2. 中国科学院苏州生物医学工程技术研究所,江苏 苏州 215000
2. Chinese Academy of Scineces, Suzhou Institute of Biomedical Engineering and Technology, Suzhou 215000, China
入水是指运动体由空气介质穿越自由液面进入到水介质的过程。该过程涉及到空泡流动、湍动涡等复杂现象,具有强非线性和非定常特性。同时多相流场与运动体运动存在耦合影响,运动体运动特性较之单一水下运动较为复杂。
19世纪初,Gekle等[1-2]对回转体垂直入水开展了数值模拟研究,获得了空泡发展演化规律和深闭合位置与弗汝德数间的关系,建立了空泡闭合射流模型。Quan等[3]基于Navier-Stokes方程对入水空泡生成、发展、颈缩和闭合过程进行模拟。Reinhard等[4]开展了二维对称模型入水过程空泡形成和扩张的数值研究,建立了基于Wagner理论和水动力占优假设的入水空泡预测数值模型,分别研究了抛物线型和对称楔形对入水空泡形成和扩张的影响规律。Iranmanesh等[5]基于VOF自由液面追踪技术开展了低弗汝德数下水平圆柱入水的数值仿真研究,研究了圆柱直径、入水速度对入水空泡流的影响。叶取源等[6]分别采用非线性自由面理论和欧拉-拉格朗日混合边界元方法模拟了锥体和圆盘入水空泡发生、发展、面闭合和深闭合等流动现象,定性地分析了运动体质量和速度对入水空泡演化过程的影响。Gong等[7]在SPH方法基础上,引入非反射边界条件(non-reflection boundary),开展了二维平面楔形体入水过程的数值模拟研究。张珂等[8 – 9]采用单相格子Boltzmann流动模型开展了圆柱体垂直入水二维和三维数值模拟,结果表明单相格子Boltzmann流动模型可以较为精确地捕捉到入水过程中的部分流动特征。王聪等[10]对球体高速入水开展数值仿真,研究了空气压力对入水空演化的影响。马庆鹏等[11]分别对球体和锥头圆柱体入水空泡及流场环境影响开展了模拟研究。王平等[12]开展了楔形体波浪中入水数值研究,研究了波浪对楔形体受力及入水姿态的影响。
凹形运动体作为一种复杂结构运动体,具有广泛的工程应用背景。目前仅有路中磊等[13 – 14]以火箭助推器入水为背景开展过“凹体”入水相关研究,其研究主要关注入水过程流场特性,对运动特性关注较少。除火箭助推器外,导弹尾罩亦属于凹形运动体。在潜射导弹冷发射过程中,导弹点火时将尾罩从一侧弹开,其运动具有典型的多自由度特性,研究尾罩入水运动特性对避免尾罩砸艇具有重要意义。本文以此为背景,开展基于重叠网格技术的凹形运动体三自由度入水过程运动特性的数值研究,分析初始垂向速度、水平迁移速度对凹形运动体三自由度入水过程运动特性及水动力特性的影响。
1 数值计算理论及方法 1.1 基本控制方程入水运动是一个非定常问题,流动参数均随时空变化,主要表现在质量扩散、动量黏滞耗散等方面。在流体流动过程中,混合相满足质量守恒和动量守恒方程。
连续性方程为:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial t}}(\rho {u_i}) = 0,$ | (1) |
动量守恒方程为:
| $\! \frac{\partial }{{\partial t}}(\rho {u_i}) \!\!+ \!\!\frac{\partial }{{\partial {x_i}}}(\rho {u_i}{u_j}) \!= \!\!\frac{{ - \partial p}}{{\partial {x_i}}}\!\! + \!\!\frac{\partial }{{\partial {x_i}}}\left[(\mu + {\mu _t})\left(\frac{{\partial {u_i}}}{{\partial {x_j}}} \!\!+\!\! \frac{{\partial {u_j}}}{{\partial {x_i}}}\right)\right] \text{。}$ | (2) |
式中:
低速入水空泡气液两相介质互不掺混,空泡壁面处两相流速基本一致,因此可采用均质平衡多相流理论[15]。本文选用的VOF多相流模型是一种适用于固定欧拉网格的界面捕捉模型,该模型可以较好描述流动过程中多相流体的界面位置。VOF模型将两相流体视为一种密度可变的混合流体,通过逐一求解计算流域内每一控制单元的控制方程得到混合流体参数,并根据各相流体所占的体积分数去实现对流体间界面的追踪。混合相密度
| ${\rho _m} = {\alpha _l}{\rho _l} + {\alpha _g}{\rho _g},$ | (3) |
| ${\mu _m} = {\alpha _l}{\mu _l} + {\alpha _g}{\mu _g} \text{。}$ | (4) |
式中:
湍流是一种具有强非线性的流动状态,同时也是最为普遍的流动状态。本文采用Realizable
| $\frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_i}}}(\rho k{u_i}) = \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\right)\frac{{\partial k}}{{\partial {x_j}}}\right] + {G_k} - \rho \varepsilon, $ | (5) |
| $\begin{split}&\frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_i}}}(\rho \varepsilon {u_i}) = \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_i}}}(\rho \varepsilon {u_i})= \\ & \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}\right] + \rho {C_1}S\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }}{\text{。}}\end{split}$ | (6) |
式中:
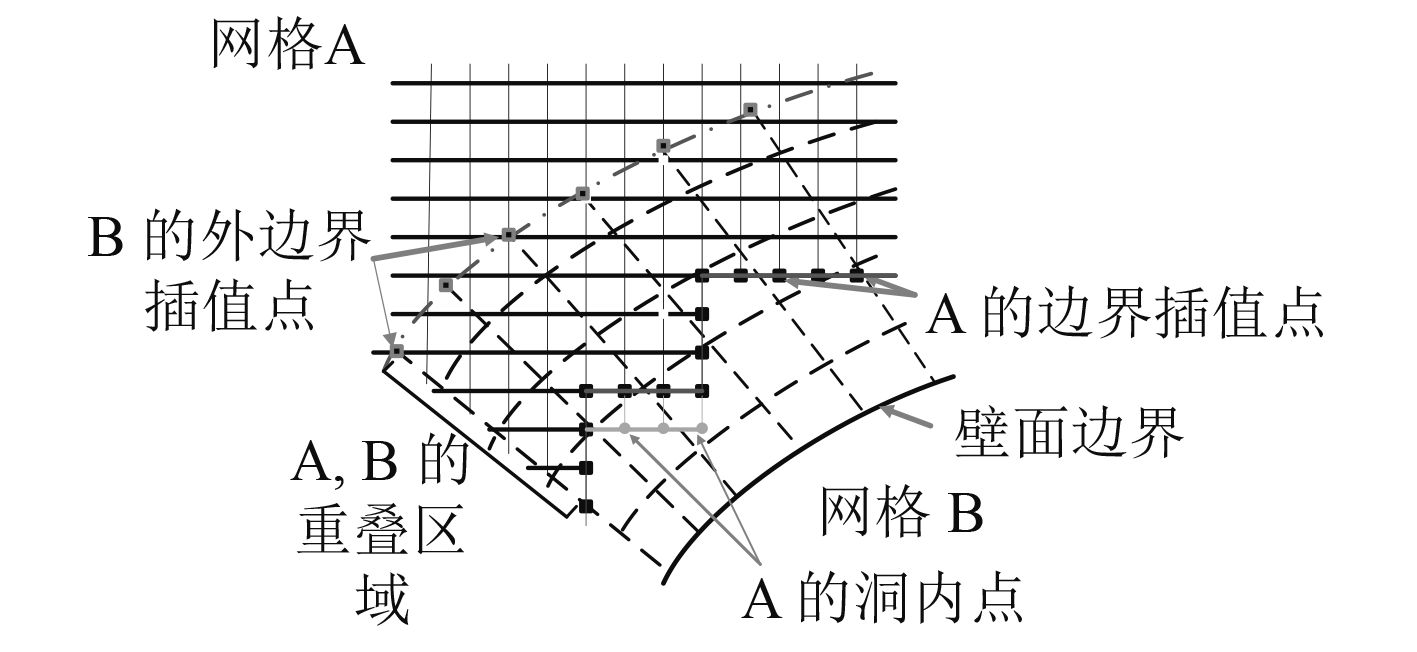
重叠网格的基本思想是对复杂流域的分解与网格的重新组合[16]。重叠网格技术将流域分解为若干个子区域,各子区域计算网格在计算中相互独立,网格之间存在重叠、嵌套和覆盖关系。在重叠区域中,各子区域计算网格通过流场信息的插值与映射进行数据交换,从而建立起了各子区域网格之间的耦合关系,为子区域流场计算提供边界条件。重叠网格的主要过程包含寻点、挖洞、建立网格重叠关系3个部分。在寻点过程中,网格A落入网格B中的节点称为洞内点,洞内点在数值求解过程中不参加计算,与洞内点紧邻的点称为边界插值点,边界插值点通过插值与映射接收来自其他子区域网格的数据信息,并将所接受的数据作为该区域求解的边界条件。如图1所示,网格A通过其边界插值点接收B网格内求解得到的流场信息,同样,网格B也从其外边界插值点获得A网格的流场数据,并将该数据作为求解边界条件。
|
图 1 重叠网格在数值计算中的实现流程 Fig. 1 The calculation princple of overlap grid |
本文基于Fluent 17.2平台,采用有限体积法离散流动控制方程;压力场与速度场的耦合选用Coupled算法;压力场的空间离散采用PRESTO!格式;各相体积率离散采用CICSAM格式;各求解变量的离散采用一阶迎风格式;对流项采用QUICK离散格式;相界面的几何重构采用Geo-Reconstruct格式。通过C语言程序,嵌入Fluent用户自定义函数定义入水运动体惯性矩及边界压力,实现模型三自由度运动。
2 计算模型及网格划分 2.1 几何模型本文计算所用凹形运动体几何模型如图2所示,模型几何参数及属性见表1。

|
图 2 凹形运动体几何模型图 Fig. 2 The geometric model of concave body |
|
|
表 1 模型几何参数及属性 Tab.1 The parameter of geometric model |
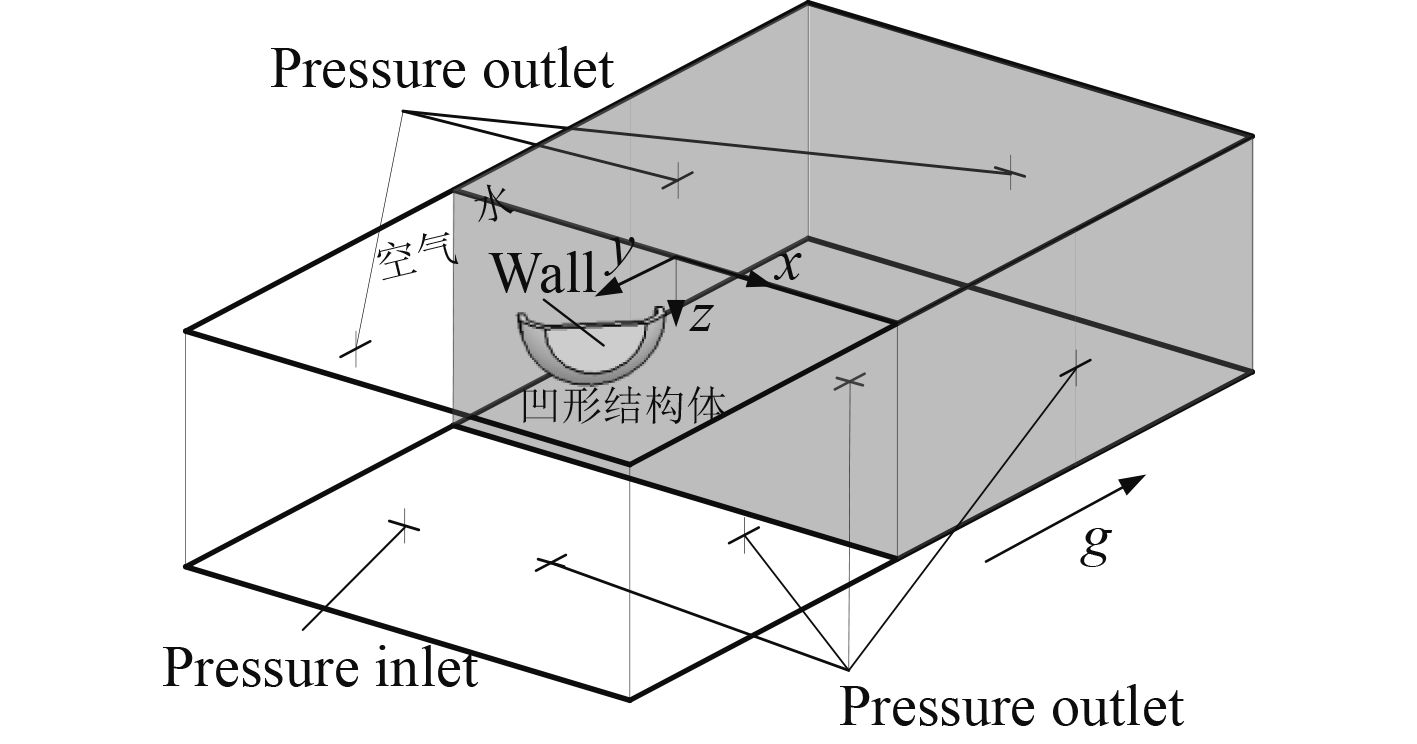
为简化计算,可假设凹形运动体在z方向不存在速度分量,且不存在绕y轴的转动速度分量。故本算例的数值计算选择在三维、三自由度情况下进行。其计算域及边界条件如图4所示,xy平面为对称平面,计算域宽为10D,高为7D,厚为10D。以触水时刻作为时间零点,触水点为坐标原点,重力方向为y负方向。
|
图 3 计算域和边界条件 Fig. 3 The simulation zone and boundary condition |
图4给出了计算域网格和子域网格的划分方式,2套网格均采用正六面体结构化网格,以较好控制网格质量和网格数量。为保证空泡区域计算精度,并保持较好的过度效果,对凹形运动体附近区域采用局部加密处理,运动体向远场过渡区域采用渐疏处理。

|
图 4 网格划分 Fig. 4 The mesh of simulation model |
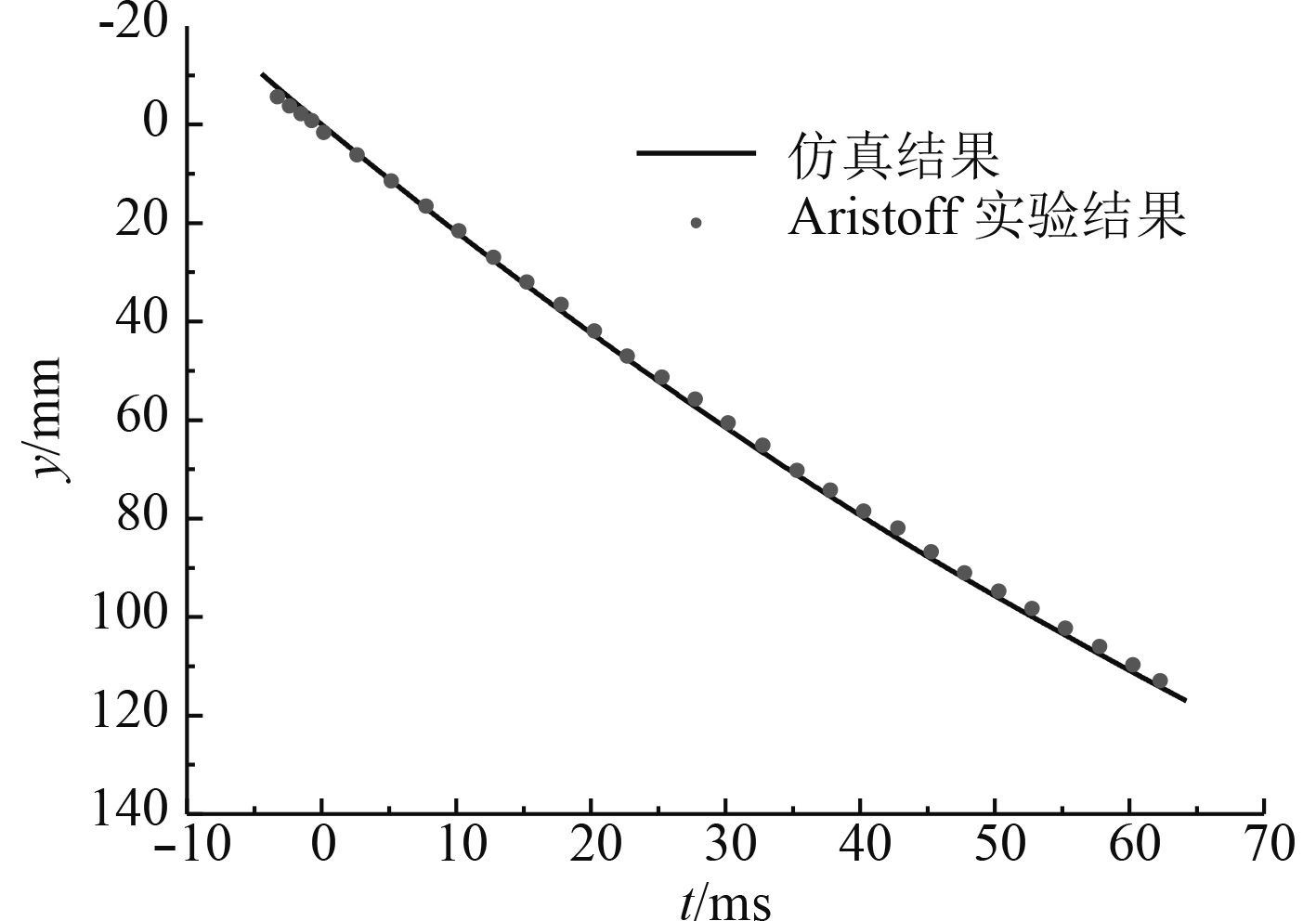
为了验证数值方法的有效性,基于上述计算方法及边界条件,对Aristoff[17]所开展的球体入水实验进行计算。实验研究所选球体直径D=25.4 mm,球体密度为2.3 g/cm3,入水速度v0=2.17 m/s。本节数值计算采用1:1的计算域模型,运动参数初始条件设置与Aristoff实验状态完全一致,计算边界条件及重叠网格划分方法与2.2节和2.3节所述相同。图5和图6分别给出了计算所得空泡形态和运动轨迹与试验的对比图,从图中可以看出,数值计算结果与实验具有较好的一致性。

|
图 5 球体入水空泡形态实验与仿真对比 Fig. 5 The comparision of experiment and numerical of the water entry cavity |
|
图 6 球体入水运动轨迹与实验结果对比 Fig. 6 The comparision of experiment and numerical of the track |
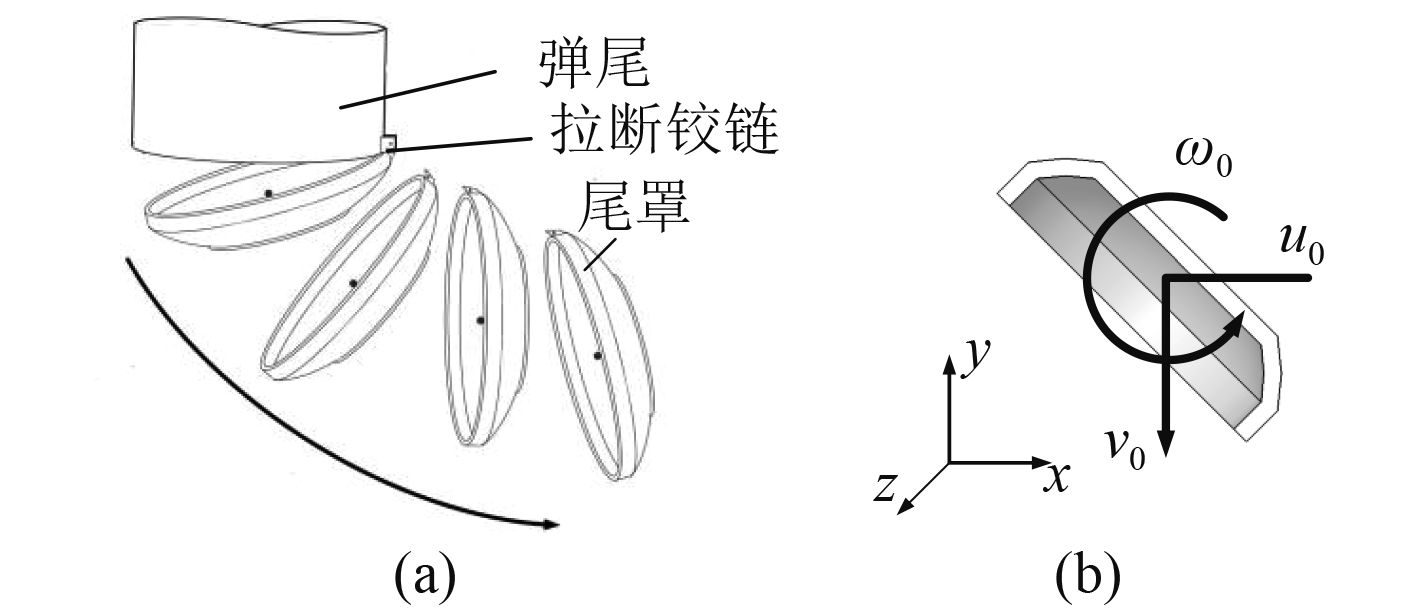
导弹尾罩在抛落时,为了避免尾罩垂向下落砸艇,往往会在导弹尾罩一侧安装拉断式铰链,使尾罩弹开后向一侧飞离,如图7所示。因此本文对凹形运动体三自由运动初始方向进行如图7所示定义,水平迁移速度沿x正方向,垂向速度沿y负方向,旋转方向正负由右手定则给出,初始角速度方向为正。
|
图 7 初始速度方向示意图 Fig. 7 The sketch of initial velocity direction |
图8给出了凹形运动体以135°倾角、垂向初始速度v0=7.5 m/s、水平迁移速度u0=2 m/s、角速度ω0=2.0 rad/s状态入水过程气液两相体积分数变化云图。在凹形运动体入水过程中,下边缘撞击自由液面,流体质点获得来自运动体的动能而产生向外排开的运动,如图8中t=0 ms所示,由于运动体凸面与凹面几何特性的差异,导致凹面尖端更易诱导空泡形成。随着入水时间的增加,喷溅液体在凹面内部闭合,形成随动空泡,如图8中t=5 ms所示。在闭合瞬间,喷溅液体在凹面上半侧产生抨击作用而形成力矩,运动体旋转方向发生改变,定义该运动为回旋运动。运动体的回旋导致由上缘诱导形成的二次空泡被横向拉伸,空泡横向发展,如图8中t=10 ms至t=15 ms所示。随着空泡的横向发展,迎流面一侧水流体在重力作用下下落,与背流面一侧空泡界面相遇,二次空泡完成闭合,如图8中t=20 ms至t=25 ms所示。二次空泡受惯性力作用继续做横向运动,逐渐与自由液面边界分离而形成了独立空泡,如图8中t=30 ms至35 ms所示。随动空泡亦由于凹形运动体旋转运动逐渐脱落形成独立空泡,如图8中t=15 ms所示。独立空泡形态脱落后受运动体凹面旋转运动形成的剪切力作用而逐渐卷曲拉长,如图8中t=15 ms至t=35 ms所示。

|
图 8 入水气液两相体积分数变化云图(v0=7.5 m/s) Fig. 8 The contour of water volume fraction on the process of water entry (v0=7.5 m/s) |
对凹形运动体所受到的水动力系数做如下定义:
| ${C_x} = \frac{{{F_x}}}{{\displaystyle\frac{1}{2}\rho v_x^2}}{\text{,}}$ | (7) |
| ${C_y} = \frac{{{F_y}}}{{\displaystyle\frac{1}{2}\rho v_y^2}}{\text{。}}$ | (8) |
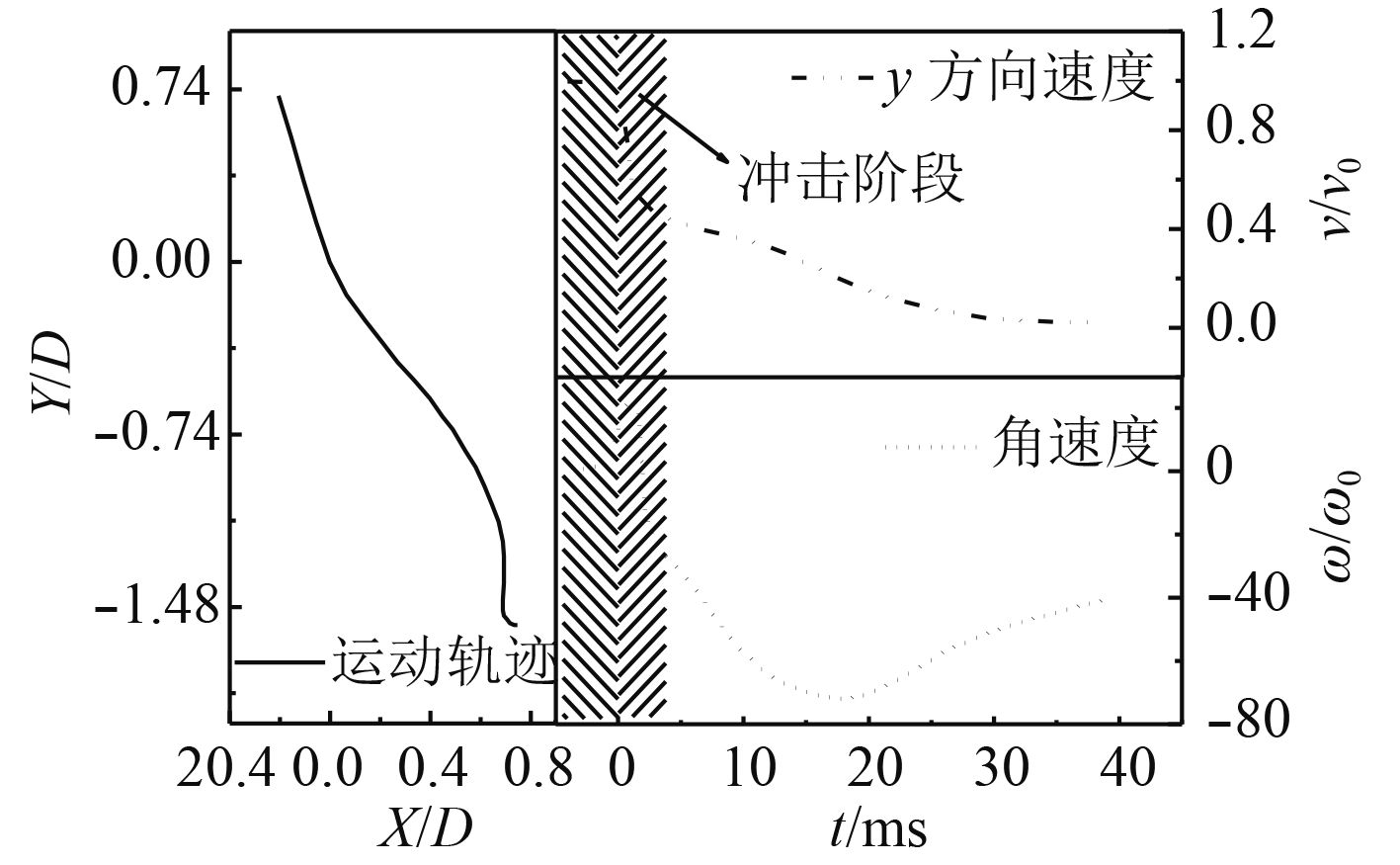
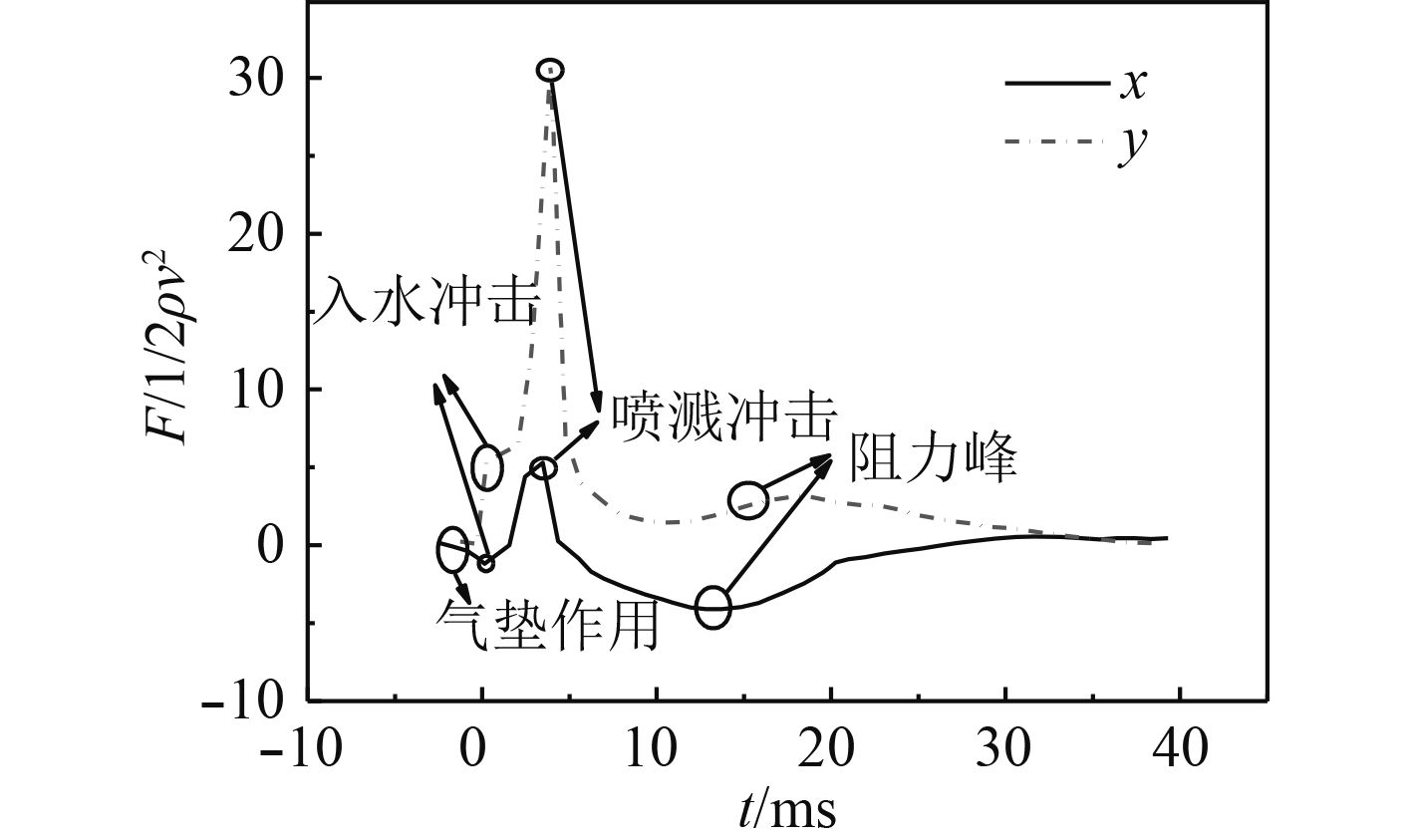
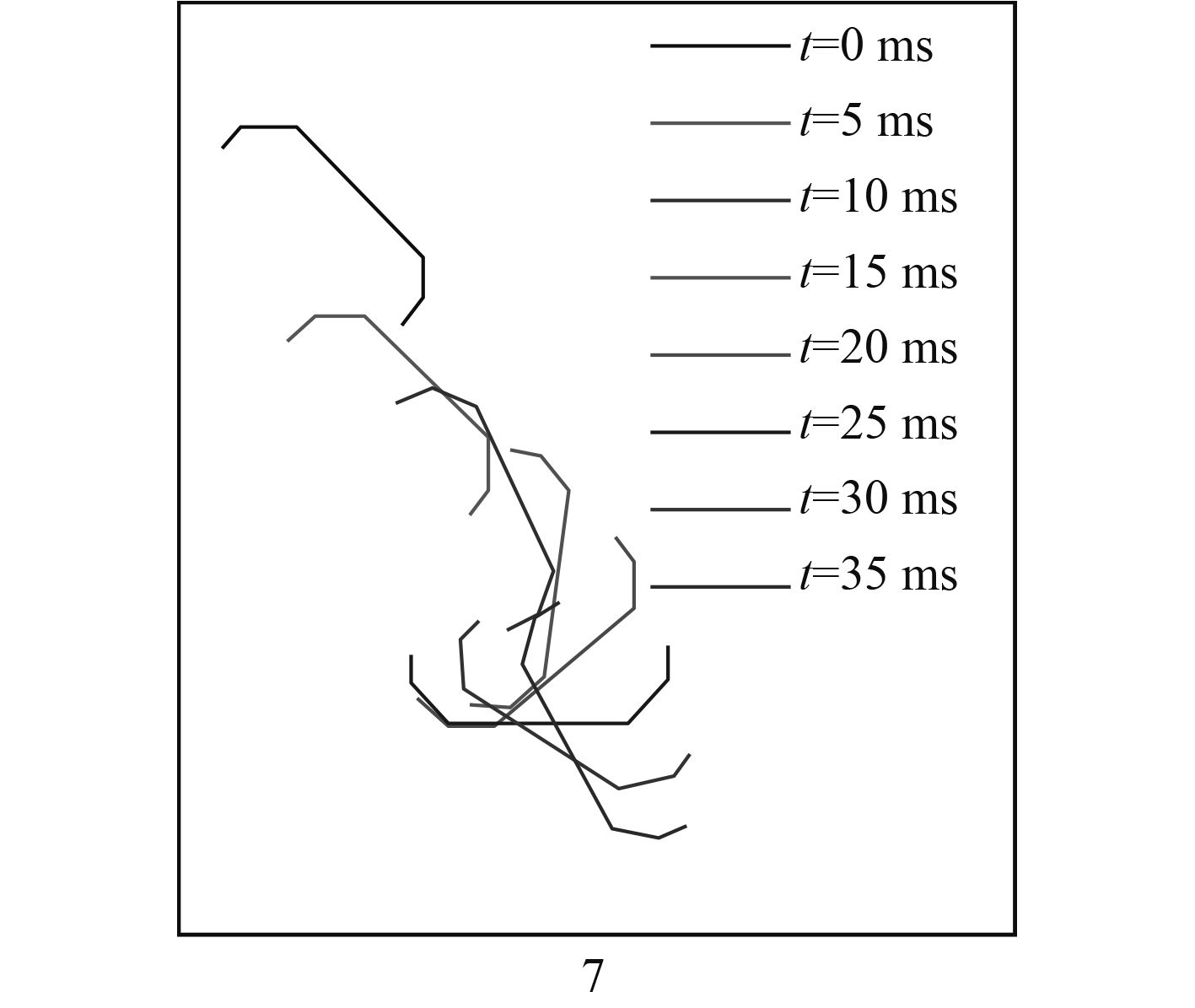
图9给出了凹形运动体入水过程运动特性曲线,图10给出了该过程水动力特性曲线,图11给出了凹形结构体位置姿态随时间变化简图。从图9中可以看出在入水之前,凹形运动体y方向速度以较小变化率减小,角速度亦呈现较为平缓的正向增加趋势;在入水后的极短时间内,y方向速度迅速减小,角速度也达到峰值,之后迅速减小为0并反向增大,称该阶段为冲击阶段;之后,y方向速度变化率逐渐减缓,速度持续减小并逐渐趋于0,角速度变化率在t=5~13 ms之间出现短暂的微幅增大,t=10 ms之后又逐渐减小,角速度达到负方向峰值后亦逐渐减小。对比图10可知,在入水之前,凹形运动体靠近自由液面,其下缘与自由液面间形成气垫,受空气垫阻力作用,y方向速度缓慢减小,由于空气垫阻力与凹形运动体所示重力形成了与角速度方向相同的力矩,导致角速度亦呈现缓慢增加趋势。在触水后,进入冲击阶段,冲击阶段主要包含入水冲击和喷溅冲击2个部分,在入水冲击过程中,凹形运动体受到入水冲击力作用,y方向速度迅速减小。y方向入水冲击力在质心处产生与角速度方向相同的力矩,x方向冲击力在质心处产生与角速度方向相反的力矩。由于y方向冲击力远大于x方向冲击力,且其值远大于空气垫阻力,因此合力矩与角速度方向相同,运动体角速度迅速增加。随着入水时间的增加,运动体背流面所形成的液体喷溅达到凹形运动体内壁面上侧(图8中t=0~5 ms之间),此时入水冲击阶段已经完成,运动体主要受喷溅冲击力作用,进入喷溅冲击阶段。喷溅冲击力在质心处所产生的力矩方向与旋转方向相反,致使角速度迅速减小并反向增加,形成回旋运动。喷溅冲击阶段结束后,凹形运动体下缘形成了空泡随动,且由于空泡内压力小于凸面处所受环境压力,导致迎流面与背流面压差形成力矩作用,该力矩方向与运动体回旋方向相同,导致角速度变化率短暂增大。在t=13 ms附近,随动空泡脱落,运动体处于全沾湿状态,其旋转受到流体阻力和转动惯性力共同作用,最终在t=18 ms时角速度达到峰值并开始减小。从图11还可以看出,由于运动体撞水面积较小,使得入水冲击较喷溅冲击弱;在t=14 ms附近,运动体在x方向的迎流面积达到最大,x方向阻力达到峰值。结合图8中t=10~16 ms阶段,由于运动体上缘与空泡尾腔分离,空泡界面与运动体边缘之间存在张力,张力的拖曳作用在y方向的分量使得y方向阻力开始微幅增大,并在t=16 ms时达到峰值。
|
图 9 入水过程运动特性曲线(v0=7.5 m/s) Fig. 9 The motion characteristic of water entry (v0=7.5 m/s) |
|
图 10 入水过程流体动力特性曲线(v0=7.5 m/s) Fig. 10 The hydrodynamic characteristic of water entry |
|
图 11 入水过程位置与姿态变化(v0=7.5 m/s) Fig. 11 The variation of position and attitude of water entry (v0=7.5 m/s) |
观察图9质心运动轨迹,发现其入水后呈现出明显的“Z”型特征,该现象由凹形结构体2个不同的运动占优阶段引起。结合图9及图11可知,在t=0~20 ms之间,y方向与x方向位移较为显著,而旋转运动相对较弱,称该阶段为平移占优阶段。在该阶段,平移运动方向与初始状态相同,而旋转运动受喷溅冲击影响,反向从0增加,导致平移运动幅值较旋转运动幅值大,运动体表现了明显的平移运动占优特征。在t=20 ms后,回旋运动角速度达到峰值并开始衰减,但其衰减速度较平移运动慢,当y方向速度趋于0时,旋转运动依然保有较大的回旋速度,导致在该阶段旋转运动较为显著,称其为旋转占优阶段。在旋转占优阶段,即t=20~25 ms期间,由回旋引起的x负方向的运动大于平移引起的x正方向的运动,导致质心轨迹回摆,t=25 ms时,凹形结构体侧壁迎流,迎流面积减小,导致横向阻力减小,x方向平移运动衰减变缓,而回旋运动衰减速度未发生明显改变,凹形运动体运动表现为向x正方向翻转,最终导致“Z”型质心轨迹形成。
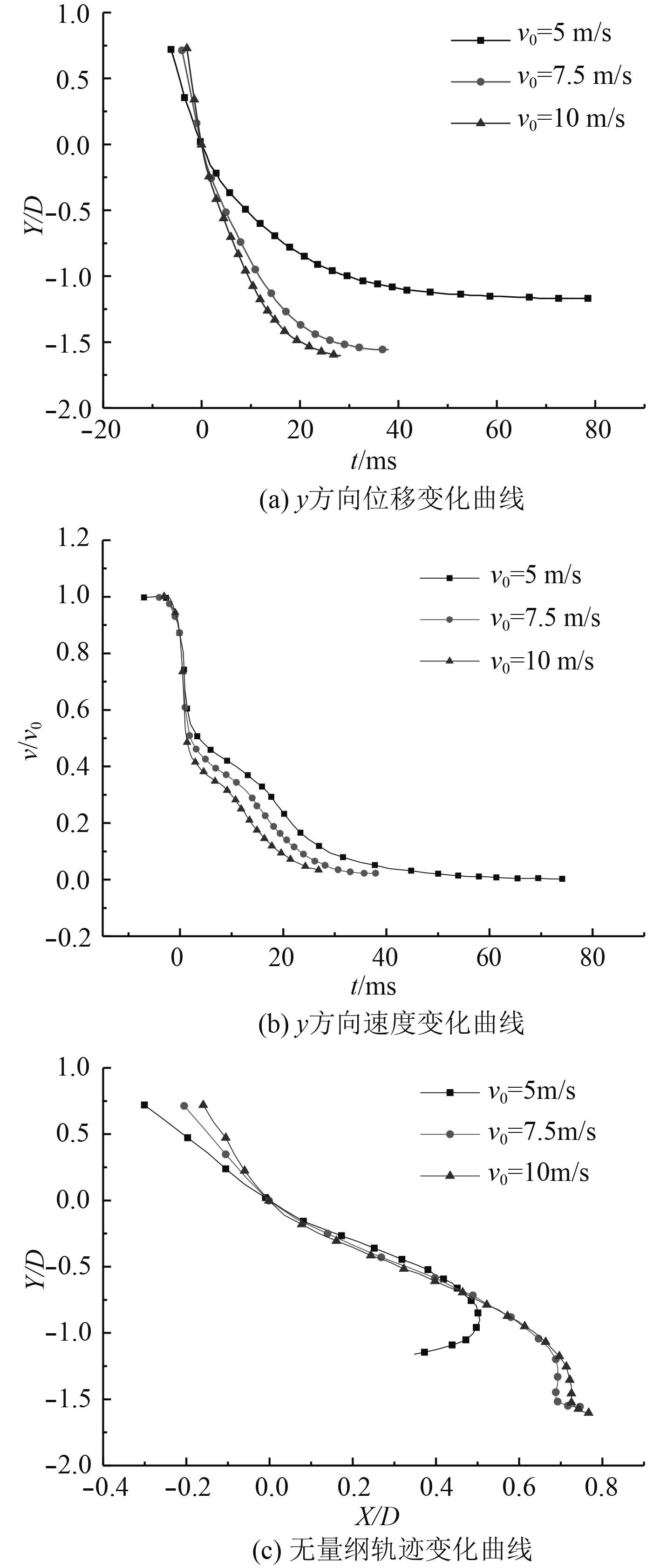
3.2 垂向速度对凹形运动体运动特性的影响考虑不同垂向速度,图12给出了凹形运动体入水过程质心平移特性变化规律,分别取初始垂向速度v0=5.0 m/s,7.5 m/s,10.0 m/s ,初始水平迁移速度u0=1 m/s,初始角速度ω0=2.0 rad/s。从图12(a)中可以看出随着垂向速度的增加,y方向速度趋于0时,其最大位移逐渐增大,但增大幅度随速度的增加而减小。由图12(b)可知,在冲击阶段,随着垂向速度的增加,速度衰减程度逐渐增大。从图12(c)中还可发现,随着垂向速度的增大,“Z”型路径逐渐平坦,表明垂向速度增加对运动体回摆存在抑制作用。
|
图 12 不同垂向速度下运动体平移特性曲线 Fig. 12 The comparision of the tranlational motion characteristic with different Y-velocity |
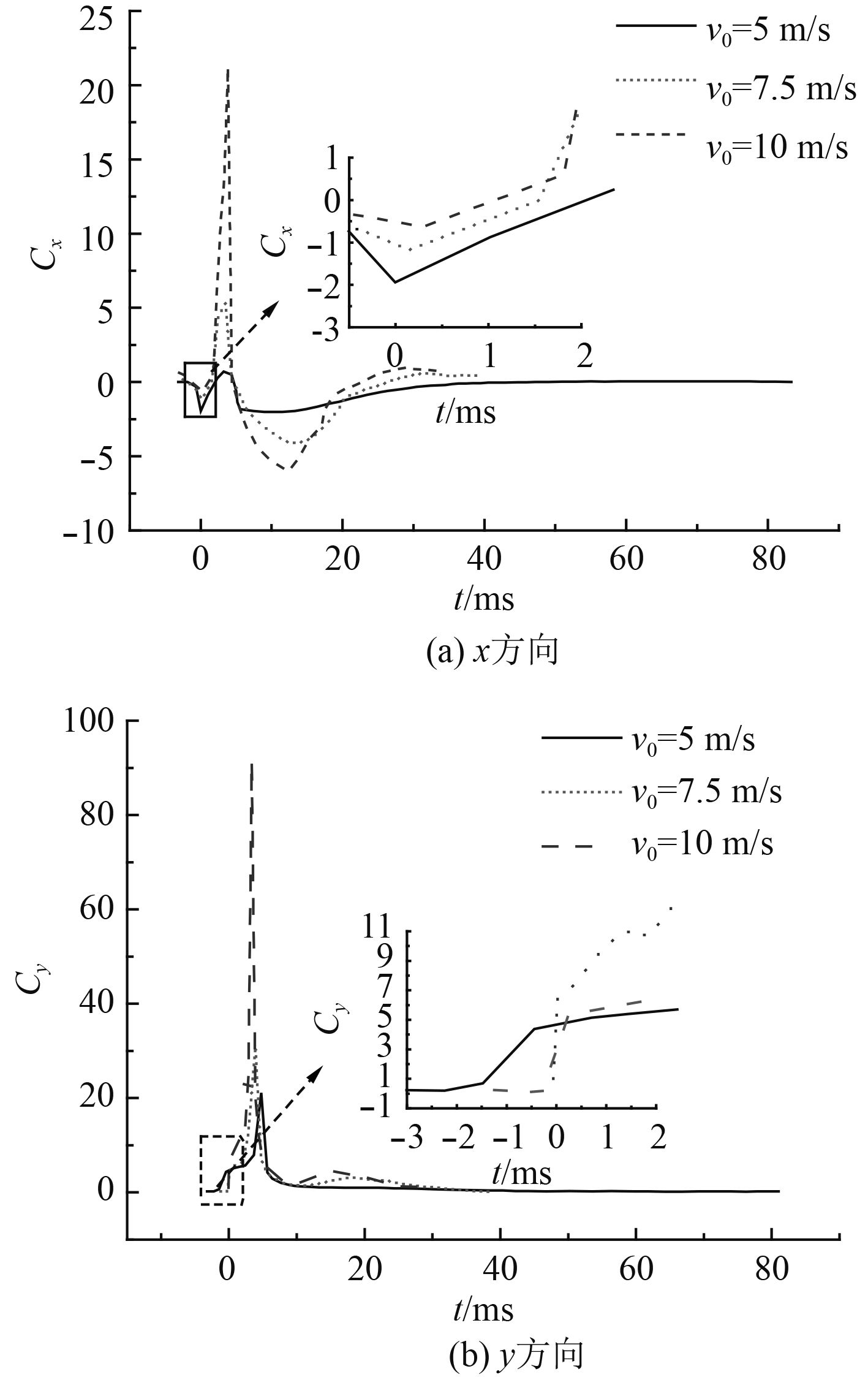
为分析上述现象原因,图13给出了运动体x方向和y方向的水动力系数变化曲线。从图13(b)可以看出,随着入水速度的增加,y方向入水冲击力以及喷溅冲击力峰值增量大幅加大,导致冲击引起的速度衰减幅度增加。在入水冲击之后,y方向受到的阻力亦随着速度增加而加大,冲击与阻力对y方向最大位移具有负激励作用,随着速度的增加,负激励增大,导致位移增加幅度减小。
|
图 13 不同垂向速度下运动体水动力系数特性曲线 Fig. 13 The comparision of hydrodynamic coefficeient with different Y-velocity |
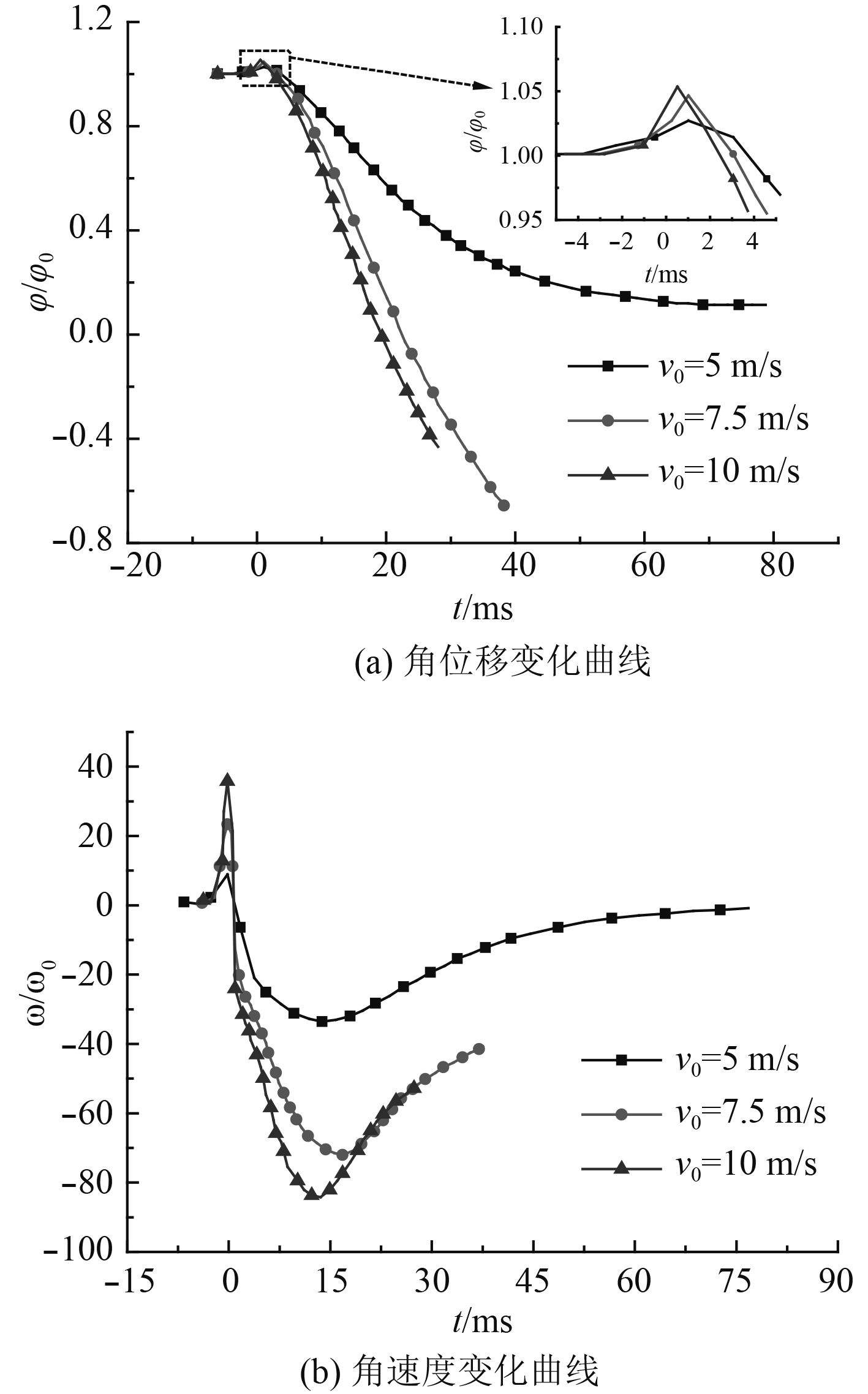
图14给出了垂向速度对旋转运动特性的影响规律,从图中可以看出,随着垂向速度的增大,入水初期角位移峰值逐渐前移,角速度峰值逐渐增大。回旋运动阶段角速度亦随着垂向速度的增大而增大。由于回旋运动主要由喷溅冲击引起,喷溅冲击力对回旋运动角速度具有正激励作用,从图13(a)可以看出,随着垂向速度的增加,喷溅冲击力大幅增加,导致回旋运动角速度增大。
|
图 14 不同垂向速度下运动体旋转运动特性曲线 Fig. 14 The comparision of the rotational motion characteristic with different Y-velocity |
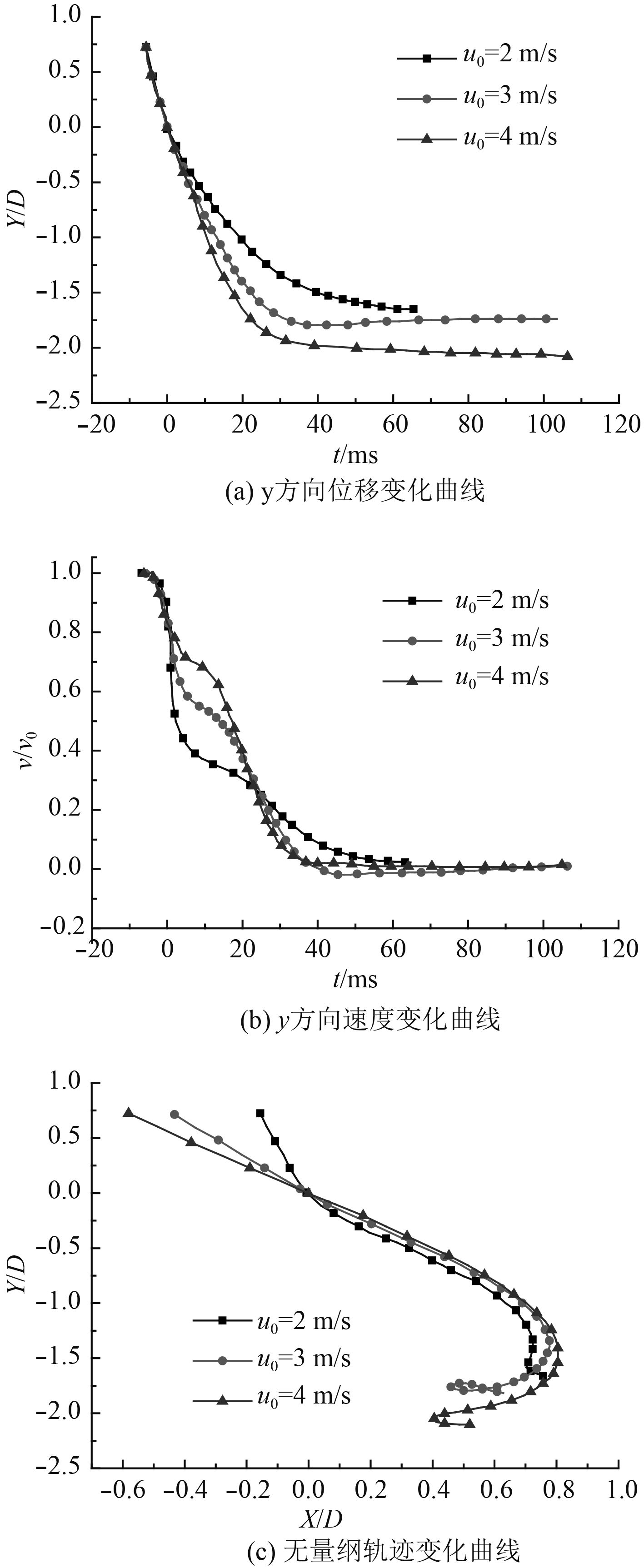
图15给出了水平迁移速度对凹形运动体平移运动的影响规律,初始水平迁移速度分别取u0=2.0 m/s,3.0 m/s,4.0 m/s,初始垂向速度取v0=6.0 m/s,初始角速度ω0=2.0 rad/s。从图15(a)中可以看出,不同水平迁移速度下,凹形运动体运动具有相同的运动趋势,且随着水平迁移速度增加,y方向速度趋于0时,其位移最大值增加。当u0=3 m/s时,回摆运动引起了质心的上漂。从图15(b)中可发现,随着水平迁移速度的增加,入水冲击阶段,y方向速度衰减幅值逐渐减小。观察图15(c)可发现,随着速度的增加,质心轨迹回摆幅值增大,质心运动轨迹的“Z”型特征随着水平迁移速度的增加而逐渐显著。
|
图 15 不同水平迁移速度下运动体平动特性曲线 Fig. 15 The comparision of the translaitonal motion characteristic with different X-velocity |
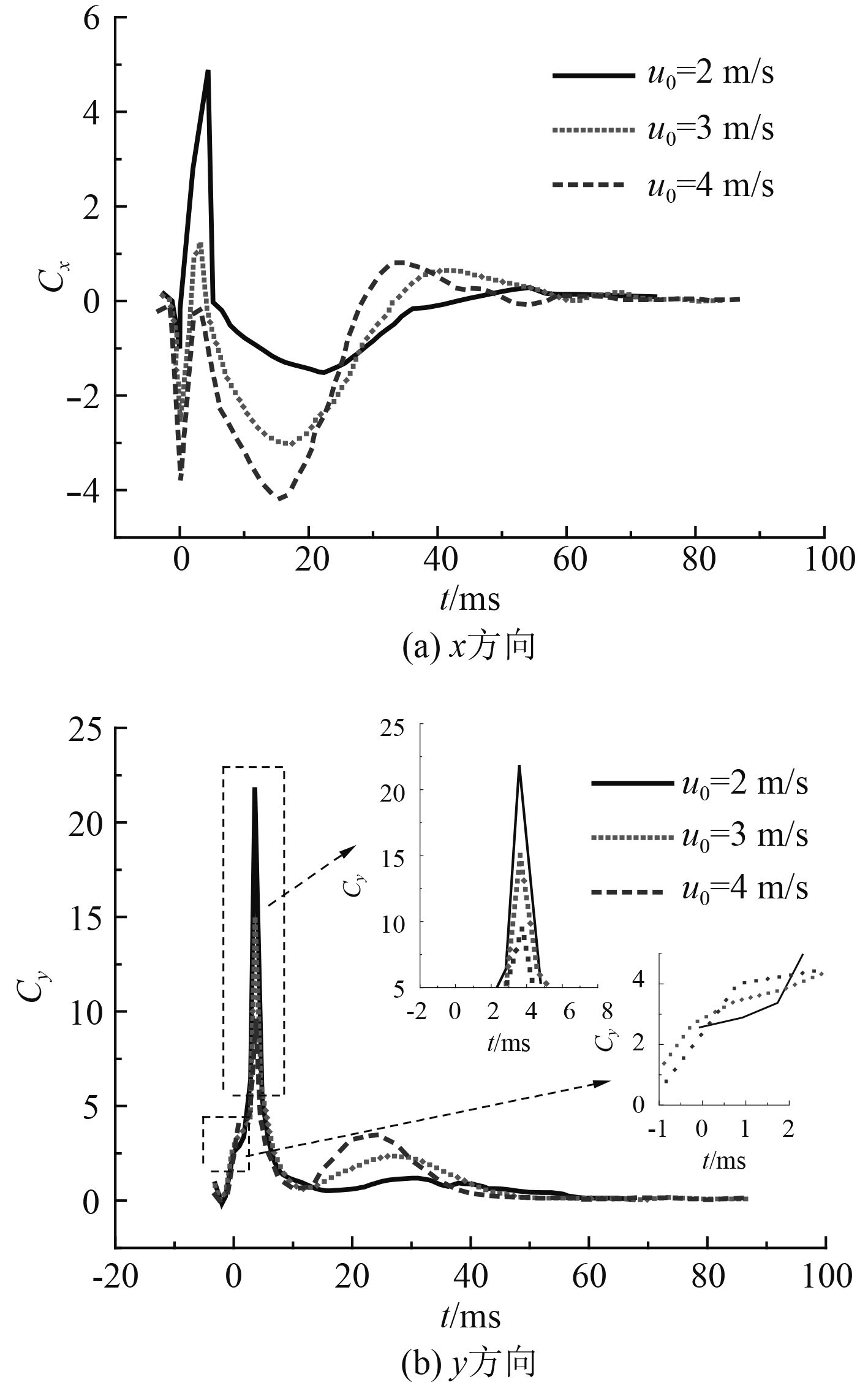
图16给出了水平迁移速度对x和y方向水动力系数的影响规律,从图中可发现,冲击阶段y方向受到的入水及喷溅冲击作用与入水瞬间速度衰减幅值呈现相同趋势。随着水平速度的增加,x方向的入水冲击力增大,但喷溅冲击力却减小。出现该现象是由于水平速度增加,喷溅到达运动体背流面时与运动体的相对速度减小,导致喷溅冲击作用减小。在冲击阶段之后,y方向所受到的阻力以及x方向阻力均随水平迁移速度的增加而增大。
|
图 16 不同水平迁移速度下运动体水动力系数特性曲线 Fig. 16 The comparision of hydrodynamic coefficeient with different X-velocity |
本文基于重叠网格技术,开展了凹形运动体入水过程运动特性数值研究,分析了初始垂向速度、水平迁移速度对凹形运动体入水过程运动特性及水动力特性的影响,得到如下结论:
1)在凹形运动体三自由度入水过程中,喷溅冲击作用对凹形运动体角运动具有重要影响,运动体在水中旋转方向与喷溅冲击形成的力矩方向相同。
2)凹形运动体入水运动存在2个运动占优阶段,在入水前期为平移运动占优,入水后期为旋转运动占优。
3)凹形运动体在下落过程中,质心运动轨迹会产生回摆而呈现“Z”型特征,垂向速度的增加对质心回摆运动具有抑制作用,水平迁移速度的增加对其具有促进作用。
| [1] |
GEKLE S, Arjan VAN DER BOS, et al. Noncontinuous froude number scaling for the closure depth of a cylindrical cavity[J]. Physical review letters, 2008, 100:084502. |
| [2] |
GEKLE S, GORDILLO J M, VAN d M D, et al. High-speed jet formation after solid object impact[J]. Physical Review Letters, 2009, 102(3): 4502. |
| [3] |
QUAN S P, HUA J S. Numerical studies of bubble necking in viscous liquids[J]. Physical Review Letters, 2008, E77: 066303. |
| [4] |
REINHARD M, KOROBKIN A A, COOKER M J. Cavity formation on the surface of a body entering water with deceleration[J]. Journal of Engineering Mathematics, 2016, 96(1): 155-174. DOI:10.1007/s10665-015-9788-8 |
| [5] |
IRANMANESH A, PASSANDIDEH-FARD M. A three-dimensional numerical approach on water entry of a horizontal circular cylinder using the volume of fluid technique[J]. Ocean Engineering, 2017, 130: 557-566. DOI:10.1016/j.oceaneng.2016.12.018 |
| [6] |
叶取源. 锥头物体垂直入水空泡的发展和闭合[J]. 水动力学研究与进展, 1989, 4(2): 33-41. YE Qu-yuan. Evolution and closure of cavity after vertical water entry of cone-head bodies[J]. Journal of Hydrodynamics, 1989, 4(2): 33-41. |
| [7] |
GONG K, LUI H. Numerical simulation of circular disk entering water by an axisymmetrical SPH model in cylindrical coordinates[C]// Proceedings of the Fifth International Conference on Fluid Mechanics, Shanghai, China, 2007. Tsinghua University Press & Springer, 2007: 372–375.
|
| [8] |
ZHANG K, YAN K, CHU X S, et al. Numerical simulation of the water-entry of body based on the Lattice Boltzmann method[C]// 29th International Conference on Ocean, Shanghai, China, 2010. ASME Offshore and Arctic Engineering, 2010: 135–145.
|
| [9] |
张珂, 颜开, 褚学森, 等. 基于LBM方法的圆盘等速入水空泡的数值模拟[J]. 船舶力学, 2010, 10: 1129-1133. ZHANG Ke, YAN Kai, CHU Xue-sen, et al. Numerical simulation of constant speed water entry cavity based on LBM[J]. Journal of Ship Mechanics, 2010, 10: 1129-1133. DOI:10.3969/j.issn.1007-7294.2010.10.008 |
| [10] |
王聪, 何春涛, 权晓波, 等. 空气压力对垂直入水空泡影响的数值研究[J]. 哈尔滨工业大学学报, 2012, 44(5): 14-19. WANG Cong, HE Chun-tao, QUAN Xiao-bo, et al. Numerical simulation of the influence of atmospheric pressure on water-cavity formed by cylinder with vertical water-entry[J]. Journal of Harbin Institute of Technology, 2012, 44(5): 14-19. |
| [11] |
马庆鹏, 魏英杰, 王聪, 等. 锥头圆柱体高速入水空泡数值模拟[J]. 北京航天航空大学学报, 2014, 40(2): 204-209. MA Qing-peng, WEI Ying-jie, WANG Cong, et al. Numerical simulation of high-speed water-entry cavity of cone cylinder[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 204-209. |
| [12] |
王平, 袁帅, 张宁川, 等. 楔形体在波浪中自由入水的数值模拟[J]. 海洋工程, 2017(5): 42-50. WANG Ping, YUAN Shuai, ZHANG Ning-chuan, et al. Numerical study of the free water-entry wedge in wave[J]. The Ocean Engineering, 2017(5): 42-50. |
| [13] |
路中磊, 魏英杰, 王聪, 等. 基于高速摄像实验的开放腔体圆柱壳入水空泡流动研究[J]. 物理学报, 2016, 65(1): 301-315. LU Zhong-lei, WEI Ying-jie, WANG Cong, et al. An experimental study of water-entry cavitating flows of an end-closed cylindrical shell based on the high-speed imaging technology[J]. Acta Physica Sinica, 2016, 65(1): 301-315. |
| [14] |
路中磊, 魏英杰, 王聪, 等. 正浮力开放腔体圆柱壳垂直入水数值计算[J]. 振动与冲击, 2016, 35(16): 79-85. LU Zhong-lei, WEI Ying-jie, WANG Cong. Numerical study on vertical water-entry of cylindrical structure with positive buoyancy and un-closed solid cavity[J]. Journal of Vibration and Shock, 2016, 35(16): 79-85. |
| [15] |
GONG K, WANG B, LUI H. Numerical simulation of wedge water entry based on two-dimensional two phase SPH model. http://www.iwwwfb.org/Abstracts/iwwwfb25/iwwwfb25_12.pdf
|
| [16] |
赵发明, 高成君, 夏琼. 重叠网格在船舶CFD中的应用研究[J]. 船舶力学, 2011, 15(4): 332-341. ZHAO Fa-ming, GAO Chen-jun, XIA Qiong. Overlap grid research on the application of ship CFD[J]. Journal of Ship Mechanics, 2011, 15(4): 332-341. DOI:10.3969/j.issn.1007-7294.2011.04.002 |
| [17] |
ARISTOFF J M, TRUSCOTT T T, TECHET A H, et al. The water entry of decelerating spheres[J]. Meeting of the Aps Division of Fluid Dynamics, 2009, 22(3): 417-422. |
 2018, Vol. 40
2018, Vol. 40
