2. 海军工程大学 舰船学院, 湖北 武汉 430033
2. School of Naval Architecture, Naval University of Engineering, Wuhan 430033, China
船模试验在船舶流体力学研究领域扮演着重要的角色,是考核理论计算方法和阐述船舶流体力学机理的关键。在船模的耐波性试验中常需要测量船模在规则波中所受的波浪作用力。这种波浪力可分为两大部分:一部分为具有零平均性质的线性振荡波浪力,其振荡频率为船模的遭遇频率
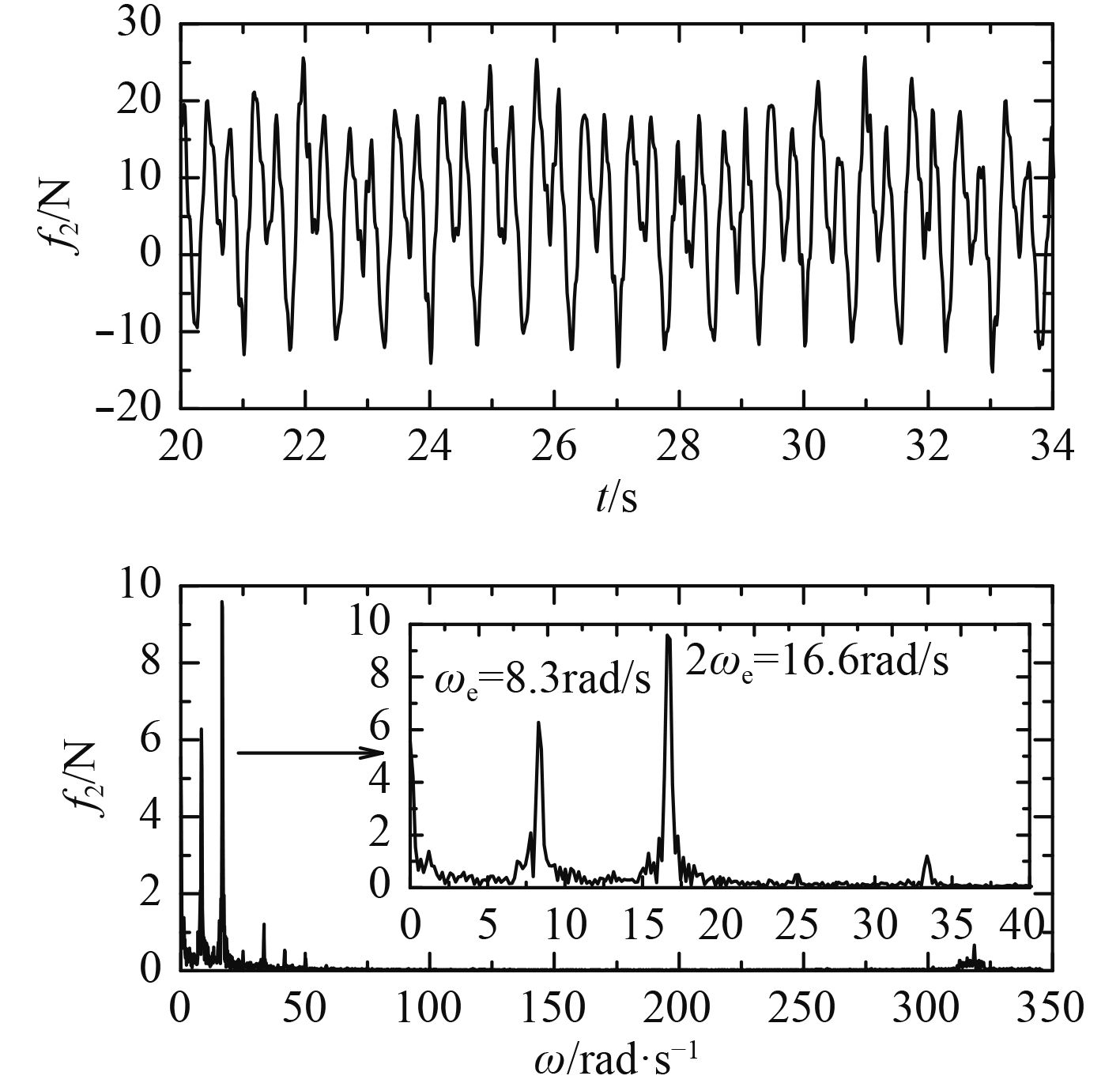
|
图 1 某船模实测首摇力矩时历过程及其幅值谱 Fig. 1 Yaw moment-time cure with its amplitude spectrum of a model ship measured in test |
经验模态分解算法(Empirical Mode Decomposition,EMD)[4]集平稳化、层次处理能力于一体,为提取船模非线性波浪力各组分提供了新思路。该方法基于信号的局部特征时间尺度,将非平稳信号分解,得到一系列不同频率的分量——本征模态函数(IMF)。相对于原非平稳、非线性信号,不同时间尺度的IMF平稳性得到很大改善。分解出最初IMF序列代表原始序列的高频组分,随着分解的进行,相应IMF的频率变小、周期增长。这些IMF可作为原序列的一组完全或几乎正交的展开基,并与最终的分解残差能够很好的重构原时间序列[5]。船模在规则波中所受波浪力的各阶组分对应着不同频率的分量,具备良好的局部尺度特征,从理论上而言,应用EMD方法进行处理,各阶波浪力组分应该能够很好的与分解得到的IMF相对应。但由于实测数据因随机因素或测量仪器等影响会带有随机误差,使得很多情况下EMD直接对信号分解提取的规律并不准确,容易出现模态混叠现象,即相同频率的信号分量被分解到不同的模态分量当中,或者不同频率的信号分量被分解到同一个模态分量当中[5]。集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[6]对EMD方法进行改进,通过加入不同随机白噪声来平衡测量数据中随机误差的影响,进而从数据中提取更准确的规律,但也因为如此,增大了EEMD分解后信号的重构误差。Yeh等对EEMD算法进行了改进,提出互补集合经验模态分解方法[7],与EEMD算法不同的是所加入的白噪声正负成对,能够极大地提高重构精度,同时减少迭代次数并提高运算效率。本文基于CEEMD算法,并辅以合适的其他信号分析手段,研究船模非线性波浪力测量信号各阶组分的提取方法。
1 EMD和CEEMD算法原理 1.1 EMD算法原理EMD方法的实质是提取本征模态函数IMF的过程。IMF分量必须满足以下2个条件:1)其极值个数和过零点数相同或最多相差一个;2)其上下包络线关于时间轴局部对称。分解方法如下[8]:
1)计算信号序列
2)对信号中计算得到的极大(小)极值点利用3次样条法进行插值,并拟合成信号的上下包络线,计算2条曲线的均值序列
3)判断
4)计算准余量函数
| $s(t) = \sum\limits_{i = 1}^n {{C_i}} + r{}_n(t)\text{。} $ | (1) |
CEEMD算法实质上是EMD算法的一种辅助算法,其核心仍是EMD,但在进行EMD前在原始信号中添加了正负对形式的白噪声,其过程如下[9]:
1)在原始信号
| $\left[ {\begin{array}{*{20}{c}} {{m_1}(t)} \\ {{m_2}(t)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1 \\ 1&{ - 1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {s(t)} \\ {w(t)} \end{array}} \right]\text{,} $ | (2) |
其中:
2)对各组信号采用EMD方法进行分解,集合中的信号都可以分解为IMF分量,其中第
3)通过多组分量组合得到分解结果如式(3)所示,残余分量记作
| ${C_j} = \frac{1}{{2N}}\sum\limits_{i = 1}^{2N} {{C_{ij}}} ,\;\;\;j = 1 \sim m\text{。} $ | (3) |
根据船模非线性波浪力测量信号的特点,本文提出如下信号处理流程:
1)低通滤波
相对于高频噪声的频率而言,船模在规则波中的遭遇频率是低频的[10],其频率往往低于5 Hz。大量的试验数据分析表明,5阶以上的高阶波浪力量值相对于1阶、甚至2阶倍频波浪力量值而言,可以忽略,因此有实际意义的高阶波浪力的频率相对于高频噪声的频率而言也是低频的。本文采用低通滤波方法去除实测波浪力信号中的高频噪声。低通滤波的具体实施方法见文献[3],高频截断频率取6
2)CEEMD求解
对过滤高频噪声的船模波浪力测量信号进行CEEMD分解,获得一系列由高频到低频排列的本征模态函数IMF。分解所得IMF中的前几个模态往往对应于随机噪声占主导的模态。另外,当信号中多倍频的高阶波浪力为小量,且量值与这些随机信号相当时,也会与随机噪声耦合在一起,存在于这几个模态当中。因此,必须要对这些模态进行甄别,为提取与船模非线性波浪力各组分相对应的有效IMF提供方便。
3)有效IMF识别
随机信号的自相关函数反映了信号与其自身在不同时间点的相似程度。对于随机噪声而言,其自相关函数在零点处最大,其余点处立即衰减为0,而不含噪信号自相关函数值在零点处最大,其余点随着时间差的增大而缓慢衰减至0[11]。本文利用随机噪声和不含噪信号自相关函数的性质差异来对噪声模态和有效模态进行识别。步骤如下:分别求取各IMF的归一化自相关函数及其方差,设定自相关函数方差的阈值,当模态分量的自相关函数方差小于阈值要求时则将相关IMF视为噪声,当自相关函数方差大于方差阈值时,则判定为有效IMF。
4)各阶波浪力提取
采用FFT-FS频谱细化技术[10]准确计算各IMF的特征频率,根据各特征频率与遭遇频率的倍数关系,依次确定高阶倍频波浪力模态及1阶波浪力模态。将1阶波浪力模态之后的各IMF及残余分量求和,所得结果为2阶低频波浪力与定常项的混合模态,采用FFT-FS方法求混合模态在频率为0处的幅值,该幅值即为定常力,将混合模态减去定常力幅值则可得到2阶低频波浪力组分。除纵荡波浪力外,其余5个方向的2阶定常波浪力就是这个定常力,对于纵荡方向而言,提取2阶定常波浪力时要扣除静水阻力。
3 船模非线性波浪力测量信号处理实例 3.1 试验概况在武汉理工大学长条形拖曳水池开展了规则波中一约束模(记作船模a)及一半约束模(记作船模b)近距离并行顶浪航行时约束模所受波浪力的测量试验。试验主要目的是研究波浪中近距离并行航行两船模之间的水动力干扰规律。船模a重173 kg,水线长3.651 m,水线宽0.462 m,设计吃水0.156 m;船b重226 kg,水线长4.352 m,水线宽0.524 m,设计吃水0.148 m,模型其他主要参数及三维轮廓参见文献[12]。两船模中对中布置,横向间距(两船模重心在横向的距离)为0.35
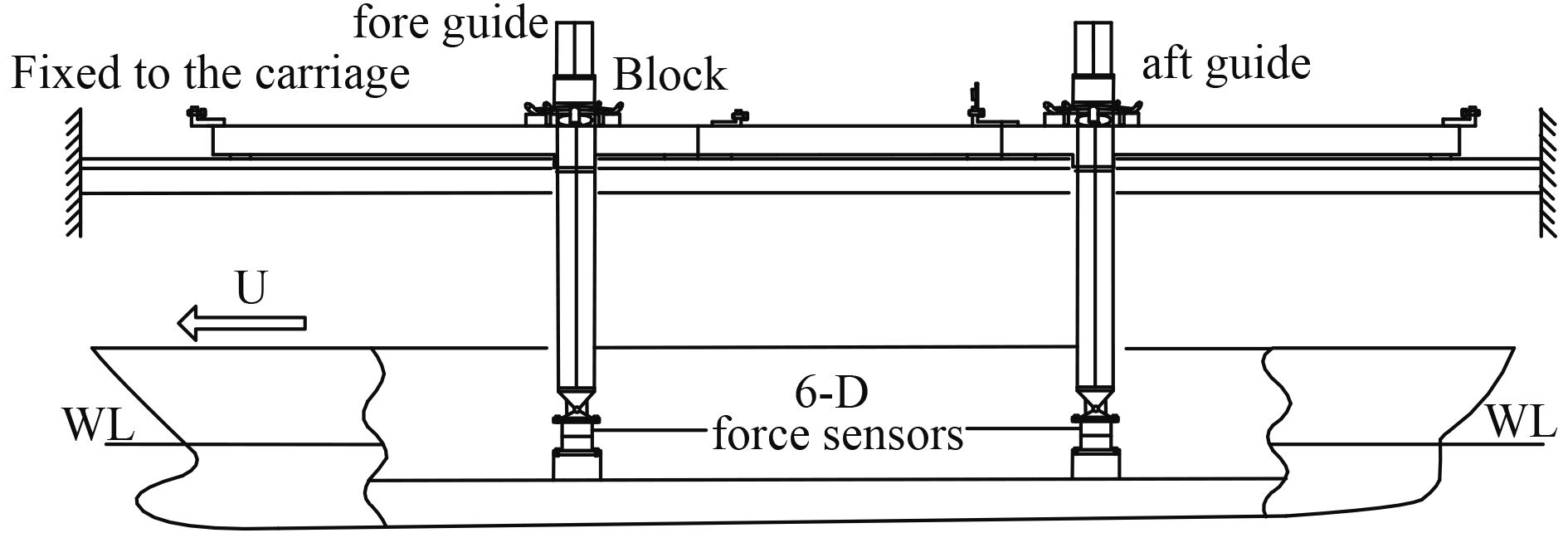
|
图 2 约束模波浪力测量装置 Fig. 2 Description of the experimental setup for the captive model |
图3及图4分别给出了当入射波波长λ为4.5 m时船a横摇力矩
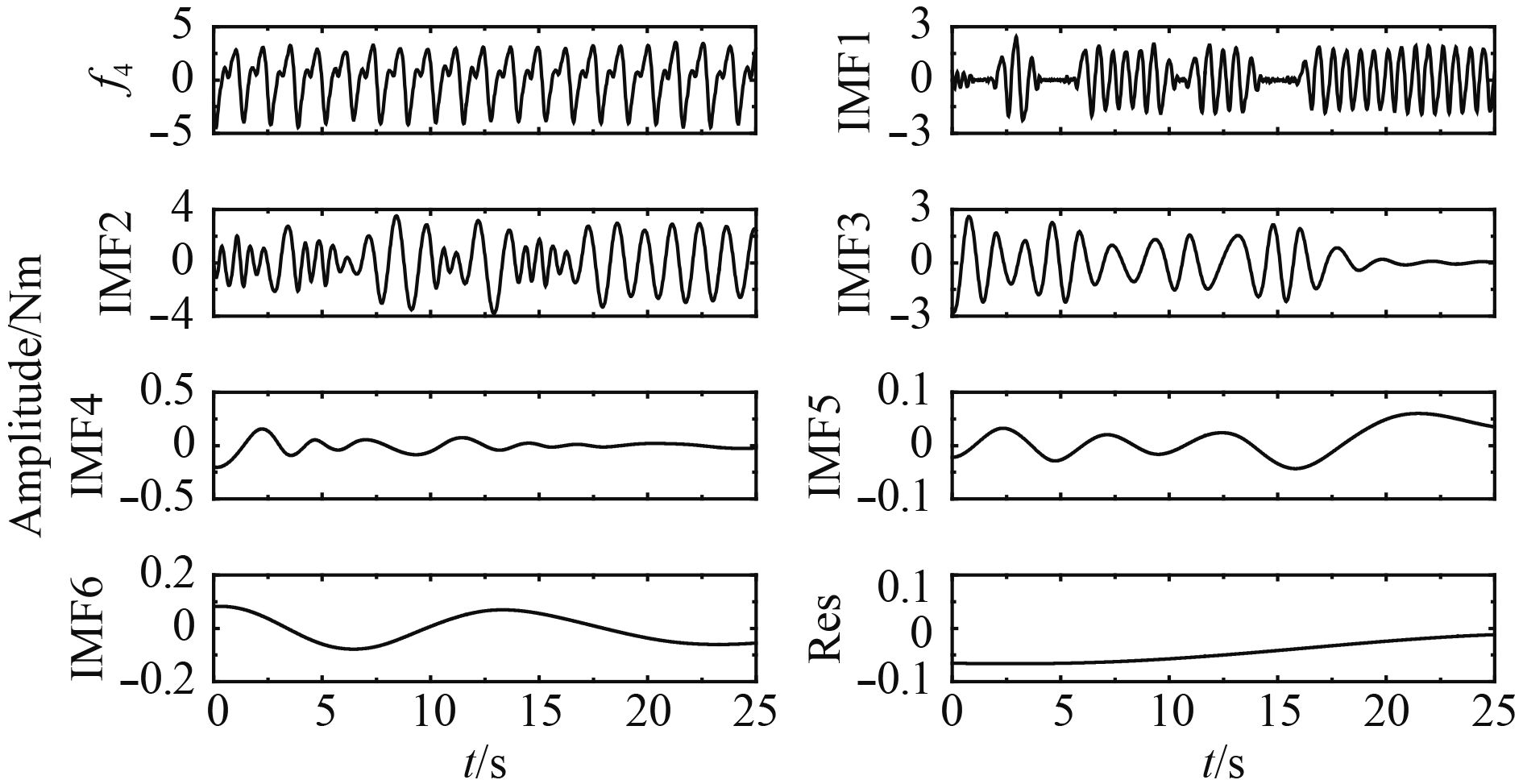
|
图 3 船a横摇力矩测量信号的EMD结果 Fig. 3 EMD results of the roll excitation moment signals on ship-a measured in the model test |
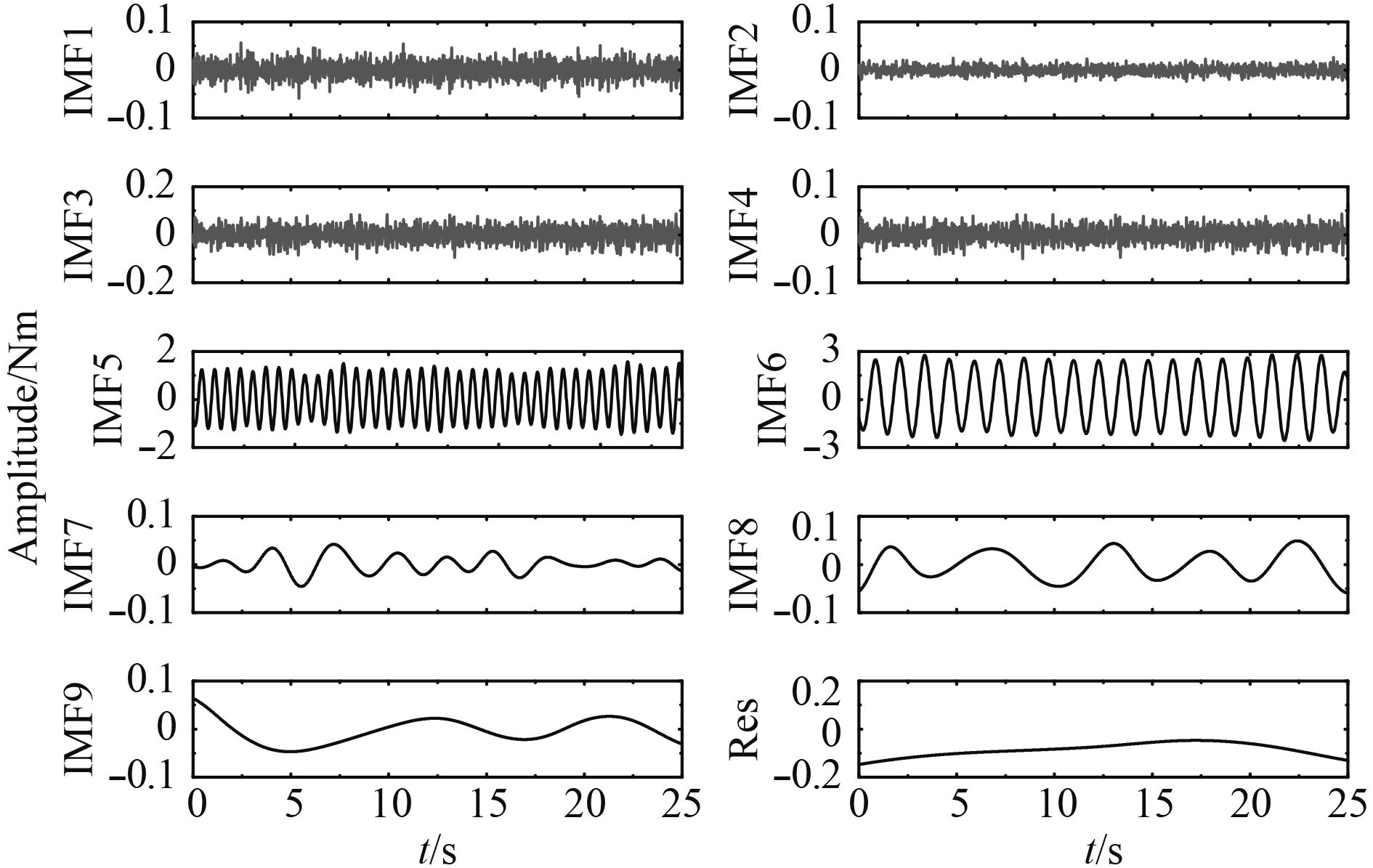
|
图 4 船a横摇力矩测量信号的CEEMD结果 Fig. 4 CEEMD results for the test signals of the roll moment on ship-a |
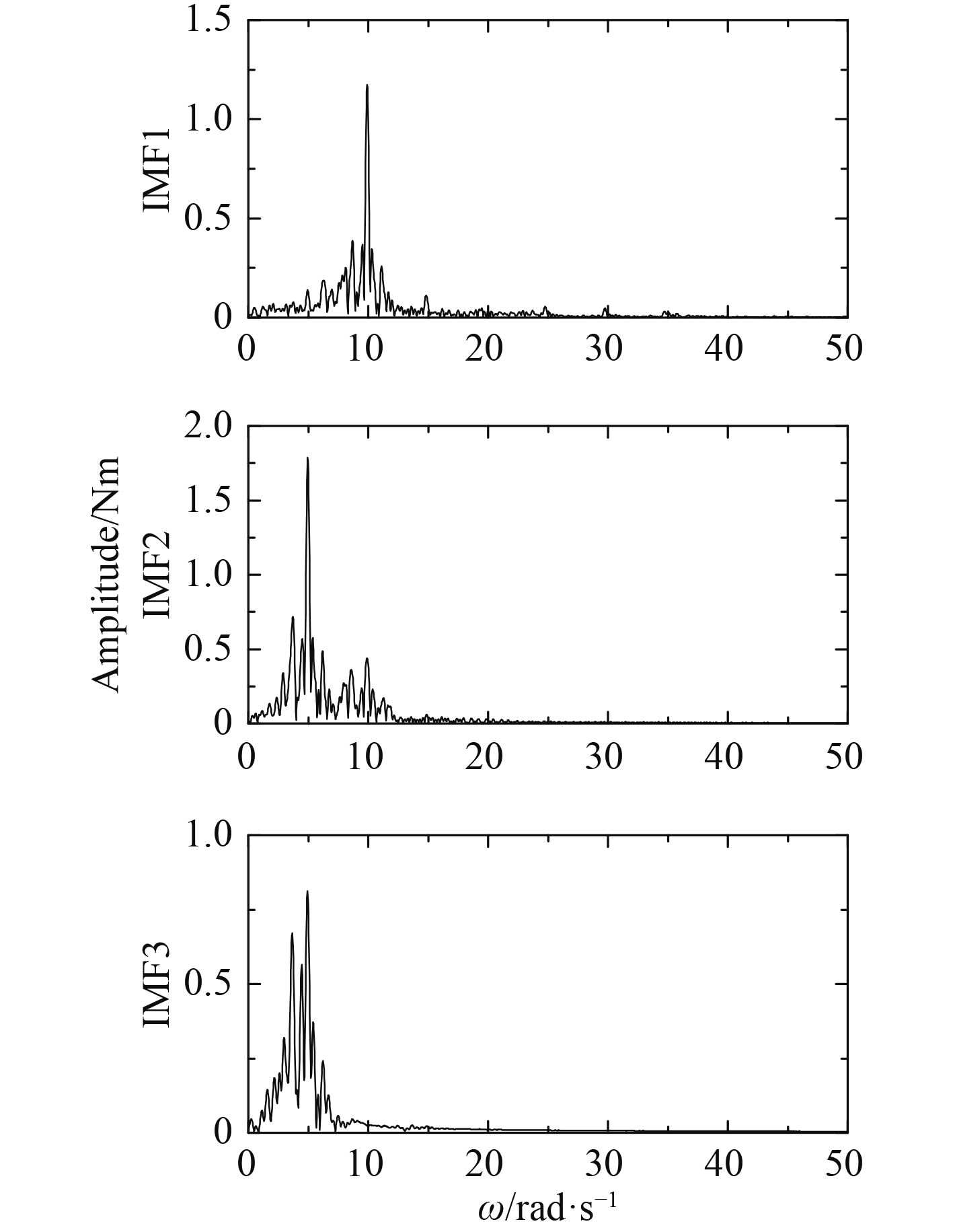
|
图 5 EMD分解所得的IMF1~IMF3对应的幅值谱 Fig. 5 Amplitude spectrums of the first three IMFs decomposed by EMD |
从图4可知采用CEEMD分解得到9个IMF分量及1个残余项,对这10个分量求取归一化自相关函数并计算方差,结果如图6及表1所示。从图6可知,前4个模态的自相关函数在零点处取得最大值,而在其余点则迅速衰减,并接近于0,非常接近随机噪声自相关函数的特性。对于其余6个分量,其自相关函数在零点处也取得最大值,但其余点随着时间差的增大缓慢变化下降至0,符合不含噪信号的特性。再从各分量归一化自相关函数的方差来看,按照文献[5]推荐的方差阈值0.03,前4个分量的方差值均小于0.03,判定这4个模态为随机噪声占主导的模态;其余6个分量方差值均大于0.03,可以判定为船模波浪力的有效模态。值得一提的是,在CEEMD分解过程中虽然人为地加入了高斯白噪声,但这种高斯白噪声和这4个噪声模态有本质区别,这4个模态中的随机噪声真实地存在于测量信号中,而人为加入的高斯白噪声由于正负成对,在合成过程中会相互抵消,不会残留在分解结果中。为进一步说明这个问题,将CEEMD所得的各分量进行重构,并与原分解信号取差值,可以得到重构误差如图7所示。从图可见重构误差可达到10–15的量级,远小于随机噪声占主导的4个模态的量级,因此分解得到的前4个IMF确实为信号中的真实分量。正是由于这些随机噪声的存在导致EMD运算所得的IMF存在模态混叠现象。而CEEMD算法由于辅助加入频率平均的高斯白噪声,使得含随机噪声的船模非线性波浪力信号变得连续,在求取IMF的过程中可以抑制随机噪声引起的极值点移位及包络线拟合偏差等问题,从而抑制模态混叠现象。图8给出了图3中IMF5,IMF6幅值谱,从图可见这2个模态没有出现模态混叠现象,根据其峰值频率可以判定IMF5对应于横摇力矩测量数据中的2阶倍频波浪力,IMF6对应于1阶波浪力。按第2节所提方法对后续模态及残差进行处理可以得到2阶定常波浪力及2阶低频波浪力组分。
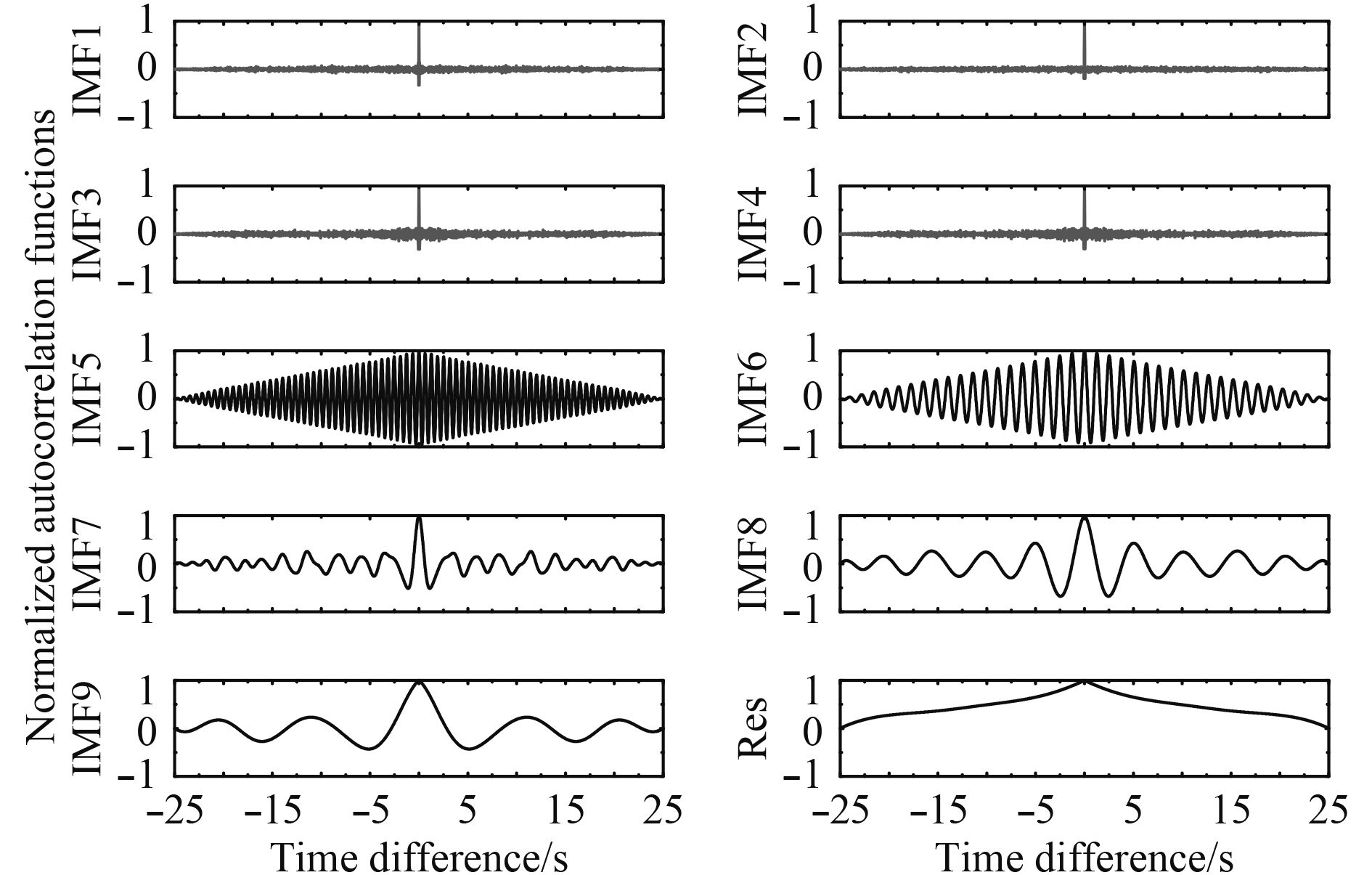
|
图 6 CEEMD分解所得的各IMF及残余项的归一化自相关函数 Fig. 6 Normalized autocorrelation curves of the IMFs and the residual term decomposed by CEEMD |
|
|
表 1 各归一化自相关函数的方差 Tab.1 Normalized autocorrelation function variance of the IMFs and the residual term |
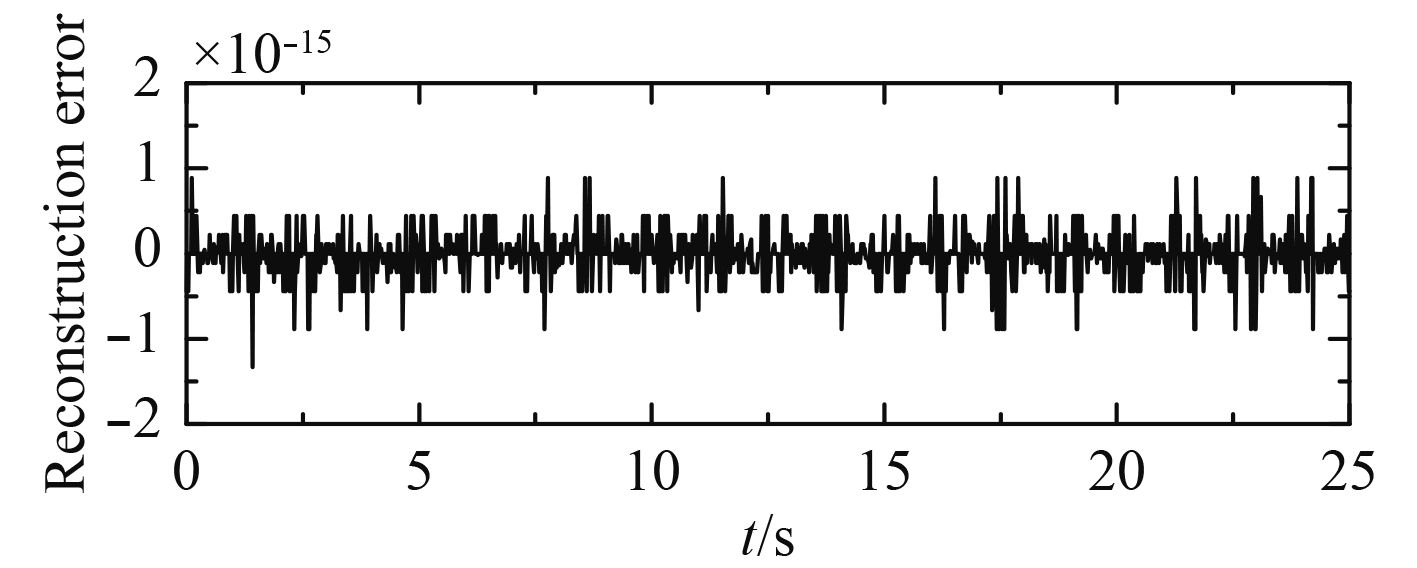
|
图 7 CEEMD的重构误差 Fig. 7 Reconstruction errors decomposed by CEEMD |
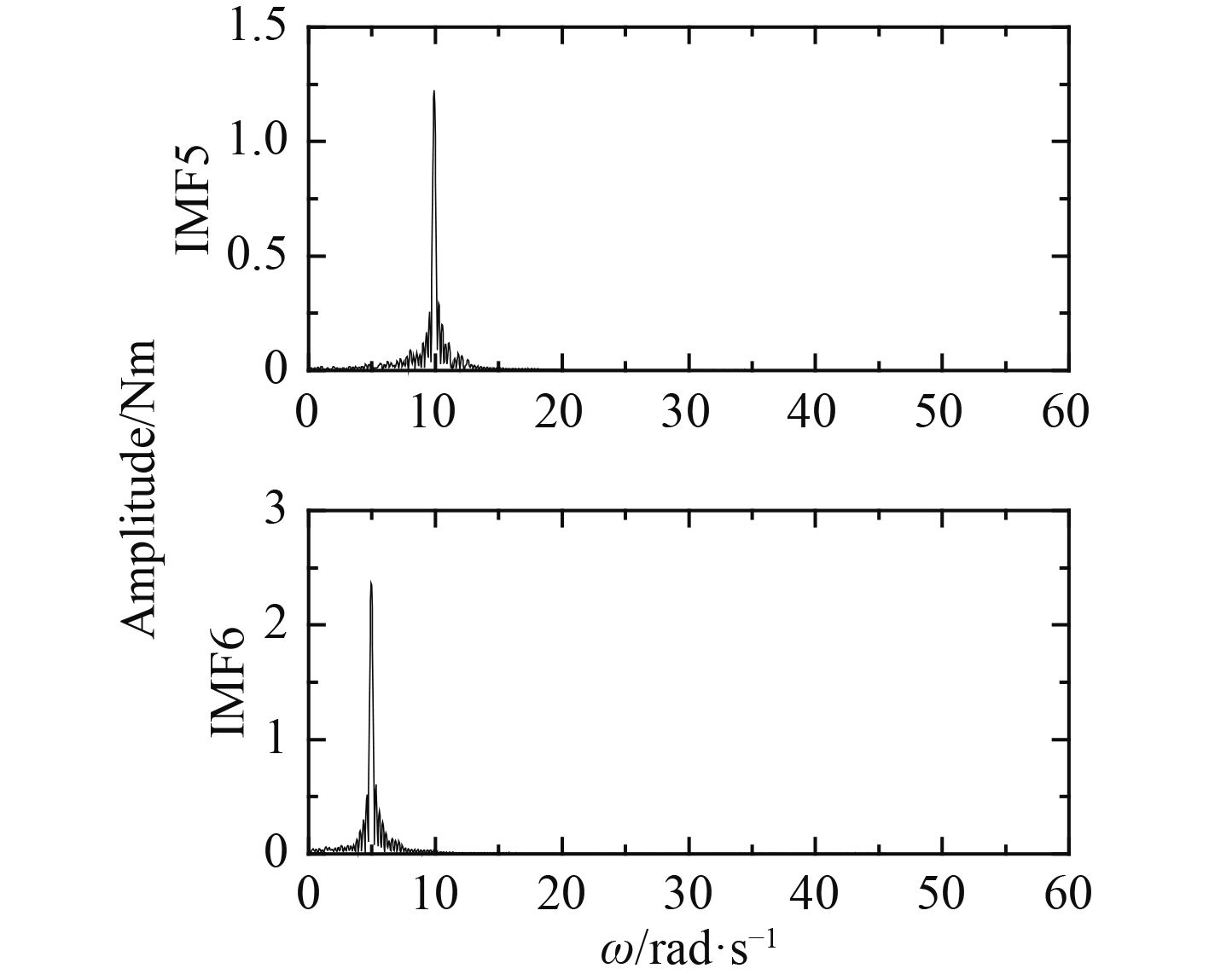
|
图 8 CEEMD所得IMF5,IMF6的幅值谱 Fig. 8 Amplitude spectrums of IMF5 and IMF6 decomposed by CEEMD |
波浪中两船近距离并行航行时,两船内侧在船长方向形成一个前宽后窄的狭长型间隙。入射波、两船摇荡产生的辐射波,入射波遭遇船体以后产生的绕射波会在这一狭窄间隙内相互干涉、衍射,形成复杂的波系干扰。由于两船内侧的狭长型间隙入口宽,出口窄,对船间流体产生阻塞作用,使得一部分波浪难以从间歇出口溢出,另一部分波浪则通过船舷后发生反射,逐步从间隙出口传播出去[13]。和单船在波浪中航行相比,这种阻塞作用和波浪的反射作用势必引起船体波浪力的变化。特别是在一些特定频率处,比如船体的共振频率或流体自身的共振频率,间隙内的波面抬升显著,作用于船体的波浪力非线性加剧,进而加剧船体的摇动运动,给船舶安全航行带来影响。因此,研究这些共振频率下船体所受波浪力的非线性特征本身就具有重要的理论和应用价值。
以本文试验为例,当入射波波长为4.5 m时,该波长与船模b船长基本相等,遭遇频率
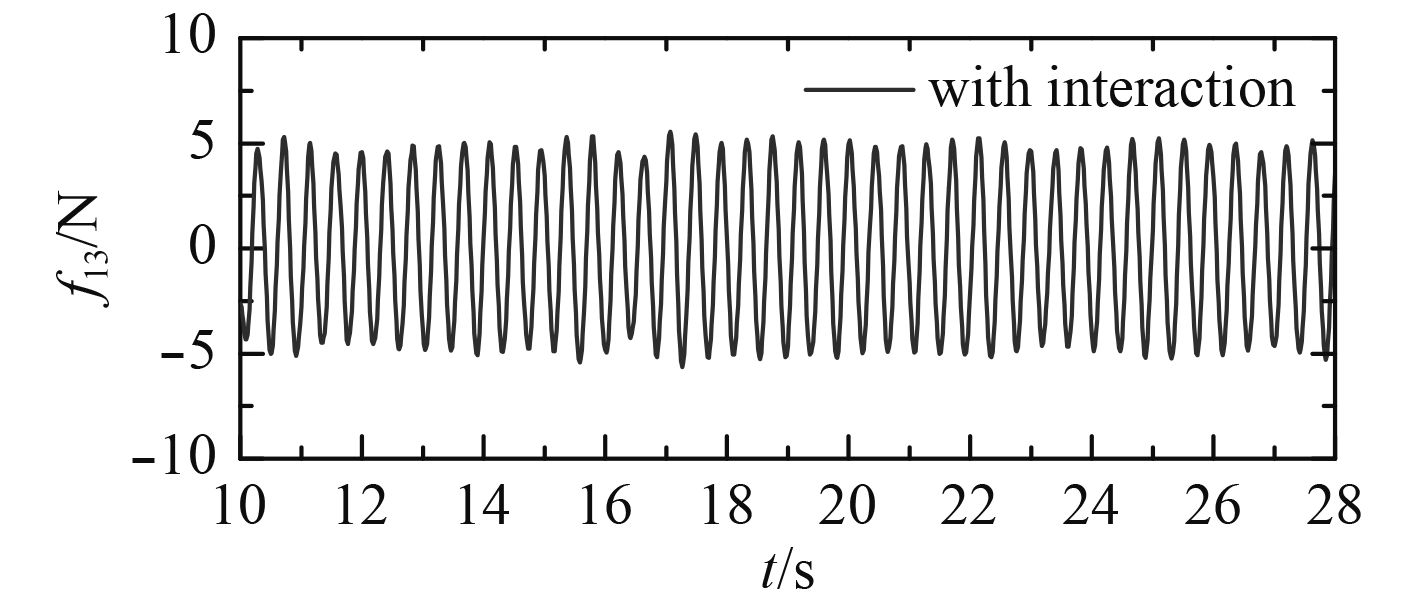
|
图 9 船模a受到的3阶倍频纵荡波浪力 Fig. 9 Third order surge forces on ship-a |
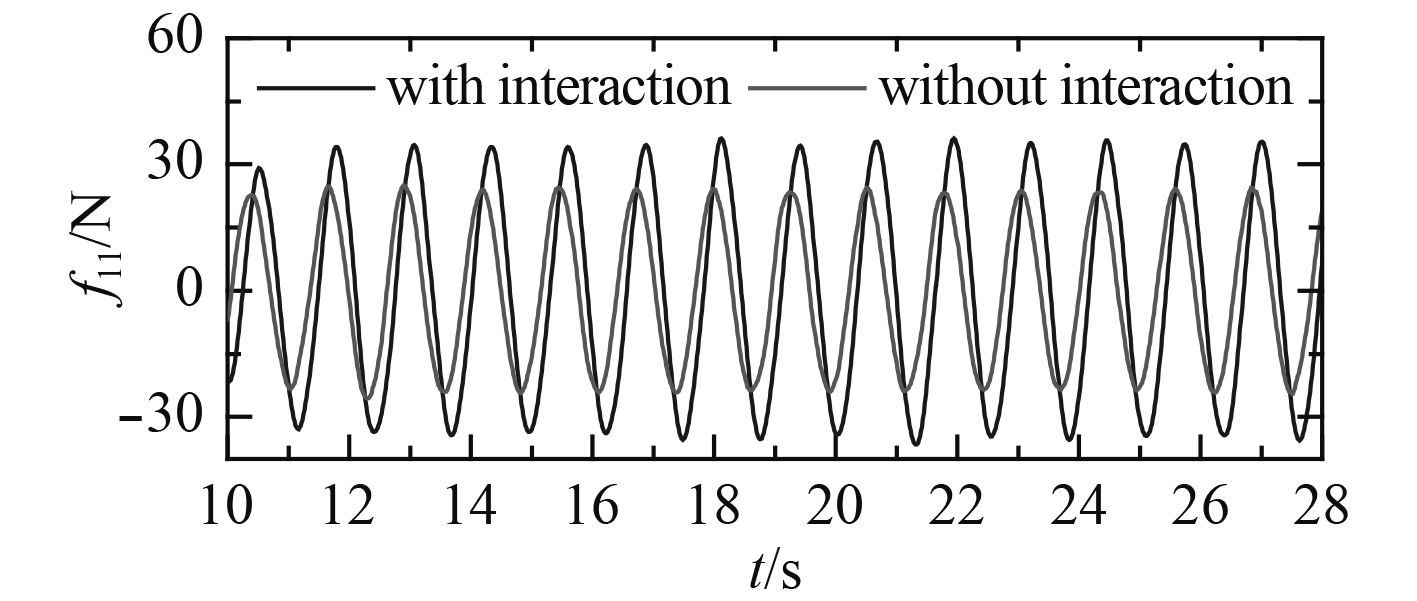
|
图 10 船模a受到的1阶纵荡波浪力 Fig. 10 First order surge forces on ship-a |
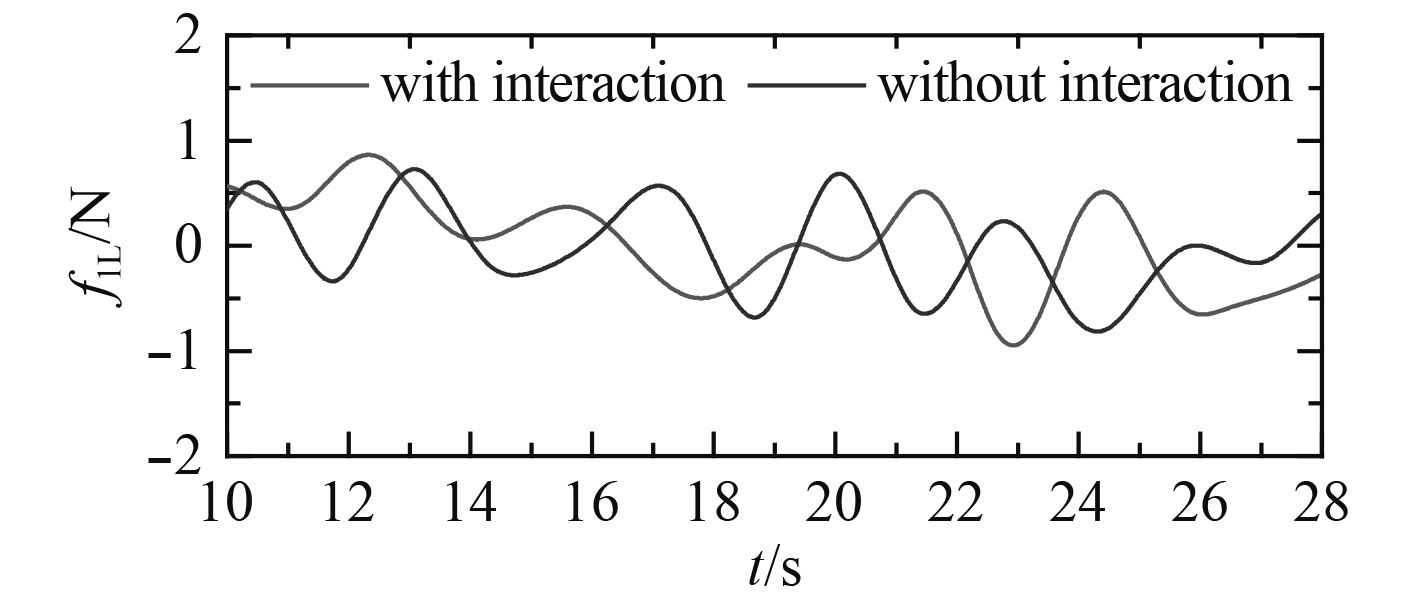
|
图 11 船模a受到的低频纵荡波浪力 Fig. 11 Second order surge forces in low frequencies on ship-a |
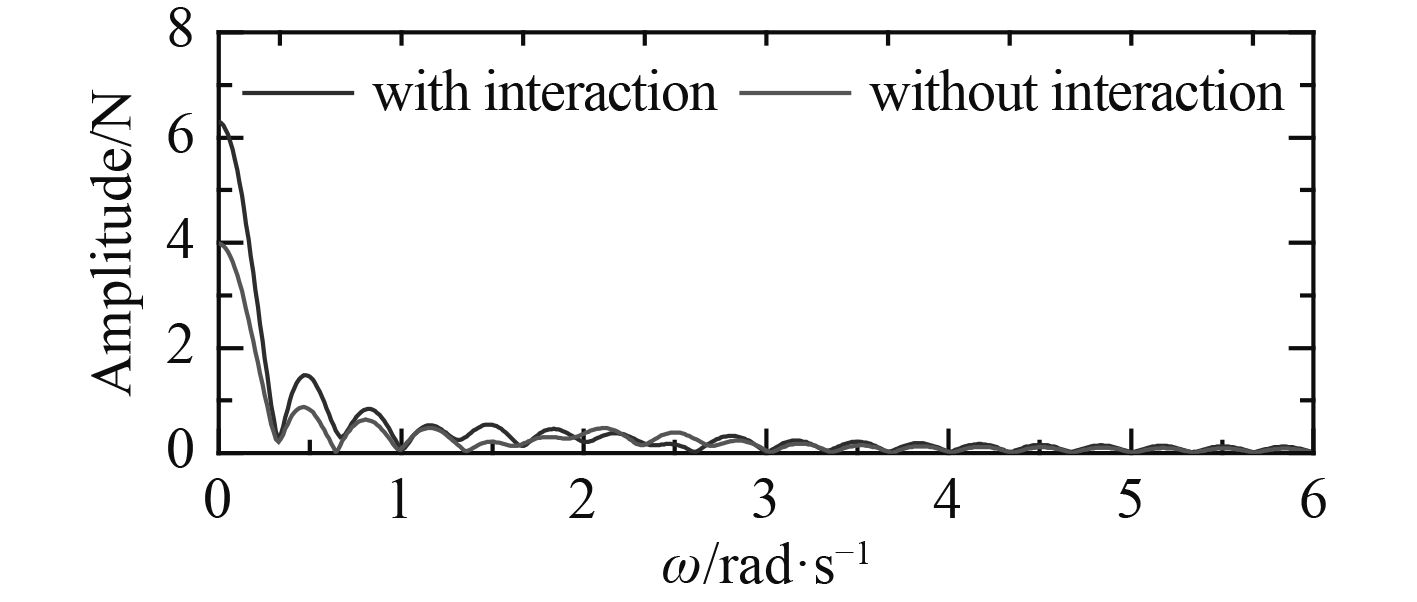
|
图 12 纵荡波浪力低频分量的幅值谱(含定常项) Fig. 12 Amplitude spectrums of the second order surge forces in low frequencies on ship-a |
使船体在波浪中产生漂移的波浪作用力称作波浪漂移力,是2阶波浪力在水平方向的分量,其成分包括定常波浪漂移力、低频波浪漂移力及2倍频波浪漂移力。波浪中近距离并行航行的两船,在定常波浪漂移力及低频波浪漂移力的作用下,会产生平均位置上的偏移,这种偏移运动可能引起两船在水平面内的相撞。对于波浪中两船横向补给作业而言,这种波浪漂移力是自动舵设计及两船航向稳定性设计的重要输入。因此两船近距离并行航行时所受波浪漂移力的研究具有重要的工程实际意义。仍以本文的试验为例,利用本文所提的信号分析方法分别对不同波长的入射波激励时船模a所受横荡波浪力及首摇力矩的测量信号进行分析,提取了各工况下横向定常漂移力
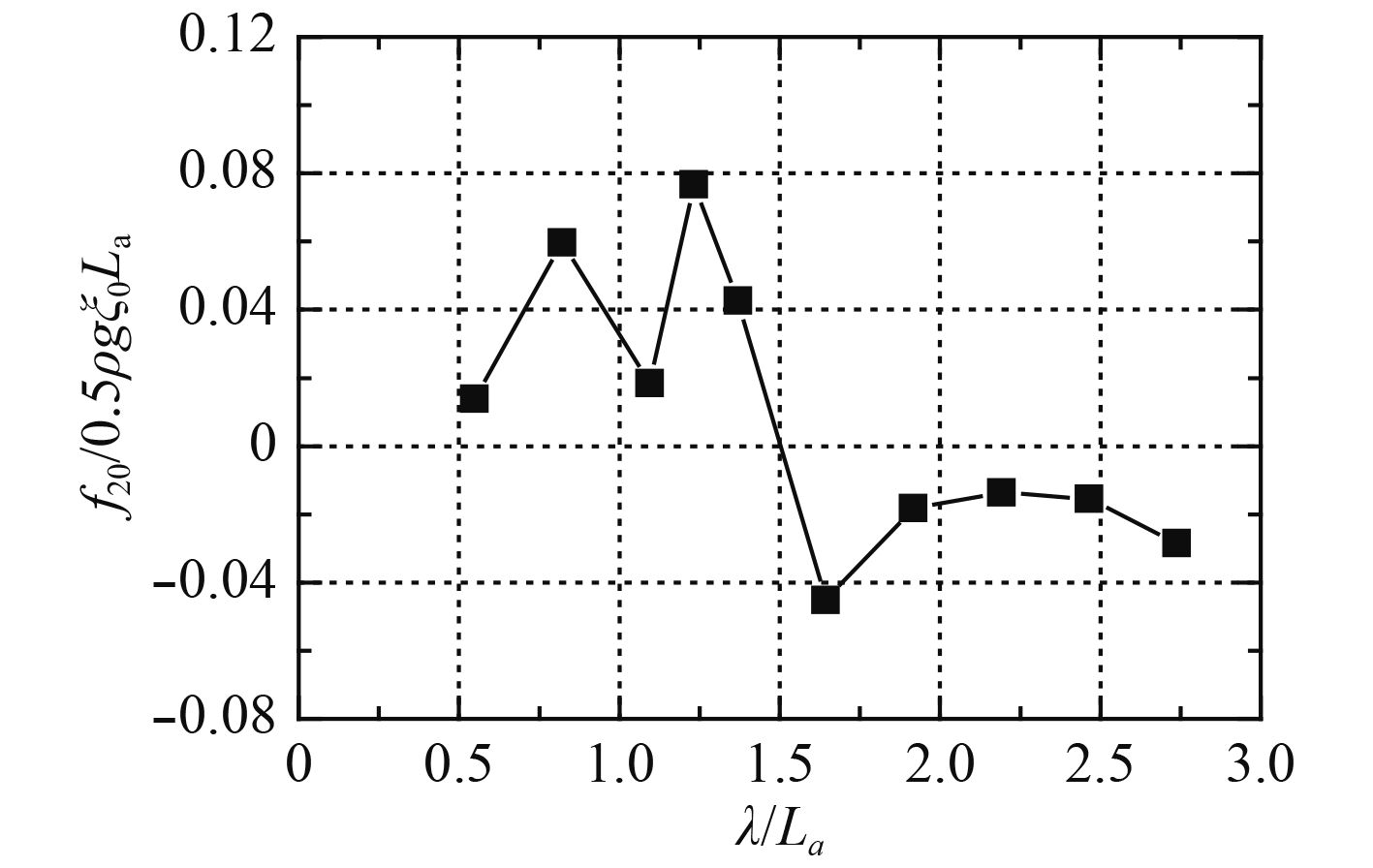
图13给出了船模a受到的无因次横向定常波浪漂移力随波长船长比的变化曲线。从图可知,当
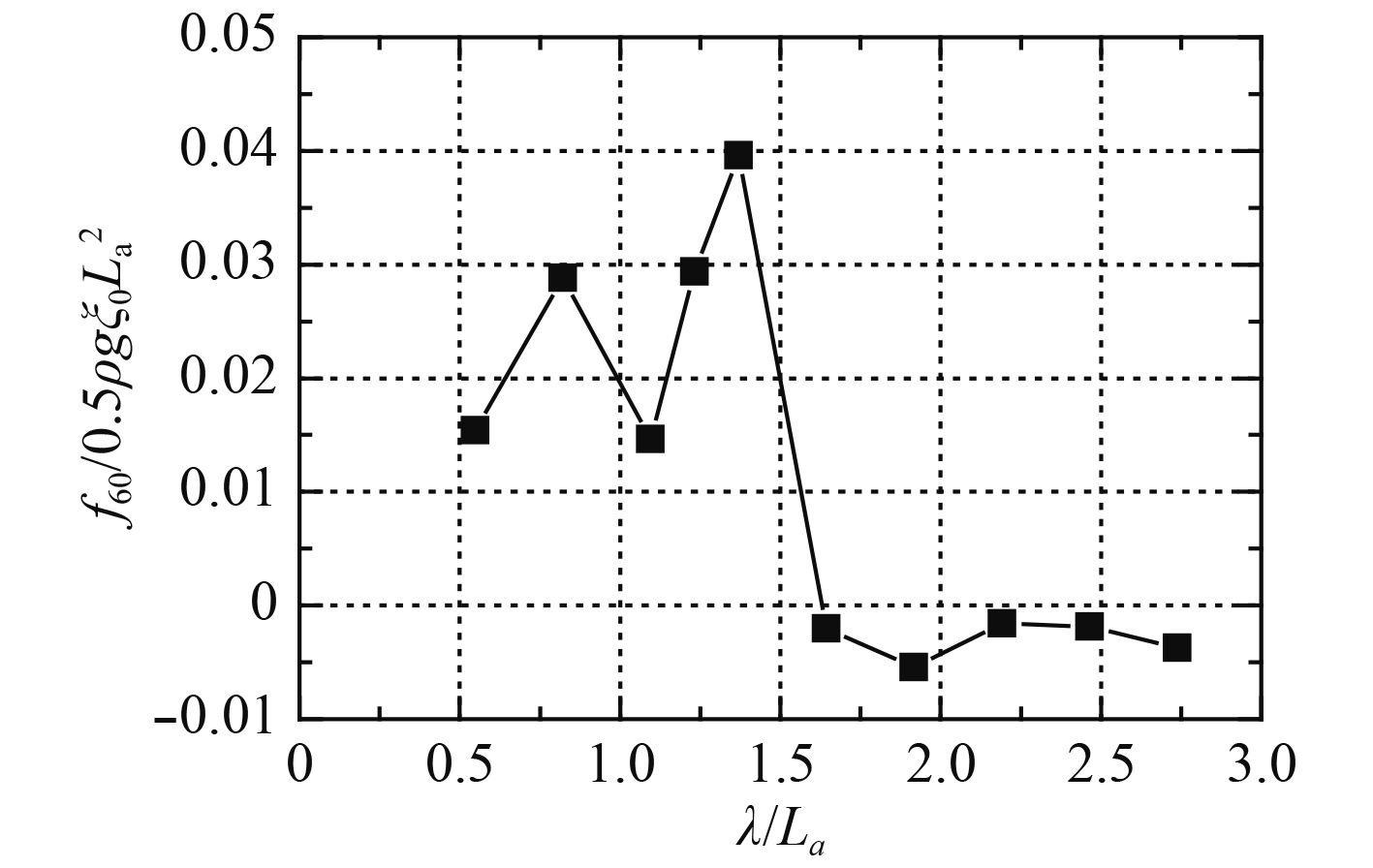
图14给出了船模a受到的无因次定常摇首力矩随波长船长比的变化曲线,其变化规律和横向定常波浪漂移力变化规律基本一致,当
|
图 13 船模a受到横向定常波浪漂移力 Fig. 13 Second order lateral drift forces on ship-a |
|
图 14 船模a受到的定常首摇力矩 Fig. 14 Second order yaw moments on ship-a |
1)直接采用EMD算法对含有随机噪声的船模非线性波浪力测量信号进行分析,会出现模态混叠现象,无法正确提取非线性波浪力中的各主要组分。
2)CEEMD算法能够过滤船模非线性波浪力测量信号中的随机噪声,并在分解过程中抑制EMD算法出现的模态混叠现象。
3)当船模非线性波浪力测量信号中高阶倍频波浪力的量值远小于信号中主成分量值时,CEEMD算法会将这些波浪力成分归于随机噪声模态中,这有利于对船模非线性波浪力主要组分的提取,消除高阶小量对主要组分提取精度的影响。
4)利用IMF归一化自相关函数的方差值能够有效识别噪声模态和有效模态。
5)本文所建立信号处理方法能够准确提取船模非线波浪力测量信号中的重要波浪力组分,为船模在规则波中的阻力增值测量,船模1阶、2阶波浪力测量等试验提供了一种可靠的数据分析方法。
| [1] |
魏泽, 赵战华, 刘家瑞. 二阶波浪力数值计算与试验方法研究[J]. 船舶力学, 2017(s1): 251-257. |
| [2] |
刘应中, 缪国平. 二维物体上的二阶波浪力[J]. 中国造船, 1985(3): 3-16. |
| [3] |
许勇, 欧勇鹏, 董文才. 基于低通滤波和经验模态分解的舰船耐波性试验信号分析方法研究[J]. 船舶力学, 2009, 13(5): 712-717. DOI:10.3969/j.issn.1007-7294.2009.05.006 |
| [4] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition method and the Hibeert Spectrum for non-stationary time series analysis[J]. Proc. Royal. Soc. London A, 1998, 454(A): 903-995. |
| [5] |
钱荣荣. 基于经验模态分解的动态变形数据分析模型研究[D]. 徐州: 中国矿业大学, 2016.
|
| [6] |
WU Zhao-hua, HUANG N E. Enstemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2011, 1(1): 1-41. |
| [7] |
YEH J R, SHIEH J S, HUANG N E. Complementary enstemble empirical mode decomposition: a noval noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010(2): 135-156. |
| [8] |
张守成, 张玉洁, 刘海生. 一种改进的EMD硬阈值去噪算法[J]. 计算机测量与控制, 2014, 22(11): 3659-3661. DOI:10.3969/j.issn.1671-4598.2014.11.062 |
| [9] |
王亚萍, 匡宇麒, 葛江华, 等. CEEMD和小波半软阈值相结合的滚动轴承降噪[J]. 振动、测试与诊断, 2018, 38(1): 80-86. |
| [10] |
许勇, 董文才, 欧勇鹏. 基于FFT-FS频谱细化技术的船模耐波性试验测量信号分析方法研究[J]. 船舶力学, 2012, 16(5): 497-503. DOI:10.3969/j.issn.1007-7294.2012.05.006 |
| [11] |
杨涛, 乐友喜, 曾贤德, 等. 基于自相关函数特性的CEEMD全局阈值去噪方法研究[EB/OL]. http://kns.cnki.net/kcms/detail/11.2982.P.20180124.1129.032.html.
|
| [12] |
XU Yong, DONG Wen-cai. Numerical study on wave loads and motions of two ships advancing in waves by using 3-D translating-pulsating source[J]. Acta Mechanica Sinica, 2013, 29(4): 494-502. DOI:10.1007/s10409-013-0062-x |
| [13] |
许勇. 波浪中近距离航行的多船水动力干扰机理研究[D]. 武汉: 海军工程大学, 2012.
|
 2018, Vol. 40
2018, Vol. 40
