0 引　言

螺旋桨空化噪声是舰艇在中高速航行时的主要噪声源，是导致舰艇暴露的重要原因^[1]。随着当前舰艇向高速化发展，空化现象在航行时出现更为频繁，对螺旋桨空化的检测引起了人们的广泛关注。当前实船螺旋桨空化的检测通常采用声学手段，通过分析螺旋桨噪声中高频带的能量变化确定空化是否出现，这种方法简单易行，但在环境变化和背景噪声起伏时，检测的准确度会下降。由于空化噪声的高度非线性和复杂性，实现空化状态的准确识别往往需要结合声信号的多方面特征。

幅度调制是包含螺旋桨在内的旋转类设备噪声信号的重要特性，螺旋桨噪声的调制特征通常与目标识别和状态评估联系在一起^[2]。国内外很多学者对调制现象的成因、调制谱结构、建模方法以及特征提取方法开展了大量研究^[3–8]，而对调制特征与空化发展之间关系没有明确的定论。

本文结合实船数据，运用小波包和解调技术，提取了螺旋桨噪声信号中的调制信息，并分析调制特征与空化发展之间的关系，旨在为螺旋桨空化的检测提供参考依据。

1 调制特征及提取方法 1.1 螺旋桨噪声的调制特征

舰船螺旋桨的转动、船尾不均匀流场中空泡崩溃的周期性或准周期性成分，使得在螺旋桨噪声中存在着“节奏”式的幅度调制，即噪声强度随着时间有规律的起伏，调制包络是慢变化的周期或准周期性过程，并为宽带舰船噪声所填充^[9]。

文献[3]将舰船噪声看作具有随机幅度、相同形状和重复周期的脉冲性随机过程处理，推导了非均匀多叶调制包络的功率谱，以4叶调制为例，其表达式为：

$\begin{split}&S\left( \omega \right) = \frac{{{{\left| {g(\omega )} \right|}^2}}}{T}\left\{ {({U_0} - {U_4}) + \frac{{2\pi }}{T}\left( {{U_4} + {U_2}\cos \frac{{\omega T}}{2}} \right.} \right. +\\&\quad \left. {\left. {\;\;\;\;\;\;\; 2{U_1}\cos \frac{{\omega T}}{4}\sum\limits_{n = - \infty }^\infty {\delta \left(\omega - \frac{{2\pi n}}{T}\right)} } \right)} \right\},\end{split}$

(1)

式中， ${U_0}$ ～ ${U_4}$ 由所用模型中脉冲随机幅度计算得出， $g(\omega )$ 为模型中单个脉冲的傅里叶谱。

从式（1）可以看出调制谱受脉冲幅值影响的同时还与脉冲的能量谱有关。

文献[4]从螺旋桨自身结构、尾流因素对空化的影响出发，对空化噪声调制解调谱进行推导，得到其表达式为：

$\begin{split}S\left( \omega \right) =& \frac{{{C_q}(N + 1)}}{T}\left\{ {{{\left| {K(\omega )} \right|}^2}{{\left| {H(\omega )} \right|}^2} }\times \right. \\&\Bigg. \sum\limits_{n = - \infty }^\infty {\delta \left(\omega - \frac{{2\pi n}}{T}\right)}+{{{\left| {\varPhi (\omega )} \right|}^2}}\Bigg\}{\text{。}}\end{split}$

(2)

式中： $K(\omega )$ 和 $H(\omega )$ 分别表征螺旋桨结构因素和尾流因素对空泡平均半径起伏的影响； $\varPhi (\omega )$ 代表环境随机因素对空泡平均半径起伏的影响。

由式（1）和式（2）可以看出，空化噪声包络谱由连续谱和与轴频对应的线谱组成，空化发展过程中噪声信号的脉冲参数变化和空泡半径变化等因素会对包络谱特性产生影响。本文主要讨论空化发展过程中与包络谱中线谱相关的特性变化。

1.2 调制特征提取方法

文献[8]对当前舰船噪声调制特征的提取方法进行介绍和仿真分析，结合空化噪声的宽带特性，从工程实用角度，本文选取检波滤波法进行空化噪声的包络谱分析。

对于一单频调制的信号：

$x\left( t \right) = A\left[ {1 + {\alpha _m}{\rm sin}\varOmega t} \right] \cos\omega t,$

(3)

其中： $A$ 为信号幅值； ${\alpha _m}$ 为调制度； $\varOmega $ 为调制频率； $\omega $ 为载波频率。

选取合适的参数对信号进行检波滤波，即可得到包含调制频率的信号：

$y\left( t \right) = \frac{{2A}}{\pi } \cdot {\alpha _m}{\rm sin}\varOmega t\text{。}$

(4)

对于空化噪声这类宽带噪声信号，其载波包含较大的频率范围，其中较低的频率会对解调后频率成分产生干扰，因此在进行检波滤波前需要进行选频处理。

针对螺旋桨空化噪声宽带非平稳特征及实船噪声干扰多、信噪比低的特点，利用小波包分析原理对螺旋桨噪声信号进行重构，得到反映螺旋桨空化特性的空化特征信号。

小波包分析包含分解及重构算法，正交小波包分解递归算法为：

$\left\{ \begin{aligned}&d_l^{j,2n} = \sum\limits_{k \in Z} {{h_{k - 2l}}d_k^{j + 1,n}}, \\&d_l^{j,2n + 1} = \sum\limits_{k \in Z} {{g_{k - 2l}}d_k^{j + 1,n}} \text{。}\end{aligned} \right.$

(5)

小波包分解系数重构算法为：

$d_l^{j + 1,n} = \sum\limits_{k \in Z} {\left[ {{h_{l - 2k}}d_k^{j,2n} + {g_{l - 2k}}d_k^{j,2n + 1}} \right]}, $

(6)

其中，系数 $\left\{ {d_l^{j,n}} \right\}$ 为信号 $f\left( t \right)$ 在分辨率为 $j$ 时的正交小波包分解系数。

对信号 $f\left( t \right)$ 进行 $k$ 层小波包分解，则将信号分解为 ${2^k}$ 个节点，每个节点信号 ${S_{k,m}}$ 对应的频带范围为：

$m{f_b} \sim \left( {m + 1} \right){f_b},$

(7)

其中 ${f_b} = {f_s}/{2^{k + 1}}$ ， ${f_s}$ 为信号采样频率， $m$ 为经Gray码转换后的第 $k$ 层分解的节点序号， $m = 0,1,...,{2^k} - 1$ 。

结合小波包选频和检波滤波方法，本文螺旋桨噪声调制特征提取步骤如图1所示。

2 螺旋桨噪声测量试验

为研究螺旋桨噪声信号调制特征与空化发展之间的关系，在某试验船上开展多工况下的螺旋桨噪声测量试验。试验海区海况平稳，近距离范围内无其他水面船只，环境干扰因素小。

该试验船螺旋桨为5叶大侧斜桨，可利用船上安装的空化监测试验装置采集螺旋桨自噪声信号，试验装置的结构如图2所示。

水听器位于船体尾部结构上，可实时采集螺旋桨部位的噪声信号，采样频率102.4 kHz，最大量程达180 dB（参考声压1 μPa），满足试验过程中的测量需求。

试验过程如下：试验船只按照规定转速在海区内直线航行，待转速稳定后采集螺旋桨噪声数据。起始转速为n r/min，转速间隔为2 r/min，共进行转速从n~n+30的16组测试，每组测试数据长度约为40 s。结合该试验船前期测试信息，该转速区间包含螺旋桨空化起始阶段。

3 数据处理及调制特征分析 3.1 空化特征信号重构

实船航行时机械噪声干扰会对空化特征的分析造成影响。机械噪声集中在低频，而空化噪声由低频线谱和高频连续谱构成，选取合适的节点信号进行重构，提取空化噪声中的高频成分用以反映空化状态，可以有效避免机械噪声带来的干扰。

根据空化噪声信号的瞬变特性，选用Daubechies 系列小波中的db4小波基对采集到的螺旋桨噪声进行小波包分解，利用小波包分解系数对信号进行重构得到节点信号 ${S_{k,m}}$ 。

定义能量分布系数：

${\lambda _{k,m}} = E({S_{k,m}})/\sum\limits_{m = 0}^{{2^k} - 1} {E({S_{k,m}})} \text{。}$

(8)

实际计算中发现，分解层数为4时，16组数据中 ${\lambda _{4,0}}$ 均在99.91%以上，即本次采集的数据中无论空化是否发生，信号能量主要集中在重构信号 ${S_{4,0}}$ 中，由于 ${S_{4,0}}$ 位于低频带，无法分离机械噪声的干扰，在分析时需要剔除。考虑采集数据时的频谱泄漏效应，去除高频段 ${S_{4,12}}$ ～ ${S_{4,15}}$ 。

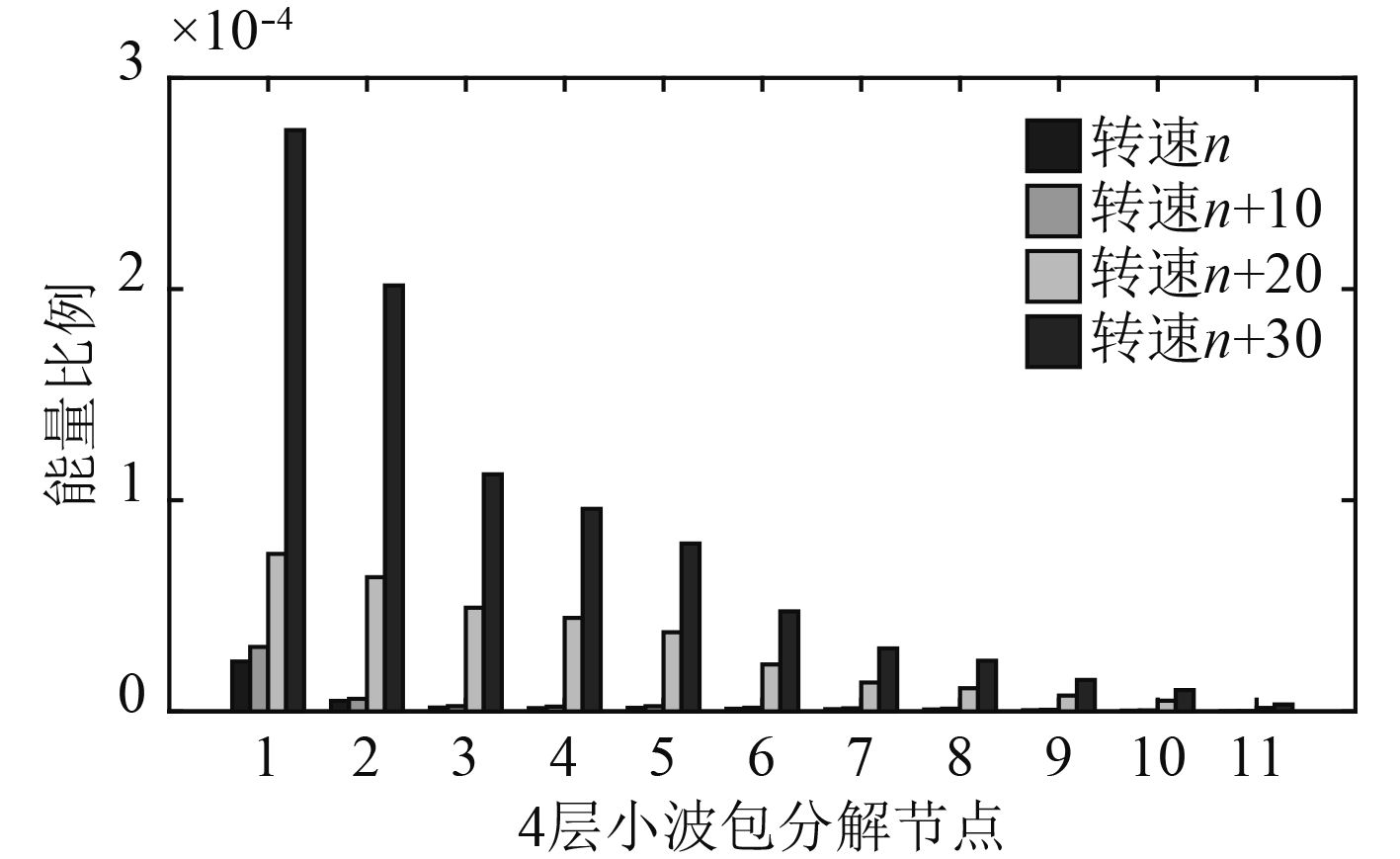
对信号进行小波包分析时，关注节点信号为 ${S_{4,1}}$ ～ ${S_{4,11}}$ ，4个转速 $n,n + 10,n + 20,n + 30$ （单位r/min）下各节点的 ${\lambda _{4,m}}$ 值如图3所示。

从图中可以看出，随着转速的升高，节点信号 ${S_{4,1}}$ ～ ${S_{4,11}}$ 能量比例出现较为明显的升高，根据空化噪声强度随转速提升而增高的关系，可以认为节点信号 ${S_{4,1}}$ ～ ${S_{4,11}}$ 反映了螺旋桨空化状态。但由于重构信号 ${S_{4,1}}$ 在 $n , n + 10$ 转时相对于 $n + 20 , n + 30$ 转时仍有较高的比例，因此对节点信号 ${S_{4,2}}$ ～ ${S_{4,11}}$ 进行组合，得到空化特征信号：

$S = \sum\limits_{i = 2}^{11} {{S_{4,11}}} \text{。}$

(9)

通过对特征信号 $S$ 的分析，可以确定螺旋桨的空化状态，并分析空化发生带来的信号调制特征变化。

3.2 空化状态判断

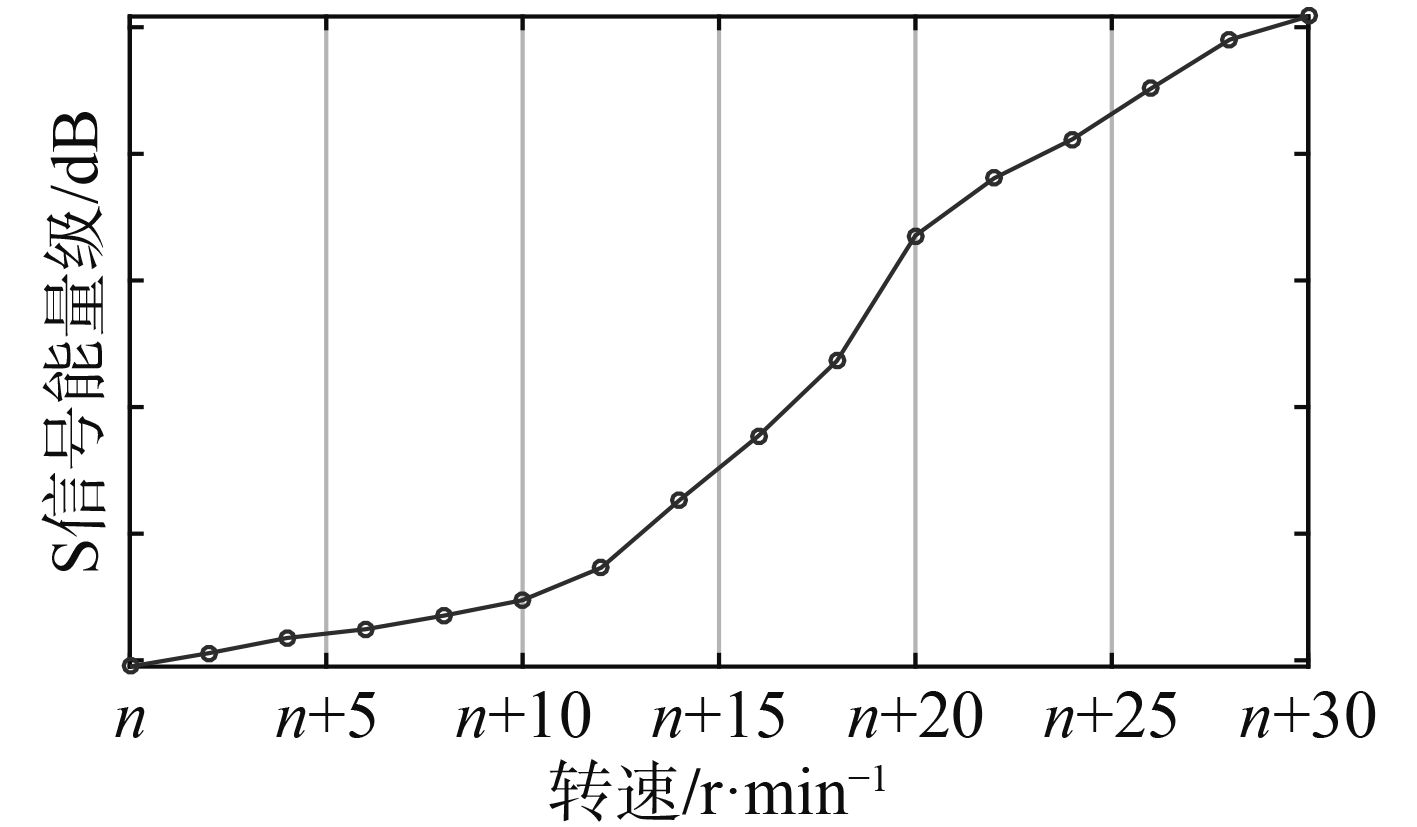
实船测试中无法通过直接观察判断螺旋桨的空化状态，需要利用间接的手段获取相关信息。在海况平稳、背景噪声干扰较小时，可以通过中高频带的信号能量变化情况评估螺旋桨的实际空化状态。图4为空化特征信号 $S$ 能量级随转速的变化曲线。

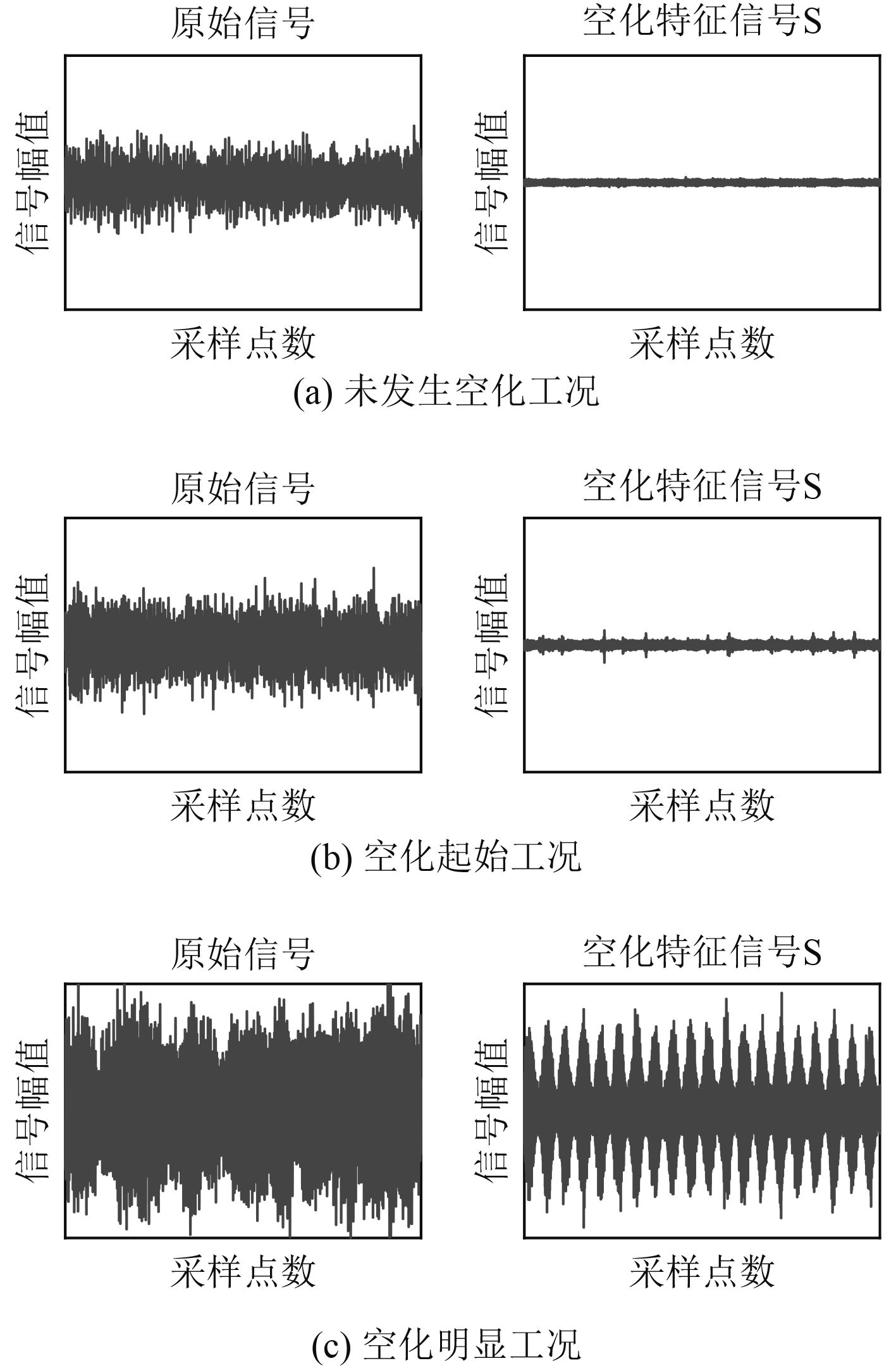
图中在转速n + 12 r/min后曲线斜率出现增大，由文献[10]中临界转速的判别方法2可知，该试验船的临界转速约为n + 12 r/min，据此将试验数据分成表1中的3组，便于对比分析。图5为螺旋桨不同空化状态下原始信号波形和经过小波包重构得到的空化特征信号波形。可以看出与原始信号相比，不同组别下重构的信号幅值、脉冲等特征存在显著变化，说明了空化特征信号重构方法的正确性。

3.3 包络谱提取与分析

由式（7）知重构信号S频带范围为6.4~38.4 kHz，根据螺旋桨轴频、叶频及低阶倍频的频率范围，选取合适参数对重构信号S进行绝对值变换、低通滤波，得到空化特征信号的包络，对包络进行谱分析，提取出与轴频、叶频相关的频率成分。

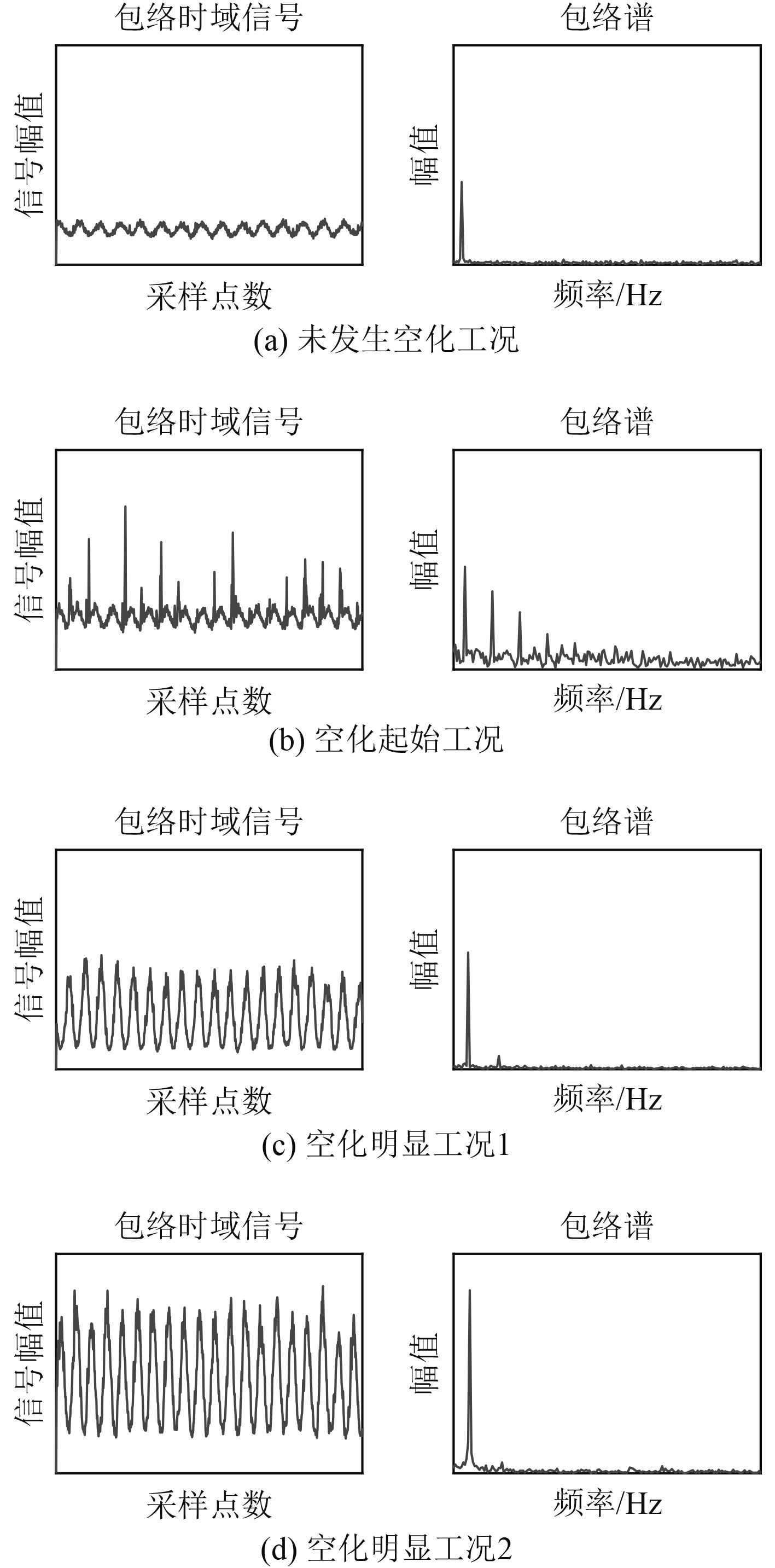
部分工况下包络时域波形和包络谱如图6所示，图中图6（a）～图6（d）对应的转速依次增加。为便于工况图像的对比并显示更多细节，图6（a）和图6（b）、图6（c）和图6（d）对应的纵坐标范围一致。

从包络时域信号可以看出，在未发生空化时，包络信号波形接近单频信号，如图6（a）所示，说明此时空化特征信号中存在着明显的幅度调制。随着螺旋桨转速的提高，包络信号中出现脉冲，引起波形的畸变，信号仍具有明显的周期性，如图6（b）所示。当空化程度进一步加深时，相互重叠的脉冲使得包络信号波形又恢复至接近单频信号，如图6（c）和6（d）所示。

各工况下包络谱中线谱均与螺旋桨轴频相对应，这与大侧斜桨的轴频调制明显、叶频调制减弱的特性相符，验证解调方法的准确性。在未发生空化时，包络谱中只存在与轴频对应的线谱，如图6（a）所示。在空化起始阶段包络谱中出现明显的谐波分量，如图6（b）所示，这与空化初期空泡分布不均匀，空泡在旋转周期的特定时刻发生溃灭，引起波形的畸变相关，这一现象在包络时域信号中有着具体的体现。同时可以观察到，当空化程度进一步加深时，轴频线谱幅值增加，同时谐波分量相对轴频明显减弱，如图6（c）和6（d）所示。

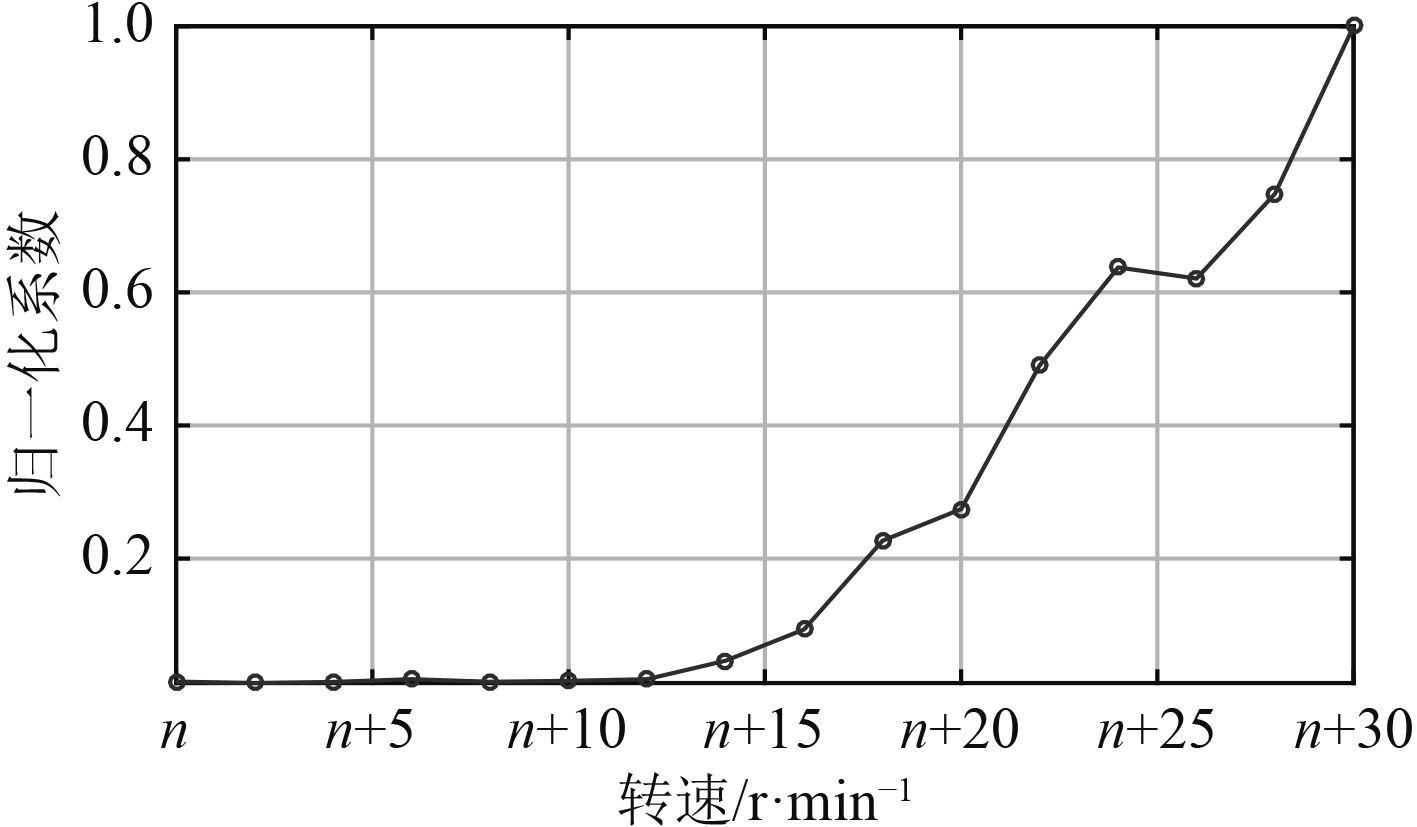
由式（4）知检波滤波解调方法提取的线谱幅值与调制度 ${\alpha _m}$ 、信号幅值 $A$ 有关，提取各工况下包络谱中轴频线谱幅值，用包络谱中轴频线谱幅值与信号有效值之比表征空化特征信号的调制程度，得到调制程度随转速的变化曲线如图7所示。

可以看出在未发生空化的转速下，调制程度保持在较低的水平，当空化出现之后，调制程度随空化的发展出现明显的增大，代表着与螺旋桨轴频相对应的能量起伏程度随着空化的发展而变化。该曲线与图4中高频带能量随转速变化曲线具有较好的对应关系，因此调制程度的变化可以作为监测螺旋桨空化状态的参量。

4 结　语

1）空化现象出现的前后，在螺旋桨噪声的中高频段均存在幅度调制，同时调制特征变化与空化的发生有关；

2）在空化发展初期，由于信号中脉冲的作用，包络谱中出现明显的谐波成分，包络谱结构发生变化；

3）螺旋桨噪声在中高频段的调制程度也可以作为空化监测的参量：在一定范围内，随着空化的发展，调制程度增强，且调制程度随转速变化曲线与中高频段能量随转速变化曲线的趋势较为吻合。