随着我国海外权益的日益增长和周边形势的复杂化,我国海上武装力量面对日益多元化的海上威胁。海军在面对恐怖分子小型快艇的迫近袭击时,中、大型水面舰艇上安装的导弹、舰炮武器费效比过高,不能即时经济的对类似小型水面目标进行精确打击。面对这种特殊需求,就需要一种自动化程度高、可舱室内遥控操作、能抵御非传统威胁、配置灵活的有效武器[1]。随着我国海洋战略的调整,对钓鱼岛海域、南海海域的巡航和执法日益频繁,从增加威慑、打击力度层面来说,设计一型通用化、模块化的武器平台能够快速提高执法船的执法能力。在我国西南边防地区,自湄公河巡航以来,由于巡航区域地理条件复杂,安全形势不容乐观,对遥控武器平台的需求也越来越迫切。基于上述背景,既可以作为独立的作战单元,也可以为其他精确制导武器提供实时作战信息支持,可广泛应用于海防、边防、反恐以及局部冲突,具备态势感知和快速精确打击的舰载遥控武器站应运而生。
舰载遥控武器站最早应用于公安边防湄公河联合巡逻,从央视披露情况可以看出,该型武器站能够经受频繁冲击振动和长时间连续工作。舰载遥控武器站当前使用最多的是海警执法船,2016年6月19日,央视报道海警21115舰访问韩国,舰载遥控武器站工作画面曝光,图1所示为某型舰载遥控武器站。

|
图 1 某型舰载遥控武器站 Fig. 1 A certain type of the naval remote controlled weapons station |
随着舰载遥控武器站的深入应用,特别是随着无人化、智能化的需求指引,遥控武器站当前急需解决一个关键问题:如何利用有限成本尽可能实现最优的控制性能,从而满足未来大批量的应用需求。从当前技术层面分析,控制系统可以从以下两点研究:
1)无位置传感器下转子位置估计
舰载遥控武器站的位置传感器检测,目前成熟的方案是在电机轴端安装机械位置传感器,如增量或绝对式的数字编码器,或者旋转变压器等[2]。这样武器站的控制精度、动态响应特性取决于传感器的性能,选择的传感器不同,其控制性能差别很大;其电机绝大多数采用安装传感器表贴式永磁同步电机(Surface-Mounted PMSM,SPMSM)驱动方式,永磁电机体积较大、电机结构相对复杂,不便于实现电机和负载的手动解脱,以实现手动和遥控模式的切换;当传感器出现故障时将严重影响控制系统性能,极易导致驱动器报警从而停止工作。此外,1套性能优异的传感器装置十分昂贵,而且方位和俯仰2轴均需要编码器,使得系统成本大大增加,这影响了舰载遥控武器站低成本大批量列装的定位。内置式永磁同步电机无位置传感器控制方案有望实现高性价比、高可靠驱动系统[3]。
2)控制算法优化,提高射击精度
舰载遥控武器站控制系统是一个多变量、非线性、强耦合的系统,对于参数摄动和外部负载扰动非常敏感,传统的PI控制方法因其算法简单、调速方便等优点,在其控制系统中得到了广泛的应用。但是PI控制方法需要系统精确的数学模型,对于舰载遥控武器站这样一个具有强后坐力、变摩擦力和变转动惯量的非线性系统,在跟踪射击状态下随机扰动难以建模表征,采用传统的控制方法很难达到系统的要求,进而难以获得理想的高精度控制性能[4]。因此,有必要研究基于PMSM控制系统的非线性控制方法。
从工程层面来讲,本文主要进行控制算法的优化,增强控制算法的鲁棒性,从而提高武器站跟踪射击时抗干扰能力,提升武器站射击精度。
关于控制系统优化的研究很多,如模糊控制在控制系统的应用研究,但是实际应用中由于模糊化、专家规则库、去模糊化的复杂应用,使得系统的控制精度受到限制;文献[5]提出了神经网络控制理论,但是通过自适应学习的系统参数整定需要比较长的数据处理时间,需要使用速度很快的微处理器来提高系统实时性,实际上增加了系统设计的成本。20世纪50年代出现的滑模变结构控制理论是一种非线性控制理论,滑模变结构控制以其对系统数学模型精确度要求不高,对系统参数摄动和外部扰动具有完全鲁棒性等优点,能够实现系统的渐进稳定性[6]。因此,有必要开展舰载遥控武器站控制系统的滑模控制研究。
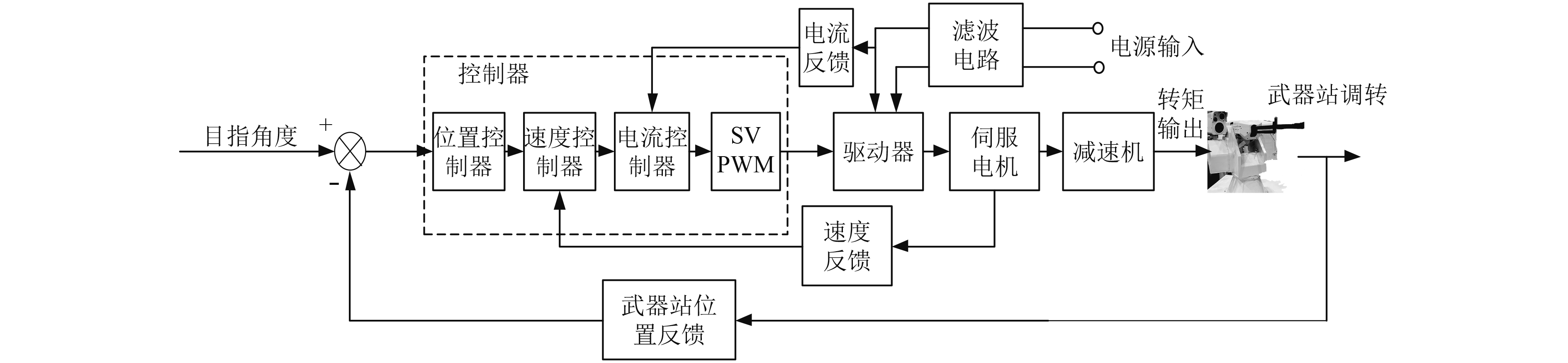
2 控制器设计 2.1 矢量控制舰载遥控武器站伺服系统闭环控制原理图如图2所示。
|
图 2 武器站伺服系统闭环控制原理图 Fig. 2 The schematic diagram of closed loop control of the servo system of the weapon station |
对于面贴式永磁同步电机,有
| $p{i_d} = {{{\rm{(}}{u_d}{\rm{ - }}{R_s}{i_d} + {\omega _r}{L_q}{i_q}{\rm{)}}} / {{L_d}}}{\text{,}}$ | (1) |
| $p{i_q} = {{{\rm{(}}{u_q}{\rm{ - }}{R_s}{i_q}{\rm{ - }}{\omega _r}{L_d}{i_d}{\rm{ - }}{\omega _r}{\psi _f}{\rm{)}}} / {{L_q}}}{\text{,}}$ | (2) |
| $p{\omega _r}{\rm{ = }}{{{\rm{(}}{P_n}{T_{em}}{\rm{ - }}{P_n}{T_l}{\rm{ - }}B{\omega _r}{\rm{)}}} / J}{\text{,}}$ | (3) |
根据以上公式,可以得到如下形式的状态方程:
| $\dot x = Ax + Bu + {B_0}{T_l}{\text{。}}$ | (4) |
其中:
式中:

|
图 3 基于矢量控制的位置控制原理图 Fig. 3 The position control schematic diagram based on the vector control |
本文中选取的面贴式永磁同步电机,有
| ${T_{em}}{\rm{ = }}\frac{3}{2}{p_n}{\psi _f}{i_q}{\text{,}}$ | (5) |
由式(3)可得:
| $J{\ddot \theta } {\rm{ = }}{T_{em}} - {T_l} - B\omega {\text{,}}$ | (6) |
武器站跟踪误差及其导数为
| $\begin{array}{l}e(t) = \theta (t) - {\theta _d}(t){\text{,}}\\\dot e(t) = \dot \theta (t) - {{\dot \theta }_d}(t){\text{,}}\end{array}$ | (7) |
其中,
设计滑模函数为
| $s(t) = ce(t) + \dot e (t){\text{,}}$ | (8) |
对滑模面S求导,根据式(6)和式(8)可得
| $\dot s(t) = c\dot e(t) + \ddot e(t) = c\dot e(t) + \frac{{{T_{em}} - {T_l} - B\omega }}{J} - {\ddot \theta _d}(t){\text{,}}$ | (9) |
为了消除系统抖振,采用变指数趋近律,得到
| $s' = - \xi \left| {\mathop {e(t)}\limits^ \bullet } \right|{\mathop{\rm sgn}} (s) - ks{\text{,}}$ | (10) |
结合式(5)、式(9)和式(10)可得相应的控制律函数为
| ${U_{SMC}} = {i_q} = \frac{{2J}}{{3{p_n}{\psi _f}}}\left[ \begin{array}{l}c\dot e(t) + \xi \left| {\dot e(t)} \right|{\rm{sgn}}(s) + \\ks{\rm{ + }}{{\ddot \theta }_d}(t) + \frac{{{T_l} + B\omega }}{J}\end{array} \right]{\text{。}}$ | (11) |
采用变指数趋近律,在远离切换面时,在常规趋近律的基础上,加入速度误差的绝对值,可以使系统加速趋近滑模面,提高系统的动态响应;当运动点接近切换面时,随着速度逐渐降低,速度误差的绝对值渐趋于0,从而保证系统平滑的到达滑模面[8]。
2.3 稳定性证明针对上述滑模控制器选用Lyapunov函数来证明其滑模平面稳定且存在滑动模态。
定义Lyapunov函数为
| ${{V = }}\frac{1}{2}{s^2}{\text{,}}$ | (12) |
对其求导,则有
| $\begin{split}{l}{{{V}}'}{\rm{ = }}s{s'} = s\left[ { - \xi \left| {\dot e(t)} \right|{\mathop{\rm sgn}} (s) - ks} \right]=\\ - \xi \left| {\dot e(t)} \right|s{\mathop{\rm sgn}} (s) - k{s^2}=\\ - \xi \left| {\dot e(t)} \right|\left[ s \right] - k{s^2}{\text{。}}\end{split}$ | (13) |
由式(13)易知
舰载遥控武器站控制系统永磁同步电机参数(标幺值)为:电机功率为
|
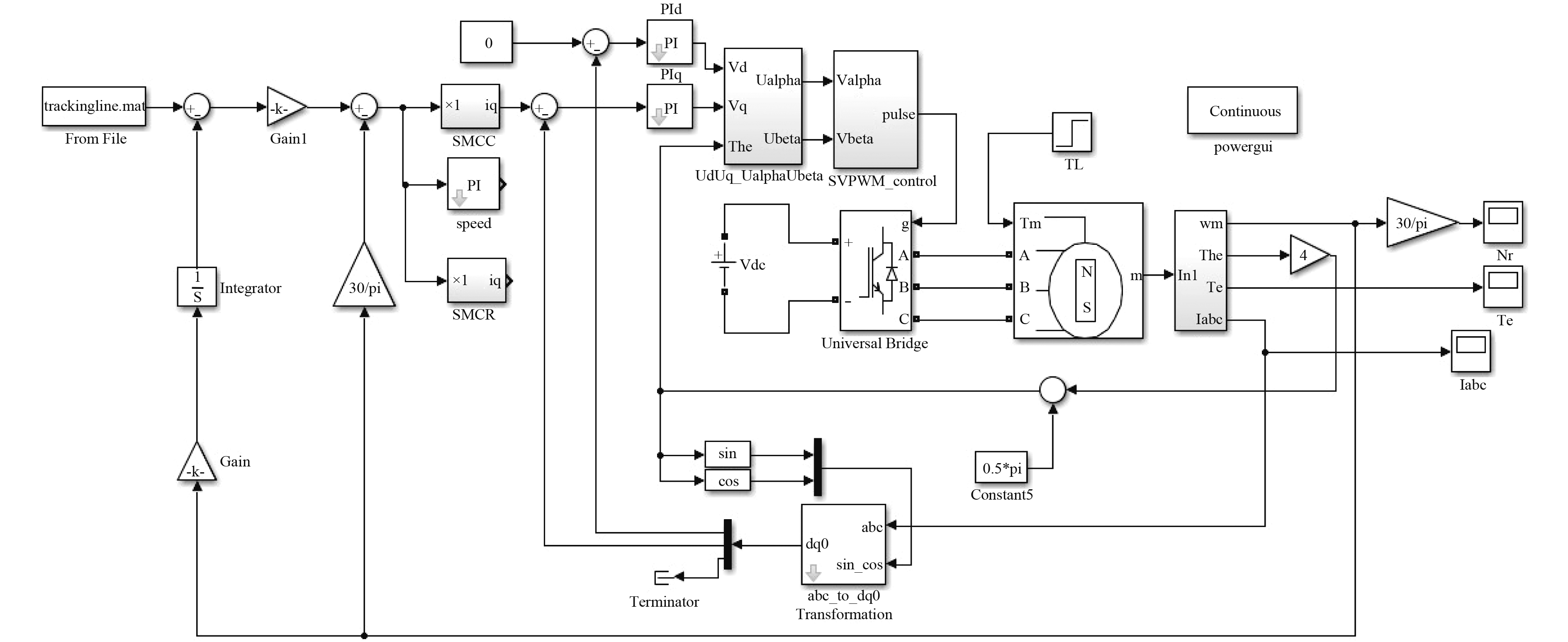
图 4 舰载遥控武器站位置控制仿真模型 Fig. 4 The position control simulation model of the naval remote controlled weapons station |
模型中位置指令输入trackingline.mat模拟上层随机指令,以验证遥控武器站伺服系统能够即时响应跟踪指令。速度环SMCC控制器是本文搭建的变指数趋近律滑模控制器,PI控制器为常规PI控制器,SMCR控制器是根据指数趋近律搭建的控制器[9]。
本文对常规PI速度控制器和变指数滑模速度控制器SMCC进行了仿真对比,仿真条件为转速参考值设定为500 r/min,在t=0.5 s突加50 N·m负载。仿真结果如图5~图8所示。

|
图 5 SMCC控制器转速响应曲线对比 Fig. 5 The comparison of speed response curve of the SMCC controller |
|
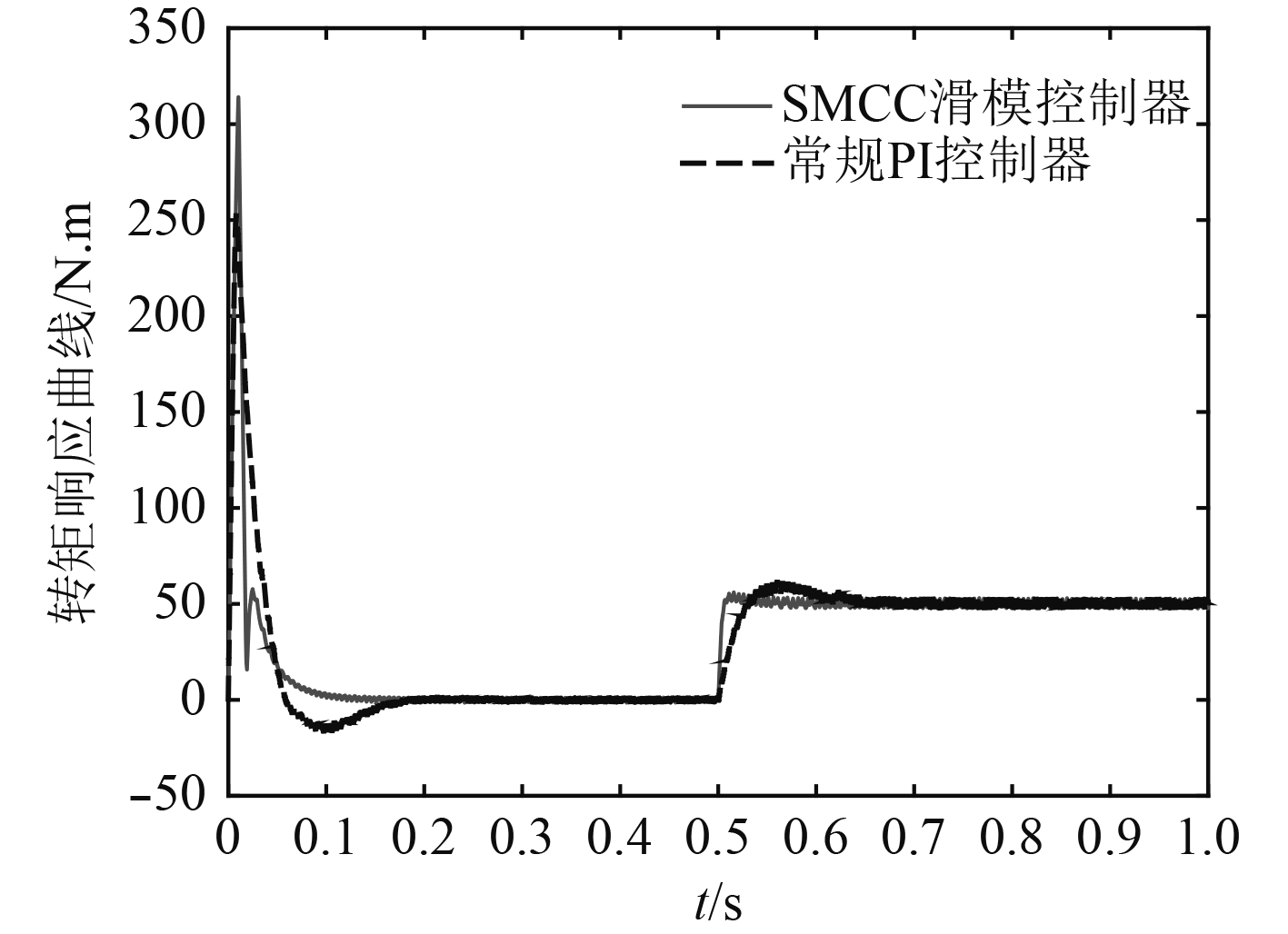
图 6 SMCC控制器转矩响应曲线对比 Fig. 6 The comparison of torque response curve of the SMCC controller |
|
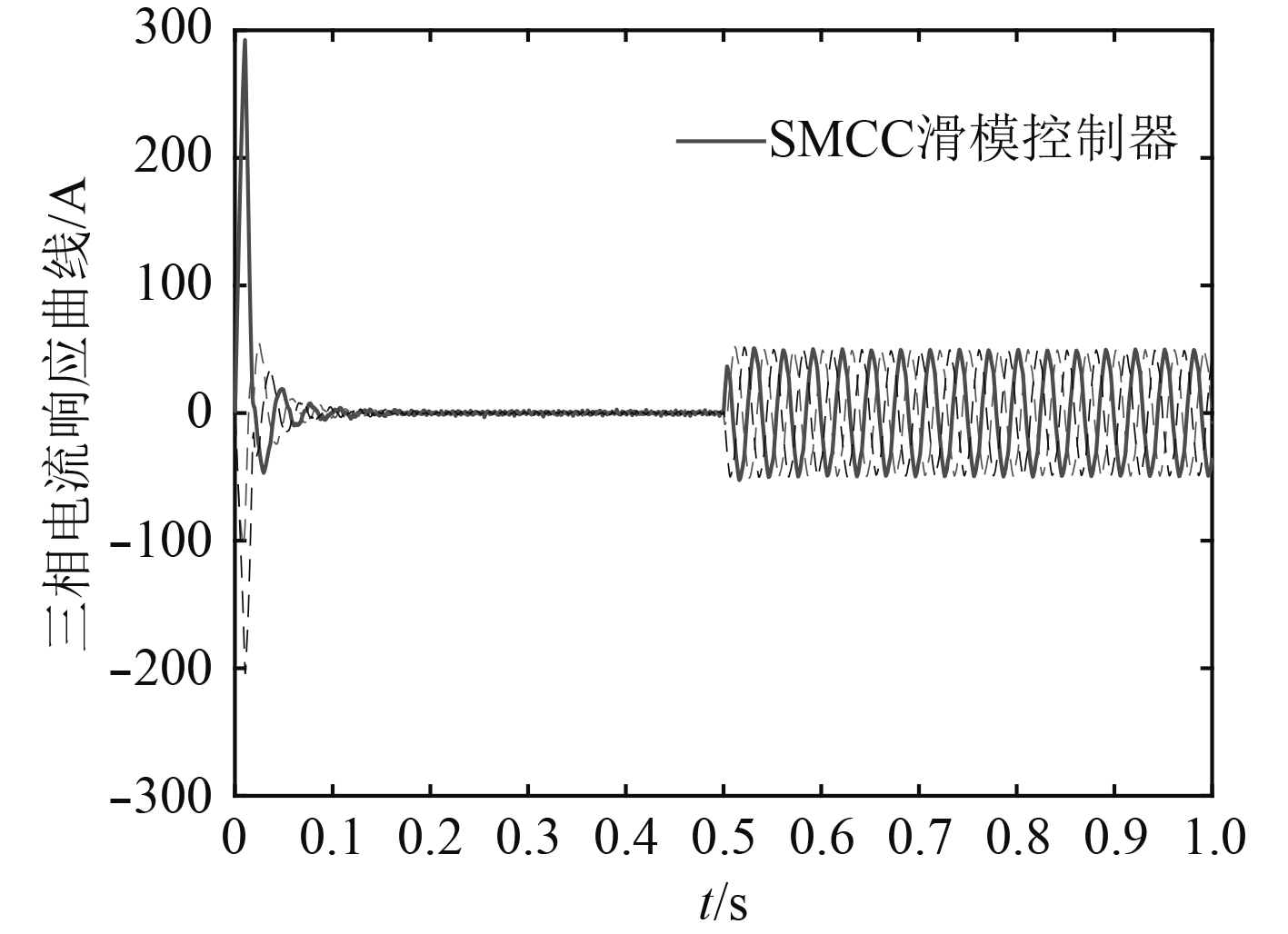
图 7 SMCC控制器下三相电流响应曲线 Fig. 7 Three phase current response curves under the SMCC controller |

|
图 8 常规PI控制器下三相电流响应曲线 Fig. 8 Three phase current response curves under the conventional PI controller |
图5转速响应曲线中武器站控制系统在速度环采用常规PI控制器时,启动阶段转速超调较大,转速最高到602 r/min,稳定时间为0.2 s。突加负载后,转速下降64 r/min,在0.66 s系统达到稳定状态。采用SMCC滑模控制器时,启动阶段控制系统基本无超调,转速稳定时间仅为0.15 s。0.5 s突加负载后,系统超调明显减少,转速仅下降12 r/min,稳定时间由0.16 s缩短为0.09 s。
图6转矩响应曲线可以明显看出,采用SMCC控制器时,系统突加负载时转矩基本无超调,且响应速度明显比采用常规PI控制器时快。
图7和图8中三相电流曲线比较可以看出,采用常规PI控制器时电流脉动较大,采用SMCC控制器时电流波形平滑,基本符合正弦曲线。
通过分析图5~图8,说明所设计的变指数趋近律滑模控制器响应速度快,抗干扰能力强,鲁棒性好。
上述模型基于采样周期和数据量限制,仿真时间有限,因此搭建基于遥控武器站数学模型的仿真系统,对SMCC速度控制器和常规PI速度控制器下的位置跟踪情况进行仿真,仿真结果如图9和图10所示。
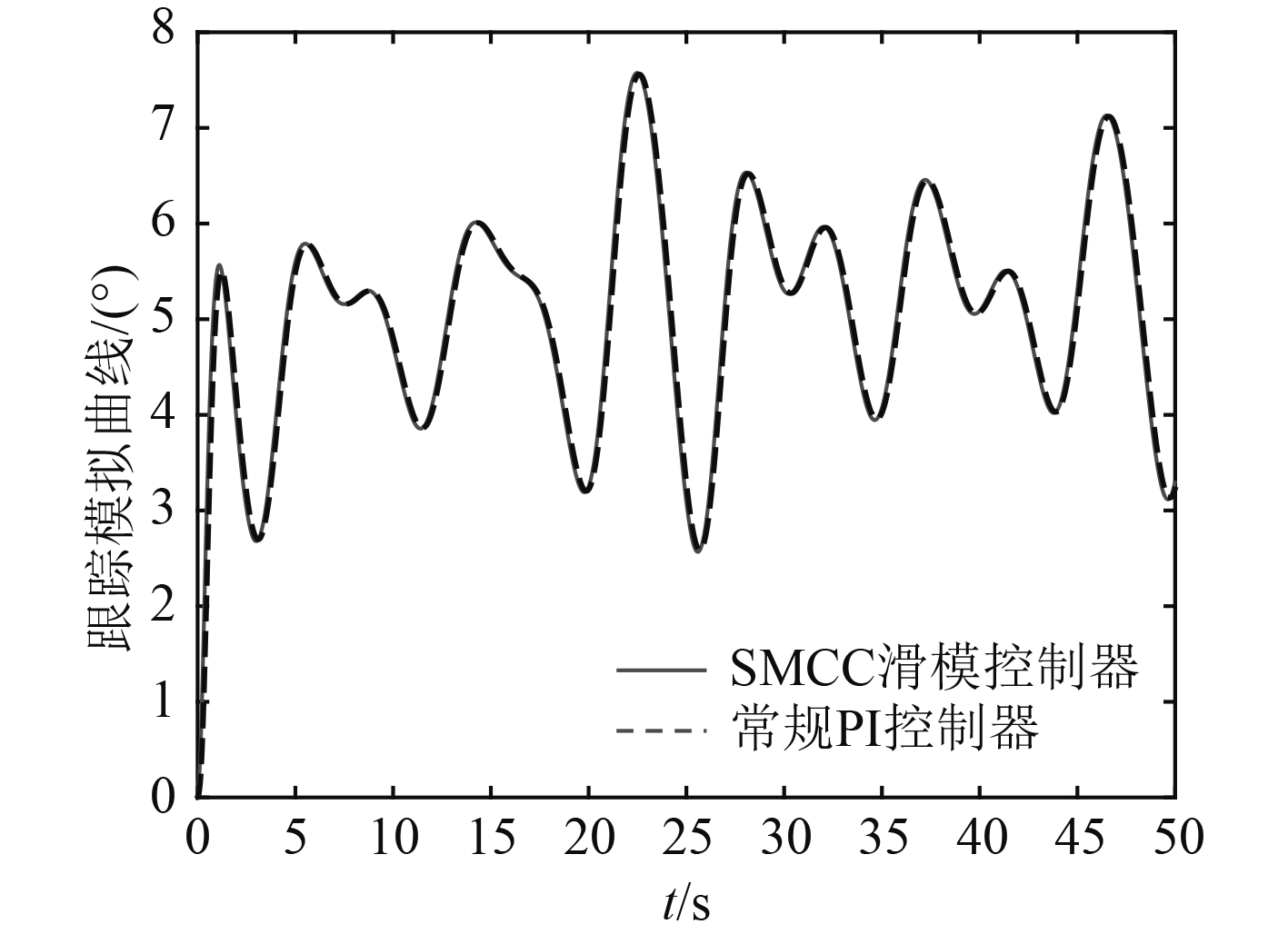
|
图 9 SMCC控制器下模拟跟踪曲线 Fig. 9 Analog tracking curve under the SMCC controller |

|
图 10 SMCC和普通PI控制跟踪误差比较曲线 Fig. 10 The comparison curves of tracking error between the SMCC and the conventional PI control |
从图9可以看出,采用SMCC控制器和常规PI控制器系统均能跟随模拟指令运动,但采用常规PI控制器相比SMCC控制器跟随时间相对滞后。从图10中可以看出,在伺服系统启动和换向阶段,采用普通PI控制的跟踪误差要远远大于SMCC控制下误差,前者的均方根植最大超过1.2°,而后者最大不超过0.5°。
通过以上仿真对比,可以看出,在矢量控制条件下,采用SMCC速度控制器的武器站控制系统具有更好的跟随性能和更强的抗扰动能力。
4 结 语针对舰载遥控武器站跟踪射击精度需求逐步提升的现状,在滑模变结构控制的基础上,兼顾减小滑模抖振,实现武器站控制系统的高精度控制,本文采用变指数趋近律,设计了变指数滑模控制器,与常规PI控制器进行对比,仿真结果表明采用所设计的控制器遥控武器站能够很好的跟随目标指令,且系统抗干扰能力强,鲁棒性好。本文设计的控制算法对舰载遥控武器站算法优化具有工程指导意义。
| [1] | 陈延伟, 李翔, 魏立新. 舰载遥控武器站发展探讨[J]. 舰船科学技术, 2010, 34(8): 3–6. http://mall.cnki.net/magazine/Article/JCKX201208013.htm |
| [2] | SUN Y, PREINDL M, SIROUSPOUR S, et al. Unified Wide-Speed Sensorless Scheme Using Nonlinear Optimization for IPMSM Drives[J]. IEEE Trans. Power Electron, 2017, 32(8): 6308–6322. |
| [3] | 张国强. 内置式永磁同步电机无位置传感器控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2017: 1–5. |
| [4] | 张伟. 基于开环光纤陀螺控制的无人作战平台稳定技术研究[J]. 国防科学技术大学博士学位论文, 2011: 50–64. http://wap.cnki.net/touch/web/Dissertation/Article/10217-2010075260.nh.html |
| [5] | 卢达, 赵光宙, 曲轶龙, 等. 永磁同步电机无参数整定自抗扰控制器[J]. 电工技术学报, 2013, 28(3): 27–34. http://www.cqvip.com/QK/94183X/201303/45148901.html |
| [6] | 崔家瑞, 高江峰, 张波, 等. 永磁同步电机滑模变结构鲁棒控制. 电机与控制学报, 2016, 20(5): 84–89. http://www.cqvip.com/QK/92879X/201208/43011075.html |
| [7] | 张晓铎. 双体船水翼电伺服控制系统设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 24–31. |
| [8] | 高键, 吴祥瑞. 基于滑模控制的船舶电力推进调速系统仿真[J]. 舰船科学技术, 2018, 40(1): 104–107. http://www.cqvip.com/QK/93337X/201504/664625170.html |
| [9] | 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2015. |
 2018, Vol. 40
2018, Vol. 40
