0 引　言

舰炮是装备在舰艇上用于对海作战、对空防御和对岸火力支援的重要武器之一。由于舰炮具有射速高、反应快、持续作战能力强、使用效费比高等优点，得到各国海军重视^[1]。随着未来海战的不断变化，舰炮面临着新的挑战和要求，不断推动着舰炮向着高精度、远射程的方向发展。舰炮伺服系统的控制精度直接影响着射击精度。同时，舰炮伺服系统是一个负载变化大、非线性因素多、扰动强的非线性系统，采用传统的PID控制算法难以实现高精度和强抗干扰性^[2]。

本文在分析舰炮伺服系统组成结构并对负载转矩进行分析的基础上，将线性自抗扰控制技术运用到位置控制器中，利用Matlab/Simulink对系统进行仿真，对比了PID，LADRC和Model-assisted LADRC控制算法的控制效果。

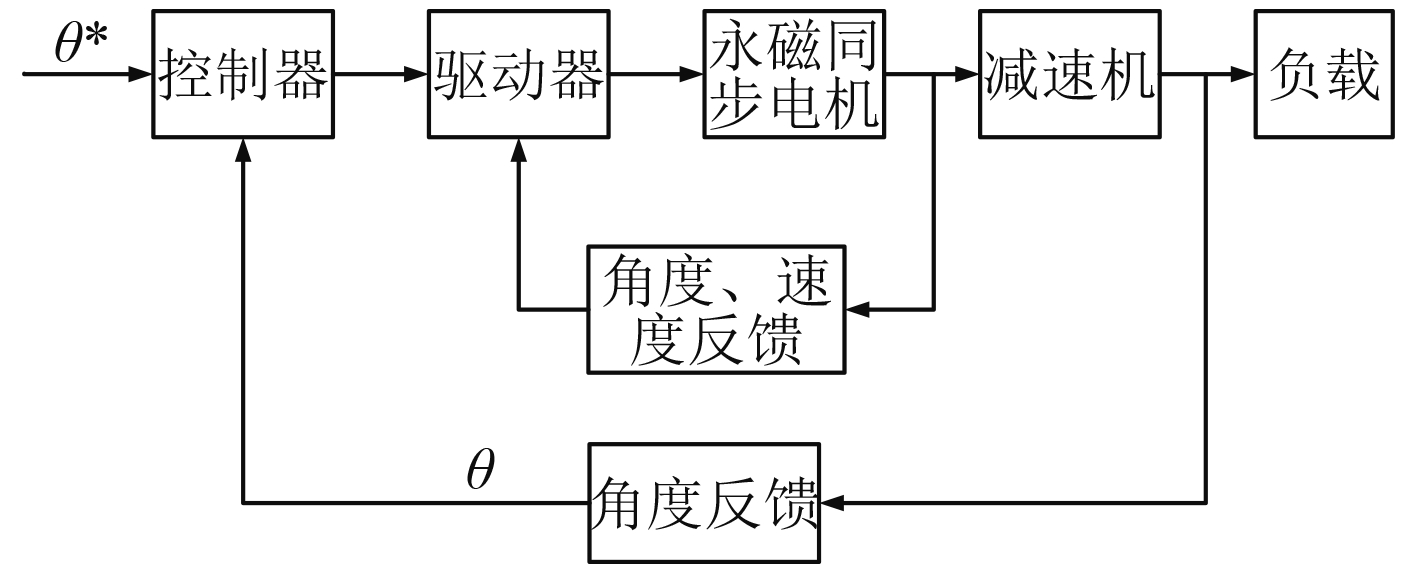
1 伺服系统建模 1.1 伺服系统组成

舰炮伺服控制系统由控制器、驱动器、三相永磁同步电机（PMSM）、减速机、反馈元件等设备组成。系统采用典型的三闭环控制结构。其中，电流环和速度环在驱动器内部实现，均选用PI控制器，本文将重点对位置环控制器进行设计。控制结构框图如图1所示。

1.2 永磁同步电机数学模型

采用矢量控制策略使i_d=0，在dq坐标系下建立永磁同步电机数学模型，其电压方程为：

$\left[ {\begin{array}{*{20}{c}} {{\!u_d\!\!\!}}\\ {{\!u_q\!\!\!}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_s}}\!\!\!\!\!\!\!&{ - {\omega _e}{L_q}}\!\! \\ {{\omega _e}{L_d}}\!\!\!\!\!\!\!\!\!&{{R_s}}\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\!i_d\!\!\!}}\\ {{\!i_q\!\!\!}}\end{array}} \right] + \frac{d}{{dt}}\left[ {\begin{array}{*{20}{c}} {{\!\psi _d\!\!\!}}\\ {{\!\psi _q\!\!\!}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0 \\ {{\!\!\omega _e}{\psi _f}} \!\!\!\end{array}} \right]\text{。}$

(1)

式中： ${u_d}$ ， ${u_q}$ 为dq轴电压； ${i_d}$ ， ${i_q}$ 为dq轴电流； ${L_d}$ ， ${L_q}$ 为dq轴电感； ${\psi _d}$ ， ${\psi _q}$ 为dq轴磁链； ${\omega _e}$ 为电角速度； ${\psi _f}$ 为转子磁链。

dq轴的磁链方程为：

$\left[ {\begin{array}{*{20}{c}} {{\psi _d}} \\ {{\psi _q}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{L_d}}&0 \\ 0&{{L_q}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}} \\ {{i_q}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\psi _f}} \\ 0 \end{array}} \right]\text{，}$

(2)

控制 ${i_d}{\rm{ = }}0$ ，那么电磁转矩：

${T_e} = {n_p}{\psi _f}{i_q}\text{，}$

(3)

在电机带动负载运动过程中有：

${T_e} - {T_L} = J\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}\text{。}$

(4)

1.3 负载分析

本文主要对水平方向的负载转矩进行分析，永磁同步电机通过减速机连接负载，运动过程中需要克服的力矩有：方向座圈的摩擦力矩、射击作用产生的附加阻力矩和惯性力矩。

1）方向座圈的摩擦力矩

$ {M_{F1}} = {f_k}G\frac{{{D_1}}}{{{d_1}}} \text{，}$

(5)

式中： ${f_k}$ 为耳轴摩擦系数； $G$ 为座圈承受的重力； ${D_1}$ 为滚道直径； ${d_1}$ 为滚珠直径。

2）后坐力附加的阻力矩

因为射击角度不同，后坐力对座圈的作用方向不同，不考虑水平分力和倾覆力矩对座圈的影响。

$ {M_{F2}} = {f_k}{P_{KH}}\sin \theta \frac{{{D_1}}}{{{d_1}}} \text{，}$

(6)

式中 ${P_{KH}}$ 为后坐力。

3）惯性力矩

$ {M_{F3}} = {J_F}\varepsilon \text{，}$

(7)

式中： ${J_F}$ 为转动惯量； $\varepsilon $ 为角加速度。

运动射击过程中需要克服的总负载力矩

$ {M_F} = {M_{F1}} + {M_{F2}} + {M_{F3}} \text{，}$

(8)

折算到电机轴总负载力矩

$ {M_{FD}} = \frac{{{M_F}}}{{i\eta }} \text{。}$

(9)

式中： $i$ 为减速比； $\eta $ 为传动效率。

从式（5）~式（7）可以看出，负载转矩在射击和运动过程中不断变化，这一变化可以看成是外界干扰。

2 模型辅助线性自抗扰控制器设计

自抗扰控制（ADRC）应用现代控制理论状态观测的原理，对系统的扰动情况进行观测和补偿，具有较强的鲁棒性^[3-4]。自抗扰控制技术已在伺服系统控制、飞行器控制及过程控制等领域中得到了很好的应用^{[5 – 7]}。文献[8]为提高火炮伺服系统的抗干扰性，采用ADRC对系统进行控制仿真，取得了较好控制效果。同时也发现其参数整定复杂，不利用工程应用。为使自抗扰技术得到更好的工程化应用，高志强提出了线性自抗扰控制（LADRC），减少了控制参数，简化了参数整定过程^[9]。

舰炮伺服系统中面临的主要干扰包括摩擦力矩、射击附加力矩等。为提高系统的控制性能所设计的线性自抗扰控制器结构，如图2所示。

系统可简化为1个二阶系统，

$ \ddot y = - {a_1}\dot y - {a_0}y + w + bu = f + {b_0}u \text{。}$

(10)

式中：y，u分别为系统输出和输入； ${a_1},{a_2}$ 可以从模型中得到，并按仿真结果进行调整；w为扰动；f为总扰动；b₀为已知部分。

令 $ {{x}} = {[y{\rm{ \dot y }}f]^{\rm{T}}} $ ，式（10）转化为扩张状态空间形式：

$ \left\{ \begin{array}{l}\dot {\boldsymbol{x}} = {{Ax}} + {{B}}u + {{E}}\dot f\text{，}\\y = {{Cx}}\text{，}\end{array} \right. $

(11)

式中：

$ \begin{gathered} {{A}} = \left[ {\begin{array}{*{20}{c}} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & { - {a_0}} & { - {a_1}} \end{array}} \right],\,\,\,\,{{B}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{b_0}} \\ { - {a_1}{b_0}} \end{array}} \right], \hfill \\ {{E}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right],\,\,\,\,{{C}} = \left[ {\begin{array}{*{20}{c}} {1} & 0 & {0} \end{array}} \right] \text{。}\end{gathered}$

构造模型辅助线性扩张状态观测器（LESO）为：

$ \left\{ \begin{array}{l}\dot {\boldsymbol{z}} = {{Az}} + {{B}}u + {{L}}\left( {y - \hat y} \right)\text{，}\\\hat y = {{Cz}}\text{。}\end{array} \right. $

(12)

把特征方程的极点放在同一位置（ $ - {\omega _0}$ ）上，取观测器的增益矩阵为：

${{L}} = {\left[ {\begin{array}{*{20}{c}} {{l_1}}&{{l_2}}&{{l_3}} \end{array}} \right]^{\rm{T}}}\text{。}$

(13)

式中： $ {l_1} = 3{w_0} - {a_1}\text{；} {l_2} = 3{w_0}^2 - 3{a_1}{w_0} - {a_0} + {a_1}^2 \text{；}{l_1} = $ $ {w_0}^3 - 3{a_1}{w_0}^2 + 3({a_1}^2 - {a_0}){w_0} + 2{a_0}{a_1} - {a_1}^3 {\text{。}}$

使得：

$\lambda \left( s \right) = \left| {s{{I}} - \left( {{{A}} - {{LC}}} \right)} \right| = {\left( {s + {\omega _0}} \right)^3}\text{，}$

(14)

式中： ${\omega _0}$ 为观测器带宽。

将线性状态误差反馈控制率（LSEF）设计为PD组合。

${u_0} = {k_p}\left( {r - {z_1}} \right) - {k_d}{z_2}\text{，}$

(15)

式中： $r$ 为给定值； ${z_1}$ 和 ${z_2}$ 为来自LESO的观测器状态； ${k_p}$ ， ${k_d}$ 分别为比例和微分系数。

根据线性自抗扰的参数整定方法^[10]，确定比例和微分系数：

${k_p} = {\omega _c}^2,{k_d} = 2{\omega _c}\text{。}$

(16)

式中： ${\omega _c}$ 为控制器带宽。

经过反复调试发现，当 ${\omega _0} = {\omega _c}$ 时，控制效果比较理想。

3 伺服系统仿真及结果分析

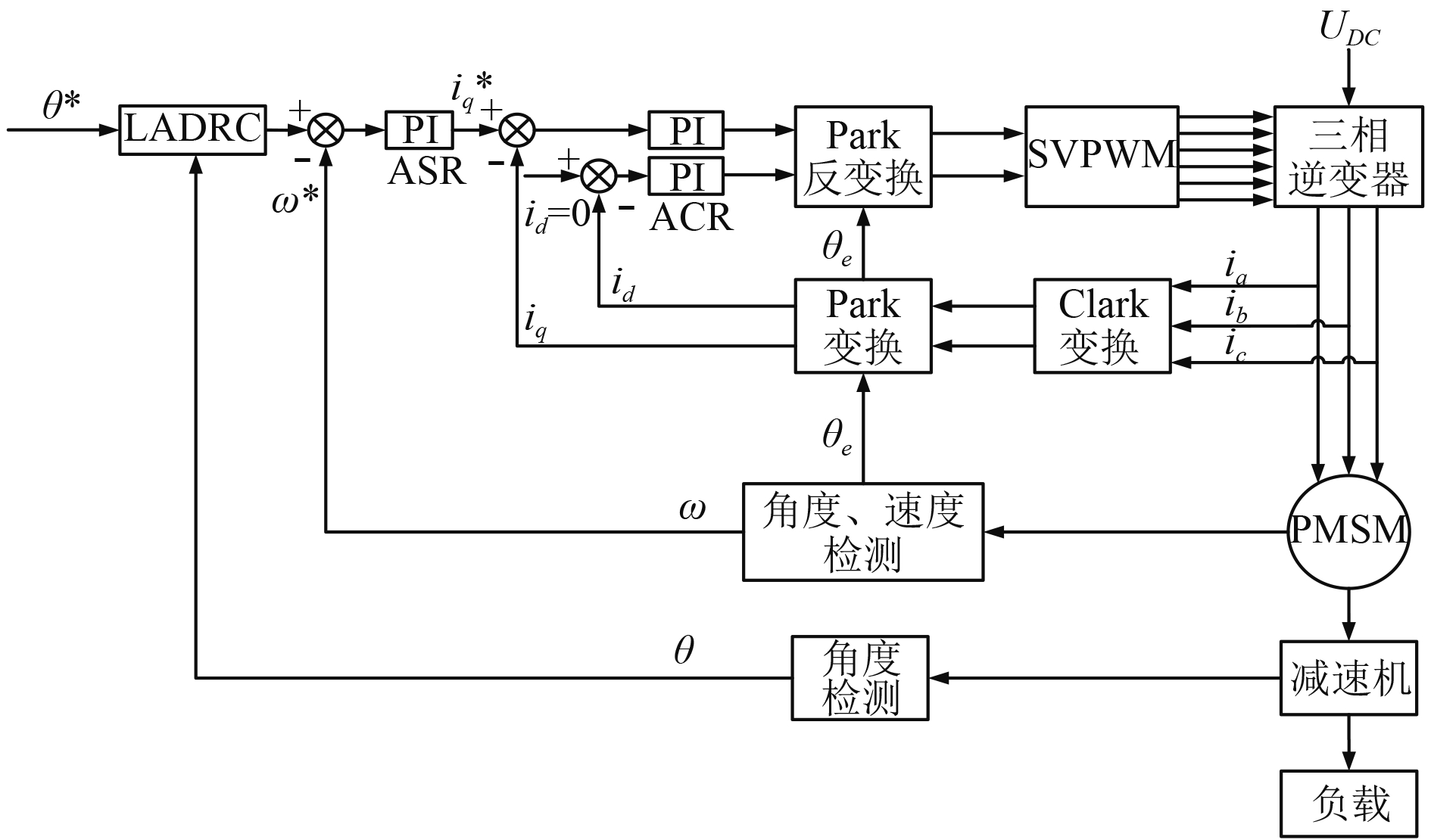
本文利用Matlab/Simulink对舰炮伺服系统进行仿真，仿真系统如图3所示。

仿真中选取电机的仿真参数为：永磁同步电机额定转矩 ${T_e} = 35$ N·m，额定转速 $N $ =3 000 r/min，定子电阻 $R = 0.06\;\;\Omega $ ，交轴、直轴 ${L_d} = {L_q} = 0.52$ mH，转子转动惯量 $J = $ 0.002 2 kg·cm²，极对数 $p = 4$ 。

阶跃调炮30°，由图4可知，采用PID算法的调节时间为0.65 s；采用LADRC的调节时间为0.48 s；而采用Model-assisted LADRC控制，系统的调节时间为0.45 s响应时间短，且超调最小。

系统稳定状态下，根据1.3节中负载转矩的分析，突加转矩扰动。如图5所示，在PID控制下舰炮水平角度有明显波动，角度最大误差为0.023°，恢复时间为0.25 s；在LADRC控制下，角度最大误差为0.003°，恢复时间为0.1 s；在Model-assisted LADRC控制下，角度最大误差为0.002°，恢复时间为0.07 s，控制效果最优。

4 结　语

本文在分析负载转矩的基础上，利用模型辅助线性扩张状态观测器对系统总扰动进行观测，并进行了补偿。通过仿真试验，对比了PID，LADRC和Model-assisted LADRC的控制效果。试验结果表明Model-assisted LADRC使系统具有更强的抗干扰性能和动态性能，且参数调节简单。