舰船配置系留索具及系留座用于为保障舰载直升机在飞行甲板的安全停放。由于舰船一般保障不止一型直升机,为提高通用性,飞行甲板系留座一般采用矩阵式。传统设计矩阵式系留座时,一般根据经验,考虑船体结构初步确定系留座间距,根据搭载的直升机需求多次调整矩阵式系留座布置并开展强度评估,直至满足所有直升机系留强度要求。由于系留座的微小变化都可能导致所有索具承载的重新分布,且很难预知系留座位置对系留载荷的影响规律,只能估计大致的调整方向,因此传统设计方法工作繁复、计算量大且难以得出理想的结果。
针对矩阵式系留座优化问题,王丹[1]使用有限元软件Ansys实现了直升机系留载荷的求解,并使用Ansys的优化设计功能对甲板系留座位置进行优化;李书[2]利用遗传算法对舰载直升机的系留点进行优化,确定了最佳系留布局形式;吴靖[3]采用包括局部搜索、全局搜索以及信息素更新的蚁群算法对舰载直升机停放时的系留座进行优选。前述研究多是针对一型舰载直升机的矩阵式系留开展优化,对于搭载两型舰载直升机的水面舰船,不同型号的直升机系留方式存在差异性,矩阵式系留座需要兼顾不同机型的需求,其优化设计鲜有涉及。
作为近年来快速发展的一种群体智能算法,粒子群优化算法(PSO)模拟鸟群,可用于求解映射关系复杂、目标函数梯度信息未知的单目标和多目标优化问题[4 – 6],因此本文针对两型舰载直升机矩阵式系留座优化,以索具载荷极值为目标函数,采用双目标模糊优化策略[7],考虑索具长度约束和索具许用载荷约束,提出了矩阵式系留座优化模型,使用粒子群算法进行寻优。最后通过保障两型舰载直升机的某型舰矩阵式系留座优化仿真算例,验证了该模型可行性和优化效果。
1 舰载直升机矩阵式系留座优化模型 1.1 目标函数对于系留于飞行甲板的舰载直升机,受到的外力包括:
1)重力。作用在机体重心,竖直向下。
2)风力。作用在形心处,设定为正侧方来风,方向为水平。
3)惯性力。作用在机体重心,沿3个座标轴方向分别为
由于直升机一般使用多根系留索具,对于此类超静定问题,其系留载荷可采用虚功原理求解。假定舰载直升机相对舰船甲板产生一刚体位移,此位移可视为仅含
| $\Delta T = EA\left(\frac{{\Delta L}}{{{L_0}}}\right)\text{,}$ | (1) |
其中:
此外,还需要根据虚功原理列出协调方程,假设
| $\frac{{\partial (U - W)}}{{\partial u}} = \frac{{\partial (U - W)}}{{\partial v}} = \frac{{\partial (U - W)}}{{\partial {\theta _z}}} = 0\text{,}$ | (2) |
由上述数学模型即可得到给定海况条件下相应系留方案下各索具的张力。
本文以所有系留索具载荷极大值为目标函数,其优化即找到一种矩阵式系留座布置,使得该布置下舰载直升机系留索具载荷极大值最小。实际的舰载直升机系留基于标准系留方案的甲板系留点,寻得最近可用的系留座得到。对于两型直升机,其目标函数为2个:
| $\left\{ {\begin{array}{*{20}{c}} {{f_1}({d_x},{d_y}) = \max ({T_{1i}}),i = 1,2,...{J_1}} \text{,} {{f_2}({d_x},{d_y}) = \max ({T_{2i}}),i = 1,2,...{J_2}} \text{。}\end{array}} \right.$ | (3) |
其中:
| $\left\{ {\begin{array}{*{20}{c}} {{f_1}({d_x}) = \max ({T_{1i}})}\text{,} {{f_2}({d_x}) = \max ({T_{2i}})} \text{。}\end{array}} \right.$ | (4) |
约束条件包括系留索具长度约束以及机身系留点的许用载荷约束。
| $\left\{\!\!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{l_{1i}} - {L_{1\max }} \leqslant 0,i = 1,2,...,{J_1}}\text{,} \\ {\begin{array}{*{20}{c}} {{T_{1i}} - {T_{1\max }} \leqslant 0,i = 1,2,...,{J_1}}\text{,} \\ {{l_{2i}} - {L_{2\max }} \leqslant 0,i = 1,2,...,{J_2}}\text{,} \end{array}} \end{array}} \\ {{T_{2i}} - {T_{2\max }} \leqslant 0,i = 1,2,...,{J_2}} \text{。}\end{array}} \right.$ | (5) |
其中:
对于矩阵式系留座,以某一型直升机系留载荷极值作为目标函数势必导致无法顾及另一型机的系留载荷,很难使得2个目标函数同时取得最优。本文兼顾两型直升机系留载荷,采用模糊策略处理双目标优化问题,主要步骤如下:
1)以A型舰载直升机的所有索具的系留载荷极值
2)以B型舰载直升机所有索具的系留载荷极值
3)进行双目标函数模糊化处理,建立单目标函数值到其隶属度函数的映射。假定隶属度函数按照线性规则确定,则隶属度函数为:
| $\eta ({f_i}) = \left\{ {\begin{array}{*{20}{c}} 1\text{,} {\displaystyle\frac{{{F_{iM}} - {f_i}}}{{{F_{iM}} - {F_{im}}}}}\text{,} 0\text{,} \end{array}} \right. \begin{array}{*{20}{c}} \!{{f_i} \leqslant {F_{im}}}\text{,}\qquad\qquad {{F_{im}} \leqslant {f_i} \leqslant {F_{iM}}}\text{,} \!{{f_i} \geqslant {F_{iM}}}\text{。}\qquad\qquad\end{array}$ | (6) |
式中,
4)综合2个目标函数隶属度:
| $F = \min (\eta ({f_1}),\eta ({f_2}))\text{。}$ | (7) |
本文优化目标取为
粒子群优化算法(PSO)优化过程如下:设计变量维数为D,群规模为N,粒子群算法设定N个粒子组成一个群体,每个粒子代表设计变量空间的一个解,第
| $\begin{gathered} {V_i}^{k + 1} = w \times {V_i}^k + {c_1} \times {r_1} \times ({({p_{best}})_i}^k - {X_i}^k)+ \\ \qquad \quad {c_2} \times {r_2} \times ({({g_{best}})^k} - {X_i}^k)\text{,} \hfill \\ \end{gathered}$ | (8) |
| ${X_i}^{k + 1} = {X_i}^k + {V_i}^{k + 1}\text{,}$ | (9) |
| $\omega = 0.9 - (0.9 - 0.4) \times k/Nummax \text{。}$ | (10) |
式中:
对优化模型中的约束采用罚函数处理,当设计变量的取值违反约束条件时,目标函数将增加一个惩罚项,以此保证粒子在可行域内寻优。
3 算例分析 3.1 舰载直升机参数某舰飞行甲板纵骨的横向间距为0.8 m,即
某A型和B型舰载直升机系留停放时旋翼中心与着舰圈中心重合,机体轴线与舰船轴线平行,舰载直升机在飞行甲板停放如图1所示。

|
图 1 舰船飞行甲板舰载直升机停放示意图 Fig. 1 Shipboard helicopter parking on the flight deck |
根据相关标准,中等海况下舰载直升机应能在飞行甲板安全系留,两型舰载直升机飞行甲板标准系留均采用8根索具方案,索具关于机身轴线对称,单个机身系留点前后2根索具也对称。给定矩阵式系留座布置后,根据直升机标准系留方案就近选择甲板系留座。
两型舰载直升机数据如表1所示。使用表1数据可求得给定甲板系留点下的两型机各索具的系留载荷。
|
|
表 1 两型舰载直升机计算数据 Tab.1 The parameters of the two helicopters |
基于双目标模糊优化的粒子群计算流程如图2所示。
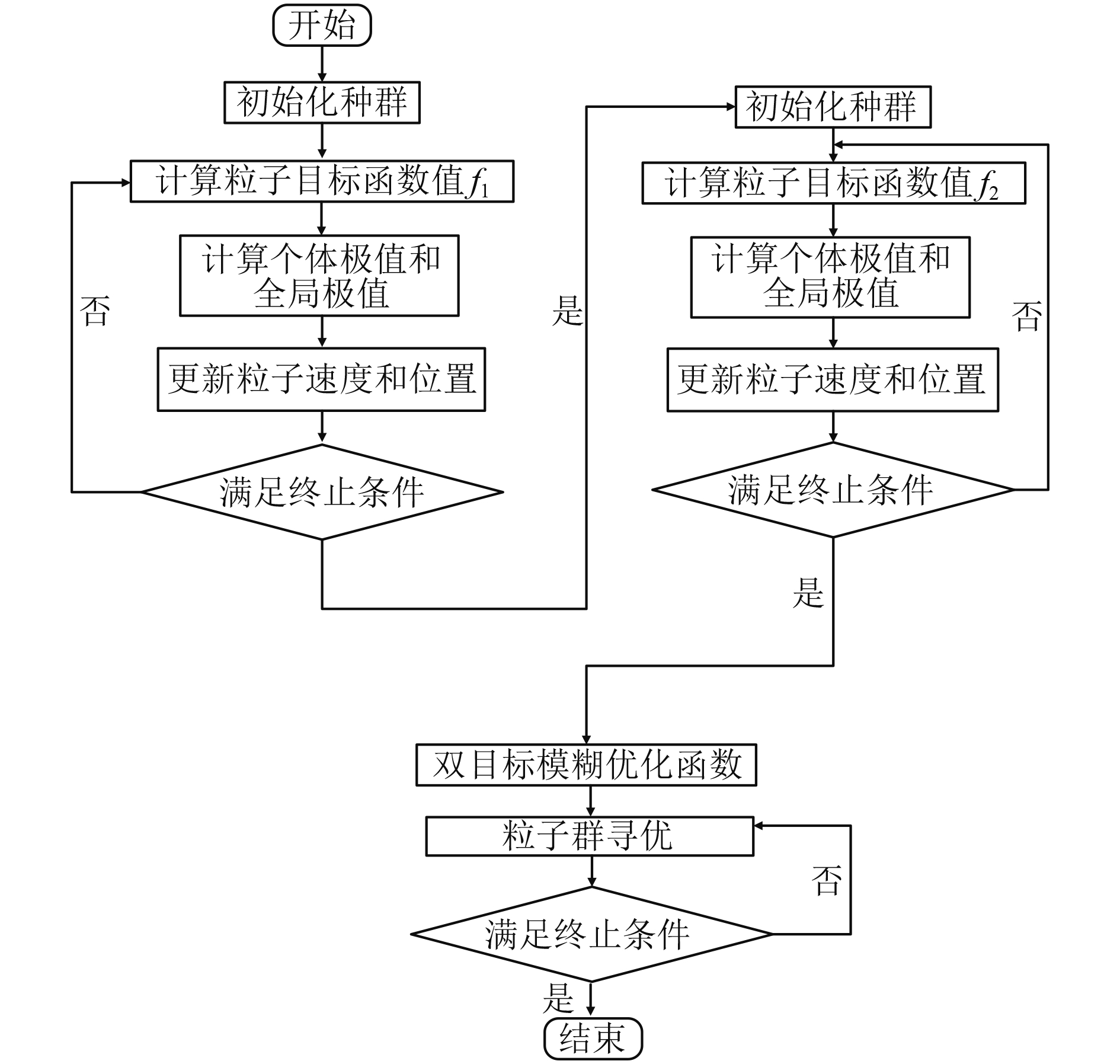
|
图 2 系留载荷粒子群优化流程图 Fig. 2 The PSO flow chart of the tie-down loads |
粒子群优化算法中种群规模取为20,最大迭代次数取100,使用上述流程对式(8)建立的双目标模糊优化后的目标函数进行寻优。
以
单目标函数

|
图 3
目标函数
|
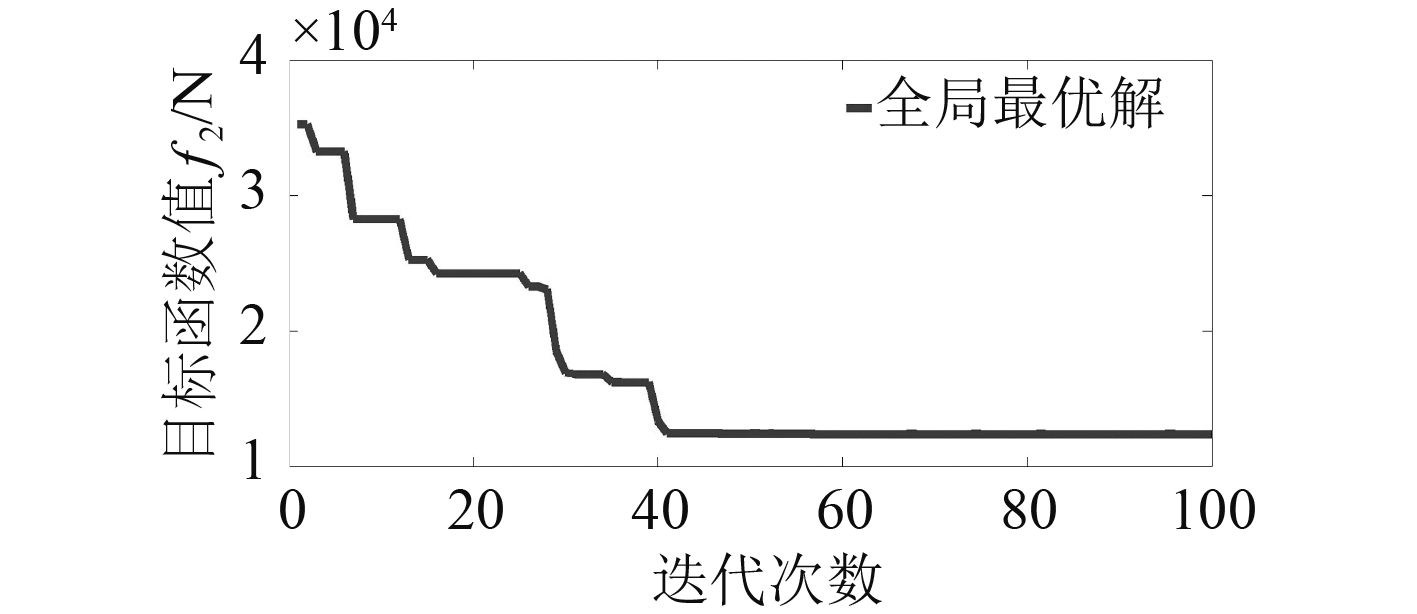
|
图 4
目标函数
|

|
图 5
双目标模糊函数
|
随迭代次数增加,种群中的粒子在惯性、全局最优以及个体最优的共同影响下,不断调整位置,直至收敛至全局最优解。粒子群算法迭代至40次左右即收敛至最优解。不同优化方法下两型舰载直升机各索具的优化结果如表2所示。
|
|
表 2 不同优化方法下索具的系留载荷对比 Tab.2 The contrast of the tie-down loads achieved by different optimal methods |
由表2可见,不同的目标函数优化对应的舰载直升机系留方案不同,甲板系留点的改变导致了索具载荷的重新分布,在不同目标函数优化方法的条件下载荷极值对应的索具编号也不同。
单目标函数
对于搭载两型舰载直升机的舰船,为保障两型机系统通用性及降低系留载荷水平,需优化矩阵式系留座设计。本文采用了索具长度约束及许用载荷约束,同时考虑两型机系留强度,提出了双目标模糊优化目标函数,建立了矩阵式系留座优化模型,基于粒子群算法开展了寻优。算例结果表明,相较于单目标函数优化,本文提出的模型能有效兼顾两型舰载直升机系留载荷的降低。
本文对兼容两型舰载直升机的通用矩阵式系留座的优化设计进行了探索,而现代舰船的航空保障能力发展迅速,兼容的舰载直升机型号越来越多,后续需要对兼容多型舰载直升机的甲板系留座多目标优化设计方法进一步研究。
| [1] | 王丹. 舰载直升机系留载荷分析及优化设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2008. |
| [2] | 李书, 何忠恒, 徐丽娜. 舰载直升机系留座的布置优化[J]. 航空学报, 2005, 26(6): 715–719. http://mall.cnki.net/magazine/Article/HKXB200506011.htm |
| [3] | 吴靖, 胡国才. 基于蚁群算法的直升机舰面系留座优选[J]. 计算机仿真, 2015, 32(7): 357–360. |
| [4] | KENNEDY J, EBERHART R. Particle swarm optimization[C]// In Proceeding of IEEE International Conference on Neural Networks, Washington, 1995:1942–1948. |
| [5] | K.E. PARSOPOULOS, M.N. VRAHATIS. Paricale swarm optimization method in multiobjective problems[C]// In Proceeding of the 2002 ACM symposium on Applied computing, 2002: 603–607. |
| [6] | KENNEDY J. Small worlds and mega-minds: effect of neighborhood topology on particle swarm performance[C]// IEEE Congress on Evolutionary Computation, 1999:1931–1938. |
| [7] | 黄梅, 王一依, 张彩萍, 马伟强, 安动. 充换电储能系统模糊双目标优化调度方法. 北京交通大学学报. 2014, 38(5): 97–102. |
 2018, Vol. 40
2018, Vol. 40
