舰船腐蚀相关静电场(由电化学腐蚀电流和防腐电流产生)是舰船目标的重要暴露源[1 – 3]。在舰艇主要电场源材料之间的采用电隔离措施是减小腐蚀相关静电场的重要方法之一[4],而采用电隔离措施方法的关键技术是根据允许的最大目标电场值估算出最小隔离电阻的大小。考虑到舰船腐蚀静电场可视为若干点电荷的叠加,点电荷的位置、强度与异种金属的位置、面积、材料的电极电位、回路内组(电隔离电阻)等参数密切相关[5],若能利用电路模型建立点电荷强度、回路内阻和水下电位的关系,即有望解决在已知目标电位条件下估算出电隔离电阻值。
1 舰船腐蚀相关静态电场不同金属在同种电解液中,其稳定电极电位不同,因此,当使用金属导线将其连接时,就形成闭合直流电路(电解偶电路),从而在回路中产生电流,使金属和电解液之间的电位差发生变化——这种现象称为电化学极化[6]。船体—螺旋桨构成的电解偶等效电路图如图1所示。
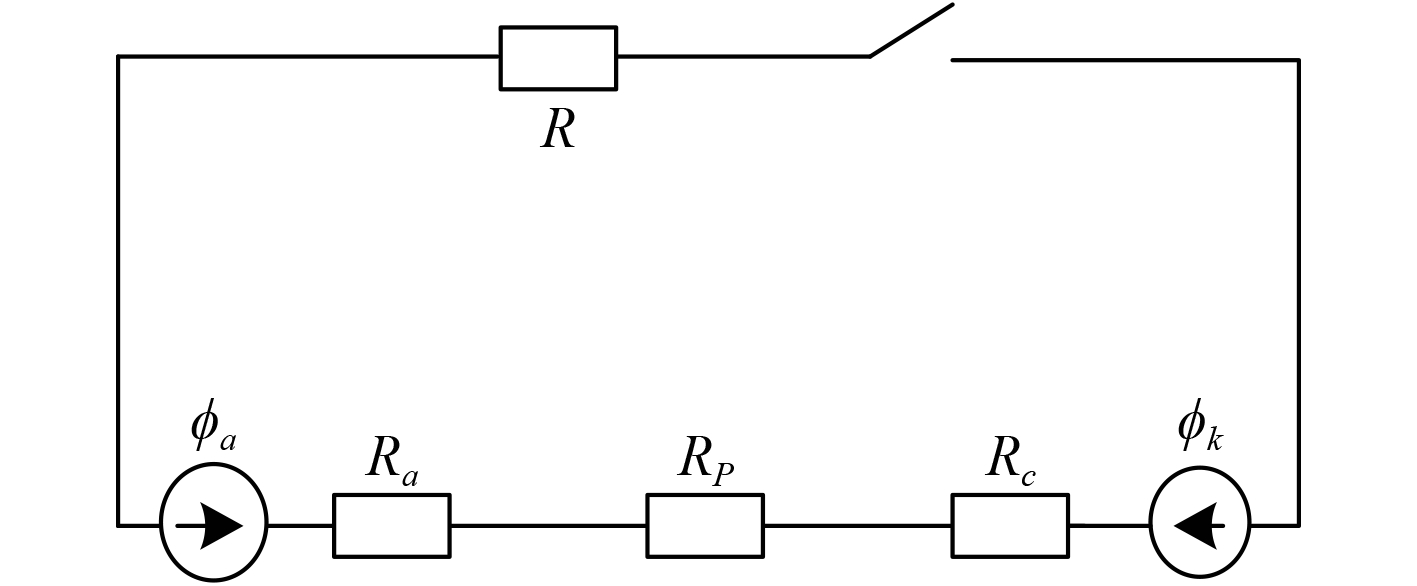
|
图 1 船体—螺旋桨构成的电解偶等效电路图 Fig. 1 Electrolytic pair equivalent circuit of hull and shaft |
图1中,
| $I = \frac{{{\varphi _a} - {\varphi _c}}}{{{R_p} + R + {R_a} + {R_c}}}\text{,}$ | (1) |
| ${R_a} = \frac{{{\beta _a} + {\rho _a}}}{{{S_a}}}\text{,}$ | (2) |
| ${R_c} = \frac{{{\beta _c} + {\rho _c}}}{{{S_c}}}\text{。}$ | (3) |
式中:
若假定舰船下方某一深度
对于非绝缘船体组成的电化学系统,“船体—螺旋桨”构成的电解偶电路是主要的腐蚀电场源。若将舰船和螺旋桨等效为半球状点电极,则式(1)中的海水电阻为
| $\begin{split} {R_p} = \frac{1}{{2\pi \sigma {a_a}}} + \frac{1}{{2\pi \sigma {a_c}}} + \frac{1}{{2\pi \sigma l}} \approx \\ \frac{1}{{2\pi \sigma {a_a}}} + \frac{1}{{2\pi \sigma {a_c}}} \text{,} \\ \end{split}$ | (4) |
式中:
由式(1)~式(4)可得“船体—螺旋桨”电解偶回路中的电流为:
| $I \approx \frac{{{\varphi _a} - {\varphi _c}}}{{\frac{{{\beta _a} + {\rho _a}}}{{{S_a}}} + \frac{{{\beta _c} + {\rho _c}}}{{{S_c}}} + \frac{1}{{2\pi \sigma {a_a}}} + \frac{1}{{2\pi \sigma {a_c}}} + R}}\text{。}$ | (5) |
由点电极的电位计算公式可知,船体和螺旋桨的正下方
| ${U_a} \approx \frac{I}{{2\pi \sigma \left( {{a_a} + d} \right)}}\text{,}$ | (6) |
| ${U_c} \approx \frac{{ - I}}{{2\pi \sigma \left( {{a_c} + d} \right)}}\text{,}$ | (7) |
即舰船下方某一深度
| $\left| {{U_a} - {U_c}} \right| \approx \left| {\frac{I}{{2\pi \sigma \left( {{a_a} + d} \right)}} + \frac{I}{{2\pi \sigma \left( {{a_c} + d} \right)}}} \right|\text{,}$ | (8) |
将式(5)代入式(8)中,并要求
| $\begin{split} R \geqslant \frac{{\left| {{\varphi _a} - {\varphi _c}} \right|}}{{\Delta {U_{\max }}}}\left[ {\frac{1}{{2\pi \sigma \left( {{a_a} + d} \right)}} + \frac{1}{{2\pi \sigma \left( {{a_c} + d} \right)}}} \right] - \\ \left[ {\frac{{{\beta _a} + {\rho _a}}}{{{S_a}}} + \frac{{{\beta _c} + {\rho _c}}}{{{S_c}}} + \frac{1}{{2\pi \sigma {a_a}}} + \frac{1}{{2\pi \sigma {a_c}}}} \right]\text{。} \\ \end{split} $ | (9) |
对于船体材料为玻璃钢或者覆绝缘层的船体,当其表面包含有多种金属时,由于金属材料的正下方具有电位的局部峰值点,若保证每种金属材料正下方
假设
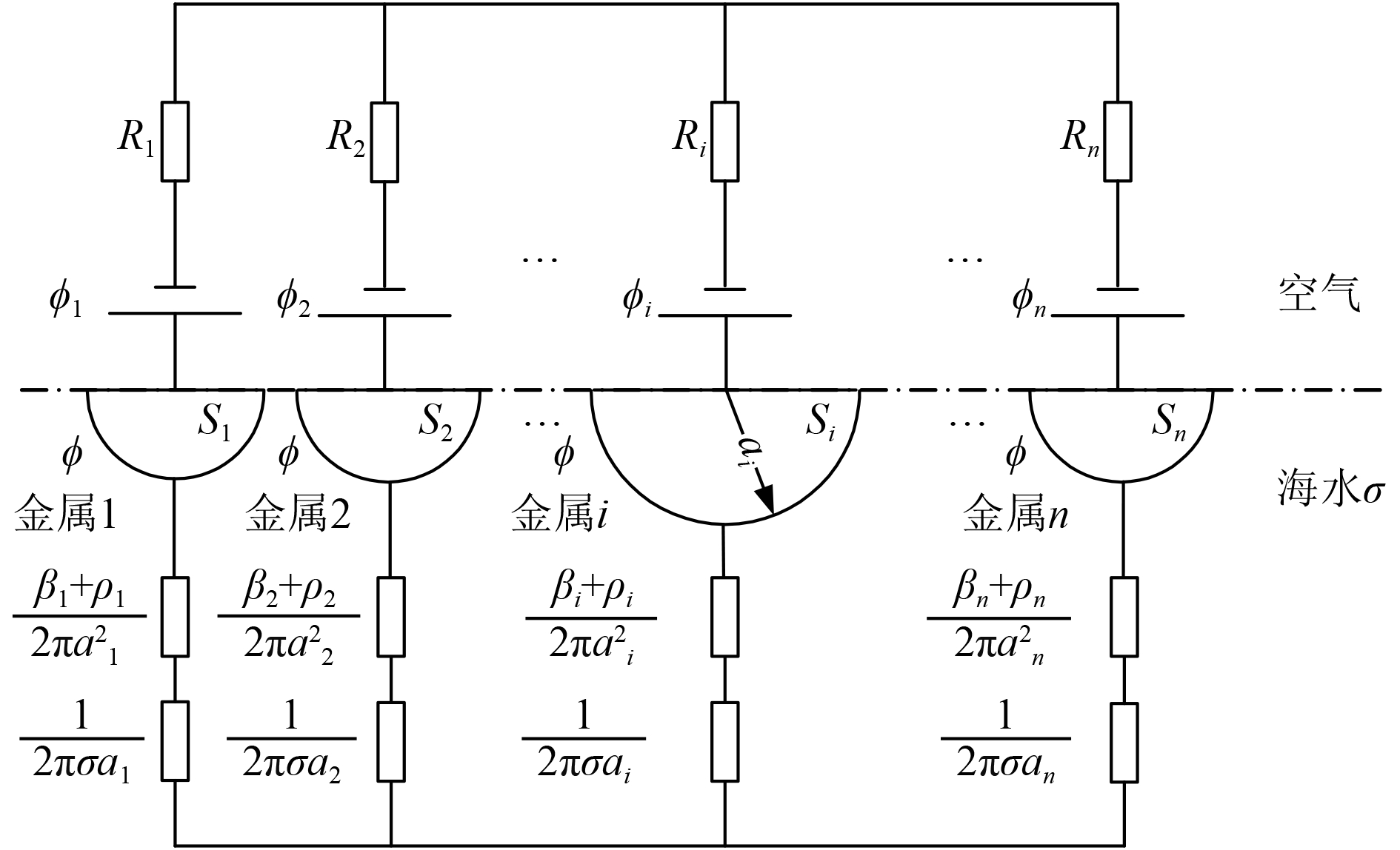
|
图 2
|
若
| ${I_i} = \frac{{\varphi - {\varphi _i}}}{{{r_i} + {R_i} + \frac{1}{{2\pi \sigma {a_i}}}}} = \frac{{\varphi - {\varphi _i}}}{{\frac{{{\beta _i} + {\rho _i}}}{{2\pi {a_i}}} + \frac{1}{{2\pi \sigma {a_i}}} + {R_i}}}\text{。}$ | (10) |
式中:
根据点电荷的电位计算公式,得到电极
| ${U_i} \approx \frac{{{I_i}}}{{2\pi \sigma \left( {{a_i} + d} \right)}}\text{,}$ | (11) |
根据
| ${R_i} \geqslant \frac{{\left| {\varphi - {\varphi _i}} \right|}}{{\Delta {U_{\max }}\pi \sigma \left( {{a_i} + d} \right)}} - \left[ {\frac{{{\beta _i} + {\rho _i}}}{{2\pi a_i^2}} + \frac{1}{{2\pi \sigma {a_i}}}} \right]\text{。}$ | (12) |
由式(12)可知,求解隔离电阻的关键是计算混合电位值
| $\begin{aligned}\frac{{{\varphi _1} {\!}-{\!} \varphi }}{{{R_{a1}}}} {\!}+{\!} \frac{{{\varphi _2} {\!}-{\!} \varphi }}{{{R_{a2}}}} {\!}+{\!} \cdots {\!}+{\!} \frac{{{\varphi _p} {\!}-{\!} \varphi }}{{{R_{ap}}}} {\!}= \\\frac{{\varphi {\!}-{\!} {\varphi _1}}}{{{R_{c1}}}} {\!}+{\!} \frac{{\varphi {\!}-{\!} {\varphi _2}}}{{{R_{c2}}}} {\!}+{\!} \cdots {\!}+{\!} \frac{{\varphi {\!}-{\!} {\varphi _q}}}{{{R_{cq}}}}\text{,}\end{aligned}$ | (13) |
式中:
| $\left\{ \begin{gathered} {R_{ai}} = \frac{1}{{2\pi {a_i}\sigma }} + \frac{{{b_{ai}} + {\rho _i}}}{{{S_i}}}\text{,} \\ {R_{cj}} = \frac{1}{{2\pi {a_j}\sigma }} + \frac{{{b_{cj}} + {\rho _j}}}{{{S_j}}}\text{。} \\ \end{gathered} \right.$ | (14) |
式中,
式(6)亦等价于
| $\left( {\sum\limits_{i = 1}^p {\frac{1}{{{R_{ai}}}} + \sum\limits_{j = p + 1}^n {\frac{1}{{{R_{ci}}}}} } } \right)\varphi = \sum\limits_{i = 1}^p {\frac{{{\varphi _i}}}{{{R_{ai}}}} + \sum\limits_{j = p + 1}^n {\frac{{{\varphi _j}}}{{{R_{ci}}}}} } \text{。}$ | (15) |
即计算得到的混合电位
具体计算混合电位
| ${\varphi _{p + 1}} \leqslant \varphi \leqslant {\varphi _p}\text{,}$ | (16) |
则
得到隔离电阻均为0时的混合电位
考虑隔离电阻
| $\overline {{R_i}} = {R_i} + \frac{1}{{2\pi \sigma {a_i}}} + \frac{{{\beta _i} + {\rho _i}}}{{2\pi a_i^2}}\text{。}$ | (17) |
根据基尔霍夫电流定律,计算包含隔离电阻值时的系统平均电位值
| ${\varphi _R} = \frac{{\sum\limits_{i = 1}^n {\frac{{{\varphi _i}}}{{\overline {{R_i}} }}} }}{{\sum\limits_{i = 1}^n {\frac{1}{{\overline {{R_i}} }}} }}\text{,}$ | (18) |
进而可得到每个电极支部的电流值为:
| ${I_i} = \frac{{\varphi - {\varphi _R}}}{{\overline {{R_i}} }}\text{,}$ | (19) |
在式(19)的基础上可得到每个点电极在其下方
| $\overline {{U_i}} = \frac{{\varphi - {\varphi _R}}}{{\overline {{R_i}} }}\frac{1}{{2\pi \sigma \left( {{a_i} + d} \right)}}\text{,}$ | (20) |
比较
| ${R_i} \geqslant \frac{{\left| {{\varphi _R} - {\varphi _i}} \right|}}{{\Delta {U_{\max }}\pi \sigma \left( {{a_i} + d} \right)}} - \left[ {\frac{{{\beta _i} + {\rho _i}}}{{2\pi a_i^2}} + \frac{1}{{2\pi \sigma {a_i}}}} \right]\text{。}$ | (21) |
而后重新根据式(17)~式(19)重新评估电极下方的电位值
为了验证上述方法的有效性,利用1艘潜艇模型进行仿真计算,其中,潜艇模型长度L为120 m,最大艇宽B为10 m,从艇首到艇尾共有6个通海阀(依次为通海阀1、通海阀2、…、通海阀6)。
艇体指挥围壳、通海阀、尾舵、前舵和螺旋桨为金属材料,其他位置为绝缘材料,其物理尺寸如表1所示。检验过程中,所采用材料的极化曲线如图3所示。由极化曲线可知,极化电阻存在非线性的关系,为了减小误差,极化电阻率选取为无电隔离措施时材料表面电位,通过Beasy软件(舰船设计阶段常用电场仿真软件,能够对水下电势和腐蚀相关磁场进行预测[7 – 9])计算得到附近的极化率值。
|
|
表 1 潜艇未覆瓦部分金属材料的尺寸 Tab.1 The size of metal materials uncovered anechoic tile part of submarine |
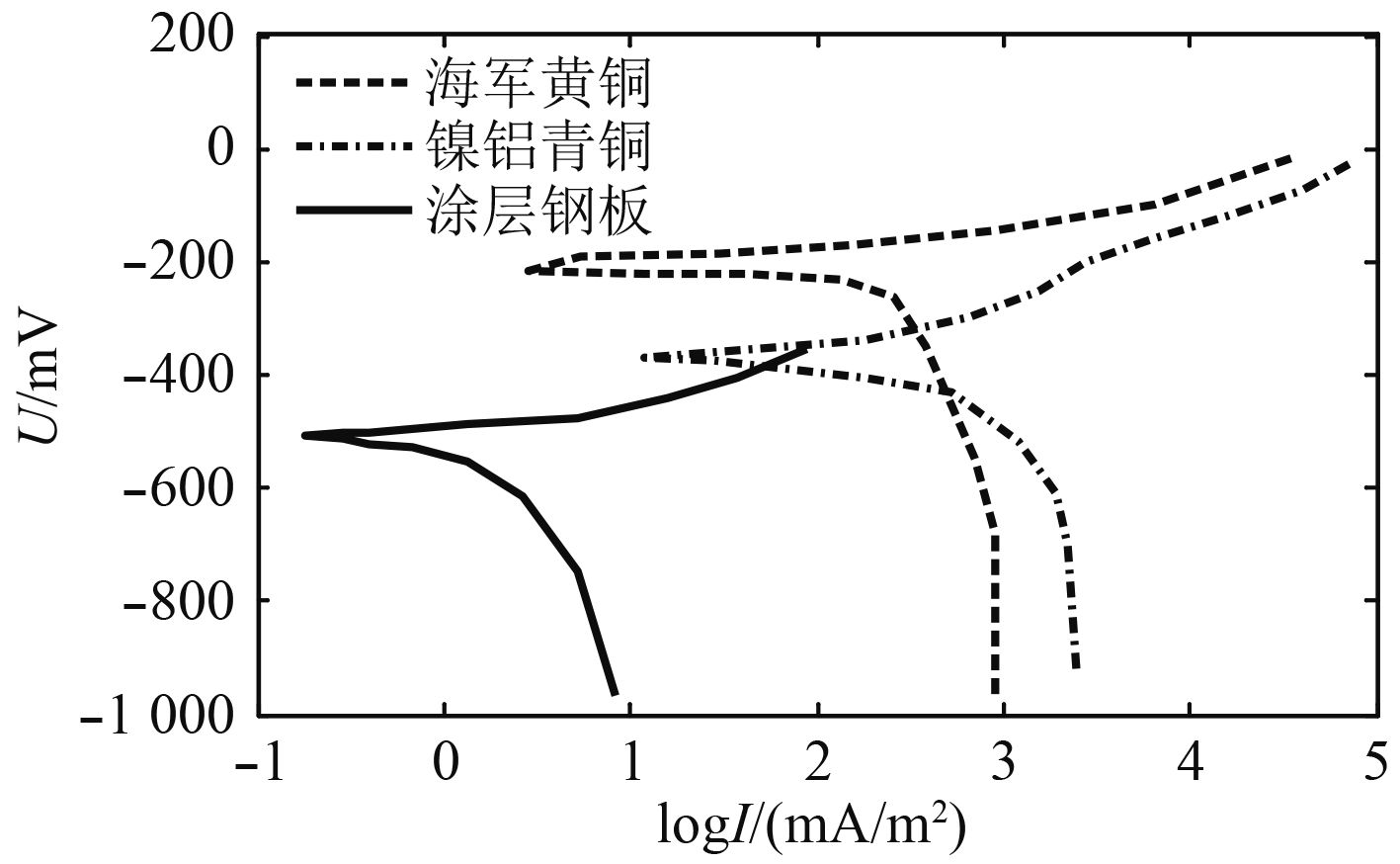
|
图 3 材料的极化曲线 Fig. 3 Polarization curve of material |
检验的具体步骤为:首先利用Beasy软件计算了隔离电阻为0时的电场值,而后采用第2节中的计算方法,估算出规定电场值条件下的最小隔离电阻值,最后将隔离电阻值代入Beasy软件,计算增加隔离电阻后的电场值,并与规定电场值进行比较。
3.1 算例1当指挥围壳、通海阀、尾舵、前舵材料为涂层钢,螺旋桨为镍铝青铜时,利用Beasy软件对无隔离电阻、自然腐蚀时的电化学系统进行建模,艇体正下方3 m的电位信号如图4所示,电位的峰-峰值为6.03 mV。
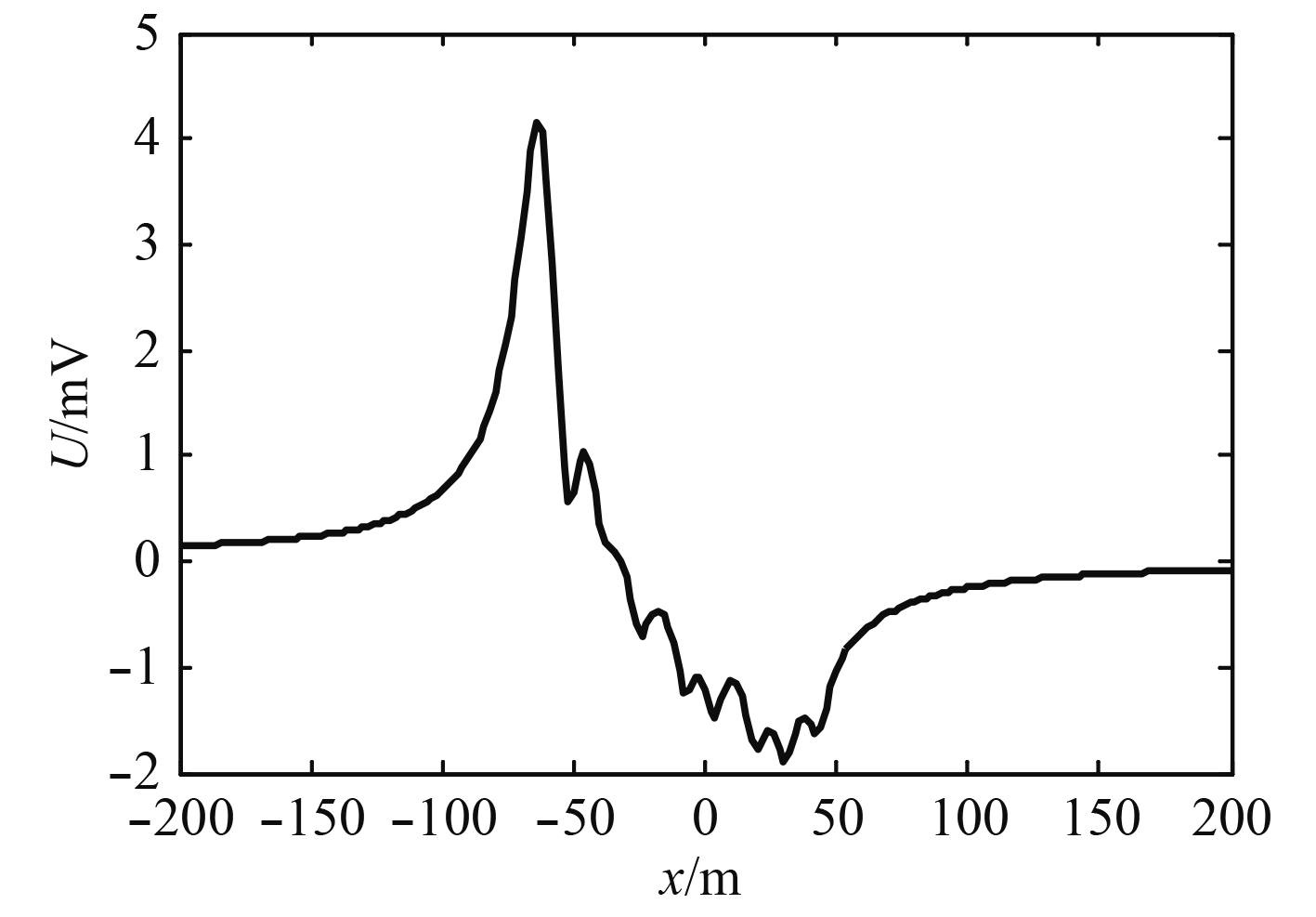
|
图 4 自然腐蚀时艇体正下方3 m的电位信号 Fig. 4 The potential signal 3 meters below the submarine on the condition of natural corrosion |
计算得到涂层钢板、镍铝青铜材料的平均电位值分别为–446 mV,–402 mV,根据平均电位值估算出涂层钢板阳极极化率和涂层电阻率和为
为了保证艇体正下方3 m处的电位峰-峰值不超过1 mV。船体虽然有绝缘层,但是金属材料仅为2种,采用第2.1节中计算得到的隔离电阻的最小值
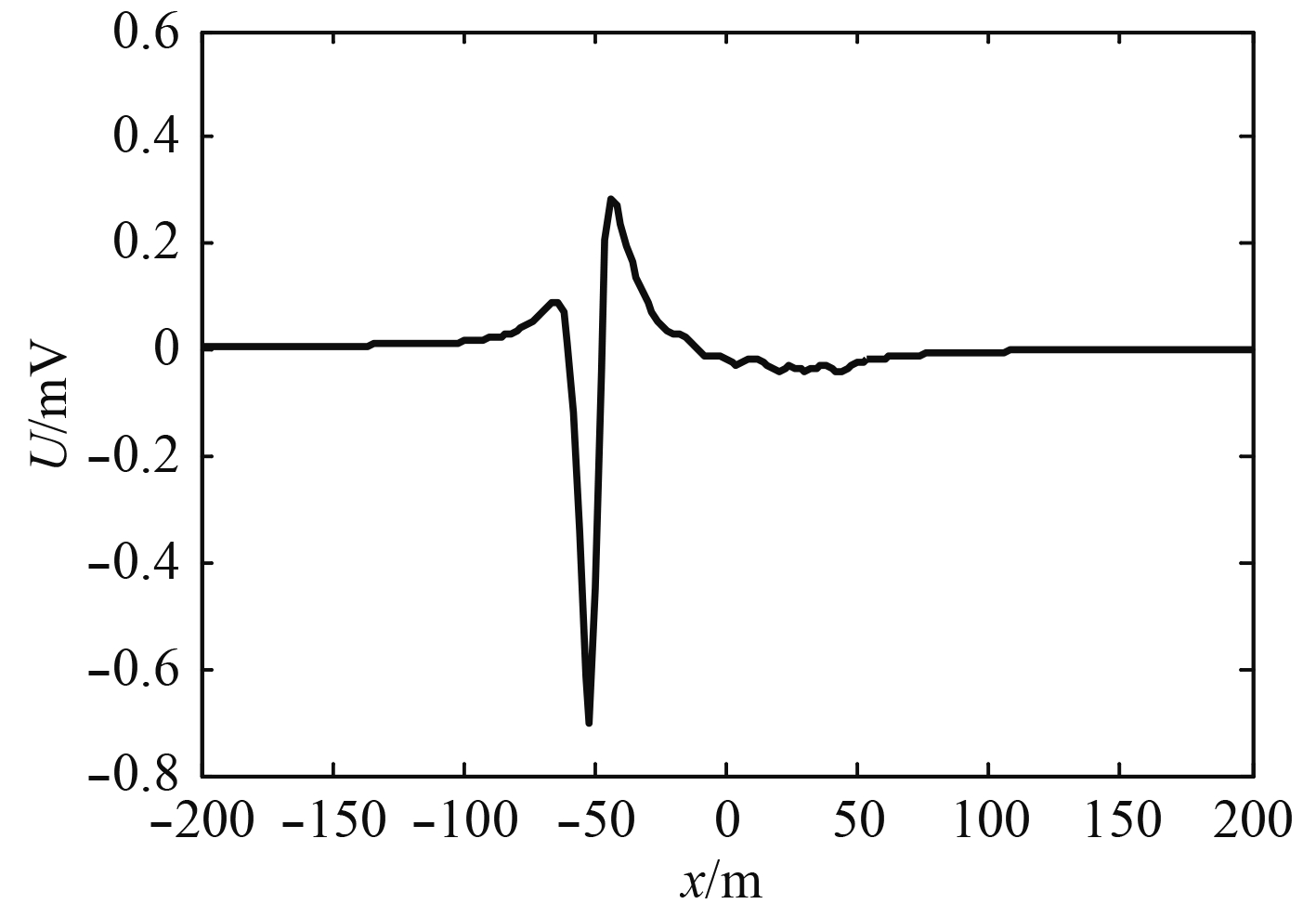
|
图 5 增加隔离电阻时艇体正下方3 m的电位信号 Fig. 5 The potential signal 3 meters below the submarine when the isolation resistance was added |
当指挥围壳、尾舵、前舵为涂层钢、螺旋桨为镍铝青铜,通海阀为海军黄铜时,利用Beasy软件对无隔离电阻、自然腐蚀时的电化学系统进行建模,艇体正下方3 m的电位信号如图6所示,其峰-峰值为27.44 mV。
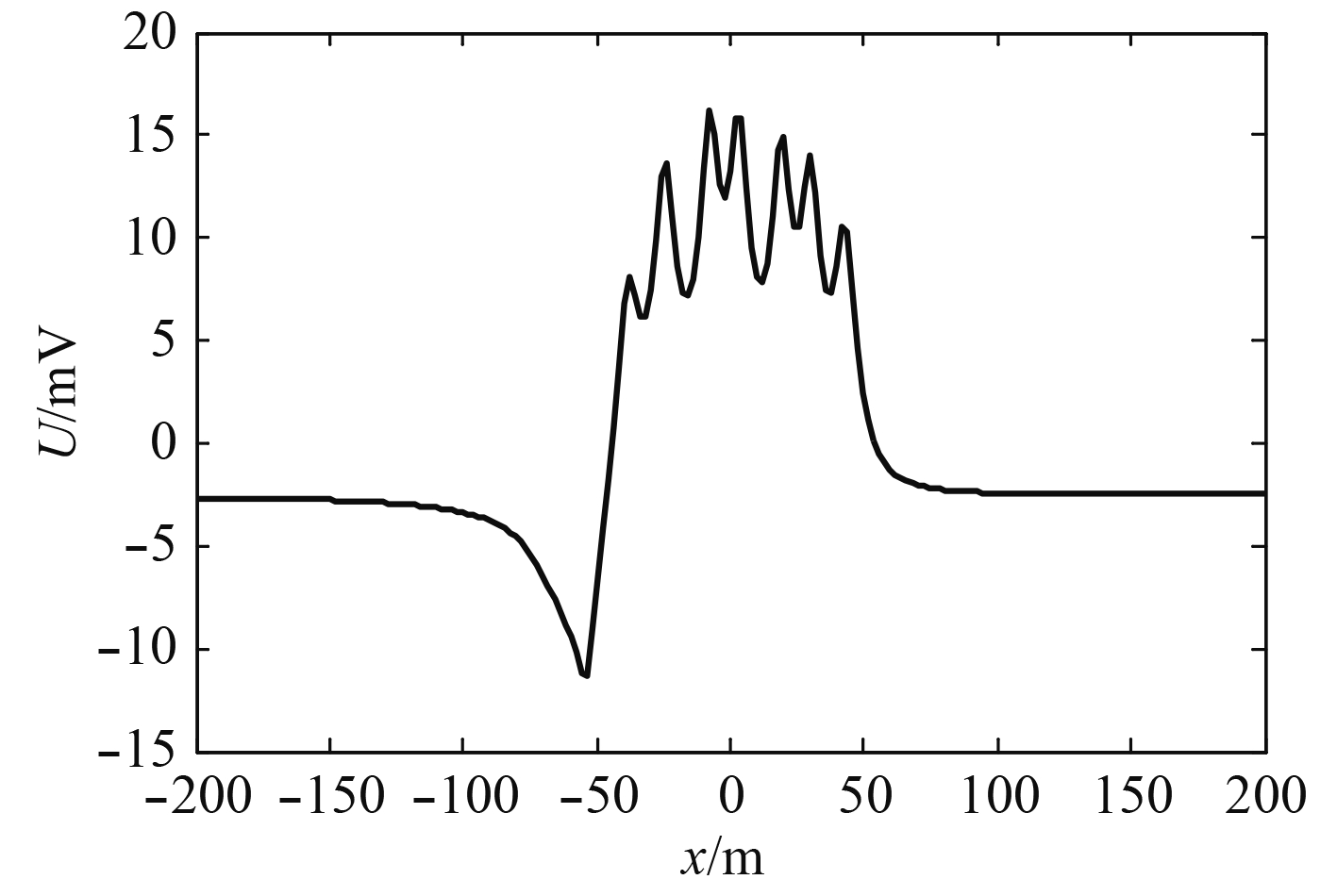
|
图 6 自然腐蚀时艇体正下方3 m的电位信号 Fig. 6 The potential signal 3 meters below the submarine on the condition of natural corrosion |
计算得到涂层钢板、镍铝青铜、海军黄铜材料的平均电位值分别为–356 mV,–350 mV,–254 mV,根据材料的极化曲线得到各个材料的极化率如表2所示。
|
|
表 2 材料的极化率 |
为了保证艇体正下方3 m处的电位峰-峰值不超过2 mV,采用第3.2节中计算得到的涂层钢板、镍铝青铜、海军黄铜的隔离电阻的最小值分别为:
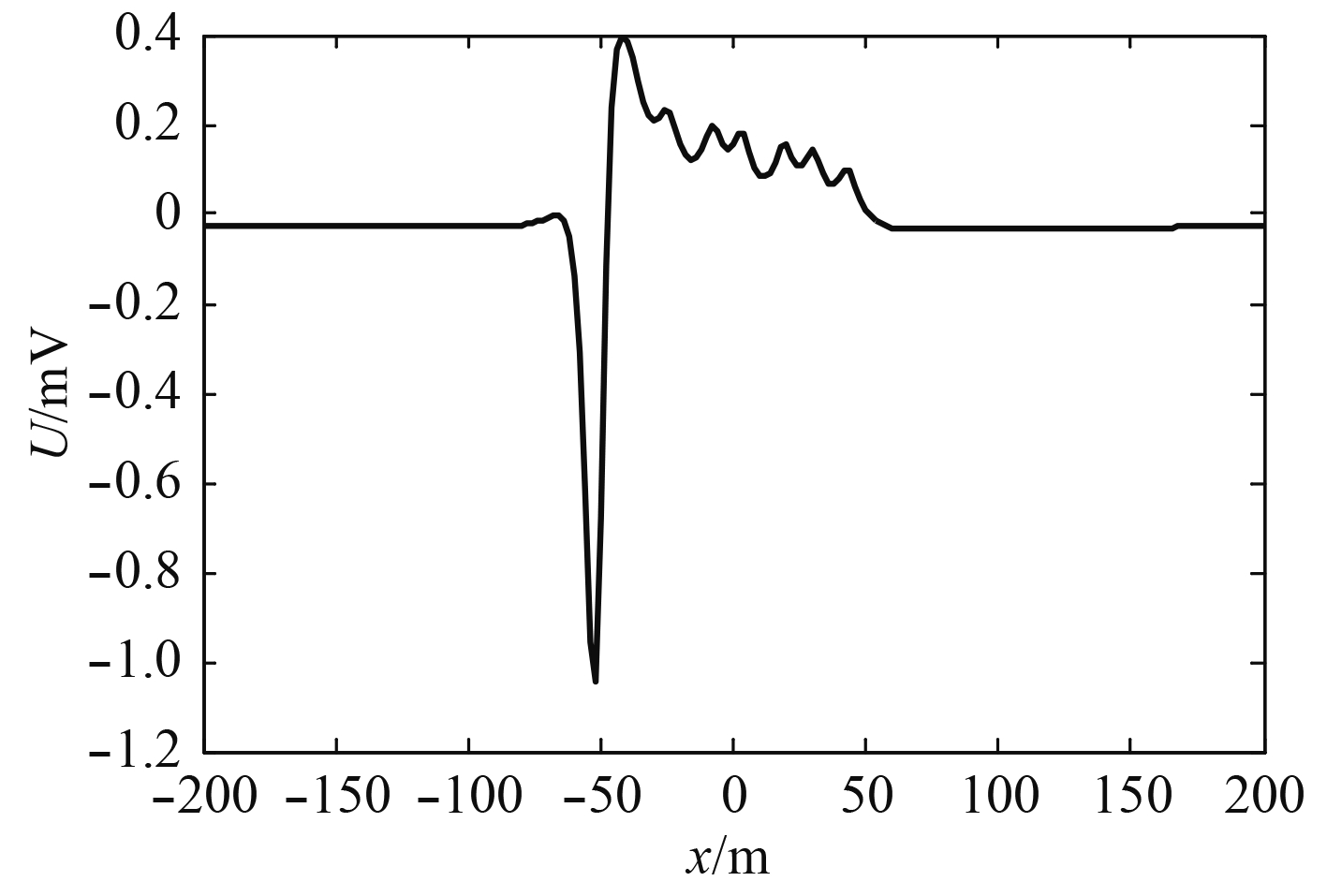
|
图 7 增加隔离电阻时艇体正下方3 m的电位信号 Fig. 7 The potential signal 3 meters below the submarine when the isolation resistance was added |
为了估算水下某一深度目标电位峰-峰值要求时船体异种金属之间允许的最小隔离电阻值,利用点电极模型建立了腐蚀电流、隔离电阻值、水下电位在非绝缘船体和绝缘船体条件下的关系,并利用Beasy软件进行检验,结果表明,所提方法能够准确预测最小隔离电阻值。
| [1] | HUBBARD J C, BROOKS S H, TORRRANCE B C. Practical measures for reduction and management of the electro-magnetic signatures of in-service surface ships and submarines[C]// Underwater Defence Technology Conference, London, 1996, 64–65. |
| [2] | DYMARKOWSKI K, UCZCIWEK J. The extremely low frequency electromagnetic signature of the electric field of the ship [C]//Underwater Defence Technology Conference, London, 2001, 1–6. |
| [3] | 龚沈光, 卢新成. 舰船电场特性初步分析[J]海军工程大学, 2008, 20(2) 1–4. http://www.cqvip.com/qk/91072A/200802/27138406.html |
| [4] | 秦一平. 舰船腐蚀相关静电场隐身技术研究[D]. 武汉: 海军工程大学, 2015. |
| [5] | 姜润翔, 林春生, 龚沈光. 基于点电荷模型的舰船静电场反演算法研究[J]. 兵工学报, 2015, 36(3): 545–551. http://www.oalib.com/paper/4453591 |
| [6] | 杨清学. 外加电流阴极保护装置在舰船防腐中的应用研究[J]. 舰船科学技术, 2016: 38(5A): 181–183. http://wuxizazhi.cnki.net/Sub/wqjs/a/JCKX201610042.html |
| [7] | 郑军林, 陈新刚, 郑春兵, 等. 舰船电场隐身技术[J]. 中国舰船研究, 2006, 1(4): 48–51. http://www.cqvip.com/qk/93256A/200705/26279117.html |
| [8] | ADEY R, BAYNHAM J. Predicting corrosion related electrical and magnetic fields using BEM[C]//In: Tracey Westwood, Underwater Defence Technology, 2000, 386–391. |
| [9] | SANTANA DIAZ E, ADEY R. Optimizing the location of anodes in cathodic protection systems to smooth potential distribution [J]. Advances in Engineering Software, 2005, 36(9): 591–598. |
 2018, Vol. 40
2018, Vol. 40
