2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai 200240, China
潜艇隐身性是其重要的性能之一。提高潜艇隐身性能有效方法之一是在潜艇表面敷设声学覆盖层以减小声波的反射,研究敷设声学覆盖层的壳体的声学性能十分必要。目前,有限元方法作为最常用的数值计算方法,经常被用来处理声学问题[1 – 3]。Kim[4]基于Kirchhoff近似的原理建立了一种新的计算敷设声学覆盖层的潜艇声目标强度的数值方法,并且用有限元方法计算了声学覆盖层敷设在与潜艇壳体具有相同厚度和相同背衬条件下的声反射系数。王曼[5]利用有限元方法,研究了水声吸声覆盖层吸声机理,分析了覆盖层空腔结构的共振特性;并且进行覆盖层反射系数的实验,实验测得的反射系数与有限元方法获取的反射系数符合较好,验证了其方法的有效性。Hennion[6]根据周期边界条件,运用Bloch理论建立声学覆盖层单个周期模型,并利用有限元方法研究了带空腔的声学覆盖层的共振吸声机理。陶猛[7]通过共振特性研究分析了Alberich型声学覆盖层的低频吸声机理,得出声学覆盖层的共振是圆柱腔体共振等结论。
以上方法主要研究了声学覆盖层敷设在简单结构体上的吸声机理。张玉玲[8]运用板块元的方法计算复杂目标敷设吸声材料前后的声目标强度,发现在低频声学覆盖层对降低声目标强度的效果不明显,在高频效果明显。板块元方法是基于基尔霍夫近似的方法,能快速预报高频段水下复杂结构物的目标强度,但是却不适用于低频段。金国梁[9]基于等效参数反演的方法研究了敷设Alberich圆柱空腔的声学覆盖层的水下无限圆柱壳体在圆柱波辐射下的低频声散射特性,并且获得了满意结果。本文研究了敷设圆台型空腔的声学覆盖层的有限长圆柱壳在平面波辐射下正横状态下的声目标强度。
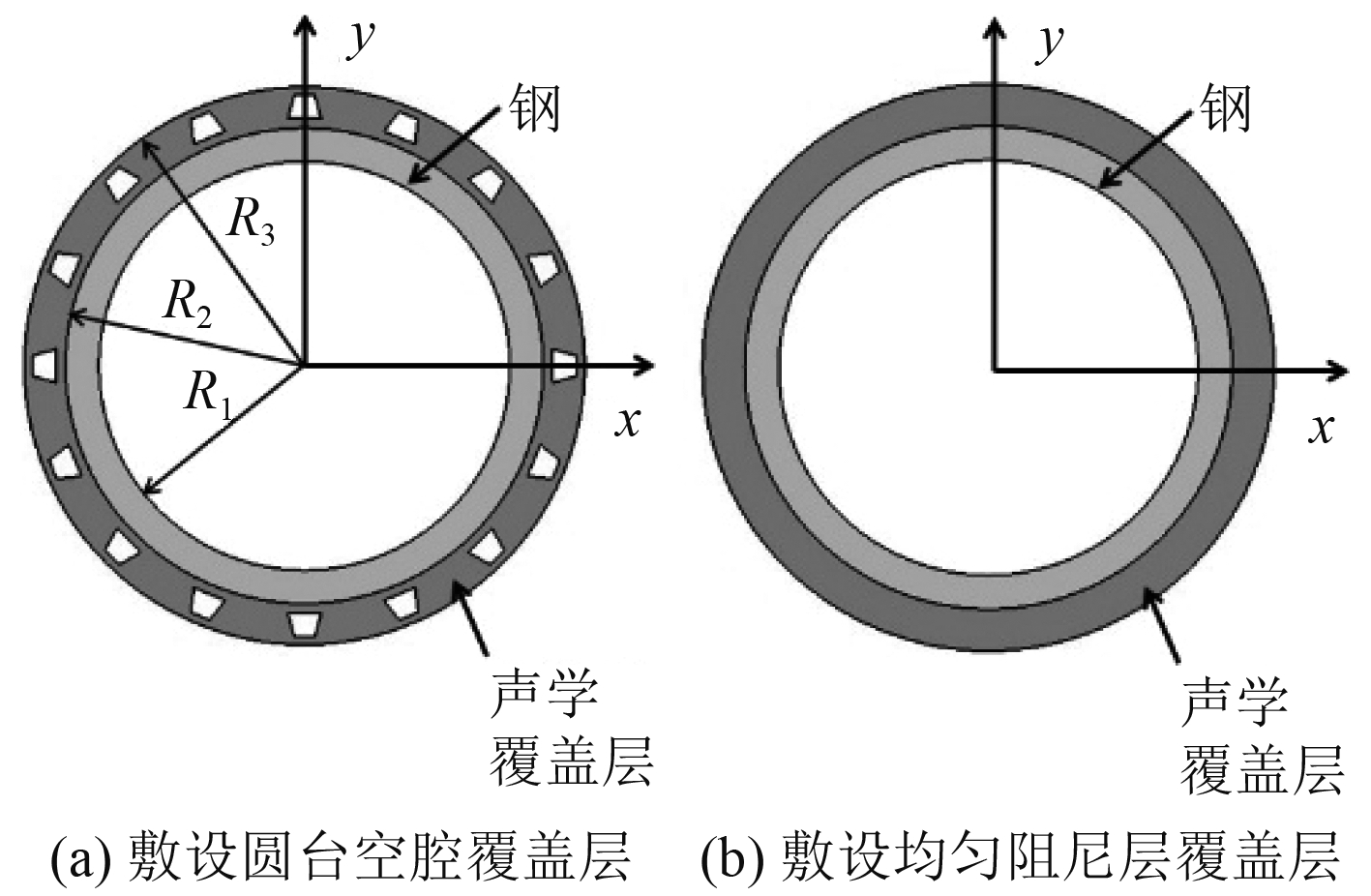
1 研究对象本文主要研究对象是长为1 m,两边简支约束的有限长圆柱壳。本文建立了2个模型,如图1所示,模型1是敷设圆台型空腔声学覆盖层的圆柱壳(图中空腔分布密度不代表实际分布情况),用于验证方法的有效性;模型2是敷设均匀阻尼层的圆柱壳,均匀阻尼层所用的物理参数为等效反演后的材料参数,2个模型的圆柱壳均为钢材。图中
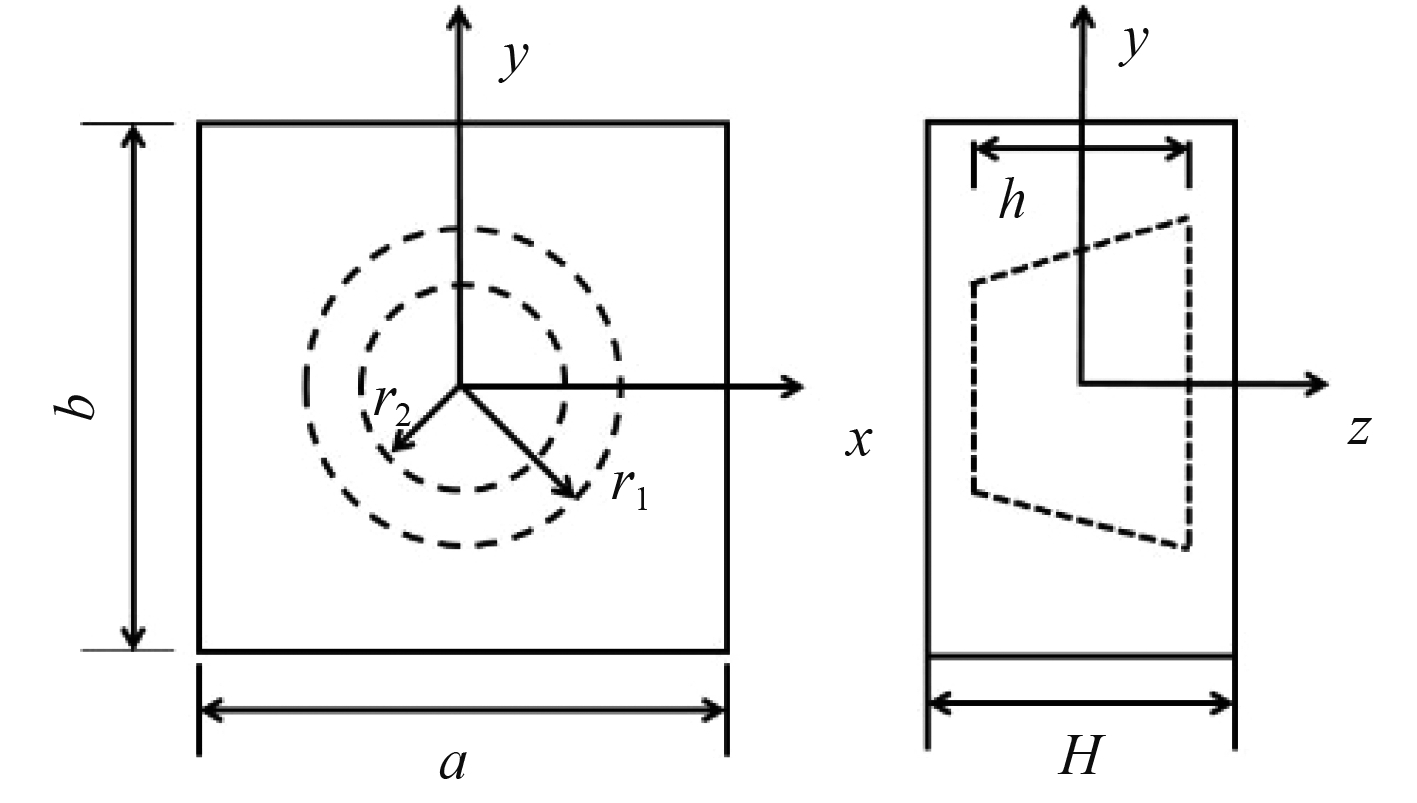
单个周期圆台空腔覆盖层的示意图如图2所示,其中
假设在远处有一个沿着x轴方向,且波振面平行yz平面的平面波入射到目标物体上,则可由有限元软件计算得到反射声场。
|
图 1 圆柱壳示意图 Fig. 1 The diagram of cylinders |
|
图 2 圆台空腔覆盖层示意图 Fig. 2 The diagram of acoustic coating which contains frustum of a cone cavity |
|
|
表 1 各结构的几何参数 Tab.1 The geometric properties of objects |
|
|
表 2 各材料的物理参数 Tab.2 The material properties of objects |
本文采用声学软件Virtual. lab的声学有限元模块计算分析了敷设声学覆盖层的水下结构物的目标强度。将声学方程进行积分化,可得以下方程:
| $\begin{array}{l}\int {_V} \overline w ({\nabla ^2}p(x,y,z) - {k^2}p(x,y,z) + \\j{\rho _0}\omega {q_0}(x,y,z)){\rm{d}}V = 0 \text{,}\end{array}$ | (1) |
其中:
再根据体积分和面积分之间的关系,可将式(1)变为下式:
| $\begin{split}\int {_V} (\nabla \overline w \cdot \nabla p){\rm{d}}V - {\omega ^2}\int {_V} (\displaystyle\frac{1}{{{c^2}}}\overline w \cdot p){\rm{d}}V = \int {_V} j\overline w {\rho _0}\omega {q_0}{\rm{d}}V - \int {_V} j{\rho _0}\omega \overline w v \cdot n{\rm{d}}S\text{,}\end{split}$ | (2) |
式中:
将式(2)进行有限元网格离散化,可得如下方程:
| $({{{K}}_a} + j\omega {{{C}}_a} - {\omega ^2}{{{M}}_a}) \cdot {{{p}}_i} = {{{P}}_i} + {{{Q}}_i} + {{{V}}_{ni}}\text{。}$ | (3) |
式中:
有限元计算声学问题时,声学边界条件十分重要,在Virtual. Lab软件中声学边界条件可采用AML技术,该方法的原理与完美匹配层(PML)原理相同,但是更加便捷,不需要人工添加吸收层网格,软件会根据模型自动定义吸收层和吸收系数,可以减少声学网格数量,从而提高计算精度及计算效率。
运用Virtual. Lab软件可得到平面波入射到结构物上后声压分布,根据式(4)可以计算得到水下结构物的目标强度。
| $TS = 20\log \frac{{{p_r}}}{{{p_i}}}\left| {_{r = 1}} \right.\text{。}$ | (4) |
式中:
本文采用参数反演法,主要思想是忽略声学覆盖层内部的声学空腔结构,利用物理参数等效前后材料的反射系数相等的原理,将声学覆盖层等效为均匀的阻尼层。等效前的反射系数可以根据充水阻抗管实验法或有限元方法模拟充水阻抗管法获得,本文采用后者以获得等效前反射系数
|
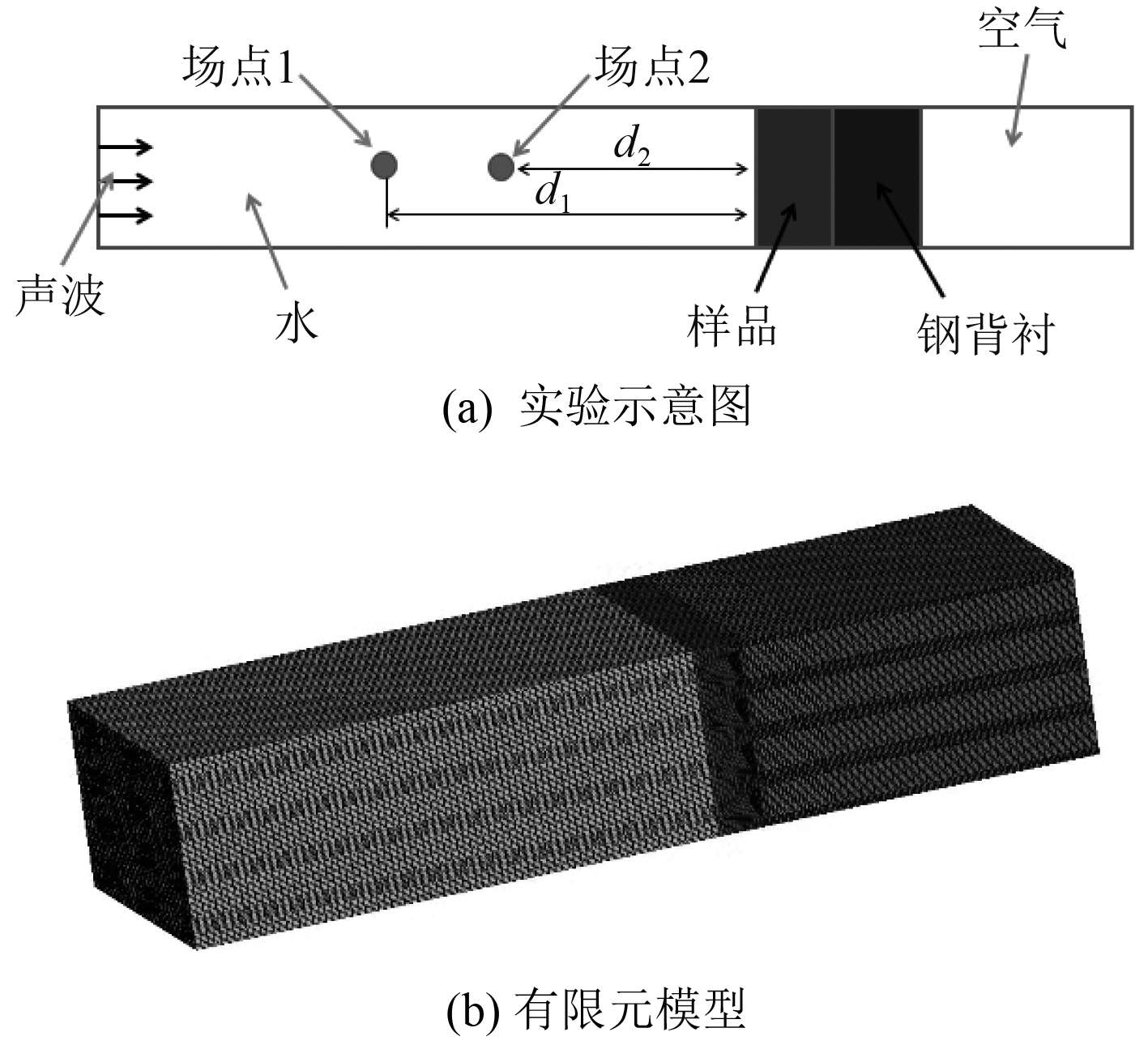
图 3 充水阻抗管法示意图 Fig. 3 The diagram of the impedance tube method |
充水阻抗管法测量材料反射系数的原理是传递函数法,在Virtual. Lab中可用场点模拟水听器。利用式(5)和式(6)可获得材料复反射系数。
| ${H_{12}} = \frac{{{p_2}}}{{{p_1}}}\text{,} $ | (5) |
| $R = \frac{{{H_{12}}{e^{i\varphi }}{e^{ik{d_2}}} - {e^{ik{d_1}}}}}{{{e^{ - ik{d_1}}} - {H_{12}}{e^{i\varphi }}{e^{ - ik{d_2}}}}}\text{。} $ | (6) |
式中:
等效后均匀阻尼层的反射系数
| $Z_{in}^{(2)} = \frac{{{Z_1} - i{Z_2}\tan {\varphi _2}}}{{{Z_2} - i{Z_1}\tan {\varphi _2}}} \cdot {Z_2}\text{,}$ | (7) |
| $Z_{in}^{(3)} = \frac{{Z_{in}^{(2)} - i{Z_3}\tan {\varphi _3}}}{{{Z_3} - iZ_{in}^{(2)}\tan {\varphi _3}}} \cdot {Z_3}\text{,}$ | (8) |
| ${R_a} = \frac{{Z_{in}^{(3)} - {Z_4}}}{{Z_{in}^{(3)} + {Z_4}}}\text{。}$ | (9) |
式中:
| ${Z_3} = {\rho _3}{C_3} = {\rho _3}\sqrt {\frac{{E(1 - \eta i)(1 - \mu )}}{{\rho (1 + \mu )(1 - 2\mu )}}}\text{。} $ | (10) |
再根据等效前后反射系数相等(即
遗传算法是根据达尔文进化论的自然选择和遗传学机理演化而来的全局搜索方法,它具有并行性、高效性等优点。在反演过程中,可以大幅提高计算效率。运用遗传算法需要定义适应度函数,如下式[9]:
| $F = \sqrt {\frac{{({R_a} - {R_0})(\overline {{R_a} - {R_0}} )}}{{\left| {{R_0}} \right|}}}\text{。} $ | (11) |
可以看出,当反演前后反射系数差值越小时,
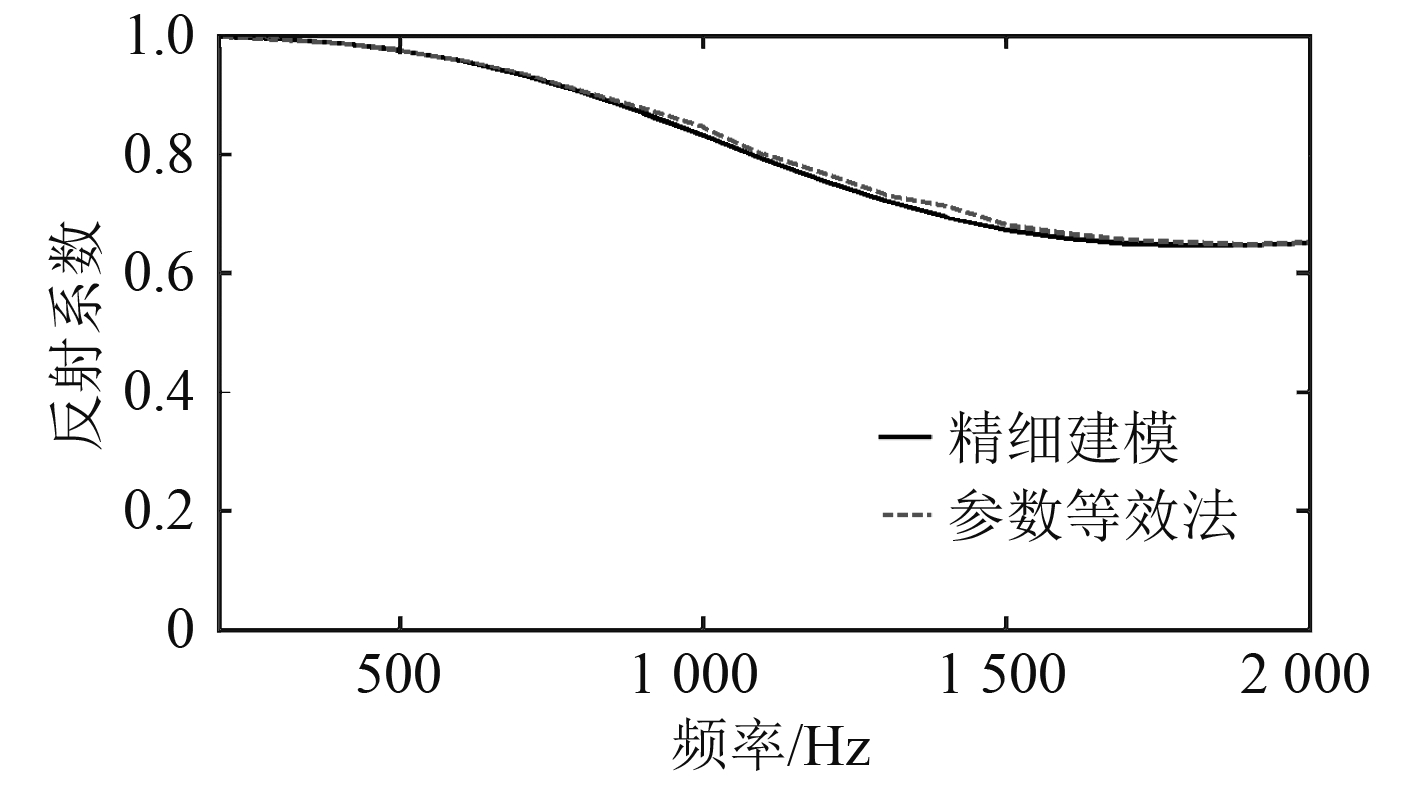
利用有限元软件模拟充水阻抗管法获得的精细建模和参数等效后声学覆盖层的反射系数如图4所示,图中实线为对圆台型空腔声学覆盖层进行精细建模所获得的反射系数,虚线为运用等效参数法后(即圆台型空腔覆盖层等效为均匀阻尼层后)所获得的反射系数。从图中可以看出,曲线趋势在2 000 Hz以下一致,且曲线基本重合,二者反射最大差值小于0.02。可以认为获得了比较可靠的等效物理参数(杨氏模量、泊松比、损耗因子)。
|
图 4 模拟充水阻抗管法获取的精细建模与等效参数法反射系数对比结果 Fig. 4 The comparison of the results of the reflection coefficient obtained from conventional FEM and equivalent parameter inversion by impedance tube method |
对敷设圆台型空腔声学覆盖层的有限长圆柱壳进行精细,再将等效后的参数用于相同圆柱壳的均匀阻尼层,运用有限元软件计算得到圆柱壳的目标强度。由于反射系数是在正入射的条件下获得的,未考虑一定角度的斜入射,因此,为了结果的有效性,只计算圆柱壳正横方向的目标强度。
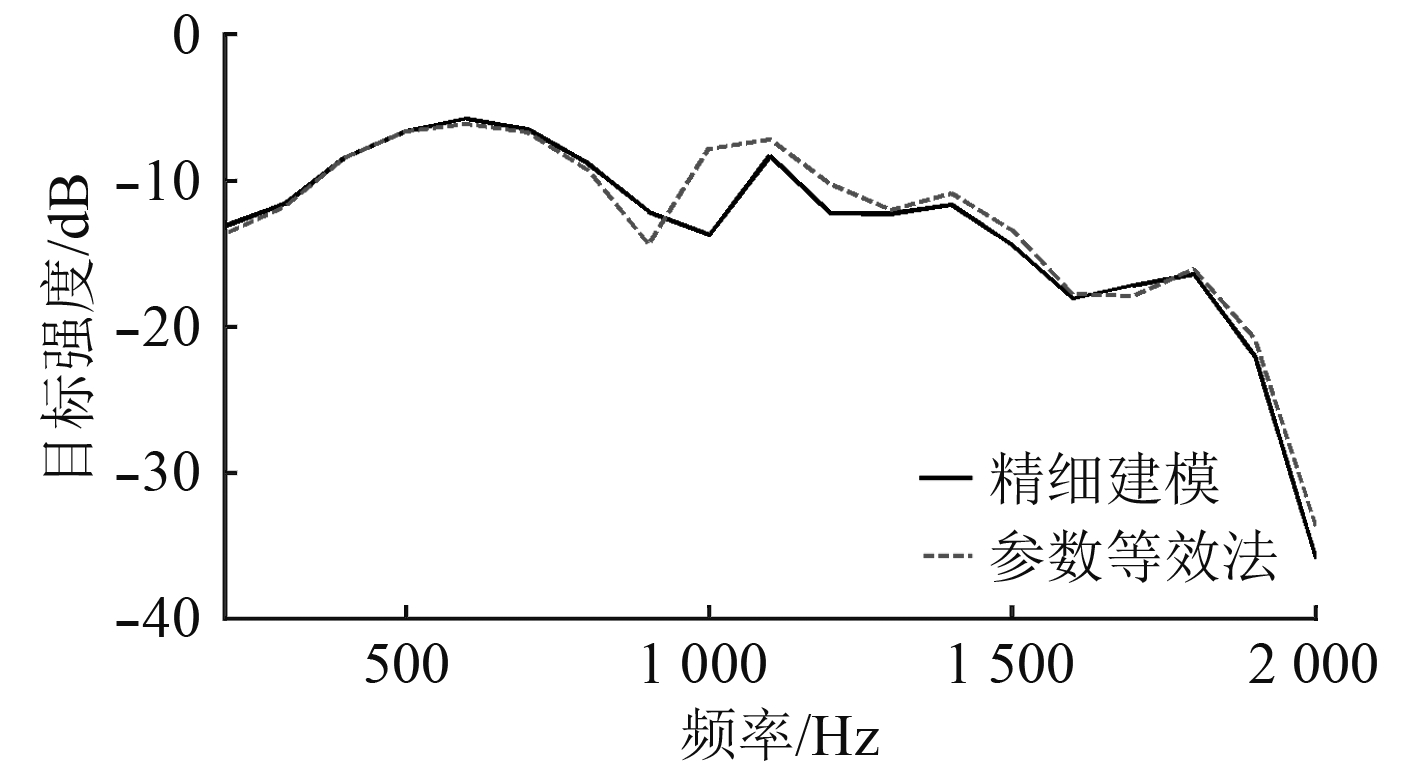
正横方向目标强度数值计算结果如图5所示,图中实线表示精细建模的圆柱壳的目标强度,曲线趋势基本一致。在200~900 Hz及1 400~2 000 Hz曲线基本重合,这与图4的结果类似;在900~1 200 Hz 两曲线谷值出现偏差,导致二者目标强度结果在1 000 Hz出现最大差值,并且值为6 dB;二者结果平均差值在1.1 dB左右。
整体看来,两者的结果基本相符,说明参数等效方法可以用于计算敷设圆台型空腔声学覆盖层的水下结构物声目标强度。
|
图 5 精细建模与等效参数法正横目标强度对比结果 Fig. 5 The comparison of the results of the acoustic target strength obtained from conventional FEM and equivalent parameter inversion |
本文运用参数等效方法计算了敷设圆台型空腔声学覆盖层的有限长圆柱壳正横状态下的声目标强度。首先基于有限元模拟充水阻抗管的方法获取声波正入射下声学覆盖层的反射系数;然后忽略声学覆盖层复杂的声学空腔结构,将其等效为均匀阻尼层;再根据等效前后反射系数相等的原理利用遗传算法反演获得均匀阻尼层的物理参数;再用模拟充水阻抗管的方法获取该均匀阻尼层的反射系数,验证反演后的参数的有效性;将阻尼层敷设在圆柱壳,用有限元软件计算圆柱壳正横方向的声目标强度,与精细建模后的目标强度进行对比,发现声目标强度与反射系数具有一定的关系,参数等效的方法可以有效地计算敷设圆台型空腔的声学覆盖层的水下结构物的目标强度,并且该方法可以减少网格数量,提高计算效率。
| [1] | CHAI Yingbin, GONG Zhixiong, LI Wei, et al. Application of Smoothed Finite Element Method to Two-Dimensional Exterior Problems of Acoustic Radiation [J]. International Journal of Computational Methods, 15(1), 2018, p. 1850029-1–35. |
| [2] | Yingbin Chai, Zhixiong Gong, Wei Li, et al. A smoothed finite element method for exterior Helmholtz equation in two dimensions [J]. Engineering Analysis with Boundary Elements, 84, 2017, p. 237–252. |
| [3] | 游翔宇, 郑文成, 李威, 等. 基于边光滑有限元法的加筋板静力和自由振动分析[J]. 计算力学学报, 2018, 35(1): 28–34. |
| [4] | Hwa-Muk Kim, Suk-Yoon Hong. Numerical Simulation of Submarines with Anechoic Coatings for Acoustic Target Strength Reduction [J]. Naval Engineers Journal, No. 124–4, 2012, p. 49–58. https://www.researchgate.net/publication/297295720_Numerical_Simulation_of_Submarines_with_Anechoic_Coatings_for_Acoustic_Target_Strength_Reduction |
| [5] | 王曼. 水声吸声覆盖层理论与实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2004. |
| [6] | Hladky-Hennion AC, Bossut R, Decarpigny JN. Analysis of the Scattering of Plane Acoustic Wave by A Periodic Elastic Structure Using the Finite Element Method: Application to Compliant Tube Gratings [J]. J. Acoust. Soc. Am. , 87(5), 1990, p. 1861–1870. |
| [7] | 陶猛, 汤渭霖. Alberich型吸声覆盖层的低频吸声机理分析[J]. 振动与冲击. Vol. 30, No. 1, 2011, p. 56–60. https://www.wenkuxiazai.com/doc/d700dd0b0740be1e650e9a0e.html |
| [8] | 张玉玲, 陶猛, 范军. 敷设吸声材料复杂目标的目标强度计算[J]. 上海交通大学学报. Vol. 43, No. 8 Aug, 2009, p. 1322–1328. http://www.cqvip.com/QK/92944X/200908/31468132.html |
| [9] | 金国梁, 尹剑飞, 温激鸿. 基于等效参数反演的敷设声学覆盖层的水下圆柱壳体声散射研究. 物理学报. Vol. 65, No. 1, 2016. |
| [10] | 詹福良, 徐俊伟. Virtual. Lab Acoustic 声学仿真计算从入门到精通[M]. 西安: 西北工业大学出版社. 2013 |
| [11] | 布列霍夫斯基赫 著(杨训仁 译). 分层介质中的波[M]. 北京: 北京科学出版社. 1960. |
 2018, Vol. 40
2018, Vol. 40
