2. 武汉第二船舶设计研究所热能动力技术重点实验室,湖北 武汉 430205
2. Key Laboratory on Thermal Energy and Power, Wuhan Second Ship Design and Research Institute, Wuhan 430205, China
核动力装置长期的运行经验表明,双端剪切断裂事故发生的概率极低,而为此引入的附加安全系统和装置使得设计成本急剧增加,但整个系统的安全性却并没有得到大幅提升[1 – 2]。因此,破前漏(LBB)技术在核动力装置安全设计中逐渐受到重视,目前国际上通用的程序包括PICEP和SQUIRT[3 – 4],国内开发的程序包括COLROPC,PICLES和CLR等[5 – 7]。
泄漏率预测是破前漏分析中极为关键的一个环节,主要涉及到临界流理论和裂纹流道阻力分析。窄缝裂纹通道内部结构比较复杂,表面有很多凹凸不平的沟槽,会对裂纹内流体流动产生一定影响,改变裂纹流道阻力特性。本研究采用数值计算技术,对窄缝裂纹通道进行参数化建模,分析裂纹几何形貌参数对流动特性的影响。
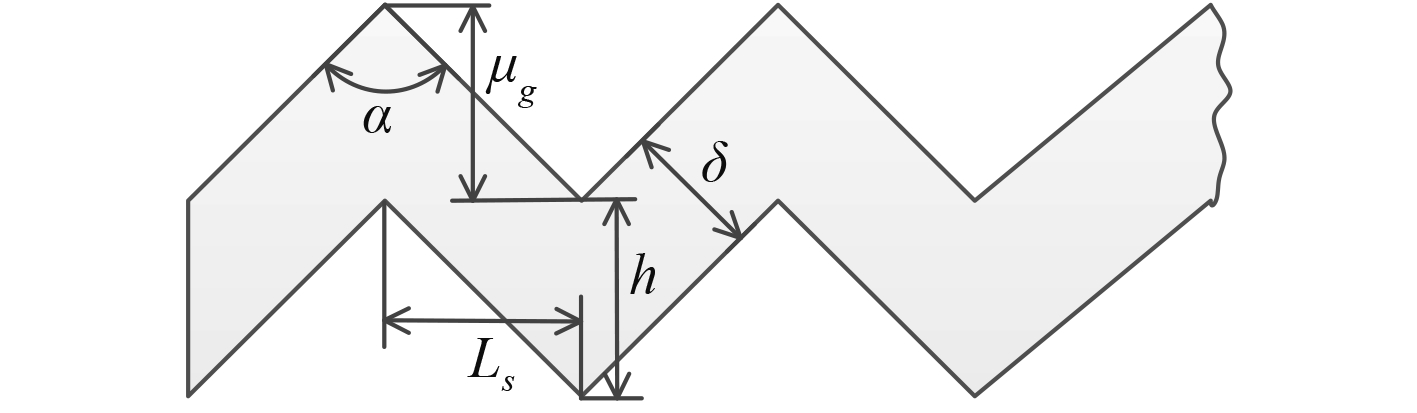
1 计算模型及网格假定裂纹内的弯折对称且均匀,对裂纹界面进行参数化建模,如图1所示。其中α为裂纹弯折角度;Ls为其中一段弯折的直线长度;μg为裂纹宏观粗擦度;h为裂纹高度;δ为裂纹张开位移(COD)。
|
图 1 裂纹几何形态建模 Fig. 1 Geometric shape modeling of crack |
上面几个参数之间的关系为:
| $\delta = h\sin \left( {\frac{\alpha }{2}} \right)\text{,}$ | (1) |
| ${L_s} = {\mu _g}\tan \left( {\frac{\alpha }{2}} \right)\text{。}$ | (2) |
因此,上面5个变量中只有3个是独立变量。本研究选择Ls,δ和μg为描述裂纹几何形态的建模参数,通过调整上述变量可得到不同的窄缝裂纹,为参数化建模计算提供基础。本研究中流道的几何参数如表1所示,δ/μG的范围为0.067~20。
|
|
表 1 流道几何参数 Tab.1 Geometry parameters of the flow path |
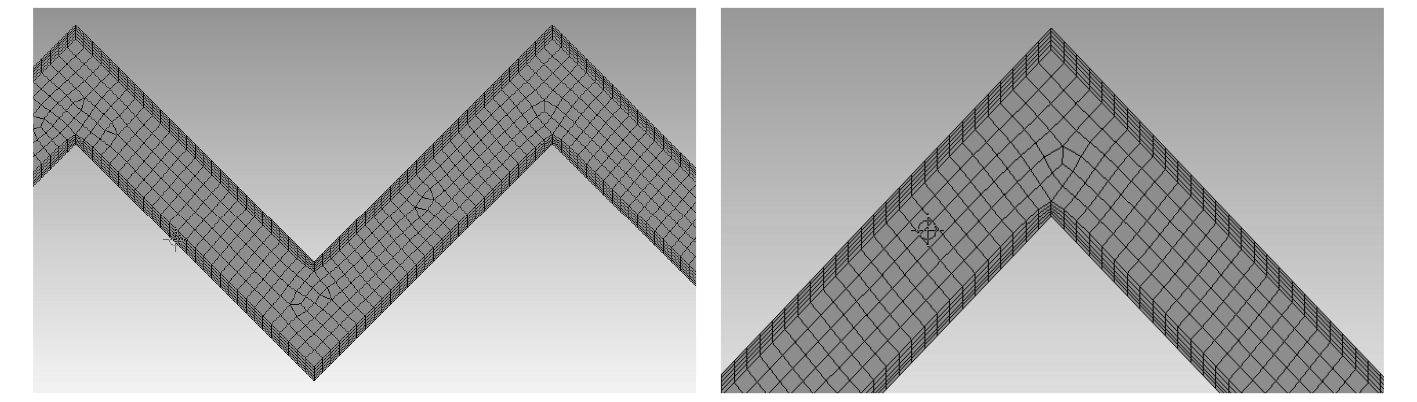
完成几何模型的构建后对流体域网格进行划分,流道壁面附近设置边界层网格,如图2所示。不同参数的窄缝流道的网格划分形式类似,根据几何参数确定网格划分策略,网格划分过程中尽量采用结构化网格,以提高计算速度和精度。
|
图 2 流道网格划分示意 Fig. 2 Shetch of the flow path meshing |
计算湍流模型为标准k-ε模型,入口边界条件为速度边界,速度范围为0.2~12 m/s,流道出口边界条件为压力出口边界,壁面局部粗糙度设定为20 μm。为了避免入口效应和出口效应的影响,在压降分析过程中分别取远离出入口的区域进行分析。
2 计算结果及分析 2.1 流场分析不同几何结构的裂纹内的流场如图3所示,入口速度和裂纹宽度分别为12 m/s和0.4 mm。从图中可以看出,当宏观粗糙度远小于裂纹宽度时(图3(a)),裂纹表面的锯齿形突起对流体流场影响不大,通道的形状不会对流体流向产生影响。随着宏观粗糙度的逐渐增加,裂纹内的弯折逐渐对通道内的流动产生影响(图(3c)),但是此时流体速度方向并未完全改变,对阻力的影响也小一些。
当宏观粗糙度增大到一定程度之后,裂缝内流道成为具有多个拐弯的窄通道(图3(e)),从图中可以看出流体在通道转弯处完全转向,单独一段直通道的流动完全发展,转弯处流体速度变化比较剧烈。随着裂纹宏观粗糙度的进一步增加,由裂纹转弯所导致的流体入口段和出口端所占份额逐渐减小,转弯所导致的局部阻力损失份额也会减小。

|
图 3 裂纹流道内速度分布 Fig. 3 The velocity in the crack flow path |
图4为不同几何结构裂纹内的湍流动能的分布情况,从图中可以看出,当宏观粗糙度很小时,湍流动能只有在壁面附近才会比较大(图4(a))。随着宏观粗糙度的进一步增加(图4(b)),裂纹通道表面的锯齿形状对湍流动能的影响愈加明显,锯齿形附近形成比较明显的湍动层。当宏观粗糙度继续增加时,通道内流体的转向所导致的影响逐渐体现(图4(c))。当宏观粗糙度增加到一定程度之后,湍流动能的剧烈增加只在转弯处附近发生(图4(g)),而且随着宏观粗糙度的增加,这种特性会越来越明显。

|
图 4 裂纹流道内湍流动能分布 Fig. 4 The kinetic energy in the crack flow path |
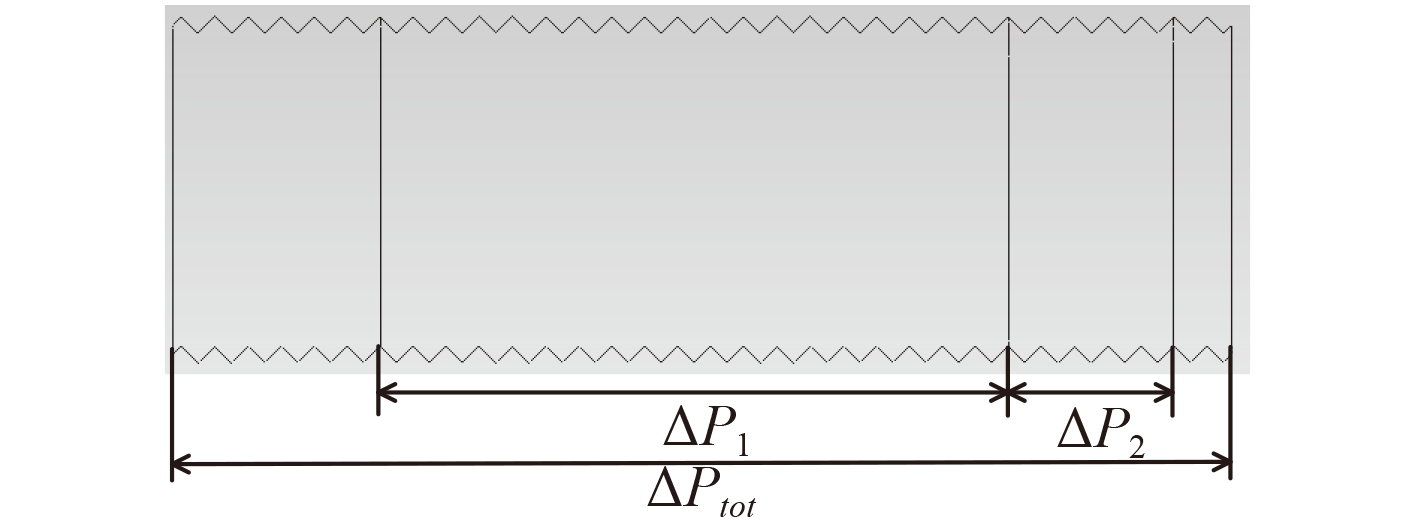
考虑到入口效应和出口效应对裂纹通道压降的影响,本研究对以下几段压降进行了计算,如图5所示。对比前面的速度分布和湍流度分布计算结果,阻力系数的计算采用图中的ΔP2。因此,裂纹通道阻力系数的计算为
| $f = \frac{{2\Delta {P_2}{D_H}}}{{L{\rho _f}u_f^2}}\text{。}$ | (3) |
其中:L为通道的长度;ρf为流体密度;uf为流体速度。
|
图 5 流道压降示意图 Fig. 5 Schematic diagram of flow pressure drop |
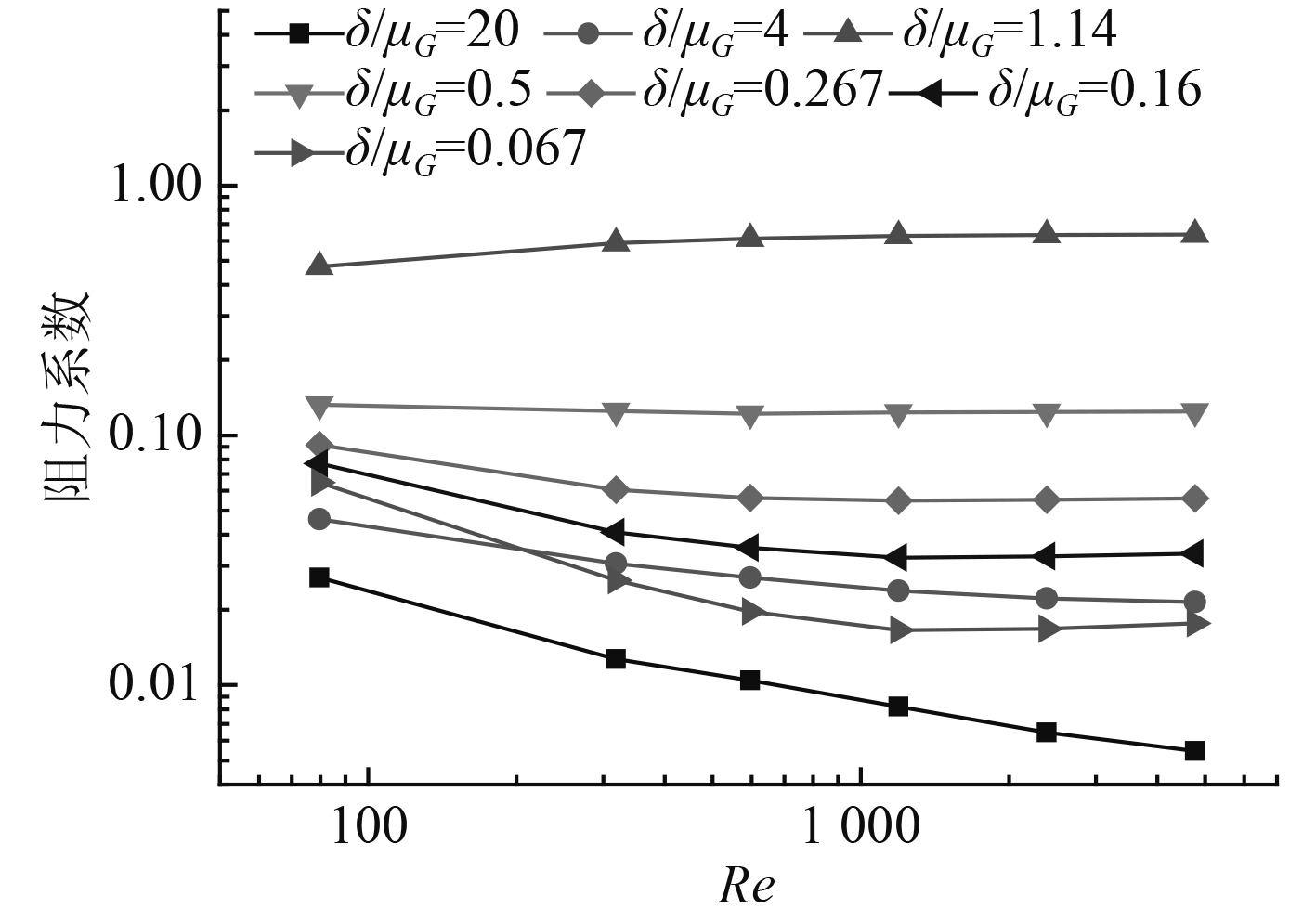
裂纹流道内不同雷诺数下的阻力系数变化如图6所示,从图中可以看出,当宏观粗糙度远小于COD时(即δ/μg =20),阻力系数随雷诺数的增加不断减小。当宏观粗糙度有所增加时(即δ/μg =4),阻力系数随雷诺数的增加仍一直减小,但是减小的速度有所下降。随着宏观粗糙度的进一步增加(即δ/μg =1.14),在本研究所计算的雷诺数范围内,阻力系数随雷诺数的增加略有增加。对于宏观粗糙度远大于COD(δ/μg =0.5)的情况,雷诺数的增加对阻力系数的影响不大。当宏观粗糙度进一步增加时(即δ/μg=0.267和δ/μg =0.16),在雷诺数增加的条件下,阻力系数先减小,随后基本不变。宏观粗糙度增加到一定程度之后(即δ/μg =0.067),阻力系数随雷诺数的增加先减小,然后有所增加,这是由于此时直管道内过渡区特性逐渐体现所导致的。
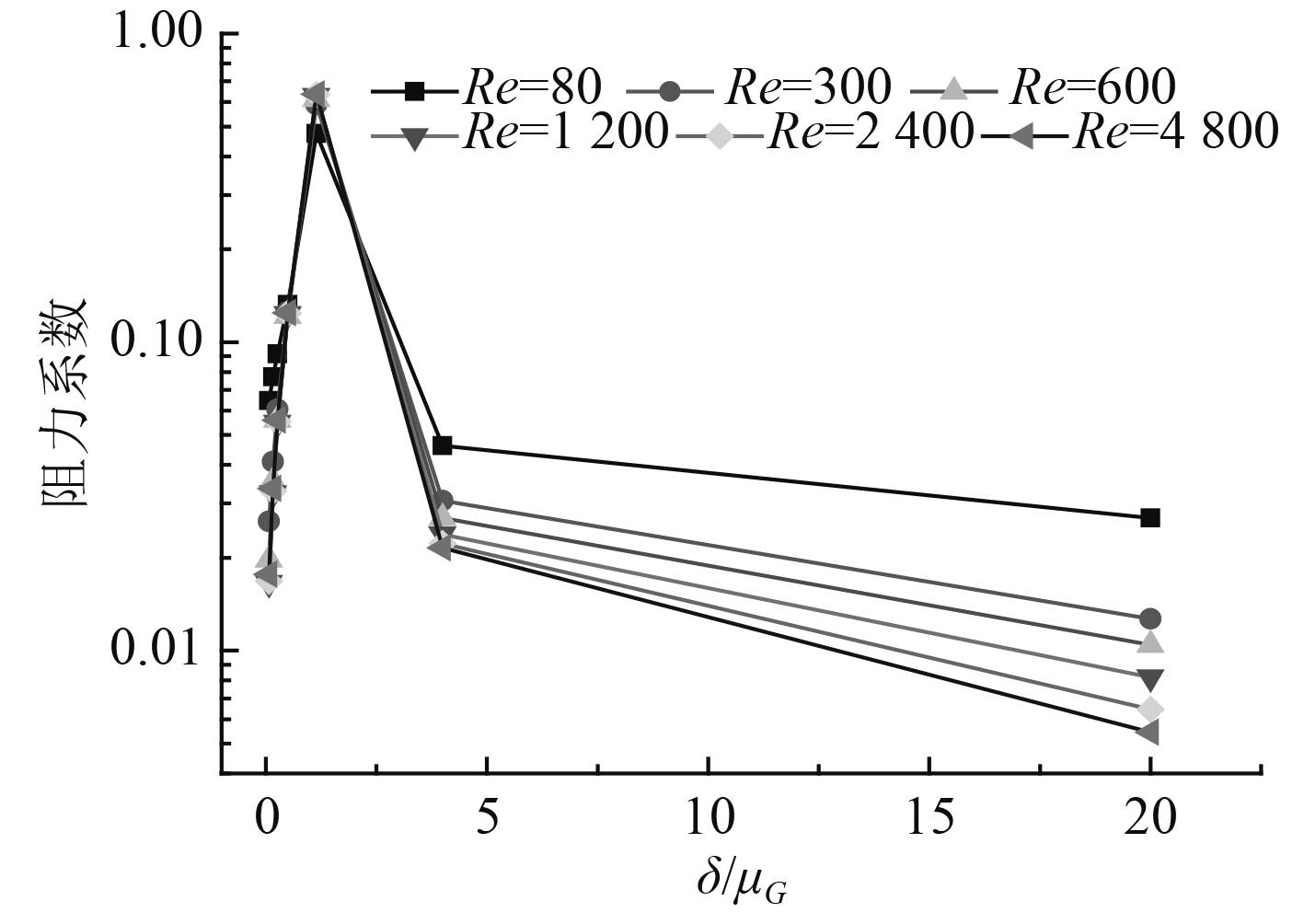
为了分析δ/μg对裂纹流动阻力系数的影响,图7示出了不同δ/μg对应的阻力系数变化。从图中可以看出在相同的雷诺数条件下,阻力系数随δ/μg的增加先增加,随后减小,转折点位于δ/μg=1附近。出现上述现象的主要原因是裂纹流道内拐弯的作用开始逐渐增强,而增强到一定程度之后直通道的作用逐渐明显,图3所示的速度分布和图4所示的湍流强度分布可以直观地说明上述问题。
|
图 6 不同雷诺数下的阻力系数变化 Fig. 6 The resistance coefficient at different Reynolds numbers |
|
图 7 对阻力系数的影响 Fig. 7 Effect of δ/μg on resistance coefficient |
本研究利用CFD技术对窄缝裂纹通道内的流体流动特性进行了研究,采用参数化建模方法对不同裂纹通道进行建模并划分网格,分析裂纹几何结构对流场、湍流动能以及流动阻力系数的影响,主要结论如下:
1)裂纹张开位移和宏观粗糙度的比值(δ/μg)会影响流场和湍流动能分布特性,当δ/μg较大时,裂纹流道接近于直管道而拐弯的作用与表面粗糙度类似,当δ/μg较小时,裂纹流道内流动特性接近于有众多拐弯的直管道,其他情况则介于上述2种情况之间。
2)受裂纹流道内流场和湍流动能分布特性的影响,裂纹流道内拐弯对于阻力系数的增强作用在δ/μg较小时比较弱,随着δ/μg的增加越来越强,但当δ/μg增加到一定程度之后拐弯对于阻力系数的增强作用会再次减弱。
| [1] | 乔红威, 刘志伟, 李琦, 李锡华. LBB裂纹稳定性分析方法研究[J]. 原子能科学技术, 2013, 47(11): 2108–2113. |
| [2] | Yann Kayser, Stephane Marie, Christophe Poussard, Christine Delaval. Leak Before Break procedure: Recent modification of RCC-MR A16 appendix and proposed improvements[J]. International Journal of Pressure Vessels and Piping, 2008, 85: 681–693. |
| [3] | Electric Power Research Institute, EPRI NP-3596-SR[R]. PICEP: Pipe Crack Evaluation Program (Revision 1), Revision 1, 1987 |
| [4] | PAUL D D, Ahmad J, Scott P M, et al. Evaluation and refinement of leak-rate estimation models, NUREG/CR-5128[R]. US: NRC, 1994. |
| [5] | 章静, 乔红威, 李朋州, 巫英伟, 田文喜, 秋穗正, 苏光辉. 管道贯穿裂纹泄漏率预测[J]. 原子能科学技术, 2015, 49(4): 660–666. |
| [6] | 吴万军, 谢海, 兰斌, 黄旋, 叶献辉. 管道裂纹泄漏率计算软件开发[J]. 核动力工程, 2015, 36(4): 65–68. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-NLSI201409002123.htm |
| [7] | 殷海峰, 梁兵兵, 徐宁. 管道泄漏率计算模型研究和程序开发[J]. 核技术, 2013, 36(4): 1–4. http://www.cqvip.com/QK/90373X/201504/664507574.html |
 2018, Vol. 40
2018, Vol. 40
