0 引　言

在“工业4.0”以及“中国制造2025”的时代背景之下，智能船舶、无人船舶成为当今造船业和船舶营运业发展的重点。实现机舱智能化、船舶智能化的前提条件是能够对船舶动力装置的重要系统或设备的未来状态进行评估，预测系统或设备的健康状态的发展趋势，为系统或设备的零部件置换策略和维修策略提供相应的依据。而能够实现状态评估的关键是对船舶动力装置系统或设备的状态参数进行准确的预测。随着船舶行业的发展，当前大多数的船舶冷却水系统采取的是中央冷却水系统的形式^[1]。海水冷却系统作为中央冷却水系统关键组成，承担着整个船舶系统与海水热量交换工作^[2]，若发生故障将会导致船舶柴油机产生的1/3左右的热量不能散发出去，妨碍柴油机甚至整个船舶系统的正常运行；海水冷却系统中海水与船舶舷外海水相通，若系统发生故障可能会导致舷外海水进入机舱，发生事故。基于上述原因，对船舶海水冷却系统的状态参数进行预测以及后续的状态评估具有十分重要的意义。目前，国内外专家学者对状态参数预测方法进行广泛研究，但大多集中在电力系统等其他领域，而针对船舶冷却水系统等方面的研究较少。郭克余^[3]提出运用ARMA时间序列的方法对船舶冷却水系统的参数进行预测，利用ARMA模型受外界环境因素影响较小并统一为时间因素处理等优点，能较为准确预测出冷却水系统未来参数，但ARMA模型在预测非线性问题方面有一定的局限性。王新全等^[4]建立了基于BP神经网络的时间序列预测模型对船舶柴油机排气温度趋势进行预测，用GA（遗传算法）对模型进行优化，通过验证表明建立的模型能够较为准确的预测船舶主机排气温度的变化趋势。虽然基于神经网络的参数预测方法在处理非线性问题上具有一定的优势，但容易受外界环境因素影响，并不适合单独用于船舶海水冷却系统的参数预测。针对如上问题，提出基于ARMA时间序列与BP神经网络相结合的船舶海水冷却系统状态参数混合预测模型，并验证其在提高船舶海水冷却系统参数预测精度方面的可行性。

1 模型的基本理论及建模过程 1.1 ARMA模型基本原理

自回归滑动平均模型（auto regression moving average model）简记为ARMA（p, q）模型，其一般表示形式为：

$\begin{split}{x_t} = {\emptyset _1}{x_{t - 1}} + {\emptyset _2}{x_{t - 2}} + \ldots + {\emptyset _p}{x_{t - p}} + {\varepsilon _t} - \\{\theta _1}{\varepsilon _{t - 1}} - {\theta _2}{\varepsilon _{t - 2}} - \ldots - {\theta _q}{\varepsilon _{t - q}}{\text{，}}\end{split}$

(1)

引进延迟算子B，k步线性延迟算子用B^k表示，使得

${{{ B}}}{x_t} = {x_{t - 1}}{\text{，}}$

(2)

${B^k}{x_t} = {x_{t - k}}{\text{，}}$

(3)

所以，式（1）可简记为

${{\phi }}\left( {{B}} \right){{\rm{x}}_t} = {\rm{\Theta }}\left( B \right){\epsilon _t}{\text{，}}$

(4)

式中： ${{\phi }}\left( {{B}} \right)\!\!=\!\!1 - {\phi _1}B - {\phi _2}{B^2} - \ldots - {\phi _p}{B^p}$ ； ${\rm{\Theta }}\left( B \right)\!=\!1 -{\theta _1}B - $ $ {\theta _2}{B^2} - \ldots - {\theta _q}{B^q}$ 。

特殊情况下，当p值为0时，ARMA（p, q）退化为q阶的滑动平均模型（moving average model）简记为MA模型^[5]；同理，当q值为0时，ARMA（p, q）退化为p阶的自回归模型（auto regression model）简记为AR模型。

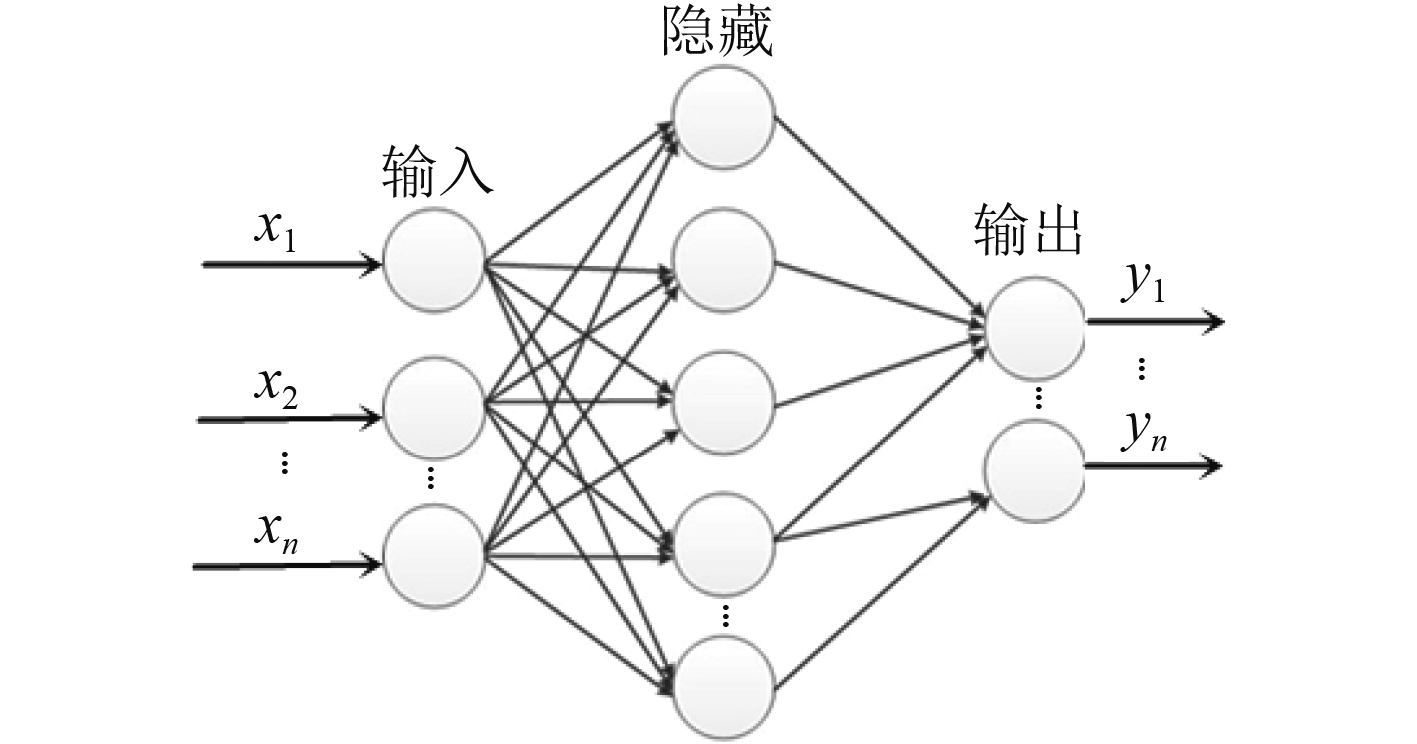
1.2 BP神经网络基本原理

BP神经网络一般为多层前向神经网络，是网络采用误差反向传播的学习算法^[6]，由输入、隐藏和输出3部分层次组成，其中隐藏层可以是单层或多层，层层之间全连接，能够模拟任何复杂非线性映射能力，构成如图1所示。

BP神经网络实现预测功能主要通过2种方法，一种是作为函数逼近器，对参数进行拟合预测；另一种是分析输入与输出的动态关系，利用带有反馈的动态神经网络对参数建立动态预测模型进行预测。当输入信号正向传播时，按图1箭头方向从输入层—隐藏层—输出层^[7]传播；当实际输出值与期望值相差较大时，则进入到逆向传播状态，即从输出层向输入层逐层调整连接权值达到减少误差的目的^[8]。BP神经网络的传递函数必须可微，多数情况下采用Sigmoid函数或线性函数作为传递函数，Sigmoid函数由下式确定：

${{f}}(x) = \frac{1}{{1 + {e^{ - x}}}}{\text{。}}$

(5)

1.3 混合预测模型的建模过程

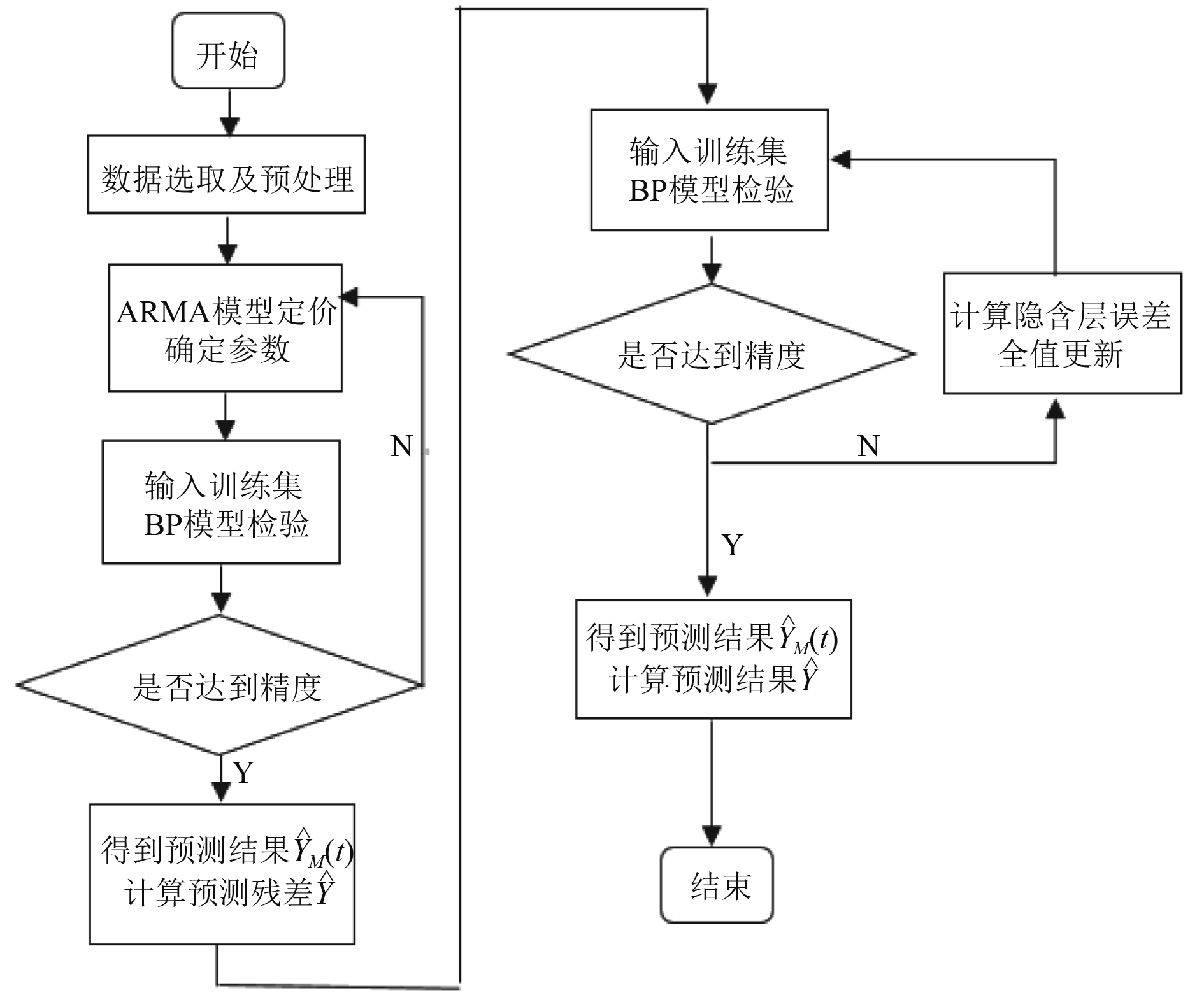
ARMA模型适用于对时间序列的线性部分进行预测，而在预测较复杂的非线性问题时误差往往较大，相反，BP神经网络具有较好的非线性问题的预测能力，而在处理线性问题时能力较弱。因此，提出一种兼备ARMA和BP神经网络各自优点的混合预测模型。混合预测模型包含ARMA线性子模型和BP神经网络非线性子模型2部分，能完整的对时间序列的线性部分和非线性部分进行预测，提高预测精度，预测框架如图2所示。

具体步骤如下：

1）要对时间序列进行预处理，若数据在一定范围内呈现一定的周期性和规律性，则说明时间序列不平稳，要对数据进行不定次差分处理，直至数据在一定范围内随机波动，没有明显的规律性。对于时间序列的平稳性检验，使用Matlab的adftest函数进行。

2）采用AIC方法对ARMA（p, q）模型定阶，定阶准则的公式为^[9]

$AIC = \ln \hat \sigma _\varepsilon ^2 + \frac{{2(p + q)}}{N}{\text{。}}$

(6)

式中： $\hat \sigma _\varepsilon ^2$ 为最大似然估计值；N为样本容量。选择使AIC值最小的p值和q值，则此ARMA（p, q）模型为最佳模型，令 ${\mathop Y\limits^ \wedge _{\rm{H}}}(t)$ 为ARMA模型的预测值，式（1）可写为：

${\mathop Y\limits^ \wedge _{{H}}}(t) = \sum\limits_{p = 1}^n {{\varphi _p}} {x_{t - p}} - \sum\limits_{q = 1}^m {{\theta _q}} {\varepsilon _{t - q}} + {\varepsilon _t}{\text{。}}$

(7)

3）利用最小二乘法对模型的参数进行估计，在实际模型定参过程中可以选用Matlab的armax（data, orders）函数来实现。对建立的ARMA（p, q）进行检验，当模型某参数显著为0要对模型重新定参，使模型达到最优。

4）模型参数确定之后将处理后的数据集输入到ARMA（p, q）模型进行训练，在Matlab中调用predict(sys, data, K)函数进行参数预测得到预测值 ${\mathop Y\limits^ \wedge _{{H}}}(t)$ ，之后根据式（8）可以得到ARMA线性子模型的预测余项即残差为：

${\mathop Y\limits^{} _M}(t) = {Y_t} - {\mathop Y\limits^ \wedge _H}(t){\text{，}}$

(8)

式中， ${Y_t}$ 为实际监测数值。

5）建立BP神经网络非线性子模型，确定模型参数和权值，将式（8）得到的预测余项 ${\mathop Y\limits^{} _M}(t)$ 作为非线性子模型的训练集，得到预测结果 ${\mathop Y\limits^ \wedge _M}(t)$ ：

${\mathop Y\limits^ \wedge _M}(t) = {a_0} + \sum\limits_{j = 1}^m {{w_j}f({a_{0j}} + \sum\limits_{i = 1}^n {{w_{ij}}{Y_{M(t - i)}}} ) + {\varepsilon _t}}{\text{，}} $

(9)

式中： ${w_j}$ 和 ${w_{ij}}$ 为BP神经网络的连接权值；m，n表示BP神经网络的输入层和隐藏层的节点数； ${a_0}$ 和 ${a_{0j}}$ 为偏置项； ${\varepsilon _t}$ 为在时间t时的预测误差；f为传递函数（5），将 ${\mathop Y\limits^{} _M}(t)$ 即ARMA线性子模型的残差作为BP非线性子模型的输入，对BP模型训练，获得预测值 ${\mathop Y\limits^ \wedge _M}(t)$ 。

6）综合式（7）、式（8）、式（9），建立混合预测模型的表达式为：

$\left\{ \begin{aligned} & \mathop {{Y_t}}\limits^ \wedge = {\mathop Y\limits^ \wedge _{\rm{H}}}(t) + {\mathop Y\limits^ \wedge _M}(t){\text{，}} \\& {\mathop Y\limits^ \wedge _{\rm{H}}}(t) = \sum\limits_{p = 1}^n {{\varphi _p}} {x_{t - p}} - \sum\limits_{q = 1}^m {{\theta _q}} {\varepsilon _{t - q}} + {\varepsilon _t}{\text{，}} \\& {\mathop Y\limits^{} _M}(t) = {Y_t} - {\mathop Y\limits^ \wedge _H}(t){\text{，}} \\& {\mathop Y\limits^ \wedge _M}(t) = {a_0} + \sum\limits_{j = 1}^m {{w_j}f({a_{0j}} + \sum\limits_{i = 1}^n {{w_{ij}}{Y_{M(t - i)}}} ) + {\varepsilon _t}}{\text{。}} \end{aligned} \right.$

(10)

式中， $\mathop {{Y_t}}\limits^ \wedge $ 为混合预测模型最终的预测结果。

2 海水冷却系统状态参数预测 2.1 海水冷却系统状态参数选取

以“育鲲轮”为目标船舶，在正常工况下，选取该船海水冷却系统非故障状态参数作为训练集，包括海水泵进、出口压力，中央冷却器海水侧进、出口温度以及中央冷却器淡水侧出口温度5种状态参数，5种状态参数正常值如表1所示。以2 h为时间间隔，对系统5种状态参数进行采集并记录为1组数据，1天采集12组数据，以前5天共60组数据作为训练集，对第6天的12组数据进行预测，并记录第6天的观测值。6天采集的简要历史数据如表2所示。

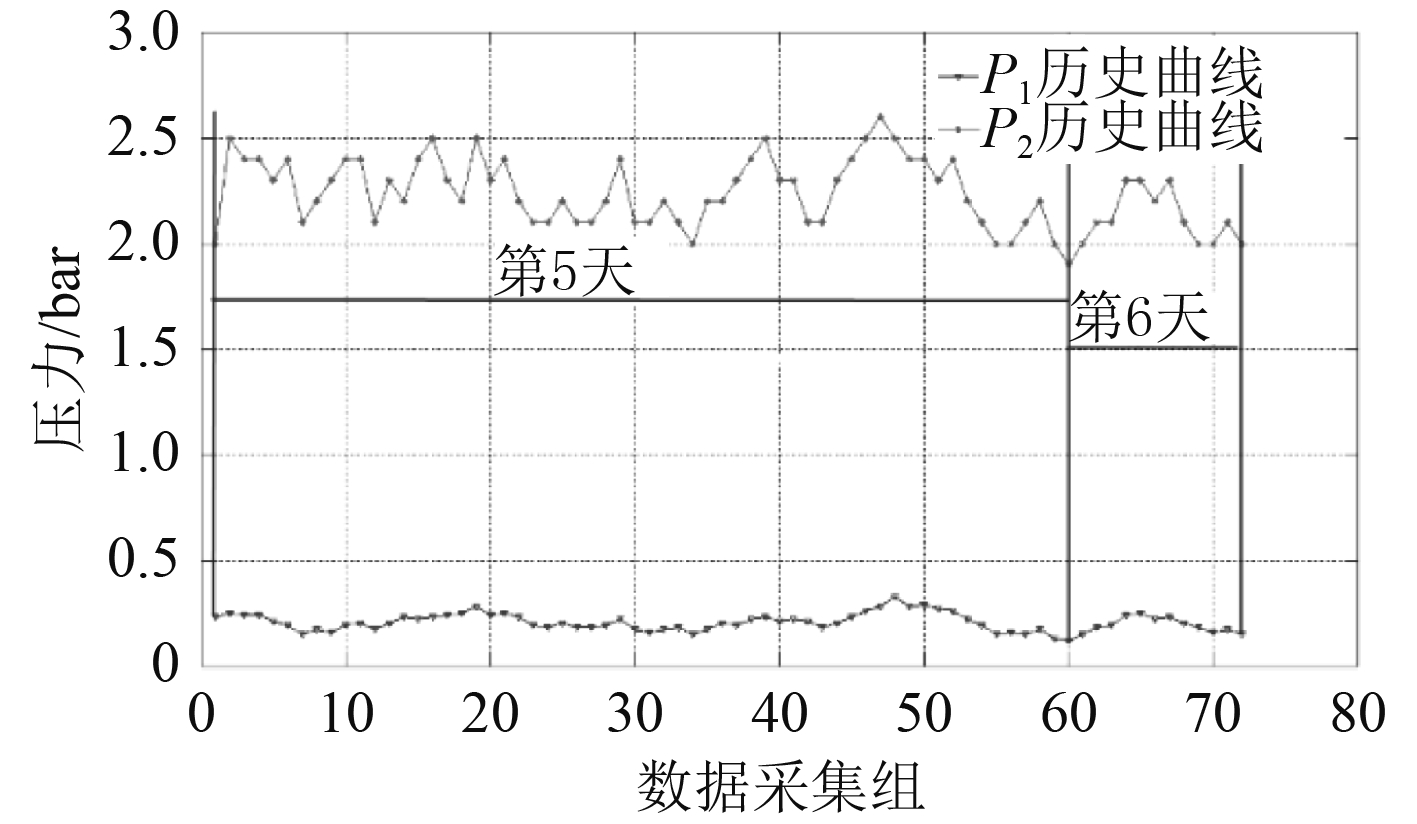
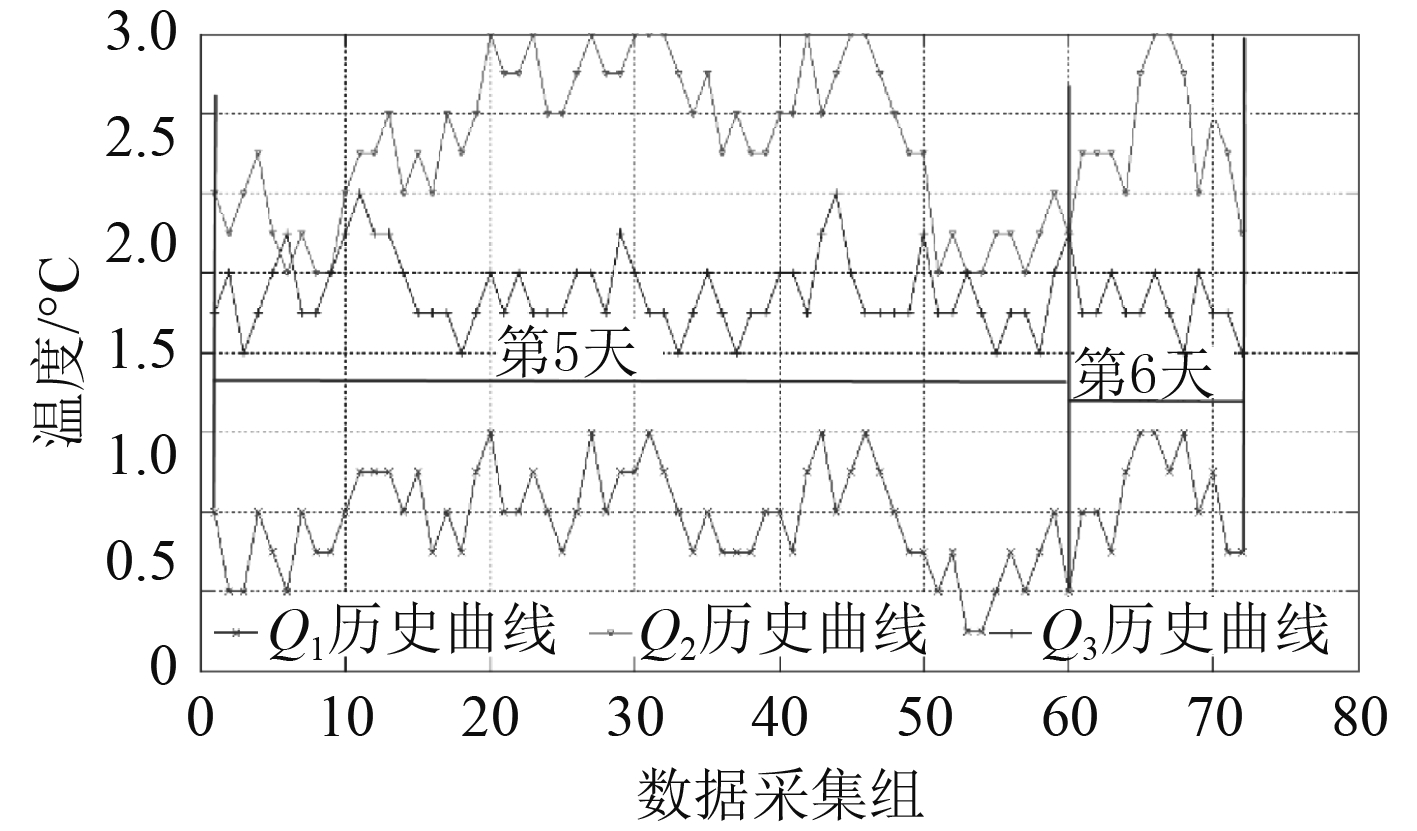
海水泵进、出口压力历史曲线P₁, P₂如图3所示，中央冷却器海水侧进、出口温度曲线Q₁, Q₂和淡水侧出口温度历史曲线Q₃如图4所示。

2.2 混合预测模型确定

在Matlab环境下，通过adftest函数对历史数据进行分析发现在采集时间内的5种状态参数平稳性良好，不需要对数据进行去趋势化处理。通过分析5种状态参数的偏自相关函数和自相关函数发现都为拖尾型，确定线性子模型为ARMA（p, q）模型^[10]。以海水泵进口压力混合预测模型建立为例，采用AIC准则对模型进行定阶，发现当p，q值为[1, 1]时AIC值最小，建立的ARMA（1，1）模型为最佳线性子模型。

在线性子模型定阶之后，在Matlab环境下运用armax(data, [p, q])函数对线性子模型参数进行估计，将海水泵进口压力前5天历史数据作为训练集对模型进行训练，利用predict(sys, data, K)函数对第6天12组数据进行预测，并与第6天实际记录数值进行比较，判断模型预测的准确性，不断调整模型参数，直至预测值达到精度要求，最终获得的第6天12组数据为 ${\mathop Y\limits^ \wedge _{\rm{H}}}(t1)$ 。模型参数确定之后，对6天的全部72组数据进行预测，通过式（8）得到线性子模型的预测残差 ${\mathop Y\limits^{} _M}(t1)$ 。建立BP非线性子模型，不断调整模型参数和连接权值，将前5天的60组预测残差进行归一化处理并作为训练样本集，对第6天的12组预测残差进行预测。BP神经网络非线性子模型采用4-9-1三层结构，设定训练次数为10 000，训练目标取0.000 5，学习速率为0.1。获得的第6天12组预测的残差数据为 ${\mathop Y\limits^ \wedge _M}(t1)$ ，将上述获得的 ${\mathop Y\limits^ \wedge _M}(t1)$ 和 ${\mathop Y\limits^ \wedge _{{H}}}(t1)$ 代入式（10）中的 $\mathop {{Y_t}}\limits^ \wedge = {\mathop Y\limits^ \wedge _{{H}}}(t) + {\mathop Y\limits^ \wedge _M}(t)$ ，获得基于混合预测模型的海水泵进口压力最终预测结果 $\mathop {{Y_{t1}}}\limits^ \wedge $ 。将第6天的海水泵进口压力观测值、ARMA模型预测值和混合预测模型预测值绘制对比曲线图如图5所示。

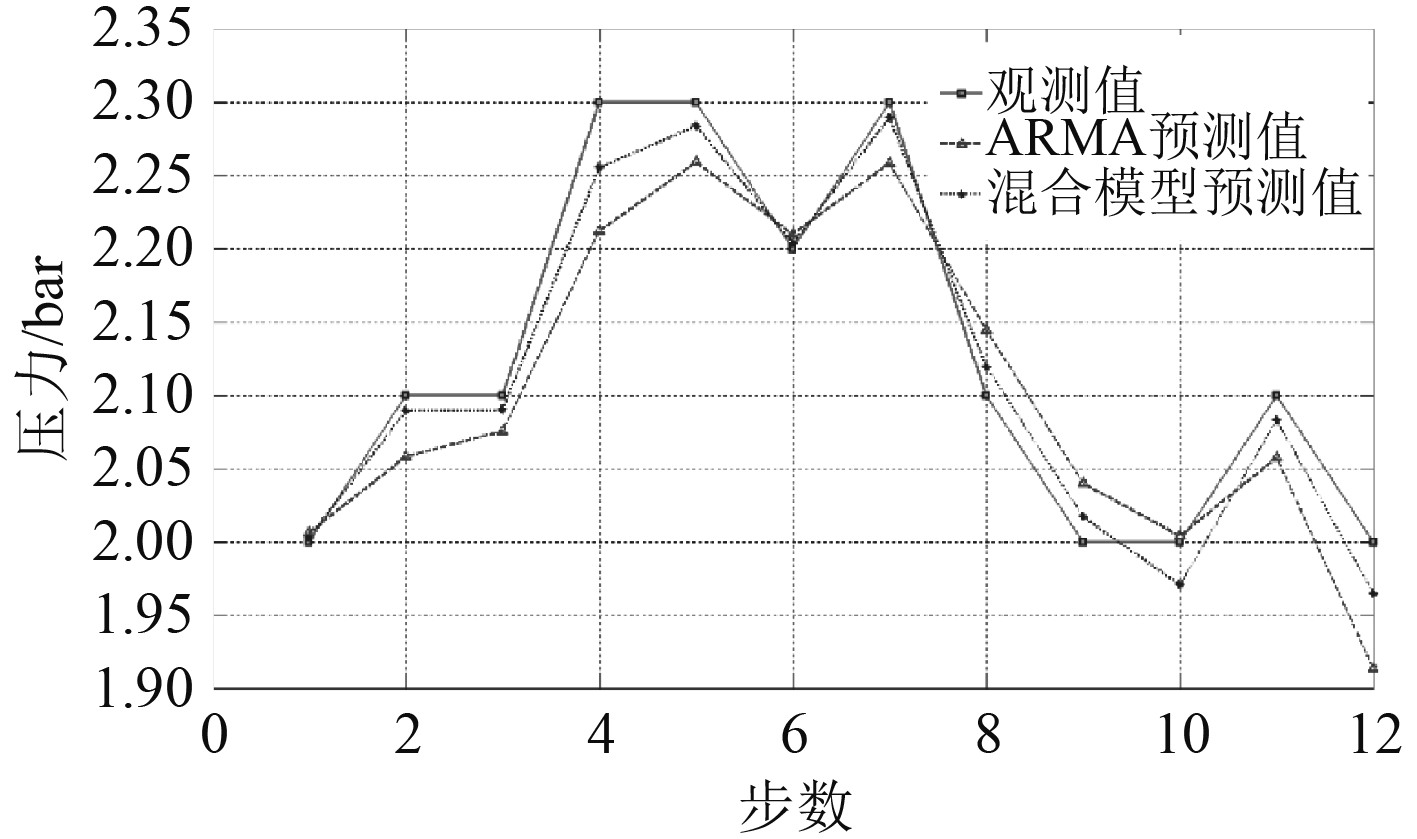
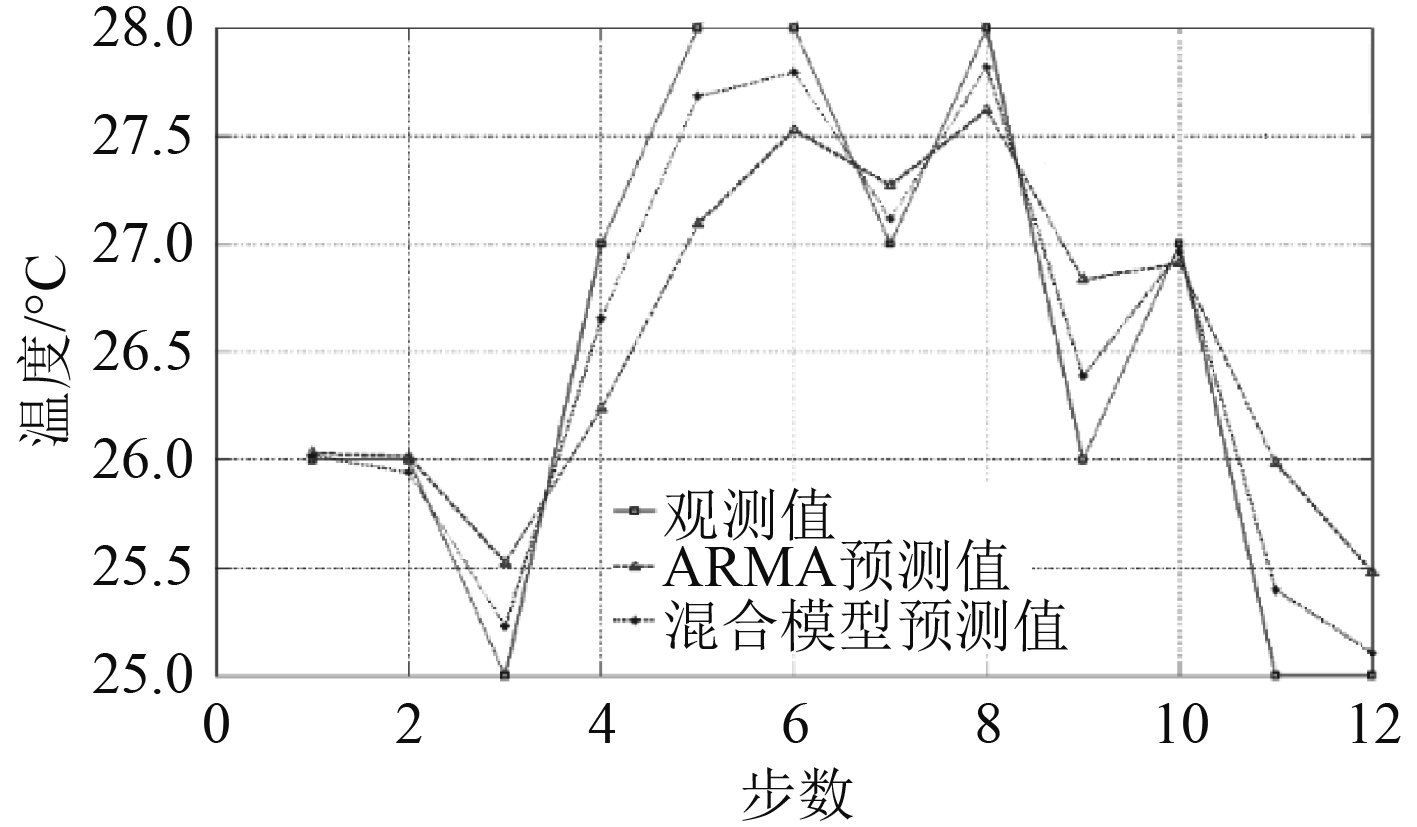
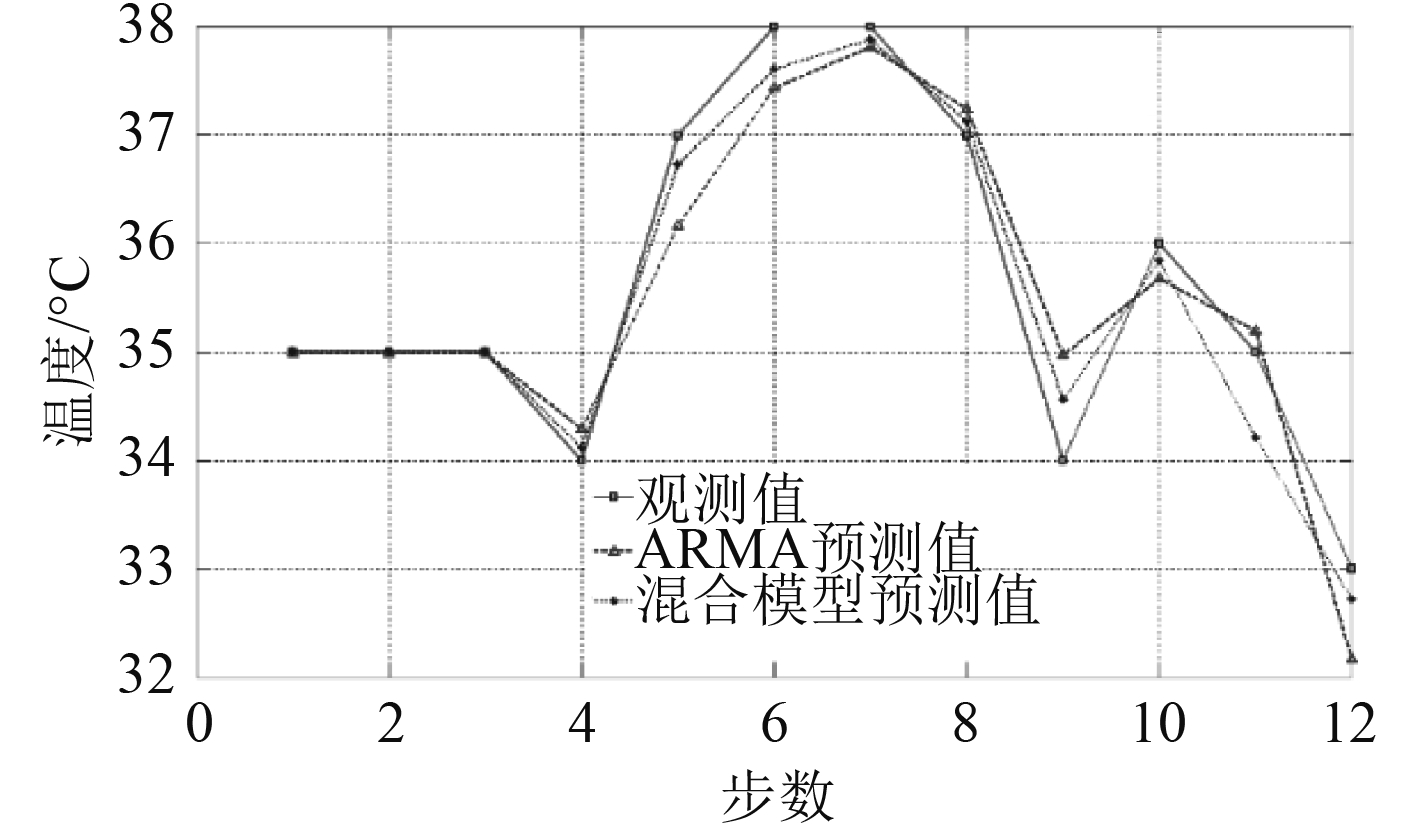
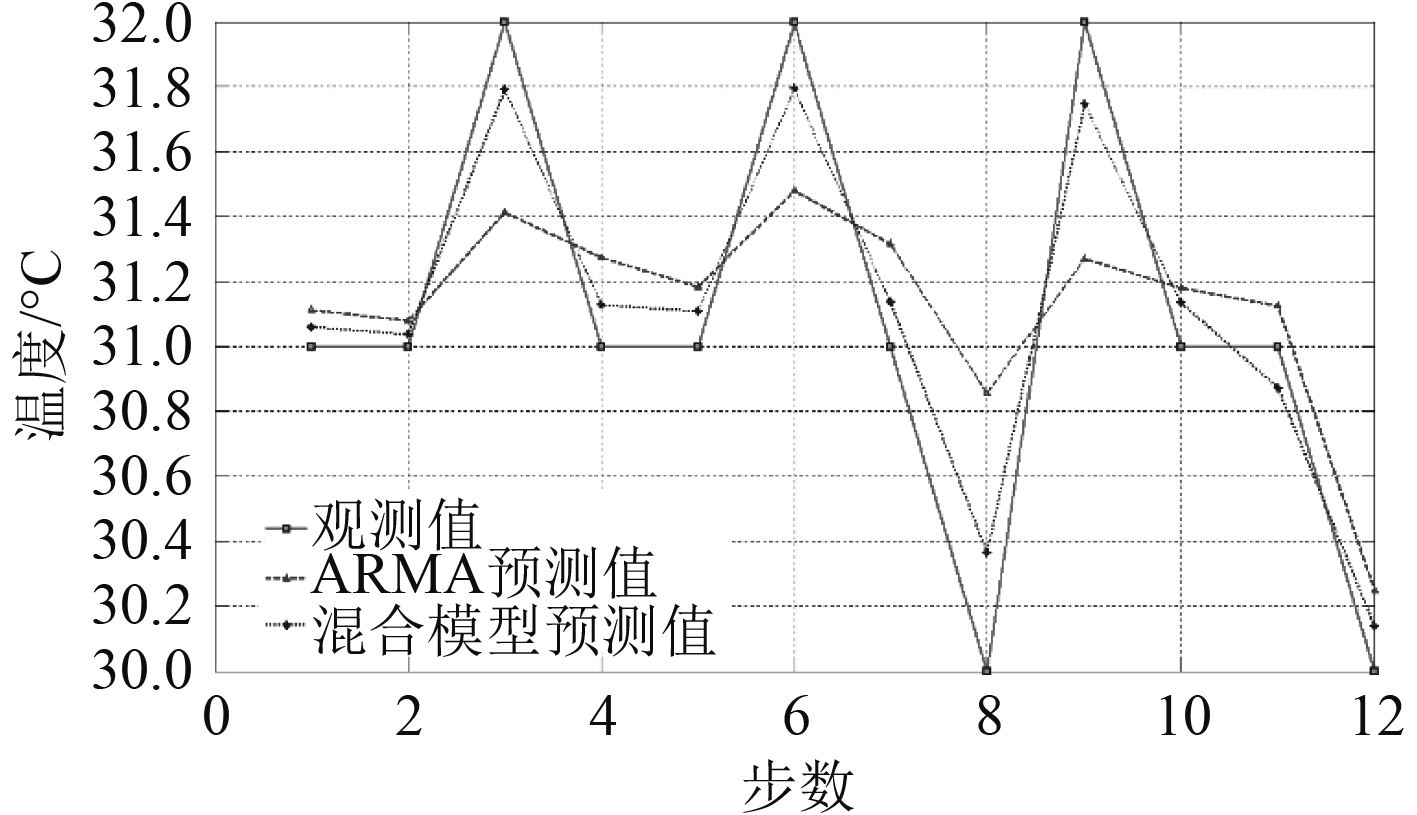
同理，分别将海水泵出口压力，中央冷却器海水进、出口温度，中央冷却器淡水出口温度前5天的历史数据输入到海水冷却系统混合预测模型，分别设置模型参数得到第6天的12组预测数值如表3所示，绘制每种状态参数观测值、ARMA模型预测值和混合预测模型预测值的对比曲线图，分别如图6 ~ 图9所示。

从绘制的数据对比图可以看出，海水冷却系统混合预测模型比ARMA预测模型的精度要高，更趋近于实际观测值，整体趋势与实际观测值更为吻合。

2.3 混合预测模型验证与分析

从5种状态参数的预测数据对比图中可以看出，混合预测模型的预测结果大部分在实际观测值以下，只有一小部分在实际观测值之上，具有一定的不确定性。在趋势预测之后采用平均绝对百分比误差法（MAPE）作为评价指标，对预测数值的准确性进行评定，如果评定效果不理想，要重新对模型进行优化处理。

平均绝对百分比误差：

$MAPE = \frac{1}{N}\sum\limits_{i = 1}^n {\left| {\frac{{{x_{fi}} - {x_{ai}}}}{{{x_{ai}}}}} \right|} \times 100\% {\text{。}}$

(11)

式中：N为预测个数； ${x_f}$ 为预测值； ${x_a}$ 为实际观测值。

分别将5种状态参数在海水冷却系统状态参数混合预测模型和ARMA模型下的预测值与实际观测值代入式（11），得到2种预测模型的MAPE值如表4所示。

将表4中基于混合预测模型得到的MAPE值与ARMA预测模型得到的MAPE值进行对比发现，基于混合预测模型得到的预测参数的MAPE值整体比ARMA模型的MAPE值要小，表明本研究建立的海水冷却系统混合预测模型比ARMA时间序列预测模型效果要好，可以提高海水冷却系统状态参数的预测精度；而且海水冷却系统状态参数混合预测模型的平均绝对百分比误差（MAPE）全部在1%以下，可以认为本研究建立的海水冷却系统状态参数混合预测模型具有很好的预测能力。

3 结　语

本研究选取“育鲲轮”海水冷却系统5种状态参数5天的历史数据作为训练集，第6天的观测值作为验证数据，建立基于ARMA线性子模型和BP神经网络非线性子模型相结合的船舶海水冷却系统状态参数混合预测模型。通过绘制不同预测模型的预测数据对比图以及运用平均绝对百分比误差法对预测结果进行验证，结果表明本研究所搭建的海水冷却系统状态参数混合预测模型可以提高参数预测精度，预测值与实际观测值更为吻合，与ARMA模型相比能更有效的预测出5种状态参数在未来一段时间的变化趋势，能更为有效地反映出海水冷却系统在未来一段时间的工作状态的变化趋势，尽早判断系统是否存在异常情况，为系统或设备的零部件置换策略和维修策略提供相应的依据，提高船舶的安全性；为系统和设备的剩余寿命预测以及实现“事后维修”向“视情维修”转变奠定基础，是实现智能船舶、无人船舶的重要一步。