0 引　言

日益减小的北极冰带，使北极的航道、地区能源、矿物资源成为新的关注点，促使了冰区船的发展^[1]。冰区环境中航行船的螺旋桨会经常性的碰撞冰块，导致桨-轴的扭振传递，相对于无冰区航行船来说，该种轴系扭振响应非常复杂。冰冲击引起的转速变化会进一步促使桨激励、主机激励、冰载荷发生非周期性改变，以往的稳态方法不能表达这些激励载荷，为提高该种轴系的安全性，应当采用时域计算方法。

目前，对冰载荷下的轴系扭振研究逐渐增多，肖能齐^[2]考虑桨-冰激励扭矩和电机电磁激励扭矩，利用傅里叶函数得到冰载荷简谐力，在频域上模拟了轴系强迫扭振；杨红军^[3]使用Matlab，对某船推进轴系在冰载荷作用下的瞬态响应做了数值计算；Ronald D. Barro^[4]结合实际瞬态扭振测量和桨-冰载荷的理论分析，分析了弹性联轴器刚度对扭振的影响；Sebastian persson^[5]剖析了稳态和瞬态2种方法，并对转速和相位对冰载荷下的轴系扭振影响进行了瞬态计算；Mr. GeirDahler^[6]对1艘散货船在冰载荷下的轴系扭振测试数据、稳态动力和瞬态动力仿真结果进行了比较分析。

对于冰载荷下的轴系扭振，考虑试验难度和成本，采用数值方法校核显得非常重要。本文利用Abaqus有限元分析软件，基于Newmark理论，针对一个柴油机推进轴系稳定运行工况下的瞬态扭振进行仿真计算，将时域与频域计算结果进行对比；同时，在考虑柴油机调速器的情况下，利用刚性轴模型，采用该时域方法计算冰载荷下轴系的扭振响应。

1 轴系扭振时域计算方法Newmark理论

轴系扭振瞬态响应动力学方程：

${ J}\ddot \theta + { C}\dot \theta + { K}\theta = {{ M}_{\text{主机}}}(t) + {{M}_{\text{浆}}}(t) + {{M}_{\text{冰}}}(t){\text{，}}$

(1)

式中：K为扭转刚度矩阵；C为阻尼矩阵；J为转动惯量矩阵； $\theta $ 为扭转角矢量； $\dot \theta $ 为扭转角速度矢量； $\ddot \theta $ 为扭转角加速度矢量；M为激励扭矩矢量（主机、螺旋桨、冰）。

Newmark $\beta $ 方法近似假设：

${\dot \theta _{t + \Delta t}} = {\dot \theta _t} + (1 - \delta ){\ddot \theta _t} \cdot \Delta t + \delta {\ddot \theta _{t + \Delta t}} \cdot \Delta t\text{，}$

(2)

${\theta _{t + \Delta t}} = {\theta _t} + {\dot \theta _t} \cdot \Delta t + (0.5 - \beta ){\ddot \theta _t} \cdot \Delta {t^2} + \beta {\ddot \theta _{t + \Delta t}} \cdot \Delta {t^2}\text{。}$

(3)

将式（2）、式（3）代入式（1），可计算经过 $\Delta t$ 时间后的角位移响应 ${\theta _{t + \Delta t}}$ 、角速度响应 ${\dot \theta _{t + \Delta t}}$ 和加速度响应 ${\ddot \theta _{t + \Delta t}}$ ，进一步可得到轴系的扭矩响应和扭振应力。

当 $\delta \geqslant 0.5$ ， $\beta = 0.25{(0.5 + \delta )^2}$ 时，此方法无条件稳定^[7-8]。

2 柴油机推进轴系扭振时域计算方法研究

本文以1艘冰区加强船上的推进轴系为研究对象，先对涉及扭振的激励扭矩进行仿真分析，再对无冰载荷下的轴系进行扭振时域分析，利用傅里叶函数将结果转换到频域，与频域方法计算结果进行对比，来验证该时域方法合理性。

2.1 研究对象

该船的冰级符号为B1，主机为二冲程6缸柴油机，曲柄半径88.5 cm，连杆长度177 cm，气缸直径40 cm，往复部件重量1 544 kg，额定功率和转速为6 810 kW，146 r/min，4叶螺旋桨，推进轴系参数如表1所示。

2.2 计算模型、激励载荷和阻尼

1）计算模型

根据推进轴系系统的参数可建立模型，如图1所示，轴段采用梁单元B32，大小为0.1 m，集中元件采用11个点单元ROTARYI，阻尼为1个CONN3D2单元。

2）激励载荷

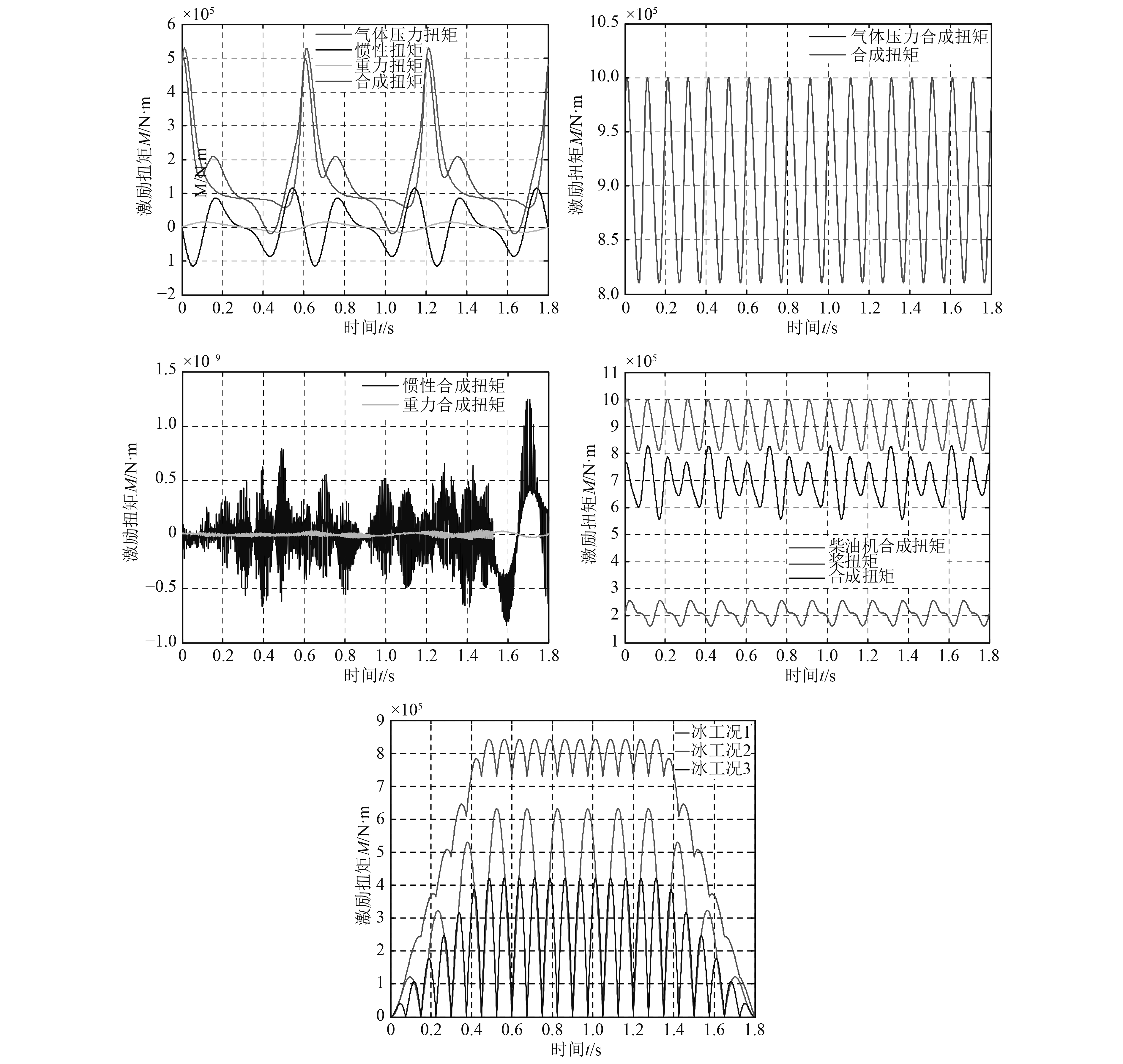
本文采用经验公式和系数^[9-10]来获得主机、螺旋桨和冰载荷（4叶桨）。通过Matlab程序对相关激励载荷进行时域仿真，如图2所示，计算转速为100 r/min。

载荷分析：可看出M_气体>>M_惯性>M_重力，后两者数量级为9–10，气缸总扭矩基本与气体压力扭矩相同；机-桨合成扭矩均为周期型激励，即为简谐力，主机扭矩约为桨的4.5倍；冰载荷中，M₂>M₁>M₃，起始和结束曲线幅值依线性斜坡函数变化，即为非稳态力，不能作为简谐力来处理，也就不适合用频域方法计算。

在时域分析中，据实际情况将激励载荷添加到有限元模型，包含主机各气缸和桨的扭矩，方向相反。

3）阻尼

通过表1中的阻尼数据和计算的桨阻尼可知，C_桨>>C_主机，相差3个数量级，所以本文只考虑螺旋桨阻尼。

2.3 轴系扭振时域计算方法的可行性验证

根据模态分析和Holzer法得到前3阶固有频率来进行对比，证明无阻尼模型合理性，如表2所示，误差均在5%以内，满足要求；

对40～160 r/min（间隔10 r/min）和64 r/min转速处敞水中的轴系扭振进行时域仿真，只考虑主机、桨激励，以及阻尼，在这些条件下，整个系统达到平衡。利用傅里叶变换，将结果从时域转到频域，与频域方法计算结果进行对比，分析时域方法可行性。

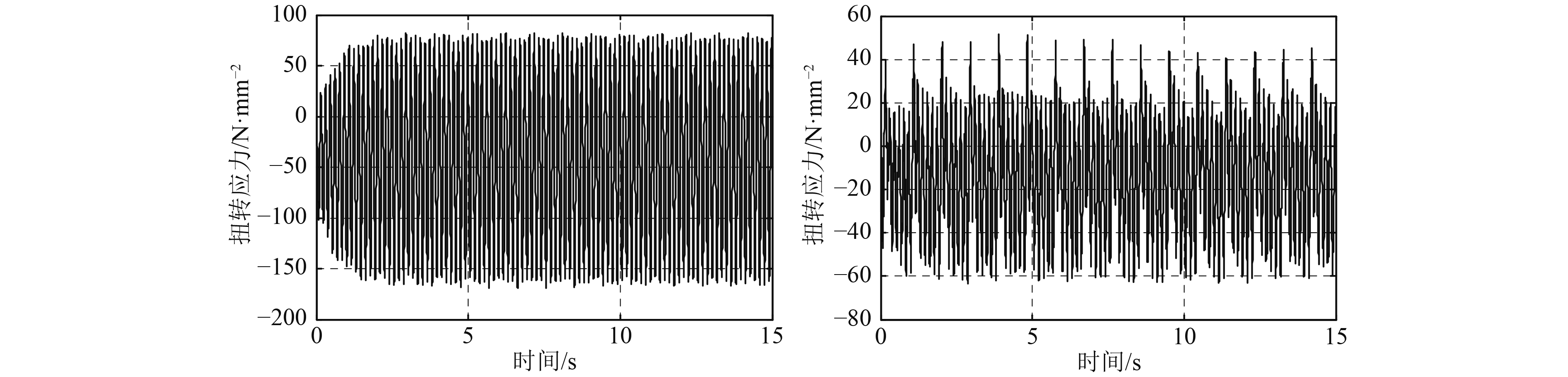
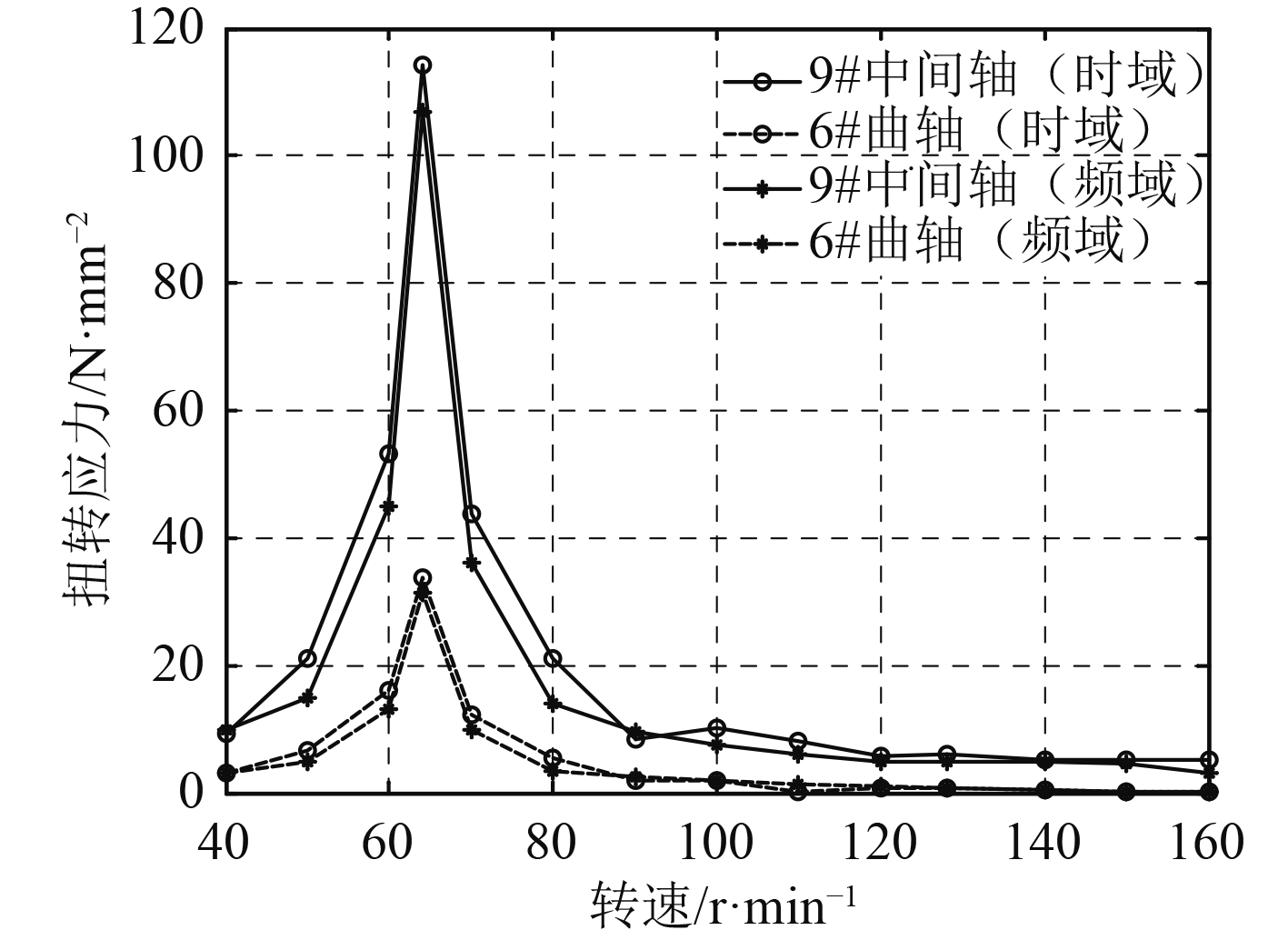
这里给出64 r/min转速处，9#中间轴、6#曲轴的时程应力曲线和傅里叶变换结果，如图3和图4所示。频域方法和Newmark时域方法计算9#中间轴、6#曲轴的6谐次扭振应力结果对比，如图5可知，时域与频域结果曲线变化趋势非常相似，而且峰值大小相当，峰值处对应转速频率基本相同，分别为6.4Hz，6.409 Hz。

经过对比2种计算结果可知：该时域方法中模型、激励载荷、阻尼的建立方式合理，可用于冰载荷下的轴系扭振计算。

3 冰载荷下柴油机推进轴系扭振的时域计算

以往针对结构振动的计算，直接在柔性结构上施加激励载荷进行求解，该情况是已知激励载荷下的计算，但是在本文中考虑到冰对桨的激励会导致螺旋桨的转速发生变化，而转速又会反过来影响主机、桨和冰3种激励载荷，3种激励载荷之间互相影响，所以本文中涉及到的冰载荷下轴系扭振计算方法有所区别。

本文中冰载荷下轴系扭振计算方法，先利用刚性轴模型，根据主机、桨和冰载荷间的平衡关系，不考虑阻尼影响，采用式（4）递推出各种激励载荷的时程曲线；然后，在考虑阻尼的情况下，将各种激励载荷施加在推进轴系的有限元模型上，计算出推进轴系的扭振响应。在实际考虑阻尼的情况下，轴系转速会低一些，实际激励载荷会比递推出来的激励载荷小，所以利用该方法计算的结果稍偏保守、安全，可以应用于计算轴系的扭振响应。

这里计算了柴油机正常发火情况，额定转速146 r/min时，冰载荷3种工况冲击下的轴系扭振响应。

3.1 激励载荷的计算

利用刚性轴模型，根据下面动力学递推公式来得到所需要的转速、各气缸（考虑柴油机惯性合成扭矩和重力合成扭矩）和螺旋桨处的激励扭矩，以及螺旋桨处的冰扭矩^[10]。公式如下：

$\delta n = \delta t\frac{{{M_{chai}} - ({M_{ow}} + {Q_{ice}})}}{{2\pi I}}\text{。}$

(4)

式中： ${M_{chai}}$ 为柴油机输出均扭矩； ${M_{ow}}$ 为螺旋桨激励扭矩； ${Q_{ice}}$ 为冰扭矩； $I$ 为系统转动惯量； $\delta t$ 为单位时间间隔； $\delta n$ 为单位时间后的转速变化。

柴油机的扭矩特点一定程度上依靠涡轮增压器的布置，在冰桨相互作用的环境中，会引起突然地过载，并带有间接地转速下降，“动态”特性会有点高。当冰冲击发生时，假定主机以全功率运行。主机转速会降低，但是由于涡轮增压器的转子运动活跃，主机会临时被提供比“静态”情况下更多的空气，会使柴油机抗冲击性提高，转速不会突然下降，该现象可以成为柴油机的控制策略或者调速器作用。可以用一个粗略的经验方法来仿真调速器模型，如下：

主机扭矩作为转速n和时间t的函数^[11]：

$T(n;t) = {T_{static}}(n) + \Delta {T_{dyn}}(t)\text{，}$

(5)

式中： ${T_{static}}(n)$ 为柴油机稳定状态运行时的输出扭矩； $\Delta {T_{dyn}}(t)$ 为冰载荷冲击下导致的柴油机补偿扭矩。

$\Delta {T_{dyn}}(t)$ 是假定能够使主机维持额定扭矩 ${T_{rated}}$ 一小段短时间，可以描述为：

$\Delta {T_{dyn}}(t) = ({T_{rated}} - {T_{static}})*(1 - t/3)\text{。}$

(6)

当 ${T_{static}} < {T_{rated}}$ 时，t从0开始，并且3 s后结束。

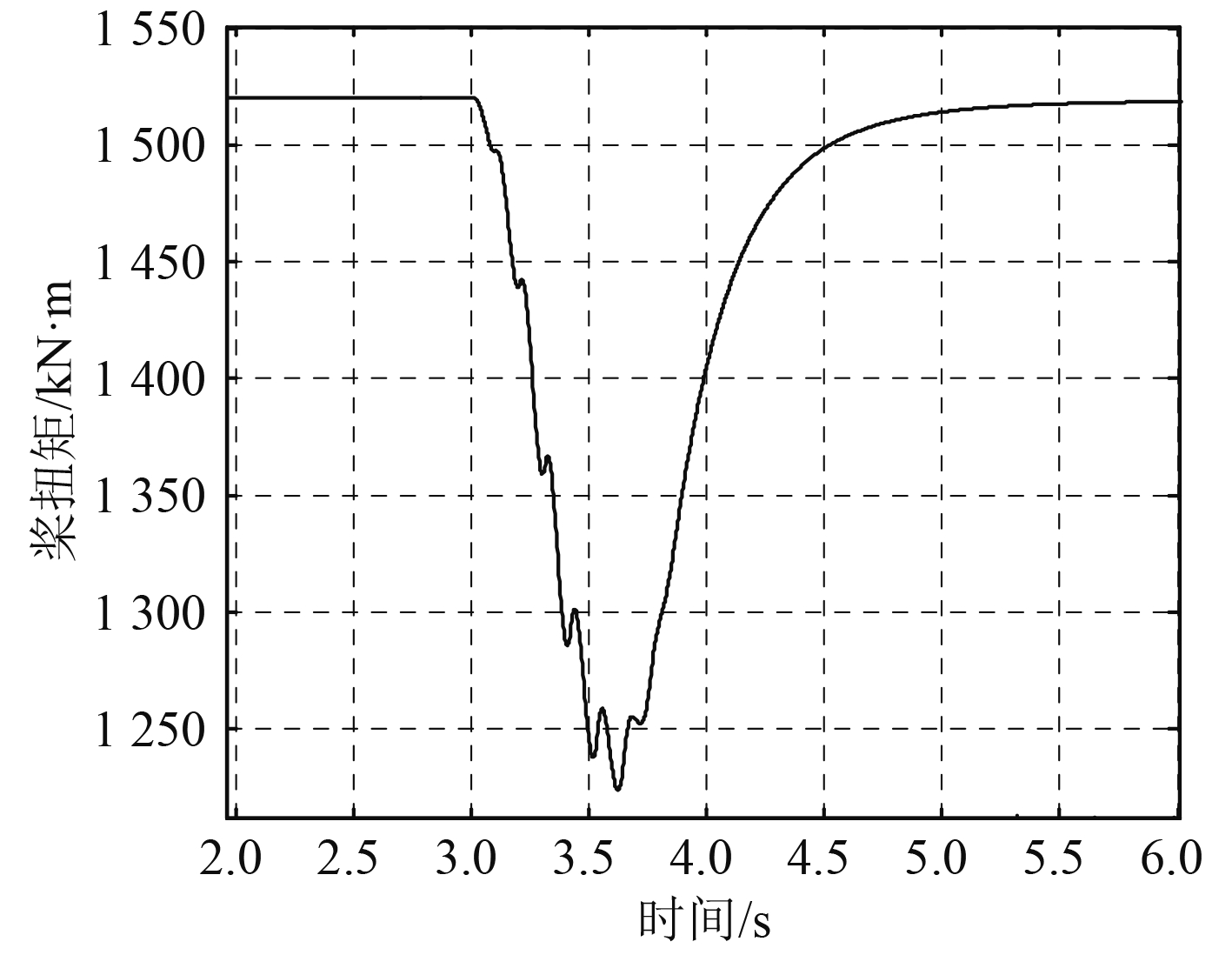
根据以上公式和各种激励载荷的计算公式，可以得到3种冰载荷冲击工况下的柴油机转速、各种激励载荷的仿真曲线，在此处，只给出工况1的激励载荷，如图6~图11所示。

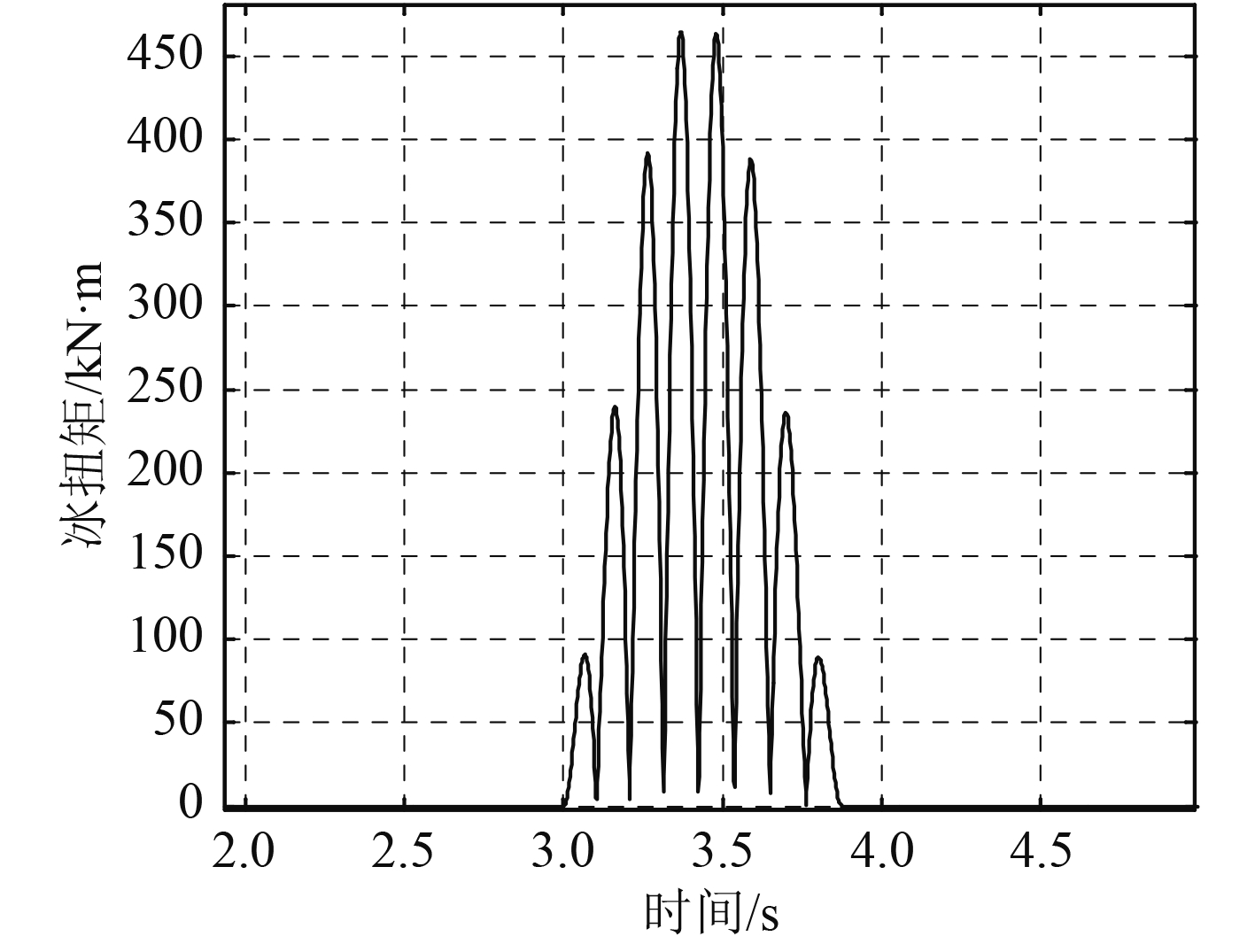
从图6~图8可以看出，均转速、柴油机总输出均扭矩、桨均扭矩，在冰载荷冲击下，由于柴油机具有自身的调速器控制策略，会比较陡地、缓慢地、有着接近周期性变化的降低，并且转速变化范围不是很大，下降过程产生下凹是因为冰载荷扭矩激励是周期性切削扭矩；对应着图9，可以看出，冰扭矩在初始和结束时，峰值呈线性变化，中间两大大峰值会引起转速、柴油机扭矩和桨扭矩曲线下边最大的2个下凹，在冰载荷倒数第3个峰值结束后，柴油机转速会一直上升，同样，柴油机扭矩和螺旋桨扭矩会跟着同步增加，根据规范^[11]计算得到冰载荷跟螺旋桨作用时间为2圈，即720°；最终，柴油机输出扭矩与螺旋桨吸收扭矩相等后，整个系统达到平衡。

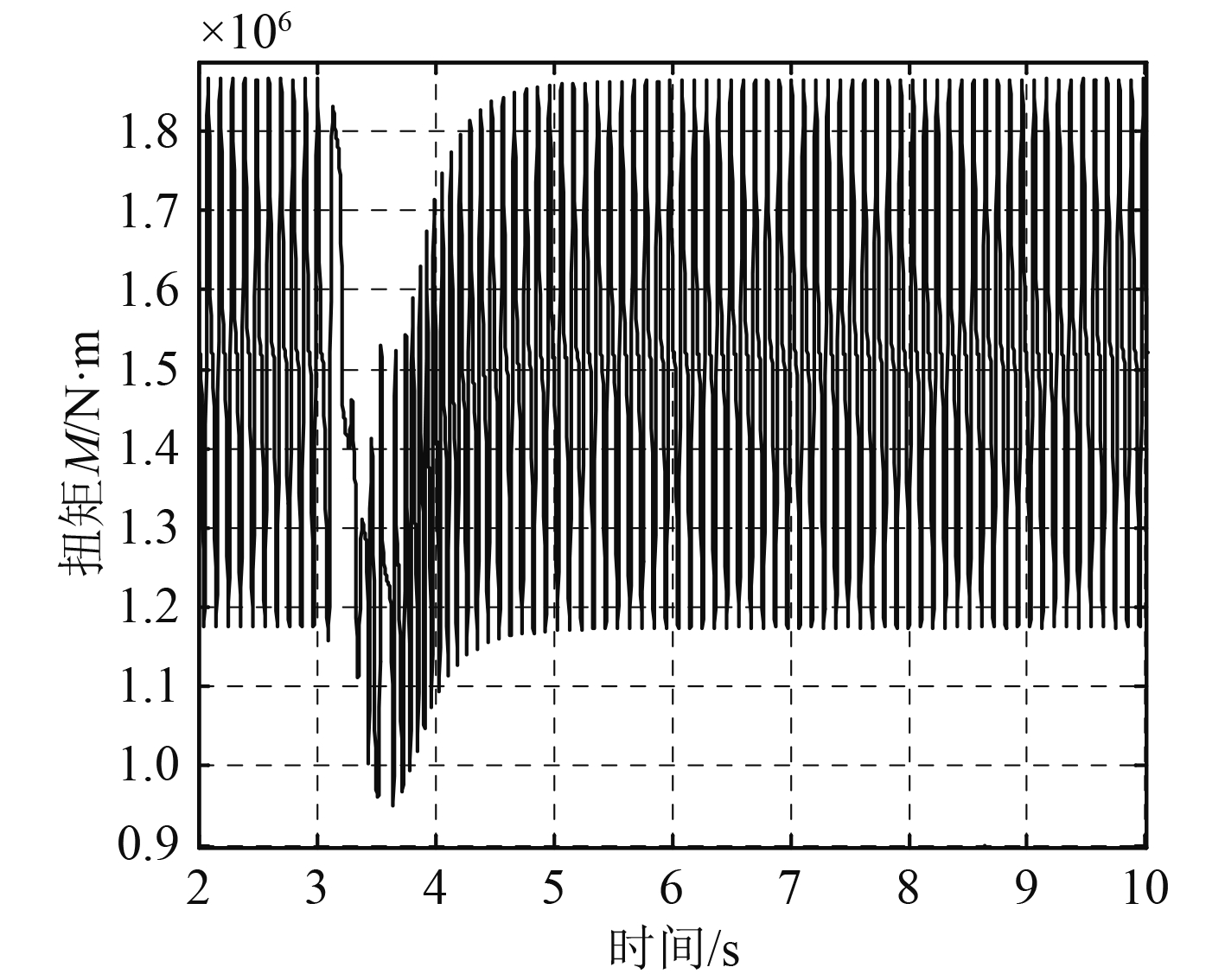
图10和图11为轴系扭振计算中使用的螺旋桨激励扭矩和柴油机6个气缸的气体压力激励扭矩，螺旋桨激励扭矩考虑螺旋桨的叶频和倍叶频激励，柴油机的气体压力激励扭矩考虑前16个谐次的简谐力。受轴系转速的影响，螺旋桨在冰载荷冲击期间，瞬态激励扭矩变化很大；柴油机气体压力激励扭矩同样是，只是不同气缸受冰载荷的影响程度不一样，主要是各气缸之间的相位角不同，导致它们产生的激励扭矩不一样，第1缸、第5缸、第6缸激励扭矩曲线相似，因为它们之间的相位角为0°，60°，300°，第2缸、第4缸、第3缸受冰载荷冲击影响依次减小，它们的相位角为240°，180°，120°，从此处可以看出，在柴油机运行过程中，与冰块碰撞时，曲轴在不同的相位角处会影响柴油机的激励扭矩，会导致轴系产生不同的扭振响应。

3.2 轴系扭振阻尼的计算

本算例中，根据表1中的数据，可以发现主机阻尼很小。根据Archer公式，经验上来说，螺旋桨均扭矩形成的系数为20，一般冰载荷冲击下桨转速变化，导致产生的系数为28，所以，计算剩余阻尼时，取该系数为8，可以计算得到阻尼系数为83 306 Nms/rad。由于螺旋桨阻尼相对主机阻尼大很多，整个系统几乎主要是螺旋桨阻尼，所以这里只考虑螺旋桨阻尼。计算公式如下：

${c_p} = A\frac{{{T_p}}}{{{n_p}}}\text{。}$

(7)

式中： $A$ 为Archer系数，取值为25~35； ${T_p}$ 为螺旋桨扭矩，N.m； ${n_p}$ 为螺旋桨转速，r/min。

3.3 冰载荷下轴系扭振的时域计算

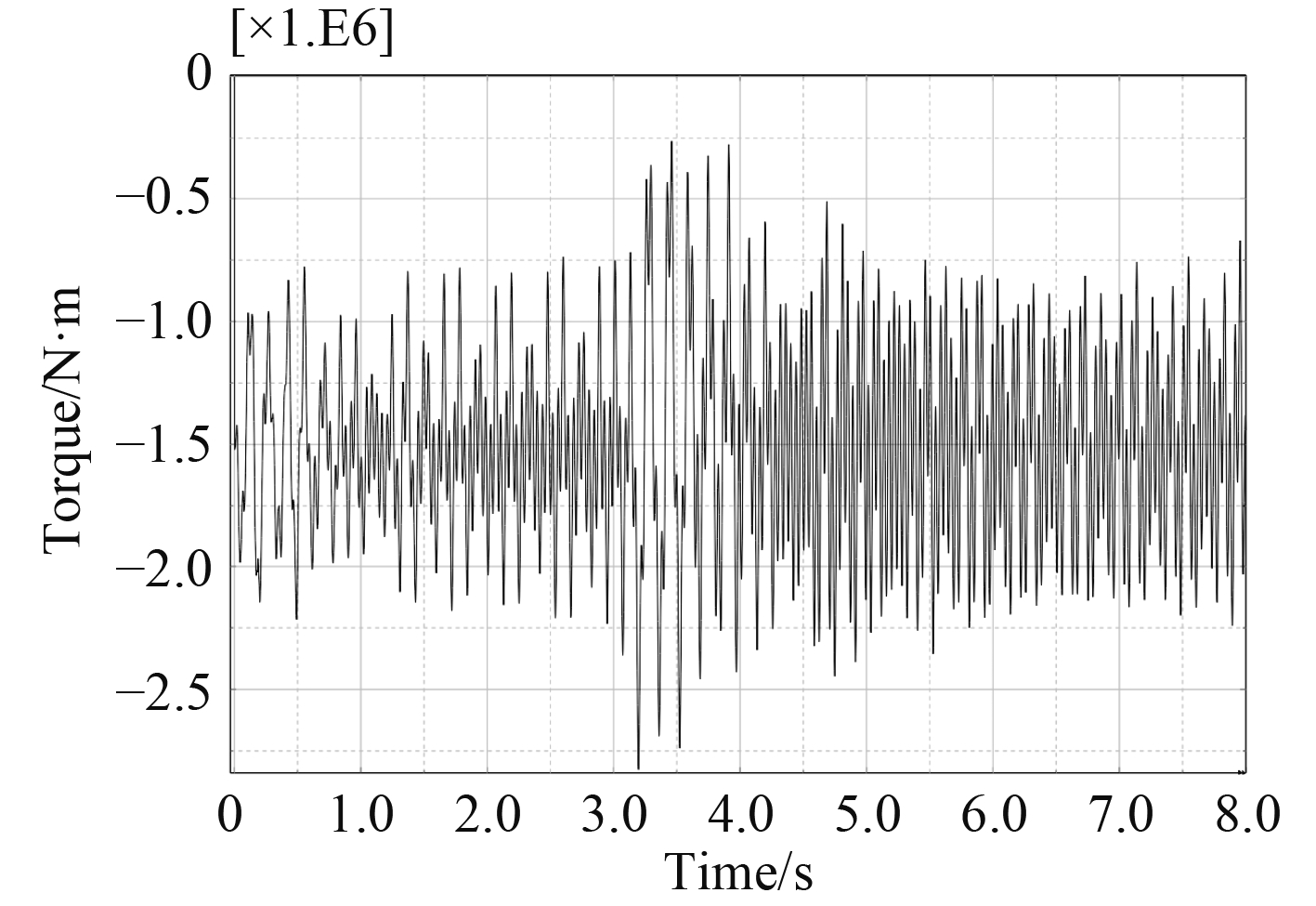
在轴系扭振时域计算时，先在轴系上施加气缸激励扭矩和螺旋桨扭矩，施加一段时间，达到一定的平衡，在第3 s时刻，施加冰载荷，可以得到轴系扭振时域响应结果。这里仅给出9#中间轴的扭振响应，工况1如图12所示，工况2如图13所示，工况3如图14所示。

根据规范[10]中的计算方法，取冰冲击下扭振响应最大值与最小值差值绝对值的一半来作为扭振最大峰值，这里对9#中间轴3种工况的扭振应力最大峰值进行了计算，9#中间轴直径为0.36 m，计算结果如表3所示，正常发火工况下柴油机额定转速无冰载荷冲击时稳态运转下9#中间轴扭振应力为12.4 MPa，对比可以看出，冰载荷冲击下的轴系扭振应力结果远大于没有冰载荷冲击的情况，所以以往的轴系扭振校核方式不再适合，需要考虑冰载荷循环次数采用专门的疲劳强度校核方法。

4 结　语

通过对轴系扭振的数值方法研究，可以得到以下结论：

1）Newmark方法可以应用于柴油机推进轴系扭振的时域仿真计算；

2）冰载荷下柴油机推进轴系的扭振计算，需要考虑调速器的影响，同时，曲轴在不同的相位角处会影响柴油机的激励扭矩，进而导致轴系产生不同的扭振响应；

3）本文提出的计算方法中，考虑到主机、桨和冰3种激励载荷由于轴转速而导致互相影响这个因素，先利用刚性轴模型，推算出各种激励载荷，然后施加在柔性有限元模型上，计算轴系扭振响应，该方法可利用通用有限元软件来进行冰载荷下轴系的扭振计算，使用范围广，可以为行业内提供参考，对提高轴系的安全性具有重要意义，同时，该种计算方式值得在其他方面进行研究和应用；

4）从有冰载荷与无冰载荷冲击下的轴系扭振应力两种结果对比来看，冰对螺旋桨冲击导致产生的轴系扭振相当严重，需要密切关注，而且对应的校核方法也需要改变。