固体氧化物燃料电池是一种直接将燃料中的化学能转化为电能的电力发生装置,打破卡诺循环(Carnot cycle)热效率的限制,具有传统热机不可比拟的高效性。其尾气含有一定量未反应的氢气,可通过催化燃烧室进一步提高尾气初温,利用燃料电池-燃气轮机热电联合循环,其系统热效率高达60%[1]。燃料电池-燃气轮机联合循环动力系统应用于下一代舰艇常规动力装置具有高效、环保、安全等优点。
西门子公司已于2000年实现100 kW级的燃料电池-燃气轮机联合发电系统的运行[2],国内联合循环系统大多尚处于理论研究阶段,目前针对系统功率匹配、参数优化研究甚少。目前国内大功率电堆制备技术尚不成熟,为实现电堆与微型燃气轮机功率匹配,提出多组电堆与微型燃气轮机联合循环系统结构。本文构建的一维分布式集中参数数学模型,在满足动态响应的前提下,适当简化模型复杂程度,节省计算成本,为探索燃料电池-燃气轮机联合发电系统在舰船电力综合系统上的应用打下坚实基础[3]。
1 构建系统数学模型目前燃料电池-燃气轮机联合循环主要有顶层循环与底层循环2种结构,分为常压型板式燃料电池与微型燃气轮机底层循环,加压型管式燃料电池与微型燃气轮机顶层循环[4]。本文多组燃料电池堆与微型燃气轮机联合循环系统结构如图1所示。

|
图 1 系统结构拓扑图 Fig. 1 System structure topology |
该系统主要由2个相同的燃料电池堆、微型燃气轮机、换热器、催化燃烧室、预重整器等组成。燃料与部分高温阳极尾气混合进入预重整器重整,再进入燃料电池阳极反应,利用阳极尚未完全反应的氢气,提高燃料电池的燃料利用率。燃料电池尾气经过催化燃烧室催化燃烧,进一步提高尾气初温。压气机出口高压空气通过换热与燃料电池尾气换热,最后通过涡轮做功。通过燃料电池堆串联实现系统燃料利用率最大,燃料电池堆并联实现系统功率最大。此系统燃料电池与燃气轮机没有工质的交换,只存在能量上的传递,故可减少整个系统的耦合关系,使得系统更加灵活可控。
1.1 燃料电池模型通入燃料电池堆的燃料气是甲烷与水蒸气的混合物,为保证不发生积碳现象,气碳比大于3,在催化剂的作用下电堆内部发生重整与置换2个可逆反应[5]:
| ${\rm{C}}{{\rm{H}}_4} + {{\rm{H}}_2}{\rm{O}} \leftrightarrow {\rm{CO}} + 3{{\rm{H}}_2}\text{,}$ | (1) |
| ${\rm{CO}} + {{\rm{H}}_2}{\rm{O}} \leftrightarrow {\rm{C}}{{\rm{O}}_2} + {{\rm{H}}_2}{\text{。}}$ | (2) |
通过重整反应速率确定甲烷消耗的速率:
| ${r_r} = {K_r}P_{_{C{H_{4,tpb}}}}^\alpha P_{_{{H_2}O,tpb}}^\beta \exp \left( - \frac{{{E_r}}}{{R{T_{fuel}}}}\right){\text{。}}$ | (3) |
式中:重整阶数α=0.85,β=–0.35;重整反应活化能Er=95 kJ/mol;重整反应速率系数Kr=8 542。实验表明甲烷的消耗速率对电堆动态性能具有一定影响,但在电堆稳态放电状态下,尾气中甲烷的剩余量可以忽略不计,甲烷的重整反应达到平衡状态:
| $\begin{split}{K_r} =& \exp ({A_r}T_{fuel}^4 + {B_r}T_{fuel}^3 + {C_r}T_{fuel}^2 + \\&{D_r}T_{fuel}^{} + {E_r})\text{。}\end{split} $ | (4) |
相对于重整反应,置换反应速率更快,可以更快达到平衡状态,使得置换反应的瞬时动态对电堆的动态效应影响忽略不计:
| $\begin{split}{K_s} =& \exp ({A_s}T_{fuel}^4 + {B_s}T_{fuel}^3 + {C_s}T_{fuel}^2 + \\&{D_s}T_{fuel}^{} + {E_s})\text{,}\end{split} $ | (5) |
阳极板与阴极板主要发生如下电化学反应:
| $\begin{split} & {{\rm{H}}_2} + {{\rm{O}}^{2 - }} \to {{\rm{H}}_2}{\rm{O}} + 2{{\rm{e}}^ - }\text{,} \\ & \frac{1}{2}{{\rm{O}}_2} + 2{{\rm{e}}^ - } \to {{\rm{O}}^{2 - }} \text{。}\end{split} $ | (6) |
阳极同时还进行着微量的
电化学反应产生电堆的电压可以由Nernst方程表示:
| $E = {E^0} - \frac{{R{T_{cell}}}}{{4F}}\ln \left(\frac{{{p^2}_{tpb,{{\rm{H}}_2}{\rm{O}}}}}{{{p^2}_{tpb,{{\rm{H}}_2}} \cdot p_{tpb,{{\rm{O}}_2}}^{}}}\right)\text{,}$ | (7) |
| ${E^0} = 1.272\;3 - 2.764\;5 \times {10^{ - 4}}{T_{cell}}\text{,}$ | (8) |
堆栈单元实际运行电压:
| ${v_f}_c = E - {\eta _{ohmic}} - {\eta _{conc}} - {\eta _{act,a}} - {\eta _{act,c}}\text{。}$ | (9) |
式中:欧姆极化
燃料电池板沿径向非常薄,温差很小,假设板沿径向方向没有温度变化。燃料电池板主要换热存在于气体流过通道时与电极发生的强制对流:
| ${q_{conv}} = hA\left( {{T_{cell}} - {T_{fuel}}} \right)\text{。}$ | (10) |
式中:
实验表明通道内气体为层流,阳极通道与阴极通道雷诺数分别取66与287,利用雷诺数
| $\begin{split}h =& 0.332\frac{k}{{{D_{fuel,air}}}}{\left( {\frac{{{C_V}\mu }}{k}} \right)^{1/3}} \times \\&{\left( {\frac{{{D_{fuel,air}}M}}{\mu }} \right)^{1/2}}{\left( {\frac{{uP}}{{R{T_{out}}}}} \right)^{1/2}}{\text{。}}\end{split}$ | (11) |
式中:
电堆温度模型约束条件为:
| ${m_{cell}}{C_{cell}}\left( T \right) \cdot \frac{{d{T_{cell}}}}{{dt}} = - {P_{fc}} - {r_3}\Delta {H_3}\left( T \right) - {q_{conv}}\text{,}$ | (12) |
| $\begin{split} & {C_{re}}\left( T \right) \cdot \frac{{d{T_{out}}}}{{dt}} = \sum {\left( {G_{in,i}^{air} \cdot h_{_{in,i}}^{air}} \right)} + \sum {\left( {G_{in,i}^{fuel} \cdot h_{_{in,i}}^{air}} \right)} -\\ & \sum {\left( {G_{_{out,i}}^{air} \cdot h_{_{out,i}}^{air}} \right)} - \sum {\left( {G_{_{out,i}}^{fuel} \cdot h_{_{out,i}}^{fuel}} \right)} - {r_r}\Delta {H_r}\left( T \right)-\\ & {r_s}\Delta {H_s}\left( T \right) + {q_{conv}} \text{。}\end{split} $ | (13) |
式中
本文微型燃气轮机选用离心式压气机,向心式涡轮。压气机系统包括过滤器、进气管道、通流部分及扩压器等部分。压气机的输入参数为大气环境条件,输出参数为压缩耗功、压气机空气出口温度及出口空气焓值[8]。
本文采用含有压力损失系数的经验公式,即压力损失和流量的平方成正比:
| $\Delta p = \frac{{{p_{in}} - {p_{out}}}}{{{p_{in}}}}{\rm{ = }}{\left( {\frac{{{G_{in}}}}{{{G_0}}}} \right)^2} \cdot \sigma {\text{。}}$ | (14) |
压气机是一个高度非线性的部件,本项目采用非线性模块化建模方法。根据相似理论,压气机的工作特性可以用压比、折合转速和折合流量以及热效率4个参数的关系来表示。在压气机数学模型中假设:工质通过压气机外壳与外界的热交换忽略不计;忽略流体质量力及动量作用的影响[9]。
质量守恒方程:
| ${G_{{\rm{in}}}} = {G_{{\rm{out}}}}{\text{,}}$ | (15) |
式中:
压气机压比、流量特性:
| $\begin{split} {\pi _C} = {f_1}\left({G_{in}}\frac{{{p_0}\sqrt {{T_{in}}} }}{{{p_{in}}\sqrt {{T_0}} }},{n_c}\frac{{\sqrt {{T_0}} }}{{\sqrt {{T_{in}}} }}\right) \text{,}\\ {\eta _C} = {f_2}\left({G_{in}}\frac{{{p_0}\sqrt {{T_{in}}} }}{{{p_{in}}\sqrt {{T_0}} }},{n_c}\frac{{\sqrt {{T_0}} }}{{\sqrt {{T_{in}}} }}\right) \text{。}\end{split} $ | (16) |
压气机耗功:
| $N{e_C} = {{{c_{pa}}{T_{in}}(\pi _C^{{m_a}} - 1)} / {{\eta _C}}}\text{,}$ | (17) |
压气机出口空气温度:
| ${T_{out}} = {{{T_{in}}[1 + (\pi _C^{{m_a}} - 1)} / {{\eta _C}}}]\text{。}$ | (18) |
涡轮模块与压气机模块类似,因此,假设:忽略涡轮内部气体容积;忽略涡轮金属蓄热作用及向外散热影响;涡轮部件注入冷却空气折算到涡轮进口;忽略流体质量力和动量作用的影响。
涡轮膨胀比、效率特性:
| $\begin{split} {\varepsilon _T} = {f_3}\left(\frac{{{G_{{\rm{in}}}}\sqrt {{T_{{\rm{in}}}}} }}{{{p_{{\rm{in}}}}}},\frac{{{n_T}}}{{\sqrt {{T_{{\rm{in}}}}} }}\right)\text{,} \\ {\eta _T} = {f_4}\left(\frac{{{G_{{\rm{in}}}}\sqrt {{T_{{\rm{in}}}}} }}{{{p_{{\rm{in}}}}}},\frac{{{n_T}}}{{\sqrt {{T_{{\rm{in}}}}} }}\right) \text{。}\end{split} $ | (19) |
式中:
涡轮做功:
| $N{e_T} = {c_{pg}}{T_{{\rm{in}}}}(1 - \varepsilon _T^{ - {m_g}}){\eta _T}\text{,}$ | (20) |
涡轮出口燃气温度:
| ${T_{{\rm{out}}}} = {T_{{\rm{in}}}}[1 - (1 - \varepsilon _T^{ - {m_g}}){\eta _T}]\text{。}$ | (21) |
燃料电池高温尾气经过催化燃烧室的催化燃烧,温度得到进一步提升。采用换热器与燃气轮机换热,替代燃气轮机燃烧室。换热器热计算有平均传热温差法和效能-传热单元数(ε-NTU)法。效能-传热单元数法收敛速度较快,但随着计算机计算速度的提升与计算成本的下降,效能-传热单元数法计算量小的优势逐步丧失,而平均传热温差法可以得到温差修正系数
在平均温差法中出口温度
| $\Delta {T_{lc}} = \frac{{T_1'- T_2''}}{{\ln \left( {{{T_1'' - T_2'} / {T_1'- T_2''}}} \right)}}\left( {\frac{{T_1'' - T_2'}}{{T_1'- T_2''}} - 1} \right)\text{。}$ | (22) |
引入温度修正系数
| $P = \frac{{T_2'' - T_2'}}{{T_1'- T_2'}},R = \frac{{T_1'- T_1''}}{{T_2'' - T_2'}}\text{。}$ | (23) |
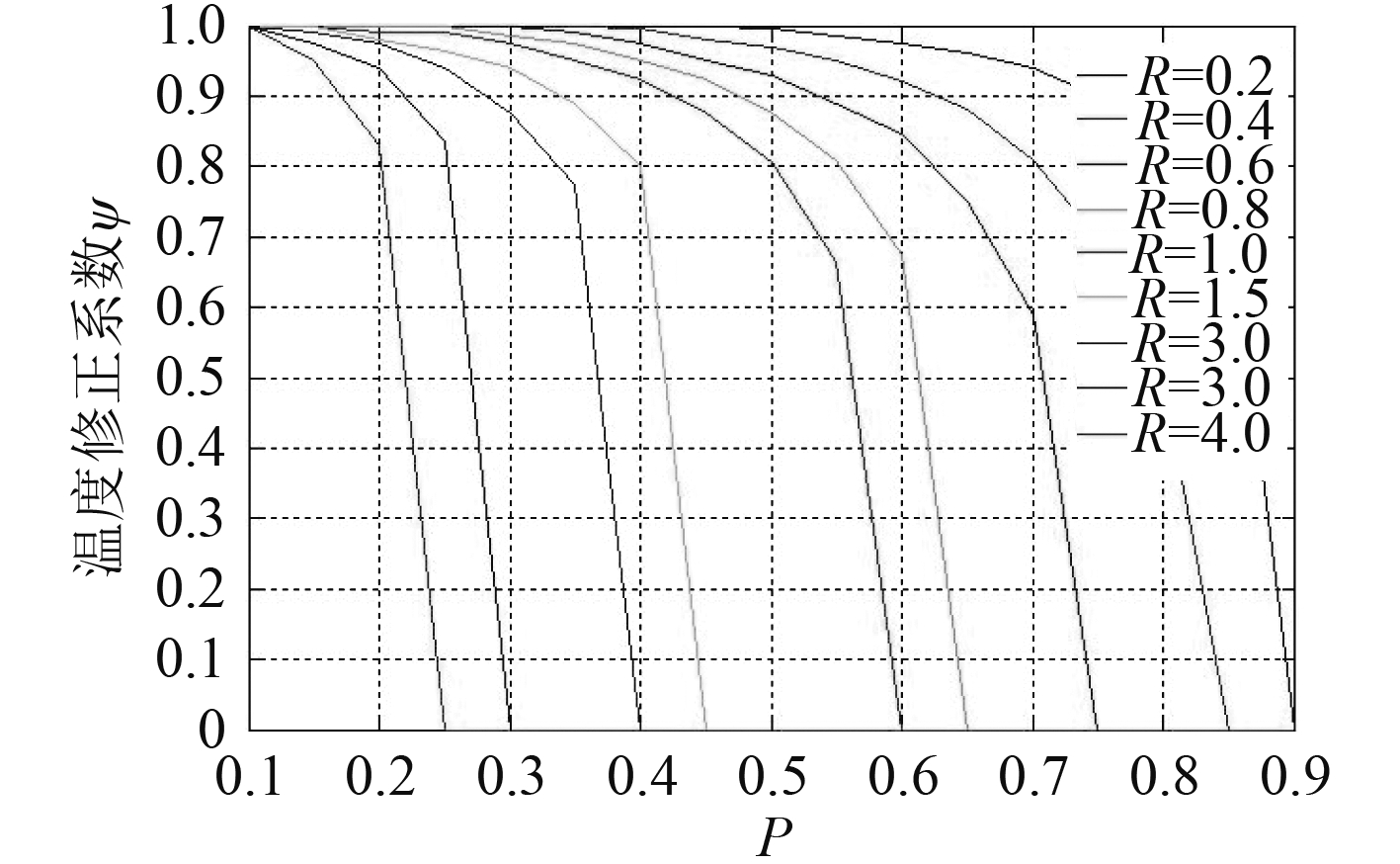
|
图 2 温度修正系数 Fig. 2 Temperature correction factor |
以系统热平衡为收敛条件:
| $\varPhi = {q_{m1}}{c_{p1}}\left( {T_1'- T_1''} \right) = {q_{m2}}{c_{p2}}\left( {T_2'' - T_2'} \right)\text{。}$ | (24) |
本文采用实验与仿真相结合的方法探究燃料电池与燃气轮机联合循环性能,并对其优化。电堆采用索福人公司生产板式电堆。单板额定功率约为50 W,本文采用25块相同燃料电池板组成电堆,实验得到燃料电池堆基础结构参数。

|
图 3 电堆连接体结构 Fig. 3 Structure of SOFC |
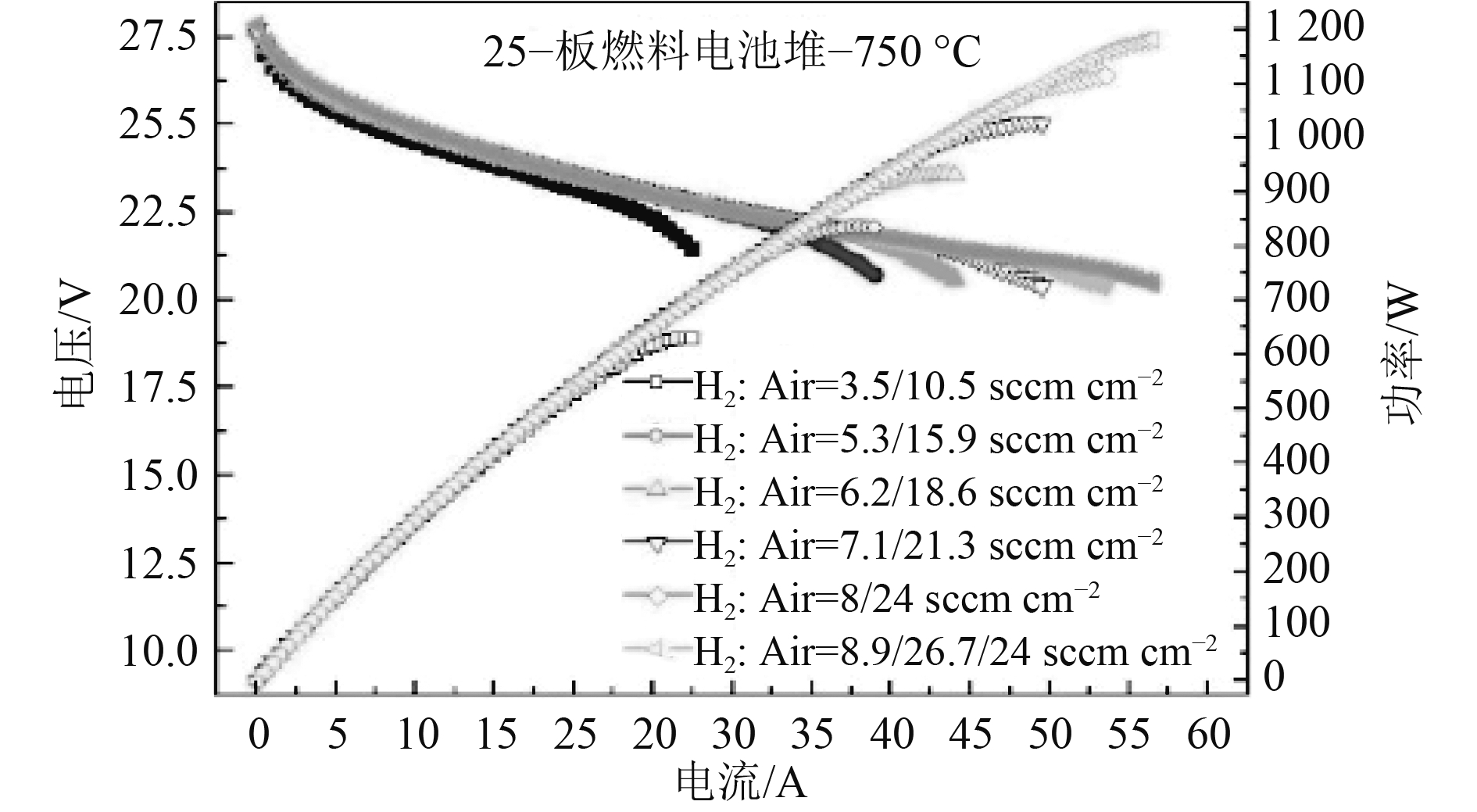
|
图 4 电堆性能参数 Fig. 4 Test curve |
燃料电池与燃气轮机联合循环仿真初始参数如表1所示,对模型进行仿真验证。
|
|
表 1 仿真初始参数 Tab.1 Modeling parameters |
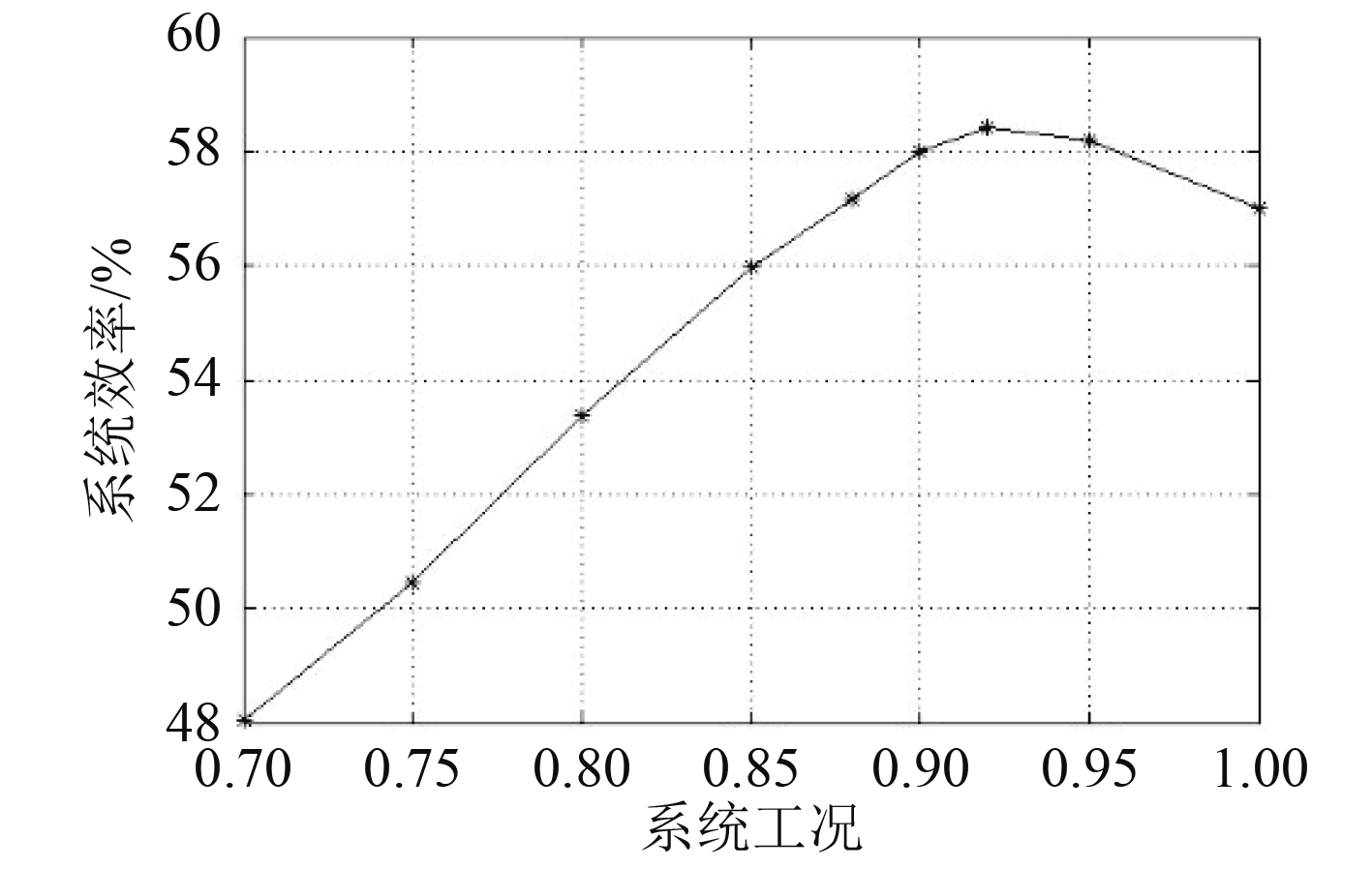
|
图 5 变工况效率特性曲线 Fig. 5 The efficiency of SOFC-GT at off-design condition |
在不同工况下,燃料电池-燃气轮机联合循环系统的效率特性如图5所示。随着工况的下降,燃料电池-燃气轮机联合循环系统效率先小幅升高后迅速下降。在联合循环系统中燃料电池输出功率约占系统总功率的80%,初始阶段工况的降低使得燃气轮机的效率降低,但燃料电池效率远大于燃气轮机效率,燃料电池输出功率占系统总输出功率比例升高,使得初始阶段系统效率会有小幅度的升高。后随着工况的进一步降低,燃料电池堆温降低,效率急剧下降,燃气轮机工作环境进一步恶化,效率大幅度降低,系统效率会迅速下降。
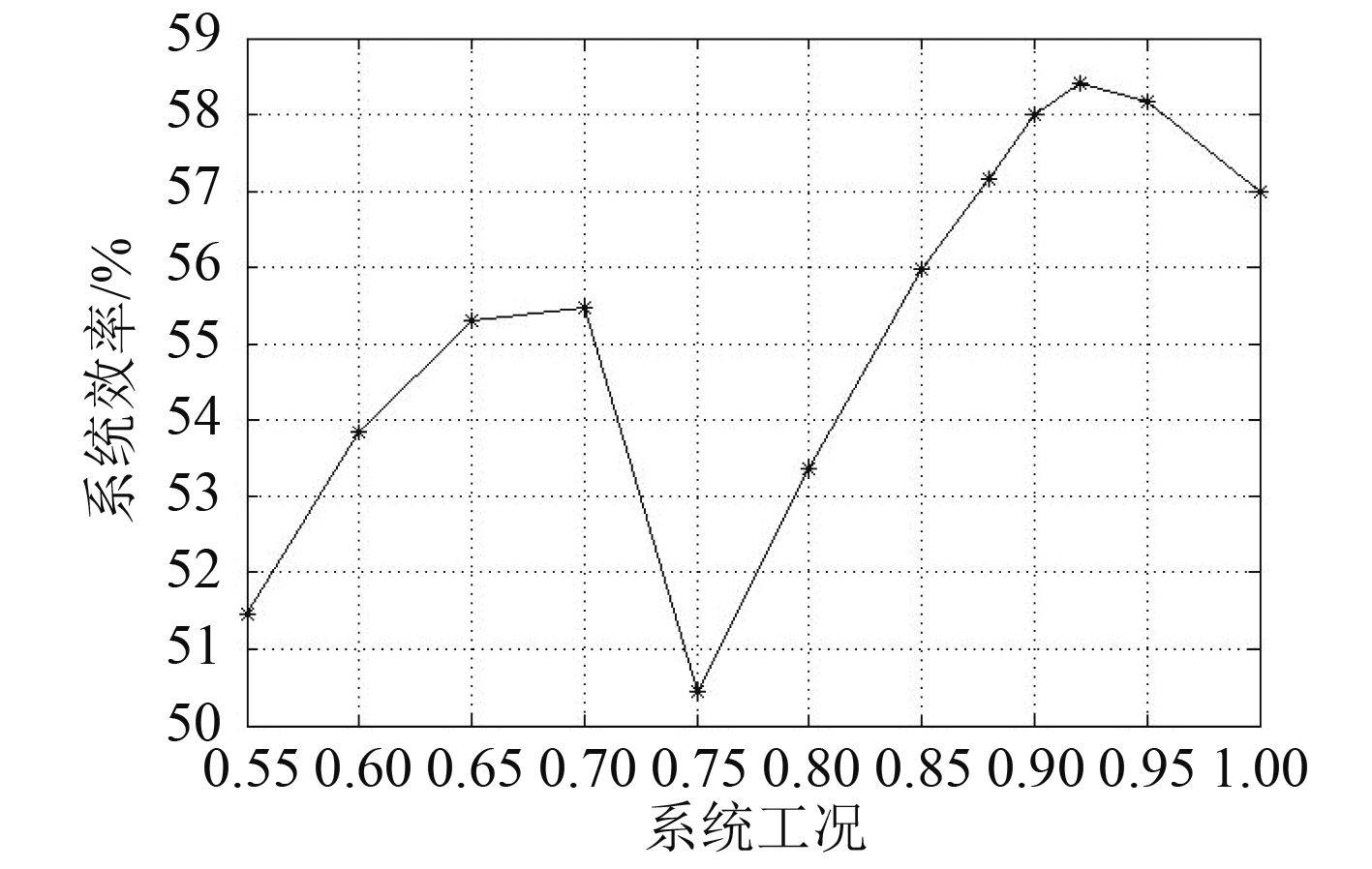
|
图 6 系统效率特性曲线 Fig. 6 The efficiency of SOFC-GT at off-design condition |
为实现燃料电池-燃气轮机联合循环在不同工况下均有较高的效率与燃料利用率,在高工况时采用双堆并联工作方式以提高系统的输出功率,在低工况是采用双堆串联工作方式以提高系统效率与燃料利用率。在0.7工况时,系统由并联状态切换到串联状态,系统效率提升7.5%左右。这种工作模式保证了系统在不同工况下,系统效率大于50%。

|
图 7 系统功率特性曲线 Fig. 7 The power of SOFC-GT at off-design condition |
随着工况的下降,各模块输出功率逐渐降低。在0.7工况时,系统由并联状态切换到串联状态,此时电堆1在1 200 W额定功率下工作,对于电堆1尾气中未能完全反应的氢气,进入电堆2的阳极进一步反应。由于此时系统尾气流量减小,使得微型燃气轮机功率大幅度下降。
3 结 语为实现燃料电池-燃气轮机联合循环系统在不同工况下均有较高的效率,提出改变循环结构的控制策略。优化系统各模块间的功率分配,实现低工况时系统效率依然大于50%,相较于原循环系统效率提高7.5%。同时多堆燃料电池与燃气轮机联合循环解决了目前电堆功率不足的限制,为大功率联合循环系统结构设计指明了方向。为燃料电池-燃气轮机联合循环动力系统在水面舰艇上的应用打下了坚实的基础。
| [1] | WU XJ, ZHU XJ, CAO GY, TU HY. Predictive control of SOFC based on a ga-rbf neural network model[J]. Journal of power Energy, 2008, 179(1): 232–239. |
| [2] | FLORIAN Leucht, WOLFGANG G. Bessler. Fuel cell system modeling for solid oxide fuel cell/gas turbine hybrid power plants, Part I: Modeling and simulation framework[J]. Journal of Power Sources, 2011(196): 1205–1215. |
| [3] |
汤根土, 骆仲泱, 倪明江, 等. 平板状阳极支撑固体氧化物燃料电池的数值模拟及性能分析[J]. 中国电机工程学报, 2005, 5(10): 116–121.
TANG Gen-tu, LUO Zhong-yang, NI Ming-jiang, YU Chun-jiang, CEN Ke-fa. Numerical simulation and performance analysis of planar anode-supported solid oxide fuel cell[J]. Proceedings of the CSEE, 2005, 5(10): 116–121. |
| [4] |
吕小静, 陆超豪, 耿孝懦, 等. 水蒸气对IT/SOFC-GT混合动力系统性能的影响[J]. 工程热物理学报, 2016, 4(4): 705–710.
LU Xiao-Jing, LU Chao-Hao, GENG Xiao-Ru, ZHU Xin-Jian, WENG Yi-Wu. Effect of Steam on the Performance of an IT-SOFC/GT Hybrid System[J]. Journal of engineering thermal physics, 2016, 4(4): 705–710. http://www.cnki.com.cn/Article/CJFDTotal-GCRB201604005.htm |
| [5] |
谭勋琼, 吴政秋, 周野, 钟浩, 李军军. 固体氧化物燃料电池的集总建模与仿真[J]. 中国电机工程学报, 2010, 6(17): 104–110.
TAN Xun-qiong, WU Zheng-qiu, ZHOU Ye, ZHONG Hao, LI Jun-jun. Solid Oxide Fuel Cell Lumped Modeling and Simulation[J]. Proceedings of the CSEE, 2010, 6(17): 104–110. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dianyjs201010011 |
| [6] |
徐泽亚, 杨晨. 管式SOFC数学模型及系统性能分析[J]. 计算机仿真, 2006, 23(6): 224–228.
XU Zeya, YANG Chen. Mathematical model of tubular solid oxide fuel cell and system performance analysis[J]. Computer Simulation, 2006, 23(6): 224–228. http://cdmd.cnki.com.cn/Article/CDMD-10731-1012411708.htm |
| [7] | ALI Volkan Akkaya. Electrochemical model for Performance analysis of a tubular SOFC[J], International Journal of energy research, 2006(1), 31: 79–98. |
| [8] |
张健. 固体氧化物燃料电池与燃气轮机联合循环特性分析[D]. 保定: 华北电力大学, 2007.
ZHANG Jian. Analysis of the characteristics of SOFC-GT system[D]. Baoding: North China Electric Power University, 2007. |
| [9] | THORUD B. Dynamic modelling and characterisation of a solid oxide fuel cell integrated in a gas turbine cycle[D]. Trondheim: Norwegian University of Science and Technology, 2005. |
| [10] |
李杨, 翁一武. 固体氧化物燃料电池-燃气轮机混合动力系统及控制策略分析[J]. 中国电机工程学报, 2010, 30(35): 94–100.
LI Yang, WENG Yiwu. Performance study and control strategies of temperature solid oxide fuel cell-gas turbine hybrid system[J]. Proceesings of the CSEE, 2010, 30(35): 94–100. http://www.cnki.com.cn/Article/CJFDTotal-ZGDC201035017.htm |
 2018, Vol. 40
2018, Vol. 40
