浮式海洋结构物为了避免受到环境扰动后发生位置漂移,需要装备能够控制其位置保持在作业条件允许的半径范围内的定位系统,常见的有动力定位、锚泊定位及锚泊辅助动力定位等方式。锚泊辅助动力定位结合了锚泊定位和动力定位的优点,既具备抵抗外载荷的能力,又能够控制半潜式平台的首向、偏移量以及对任意可能断裂的锚泊线进行补偿。当外载荷较小时,锚泊系统能提供足够的回复力使平台保持在允许作业半径内而不需要推进器开动,从而降低动力定位系统的燃油消耗;当外载荷超过锚泊系统的回复力极限,动力定位能够阻止平台的动态运动并抵消部分外载荷,防止锚泊线出现应力过大导致的断裂。因此根据环境载荷提前预估半潜式平台可能的位置能够加强系统的定位能力、节约成本及增大可变载荷。Smith等[6]基于悬链线方程采用拉格朗日迭代求解深水两成分锚泊线的回复力。Liu等[2]对规则波浪条件下的采用锚泊系统的半潜式平台的运动响应进行了数值研究,并用2种不同的方式评估锚泊系统对平台运动响应的影响。Qiao等[3]对2种静力特性及布锚方式相同的锚泊系统进行了非线性时域耦合分析,并研究了两者对平台运动及系泊线张力的影响。Guo等[4]研究了悬链式锚泊线在动态响应下的非线性回复力问题。余龙等[5]通过准静定法研究了不同锚泊线组成对锚泊系统回复力的影响。
锚泊系统的锚泊线并不总是交于一点,因此半潜式平台在外载荷及锚泊线张力的共同作用下既产生位移,首向又会发生改变,称这样的系统为非汇交锚泊系统。但如果假设锚泊系统的所有锚泊线总是交于一点,则平台只产生位移,首向不发生变化,称之为汇交锚泊系统。汇交锚泊系统是对实际系统的一种简化,但进行相关仿真计算时更加简单方便。本文通过提出的平台位移计算方法比较汇交和非汇交锚泊系统之间的性能差异,具体的研究方法和相关结论可为半潜式平台的定位控制及计算提供参考。
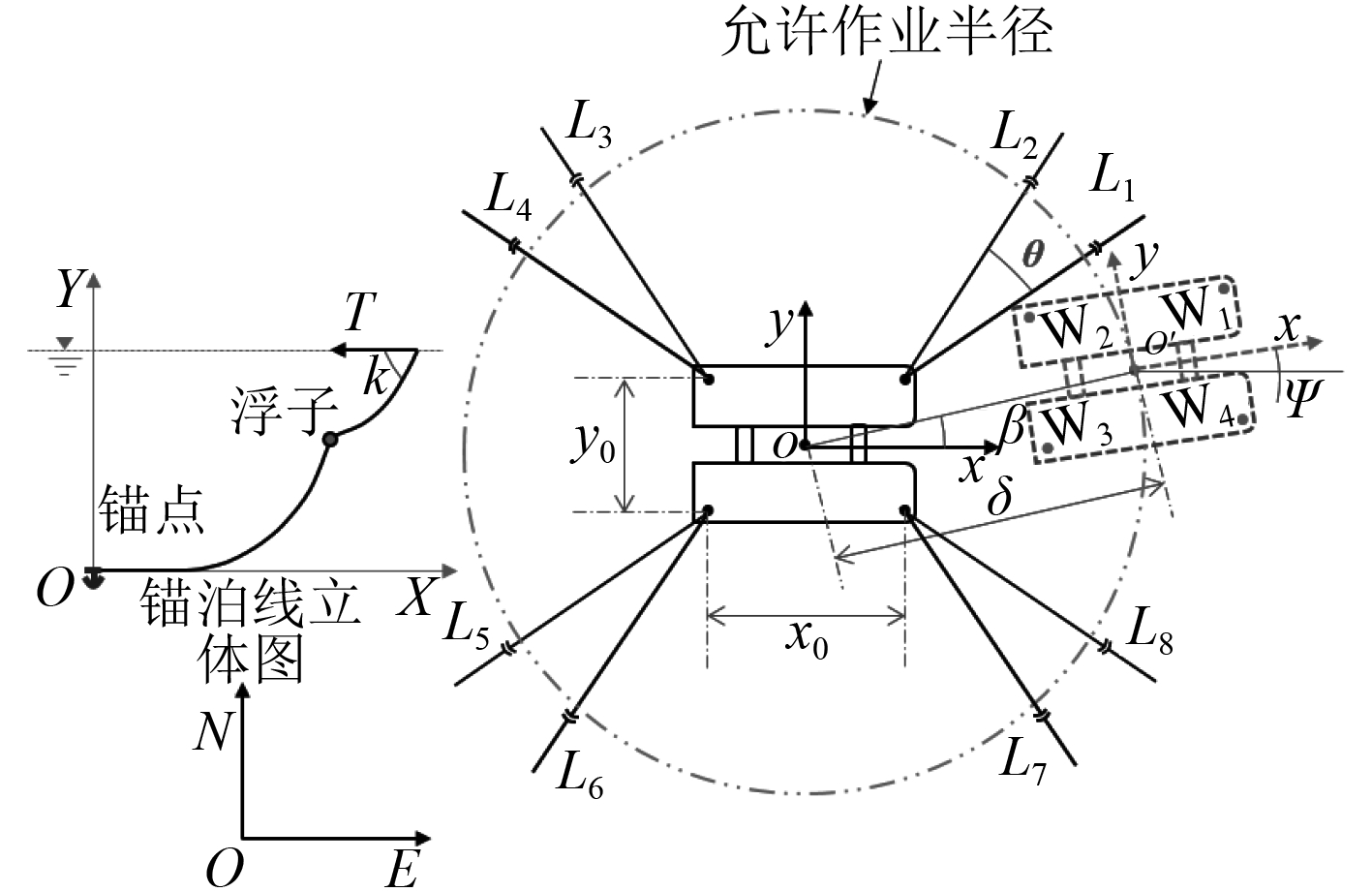
1 计算方法以平台中心为坐标原点,水平方向中线为x轴,首向为x轴正向,纵向中线为y轴,左舷为y轴正向建立海洋平台船体坐标系。平台采用8点对称式布锚,锚泊线编号为L1~L8,虚线为平台受到环境扰动后的位置,如图1所示。
|
图 1 锚泊系统在外载荷下的位置变化图 Fig. 1 The position change of the mooring system under external interference |
图中,编号分别为W1,W2,W3,W4的4台锚绞机布置在平台的4个角上,每台锚绞机控制2条锚泊线,其夹角设为θ,相邻锚绞机之间的距离分别为x0和y0。若平台位置变化后其中心由O点移动到O′点,直线位移大小为δ m,位移方向为β。由于所有锚泊线不交于一点,因此当平台位置变化后其首向会发生改变,设变化角度为ψ。
1.1 回复力计算已知平台位移δ、方向α及转角ψ,可求出平台位移后锚绞机在北东(NE)坐标系下的位置为:
| $\begin{split}{X_{Wi}} = \rm{sgn} \left[ {\sin (\frac{\pi }{4} + \frac{\pi }{2}i)} \right] \times \frac{{{x_0}}}{2}\cos \psi +\;\;\;\;\;\;\;\;\;\;\;\; \\\rm{sgn} \left[ {\sin (\frac{\pi }{2}i - \frac{\pi }{4})} \right] \times \frac{{{y_0}}}{2}\sin \psi + \delta \cos \alpha \text{,}\end{split}$ | (1) |
| $\begin{split}{Y_{Wi}} = \rm{sgn} \left[ {\sin (\frac{\pi }{4} + \frac{\pi }{2}i)} \right] \times \frac{{{x_0}}}{2}\sin \psi +\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \rm{sgn} \left[ {\sin (\frac{\pi }{2}i - \frac{\pi }{4})} \right] \times \frac{{{y_0}}}{2}\cos \psi + \delta \sin \alpha\text{。}\end{split}$ | (2) |
式中,XWi,YWi分别为锚绞机Wi的横坐标和纵坐标,i=1,2,3,4。
定义平台位移后锚泊线的水平长度与其初始状态下的水平长度之差为等效位移ΔL,则
| $\Delta {L_j} = \sqrt {{{\left( {{X_{Wi}} - {X_j}} \right)}^2} + {{\left( {{Y_{Wi}} - {Y_j}} \right)}^2}} - L\text{。}$ | (3) |
式中:Xj,Yj分别为与第j根锚泊线连接的锚在NE坐标系下的横坐标和纵坐标,i=1,2,3,4;j=1,2,…,8,锚绞机和锚泊线存在对应关系,例如W1对应L1和L2,以此类推;L是锚泊线在预张状态下的水平长度。
在锚固点不变时,锚绞机的等效位移ΔL即为相应锚泊线长度的变化,假设8根锚泊线的材质及组成完全一致,因为锚泊线顶端水平张力与位移呈现非线性关系,无法用统一的数学方程加以描述,可以采用级数对其进行逼近,设锚泊线顶端水平张力与等效位移的关系为
| $T = {T_0} + g(\Delta L,\kappa ) = {T_0} + \sum\limits_{i = 1}^n {{a_i}{{(\Delta L)}^i}} \text{。}$ | (4) |
式中:T0为锚泊线在预张状态下的水平分力;κ为锚泊线顶端张力与海平面的夹角,其值与ΔL满足函数关系;ai为待求的参数;n的大小与单根锚泊线的应力模型有关。
已知锚泊线顶端水平张力与等效位移的关系函数,可以求出锚泊线水平张力T,其与NE坐标系中E轴的夹角为λ:
| ${\lambda _j} = \arctan \left( {\frac{{{Y_{Wi}} - {Y_j}}}{{{X_{Wi}} - {X_j}}}} \right)\text{。}$ | (5) |
已知锚泊线顶端的水平张力T及夹角λ,通过力的合成可求出锚泊系统的静回复力F和方向β:
| $F = \sqrt {\begin{split}{\left( {\sum\limits_{j = 1}^8 {{\rm{sgn}}\left[ {\sin (\frac{{3\pi }}{8} + \frac{\pi }{4}j)} \right] \times {{\rm{T}}_j}\cos {\lambda _j}} } \right)^2} + \\ {\left( {\sum\limits_{j = 1}^8 {{\rm{sgn}}\left[ {\sin (\frac{\pi }{4}j - \frac{\pi }{8})} \right] \times {{\rm{T}}_j}\sin {\lambda _j}} } \right)^2}{\text{,}}\end{split}} $ | (6) |
| $\begin{split}\beta = & \arctan \left( {\sum\limits_{j = 1}^8 {{\rm{sgn}}\left[ {\sin (\frac{\pi }{4}j - \frac{\pi }{8})} \right] \times {{\rm{T}}_j}\sin {\lambda _j}} /} \right.\\& \left. {\sum\limits_{j = 1}^8 {{\rm{sgn}}\left[ {\sin (\frac{{3\pi }}{8} + \frac{\pi }{4}j)} \right] \times {{\rm{T}}_j}\cos {\lambda _j}} } \right)\end{split}\text{。}$ | (7) |
式中,Tj和λj分别是第j根锚泊线提供的水平张力及作用方向。
设M是首摇方向的平台力矩,则
| $M = \sum\limits_{j = 1}^8 {{T_j}d\left[ { - \cos {\lambda _j}\sin ({\mu _i} + \psi ) + \sin {\lambda _j}\cos ({\mu _i} + \psi )} \right]}\text{。} $ | (8) |
式中:d为锚绞机到平台中心的距离;μi为锚绞机Wi与平台中心的连线和船体坐标系下x轴的夹角。
1.2 公式拟合对锚泊线顶端的水平张力进行计算时,首先要确定式(4)中的待求参数。以三段式组合锚泊线为研究对象,上段钢链与锚绞机相连,中段钢缆,下段钢链与锚相连。在钢缆中串联浮子改善锚泊系统的静力特性[6],并考虑其尺度作用,材质参数如表1所示。海洋平台的工作水深设为300 m,海流的切向和法向阻力系数分别为0.024和1.2[7],流速分布为均匀流1.2 m/s。锚泊线在预张状态下的长度为1 500 m,上段锚链的长度为50 m,下段锚链的长度为595 m,将整串浮子的起点位置安置在距锚泊线顶端550 m处,浮子尺度为5 m,浮子和锚链的直径为等效直径。
|
|
表 1 锚泊线材料特性 Tab.1 Line physical properties |
在锚泊线顶端施加预紧力,能使平台在一定的外载荷下正常作业而不需要锚绞机运行,选择合适的预紧力能够增强锚泊系统抵抗外载荷的能力[8]。
对锚泊系统的所有锚泊线预加某初始张力,使平台处于平衡位置,当外载荷作用于平台后,平台发生位移。在锚绞机不动作的情况下,背离外载荷方向的锚泊线中总有一根受力最大。以受力最大的锚泊线为研究对象,当平台处于允许工作半径时,此锚泊线刚好达到安全应力的临近点,这时的锚泊线初始张力即为最佳预紧力。
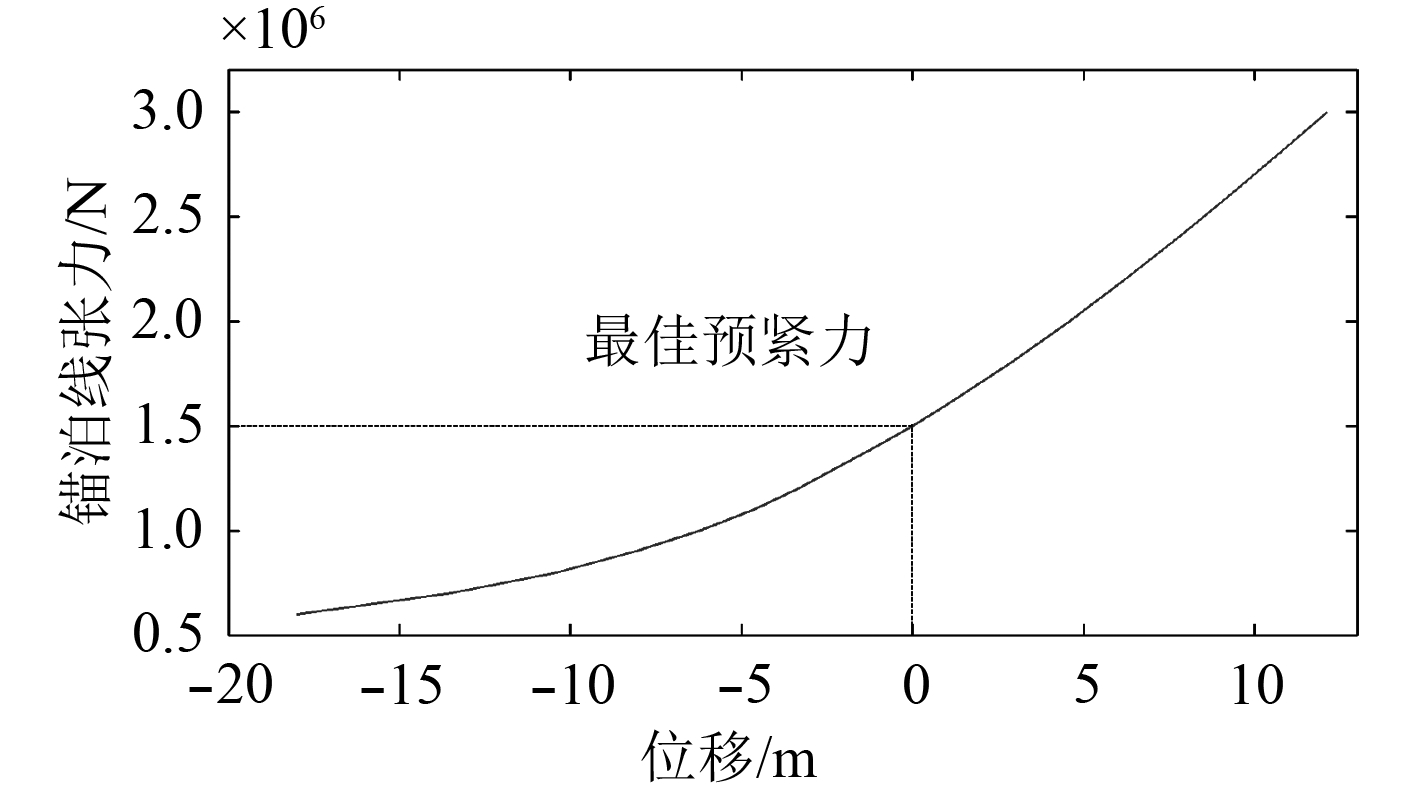
本文锚泊线采用的安全系数为2。通常规定平台的工作半径为水深的3%~5%,本文将平台的正常作业半径设为12.123 m。以锚泊线顶端位移为x轴,锚泊线顶端张力为y轴建立平面直角坐标系。当锚泊线顶端位移为12.123 m,顶端张力刚好处于安全应力的临界点(2 920 875 N)时,其张力-位移曲线与x=0的交点即为锚泊线的最佳预紧力。根据给出的锚泊线参数,使用分段外推法[9]在Matlab中搭建锚泊线的应力模型,得出单根锚泊线顶端张力与位移的关系曲线,如图2所示。
|
图 2 锚泊线张力-位移曲线 Fig. 2 The tension-movement curve of mooring line |
从图中可知,锚泊线的最佳初始预张力为1 500 261 N。
继续使用搭建的锚泊线应力模型,得出单根锚泊线水平张力与位移的关系,并对式(4)中的参数进行求解,得到锚泊线顶端水平张力与等效位移的函数关系为
| $\begin{split}T = & {T_0} + g(\Delta L) = 1\;386\;989 + 1.085\;6 \times {10^{ - 5}}{(\Delta L)^9}+ \\ &2.152\;1 \times {10^{ - 4}}{(\Delta L)^8}- 3.929\;7 \times {10^{ - 3}}{(\Delta L)^7} - \\ &0.075\;248{(\Delta L)^6} + 0.626\;44{(\Delta L)^5}+ 7.245\;6 {(\Delta L)^4} - \\ &77.946{(\Delta L)^3} + 234\;9.4{(\Delta L)^2} + 971\;93\Delta L\text{,}\end{split}$ | (9) |
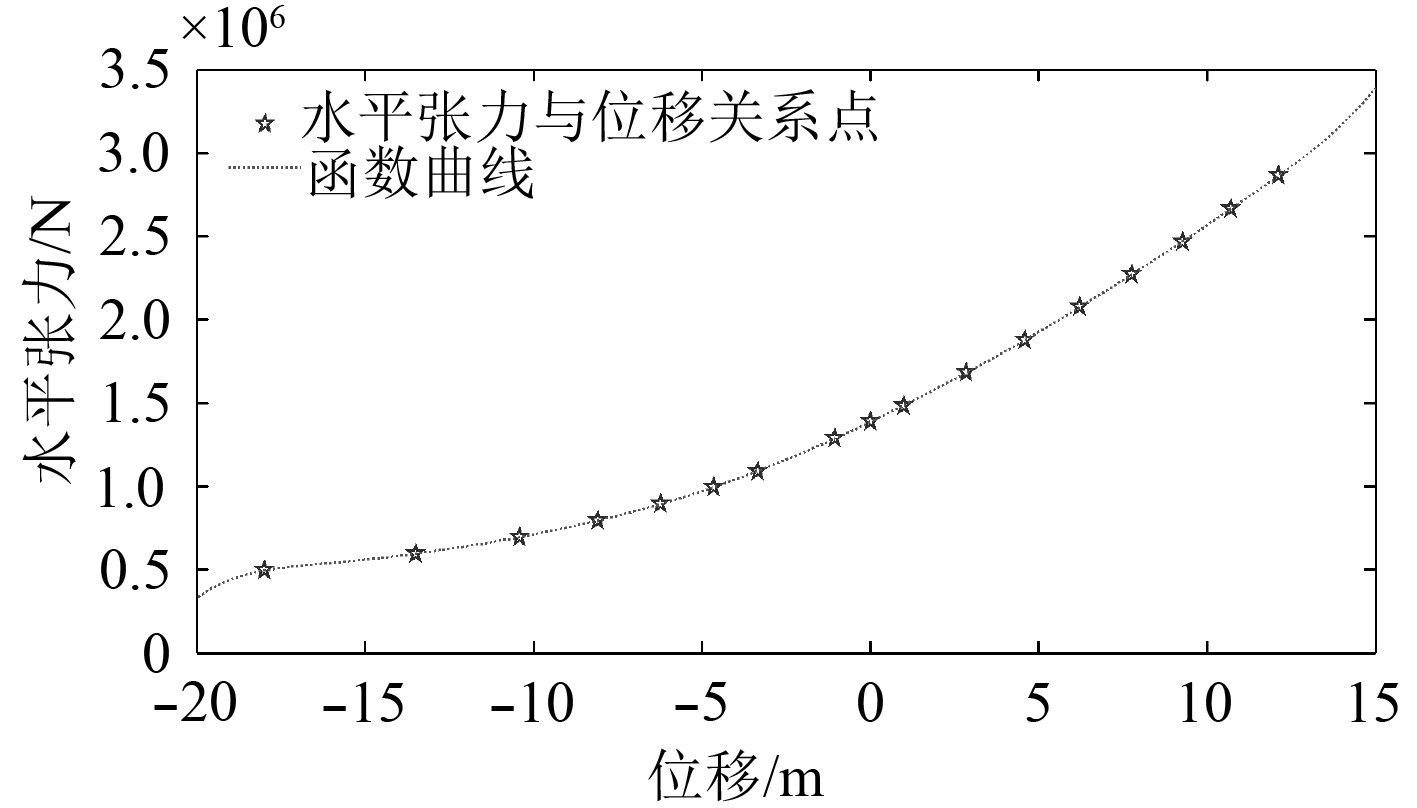
所得函数图形与通过仿真得到的锚泊线顶端水平张力和位移关系点的差异如图3所示。
|
图 3 锚泊线水平张力-位移曲线 Fig. 3 The horizontal tension-movement curve of mooring line |
从图中可以看出,函数曲线较好地反映了锚泊线水平张力与位移的关系,式(9)可以用于锚泊系统静回复力的计算。
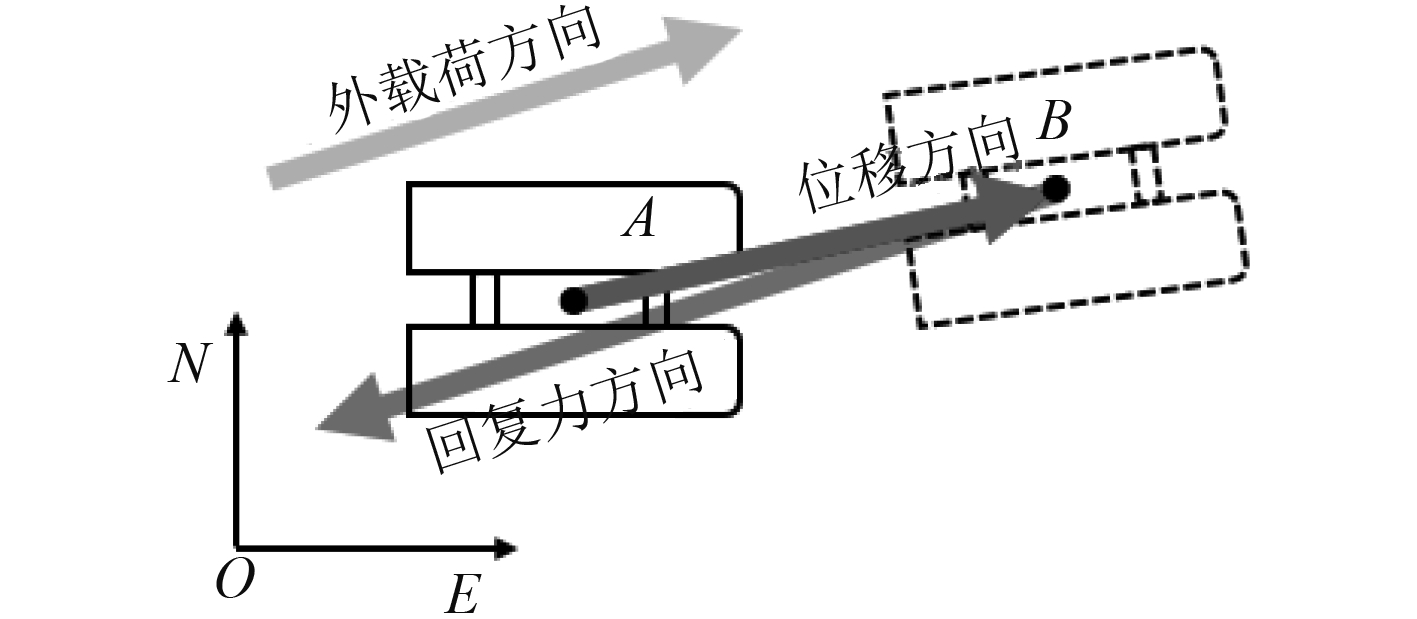
2 求解与验证定义位移方向、回复力方向及外载荷方向都是其与E轴的夹角。平台在外载荷的影响下从A点移动到B点,此时回复力与外载荷方向大小相等,方向相反,三者的关系如图4所示。
|
图 4 方向示意图 Fig. 4 Direction diagram |
已知外载荷大小及方向,使用数值求解的方法得出平台的位移方向及大小。但是,在求解之前,需要验证平台的位移方向与外载荷方向是否一致,即位移方向与回复力方向是否相等。如果两者方向不相等,需要在整个NE坐标系下寻找平台位置,使其在此位置下的回复力与外载荷刚好抵消;如果两者方向相等,或者偏差很小,则只需在外载荷方向上寻找平台位置,这样能够大大减小求解范围,提高求解速度。
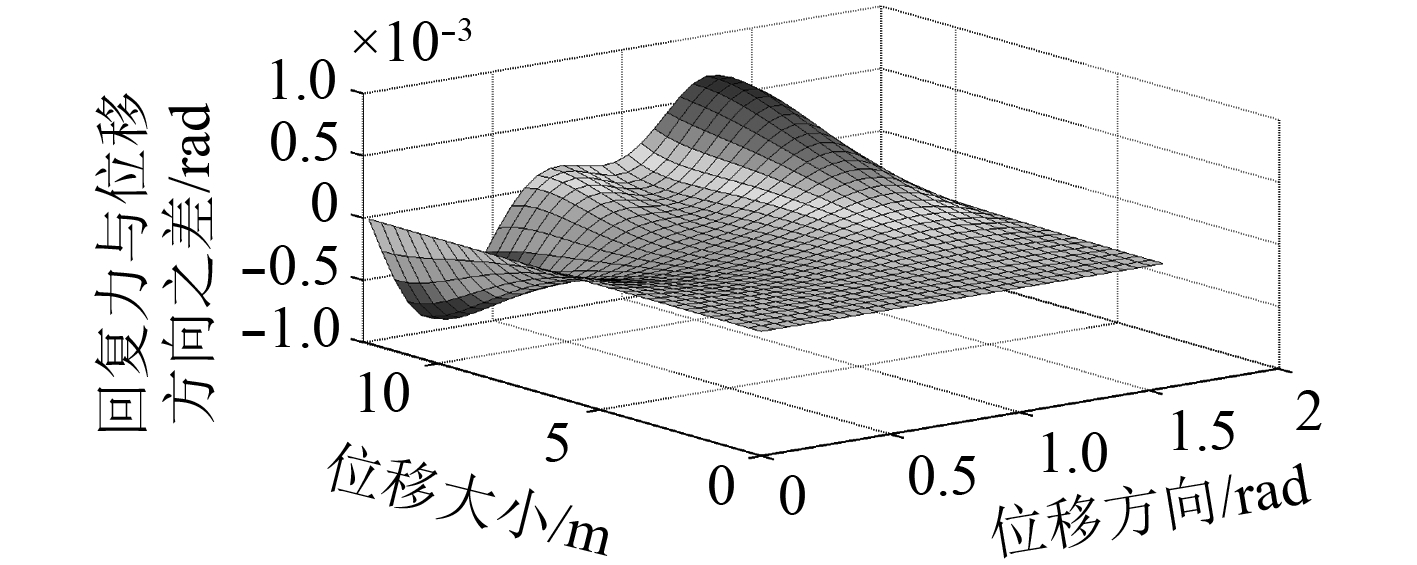
锚泊系统采用θ=π/4的布锚方式,根据之前推导的回复力计算公式,在Matlab中搭建锚泊系统的回复力模型,比较平台在允许工作半径内回复力方向β与位移方向α的差异,如图5所示。
|
图 5 回复力方向与位移方向差异图 Fig. 5 The direction difference between the restoring force and movement |
从图中可以看出,平台位移越大,回复力方向与位移方向之间的差距越大,但是两者在允许作业半径内的最大的差值仅为0.000 89 rad,因此可以认为锚泊系统的回复力方向与平台位移方向相等,即平台的位移方向与外载荷方向一致。
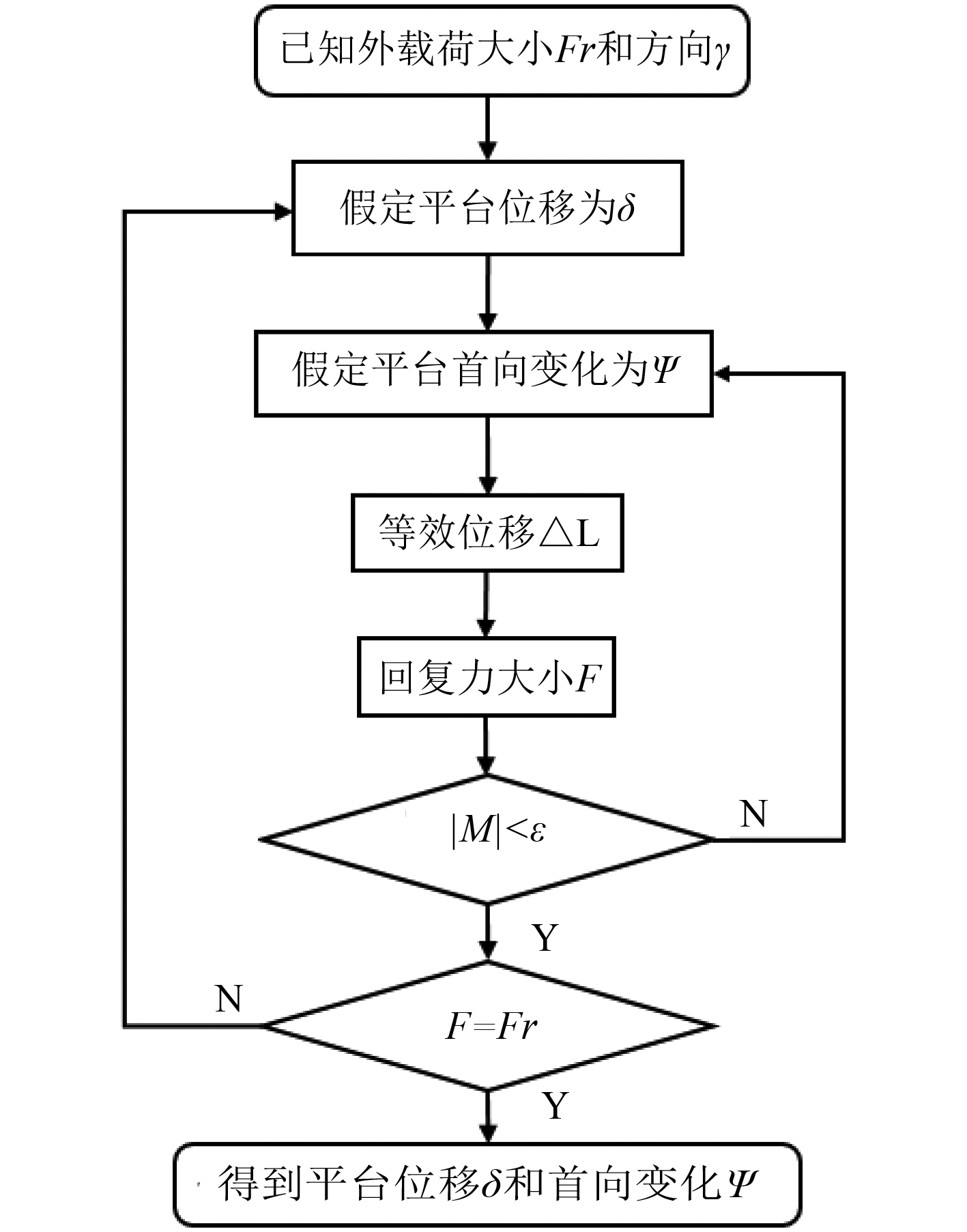
2.1 求解方法根据之前的公式推导和仿真分析,可以在已知外载荷大小及方向的情况下,求解平台的位移及首向变化。当布锚夹角θ以及锚泊线材质组成确定后,通过建立的NE坐标系得到预张状态下的锚绞机及锚固点坐标。已知外载荷大小Fr与方向γ,因为位移方向α与外载荷方向一致,所以只需假设位移大小为δ和平台首相变化为ψ,即可根据式(1)、式(2)、式(3)求出锚绞机坐标及锚泊线顶端的等效位移。将等效位移代入式(9)中,就能求出每根锚泊线的张力,最后经过式(6)求出平台的回复力大小。调整位移大小δ直到回复力大小与外载荷大小之差满足一定精度。因为位移方向确定后,位移大小与平台首向变化存在一一对应的关系,因此相当于只有一个自变量,结果存在唯一解。具体计算流程如图6所示。其中,ε是一个足够小的值。
|
图 6 求解流程图 Fig. 6 The solution flow chart |
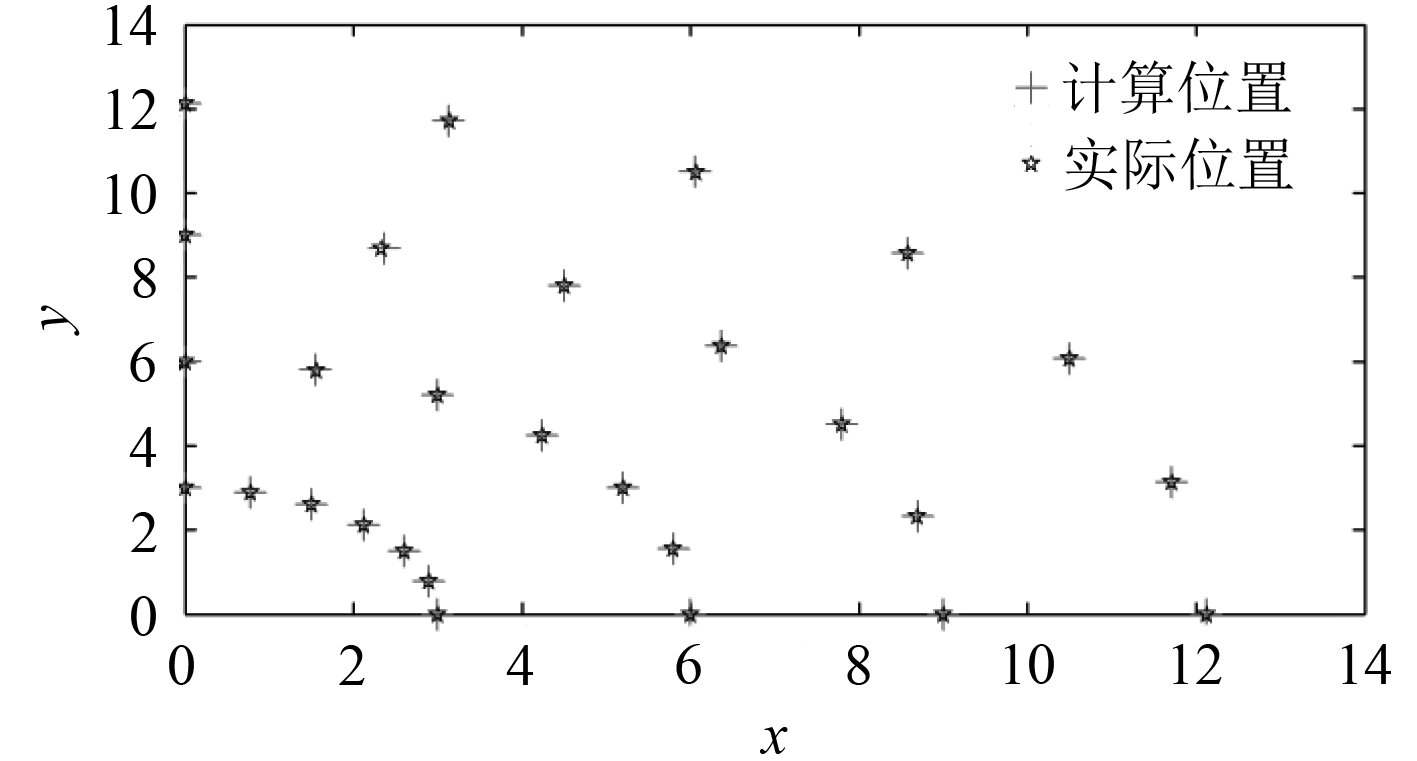
给定平台一个实际位置,可以得出平台在此位置下的回复力大小及方向。将计算得出的回复力假设为外载荷,通过图6给出的求解方法得出平台的计算位置。比较平台的实际位置与计算位置,来验证方法的可行性,仿真结果如图7所示。
|
图 7 坐标差异图 Fig. 7 The coordinate difference chart |
从图中可以看出,平台的实际位置与计算位置差异很小,所以本文给出的计算平台在外载荷下位移的方法具备可行性和准确性。
3 汇交和非汇交锚泊系统的差异实际的锚泊辅助动力定位系统中,所有的锚泊线并不会交于一点。但采用非汇交方法对平台位置进行计算时,由于计算量偏大会导致控制器的时效性较差,进而影响动力定位系统中的推进器对前馈的补偿。本节借助上节给出的平台位移计算方法,研究汇交和非汇交锚泊系统的差异,进而探讨使用汇交锚泊系统代替非汇交系统的可行性。
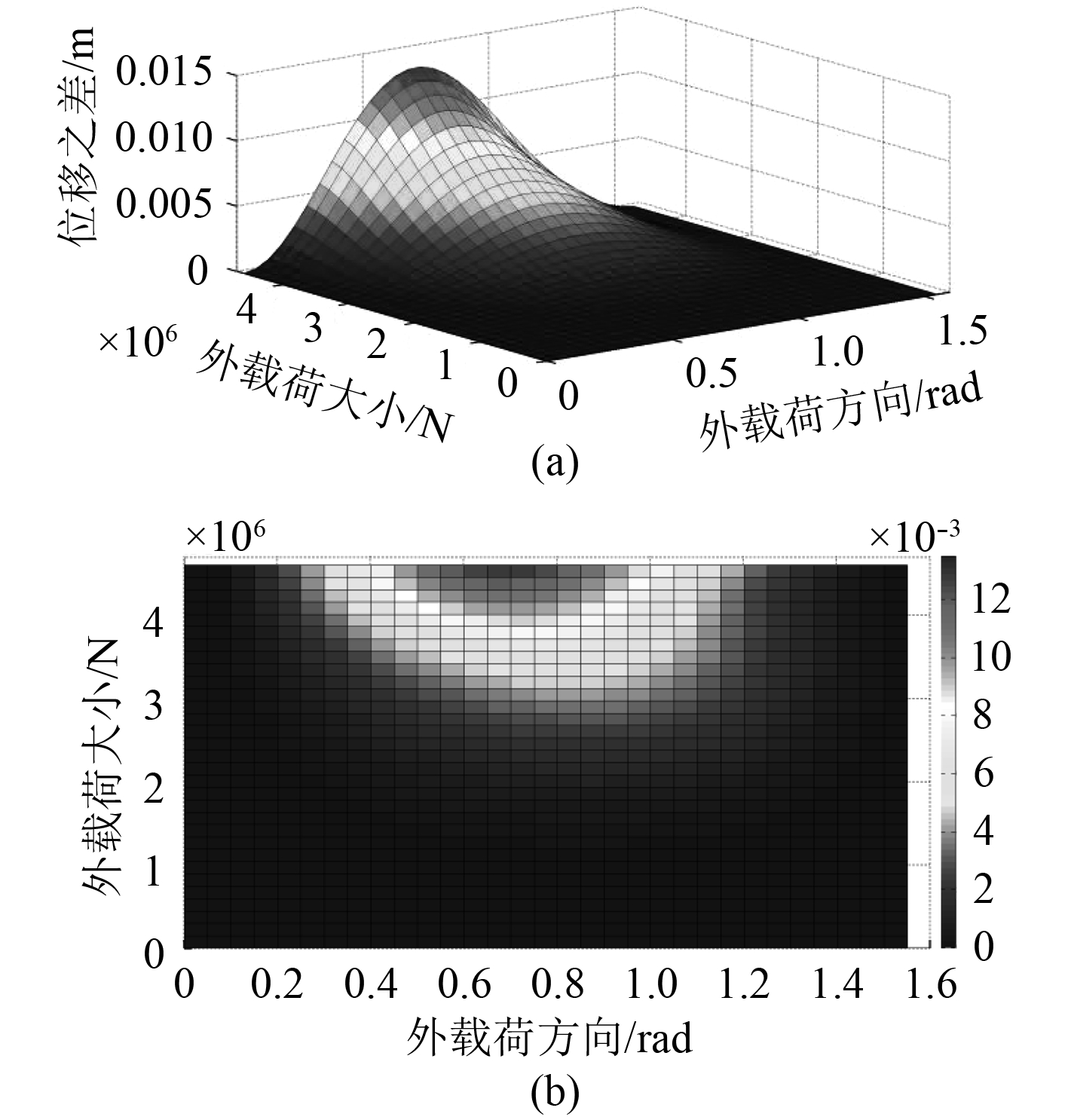
3.1 位移差异锚泊系统的定位能力是由所有分布在平台四周的锚泊线共同决定的,在相同的外载荷下,平台的位移越小,说明锚泊系统的定位性能越好,推进器工作的频率越小。本文采用对称式布锚,因为流速对锚泊线的偏移量几乎没有影响,所以只研究外载荷方向γ在0~π/2 rad范围内,非汇交与汇交锚泊系统的平台位移差异,如图8所示。
|
图 8 位移差异图 Fig. 8 The movement difference diagram |
从图中可以看出,随外载荷的增大,非汇交与汇交锚泊系统的位移差异逐渐增大。当外载荷大小为4 597 207 N,外载荷方向为0.75 rad时,两者的位移差异最大,为0.013 5 m,相比于此时位移大小为12.272 9 m的非汇交平台,两者的位移差异可忽略不计。
为了更加直观比较汇交和非汇交锚泊系统对平台位移的影响,给两者施加同样的外载荷。其中,外载荷大小为:
| $Fr = \left\{ {\begin{aligned}&{3900000 \times \sin (0.053t),\quad\quad\quad\quad\,\quad\quad\quad\quad\quad t \leqslant30}\text{;}\\&{3950000 + 600000\sin \left[ {0.08 \times (t - 30)} \right],\;\;\;30 < t \leqslant 70}\text{;}\\&{3859138 - 2000000\sin \left[ {0.05 \times (t - 70)} \right],70 < t\leqslant 100 }\text{。}\end{aligned}} \right.$ | (11) |
外载荷方向为:
| $\gamma = \left\{ {\begin{array}{*{20}{c}}{0.4 \times \sin (0.05t),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \leqslant 30}\text{;}\\{0.4 + 1.15\sin \left[ {0.04 \times \left( {t - 30} \right)} \right],\;30 < t \leqslant 70\;}\text{;}\\{1.55 - 1.2\sin \left[ {0.05 \times \left( {t - 70} \right)} \right] ,\;70 < t \leqslant 100 }\text{。}\end{array}} \right.$ | (12) |
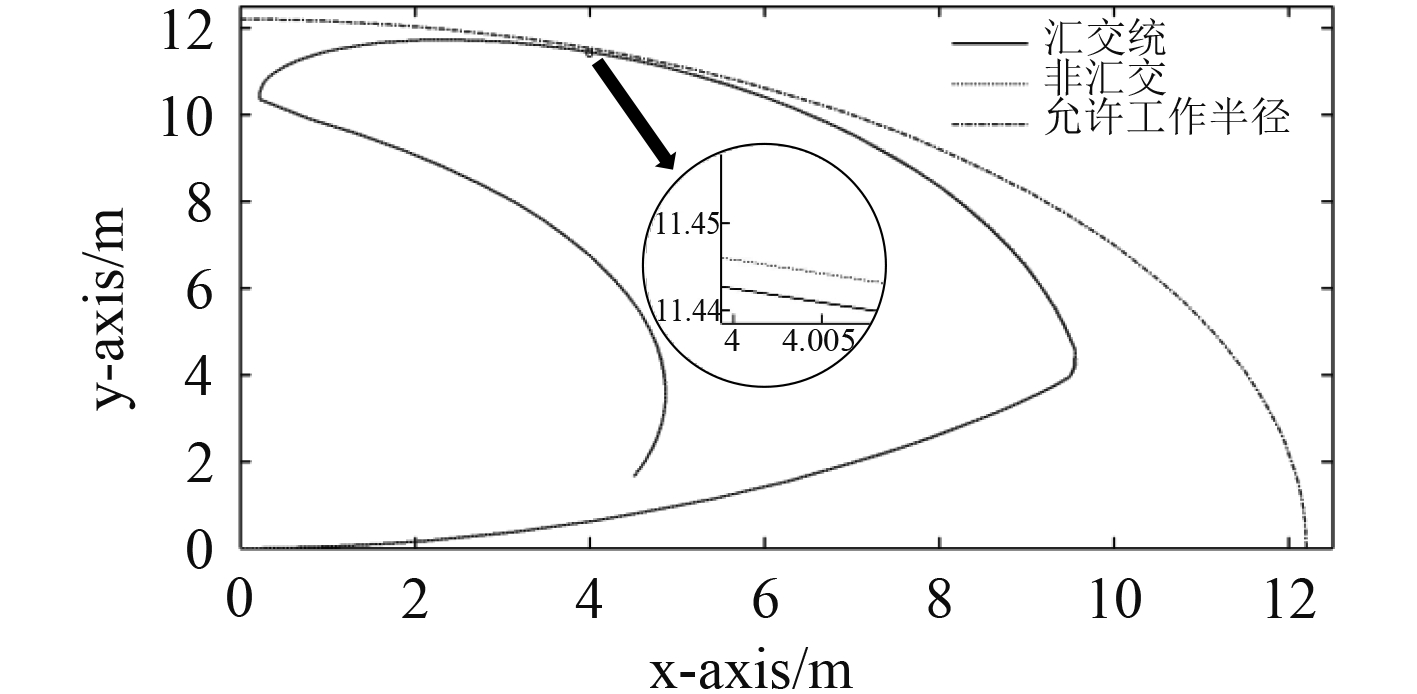
两者在外载荷下的平台运动轨迹如图9所示。
|
图 9 运动轨迹差异图 Fig. 9 The trajectory difference chart |
从图中可以看出,在允许工作半径内,汇交和非汇交锚泊系统的平台在相同外载荷下的运动轨迹差异可忽略不计。
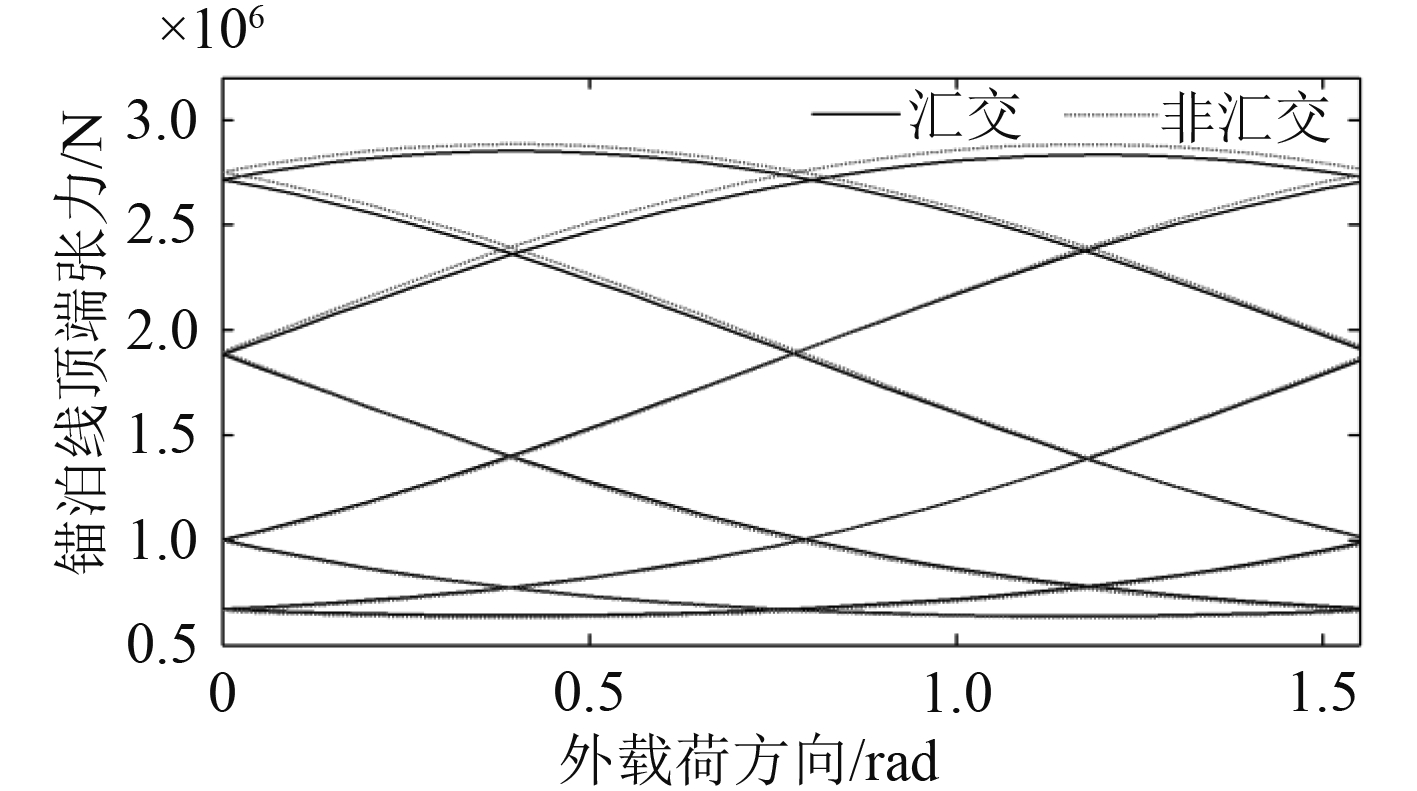
3.2 锚泊线受力差异研究汇交和非汇交锚泊系统的差异,不能单单考虑平台在相同外载荷下的位移差异,也要考虑锚泊线的受力,特别是所有锚泊线的受力均匀程度。锚泊线在外载荷的影响下受力越均匀,则锚泊线发生断裂的可能性就越低。汇交与非汇交锚泊系统的8根锚泊线在4 500 000 N外载荷下的应力差异如图10所示。
|
图 10 锚泊线受力差异图 Fig. 10 The tension difference of all mooring lines |
从图中可以看出,当锚泊线张力大于初始预张力时,汇交锚泊系统的锚泊线的受力比非汇交偏小;反之则偏大。当外载荷方向为1.05 rad时,锚泊线L6的顶端张力差异最大,为52 283 N,而此时非汇交系统中对应锚泊线的顶端张力为2 856 725 N,相对差异并不大。
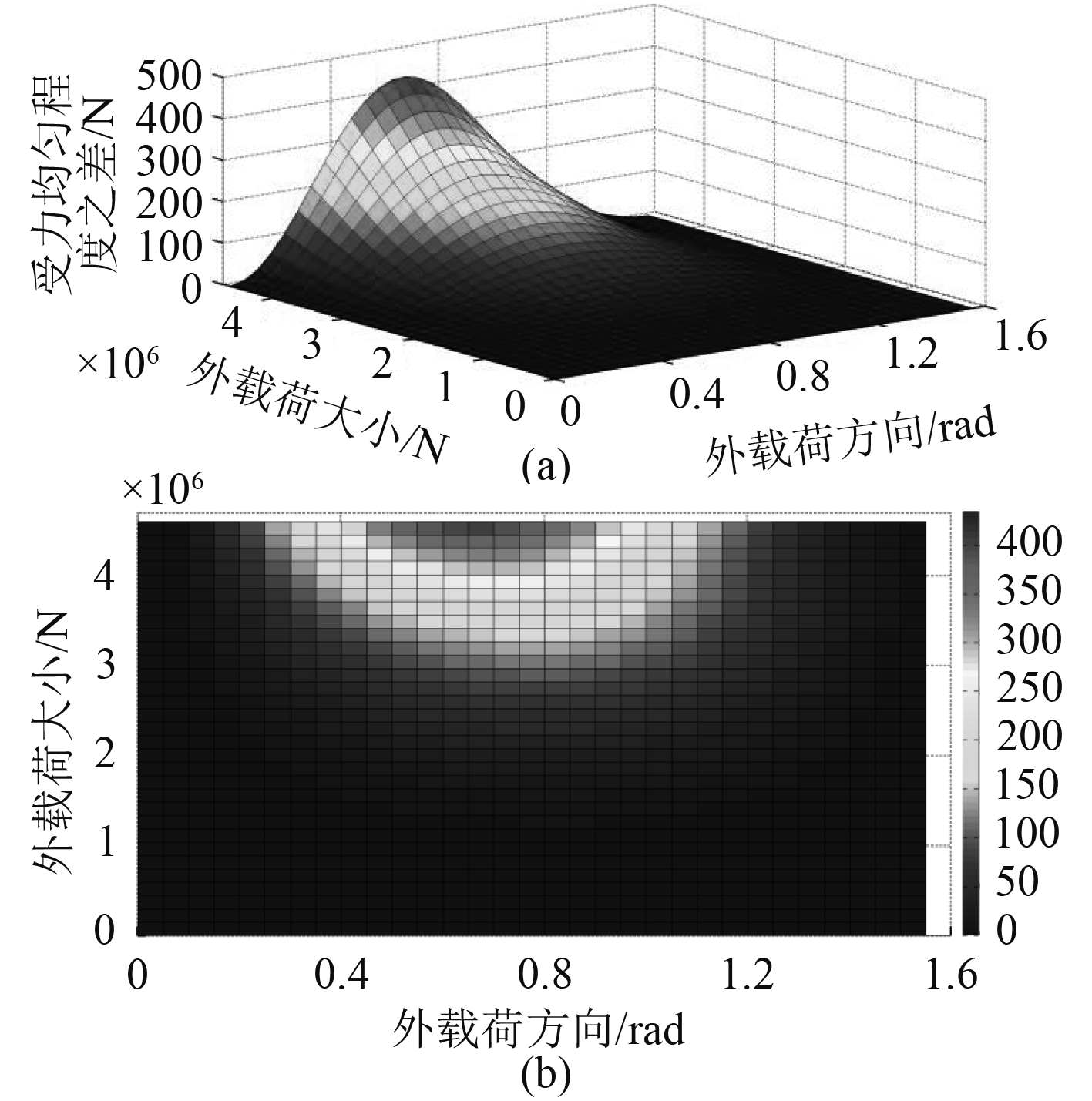
用8根锚泊线受力的标准差表示锚泊线受力的均匀程度,两者的锚泊线受力均匀性差异如图11所示。
|
图 11 受力均匀性差异图 Fig. 11 The difference diagram of tension uniformity |
从图中可以看出,随外载荷的增大,汇交和非汇交锚泊系统的锚泊线受力均匀性差异越来越大。当外载荷大小为4 597 207 N,外载荷方向为0.65 rad时,两者的锚泊线受力标准差差异最大,为433.67 N,相比于此时受力标准差大小为870 332.35 N的非汇交锚泊系统,差异可忽略不计。
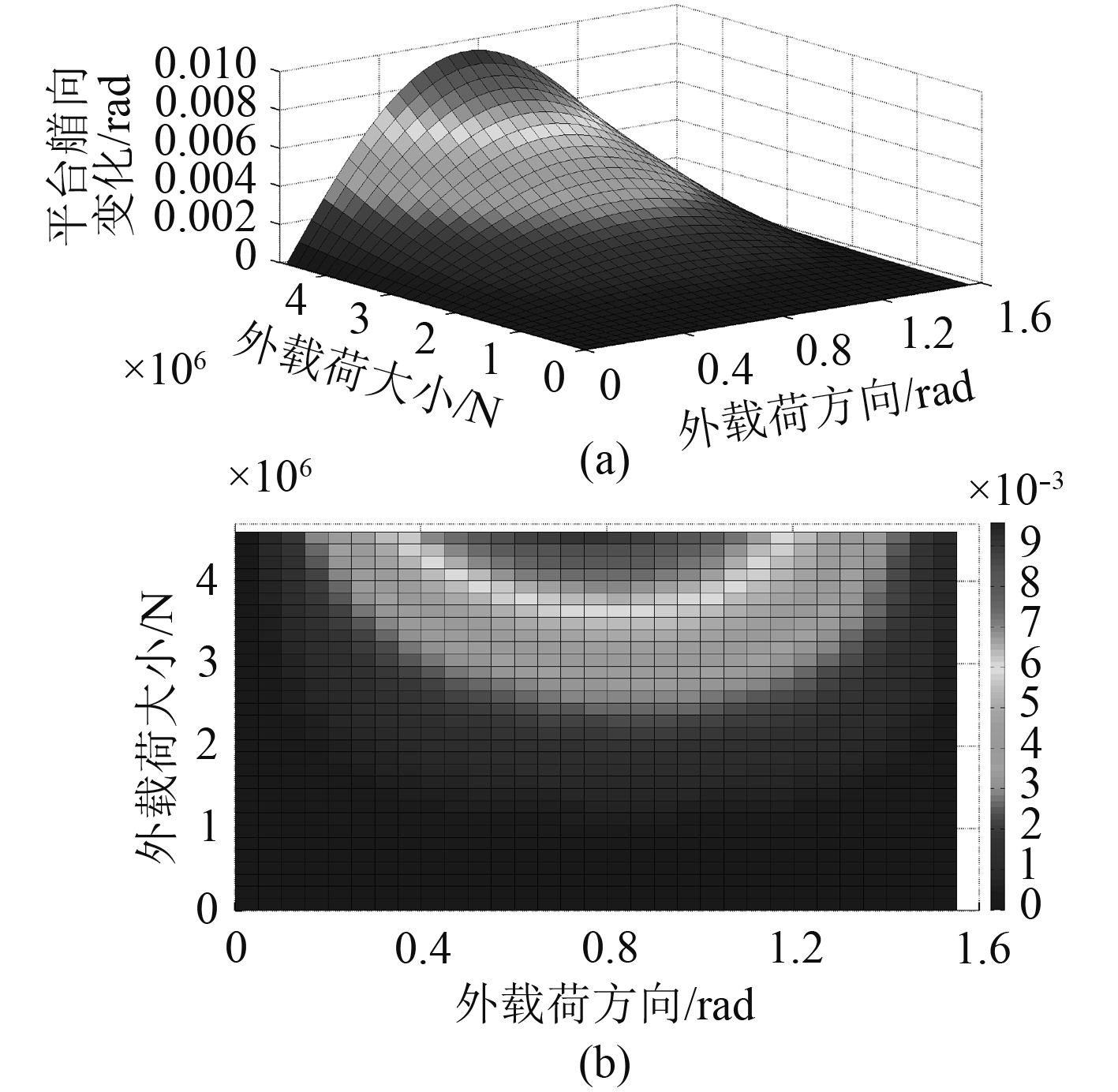
3.3 平台的首向差异非汇交锚泊系统的锚泊线并不总交于一点,因此平台在外载荷的影响下既发生位移,首向又发生变化。下面研究外载荷大小及方向对平台首向ψ的影响,如图12所示。
|
图 12 平台首向变化图 Fig. 12 The difference diagram of platform bow |
从图中可以看出,随外载荷的增大,平台首向变化逐渐增大。平台在0~π/2 rad范围内的首向变化都为正值,即平台转动方向全部都为逆时针。当外载荷大小为4 597 207 N,外载荷方向为0.7 rad时,平台的首向变化最大,为0.009 69 rad。所以非汇交锚泊系统对平台首向的影响可忽略不计。
综上所述,与实际系统相比,汇交锚泊系统在平台位移、锚泊线受力以及平台首向方面存在的差异很小,可忽略不计。在进行相关计算时可假设锚泊系统的所有锚泊线总交于一点。
4 结 语本文提出一种计算半潜式平台在外载荷下位移的方法,并验证了其可行性。通过比较汇交锚泊系统与实际系统的差异,简化了求解模型,使控制器能够提前预估平台在外载荷下的位置,进而提高推进器的工作效率与控制精度。基本结论如下:
1)本文给出的半潜式平台位移计算方法具备可行性及准确性。
2)采用锚泊定位的半潜式平台的位移方向与外载荷方向基本一致,其首向在外载荷的影响下变化也很小。
3)在对锚泊系统的受力及平台位移进行计算时,可使用汇交锚泊系统代替非汇交系统。
本文所做的研究工作及相应结论可为锚泊辅助动力定位系统控制器的设计提供参考。
| [1] | SMITH R J, MACFARLANE C J. Statics of a three component mooring line[J]. Ocean Engineering, 2001, 28(7): 899–914. |
| [2] | LIU Y C, PENG Y, WAN D C. Numerical investigation on interaction between a semi-submersible platform and its mooring system[C]//ASME 2015 34th International Conference on Ocean. Newfoundland: Ocean, Offshore and Arctic Engineering Division, 2015: 8–12. |
| [3] | QIAO D S, WU F, OU J P. Coupled analysis of a semisubmersible platform with two types of mooring systems[C]//Proceedings of the International Offshore and Polar Engineering Conference. Busan: International Society of Offshore and Polar Engineers, 2014: 993–1000. |
| [4] | GUO S X, CHEN W M, FU Y Q. Non-linearly Restoring Performance of SFT’s Catenary Mooring-lines under Consideration of its Dynamic Behaviors[J]. Procedia Engineering, 2016, 166: 204–209. |
| [5] | 余龙, 谭家华. 基于准静定方法的多成分锚泊线优化[J]. 海洋工程, 2005, 23(1): 69–73. |
| [6] | 闫俊, 乔东生, 欧进萍. 深水悬链锚泊线串联浮筒系统静力特性分析[C] //第十六届中国海洋(岸)工程学术讨论会论文集(上册). 大连: 中国海洋工程学会, 2013: 339–344. |
| [7] | 郝春玲, 滕斌. 不均匀可拉伸单锚链系统的静力分析[J]. 中国海洋平台, 2003, 18(4): 19–22+34. |
| [8] | AHMED M O, YENDURI A, KURIAN V J. Behavior of Mooring Systems for Different Line Pretensions[J]. Applied Mechanics and materials, 2014, 567: 204–209. |
| [9] |
王冬姣. 索-链-浮子/沉子组合锚泊线的静力分析[J]. 中国海洋平台, 2007, (06): 16–20.
WANG D J. Static analysis of a wire rope-chain-buoy/sinker Mooring line[J]. China Offshore Platform, 2007, 16(05): 16–20. http://www.doc88.com/p-1856918329321.html |
 2018, Vol. 40
2018, Vol. 40
