2. 江苏科技大学,江苏 镇江 212003, China;
3. 中国船舶重工集团公司第七一一研究所, 上海 201108
2. Jiangsu University of Science and Technology, Zhenjiang 212003, China;
3. The 711 Research Institute of CSIC, Shanghai 201108, China
船舶减振支架是一种具有优良减振性能的隔振装置,使用弹性体将柴油机和齿轮箱等会发生振动行为的设备固定在减振支架上,能够有效防止设备在使用过程中因振动而对船体造成损伤。由于振动疲劳的影响,极易导致船舶减振支架结构在工作过程中突然发生疲劳断裂事故。为了区别于常规疲劳问题,通常将这种由振动所导致的疲劳破坏称为振动疲劳。尤其当载荷的频率等于或接近结构的某一阶或某几阶固有频率时,会发生共振疲劳[1]。
凡服役在振动环境中的工程结构都把抗疲劳作为结构设计的重要准则之一,但是以往工程师在结构抗疲劳设计阶段,仍然利用静态疲劳理论,等产品试制出来后再进行振动校核或振动测试,对不符合要求的设计进行局部补救。这种不合理的设计理念为今后发生事故埋下了隐患,例如汽轮发电机组转子曾因振动引起疲劳断裂,斜拉桥由于斜拉索的的剧烈振动导致疲劳损伤[2]。
最近5年,有关学者对振动疲劳的研究主要有Seung-Ho Han等[3]对汽车进行振动疲劳分析,考虑了车身内由多点点焊接头累积疲劳损伤引起的频率响应变化;孙刚等[4]通过振动疲劳实验方法研究了温度与修复层振动疲劳寿命的关系,分析了修复层的成分及组织随温度的形貌变化。目前,残余应力对船舶专用的减振支架结构进行振动疲劳分析的研究较少,更无可借鉴的例子。因此,本文针对某船舶隔振装置的减振支架,对其进行结构振动疲劳及残余应力影响研究。研究工作将对提高减振支架的运行安全性和可靠性提供相关依据,同时对船舶降噪具有实践性的指导和参考意义。
1 振动疲劳理论基础 1.1 振动疲劳简介随机加载条件下的疲劳计算可根据压缩的频域信号,将随机载荷及响应信号用功率谱密度(PSD)函数分类,从而将动态结构模拟成一个线性传递函数[5]。
1.2 功率谱密度(PSD)的惯性矩惯性矩即为功率谱密度函数曲线下包括的面积,n阶惯性矩
| ${M_n} = \int {{f^n}G(f){\rm{d}}f} {\text{,}}$ | (1) |
式中:f为频率;G(f)为频率f处的单边PSD值。
不规则因子
| $\gamma = \frac{{{E_0}}}{{{E_P}}} = \frac{{\sqrt {{{{m_2}}/{{m_0}}}} }}{{\sqrt {{{{m_4}}/{{m_2}}}} }} = \frac{{{m_2}}}{{\sqrt {{m_0}{m_4}} }}{\text{。}}$ | (2) |
式中:E0为零交叉点的期望数;EP为峰值的期望数;
1.3 基于宽带信号的疲劳分析Dirlik用Monte Carlo技术进行全面的计算机模拟得到了基于宽带信号的振动疲劳分析[5],式(3)给出了Dirlik方法的数学表达式为:
| ${N_S} = {E_P}{\rm{-}}T{\rm{-}}P(S){\text{。}}$ | (3) |
式中:NS为时间长度为T、应力幅值为S的应力循环次数。
P(S)为由1个指数分布和2个瑞利(Rayleigh)分布近似给出的雨流幅值概率密度函数,即
| $P(S) = \displaystyle\frac{{\displaystyle\frac{{{D_1}}}{Q}{e^{\displaystyle\frac{{ - Z}}{Q}}} + \displaystyle\frac{{{D_2}}}{{{R^2}}}{e^{\displaystyle\frac{{ - {Z^2}}}{{2{R^2}}}}} + {D_3}Z{e^{\displaystyle\frac{{ - {Z^2}}}{2}}}}}{{2\sqrt {{m_0}} }}{\text{,}}$ | (4) |
其中
据Miner线性累积损伤理论,连续变化循环应力的构件累积损伤度[6]
| $D = \int {\frac{{{n_S}}}{{{N_S}}}} {\text{,}}$ | (5) |
式中:nS为应力幅值为S时的实际循环数;NS为应力幅值为S时的破坏循环数;D为累积损伤度;一般情况下当D=1时,构件发生破环。
根据强度理论,疲劳曲线在其有限寿命范围内的曲线方程为:
| ${S^{m}}{N_S} = {\rm{C}}{\text{,}}$ | (6) |
式中:C和m为材料常数,由疲劳试验确定。
式(1)为宽带随机载荷的寿命预测,将式(5)和式(6)代入式(3)获得构件的疲劳寿命为:
| $T = \frac{{{N_S}}}{{{E_P}P(S)}} = \frac{{\rm{C}}}{{{E_P}\int {{S^m}P(S){\rm d}S} }}{\text{。}}$ | (7) |
由于支架外载荷属于宽频的随机激励,所以振动疲劳分析方法采用了Dirlik法。
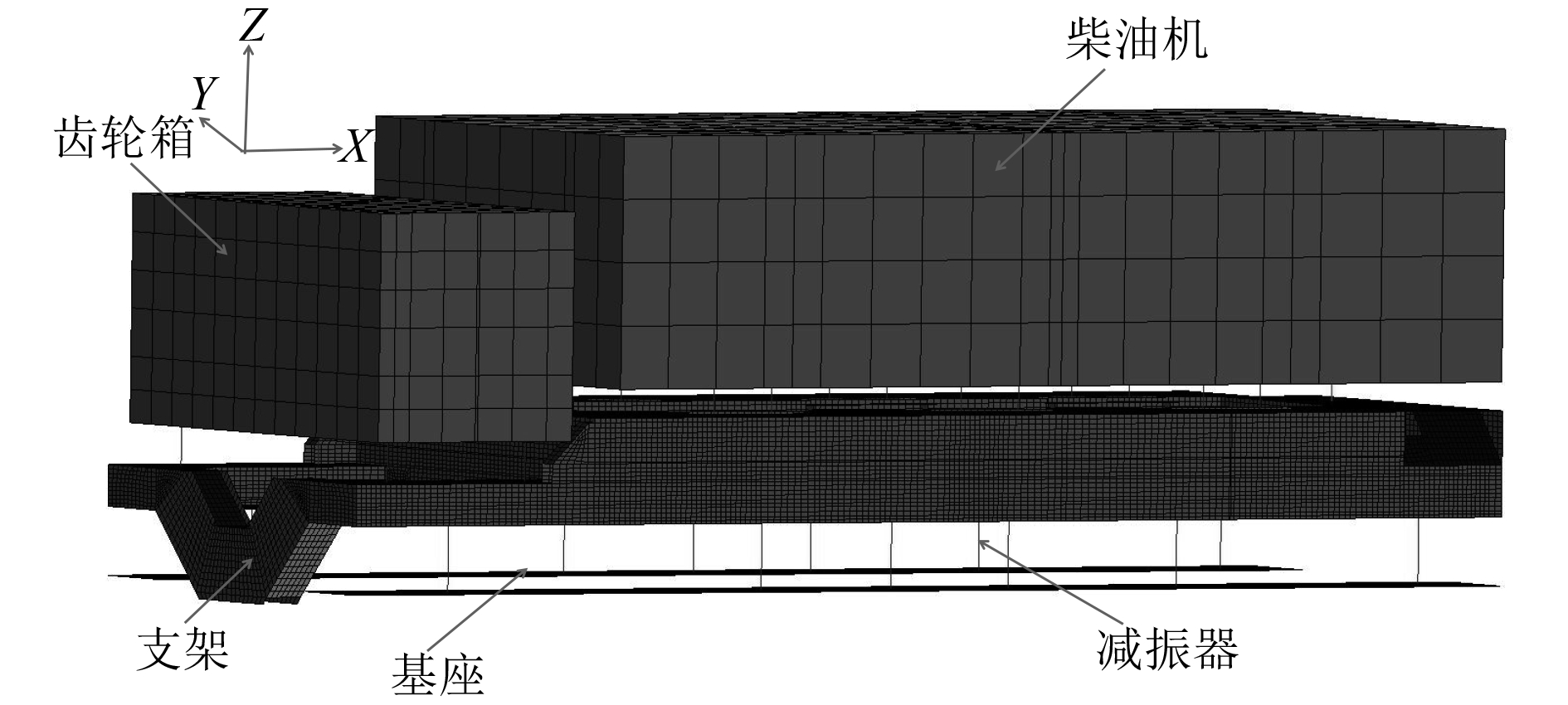
2 船舶减振支架结构有限元建模及加载船舶减振支架长5 m、宽1.8 m、高1.557 m,板厚大部分为8 mm,用MSC.Patran有限元软件进行建模。图1为船舶减振支架结构整体有限元模型,减振支架通过减振器与齿轮箱、柴油机及基座相连,齿轮箱与柴油机之间通过一根弹性轴相连,支架的材料属性如表1所示。
|
|
表 1 支架结构材料参数 Tab.1 Material parameters of structure |
减振支架采用壳单元,柴油机和齿轮箱为实体模型,减振器和弹性轴采用弹簧单元进行有限元建模。
柴油机和齿轮箱工作载荷1和工作载荷2分别加载在其重心处,其部分实测数据如表2所示。
|
|
表 2 加载载荷 Tab.2 The loads |
|
图 1 船舶减振支架结构整体有限元模型 Fig. 1 The entire finite element model of the shock reduction support |
任何结构或部件都有固有频率和相应的模态振型,这些属于结构或部件自身的固有属性。模态分析用于确定结构的固有频率和振型,其分析结果为后面的频率响应分析作基础。对于无约束的支架,前6阶模态为刚体模态,计算所得第7~12阶模态如表3所示。
|
|
表 3 支架第7~12阶模态固有频率 Tab.3 Natural modal frequencies from 7 to 12 orders of the support |
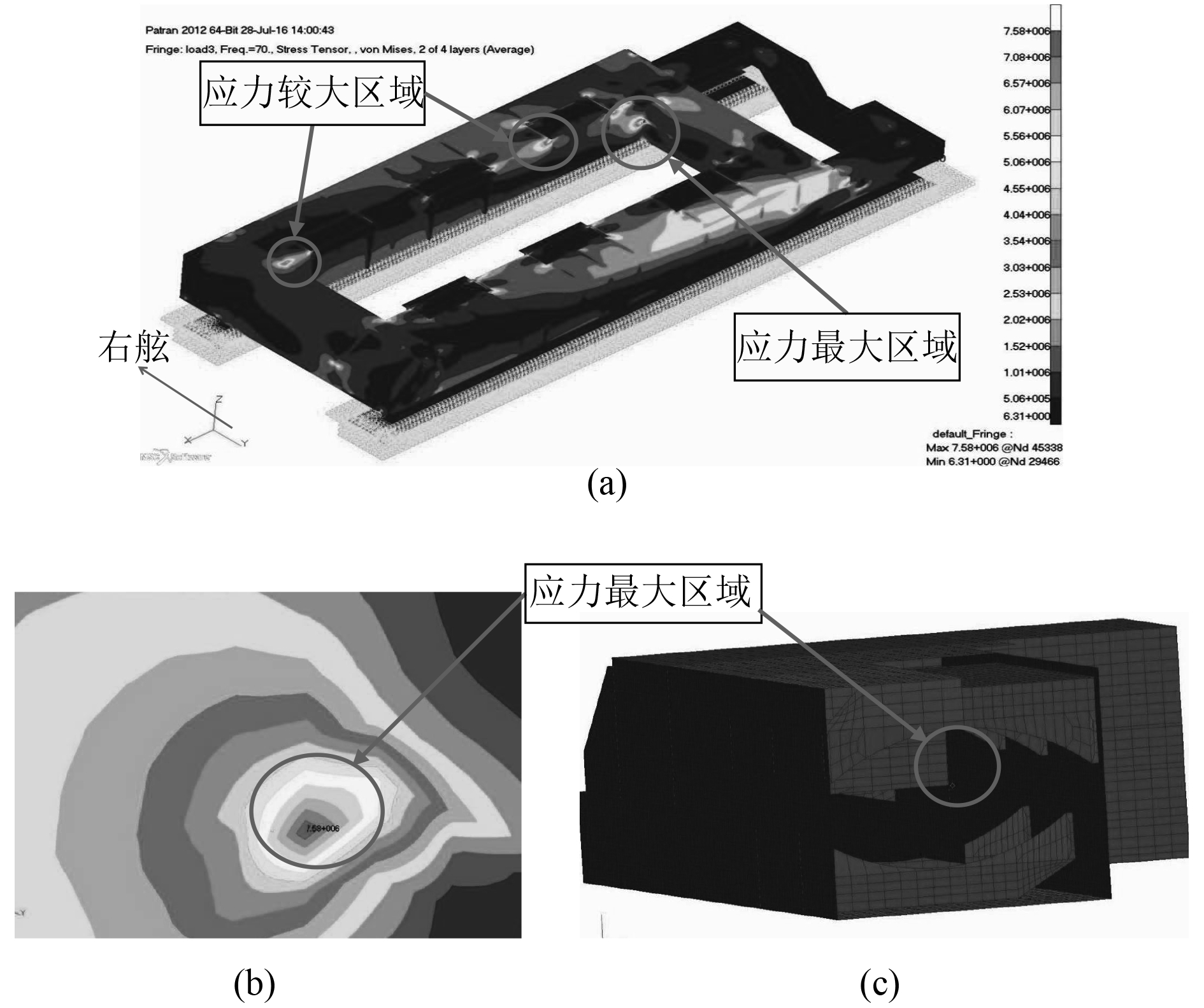
对减振支架整体结构进行载荷1和载荷2共同作用下的频率响应分析。计算结果可知,当频率为70 Hz时,应力响应最大为7.58 MPa,位于中间梁右舷垂直相交连接处,如图2减振支架应力分布图2(a)所示,图2(b)和图2(c)为应力最大区域局部放大图。应力最大的一部分原因主要是其在板架连接处,应力较为集中。而位于支架上表面开孔的局部部位也有应力比较集中的区域,即应力较大区域,约为5.06 MPa。本次计算分析应力较小的原因是输入的载荷较小。应力最大区域和应力较大区域均有可能成为疲劳热点,易产生振动疲劳破坏,因此有必要对这些部位进行疲劳分析和研究。
振动疲劳破坏易发生的部位通常是共振中应变大且有缺陷或应力集中的部位,如果该部位正好处于某几阶重要模态振型的节线处,问题将变得更加严重。结合3.1节模态分析中的第8阶模态可知,减振支架的频率为70 Hz,此时最容易发生共振破坏。因此,在船舶作业时,应避免结构达到此频率。
为了较好的进行振动疲劳分析,符合结构疲劳计算要求,将减振支架应力最大区域附近网格加密,重新进行频率响应分析,发现应力最大点的位置更接近于中间梁右舷垂直焊缝位置,所以接下来的振动疲劳分析都是采用的网格加密过后的船舶减振支架有限元模型。
|
图 2 减振支架应力分布 Fig. 2 Stress distribution of the shock reduction support |
使用有限元软件MSC.Fatigue进行支架的振动疲劳分析主要包括载荷谱的处理、材料疲劳S-N曲线的确定、单位载荷下支架的应力响应分析。根据支架结构的材料参数,并进行相关修正,得到如式(8)所示的S-N曲线为:
| $\lg S = 3.571 - 0.133 \; 9\lg N{\text{。}}$ | (8) |
采用本文第1节振动疲劳理论,对减振支架整体结构进行柴油机和齿轮箱(载荷1和载荷2)共同工作下的不考虑残余应力影响的振动疲劳分析,得到寿命为3329.53年,且破坏位置在应力最大区域。
4.2 修正S-N曲线由4.1节可知,在没有考虑焊接残余应力时,支架振动疲劳寿命是3329.53年。但是支架结构实际上为焊接构件,不可避免会存在或大或小的焊接残余应力,采用经过计量检定合格的LM-12型残余应力检测仪和盲孔法对支架应力最大值区域附近的3个测点进行初始残余应力测量。为了降低焊接残余应力,对支架进行振动时效以释放部分残余应力。并测量了测点振动时效后的焊接残余应力剩余值,共进行了4次,总的残余应力释放量为4次释放量的总和。
初始焊接残余应力经过振动消除后,还留有较大的剩余,最大达到453.6 MPa,会对支架结构的频率响应分析和振动疲劳寿命产生较大的影响。
为了考虑经过振动释放后的残余应力对减振支架结构疲劳强度的影响,根据式(9)的Goodman公式[7 – 8]对S-N曲线进行修正,从而得到可以考虑残余应力影响的S-N曲线,这将会使计算结果更合理,并且更接近实际工作情况。
| ${S_{\rm{a}}} = {S_e } \left(1 - \frac{{{S_m}}}{{{S_u}}}\right){\text{,}}$ | (9) |
式中:Sa为应力幅;Se为等效应力;Sm为平均应力;Su为材料极限抗拉强度,本文为780 MPa。
为得到考虑残余应力影响的S-N曲线,首先在式(8)中取2组A(Sa1,N1),B(Sa2,N2)值,然后将残余应力100 MPa作为平均应力Sm代入式(9)中,得到2个等效应力Se1,Se2,再代入S-N公式(8)中求得等效应力下的寿命(N3,N4),最后得到数据C(Sa1,N3),D(Sa2,N4),由C,D得到如式(10)所示新的S-N曲线公式:
| $\lg S = 3.5114 - 0.1339\lg N{\text{。}}$ | (10) |
根据新的S-N曲线式(10)进行含残余应力的振动疲劳寿命分析,得出减振支架寿命为494.67年,而无残余应力时寿命3329.53年是考虑残余应力100 MPa影响时寿命的6.73倍。为了获得不同残余应力对支架振动疲劳寿命的影响,分别求出残余应力为200 MPa、300 MPa、400 MPa及残余应力最大值453.6 MPa时的S-N曲线,并进行振动疲劳寿命计算,结果如表4所示。分析得寿命最低部位均与图2应力最大区域位置相同,即中间梁右舷垂直相交连接处。
|
|
表 4 考虑残余应力影响的支架振动疲劳寿命对比表 Tab.4 Comparison of vibration fatigue life with different residual stresses |
由表4可知,焊接残余应力对支架振动疲劳寿命影响较大,虽然应力值仅从无增加到453.6 MPa,但是寿命却从之前的3 329.53年降至0.096年(约35.07天),在残余应力仅为300 MPa时支架寿命就无法符合设计要求的20年。
5 结 语1)本文船舶减振支架结构模态分析中第8阶模态为70.8 Hz,而频率响应分析中支架应力最大时频率为70 Hz,由此可见支架在70 Hz时容易发生共振,在使用过程中应避免支架达到此频率。
2)焊接残余应力对支架结构振动疲劳寿命的影响较大。要防止支架结构的振动疲劳破坏,应尽量降低支架结构关键部位的残余应力,将关键部位的焊缝连接处进行调整,使得焊缝与结构的应力集中部位远离,尽量防止多重不利因素的影响。
| [1] | 张坤, 薛璞, 胡海涛, 等. 含高频的载荷下飞机薄壁结构振动疲劳寿命分析[J]. 机械科学与技术, 2012, 31(4): 639. http://www.cnki.com.cn/Article/CJFDTOTAL-HKGJ201607019.htm |
| [2] | 刘文光. 结构共振疲劳试验及裂纹构件的振动疲劳耦合分析[D]. 南京: 南京航空航天大学. 2010: 2–3. |
| [3] | Seung-Ho HAN, Dae-Gyun AN, Seong-Jong KWAK, et al. Vibration fatigue analysis for multi-point spot-welded joints based on frequency response changes due to fatigue damage accumulation [J]. International Journal of Fatigue, 2013: 171. |
| [4] | 孙刚, 陈学明, 马国佳, 等. 基体温度对TC11钛合金EB-PVD修复层组织及振动疲劳寿命的影响[J]. 中国表面工程, 2015, 28(2): 59. |
| [5] | 王国军. Msc.Fatigue 疲劳分析实例指导教程[M]. 北京: 机械工业出版社, 2009, 167–170. |
| [6] | 孟彩茹, 卢博友. 基于PSD的随机载荷下振动疲劳寿命估算[J]. 机械设计, 2009, 26(5): 73–74. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jxsj200905023 |
| [7] | 方洪渊. 焊接结构学[M]. 北京: 机械工业出版社, 2010. |
| [8] | 格尔内. 焊接结构的疲劳. 周殿群, 译[M]. 北京: 机械工业出版社, 1998. |
 2018, Vol. 40
2018, Vol. 40
