舰船在海洋表面航行时,非流线型的舰面建筑会产生随甲板风变化的空气尾流,以往大量的研究[1 – 7]均将甲板风中的自然风简化为均匀来流,但实际中,由于受到海洋表面的摩擦作用,空气的水平运动受到阻碍,其速度逐渐减慢,形成大气边界层。2003年,Polsky[8]在利用CFD方法研究舰载风速仪测量精度时发现,引入大气边界层速度梯度前后,90°来流条件下特定位置的风向角方向改变量大于90°,幅值也发生较大变化,且与实船测量结果吻合更好;2008年,Forrest等[9]在研究英国皇家海军公爵级护卫舰Type 23的尾流场时发现,增加大气边界层速度梯度模型后,CFD预测的湍流度与实船测量结果吻合度更高,但速度值与实船测量结果吻合度反而更差,因此,Forrest等猜测可能海上的大气边界层条件与模拟的速度梯度模型不完全一样;2013年,Murray等[10]利用实船测量结果验证美国巡逻训练艇YP676 CFD仿真结果时发现,由于CFD仿真中没有考虑大气边界层的影响,其计算得到的速度剖面与实船测量结果截然不同。
上述研究证明大气边界层中的速度梯度对尾流场的影响不可忽略,但他们在CFD仿真中仅加载了速度梯度模型,并没有研究湍流强度对流场特性的影响。为了进一步研究大气边界层对舰船尾流特性的影响,本文利用CFD方法对不同边界条件下SFS2空气尾流进行数值模拟,系统分析大气边界层对甲板空气尾流特性的影响。
1 仿真方法 1.1 湍流模型舰船周围的空气流动可视为三维低速不可压高雷诺数湍流流动,且实际工程应用中主要关心湍流统计平均量,因此本文选用标准k-ε模型进行仿真模拟。标准k-ε模型适用于高雷诺数湍流,具有经济普适性,文献[3, 12–13]的研究中均采用了标准k-ε模型,且得到了很好的预测结果。
1.2 几何模型与网格划分本文利用Ansys ICEM对图1中所示的SFS2划分结构化网格,典型护卫舰简化模型SFS2坐标原点位于飞行甲板起始位置的中点,x正方向由船首指向船尾,y正方向由左舷指向右舷,z正方向由下指向上,机库高度H=6.096 m,飞行甲板长度L=4.5H,飞行甲板宽度B=2.25H。
|
图 1 SFS2几何模型 Fig. 1 Simple frigate shape (SFS) dimensions |
对于近壁网格采用壁面函数法处理,近壁网格的第1层网格到壁面的距离在对数区内,即无量纲化的避免距离y+在30~60之间。SFS2船体表面网格分布如图2中所式,经网格无关性验证后的SFS2的网格数量为1.89×107。基于飞行甲板宽度B和入口平均速度UB=20.6 m/s的流动雷诺数Re=1.83×107。

|
图 2 SFS2网格分布 Fig. 2 Structured mesh for SFS2 |
计算区域入口设置为速度入口,风向角包括0°和右舷45°两种工况;出口为压力出口;其他边界均设置成自由边界,并使用滑移条件设置三向速度分量。均匀来流条件下将静止的海平面设置成无粘壁面;考虑大气边界层模型时,将海平面设置为无滑移壁面,并将大气边界层的影响通过用户自定义函数(UDF)输入到入口边界条件中。
大气边界层中的平均风速剖面选择指数律,如下式:
| $U\left( z \right) = {U_{ref}}{\left( {\frac{z}{{{z_{ref}}}}} \right)^n}{\text{,}}$ | (1) |
式中:z为水面以上的任一高度;U(z)为z高度处的平均风速;zref为参考高度,取300 m;Uref为参考高度处的平均风速,取20.6 m/s;n为地形表面粗糙度指数,取0.125。
大气边界层中的湍流强度定义为脉动风速标准方差与平均风速的比值,如下式:
| ${I_i}\left( z \right) = \frac{{{\sigma _i}\left( z \right)}}{{U\left( z \right)}}{\text{,}}$ | (2) |
其中,σi(z)为三向脉动风速。本文只考虑起主要作用纵向湍流度Iu(z)。
2 仿真方法的验证为了验证仿真结果的有效性,论文设计了SFS2缩比模型的风洞实验。实验采用PIV技术对1/60的SFS2缩比模型开展流场速度测量。如图3所示,实验段截面为4.5 m×3.5 m,为模拟均匀来流大气边界条件,实验时模型放置在航空地板上,航空地板距离风洞地板1.45 m。风洞风速为25.7 m/s,测量工况为0°风向角。

|
图 3 SFS2风洞实验模型 Fig. 3 SFS2 model in the test section of the wind tunnel |
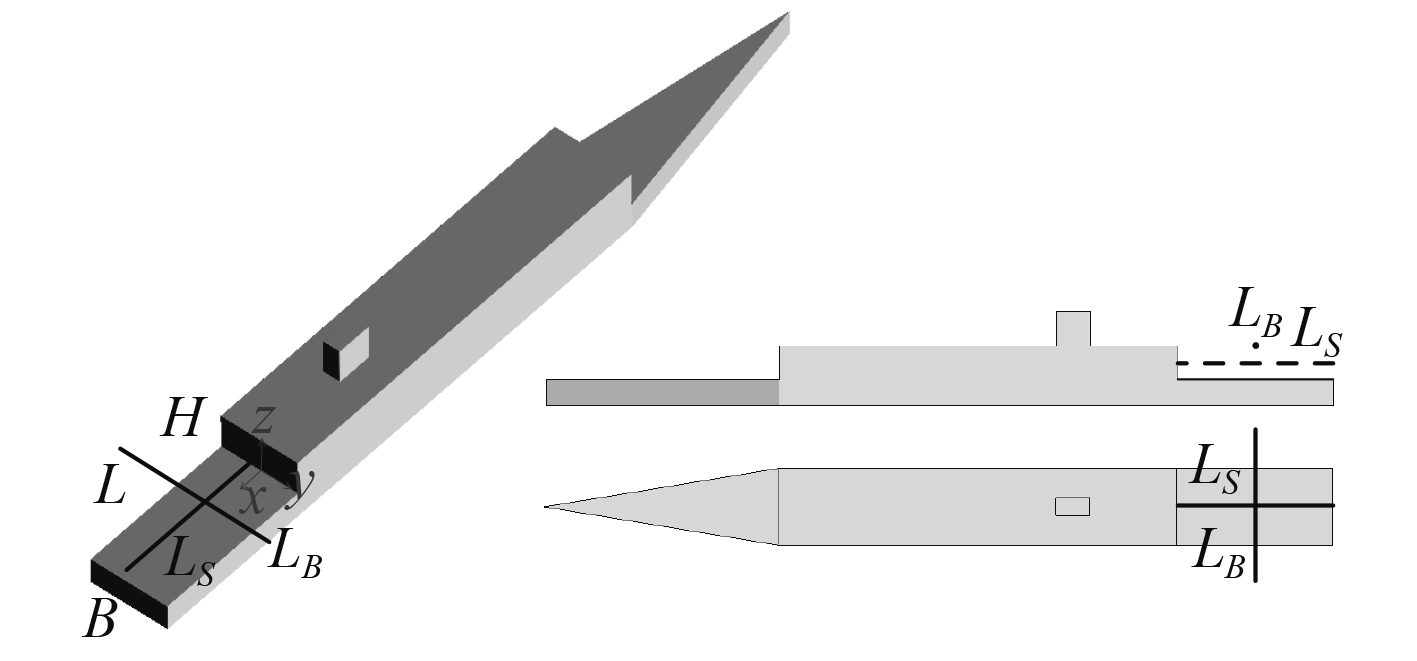
风洞实验和CFD仿真计算得到的图1中所示的SFS2中纵线LS上的无量纲化速度分布如图4中所示。对比结果显示,虽然CFD预测的垂向速度及回流区以外纵向速度值均略低于风洞实验结果,但CFD仿真计算和风洞实验得到的纵向速度和垂向速度变化趋势完全一致,且纵向和垂向速度方向发生变化的位置完全重合,这表明风洞试验和CFD仿真预测的回流区位置相同。对比结果显示,CFD仿真和风洞实验结果吻合度较高,证明本文中运用的数值方法合理可信,可用于舰船空气尾流场的研究。
|
图 4 SFS2 CFD与实验结果对比 Fig. 4 Comparison of CFD and experimental for SFS2 |
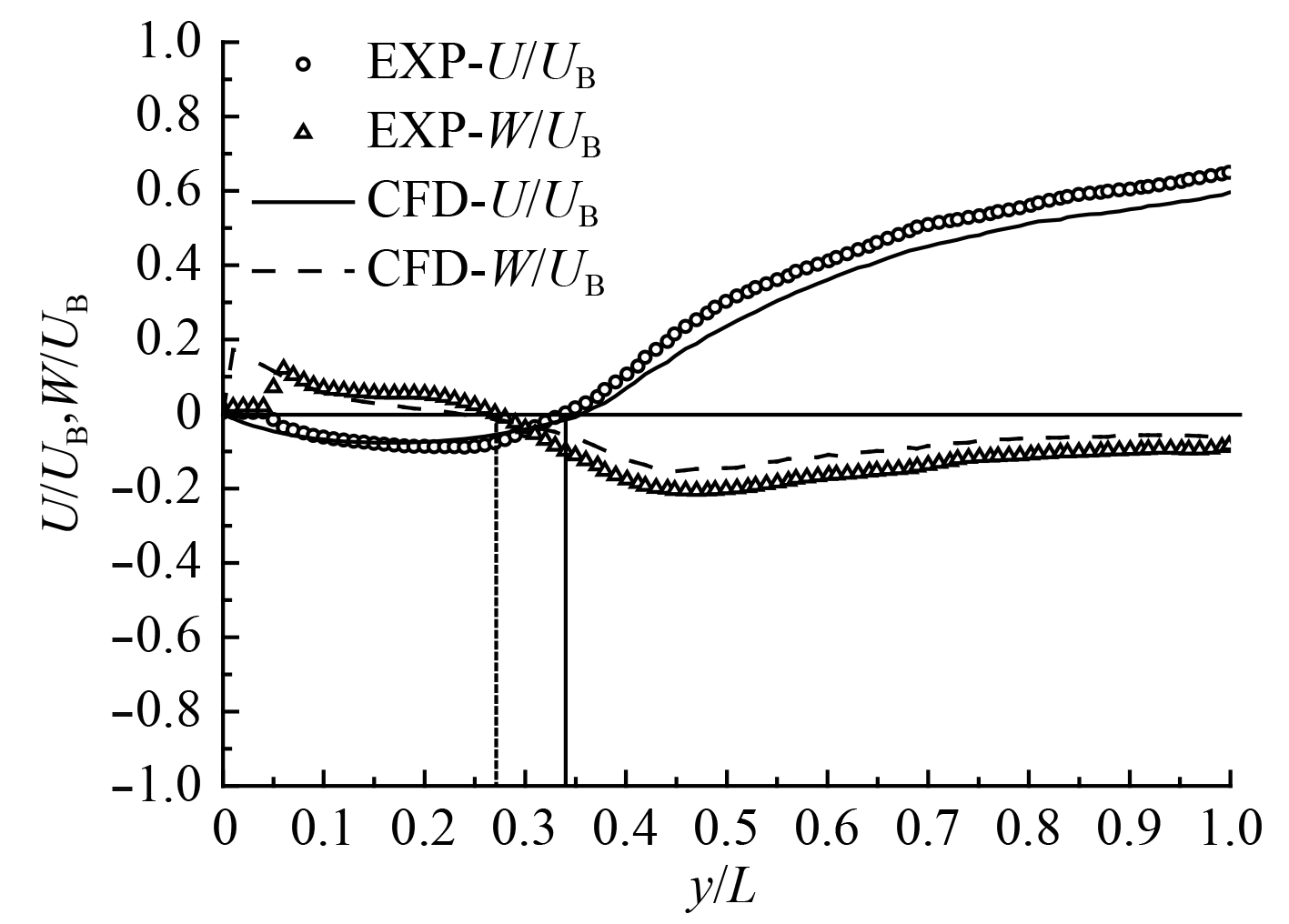
不同边界条件下SFS2在0°和右舷45°风向角时图1中所示的LB位置计算结果分别如图5和图6所示。图中,U(z)表示入口来流仅考虑大气边界层中的速度梯度;ABL表示入口来流同时考虑了速度梯度和湍流特性的影响。计算结果显示考虑大气边界层条件后,CFD预测的速度值与不考虑大气边界层条件时存在一定的差距。在大气边界层条件的影响下0°风向角时LB位置三向速度值及变化梯度均明显减小,且只考虑速度梯度的影响时其速度值相对更小,而同时考虑速度梯度和湍流特性的影响时纵向速度的变化梯度更小。
|
图 5 0°风向角时不同边界条件下速度对比 Fig. 5 Comparison of velocity of headwind in different boundary conditions |
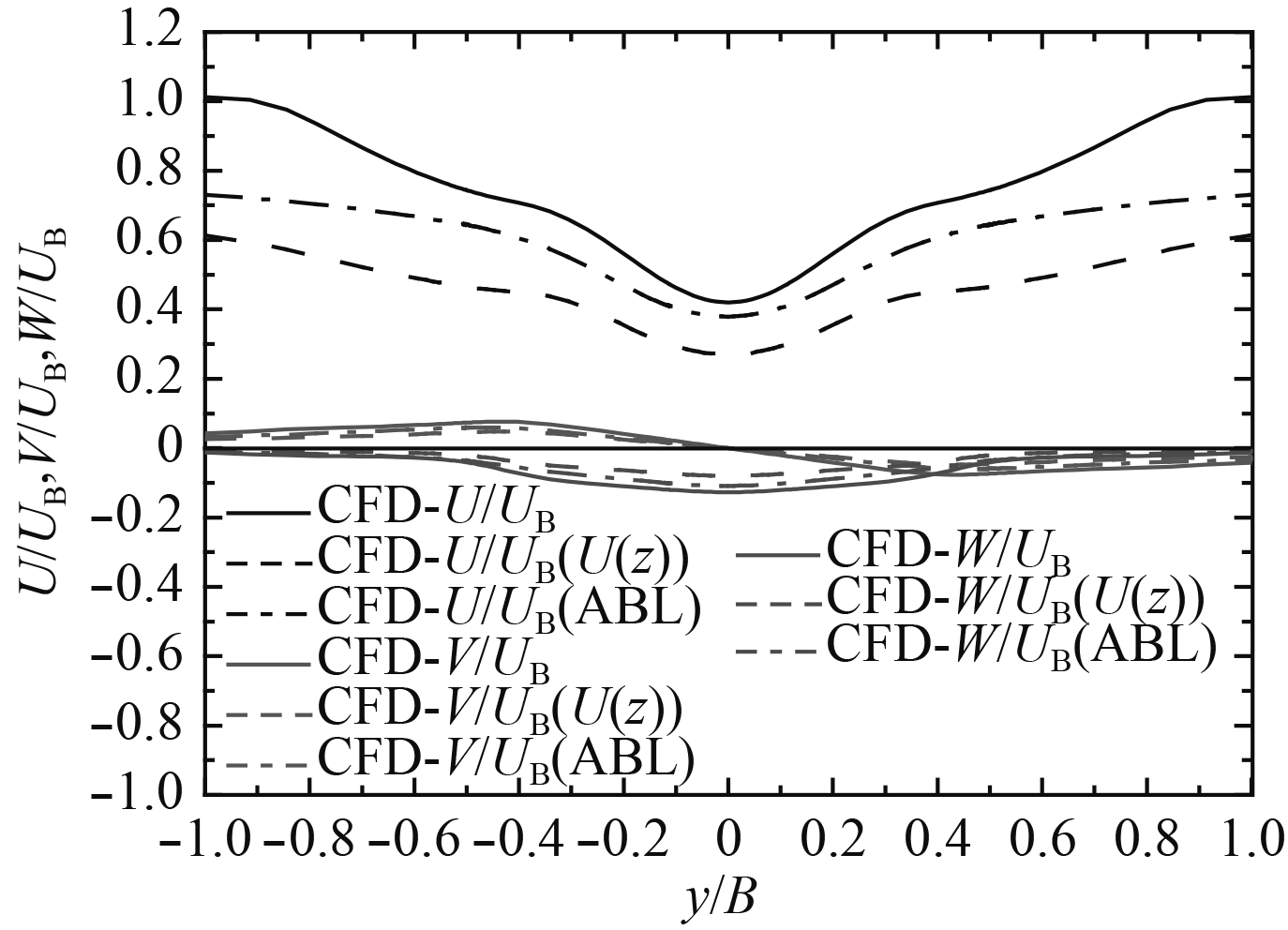
右舷45°风向角时,纵向速度的变化规律与0°风向角时相同,但横向和垂向速度的变化规律略有不同。在右舷位置考虑大气边界层影响时速度值仍低于无大气边界层影响时的值,在左舷某些位置其速度值反而比不考虑大气边界层影响时更高,与0°风向角相同的是考虑大气边界层影响后速度梯度均有所减小。
|
图 6 45°风向角时不同边界条件下速度对比 Fig. 6 Comparison of velocity of green 45° in different boundary conditions |
图7对比了0°风向角时3种边界条件下飞行甲板长度方向25%、50%、75%和100%位置处无量纲纵向速度U和横向速度V的云图分布,可以发现,3种边界条件下速度变化趋势相同,但只考虑速度梯度大气边界层条件时的速度值最低,均匀来流条件下的速度值最高,且此规律在4个不同位置截面上均适用。另外可以观察到,在均匀来流条件下100%截面上速度梯度较大,但在速度梯度边界条件下,100%截面上速度均匀性非常好。
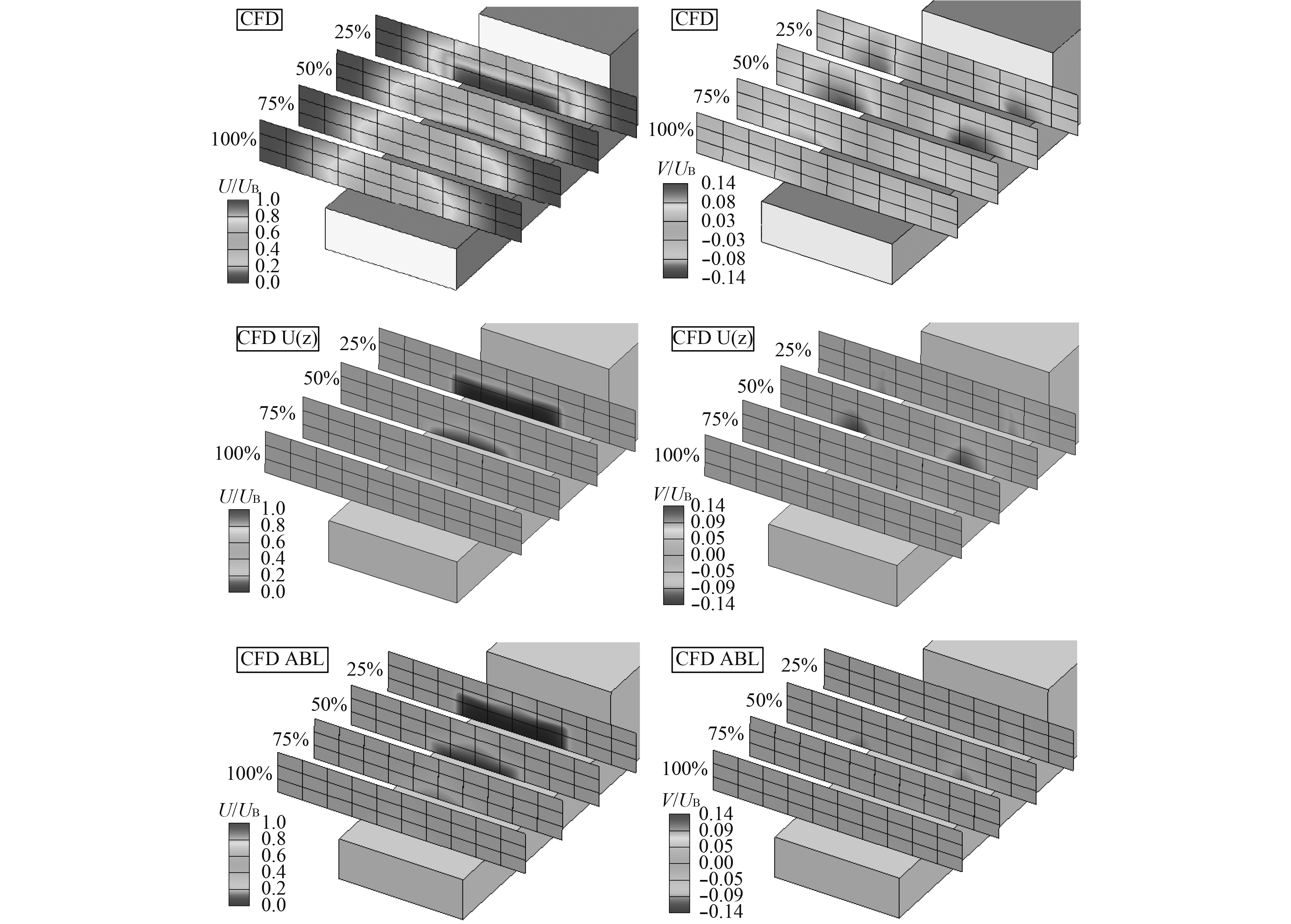
|
图 7 0°风向角时不同边界条件下SFS2截面速度云图对比 Fig. 7 Comparison of x, y-component velocity contours for different slices of SFS2 with headwind |
综合对比结果显示,相比于均匀来流入口边界条件,大气边界层条件中的速度梯度减小了入口处气流流动动能的输入,故其预测的尾流场中纵向速度值降低。湍流特性中湍动能的存在又增加了能量的输入,故完全大气边界层条件下预测的流场物理量数值居于均匀来流和速度梯度条件预测值之间,但湍流特性的存在会减弱固体壁面至大气边界层厚度位置之间的动量传递,故其预测的速度梯度较其他2种边界条件下的速度梯度更小。从不同条件下SFS2空气尾流场预测结果中可知,大气边界层条件中速度梯度与湍流特性对流场产生的影响不可忽略。
4 结 语通过对不同边界条件下SFS2空气尾流特性研究得出以下结论:
1)基于k-ε模型和壁面函数的CFD仿真方法可以用于预测舰船空气尾流;
2)大气边界层条件中的速度梯度会减小气流流动动能的输入;
3)湍流特性中湍动能会增加入口能量的输入;
4)湍流特性会减弱固体壁面至大气边界层厚度位置之间的动量传递;
5)大气边界层条件中速度梯度与湍流特性对流场产生的影响不可忽略。
本文是基于稳态计算实现了风速梯度和湍流特性的模拟,而非时间精确的瞬态计算,大气边界层中湍流积分尺度和脉动风功率谱对舰船空气尾流场的影响还需继续做深入的探讨和研究。另外,如何实现对不同大气边界层条件的准确描述,及如何在数值计算中准确复现真实大气边界层条件,将是未来需要继续深入研究的问题。
| [1] | TAI T C, CARICO D. Simulation of DD-963 ship airwake by navier-stokes method[J], Journal of Aircraft, 32(6), 1995: 1399–1401. |
| [2] | LIU J, LONG L N, MODI A. Higher order accurate solutions of ship airwake flow fields using parallel computer[C]//American Helicopter Society 54th Ann ual Forum. Washington, 1998: 1–13. |
| [3] | SYMS G F. Numerical simulation of frigate airwakes[J]. International Journal of Computational Fluid Dynamics, 2004, 18 (2): 199–207. |
| [4] | SEZER-UZOL N, SHARMA A, LONG L N. Computational fluid dynamics simulations of ship airwake[J]. Journal of Aerospace Engineering, 2005, 219(5): 369–392. |
| [5] | YESILEL H, EDIS F O. Ship airwake analysis by CFD methods[C]//AIP Conference Proceedings. Corfu, 2007: 674–677. |
| [6] | ZHANG F, XU H. BALL N G. Numerical simulation of unsteady flow over SFS2 ship model[C]//47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition. Orlando, 2009: 1–10. |
| [7] | POLSKY S A, GHEE T A, BUTLER J, et al. Application of CFD to anemometer position evaluation: a feasibility study[C]//29th AIAA Applied Aerodynamics Conference, Honolulu, AIAA, 2011: 1–14. |
| [8] | QUON E W. Data transfer strategies for overset and hybrid computaional methods[D]. Georgia: Georgia Institute of Technology, 2014. |
| [9] | POLSKY S A. CFD prediction of airwake flowfields for ships experiencing beam winds[C]//21st Applied Aerodynamics Conference. Orlando, 2003: 1–12. |
| [10] | MURRAY R. S, ANIL K, PINHAS B T, et al. Validation of computational ship air wakes for a naval research vessel[C]//American Institute of Aeronautics and Astronautics. Orlando, 2013: 1–25. |
| [11] | RAHIMPOUR, P OSHKAI. Experimental investigation of airflow over helicopter platform of a polar icebreaker[C]//2015 IEEE. Orlando, 2015: 1–8. |
| [12] | 黄斌, 徐国华, 史勇杰. 舰船飞行甲板真实流场特性试验研究[J]. 航空学报, 2001, 22(6): 500–504. http://www.cnki.com.cn/Article/CJFDTotal-JCKX201505005.htm |
| [13] | 王祎. 载机舰在风、浪中的气流场数值模拟研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. |
 2018, Vol. 40
2018, Vol. 40
