2. 海军工程大学 舰船工程系,湖北 武汉 430033
2. Department of Naval Architecture, Naval University of Engineering, Wuhan 430033, China
对于舵叶、机翼、螺旋桨、风机叶片等翼型结构,在工作载荷作用下,其主要变形模式为沿翼展方向发生弯曲变形,因此剖面惯性矩对结构的强度刚度性能极为重要。为了提高剖面惯性矩,往往对翼蒙皮离中性轴距离较远的中间区段进行局部加厚,形成与风机叶片类似的梁帽结构[1 – 2],以获得较高的材料利用率。如何精确确定中间加厚段的范围,以最少的材料获得较优的刚度和强度,是一个需要研究的问题。以往的研究主要借助有限元软件结合优化算法对翼型结构进行优化设计[3 – 6],其过程复杂,计算成本较高,若能提出一种简单的工程优化方法,会大大节约设计初期成本。
本文首先对变厚度剖面的比惯性矩(剖面惯性矩与面积的比值)进行理论推导,分析了影响比惯性矩的主要因素;然后针对复杂翼型剖面进行离散处理,采用数值分析方法编程计算,分析了中间加强区段的厚度及范围对比惯性矩的影响规律,根据最大比惯性矩提出了最优加厚区间概念,得到了最优分点位置坐标;在此基础上,针对常见的船用舵翼型NACA0012~NACA0025[7],总结了最优分点位置并绘制成图谱,以便为舵翼变厚度设计提供参考。本文所提出的方法简单有效,便于工程应用,尤其适用于复合材料舵翼蒙皮初期设计阶段,对于含加强筋的蒙皮,亦可通过将加强筋等效为蒙皮厚度[8 – 9]的方式进行设计。
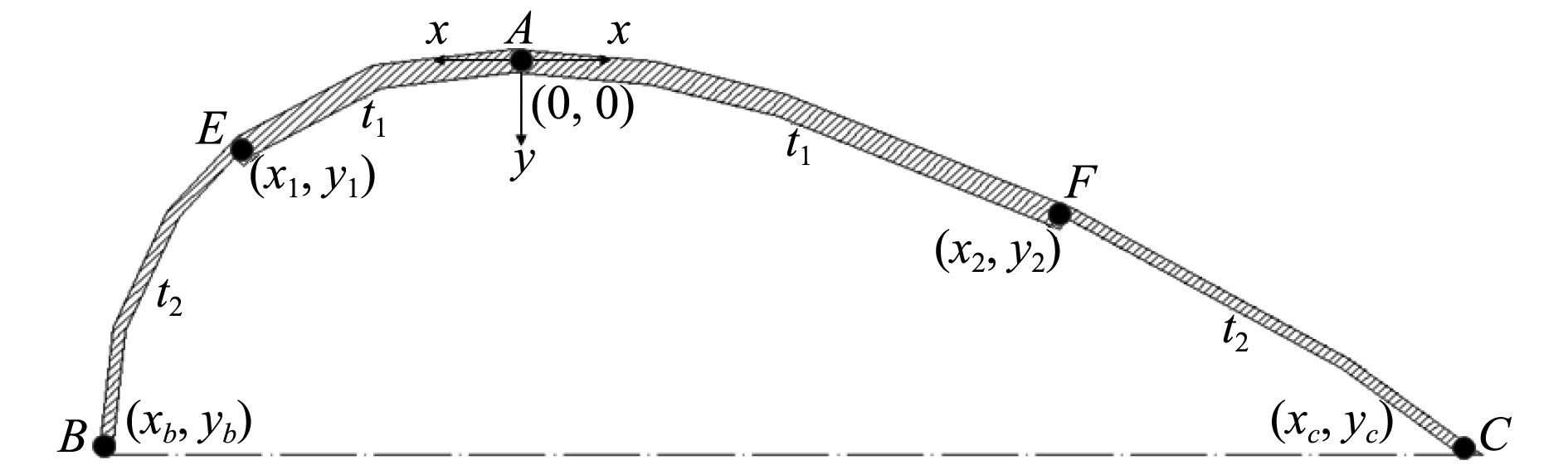
1 比惯性矩及其影响因素典型的翼剖面型线如图1所示,因对称只取其一半,BC为剖面中线,A为剖面最高点。假设EAF为中间加厚段,其厚度为t1,BE和CF为两边未加厚段,其厚度为t2。为了计算方便,取翼型线最高点A作为原点,并以该点为分界点将翼型线分为AB与AC两段曲线,2段曲线分别采用共原点的2个独立坐标系。
|
图 1 翼剖面及坐标系 Fig. 1 Wing profile and coordinate system |
以AB段为例(AC段计算方法相同),假设AB段的型线函数
AE加厚段长度、面积及惯性矩分别为
| ${l_{AE}} = \int_0^{x_1} {\sqrt {1 + y{'^2}} } {\rm{d}}x\text{,}$ |
| ${s_{AE}} = {l_1} \cdot {t_1}\text{,}$ |
| ${j_{AE}} = \int_0^{{x_1}} {\sqrt {1 + y{'^2}} } \cdot {t_1} \cdot {({y_B} - y)^2}{\rm{d}}x\text{。}$ |
EB未加厚段长度、面积及惯性矩分别为
| ${l_{EB}} = \int_{{x_1}}^{{x_B}} {\sqrt {1 + y{'^2}} } {\rm{d}}x\text{,}$ |
| ${s_{EB}} = {l_2} \cdot {t_2}\text{,}$ |
| ${j_{EB}} = \int_{{x_1}}^{{x_B}} {\sqrt {1 + y{'^2}} } \cdot {t_2} \cdot {({y_B} - y)^2}{\rm{d}}x\text{。}$ |
则AB段比惯性矩为
| $\begin{split}&j/s = \frac{{{j_1} + {j_2}}}{{{s_1} + {s_2}}} =\\&\frac{{{t_1}/{t_2} \cdot \int_0^{{x_1}} {\sqrt {1 + y{'^2}} } \cdot {{({y_B} - y)}^2}{\rm{d}}x + \int_{{x_1}}^{{x_B}} {\sqrt {1 + y{'^2}} } \cdot {{({y_B} - y)}^2}{\rm{d}}x}}{{{t_1}/{t_2} \cdot \int_0^{{x_1}} {\sqrt {1 + y{'^2}} } {\rm{d}}x + \int_{{x_1}}^{{x_B}} {\sqrt {1 + y{'^2}} } {\rm{d}}x}}\end{split}\text{。}$ |
从式中可以看出,比惯性矩只和
假设将翼型线AB段离散成N段,节点坐标依次为
| ${d_i} = \sqrt {{{({x_i} - {x_{i - 1}})}^2} + {{({y_i} - {y_{i - 1}})}^2}} \text{,}$ |
AE段面积与惯性矩为
| ${s_A} = \sum\limits_{i = 1}^M {{d_i}} \cdot {t_1}\text{,}$ |
| ${j_A} = \sum\limits_{i = 1}^M {{d_i} \cdot {t_1} \cdot {{\Bigr({y_{\max }} - \frac{{{y_i} + {y_{i - 1}}}}{2}\Bigr)}^2}} \text{。}$ |
EB段面积与惯性矩为
| ${s_B} = \sum\limits_{i = M + 1}^N {{d_i}} \cdot {t_2}\text{,}$ |
| ${j_B} = \sum\limits_{i = M + 1}^N {{d_i} \cdot {t_2} \cdot {{\Bigr({y_{\max }} - \frac{{{y_i} + {y_{i - 1}}}}{2}\Bigr)}^2}} \text{。}$ |
则AB段比惯性矩为
| $j/s = \frac{{{t_1}/{t_2} \cdot \sum\limits_{i = 1}^M {{d_i} \cdot {{\Bigr({y_B} - \frac{{{y_i} + {y_{i - 1}}}}{2}\Bigr)}^2}} + \sum\limits_{i = M + 1}^N {{d_i} \cdot {{\Bigr({y_B} - \frac{{{y_i} + {y_{i - 1}}}}{2}\Bigr)}^2}} }}{{{t_1}/{t_2} \cdot \sum\limits_{i = 1}^M {{d_i}} + \sum\limits_{i = M + 1}^N {{d_i}} }}\text{。}$ |
以复合材料船用舵为研究对象,对翼剖面比惯性矩随
|
|
表 1 NACA翼型型值 Tab.1 NACA airfoil value |
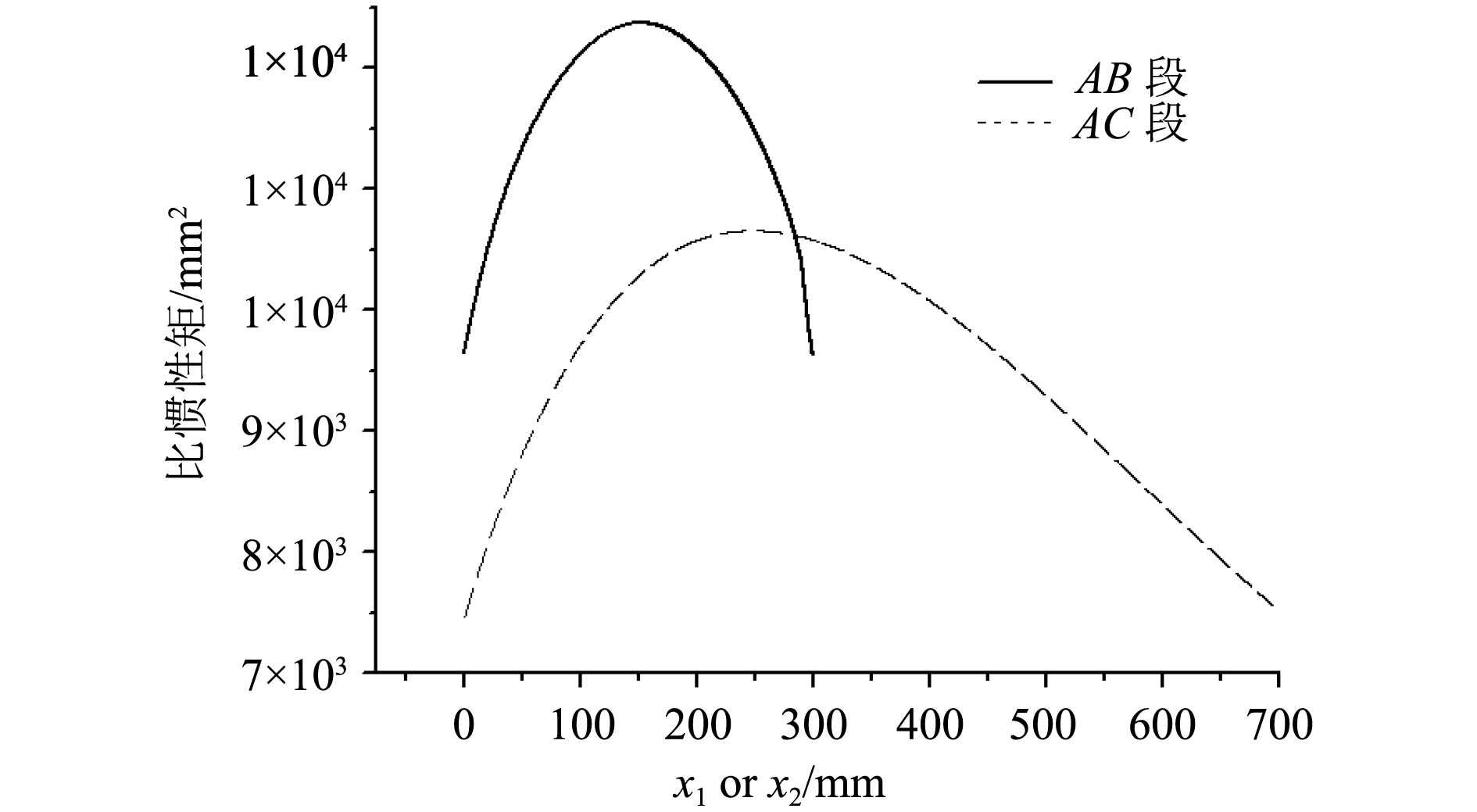
首先对特定翼型特定厚度比的情况进行研究,采用第1节中的数值公式编程计算,代表翼型为NACA0025,计算时取弦长为1 m,注意将型值转换为图1坐标系中对应坐标。经过计算,绘制翼型NACA0025在特定厚度比(
当厚度比
|
图 2 比惯性矩/分点坐标曲线 Fig. 2 Specific moment/point coordinate curve |
|
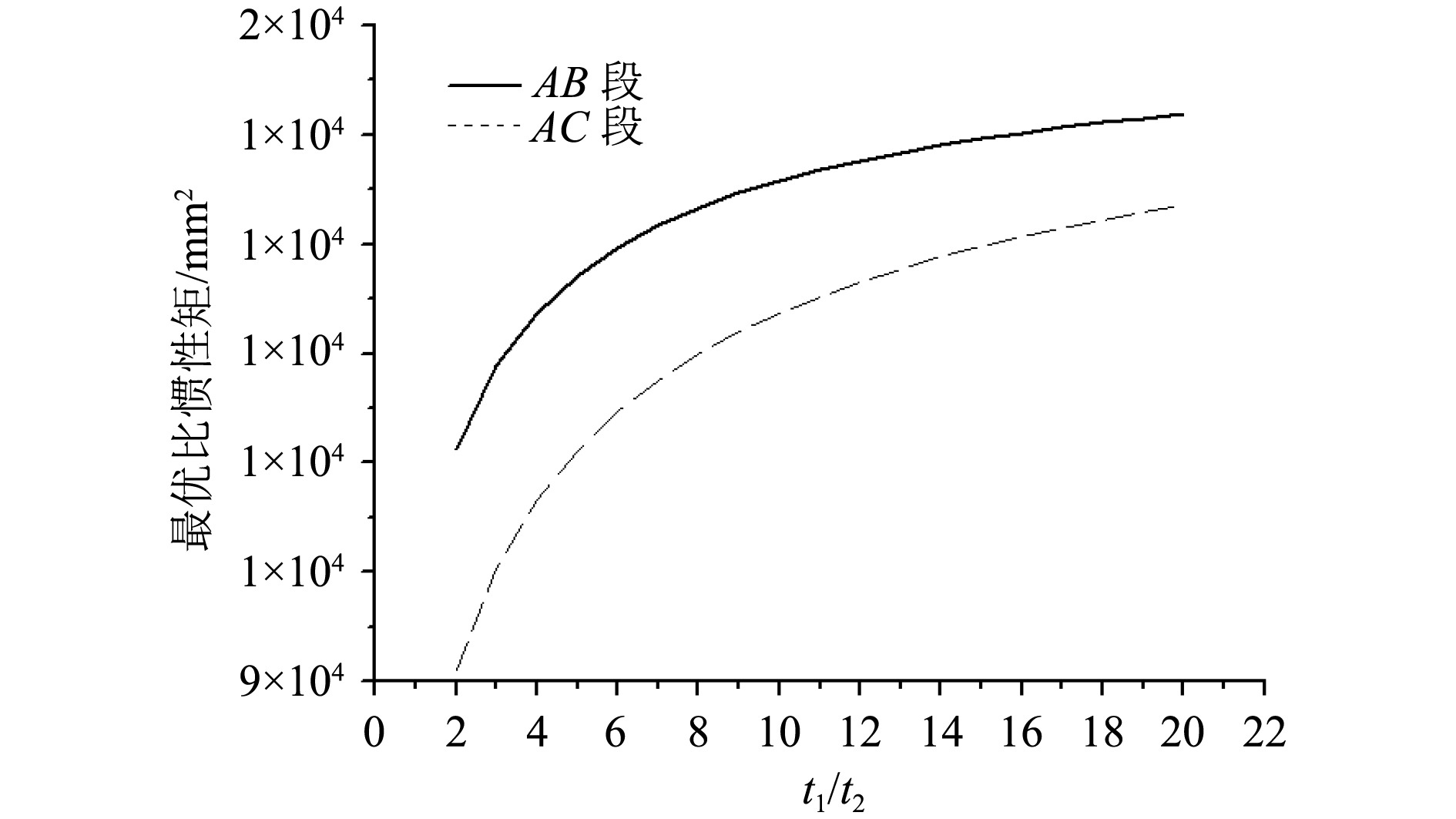
图 3 最优比惯性矩/厚度比曲线 Fig. 3 Optimal specific moment/thickness ratio curve |
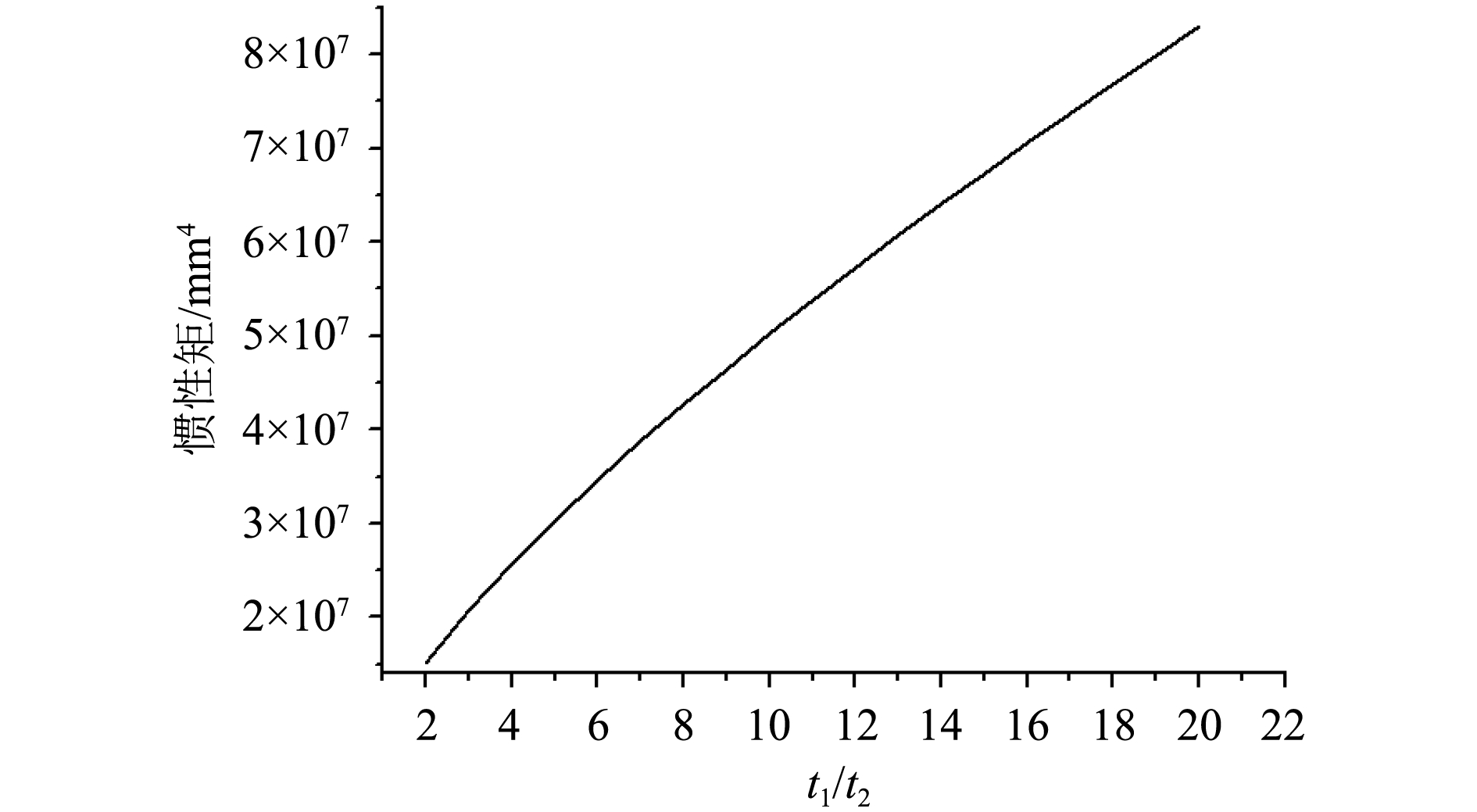
在应用该方法确定加厚区间时,可先根据局部强度要求及最小工艺厚度要求确定最小厚度t2;由以上分析可知,厚度比
|
图 4 最优惯性矩/厚度比曲线 Fig. 4 Optimal moment of inertia / thickness ratio curve |
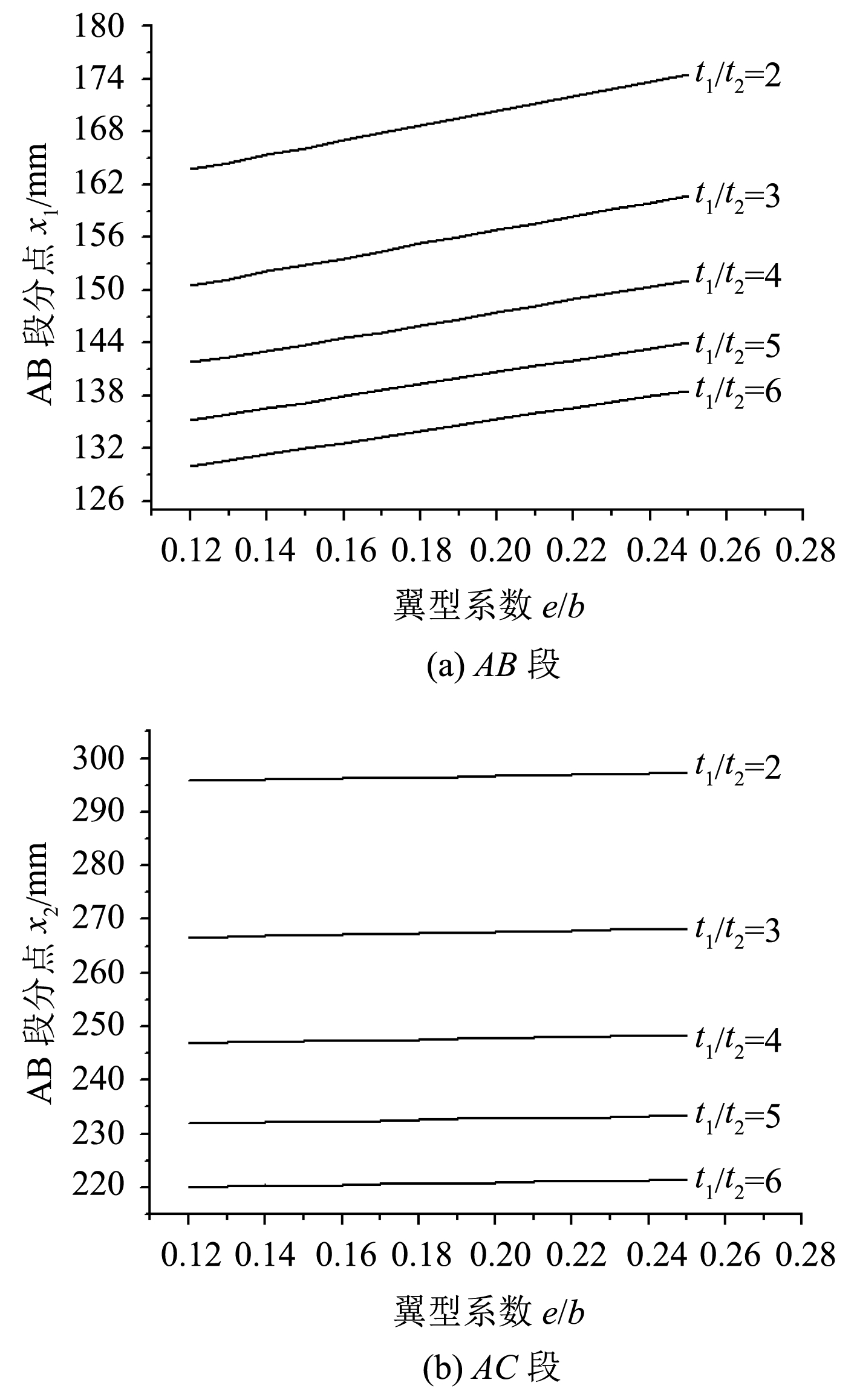
实际上,船用舵以NACA0012-NACA0025翼型使用居多,因为在该范围内,舵叶的升力系数较大,超出该范围,升力系数较小[7]。此外,对于复合材料舵,蒙皮最小工艺厚度约5 mm,最大厚度受工艺与声学性能限制一般不超过30 mm,因此蒙皮厚度比范围一般为2~6。因此,针对该范围内NACA0012-NACA0025翼型的最优比惯性矩进行研究,并将对应的最优分点位置x1和x2绘制成图谱,以供设计参考,如图5所示。分析可得出以下结论:1)对于弦长1 m的常见船用舵翼型,加厚段的最优分点位置坐标x1的分布范围为[130 mm,174 mm],x2的分布范围为[220 mm, 297 mm];2)随着厚度比
|
图 5 最优分点坐标图谱 Fig. 5 Optimal point coordinate map |
某船用舵为变截面变翼型舵,其展长为3 200 mm,大端面翼型NACA0018,弦长2 400 mm,小端面翼型NACA0016,弦长1 600 mm。采用玻璃钢复合材料设计,根据惯性矩要求确定优化前的蒙皮平均厚度为12.8 mm。在保证蒙皮质量不变的前提下,根据上述加厚区间优化设计方法,首先由局部强度限制两边未加厚段的厚度为6 mm,再由
大端面分点坐标
x1=146.0×2.4=350.4(mm),x2=247.5×2.4=594.0(mm);
小端面分点坐标
x1=144.6×1.6=231.4(mm),x2=247.2×1.6=395.5(mm)。
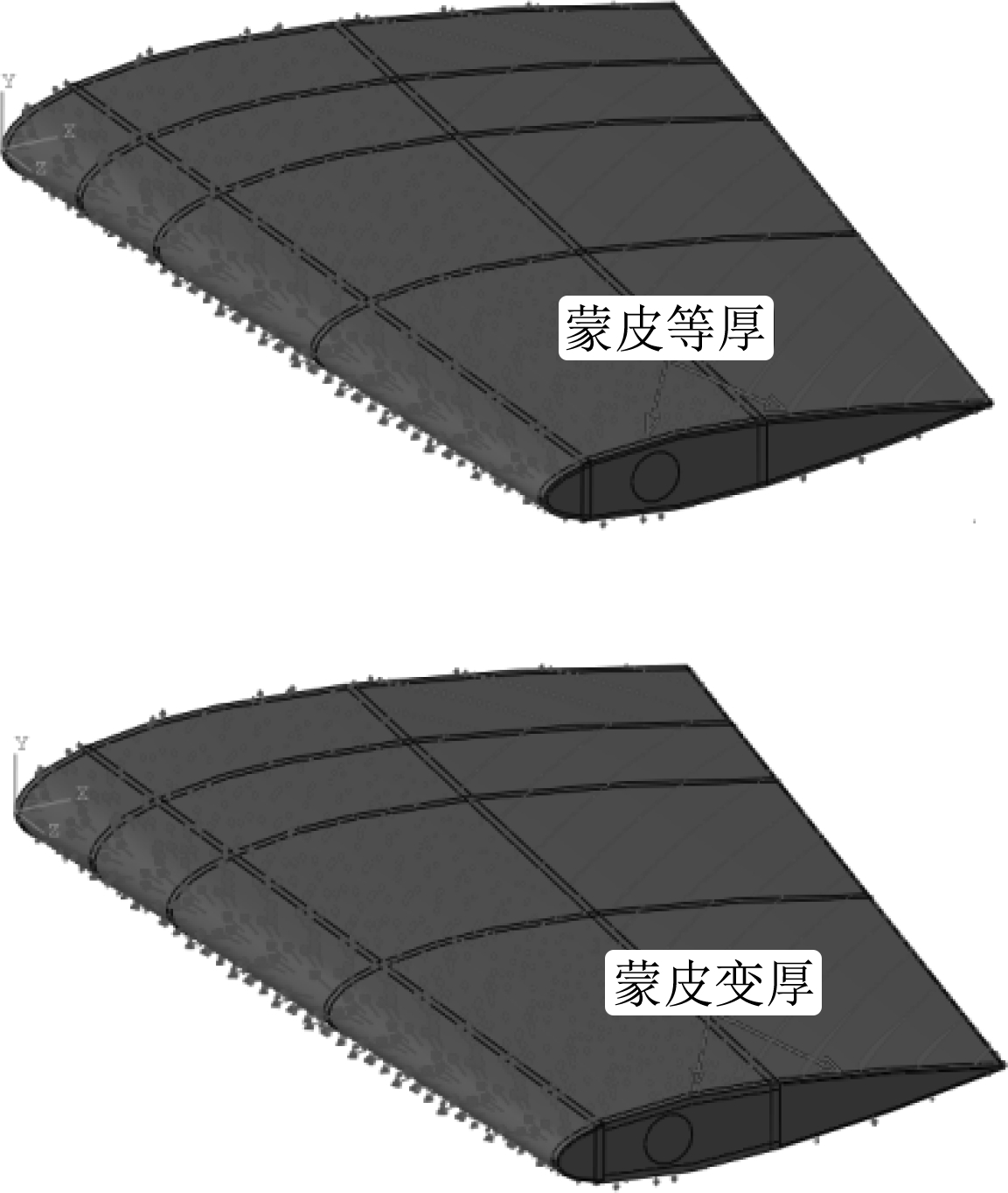
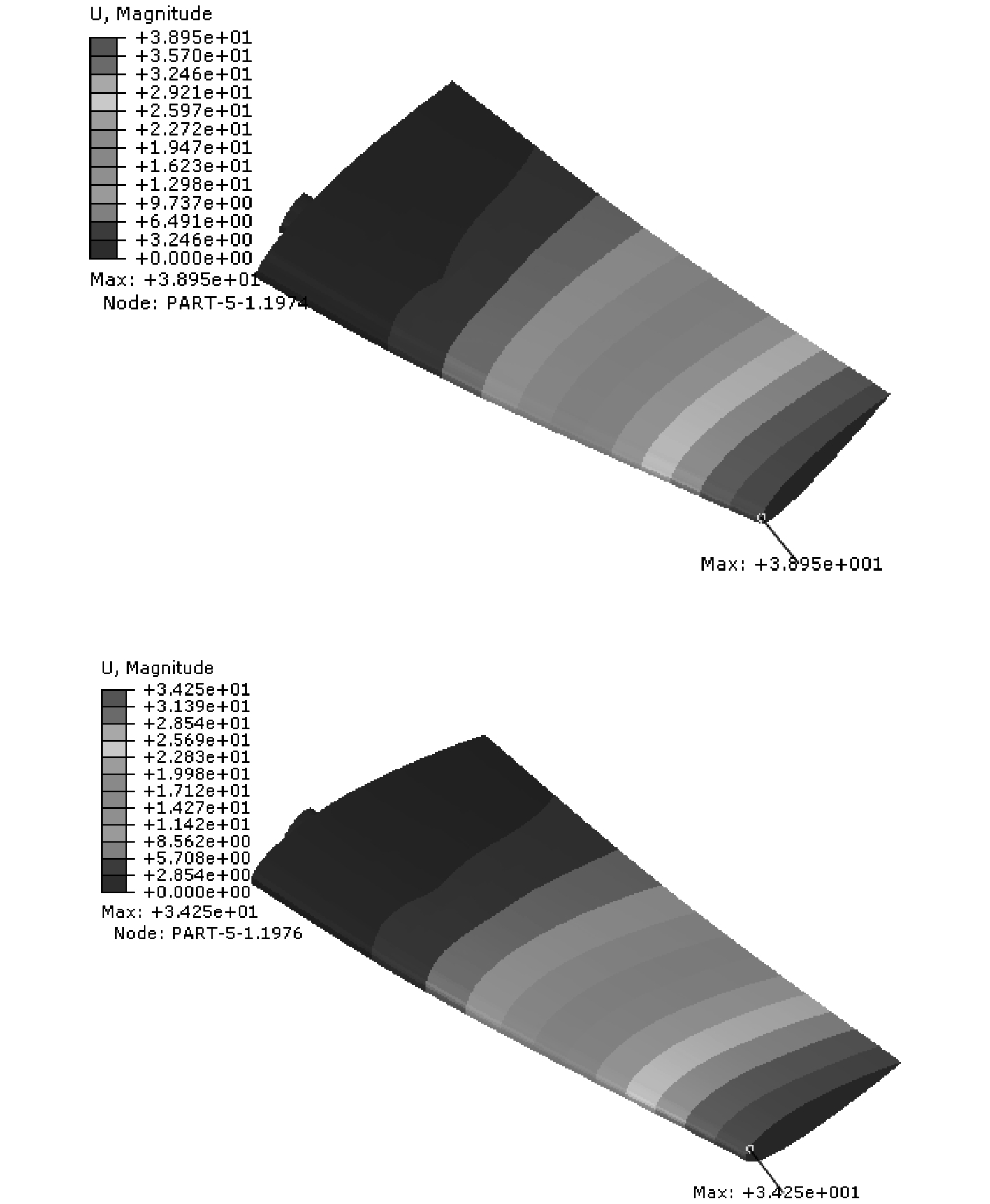
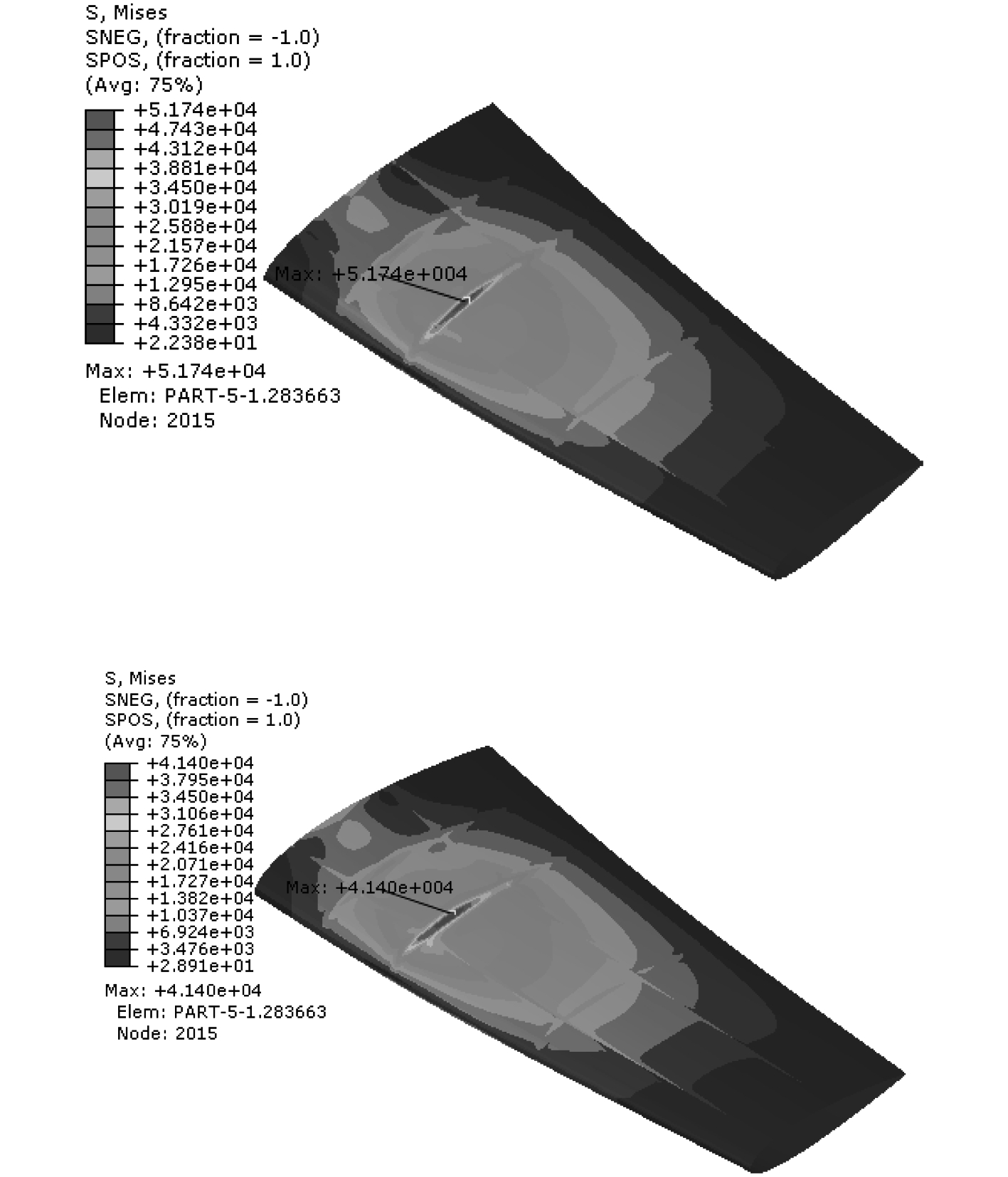
4.2 结果分析通过Abaqus有限元软件,对优化前后的舵叶进行建模,并在舵轴端施加固支边界约束,在舵叶表面施加操舵水动力载荷,如图6所示。计算所得位移和蒙皮应力分布如图7和图8所示。优化前最大位移为38.95 mm,优化后最大位移为34.25 mm,减小了12.1%;优化前最大应力为51.74MPa,优化后最大应力为41.40MPa,减小了20.0%。从优化结果来看,优化后舵叶的强度与刚度都得到了较大提高,说明该方法的优化效果比较明显。
|
图 6 优化前后舵叶模型 Fig. 6 Comparison of rudder model before and after optimization |
|
图 7 优化前后舵叶位移 Fig. 7 Comparison of rudder deformation before and after optimization |
|
图 8 优化前后蒙皮应力 Fig. 8 Comparison of skin stress before and after optimization |
本文基于比惯性矩最大原则,提出了一种确定翼型结构最优加厚区间的工程优化方法,在此基础上将常用舵翼的最优加厚区间绘制成图谱,基于图谱分析了最优加厚区间变化规律,并通过一算例阐述了图谱使用方法,验证了该方法的有效性。经过研究,本文得出的主要结论如下:
1)在翼型与加厚比
2)随着厚度比
3)随着翼型系数e/b的增大,同一厚度比的分点坐标x1,x2呈现线性变化,这说明对于变截面变翼型(厚度比不变)的船用舵,只需确定两端面的最优分点位置,即可线性确定其他舵剖面的分点,极大地扩展了该方法的实用性和适用范围。
| [1] | 胡燕平, 戴巨川, 刘德顺. 大型风力机叶片研究现状与发展趋势[J]. 机械工程学报, 2013, 49(20): 140–147. http://www.cqvip.com/qk/86583b/201110/39568309.html |
| [2] | 冯消冰, 孙树力. 2 MW风机叶片梁帽与腹板的强度优化设计[J]. 合成材料老化与应用, 2015, 44(2): 21–27. http://www.cqvip.com/QK/93456A/201502/664572732.html |
| [3] | VITALE A J, ROSSI A P. Computational method for the design of wind turbine blades[J]. International Journal of Hydrogen Energy, 2008, 33(13): 3466–3470. |
| [4] | 李丹, 姚卫星. GFRP风机叶片结构设计的二级优化方法[J]. 南京航天航空大学学报, 2011, 43(5): 598–601. http://or.nsfc.gov.cn/bitstream/00001903-5/72867/1/1000004601243.pdf |
| [5] | 廖猜猜, 王建礼, 石可重, 等. 风力叶片截面刚度优化设计[J]. 工程热物理学报, 2010, 31(7): 1127–1130. http://www.oalib.com/paper/4856035 |
| [6] | CAI Xin, ZHU Jie, PAN Pan, et al. Structural optimization design of horizontal-axis wind turbine blades using a particle swarm optimization algorithm and finite element method[J]. Energies, 2012, 5(11): 4683–4696. |
| [7] | 梅琴生. 船用舵[M]. 北京: 人民交通出版社, 1981. |
| [8] | QUYANG X, YU X Q, WANG Y. Flutter analysis for wing structure using finite element modeling with equivalent stiffness[J]. Journal of Vibroengineering, 2014, 16(3): 1483–1493. |
| [9] | 王宇, 欧阳星, 余雄庆. 采用等效有限元模型的复合材料机翼结构优化[J]. 复合材料学报, 2015, 32(5): 1487–1494. http://www.cqvip.com/QK/95343A/201501/664032299.html |
 2018, Vol. 40
2018, Vol. 40
