2. 广州市顺海造船有限公司,广东 广州 511440
2. Guangzhou Shunhai Shipyards Ltd., Guangzhou 511440, China
与传统单体船相比,双体船拥有更宽阔的甲板面积、较大的横稳心半径以及较小的兴波阻力等优点,其作为海洋环境参数监测无人船的一种结构形式已经引起人们的重视,双体船已经成为海洋科学研究无人船乐意采用的船型之一[1]。
船舶在波浪中航行时,波浪扰动作用引起的摇荡运动与波浪相互作用致使其总阻力的增加,航速降低,进而影响船舶操纵和推进等性能,如何减小船舶在波浪中的阻力是优良船型设计过程中不得不面对的问题[2]。对双体无人船尤为如此。一方面,双体无人船拥有2个片体使其湿表面积较等排水量的单体船大,使得其摩擦阻力相对较大,低速静水阻力也相对较大,恰当的设计可产生的有利兴波干扰又使得双体船在高速航行时兴波阻力较等排水量的单体船小[3],静水阻力也较小;另一方面,海洋科学研究双体无人船的船长通常远小于海浪波长,波浪中摇荡运动响应较大,波浪增阻占总阻力的比例将大为增加,双体船在波浪中航行时,通过对设计变量进行优化可减小双体船在波浪中纵摇和升沉运动响应从而削弱波浪增阻。
1 细长体理论与波浪增阻 1.1 细长体理论细长体方法基于MICHELL[4]提出的运用一阶线性方法对船舶兴波阻力进行求解的积分方程,是一种通过计算细长船体在静水中航行时兴起的远场波系自由液面的能量来求解船体兴波阻力的数值方法[5],Michell积分表达式为:
| $\begin{split}\!\!\!\!\!\!&{R_{\rm{w}}} = \frac{{4\rho {g^2}}}{{{\rm{\pi }}{v^2}}}\mathop \int_1^\infty ({I^2} + {J^2})\frac{{{\lambda ^2}}}{{\sqrt {{\lambda ^2} - 1} }}{\rm{d}}\lambda \text{,} \\ & I = \int_0^\infty \int_{ - \infty }^\infty f(x,z){e^{\displaystyle\frac{{ - {\lambda ^2}gz}}{{{v^2}}}}}\displaystyle\frac{{\cos \lambda gx}}{{{v^2}}}\operatorname{d}\!x{\rm{d}}z \text{,} \quad\quad\quad(1) \\ & J = \int_0^\infty \int _{ - \infty }^\infty f(x,z){e^{\displaystyle\frac{{ - {\lambda ^2}gz}}{{{v^2}}}}}\frac{{\sin \lambda gx}}{{{v^2}}}{\rm{d}}x{\rm{d}}z \text{,} \\ & \lambda = \frac{{m{v^2}}}{g} \text{。} \end{split} $ |
式中:ρ和g为常量,分别为流体密度和当地重力加速度;v为船体远前方来流速度,即航速;m为常数;x和z为空间积分变量;I,J,λ为中间变量。
在细长体方法中,船体湿表面被离散为若干四边形面元,面元源强的表达式为:
| $\sigma = \frac{{{U_x}}}{{2{\rm{\pi }}}}\frac{{{\rm{d}}y}}{{{\rm{d}}x}} \cdot {S'_0}\text{,}$ | (2) |
式中:S0′为面元在船体中纵剖面上的投影面积;Ux为船体远前方来流速度x方向的分量;dy/dx为水线在面元形心处的斜率。
式(2)在面元形心处水线斜率趋向无穷大或面元在船体中纵剖面上的投影面积无穷小时失效,因而式(2)无法求解方尾处的源,将该式应用在求解高速方尾船兴波阻力时常常会因忽略方尾处的源强而出现较大偏差。针对式(2)的局限性,COUSER[6]给出了更加灵活的面元源强表达式,如下式所示:
| $\sigma = \frac{{ - 1}}{{2{\rm{\pi }}}}\hat n \cdot U \cdot {S_0}\text{,}$ | (3) |
式中:U为船体远前方来流速度;
式(3)不含水线斜率项dy/dx以及投影面积项S0′,有效减轻了求解方尾船兴波阻力时忽略方尾源强所带来的偏差。INSEL[7]将兴波阻力用有限水深下源的Eggers远场系数来表示,给出了源的兴波阻力计算公式:
| ${R_{{\rm{wp}}}} \!=\! \frac{{\rho gB}}{4}\left\{ \begin{gathered} \zeta _0^2\left[ {1 - \frac{{2{k_0}H}}{{\sinh (2{k_0}H)}}} \right] + \hfill \\ \mathop \sum \limits_{m = 1}^\infty \zeta _m^2\left[ {1 \!-\! \frac{{{{\cos }^2}{\theta _m}}}{2}\left( {1 \!+\! \frac{{2{k_m}H}}{{\sinh (2{k_m}H)}}} \right)} \right] \hfill \\ \end{gathered} \right\}\text{,}$ | (4) |
式中:km,θm及ζm分别为第m个谐波的波数、波倾角和波高;B,H分别为水池宽度和水池深度。
式(4)中,第m个谐波波高ζm满足关系式ζm2=ξm2+ηm2,点(xσ,yσ,zσ)处源强的自由表面波高项ηm,ξm为:
| $\begin{gathered} \left| {\begin{array}{*{20}{c}} {{\xi _m}} \\ {{\eta _m}} \end{array}} \right| = \frac{{16{\rm{\pi }}U}}{{Bg}} \cdot \frac{{\bar k + {k_m}{{\cos }^2}{\theta _m}}}{{1 + {{\sin }^2}{\theta _m} - \bar kH{\rm{sech}}\left( {{k_m}H} \right)}} \times \hfill \\ \mathop \sum \limits_\sigma \left[ \begin{gathered} {\sigma _\sigma }{e^{ - {k_m}H}} \cdot \hfill \\ \cosh \left[ {{k_m}(H + {z_\sigma })} \right]\left| {\begin{array}{*{20}{c}} {\cos ({k_m}{x_\sigma }\cos {\theta _m})} \\ {\sin ({k_m}{x_\sigma }\cos {\theta _m})} \end{array}} \right|\left| {\begin{array}{*{20}{c}} {\cos \displaystyle\frac{{m{\rm{\pi }}{y_\sigma }}}{B}} {\sin \displaystyle\frac{{m{\rm{\pi }}{y_\sigma }}}{B}} \end{array}} \right| \hfill \\ \end{gathered} \right] \text{。}\hfill \\ \end{gathered} $ | (5) |
式中:ξm,ηm分别为偶次谐波波高和奇次谐波波高;σσ为点(xσ,yσ,zσ)处的源强;
Michell积分以流动为对称绕流、船体长宽比足够大为前提条件,因此,对于双体船,每个船体应关于各自的中纵剖面左右对称且均拥有足够大的长宽比,以保证足够的计算精度。
1.2 波浪增阻波浪增阻是由船舶在波浪扰动下产生的摇荡运动(主要是纵摇与垂荡)与波浪相互作用引起的。不规则波中总波浪增阻可表示为规则中波浪增阻的叠加:
| $\overline {{R_{aw}}} = 2\int_0^\infty {{C_{aw}}} \cdot {S_\zeta }({\omega _e}){\kern 1pt} \;\partial {\omega _e}\text{,}$ | (6) |
| ${C_{aw}}{\rm{ = }}\frac{{{R_{aw}}({\omega _e})}}{{\zeta _0^2}}\text{。}$ | (7) |
式中:Caw为规则波中波浪增阻系数;Sζ(ωe)为遭遇波海浪谱;ωe为波浪遭遇频率;Raw(ω)为规则波中波浪增阻;ζ0为遭遇波波幅。SALVESEN[8](1978)给出了规则波中切片波浪增阻表达式:
| ${R_{aw}}{\rm{ = }}\frac{{ik}}{2}({\eta _3}{\hat F_3} + {\eta _5}{\hat F_5}) + {R_7}\text{,}$ | (8) |
其中:
| ${\hat F_3} = \zeta {\int e ^{ - ik\xi }}{e^{ - kz}}[c(\xi ) - {\omega _0}({\omega _e}{a_{33}}(\xi ) - i{b_{33}}(\xi ))]{\rm d}\xi \text{,}$ | (9) |
| ${\hat F_5} \!=\! - \zeta {\int e ^{ - ik\xi }}{e^{ - kz}}[c(\xi ) - {\omega _0}(\xi + \frac{{iU}}{{{\omega _e}}})({\omega _e}{a_{33}}(\xi ) - i{b_{33}}(\xi ))]{\rm d}\xi \text{,}$ | (10) |
| ${R_7}{\rm{ = }}\frac{{{\zeta ^2}k{\omega _0}^2}}{{2{\omega _e}}}\int {{e^{ - 2kz}}} {b_{33}}(\xi ){\rm d}\xi \text{。}$ | (11) |
式中:k为波数;η3,η5为复数形式的垂荡、纵摇;ζ为当地的波高;
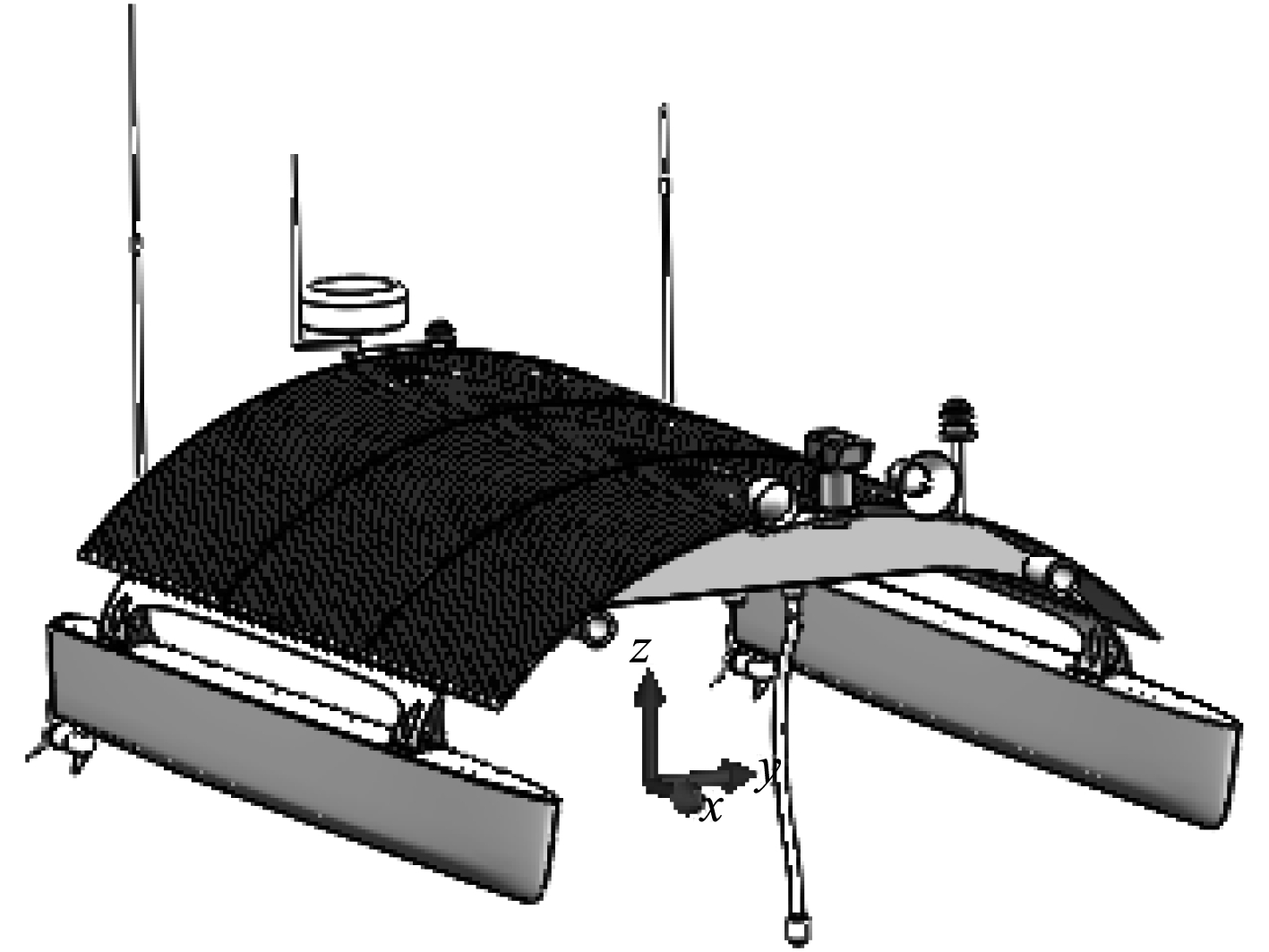
采用本课题组研发的一种远距离遥控采样太阳能双体无人船为计算对象,该船利用水密的圆弧形箱式连接桥结构将2个片体连接起来并在圆弧形箱式连接桥结构上表面覆盖柔性太阳能薄膜,储能锂电池放置在片体内部,其示意图如图1所示。船体坐标系原点定义在双体无人船中纵剖面、基平面与中横剖面交点上。
运用Hullspeed[9]中的细长体方法计算双体无人船的静水阻力。建立双体无人船船体简化曲面模型,运用Hullspeed划分细长体网格(Slender Body Mesh),将无人船船体湿表面离散为四边形面元,并对方尾使用虚拟附体法进行修正使船尾水线封闭,示意图如图2所示。计及片体间黏性干扰的形状因子(1+βkh)根据Molland公式确定,即
| $(1 + \beta {k_h}) = 3.03{({L_{wl}}/{\nabla ^{1/3}})^{ - 0.4}}\text{。}$ | (12) |
式中:Lwl为水线长;
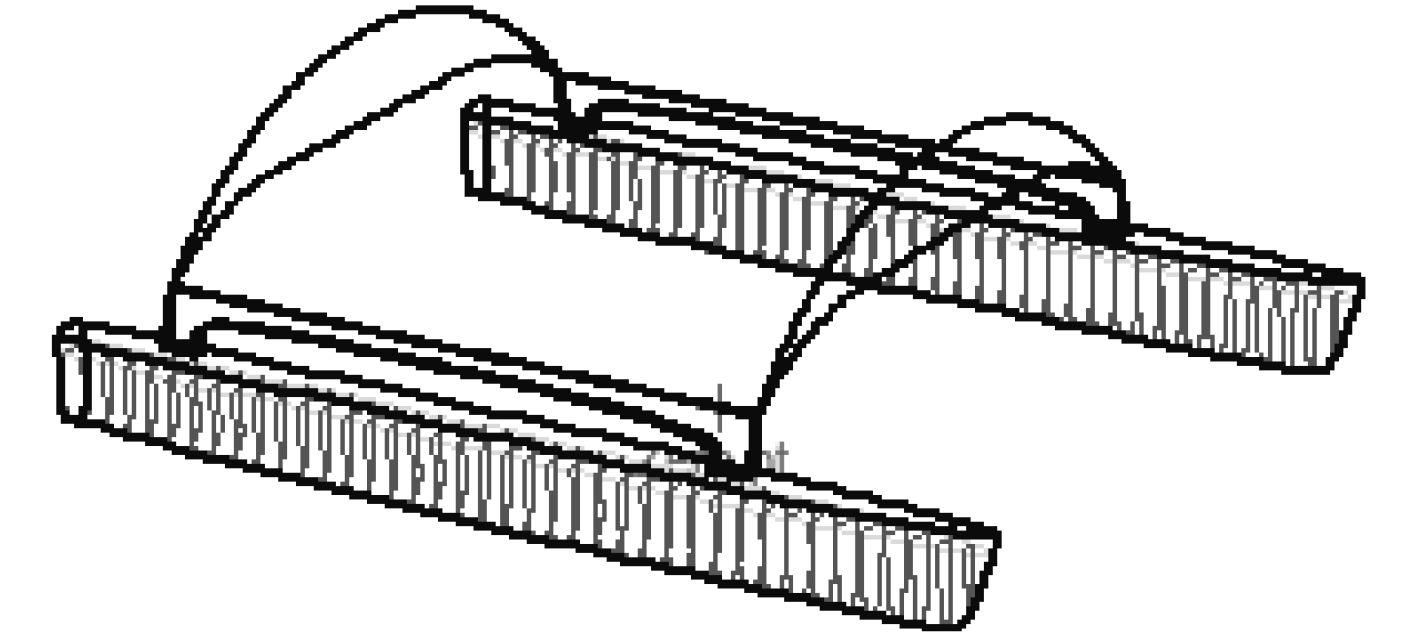
运用Seakeeper中SALVESEN[8]提出的方法计算双体无人船的波浪增阻。计算中,将双体无人船片体水线以下船体空间离散为若干切片,示意图如图3所示。计算中所选遭遇波海浪谱为P-M谱,浪向角180°,特征风速20 kn。
|
图 1 计算模型与船体坐标系 Fig. 1 The model for calculation and ship coordinate system |

|
图 2 细长体网格 Fig. 2 The slender body mesh |
|
图 3 船体切片 Fig. 3 The hull section |
根据均匀设计的原理,在保持排水量Δ、方形系数Cb等船体参数不变的前提下均匀改变片体水线长Lwl并得到对应的水线宽Bwl。
|
|
表 1 不同片体长宽比方案 Tab.1 Scheme of different Lwl/Bwl |
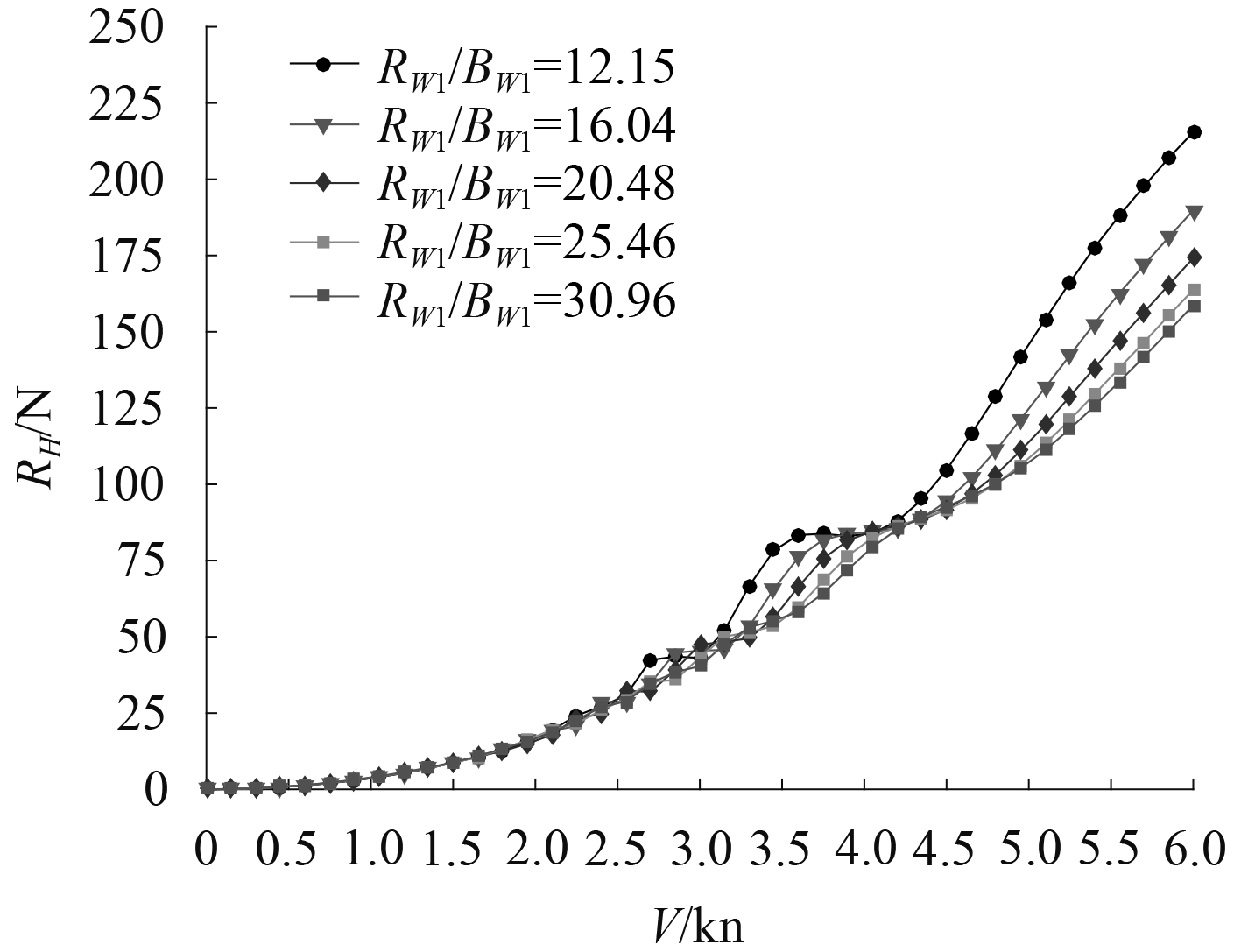
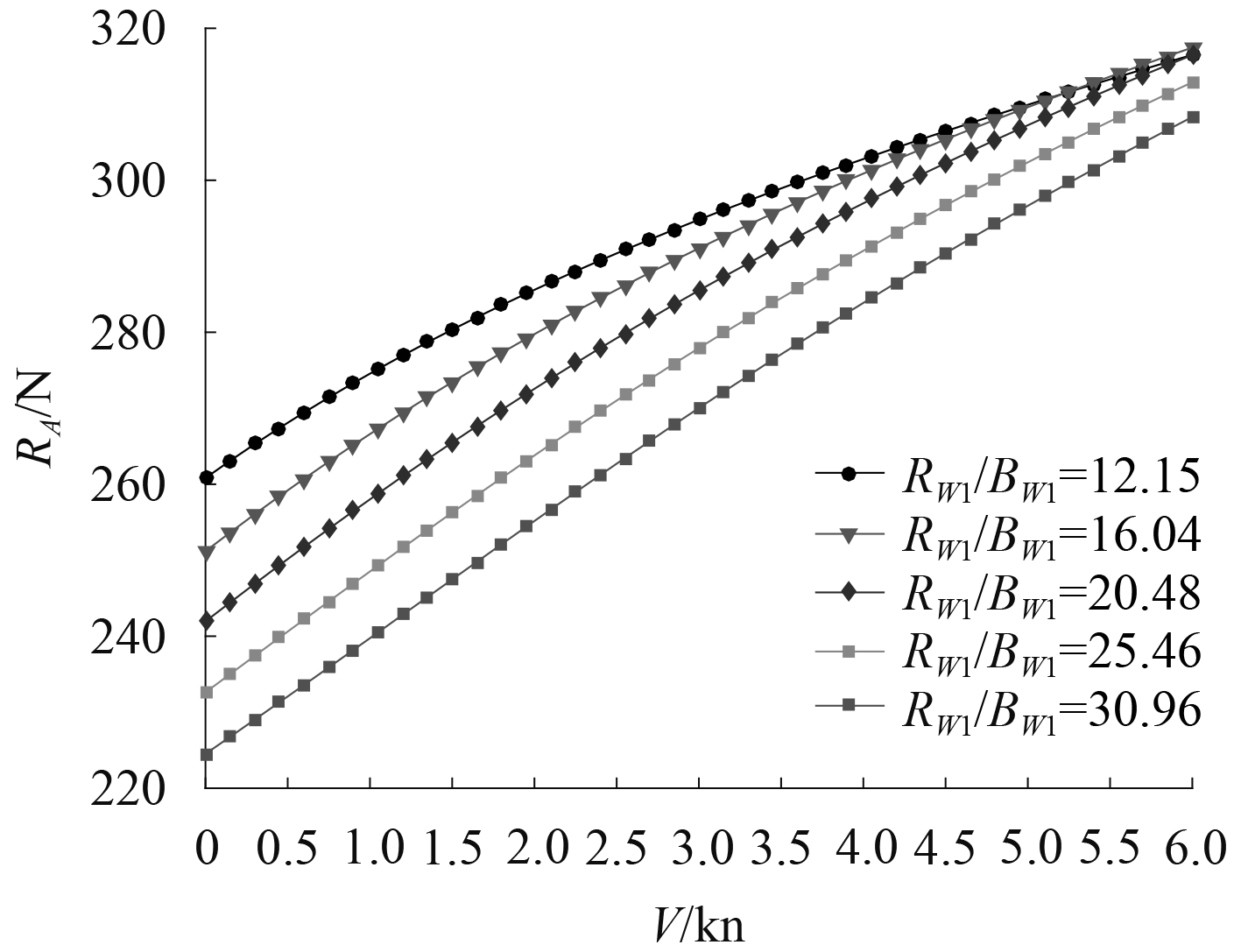
图4为不同片体长宽比下双体无人船静水阻力曲线,在航速较低时,不同片体长宽比Lwl/Bwl下静水阻力RH相差不大,随着航速的增大,不同片体Lwl/Bwl的双体无人船静水阻力曲线逐渐分离,片体较细长的双体无人船静水阻力较小;如图5所示,波浪增阻RA随航速的增大而增大,片体较细长的双体无人船波浪增阻较小且随着航速的增大不同片体长宽比的双体无人船波浪增阻曲线逐渐收拢,差异减小。
|
图 4 不同Lwl/Bwl静水阻力曲线 Fig. 4 Calm water resistance curves of different Lwl/Bwl |
|
图 5 不同Lwl/Bwl波浪增阻曲线 Fig. 5 Added resistance-in-wave curves of different Lwl/Bwl |
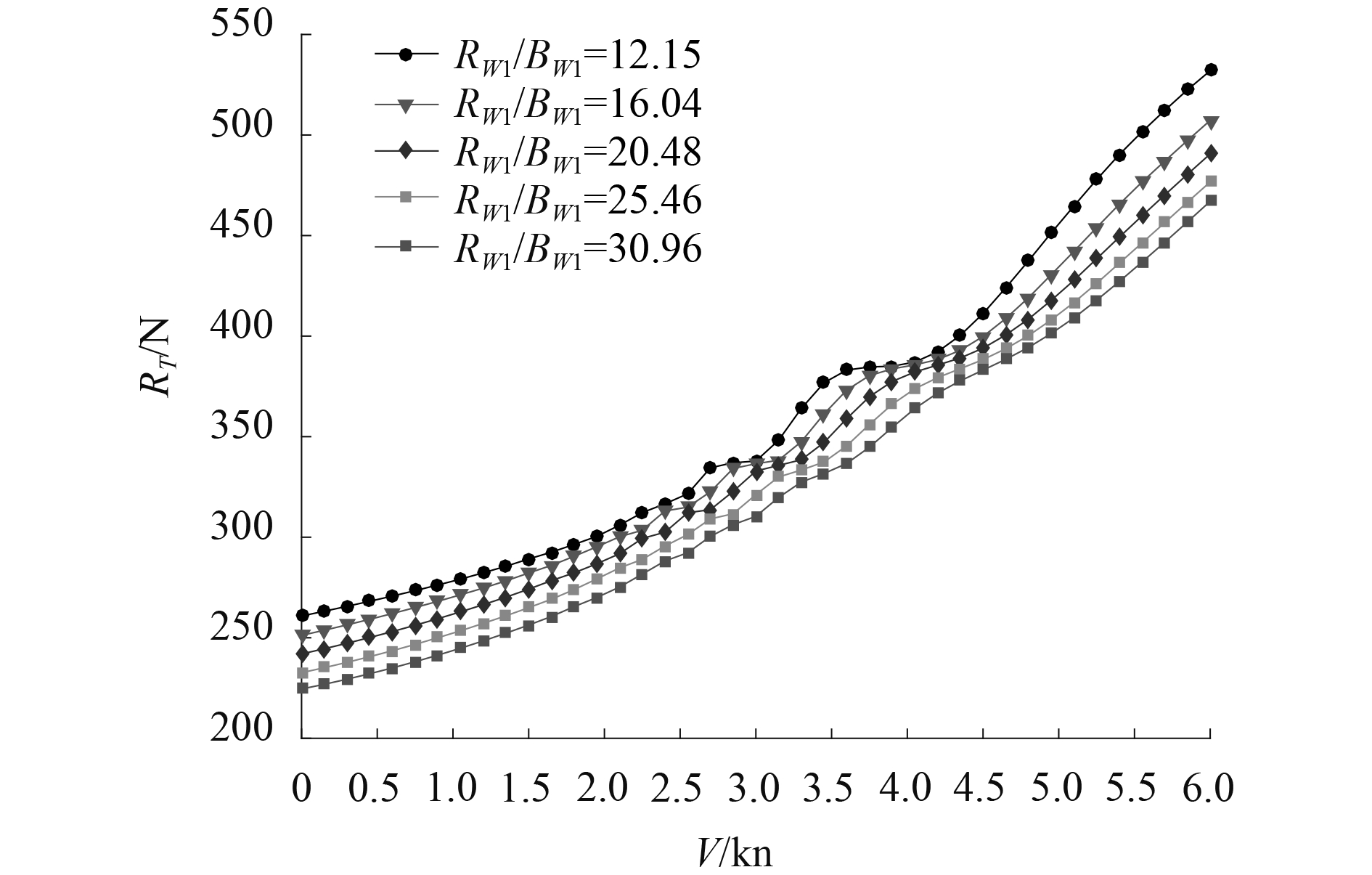
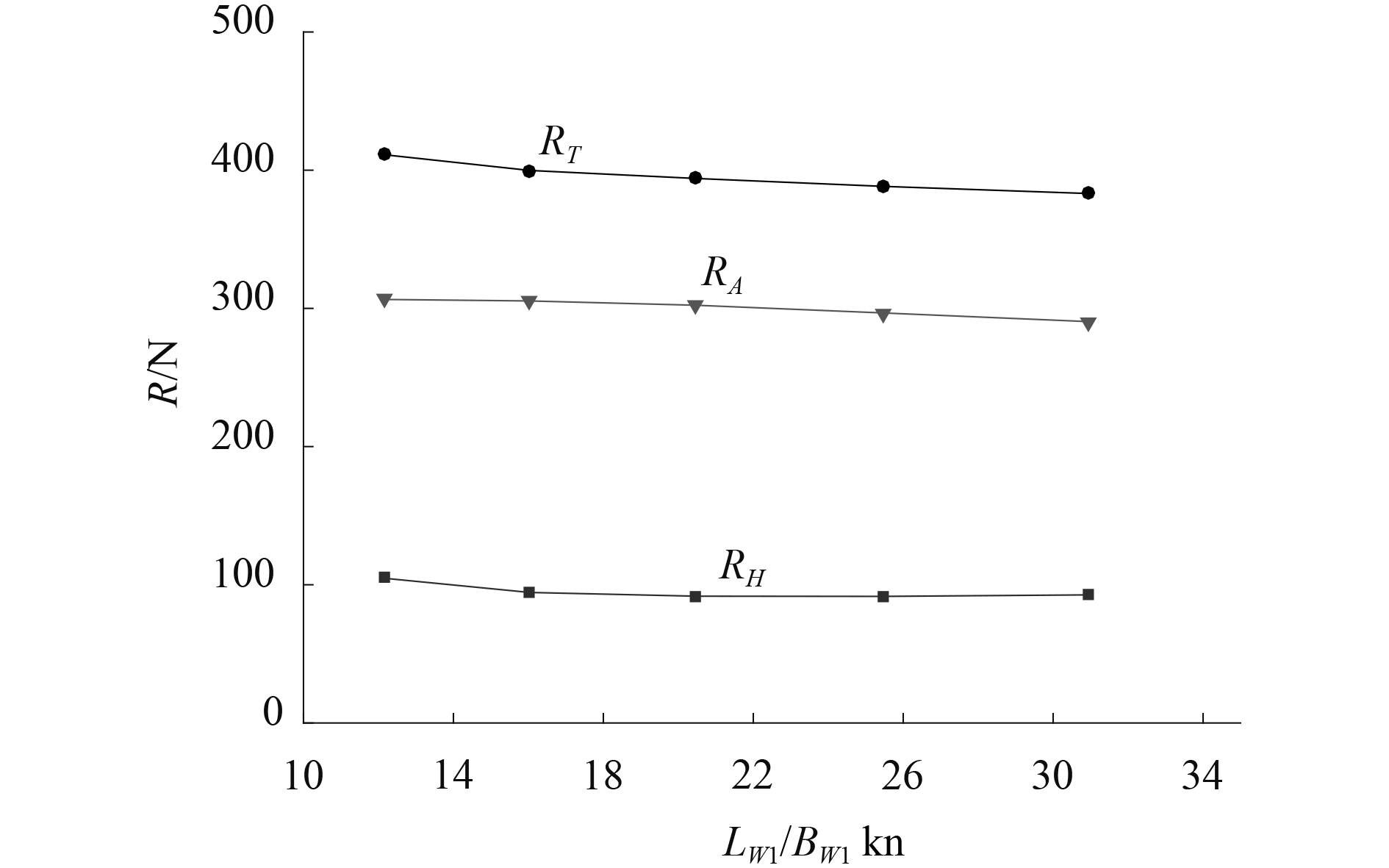
将某一片体长宽比的双体无人船静水阻力曲线与该双体无人船波浪增阻曲线线性叠加得到不同片体长宽比双体无人船的总阻力曲线,如图6所示。由图6可知,在给定的海况下,随着片体长宽比增大,各航速下的双体无人船总阻力均减小,因而较大的片体长宽比对降低总阻力有利。图7给出了设计航速V=4.5 kn时静水阻力、波浪增阻以及总阻力随片体长宽比变化曲线。综上,从减小总阻力的角度出发,片体长宽比越大越好。
|
图 6 不同Lwl/Bwl总阻力曲线图 Fig. 6 Total resistance curves of different Lwl/Bwl |
|
图 7 V=4.5 kn时阻力与长宽比关系曲线 Fig. 7 Relationship curves of resistance and Lwl/Bwlat V=4.5 kn |
本课题组研发的双体无人船在片体内部沿船长方向放置若干储能锂电池,锂电池厚度为68 mm。故为保证锂电池能正常安装且片体有足够的结构强度,实取片体水线宽度170 mm。
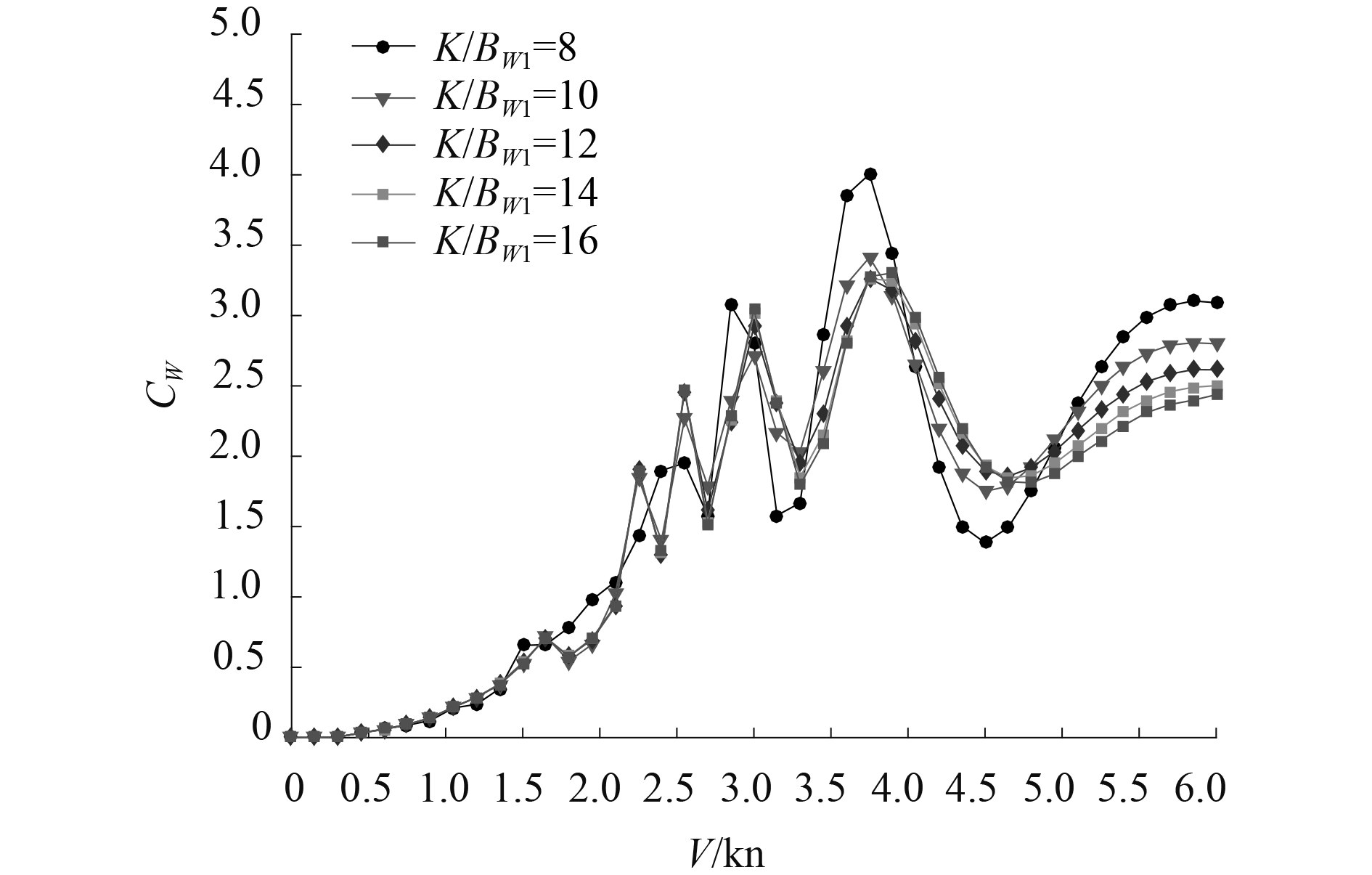
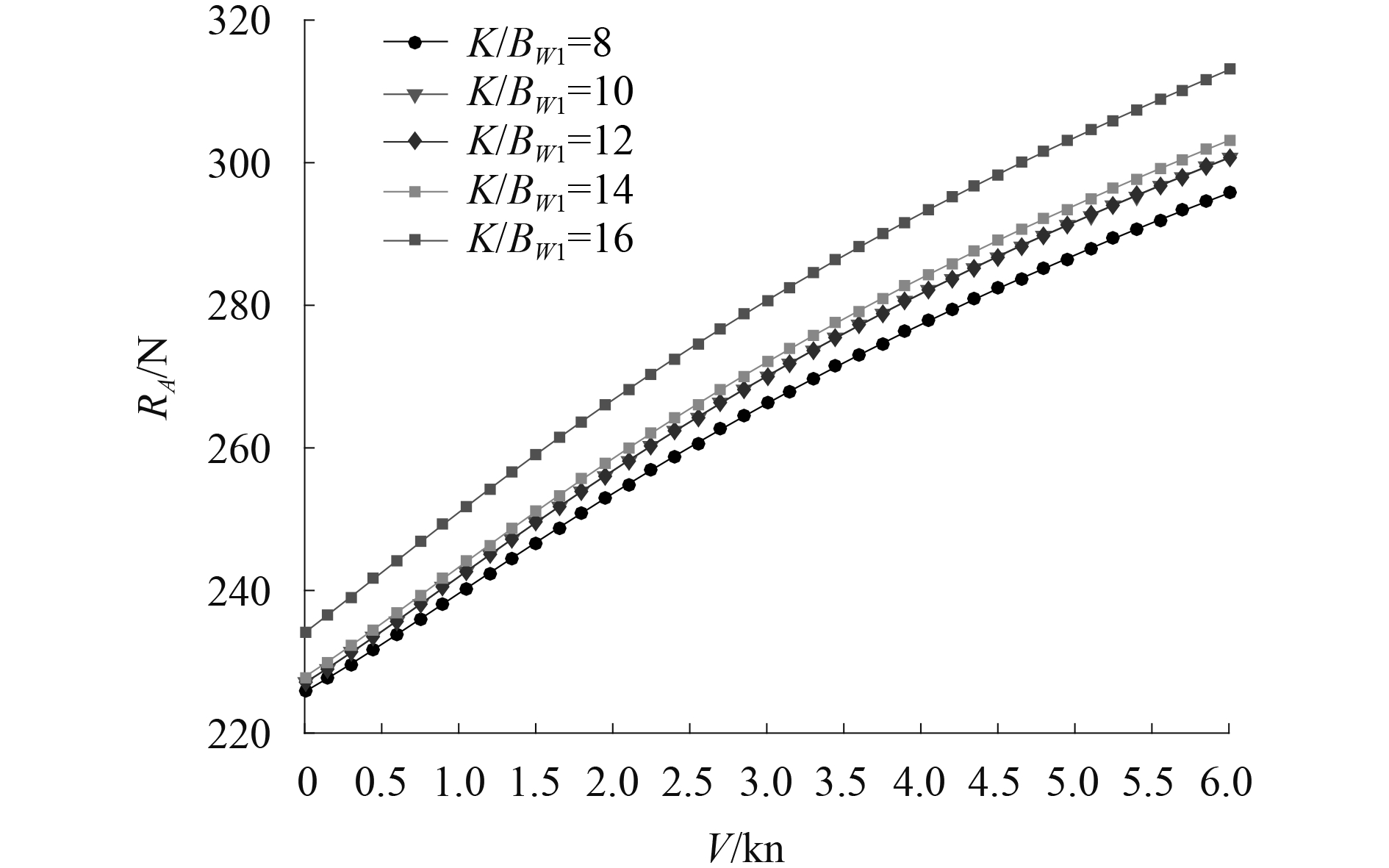
4 片体间距对双体无人船阻力的影响研究在片体长宽比优化的基础上根据均匀设计的原理均匀改变片体间距K,分别计算不同片体相对中心距K/Bwl下双体无人船静水阻力以及波浪增阻。片体相对中心距与兴波干扰密切相关,不同K/Bwl会产生的不同的兴波干扰,“有利干扰”使静水阻力降低,而“不利干扰”则使静水阻力增加。图8与图9分别给出了不同片体相对中心距K/Bwl下兴波阻力系数以及静水阻力随航速变化曲线,低航速下粘性阻力占静水阻力主要部分,不同片体相对中心距K/Bwl的兴波阻力系数以及静水阻力基本一致,随着航速的增加,在设计航速4.5 kn(Fr=0.396)附近较小的K/Bwl兴波干扰较有利,静水阻力较小,当V>5.0 kn(Fr=0.440)时,较大的K/Bwl兴波干扰较有利,静水阻力较小。
|
图 8 不同K/Bwl兴波阻力系数曲线 Fig. 8 Wave-making resistance coefficient curves of different K/Bwl |

|
图 9 不同K/Bwl下静水阻力曲线 Fig. 9 Calm water resistance curves of different K/Bwl |
计算不同片体相对中心距K/Bwl下双体无人船波浪增阻,图10给出了不同片体相对中心距K/Bwl下双体无人船波浪增阻随航速变化曲线,片体相对中心距K/Bwl较小的对应波浪增阻较小,因而从减小波浪增阻的角度考虑双体无人船片体相对中心距K/Bwl越小越好。将静水阻力曲线与波浪增阻曲线线性叠加得到不同K/Bwl下双体无人船总阻力曲线如图11所示,较小的片体相对中心距K/Bwl对总阻力也有利。
|
图 10 不同K/Bwl下波浪增阻曲线 Fig. 10 Added resistance-in-wave curves of different K/Bwl |

|
图 11 不同K/Bwl下总阻力曲线 Fig. 11 Total resistance curves of different K/Bwl |
本课题组研发的双体无人船在箱式连接桥结构的圆弧形上表面横向覆盖柔性太阳能薄膜,为保证太阳能薄膜受光面积和光电转换效率,箱式连接桥结构的圆弧形上表面半径不宜过小,故经对比分析实取片体相对中心距K/Bwl=14.0,片体间距K=238 0 mm。
5 LCG对双体无人船阻力的影响研究LCG与无人船纵倾角密切相关进而影响无人船的阻力性能。求解片体长宽比及片体相对中心距优化结果在不同重心纵向坐标LCG下双体无人船纵倾角,如表2所示。根据纵倾角建立各重心纵向坐标LCG对应的船体曲面模型并分别计算不同重心纵向坐标LCG下双体无人船静水阻力以及波浪增阻。
|
|
表 2 不同重心纵向位置方案 Tab.2 Scheme of different longitudinal center of gravity |
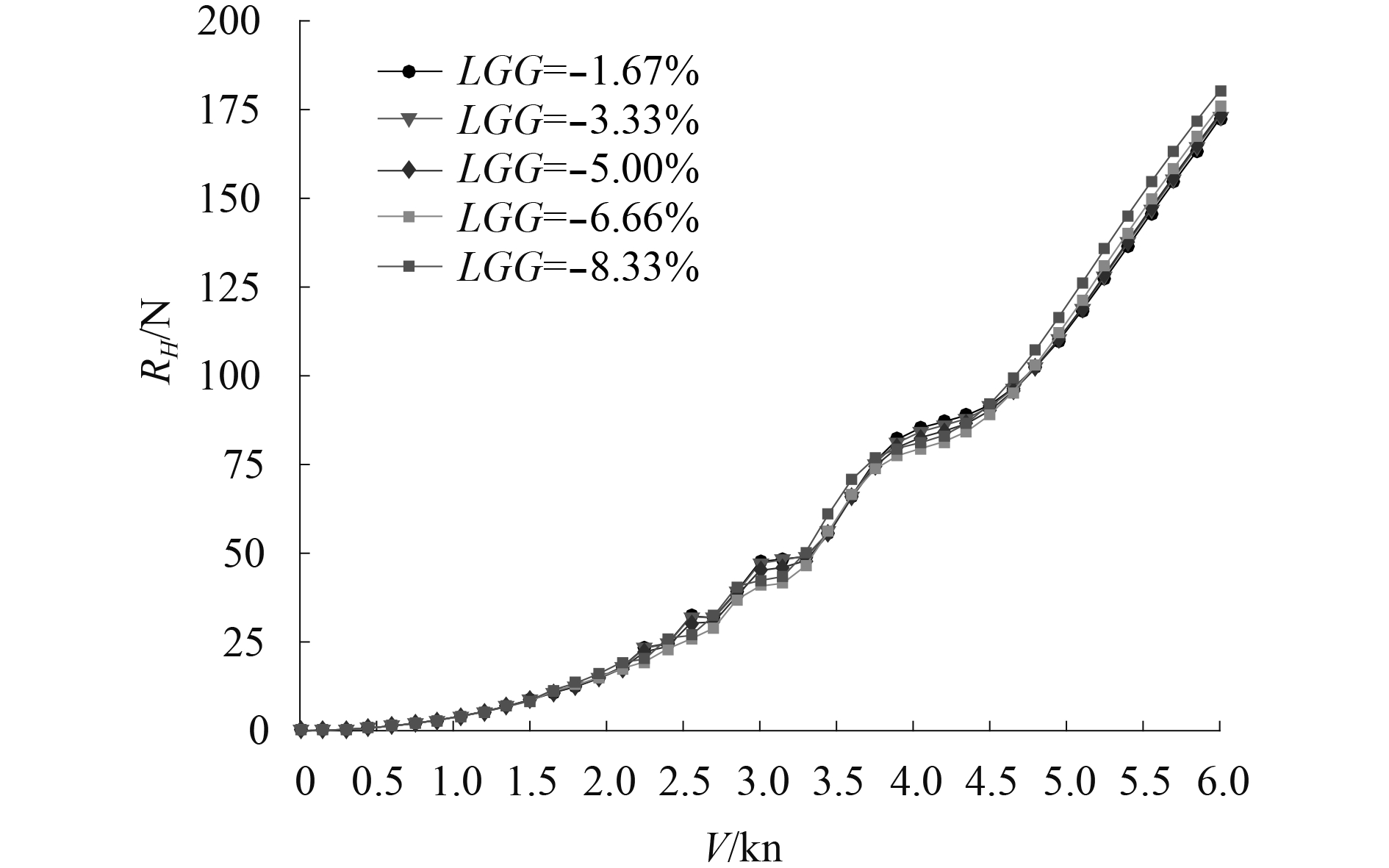
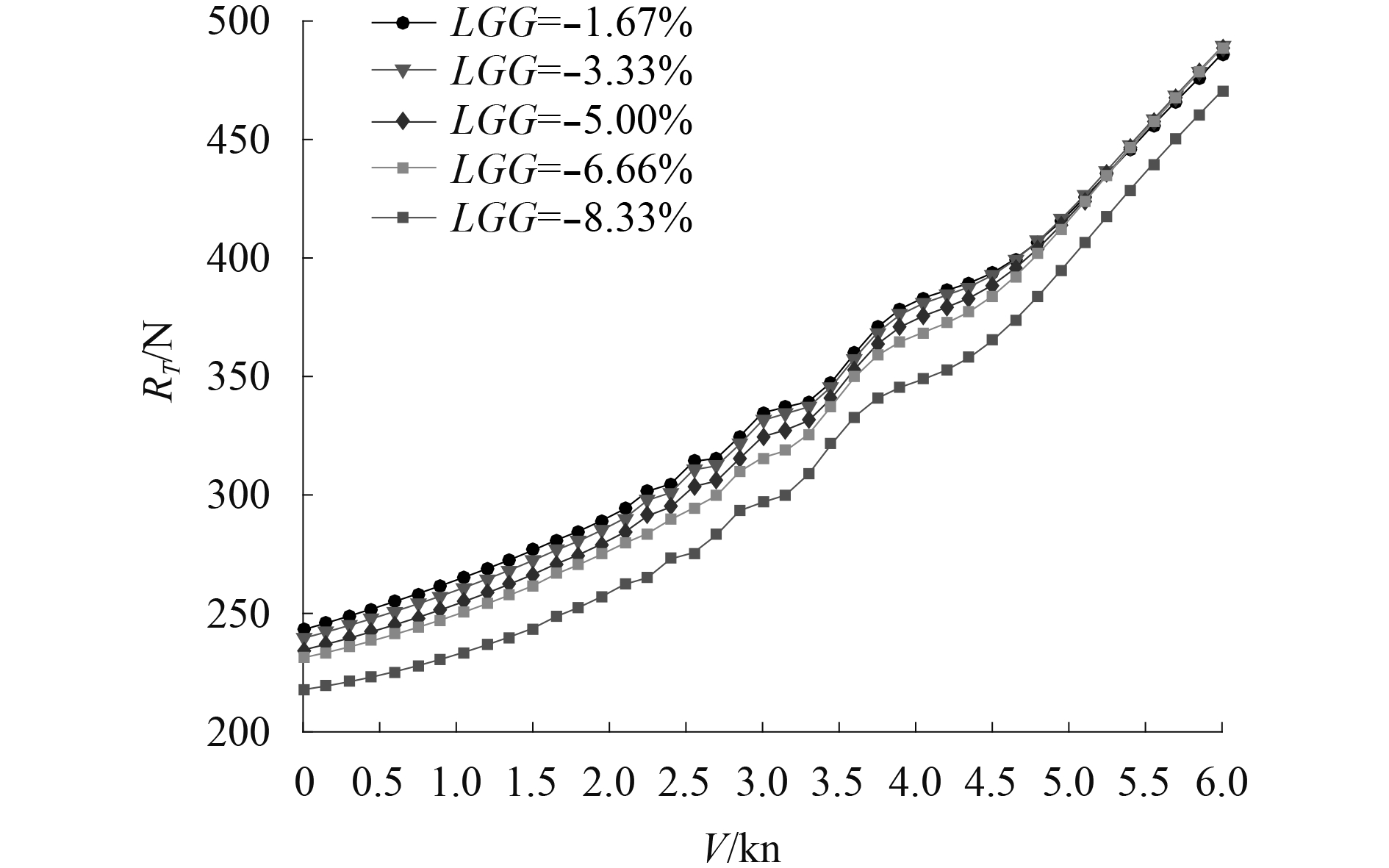
如图12所示,不同重心纵向坐标LCG的双体无人船静水阻力曲线差异不显著,在各航速的下静水阻力标准差不大于3.6 N,设计航速V=4.5 kn(Fr=0.396)时标准差不大于1.25 N;图13和图14为不同重心纵向坐标LCG的双体无人船波浪增阻曲线和总阻力曲线,由图可知,随着重心后移,纵倾角β增大,双体无人船波浪增阻以及总阻力均减小。因而适当偏后的重心位置对降低双体无人船总阻力有利。考虑到LCG=–8.33%Lwl时片体艉封板完全淹没,结合双体无人船总体布置实际情况,实取LCG=–6.66%Lwl。
|
图 12 不同LCG静水阻力曲线 Fig. 12 Calm water resistance curves of different LCG |

|
图 13 不同LCG下波浪增阻曲线 Fig. 13 Added resistance-in-wave curves of different LCG |
|
图 14 不同LCG总阻力曲线 Fig. 14 Total resistance curves of different LCG |
|
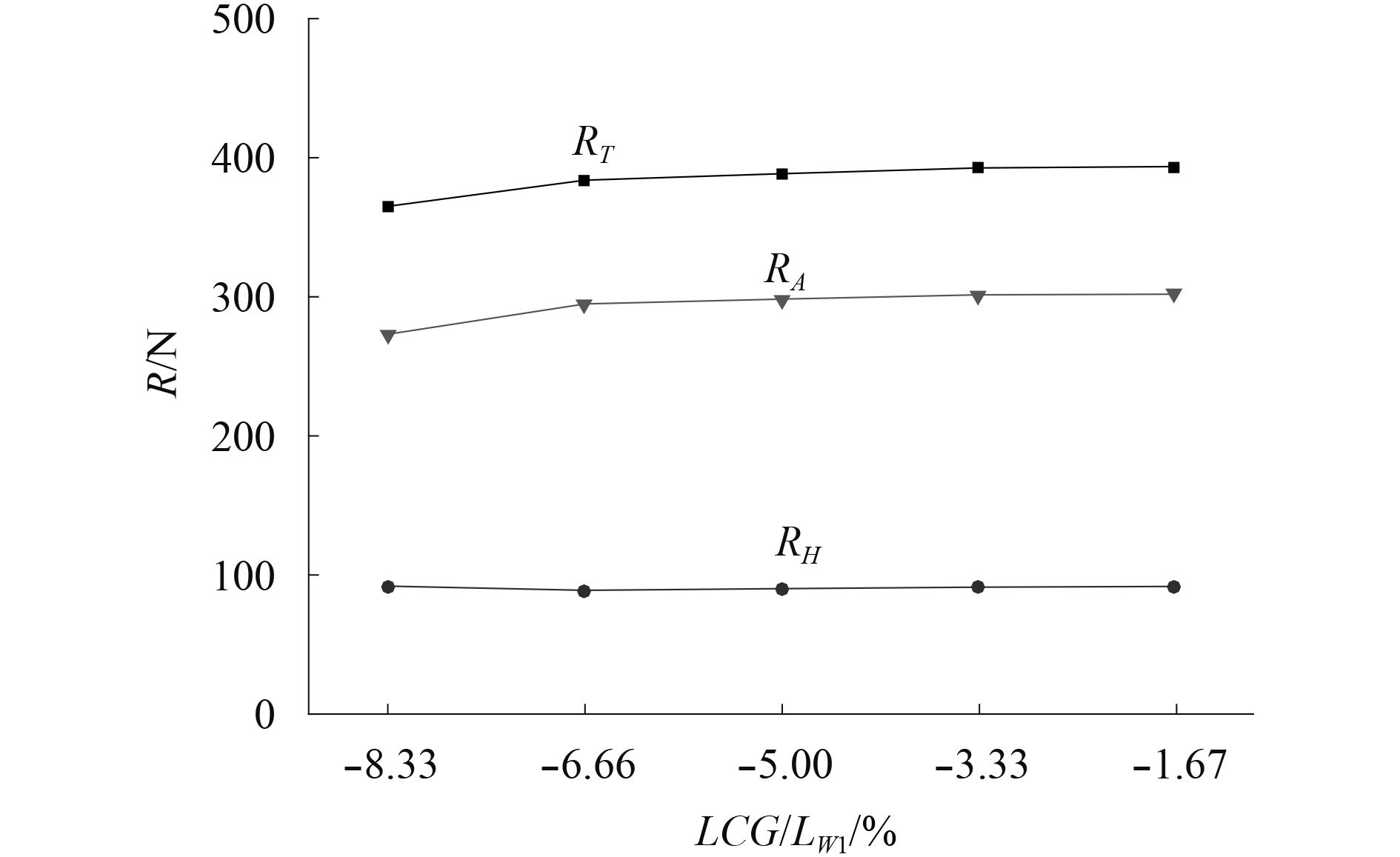
图 15 V=4.5 kn下阻力与LCG关系曲线 Fig. 15 Relationship curves of resistance and LCG at V=4.5 kn |
以片体长宽比、片体间距以及重心纵向位置为设计变量,建立不同的双体无人船数学模型,分析了各方案的静水阻力、波浪增阻并对比了各方案的总阻力性能,探讨了基于最小阻力的双体无人船优化方法。研究表明:
1)较大的细长比对降低双体无人船总阻力较有利。在等排水量的前提下,细长的片体对降低高速静水阻力、波浪增阻均有利,因而设计中宜采用大长宽比片体;但考虑到于片体内部锂电池布置对片体水线宽度的限制等因素,双体无人船片体宽度又不宜过小。片体长宽比最终优选为20.48。
2)从总阻力最小的角度考虑,较小的片体间距对降低总阻力较有利。片体间距对静水阻力的影响与航速有关,低航速下片体间距对静水阻力影响不小明显,航速较高时片体间距与静水阻力正相关或负相关;而较大的片体间距不利于减小波浪增阻。
3)较靠后的重心对降低总阻力较有利。结果显示,适当的尾倾可以降低双体无人船波浪增阻从而降低总阻力。
| [1] | J MANLEY, T VANECK. High fidelity hydrographic surveys using an autonomous surface craft[C]//Pro-ceedings of Oceans Community Conference’98, MTS, Baltimore, MD, September, 1998. |
| [2] | 盛振邦, 刘应中. 船舶原理(上)[M]. 上海: 上海交通大学出版社, 2004, 220–223. |
| [3] | 邓芳, 邓魏彬.双体船阻力性能计算及船型设计优化[J].青岛科技大学学报(自然科学版), 2015,36(1):72–76. http://www.cnki.com.cn/Article/CJFDTOTAL-CBLX200602003.htm |
| [4] | J. H. MICHELL. The wave-resistance of a ship[J]. Philosophical Magazine(series 5),1898,45(272): 106–123. https://www.researchgate.net/publication/297924730_Simplified_approach_for_predicting_the_wave_resistance_of_a_ship |
| [5] | 杨显原,吴家鸣,陈宇庆. 基于兴波干扰的三体船构型数字化优化方法[J]. 船舶工程,2017,39(S1):53–57. http://www.cnki.com.cn/Article/CJFDTOTAL-CBLX200602003.htm |
| [6] | COUSER P R, WELLICOME J F, MOLLAND.A F. An improved method for the theoretical prediction of the wave resistance of transom-stern hulls using a slender body approach[J].International Shipbuilding Progress,1998, 45(444):331–349. |
| [7] | INSEL M, MOLLAND A F. An investigation into the resistance components of high speed displacement catamarans[D]. Southampton: University of Southampton,1990:1–20. |
| [8] | NILS Salvesen. Added resistance of ships in waves[J]. Journal of Hydronautics, 1978, 12(1):24–34. |
| [9] | FORMATION DESIGN SYSTEMS. Hullspeed user manual[M]. Formation Design Systems Pty Ltd, 2009. |
 2018, Vol. 40
2018, Vol. 40
