2. 武汉第二船舶设计研究所,湖北 武汉 430205;
3. 大连船舶重工集团,辽宁 大连 116021
2. Wuhan Second Ship Design and Research Institute, Wuhan 430205, China;
3. Dalian Shipbuilding Industry Co., Ltd, Dalian 116021, China
疲劳破坏是船舶与海洋工程结构破坏的主要模式之一。目前,船舶与海洋工程结构疲劳强度评估的实用方法仍然是基于S-N曲线的疲劳累积损伤理论,且主要可分为简化算法或基于频域谱分析的直接计算法[1 – 2]。
如何确定交变应力的功率谱密度与应力范围S的概率密度之间的关系,是频域谱分析直接计算方法中的关键问题。通常将某一海况中交变应力认为一均值等于0的理想窄带平稳正态随机过程,此时应力峰值服从Rayleigh分布,疲劳累积损伤容易求解,现有规范中多采用这种方法。然而,船体结构应力存在宽带谱特点[1]。此时交变应力范围的概率密度函数不再服从Rayleigh分布,仍按理想窄带假设方法计算疲劳损伤值偏大,设计偏于保守[2 – 4]。
由于宽带高斯应力过程疲劳损伤计算的复杂性,很多学者采用窄带近似对其进行计算,并采用一个修正系数来得到较为准确的损伤值[5 – 9]。该方法以基于对交变应力时间历程的雨流计数统计得到的疲劳损伤结果作为衡准,窄带计算的结果对其进行“雨流修正”,这种方法在得到修正系数以后相对比较简单,Wirsching和Light方法在规范中[2 – 4]得到应用。
本文对基于“雨流修正”的宽带高斯应力过程疲劳损伤计算方法进行研究,并采用谱分析直接计算方法,对考虑宽带效应的船体结构疲劳强度分析。并通过算例分析,对各修正方法分析结果进行比较研究。
1 应力的响应谱计算谱分析法利用传递函数由海洋波浪谱来预测结构中的波浪诱导应力谱。假定船舶与海洋工程结构为线性系统,系统的输入为作用在结构上的波浪过程
设
| ${G_{XX}}\left( \omega \right) = {\left| {H\left( \omega \right)} \right|^2}{G_{\eta \eta }}\left( \omega \right)\text{,}$ | (1) |
式中:
| ${m_n} = \int_0^{ + \infty } {{\omega ^n}{G_{XX}}(\omega ){\rm d}\omega } \text{。}$ | (2) |
将频率
| ${m_n} = \int_0^{ + \infty } {\omega _e^n \cdot {G_{XX}}({\omega _e}){\rm d}{\omega _e}} \text{。}$ | (3) |
另外,为得到给定时间内的应力循环次数,要用到交变应力过程的跨零率
| ${f_0} = \frac{1}{{2\pi }}\sqrt {\frac{{{m_2}}}{{{m_0}}}} \text{,}$ | (4) |
带宽系数
| $\varepsilon = \sqrt {1 - \frac{{m_2^2}}{{{m_0}{m_4}}}} \text{,}$ | (5) |
不规则系数
| $\alpha = \sqrt {\frac{{m_2^2}}{{{m_0}{m_4}}}} \text{。}$ | (6) |
在船舶与海洋工程中,海洋波浪的长期状态通常看成是由许多短期海况的序列所组成。对每一短期海况,通常是把波浪作为一个平稳正态随机过程来研究。
当交变应力过程假设均值为0的窄带平稳随机过程时,根据随机过程理论可知,其应力峰值服从Rayleigh分布,概率密度函数为
| ${f_Y}(y) = \frac{y}{{\sigma _X^2}}\exp \left( { - \frac{{{y^2}}}{{2\sigma _X^2}}} \right){\text{,}} \; 0 \leqslant y < + \infty {\text{。}}$ | (7) |
式中:
对于每一个短期海况,根据随机过程理论可知,应力峰值服从Rayleigh分布,用概率论中随机变量函数的概率密度的计算方法,可得应力范围的概率密度函数为
| ${f_S}(S) = \frac{S}{{4{m_0}}}\exp \left( { - \frac{{{S^2}}}{{8{m_0}}}} \right), \;\; 0 \leqslant S < + \infty \text{,}$ | (8) |
当交变应力过程为一般带宽时,应力峰值的概率密度函数为Rice分布:
| $\begin{split}& fY(y) = \displaystyle\frac{\varepsilon }{{\sqrt {2\pi } \sigma X}}\exp \left( - \displaystyle\frac{{{y^2}}}{{2\sigma {X^2}{\varepsilon ^2}}}\right) + \\& \frac{{\alpha y}}{{\sigma {X^2}}}\Phi \left(\frac{{\alpha y}}{{\sigma X\varepsilon }}\right) \exp\left( - \frac{{{y^2}}}{{2\sigma {X^2}}}\right), - \infty < y < + \infty {\text{,}}\end{split}$ | (9) |
式中:Φ为标准正态分布函数。
由于标准正态分布函数的存在,在后续应力范围及疲劳损伤的推导过程中,会产生一误差函数,造成疲劳累积损伤不能得到解析解。
在船舶与海洋工程领域,通常采用将各短期海况下交变应力过程的标准差和跨零率与原过程相同的窄带平稳随机过程近似地替代原来的宽带过程,即Rayleigh分布模型描述应力峰值及范围分布,在此基础上进行累积损伤计算并对计算结果进行“雨流修正”。
3 带宽修正方法以基于对交变应力时间历程的雨流计数统计得到的疲劳损伤结果作为衡准,其他窄带计算结果对其进行“雨流修正”。修正系数主要交变应过程的功率谱密度的相关参数表达。典型修正方法如下:
Wirsching-Light方法的修正系数为
| ${\lambda _{W,L}} = a + (1 - a){(1 - \varepsilon )^b}\text{,}$ | (10) |
式中,a,b为与S-N曲线参数m相关的表达式,具体为
| $\begin{array}{l}a = 0.926 - 0.033m\text{,}\\b = 1.587m - 2.323\text{。}\end{array}$ | (11) |
Ortiz-Chen方法的修正系数为
| ${\lambda _{O,C}} = \frac{1}{\alpha }{\left( {\sqrt {\frac{{{m_2}{m_k}}}{{{m_0}{m_{k + 2}}}}} } \right)^m}{\text{,}}k = 2.0/m{\text{。}}$ | (12) |
式中,
Chaudhury-Dover方法的修正系数如下式:
| ${\lambda _{C,D}} = \frac{{{\varepsilon ^{m + 2}}\Gamma (m/2 + 1/2)}}{{2\sqrt \pi \Gamma (m/2 + 1)}} + \frac{3}{4}\alpha \text{。}$ | (13) |
将各短期海况下采用等效窄带平稳随机过程近似时,设所考虑的船舶在第
| ${D_{Ra,ij}} = \frac{{{T_{ij}}{f_{0ij}}}}{A}\int_0^{ + \infty } {{S^m}{f_{Sij}}(S){\rm d}S} \text{,}$ | (14) |
式中,
将式(8)代入式(14),可得
| ${D_{Ra,ij}} = \frac{{{T_{ij}}{f_{0ij}}}}{A}{\left( {2\sqrt {2{m_{0ij}}} } \right)^m}\Gamma \left(1 + \frac{m}{2}\right){\text{。}}$ | (15) |
考虑雨流修正后,各短期海况下累积损伤度
| $\begin{aligned}& {D_{ij}} = {\lambda _{ij}}{D_{Ra,ij}} = \\& {\lambda _{ij}}\displaystyle\frac{{{T_{ij}}{f_{0ij}}}}{A}{\left( {2\sqrt {2{m_{0ij}}} } \right)^m}\Gamma \left(1 + \displaystyle\frac{m}{2}\right){\text{。}}\end{aligned}$ | (16) |
设船舶寿命期为
| $\begin{split}& D = \sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{D_{ij}}} } = \\& \displaystyle\frac{T}{A}\Gamma \left(1 + \displaystyle\frac{m}{2}\right)\sum\limits_{i = 1}^{{n_S}} {\sum\limits_{j = 1}^{{n_H}} {{\lambda _{ij}}{p_i}{p_j}{f_{0ij}}} } {\left( {2\sqrt {2{m_{0ij}}} } \right)^m}\text{。}\end{split}$ | (17) |
式中:
基于雨流计数方法的疲劳累积损伤计算适用于时域内随机载荷作用下的结构疲劳分析。该方法中,对应力的时间历程采用雨流计数法进行计数统计,获取疲劳应力的均值和范围。利用miner线性累积损伤理论,对计数结果直接计算损伤。
船舶结构疲劳分析的直接计算中,在得到各短期海况的交变应力功率谱密度函数后,按式(18)得到交变应力的时间历程,从而应用基于雨流计数方法进行疲劳累积损伤计算。
| ${\sigma _{ij}}(t) = \sum\limits_{k = 1}^n {\sqrt {2{G_{XXij}}({\omega _k})\Delta {\omega _k}} \cos ({\omega _k}t + {\xi _k})} \text{,}$ | (18) |
式中,
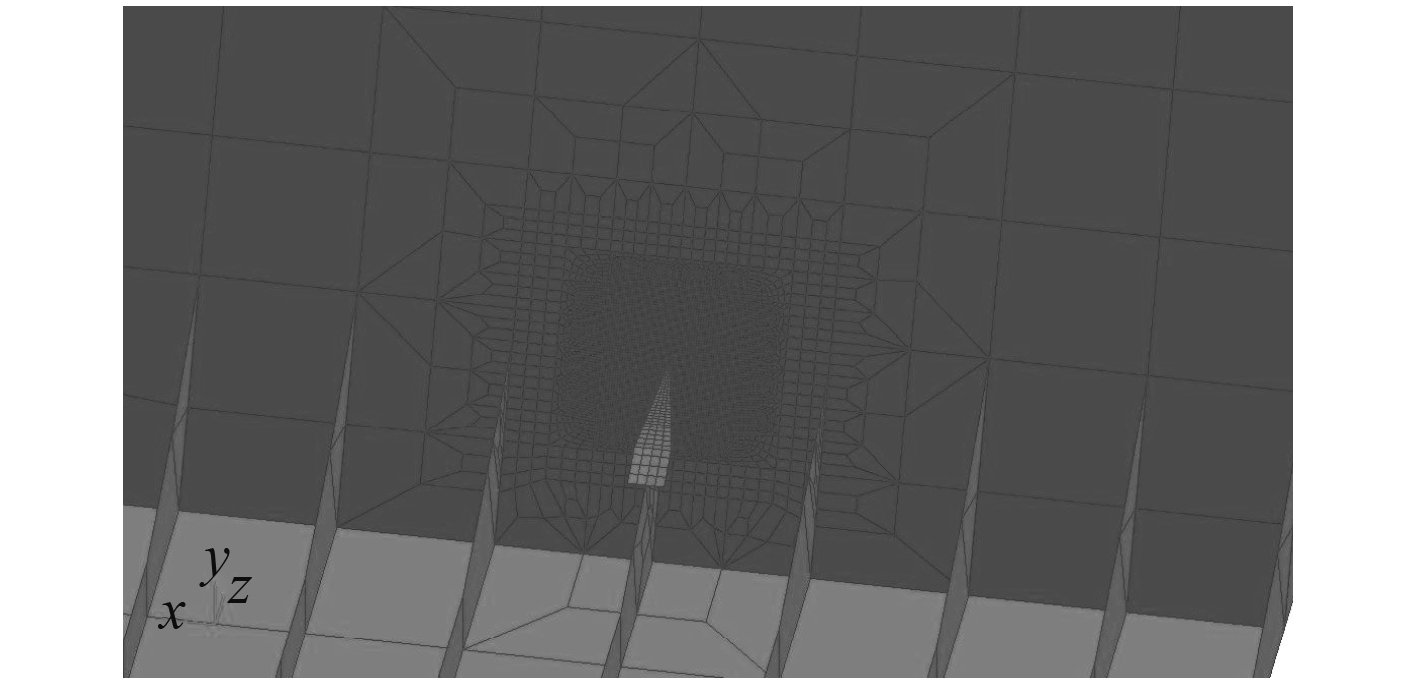
以1艘7wDWT散货船为例,采用雨流修正的方法进行疲劳累积损伤分析,有限元模型如图1所示。参照规范,选取如表1所示的疲劳破坏热点部位,进行有限元模型网格细化,图2给出了热点6的局部精细有限元模型图。

|
图 1 例船有限元模型 Fig. 1 The FEM model of one ship |
|
图 2 舷侧肋骨顶端细化点 Fig. 2 Fining point at the top of side frame |
|
|
表 1 疲劳节点位置 Tab.1 The position of fatigue node |
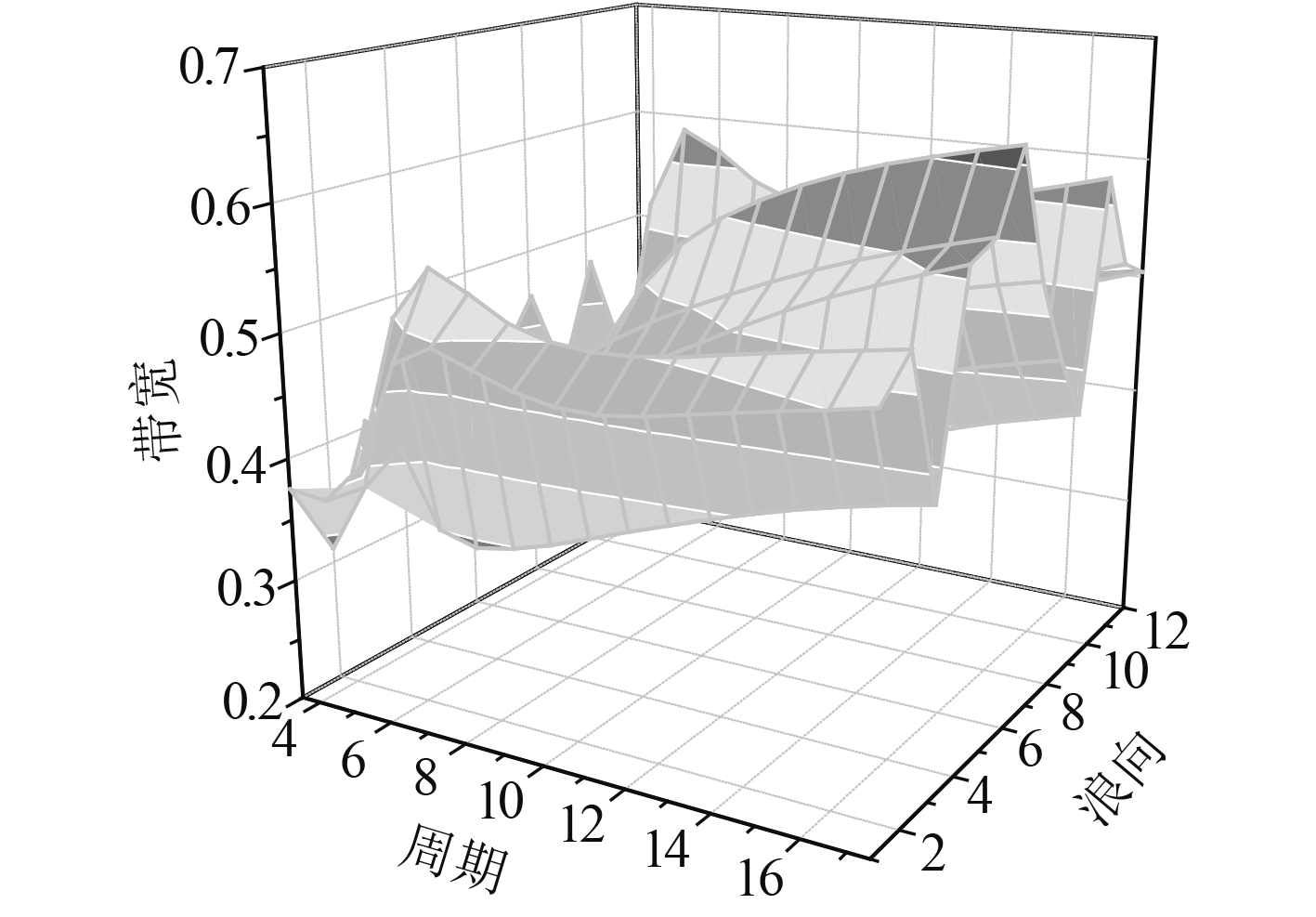
在对例船进行疲劳强度分析时,选取了疲劳问题突出的轻压载、重压载、隔舱装载等3个具有代表性装载工况进行计算。图3给出了热点6在重压载工况下的带宽系数,带宽系数大多数在0.4以上,在局部海况下达到了0.6以上,交变应力过程呈现明显的宽带谱特点。采用各修正方法所得结果
|
图 3 热点6带宽图(重压载) Fig. 3 The bandwidth map of hot spot 6 (heavy load) |
|
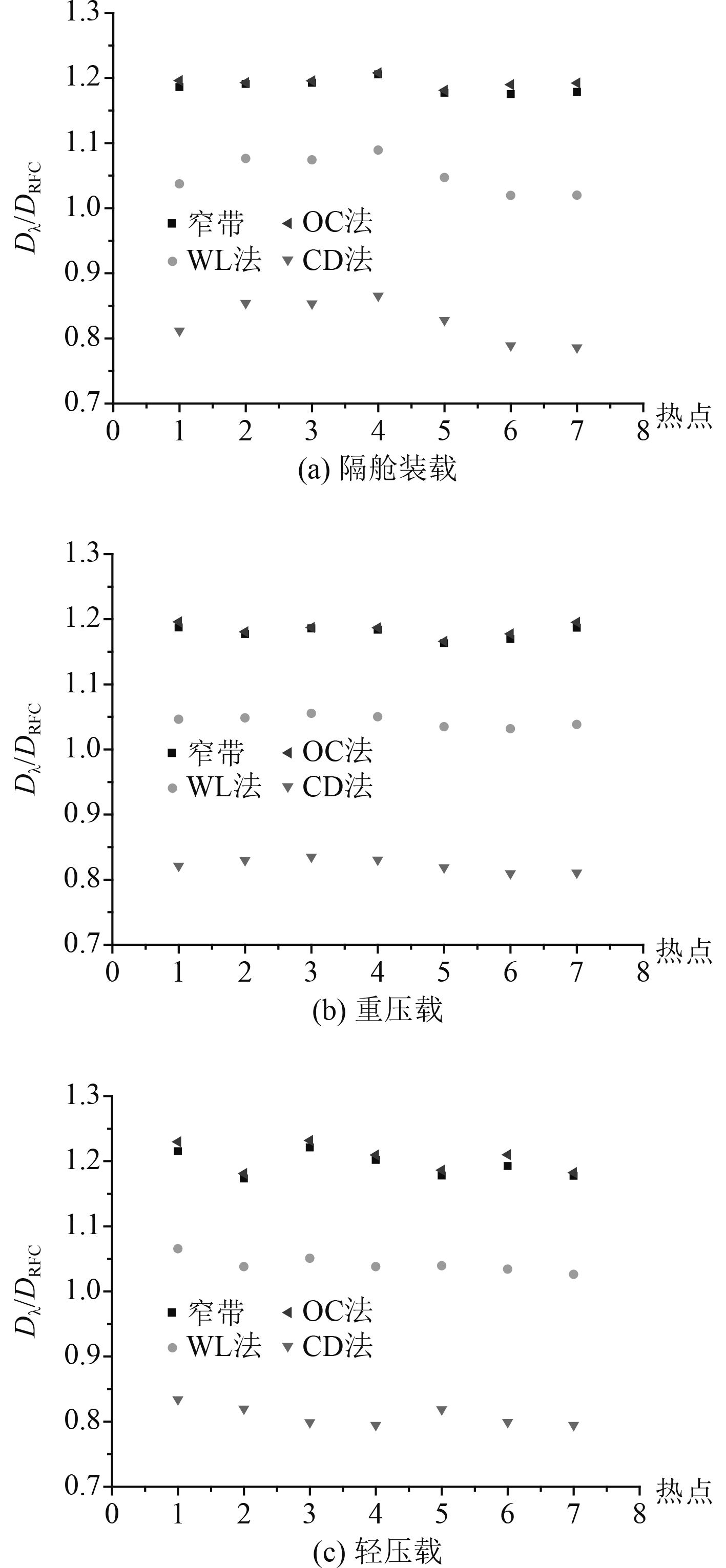
图 4 典型装载工况下损伤结果比较 Fig. 4 Comparison of damage results under typical loading conditions |
从图4结果可以看出,Ortiz-Chen法的修正效果不明显,Chaudhury-Dover法的修正结果比雨流计数结果小很多,Wirsching-Light法与雨流计数结果较为接近。
考虑上述修正后,疲劳累积损伤结果如表2所示。
|
|
表 2 累积损伤计算结果 Tab.2 The results of cumulative damage calculation |
本文针对基于不同雨流修正方法的宽带疲劳损伤进行了研究。通过算例分析表明,各短期海况下,船舶结构交变应力过程的功率谱密度的带宽系数大多在0.4~0.6之间;按照窄带近似方法进行损伤计算时,所得结果与雨流计数结果相比保守;同时,各修正方法中,Wirsching-Light法与雨流计数结果较为接近。
| [1] | 胡毓仁, 李典庆, 陈伯真. 船舶与海洋工程结构疲劳可靠性分析[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010. |
| [2] | DNV, Classification Note No. 30. 7: Fatigue Assessment of Ship Structure, Det Norske Veritas, 2010. |
| [3] | ABS, Guidance Notes on Spectral-based Fatigue Analysis for Vessels, American Bureau of Shipping, 2004. |
| [4] | 中国船级社. 船体结构疲劳强度指南[S]. 北京: 人民交通出版社, 2007 |
| [5] | WIRSCHING, P. H. & LIGHT, M. C. Fatigue under wide band random stresses[J]. Journal of the structural Division, ASCE (American Society of Civil Engineers). 1980, 106(7): 1593–1607. |
| [6] | ORTIZ CHEN. Fatigue damage prediction for stationary wide band stresses[C]// 5th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP), 1987, Vancouver, BC, Canada. |
| [7] | CHAUDHURY G K, DOVER W D. Fatigue analysis of offshore platform subject to sea wave loadings[J]. Int J Fatigue, 1985, 7: 13–19. |
| [8] | LUTES, L, LARSON, M. L. Improved spectral method for variable amplitude fatigue prediction[J]. Journal of the Structural Division. ASCE, 1990, 116: 1149–1164. |
| [9] | 李晓飞, 胡毓仁. 宽带波浪载荷下海洋结构物内应力范围及疲劳损伤分析[J]. 海洋工程, 2008, 04: 35–38. |
| [10] | GAO Z, MOAN T. Frequency-domain fatigue analysis of wide-band stationary Gaussian processes using a trimodal spectral formulation. International Journal of Fatigue, 2008, 30: 1994–1955. |
 2018, Vol. 40
2018, Vol. 40
