研究潜体近水面航行时的兴波现象及其力学特性,一直是一项具有重要工程意义的课题。尤其近几年各类附加水翼新概念船型的大量涌现,使得潜体兴波研究显得更为重要。由于计算效率的限制,以往对潜体兴波研究主要采用定常方法。如Farell改进了Havelock源格林函数,推导得到潜航回转椭球体在Neumann-Kelvin问题下的半解析理论解[1];Doctors和Beck研究了潜体在Neumann-Kelvin问题下,采用Havelock源计算的收敛性[2]。随着时代的发展,时域方法以其可以计算非定常兴波,得到运动物体实时兴波信息,便于仿真模拟和后处理等优点,吸引了越来越多学者的注意。
自从Hess和Smith[3]第一次应用面元法求解三维物体绕流问题以来,面元法在船舶与海洋工程领域得到了广泛的应用。其中Rankine源形式简单,具有较高灵活性,且易于推广到非线性计算,已经有不少学者尝试使用Rankine源处理兴波问题[4 – 5]。
然而,传统的面元法在求解问题时,需要计算每个面元与配置点之间的相互作用,生成一个N阶方阵(N为离散面元个数)。一方面储存这个N阶稠密矩阵需要大量的内存空间,另一方面求解该矩阵也将耗去大量时间。例如采用高斯消去法直接求解,时间复杂度将达到O(N3),即使使用迭代法求解,时间复杂度也有O(N2)。计算效率上的缺陷将面元法的应用限制在了小规模流场,更遑论时域计算时需要进行多次时间步进迭代,计算规模将被进一步压缩。为克服传统面元法这一局限性,引入快速多极子法,可同时减小存储量与时间复杂度。
快速多极子法最早由Rokhlin[6]于1985年提出,用来加速二维势流问题的求解。此后Liu[7],Nishimura[8]及Yoshida[9]等将快速多极子法和边界元法结合,并对其进行深入研究。多极子法与边界元法的结合已被证实可以大幅度提高其计算效率,适用于求解大规模势流问题[10 – 11]。
本文结合多极子法与面元法,对三维潜体的兴波特性进行时域研究,将所得结果与传统方法结果进行比较,证明多极子面元法高精度与高效率的特性。
1 潜体兴波问题描述
|
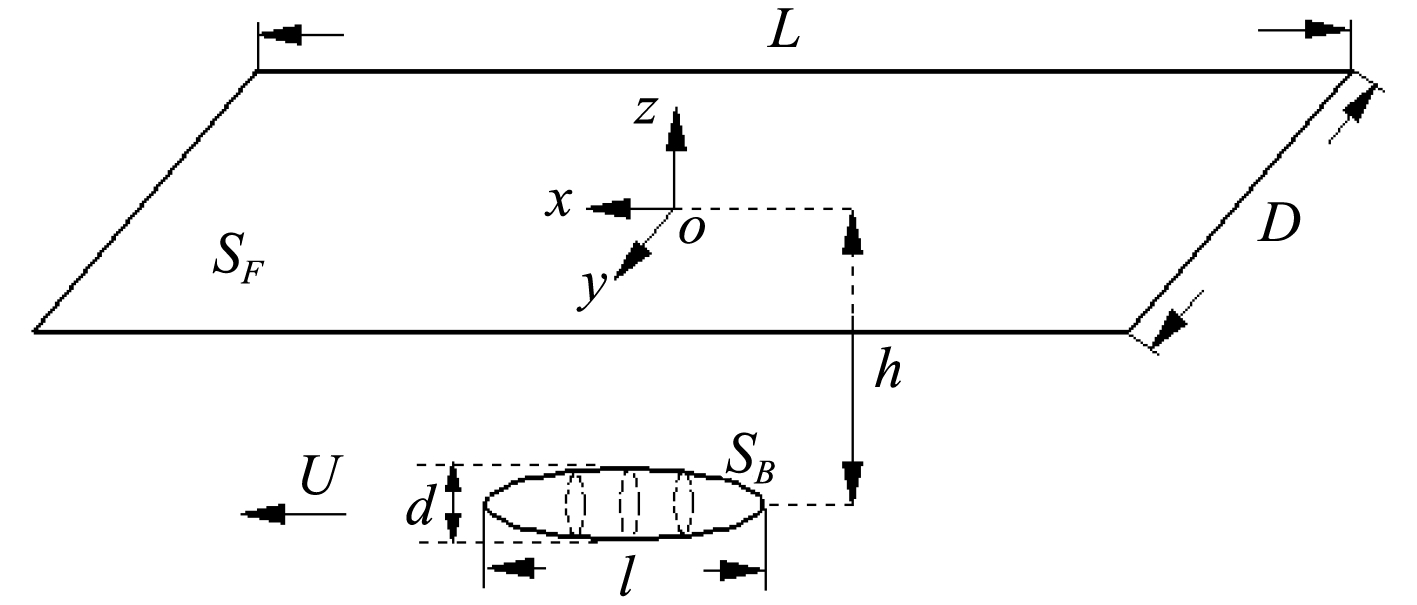
图 1 计算流场示意图 Fig. 1 The schematic of computational flow field |
考虑如图1所示的计算流场,O-xyz为三维笛卡尔直角坐标系,xy平面与自由面平行,潜体沿x轴方向以速度U运动,z轴垂直向上,整个流场边界由潜体物面SB和自由面SF组成。潜体的特征长度为l,特征宽度为d,潜体中心距自由表面深度为h。对于时域兴波问题,自由面条件中对流项起到主要作用,足够远处将自由水面截断,截断边界上的反射对势流解的影响并不敏感[12]。因此本文中采用截断有限自由表面代替无限自由表面,其长为L,宽为D。假设流体无压、无粘并且无旋,流场中存在一速度势
| ${\nabla ^2}\varphi = 0\text{。}$ | (1) |
在潜体表面SB上满足不可穿透条件,即
| $\frac{{\partial \varphi }}{{\partial n}} = {{U}} \cdot {{n}}\text{,}$ | (2) |
其中
| $\frac{{\partial \eta }}{{\partial t}} = - \tilde \nabla \varphi \cdot \tilde \nabla \eta + \frac{{\partial \varphi }}{{\partial z}} , \; z = \eta (x, y, t)\text{,}$ | (3) |
其中,
| $\frac{{\partial \varphi }}{{\partial t}} = - g\eta - \frac{1}{2}{\left| {\nabla \varphi } \right|^2}, \; z = \eta (x, y, t)\text{。}$ | (4) |
在本文时域兴波问题中,假设潜体由静止快速启动至匀速运动状态,且在自由面SF上初始条件(t=0)为:
| $\varphi = 0, \; \frac{{\partial \varphi }}{{\partial t}} = 0 , \; \eta = 0\text{。}$ | (5) |
首先将整个流场的边界划分成N个离散面元,其中前NB个为三角形常数面元,用于表征潜体表面;后NF个为四边形常数面元,用于表征自由水面,则有N=NB+NF。第i个面元的的面积为Si,其上均匀分布强度为σi的面源。此时,可得到流场中任一点的诱导速度势
| $\varphi ({{x}}) = \sum\nolimits_{i = 1}^N {\frac{{{\sigma _i}}}{{4\pi }}} \iint_{{S_i}} {\frac{1}{r}{\rm d}S} , \; {{x}} \in \varOmega \text{,}$ | (6) |
诱导速度
| $\nabla \varphi ({{x}}) = \sum\nolimits_{i = 1}^N {\frac{{{\sigma _i}}}{{4\pi }}} \iint_{{S_i}} {\nabla \frac{1}{r}{\rm d}S}, \; {{x}} \in \varOmega \text{,}$ | (7) |
式中,
此外,选取每一个常数面元的中点为配置点,在每一个配置点上满足已知的边界条件,例如在t=0初始时刻,潜体物面上的配置点应满足式(2),而自由表面上的配置点应满足式(5)中的
| $\frac{{\partial {\varphi _i}}}{{\partial {n_i}}} \!=\! \sum\nolimits_{j = 1}^N {\frac{{{\sigma _j}}}{{4\pi }}} \iint_{{S_j}} {\frac{{\partial (\frac{1}{r})}}{{\partial {n_i}}}{\rm d}S} \!= \!{{U}} \cdot {{{n}}_{i}}, \; (i \!=\! 1, \cdots , {N_B})\text{,}$ | (8) |
| ${\varphi _i} \!=\! \sum\nolimits_{j = 1}^N {\frac{{{\sigma _j}}}{{4\pi }}} \iint_{{S_j}} {\frac{1}{r}{\rm d}S} \!=\! 0, \; (i \!=\! {N_B} \!+\! 1, \cdots , {N_B} \!+\! {N_F})\text{。}$ | (9) |
采用高斯积分计算上述线性方程组中的积分项,但当
| ${ A}\sigma = B \text{,}$ | (10) |
其中,
求解线性方程组(10)可得到每个面元上面源强度
| $p = - \rho \frac{{D\varphi }}{{Dt}} - \frac{1}{2}\rho {\left| {\nabla \varphi } \right|^2} + \rho \nabla \varphi \cdot {{U}} - \rho gz\text{,}$ | (11) |
其中,
| ${R_L} = - \sum\nolimits_{i = 1}^{{N_B}} {\iint_{{S_i}} {{p_i} \cdot {n_{iz}}{\rm d}S}} \text{,}$ | (12) |
| ${R_W} = - \sum\nolimits_{i = 1}^{{N_B}} {\iint_{{S_i}} {{p_i} \cdot {n_{ix}}{\rm d}S}} \text{。}$ | (13) |
其中
| ${C_L} = {R_L}/\frac{1}{2}\rho {U^2}{S_B},\;\;{C_w} = {R_w}/\frac{1}{2}\rho {U^2}{S_B}\text{。}$ | (14) |
对于整个时域计算过程则采用时间步进法。假设已知
| $\frac{{{\varphi ^{[n + 1]}} - {\varphi ^{[n]}}}}{{\Delta t}} = {{(\partial \varphi } / {\partial t}}{)^{[n]}}\text{,}$ | (15) |
| $\frac{{{\eta ^{[n + 1]}} - {\eta ^{[n]}}}}{{\Delta t}} = {{(\partial \eta } / {\partial t}}{)^{[n]}}\text{。}$ | (16) |
在
常数面元法的优点在于公式推导简单,易于应用;但为了提高精度,需要增加离散面元数目,使得计算规模增大、计算效率降低。此外,不少学者尝试使用高阶面元法求解势流问题,如Liu Y H[15],Romate J E[16]等。尽管计算精度和效率有所提升,高阶面元法仍无法有效克服传统面元法求解大规模流场问题的缺陷。因此,本文采用快速多极子方法加速传统常数面元法计算,求解大规模流场时域兴波问题。
3 多极子面元法传统面元法计算时,线性方程组(10)中系数矩阵
快速多极子法与传统面元法的结合过程和其与传统边界元法结合过程相同,详细内容可参考文献[7 – 9]。本节将简要介绍快速多极子方法的主要思想、基本公式和与面元法结合后的计算步骤。
3.1 多极子法主要思想
|
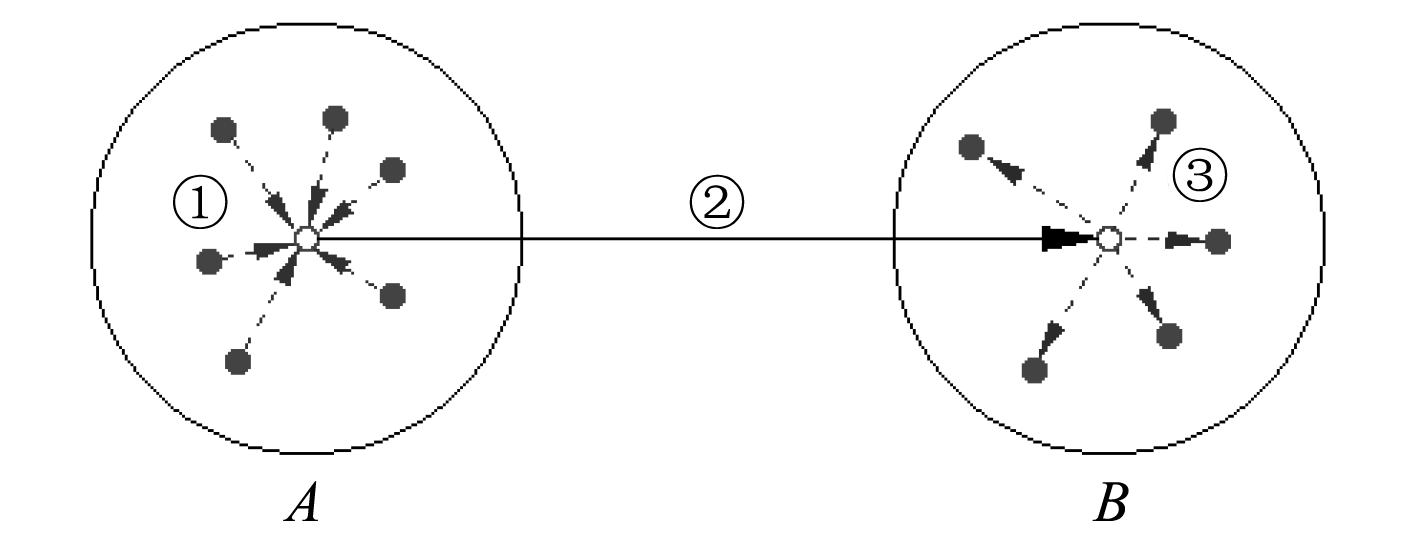
图 2 多极子计算示意图 Fig. 2 The schematic of multipole calculation |
|
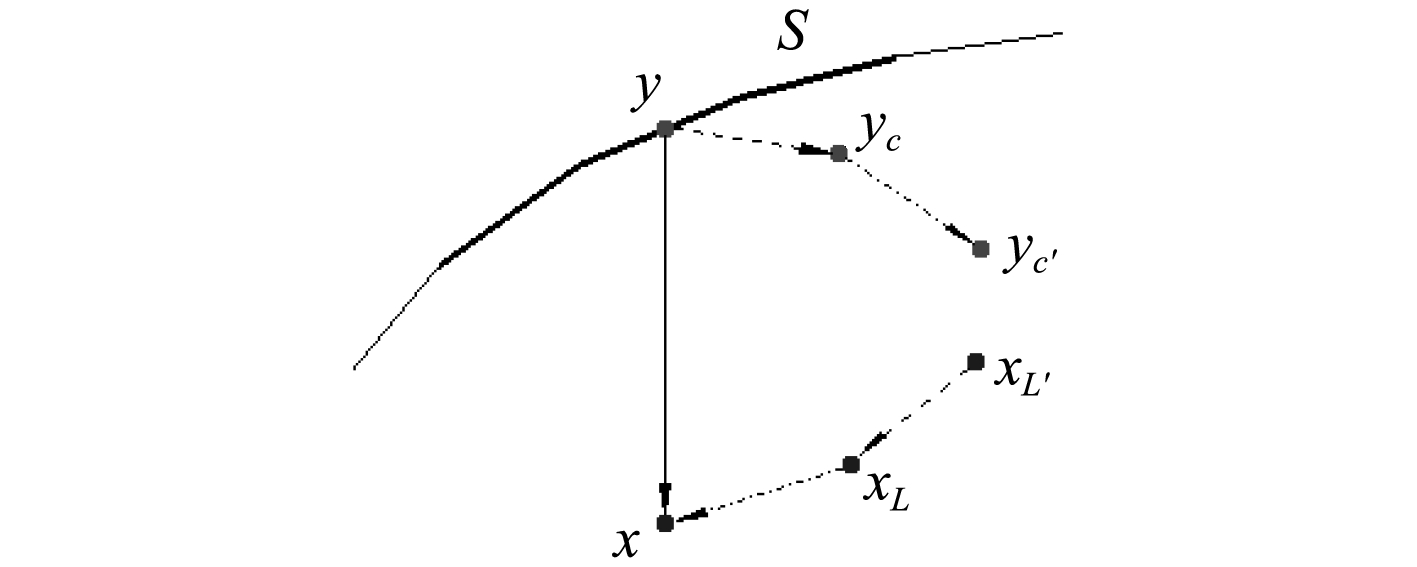
图 3 多极子展开关键点 Fig. 3 Related points in multipole expansion |
以粒子在粒子群中受力为例,两两直接计算再求和策略的计算量级是O(N2),其中N 表示粒子数量。快速多极子法将所有粒子按其空间位置分成不同的集合(如图2中的A和B),首先将粒子对外的作用力汇聚到集合内一点(如图2中的①过程),其次计算集合与集合之间的相互作用力(如图2中的②过程),最后将集合所受到的外界作用力分配到集合内每一个粒子(如图2中的③过程)。对于相距很近的粒子,相互间作用力直接计算得到;而对于相距较远的粒子,相互间的作用力则采用上述多极子方法展开得到,从而将计算量级减少至O(N∙LogN)[7–9]。其中区分粒子间距关系,可采用树状结构划分策略[17]加以实现。在传统面元法中,主要过程在于计算边界离散面元间的相互作用,因此可以采用快速多极子方法来提高计算效率。
3.2 多极子法基本公式关于多极子法公式具体推导请参见文献[7-9],这里以面元法中三维Rankine源诱导速度势核函数多极子展开为例,其展开形式如下:
| $\begin{split}G({{x}}, {{y}}) = & \frac{1}{{4\pi r}} = \frac{1}{{4\pi }}\sum\limits_{n = 0}^\infty \sum\limits_{m = - n}^n \overline {{S_{n, m}}} ({{x}} - {{{y}}_{c}}) \times \\& {R_{n, m}}({{y}} - {{{y}}_{c}} ) , \; \left| {{{x}} - {{{y}}_{c}}} \right| > \left| {{{y}} - {{{y}}_{c}}} \right|\text{,}\end{split}$ | (17) |
式中
| ${R_{n, m}}({{x}}) = \frac{1}{{(n + m)!}}P_n^m(\cos \theta ){e^{im\varphi }}{r^n}\text{,}$ | (18) |
| ${S_{n, m}}({{x}}) = (n - m)!P_n^m(\cos \theta ){e^{im\varphi }}\frac{1}{{{r^{n + 1}}}}\text{。}$ | (19) |
式中
| $P_n^m(x) = {(1 - {x^2})^{\textstyle\frac{m}{2}}}\frac{{{\rm d}m}}{{{\rm d}{x^m}}}{P_n}(x)\text{,}$ | (20) |
式中
| $\begin{split} {F_i}({{x}}, {{y}}) =& \frac{{\partial G({{x}},{{y}})}}{{\partial {x_i}}} = \frac{1}{{4\pi }}\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {\overline {{S_{n,m}}} ({{x}} - {{{y}}_c}) \times } }\\ & \frac{{\partial {R_{n,m}}({{y}} - {{{y}}_c})}}{{\partial {x_i}}},\left| {{{x}} - {{{y}}_c}} \right|\left. > {{{y}} - {{{y}}_c}} \right|\text{,}\end{split} $ | (21) |
式中
得到核函数的展开形式后,即可得到积分方程的展开形式如下:
| $\begin{split}\iint_{{S_i}} {G({{x}}, {{y}}){\sigma _i}{\rm d}S} =& \frac{1}{{4\pi }}\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {\overline {{S_{n,m}}} ({{x}}, {{y}}) \times } } \\& {M_{n,m}}({y_c}),\left| {{{x}} - {{{y}}_c}} \right|>\left| {{y}} - {{{y}_c}} \right| \text{,}\end{split} $ | (22) |
| $\begin{split} \iint_{{S_i}} {{F_i}({{x}}, {{y}}){\sigma _i}{\rm d}S} =& \frac{1}{{4\pi }}\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {\overline {{S_{n,m}}} ({{x}} - {{{y}}_c})} } \times \\&{{\tilde M}_{n,m}}({{{y}}_c}),\;\left| {{{x}} - {{{y}}_c}} \right|>\left| {{{y}} - {{{y}}_c}} \right| \text{。}\end{split} $ | (23) |
式中
| ${M_{n, m}}({{{y}}_{c}}) = \iint_{{S_i}} {{R_{n, m}}({{y}} - {{{y}}_{c}}){\sigma _i}{\rm d}S}\text{,}$ | (24) |
| ${\tilde M_{n, m}}({{{y}}_{c}}) = \iint_{{S_i}} {\frac{{\partial {R_{n, m}}({{y}} - {{{y}}_{c}})}}{{\partial {x_i}}}{\sigma _i}{\rm d}S}\text{。}$ | (25) |
同时还可以将多极子动量矩中心从
| $\begin{split} {M_{n,m}}({{{y}}_{c}}) \!=\! & \iint_{{S_i}} {{R_{n,m}}({{{y}}_{c}}){\sigma _i}{\rm d}S} \!=\!\! \\& \sum\limits_{n' = 0}^n {\sum\limits_{m' \!=\! - n'}^{n'} {{R_{n',m'}}({{{y}}_{c}} - {{{y}}_{c}}) \cdot {M_{n \!-\! n',m \!-\! m'}}({{{y}}_{c}}} } )\text{,}\end{split}$ | (26) |
上式对
对于核函数的局部展开系数则定义如下:
| $\!\!\!\!\!\!\!\!\iint_{{S_i}} {G({{x}}, {{y}}){\sigma _i}{\rm d}S} = \frac{1}{{4\pi }}\sum\limits_{n = 0}^\infty {\sum\limits_{m = - n}^n {{R_{n, m}}({{x}} - {{{x}}_{{L}}}) \cdot {L_{n, m}}({{{x}}_{{L}}}} } )\text{,}$ | (27) |
式中的局部展开系数
| $\begin{split}{L_{n,m}}({{{x}}_{L}}) = & {( - 1)^n}\sum\limits_{n' = 0}^n {\sum\limits_{m' = - n'}^{n'} {\overline {{S_{n + n',m + m'}}} ({{{x}}_{L}} - {{{y}}_c}) \times } } \\& {M_{n',m'}}({{{y}}_{c}}), \left| {{{{y}}_{c}} - {{{x}}_{L}}} \right| > \left| {{{x}} - {{{x}}_{L}}} \right| \text{。}\end{split} $ | (28) |
式中
| ${L_{n, m}}({{{x}}_{{{L'}}}}) = \sum\limits_{n' = n}^\infty {\sum\limits_{m' = - n'}^{n'} {{R_{n' - n, m' - m}}({{{x}}_{{{L'}}}} - {{{x}}_{{L}}}) \cdot {L_{n', m'}}({{{x}}_{{L}}}} } )\text{,}$ | (29) |
上式所示局部展开同样适用于诱导速度核函数
在此只简要介绍多极子面元法的计算步骤,具体请参见文献[18]。
|
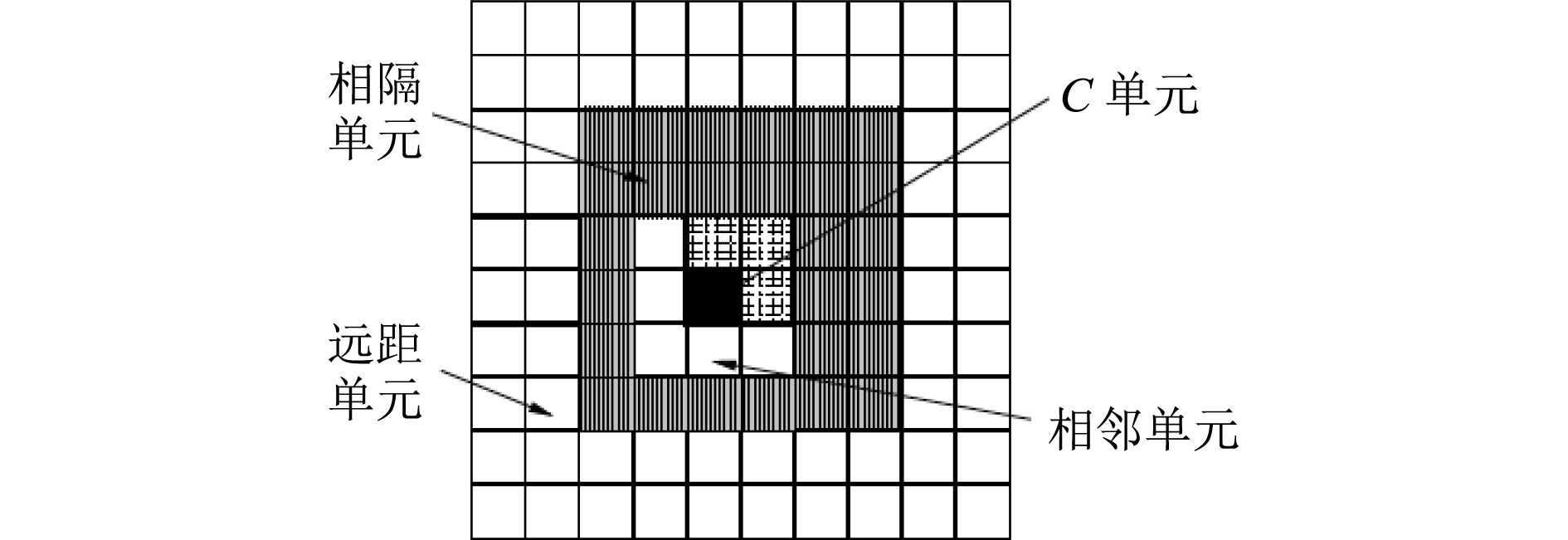
图 4 正方形单元相互关系 Fig. 4 Relations between square cells |
|
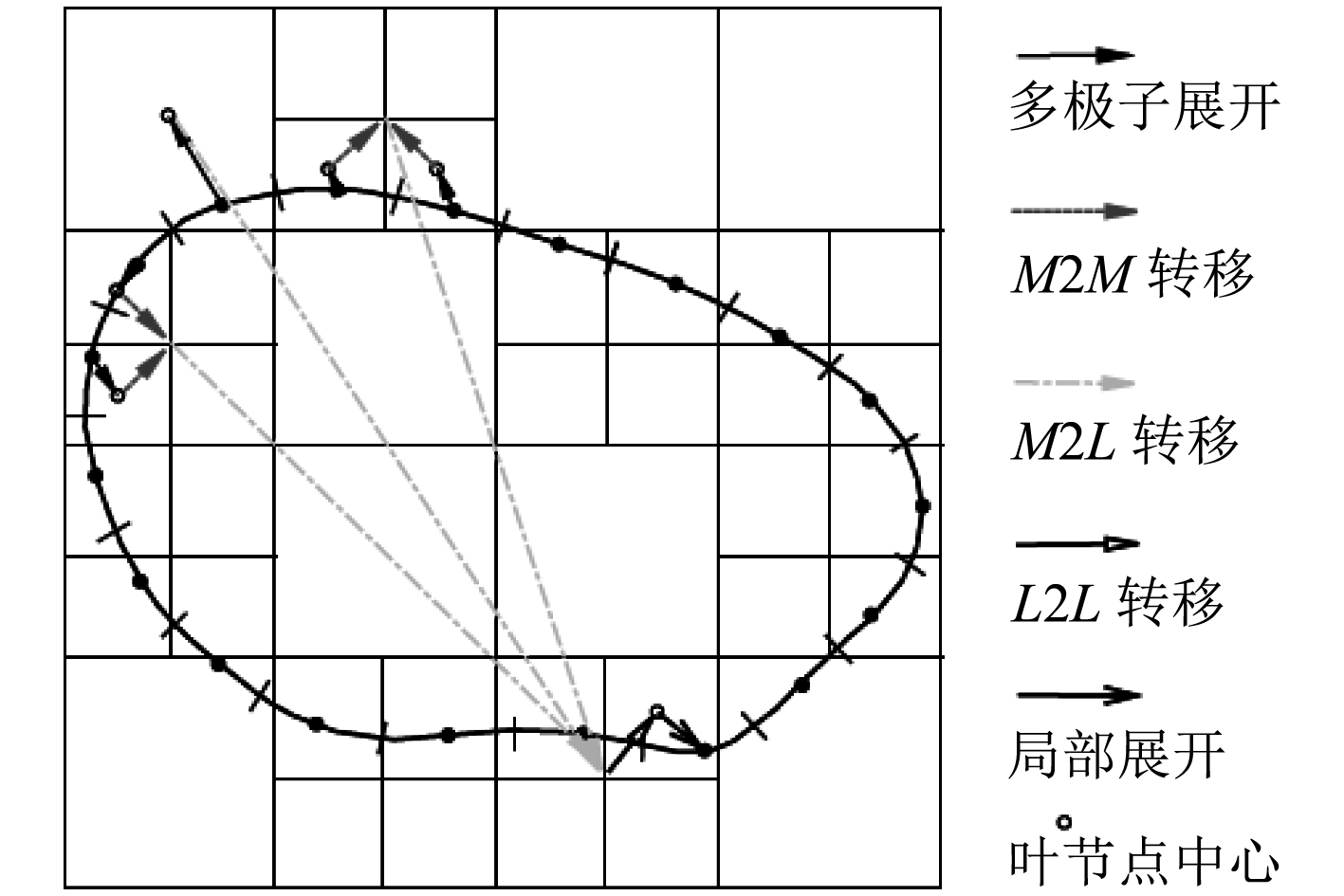
图 5 向上和向下传递过程 Fig. 5 Upward and downward passes |
步骤1与传统面元法一样对边界进行单元离散,布置面源,选取配置点。
步骤2划分树状结构。以二维问题为例,利用逐层嵌套的正方形来划分空间树状结构。首先利用一个足够大的正方形包围整个边界S,并定义其层级数为0级。考察第L层级的正方形单元C,将其均分为4个小正方形单元,层级为L+1,正方形单元C是它们的父单元。若某离散边界单元的中点位于小正方形内,则认为其属于该小正方形单元。对于4个小正方形单元,分成3种情况。若该小正方形单元内离散边界单元数为0,则将它舍弃,不计入树状结构内;若该小正方形单元内离散边界单元数大于0,且不大于事先给定的常数p时,将其定义为叶单元,不再往下划分;若该小正方形单元内离散边界单元数大于常数p时,则继续将其往下划分。如此嵌套割划,直到最后一层均为叶单元,或达到规定最大层数则停止。对于正方形单元之间的空间关系,定义如下(见图4):若2个正方形单元共用一个角点,则定义它们为相邻单元;若2个正方形单元不相邻,但其父单元相邻,则定义它们为相隔单元;若2个正方形单元的父单元也不相邻,则定义它们为远距单元。
步骤3向上传递。首先通过式(24)或式(25)计算各个叶单元的多极子动量矩,其次利用式(26)将叶单元的多极子动量矩转移到其父单元中。以此类推,多极子动量矩不断上聚,直至第2层。
步骤4向下传递。对于相隔单元,通过式(28)计算其作用;对于远距单元,则利用式(29)将父单元通过
步骤5近场远场作用叠加。对于某叶单元C中的配置点
步骤6利用GMRES求解式(10),若迭代误差小于设定值,则终止运算,否则返回第3步进行下一步迭代。本文中迭代误差设定值均取为10–4。
4 计算结果与分析 4.1 近水面回转椭球体匀速直航兴波问题本节将以近水面回转椭球体匀速直航产生的兴波波形和兴波升力、阻力为切入点,阐述如何选取合适的自由面计算域和自由面及物面网格密度,验证使用多极子面元法计算潜体兴波问题的可行性,并将多极子面元法与传统面元法进行计算效率对比。
计算模型为回转椭球体,长轴长l=1.0 m、短轴长d=0.2 m的回转椭球在自由水面下(球心距静水面距离为h=0.16 m)从静止状态突然启动,达到常速U=1.566 m/s并沿
|
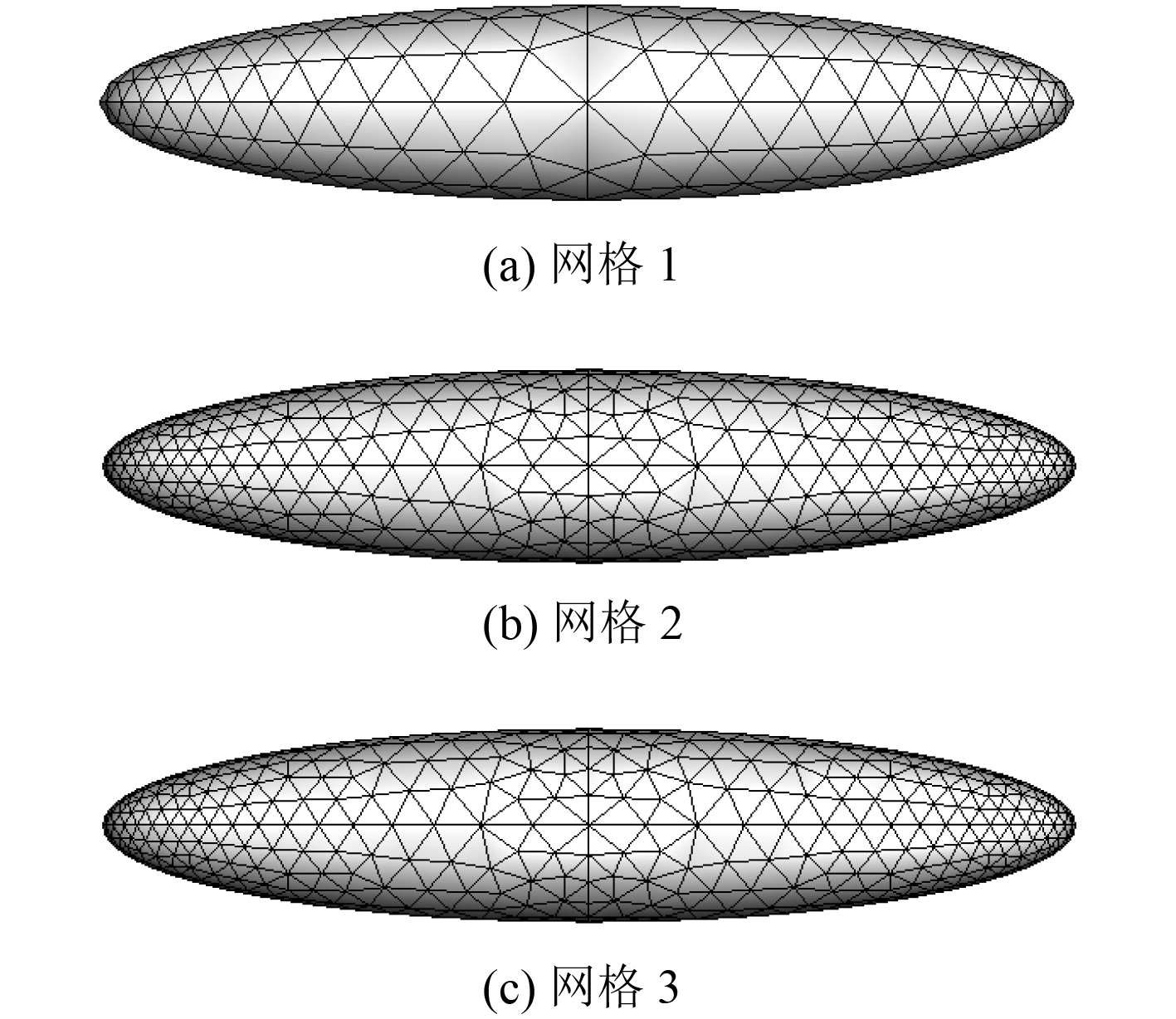
图 6 椭球网格划分 Fig. 6 The mesh generation of elipsoid |
自由面的网格密度和时间步长会直接影响到计算量、波面的光滑程度以及兴波水动力学参数的准确性,网格和时间步长的选取参照的是Dommermuth等人通过大量数值试验得到的经验公式[19]:
| ${(\Delta t)^2} \leqslant \frac{8}{\pi }\frac{{\Delta x}}{g} , \; \Delta x \leqslant \frac{8}{\pi }\frac{{U_x^2}}{g}\text{。}$ | (30) |
其中:
自由面为一足够大的长L=20 m,宽D=6 m的矩形平面,对称于坐标系原点。椭球球心初始坐标为x=–7.5,y=0,沿
椭球网格划分如图6(b)所示。自由面网格密度有3套,其中粗网格选取为100×30,网格间距为
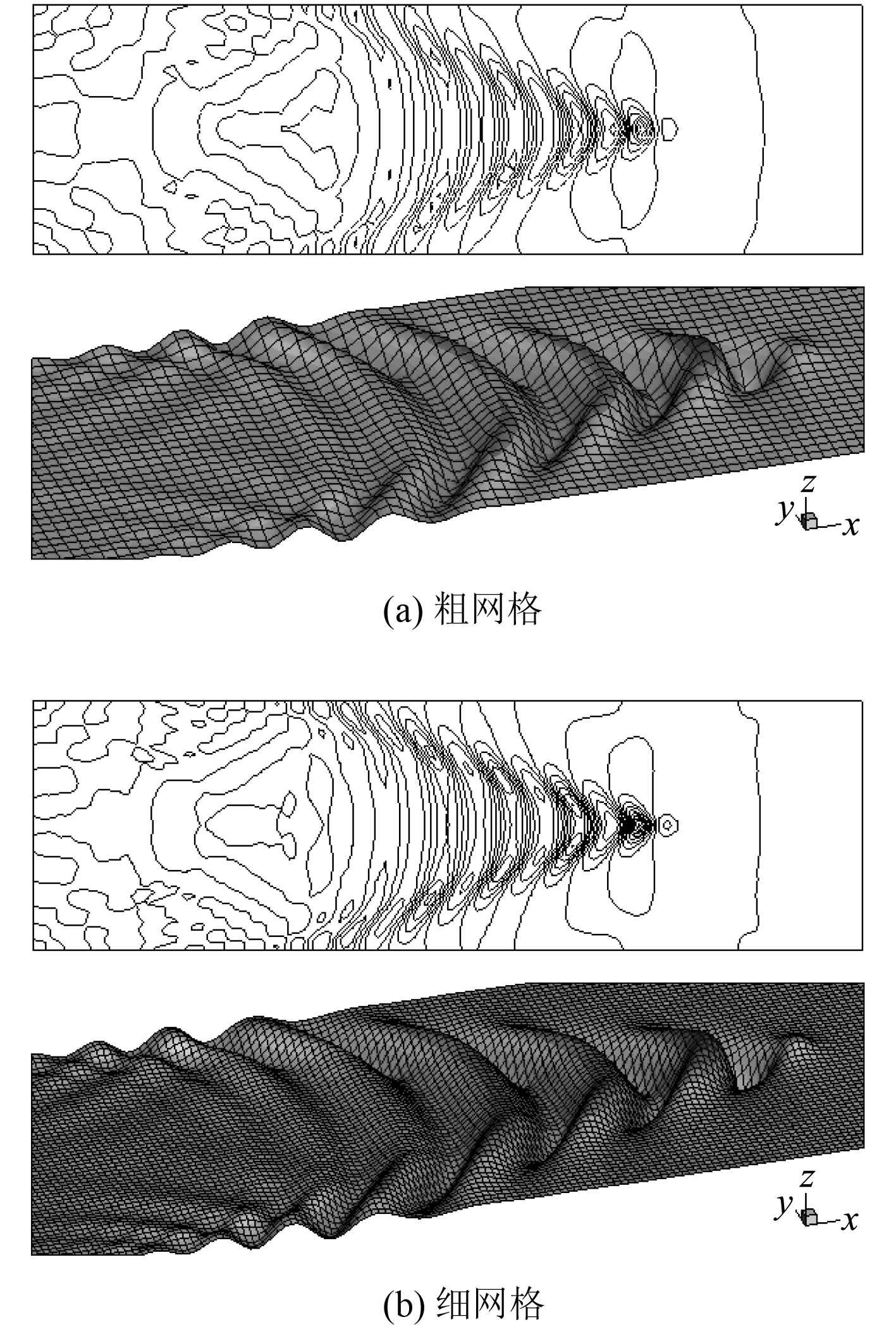
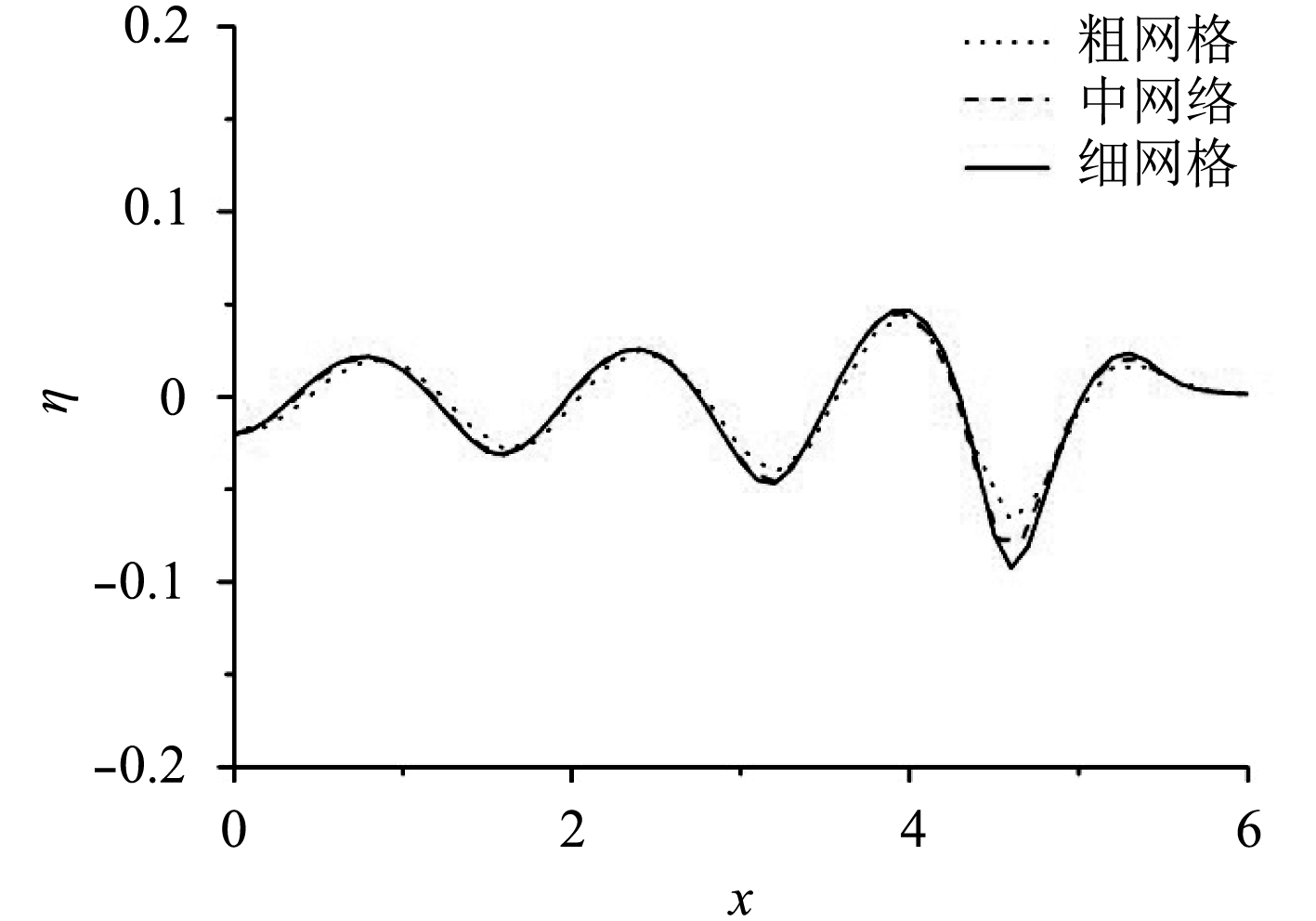
图7为t=8 s时波面图,经过对比可发现,粗网格与细网格所描绘出的波面波形图及等高线图基本一致,但粗网格仍有一些波面锯齿,而细网格的波面则光滑许多。对比图8亦可发现,3种网格描绘出的自由面中剖线二维波形图在第一个波谷处有比较明显的差别,除此之外中网格和细网格的结果完全贴合,而粗网格则与其他2种网格差别较大。
|
图 7 t=8 s时波面图 Fig. 7 The wave surface at t=8 s |
|
图 8 t=8 s时自由面二维波形图(y=0) Fig. 8 The 2D waveform of free surface at t=8 s (y=0) |
|
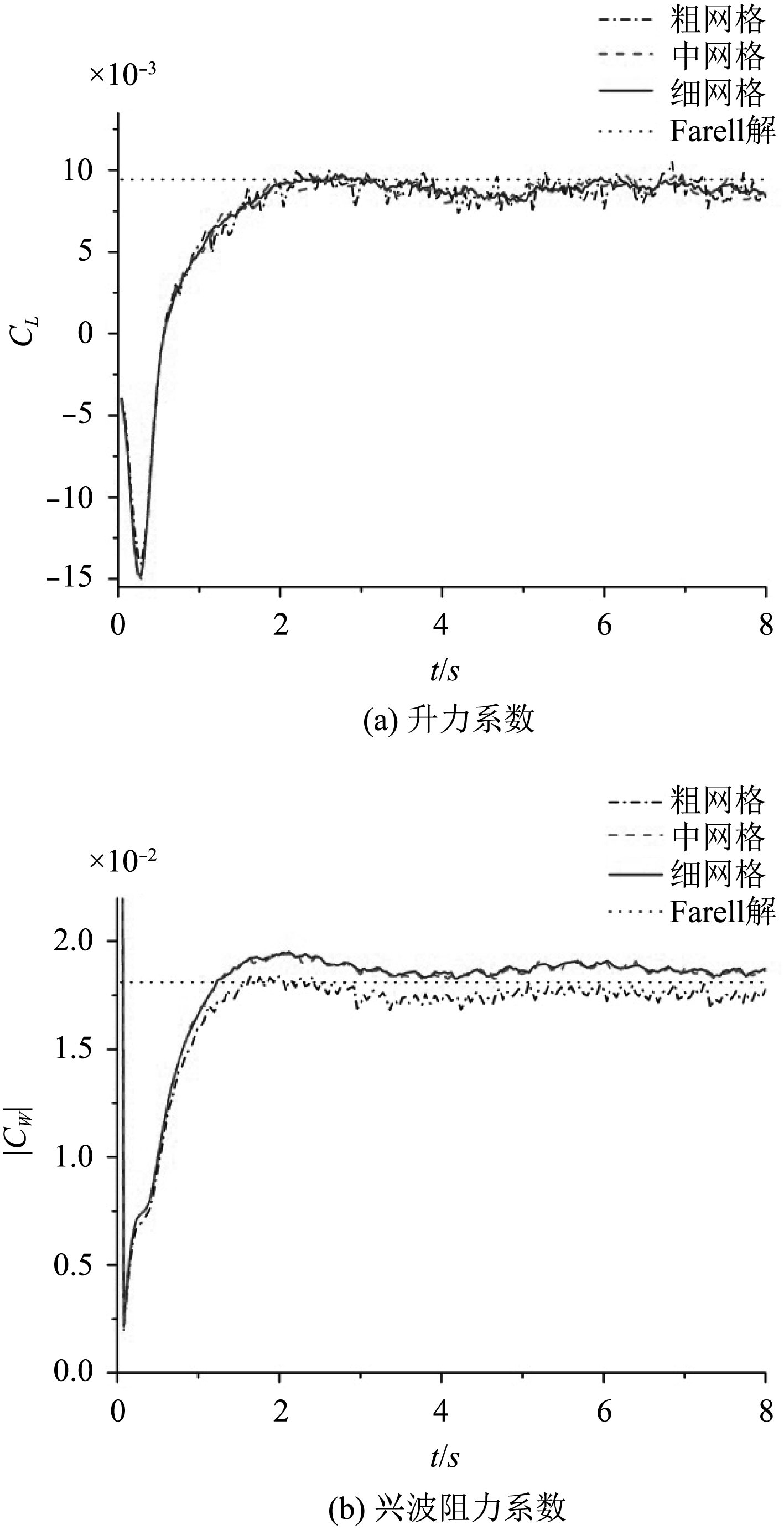
图 9 兴波水动力参数随时间变化情况 Fig. 9 The change of wave making hydrodynamic parameters over time |
其次考察兴波导致的椭球体升力、阻力。图9(a)为升力系数随时间变化情况,图9(b)为兴波阻力系数随时间变化情况。图中圆点直线为Farell解[1],3种网格所计算得到的力学系数都能收敛到Farell解附近。然而粗网格结果,特别是其升力系数的波动很大,毛刺明显;中网格和细网格的毛刺较粗网格有所减少,但仍然比较明显。此外,粗网格计算得到的升力系数收敛值和其他2种网格比较吻合,但兴波阻力收敛值有比较明显的差别,显示粗网格密度并不够,计算精度低;同时随着自由面网格不断加密,其计算结果也将逐渐收敛。
使用静网格固然能描述潜体的整个尾后兴波波面,但其取的自由面计算域过大,网格数量过多,时间效率低下;此外有大片自由面区域在长时间内兴波影响很小,是一种计算资源浪费。为了能提高计算效率,减少计算资源浪费,使用能随潜体一起前进的动网格来进行兴波时域计算。
4.1.2 自由面动网格与网格密度自由面为一个长L=8 m,宽D=5 m的矩形平面,初始时刻对称于坐标系原点。椭球球心初始坐标为x=–7.5,y=0,沿
椭球网格划分有3套(见图6)。自由面网格密度选取为80×50,网格间距
|
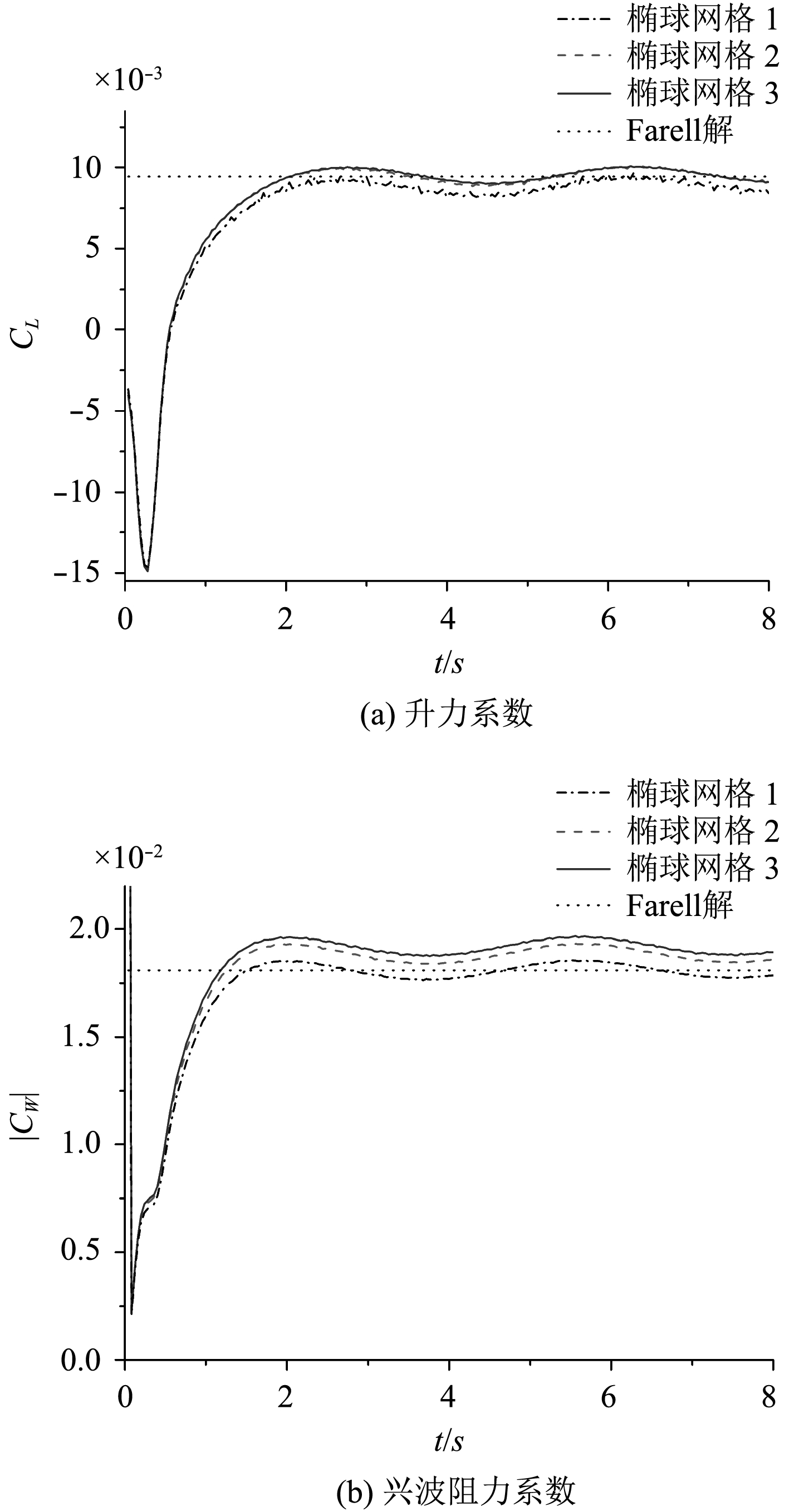
图 10 不同物面网格下兴波水动力参数随时间变化情况 Fig. 10 The change of wave making hydrodynamic parameters over time in different object surface mesh |
从图10中可以看到,虽然动网格的网格密度与静网格中细网格密度相同,但其计算结果中的毛刺现象却有大幅度改善,究其原因可能是静网格所取的自由面计算域过大,潜体相对网格的位置变化明显,在网格密度不够绝对密的情况下毛刺就会比较多,从图9中也可看出,当自由面静网格加密后,毛刺现象有所改善。此外,1304面元的椭球网格2和2640面元的椭球网格3所计算得到的升力曲线完全一致,兴波阻力曲线有略微差别,但只在1.8%左右;而528面元的椭球网格1则与其他2种网格计算结果差别较大,因此可认为随着椭球网格数量的增加,计算结果将逐渐收敛,同时1304面元的椭球网格2精度已经足够。
此外,考察自由面横向网格密度变化率q的影响,q=1代表横向网格均匀分布,q>1代表中纵线附近网格密,横向两端网格疏。表1显示了不同横向网格密度变化率下计算所得结果,其中2种网格布置的横向网格数相同,均为50个。由表中可看出横向网格变化率对计算结果的影响很小,几乎可以忽略不计。
|
|
表 1 不同横向网格密度变化率下兴波水动力学系数 Tab.1 The wave making hydrodynamic parameters in different changing rate of transverse mesh density |
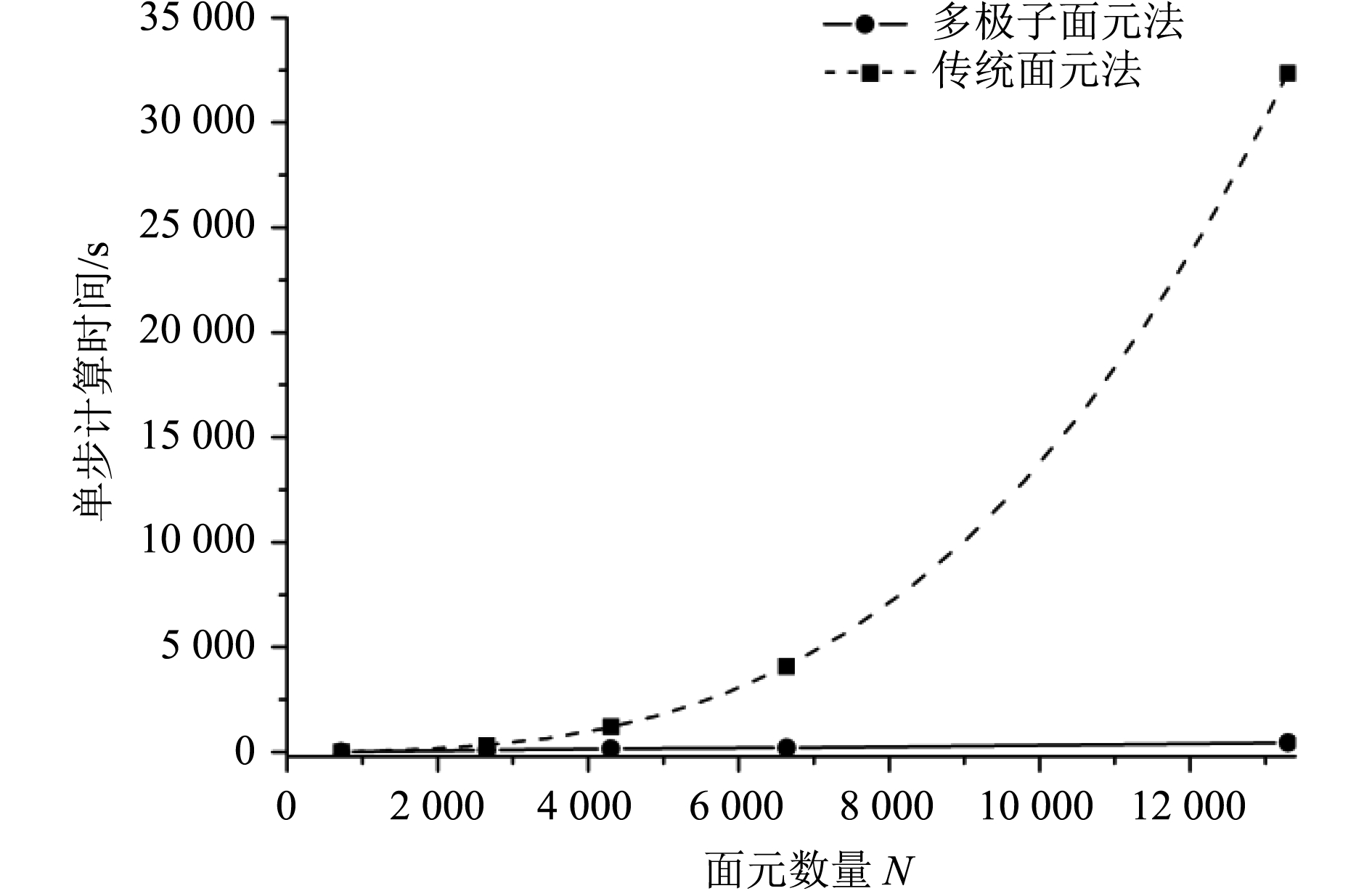
多极子法对传统面元法的改进,首先体现在内存使用量上,传统面元法需要占用O(N2)的内存,普通台式计算机无法驾驭面元数量过万的问题,但多极子面元法只需要占用O(N)的内存,使得普通台式计算机也可以计算面元数量达到数百万甚至数千万的大规模问题。表2和图11是分别采用多极子面元法和传统面元法进行时域单步计算的效率对比,计算环境为1.9 GB内存和2.50 GHz*2处理器。从图表中可以看出,当面元数较小时,使用多极子面元法和传统面元法所需要的计算量相近,甚至当面元数只有数百个时,传统面元法还要略优于多极子面元法;然而随着面元数的增长,多极子面元法所需的计算量近似线性增长,而传统面元法所需的计算量却是以三次方的速度增长,当面元数上万时,使用传统面元法求解不仅在内存上受到限制,在计算时间上也显得不现实。此外,由于时域问题较定常问题要多一个时间维度,因此利用多极子面元法来计算时域问题的可行性和高效性不言而喻,具有巨大的应用潜力。
|
|
表 2 多极子面元法和传统面元法单步计算效率比较 Tab.2 Comparison of single-step computational efficiency between FMBEM&BEM |
|
图 11 多极子面元法和传统面元法单步计算效率比较 Fig. 11 Comparison of single-step computational efficiency between FMBEM&BEM |
|
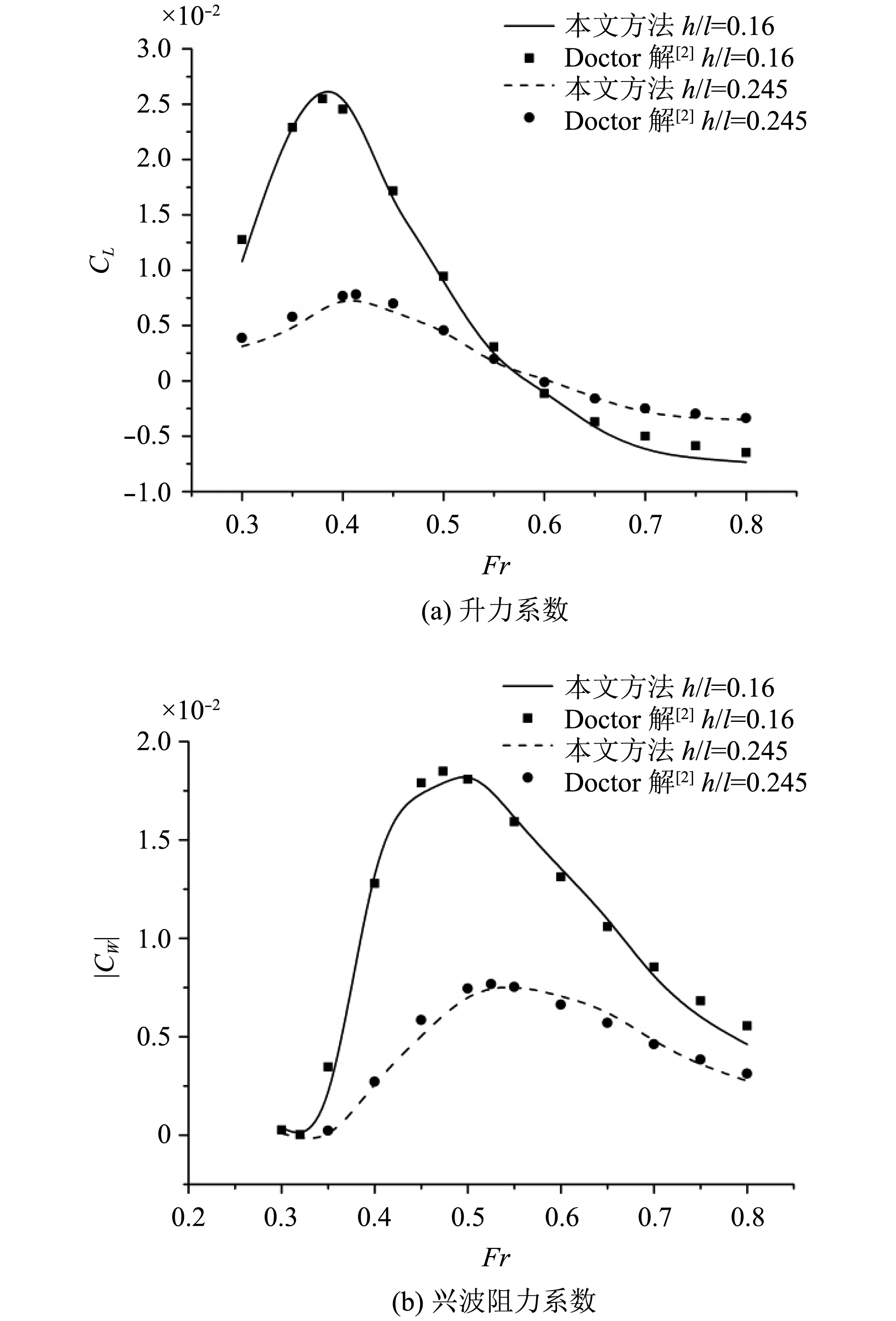
图 12 兴波水动力参数 Fig. 12 The wave making hydrodynamic parameters |
本小节将以近水面椭球匀速直航达到稳定状态后所产生的升力和兴波阻力为切入点,说明不同航速和下潜深度对其定常兴波的影响。计算模型与上节一样为回转椭球体,长轴长l=1.0 m、短轴长d=0.2 m,改变航速
自由面采取动网格,为一个长为
兴波水动力系数如图12所示,其中图12(a)是升力系数随Froude数变化情况,图12(b)是兴波阻力系数随Froude数变化情况。与Doctor解[2]相比,本文方法所得结果在
从计算结果来看,本文所开发的快速多极子面元法可以较准确地预报近水面潜体时域兴波特性,定常兴波计算结果与已有研究结果吻合良好,证明了其合理性与可靠性;且相较于传统面元法,有效地克服了计算规模和效率的局限性,引进了运动网格提高计算精度和效率。本文方法将进一步改进和发展,以计算完全非线性兴波问题、船体兴波问题等,具有较大的应用前景。
| [1] | FARELL C. On the wave resistance of a submerged spheroid[R]. 1972. |
| [2] | DOCTORS L J, BECK R F. Convergence properties of the Neumann-Kelvin problem for a submerged body[J]. Journal of Ship Research, 1987, 31(4). |
| [3] | HESS J L, SMITH A M. Calculation of non-lifting potential flow about arbitrary three-dimensional bodies[R]. DOUGLAS AIRCRAFT CO LONG BEACH CA, 1962. |
| [4] |
高志亮, 田晟, 邹早建. 浅水中下潜物体有航速辐射问题的数值解[J]. 船舶力学, 2012, 16(8): 868–876.
GAO Zhi-liang, TIAN Sheng, ZOU Zao-jian. Numerical solution of the radiation problem with forward speed for a submerged body in shallow water[J]. Journal of Ship Mechanics, 2012, 16(8): 868–876. http://industry.wanfangdata.com.cn/dl/Magazine?magazineId=cblx&yearissue=2012_8 |
| [5] | ZHANG B. Shape optimization of bow bulbs with minimum wave-making resistance based on Rankine source method[J]. Journal of Shanghai Jiaotong University (Science), 2012, 17: 65–69. |
| [6] | ROKHLIN V. Rapid solution of integral equations of classical potential theory[J]. Journal of Computational Physics, 1985, 60(2): 187–207. |
| [7] | LIU Y J, NISHIMURA N. The fast multipole boundary element method for potential problems: a tutorial[J]. Engineering Analysis with Boundary Elements, 2006, 30(5): 371–381. |
| [8] | NISHIMURA N. Fast multipole accelerated boundary integral equation methods[J]. Applied Mechanics Reviews, 2002, 55(4): 299–324. |
| [9] | YOSHIDA K. Applications of fast multipole method to boundary integral equation method[J]. Kyoto: Kyoto University, 2001. |
| [10] | LIN Z, LIAO S. Calculation of added mass coefficients of 3D complicated underwater bodies by FMBEM[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(1): 187–194. |
| [11] | CUI Y, QU J, YANG A, et al. Fast Multipole Boundary Element Method of Potential Problems[J]. Journal of Networks, 2014, 9(01): 108–114. |
| [12] |
李谊乐, 刘应中, 缪国平. Bankine 源高阶边界元法求解势流问题[J]. 水动力学研究与进展(A辑), 1999, 1.
LI Yi-le, LIU Ying-zhong, LIAO Guo-ping. Potential Flow Solution Using Higher—Order Boundary Element Method with Rankine Source [J]. Journal of Hydrodynamics (Ser. A), 1999, 1. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sdlxyjyjz199901010 |
| [13] |
李广年, 陈庆任, 谢永和, 等. 基于时域面元法的非对称双体船兴波阻力计算[J]. 水动力学研究与进展A辑, 2013, 3: 015.
LI Guang-nian, CHEN Qing-ren, XIE Yong-he. Computational research on wave-making resistance of asymmetric catamaran based on the panel method in time domain [J]. Journal of Hydrodynamics (Ser. A), 2013, 3: 015. http://www.cnki.com.cn/Article/CJFDTOTAL-CANB2013S1006.htm |
| [14] | 王献孚, 韩久瑞. 机翼理论[M]. 1987. |
| [15] | LIU Y H, KIM C H, LU X S. Comparison of higher-order boundary element and constant panel methods for hydrodynamic loadings[C]//The First ISOPE European Offshore Mechanics Symposium. International Society of Offshore and Polar Engineers, 1990. |
| [16] | ROMATE J E. The numerical simulation of nonlinear gravity waves in three dimensions using a higher order panel method[J]. 1989. |
| [17] | ZWILLINGER D. CRC standard mathematical tables and formulae[M]. CRC press, 2011. |
| [18] |
林志良. 比例边界有限元法及快速多极子边界元法的研究与应用[D]. 上海: 上海交通大学, 2010.
LIN Zhi-liang. Research and Application of Scaled Boundary FEM and Fast Multipole BEM [D]. Shanghai: Shanghai Jiao Tong University, 2010. |
| [19] | DOMMERMUTH D G, YUE D K P. Numerical simulations of nonlinear axisymmetric flows with a free surface[J]. Journal of Fluid Mechanics, 1987, 178: 195–219. |
| [20] |
冯大奎. 绕船舶自由面流动的时域分析和数值计算[D]. 武汉: 华中科技大学, 2008.
FENG Da-kui. Time Domain Analysis and Numerieal Simulation on the Free Surfaee Flow around the ship [D]. Wuhan: Hua zhong University of Science and Technology, 2008. |
 2018, Vol. 40
2018, Vol. 40
