2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 武汉理工大学 高性能舰船技术教育重点实验室,湖北 武汉 430063
2. China Ship Development and Design Center, Wuhan 430063, China;
3. Departments of Naval Architecture, Ocean and Structural Engineering, School of Transportation, Wuhan University of Technology, Wuhan 430063, China
处于中垂工况下的船舶,甲板和与甲板相邻舷侧结构的屈曲失效是船体梁整体失效的一种重要模式[1 – 3]。然而,由于甲板结构的极限破坏是一个渐进的过程,同时涉及到几何非线性和材料非线性问题,又存在板和筋的多种组合失效模式,其屈曲失效过程十分复杂。试验研究方法以其直观性的特点在船舶结构极限强度研究领域具有举足轻重的地位,对深入认识结构的整个失效过程有着重要的意义[4]。
由于海洋工程工作性质的需求,很多海洋工程船舶在甲板上布置有较大的开口,这些开口的存在,破坏了结构的连续性,降低了甲板结构在中垂工况下的极限承载能力。船舶甲板结构为船舶总纵强度的重要承力结构,对于船舶总纵强度有着重要的影响。为保证船舶航行的安全性,有必要对甲板结构进行改进,以提高甲板结构在中垂工况下的极限承载能力。为研究具有大开口甲板板架的稳定性问题,本文设计了具有大开口的甲板板架模型,开展了轴向受压极限强度模型试验,观测得到了船体甲板板架结构在轴向压力作用下崩溃的整个过程,并进行数值仿真分析。该试验对通用有限元软件计算船体甲板结构稳定性的方法进行验证,在此基础上,本文对原有的甲板结构进行改进设计,并利用经过试验验证的有限元方法,对改进方案进行了计算分析,可为船舶甲板结构稳定性设计提供一定的参考依据。
1 甲板板架结构轴压稳定性试验及数值仿真分析 1.1 甲板结构模型本文选取某布置有大开口的船舶强力甲板为研究对象,设计了缩比模型。由于无法精确评估舷侧结构、纵横舱壁结构以及相邻甲板结构对该强力甲板稳定性的影响,故设计模型时,将舷侧、纵横舱壁以及相邻甲板板架也考虑在设计范畴内。图1为该结构CAD图,模型长度为3.37 m,宽度为2.58 m,高度为0.465 m,中部大开口处为实验模型核心段,两端为延伸段,以消除边界条件的影响。各构件具体尺寸如表1所示。模型采用Q345B钢建造。

|
图 1 强力甲板结构CAD图 Fig. 1 The CAD diagram of the powerful deck structure |
|
|
表 1 强力甲板结构主要构件尺寸 Tab.1 The main component dimensions of the powerful deck structure |
将钢制模型置于由2个门架组成的自平衡加载系统中,模型采用一端固支、一端简支的边界条件[5]。固支端使用工装固定在横梁上,简支端使用液压千斤顶系统施加轴向载荷。
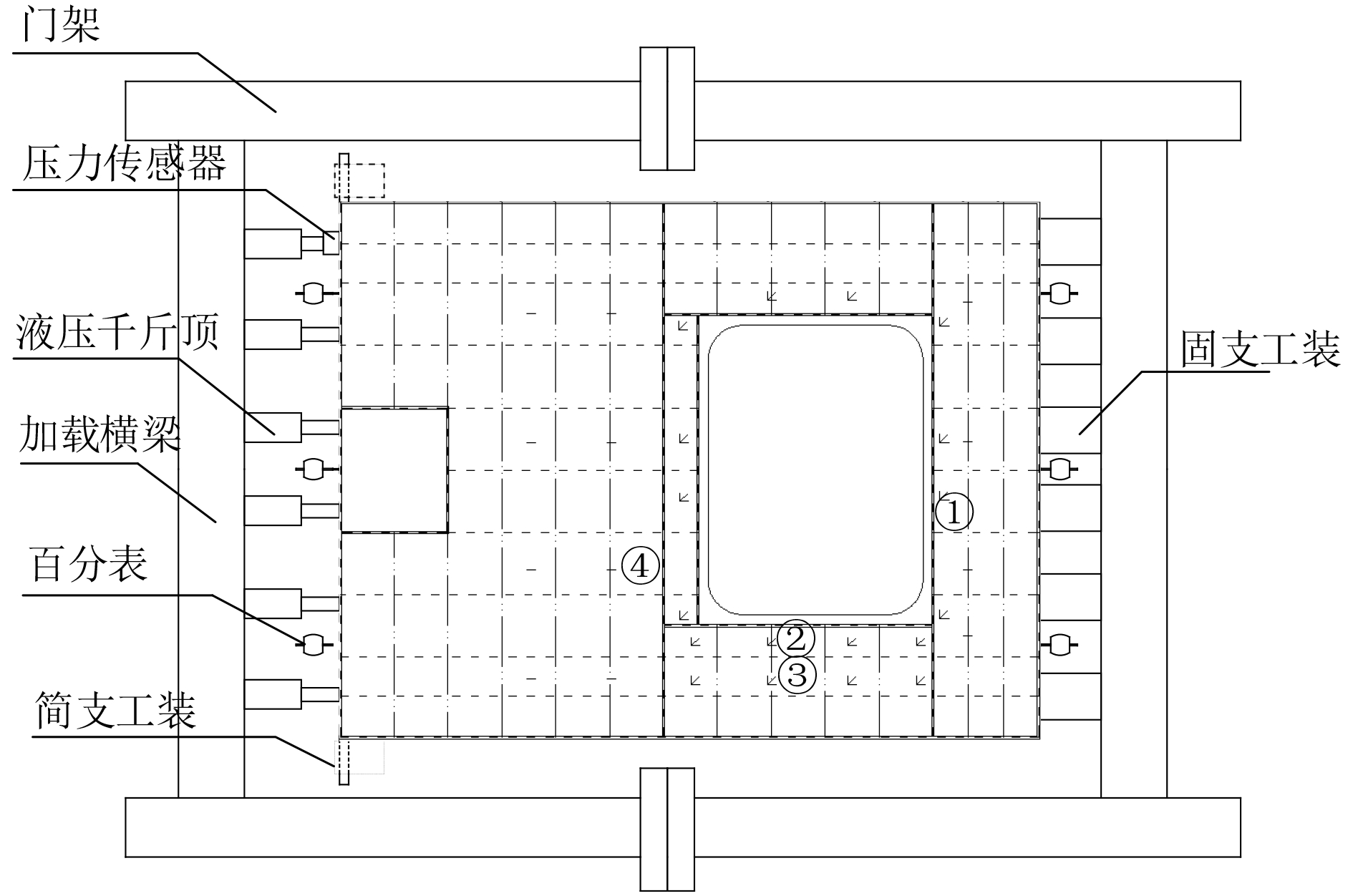
模型所受轴向载荷使用压力传感器测量,压力传感器布置于液压千斤顶和模型加载端之间。模型两端分别对称布置3个百分表,以测量结构的轴向变形。模型上布置有66个应变测点,大开口周围为主要关注区域,均布置三相应变片,其余区域主要布置单向应变片。试验加载及数据采集系统如图2所示。
为模拟简支边界条件,在图2中结构左端甲板与舷侧板交界处布置横向销轴,销轴可在固定于地基上的方钢内沿模型长度方向自由滑动,但是无法沿模型高度方向运动。从而限制了模型左端高度方向的位移,放开了长度方向的位移和宽度方向的转角,满足简支边界条件的需求,工装如图3(a)所示。为模拟固支边界条件,使用十字支柱将图1 中结构的右端固定在横梁上,如图3(b)所示。
|
图 2 试验加载示意图 Fig. 2 Schematic diagram of the test load |

|
图 3 模型边界条件 Fig. 3 The boundary condition of the model |
为了减小焊接残余应力的影响,在破坏性试验开展之前进行3次线弹性范围内的载荷加载[6],同时调试应变测点及数据采集系统。加载过程采用逐步加载方式,设置每级载荷为60 kN。第1次预加载最终载荷为360 kN,然后逐级卸载至0;第2次和第3次预加载最终载荷均为600 kN,然后逐级卸载至0。预加载之后进行破坏性试验,开始先以60 kN为一个载荷增量步,当载荷达到900 kN的时候,将载荷增量步调整为30 kN,直至结构屈曲失效,无法继续承载。
在逐级加载的过程中,每达到一个载荷点,待压力传感器读数稳定后,同时采集压力传感器读数,百分表读数和各应变测点读数。在压力传感器的读数突然下降的时候,采集最后一组数据。
1.4 试验结果破坏试验前为3次预加载试验,通过监测预加载试验过程中位移载荷曲线,发现结构线性阶段的回复性较好。3次试验载荷全部卸载完后,结构的位移都能回到原点。且随着加载次数的增加,结构位移载荷关系具有良好的线性关系。
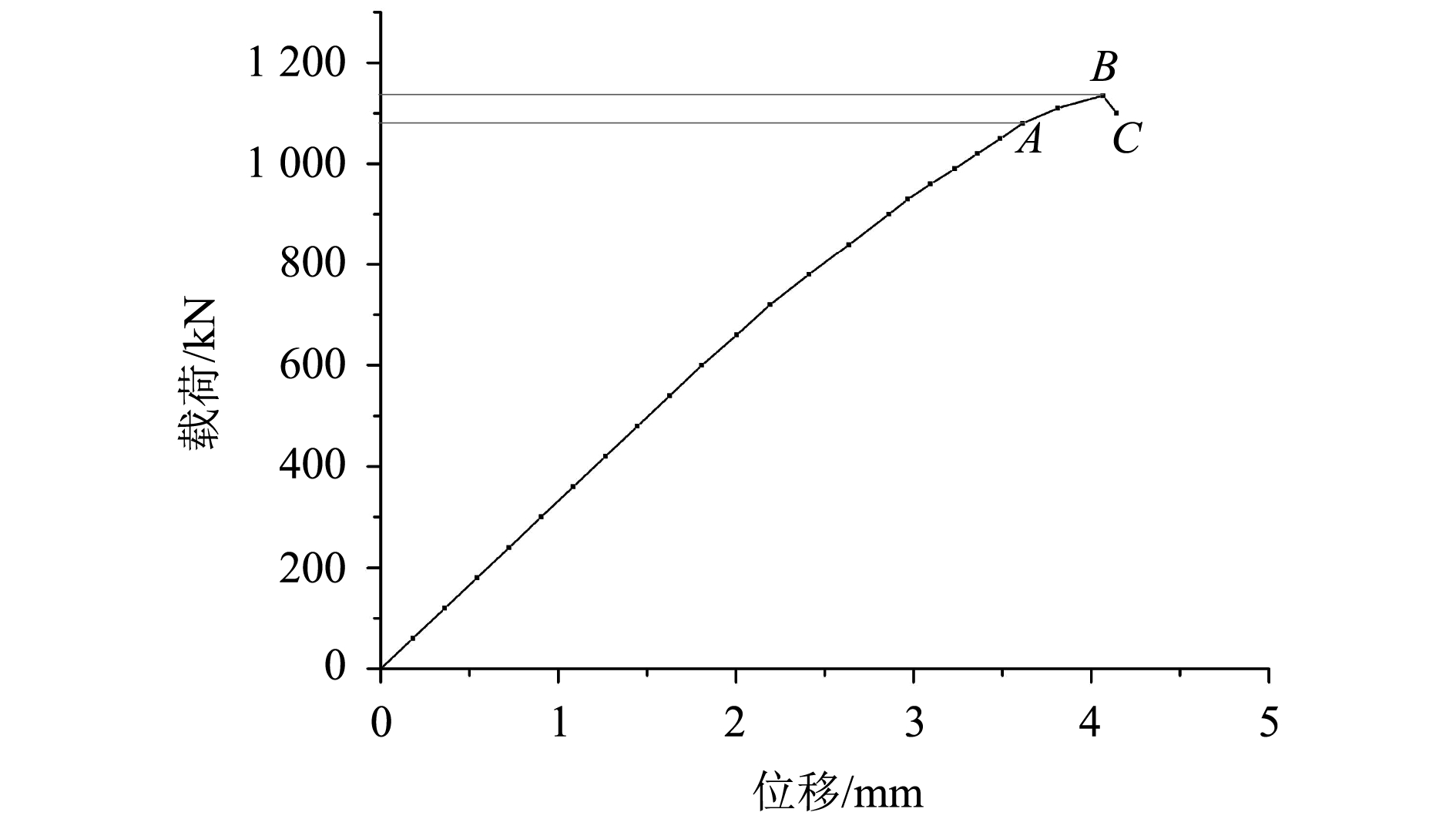
破坏试验中,当载荷增加至1 134.6 kN时,随着液压油顶位移的增加,压力传感器的读数突然急剧下降,结构发生崩溃,无法继续承载。图4所示为破坏试验中结构的位移载荷曲线,其中位移值取模型两端百分表读数的3个差值的平均值。从图4可以看出,当载荷小于1 080 kN时,结构位移载荷曲线基本呈线性增长关系,说明此区间内,结构基本处于线弹性变形范围,未到达材料的屈服或者结构的屈曲。当载荷超过1 080 kN时,随着载荷的进一步增大,结构位移的增长速度加快,结构大开口甲板处开始隆起,此时结构已经开始进入屈曲阶段。但是由应变片记录的数据看来,此时材料仍未屈服。随着载荷的持续增长,模型轴向变形明显增加,甲板大开口处以及对应舷侧板和纵舱壁,局部隆起逐渐变为明显褶皱现象。当载荷达到1 134.6 kN时,曲线到达B点,随着位移的增大,载荷逐步减小,至C点,此即结构已经完全失去承载能力,褶皱处材料也随之进入塑性阶段。
|
图 4 破坏试验结构载荷位移曲线 Fig. 4 The load-displacement curve of structure in destructive testing |
实际工程设计中,无法用试验方法对所有设计结构的稳定性进行研究校核。所以设计工作中,非线性有限元以其成本低、周期短的特点得到广大设计工作者的青睐。为进一步研究非线性有限元方法在计算甲板稳定性方面的适用性,对该甲板板架结构的极限强度进行计算分析。该甲板板架结构有限元模型使用hypermesh软件建模,网格大小为30 mm,整个模型划分网格29 057个,节点30 157个。在钢制模型建造过程中,使用超声波测厚仪测量每块钢板的实际厚度,测量精度为0.01 mm。且对模型材料开展力学性能试验,测量其实际的各项参数。计算采用的有限元模型以及材料模型均采用上述精确测量的几何及材料参数。
1.6 有限元模型边界条件按照试验模型边界条件,加载端为简支边界条件,固定端为固支边界条件。在Abaqus软件中,取模型长度方向为x,宽度方向为y,高度方向为z,约束模型的固定端所有自由度,约束加载端z方向的位移和x和z方向的转角。边界条件设置如表2所示。
|
|
表 2 模型两端边界约束条件 Tab.2 Boundary constraints on both ends of model |
结构的初始缺陷对其极限承载能力的影响不可忽视。于是在计算过程中将结构的1阶特征值屈曲模态引入有限元模型中以模拟该结构的初始变形。比例系数按照经验公式选取[7]:
| $\frac{{{w_{opl}}}}{t} = 0.1{\beta ^2}{\text{,}}$ | (1) |
其中,
将有限元软件的计算结果与试验结果从破坏模式、极限载荷和失效路径3个方面进行对比分析。
1)破坏模式对比
通过对试验过程的观测发现,结构大开口处甲板的局部屈曲导致了结构的整体失效。大开口甲板板屈曲,伴随纵骨侧向失稳,纵舱壁和舷侧板均屈曲失效。仿真计算结果亦为大开口处甲板的局部屈曲以及纵舱壁和舷侧板的屈曲失效,如图5所示。

|
图 5 试验与仿真结果破坏模式对比 Fig. 5 Comparison of test and simulation results failure patterns |
2)极限载荷与失效路径对比
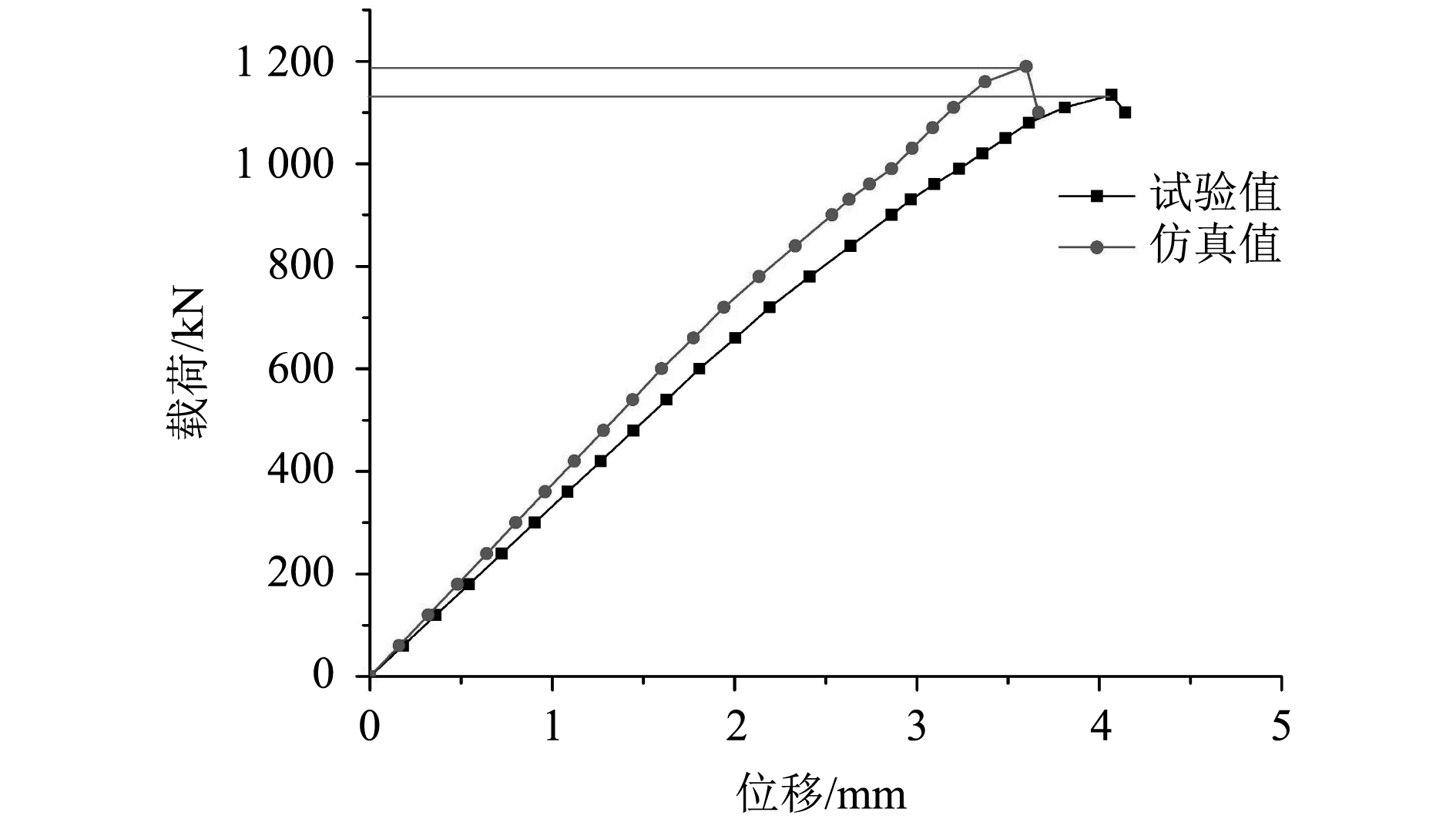
对比有限元软件计算得到的结构位移载荷曲线和试验所得位移载荷曲线,如图6所示。
由图6可见,试验结果和数值仿真结果中,载荷随位移的变化趋势基本一致。但是二者斜率略有不同。相同载荷下,轴向位移的试验值较仿真值大。究其原因,可认为是本文的数值计算未能在模型中施加焊接残余应力,且初始变形以1阶特征值模态代替,比例系数使用经验公式计算,无法精确输入板材和筋条的初始变形。上述2点原因都会导致计算模型比实际模型偏安全,所以计算结果中曲线的斜率会略大于试验得到曲线的斜率。
对比数值计算的极限载荷和试验的极限载荷,如表3所示。试验所得结构极限载荷为1 134.6 kN,数值计算结果所得结构极限载荷为1 189.54 kN,数值计算结果较试验结果,误差为4.84%。
|
|
表 3 极限载荷对比 Tab.3 Comparison of ultimate loads |
|
图 6 试验与仿真失效路径对比 Fig. 6 Comparison of test and simulation failure paths |
由以上的对比分析可见,非线性有限元的计算结果较为可靠,在结构屈曲破坏模式,失效路径以及极限承载能力的模拟上,都有较高的精度。如果能将结构的焊接残余应力以及包含骨材在内的初始变形导入至有限元模型中,计算精度或许可以得到进一步地提高。
2 甲板板架结构稳定性改进方法 2.1 结构失效诱因分析通过试验过程中的观测,发现随着载荷的增大,甲板与纵舱壁连接处的边缘甲板(图5右上小图)处最先开始出现隆起;随着载荷的进一步增大,褶皱开始沿甲板宽度方向向舷侧蔓延,同时沿纵舱壁高度方向向下蔓延;结构继续承载,待甲板完全屈曲后,随着舷侧板的屈曲发生,结构最终失去承载能力。从模型底部观测可发现,甲板板发生严重褶皱处,伴随有纵骨的侧倾失稳,如图7所示。
由此可见,甲板板的厚度不足及纵骨的尺寸较小为该结构屈曲失效的主要诱因。由结构图可见,失效处并未因为布置有大开口而增加纵骨尺寸。

|
图 7 屈曲失效处底部视图 Fig. 7 The bottom view of the buckling failure |
本文对设计板架的原型板架进行纵向轴压载荷下的稳定进行仿真。应力集中现象首先在纵舱壁上方甲板边板处出现并有向舷侧扩展的趋势,随着轴压载荷增加,舷顶列板与甲板边板产生了应力集中现象,达到了材料的屈服极限,纵舱壁上方的甲板产生大的塑性变形,甲板纵骨出现严重侧倾,继续增大载荷,甲板大开口处产生严重皱褶,结构失稳。
通过对结构失效模式和失效过程的分析,发现原型板架失效原因与设计模型板架的失效原因一致,在大开口区域的甲板板厚较小、纵骨尺寸较小,导致在此板架结构中,甲板大开口区域附近的结构强度最弱。当受到轴向载荷作用时,在此处首先发生结构的屈服及屈曲现象。
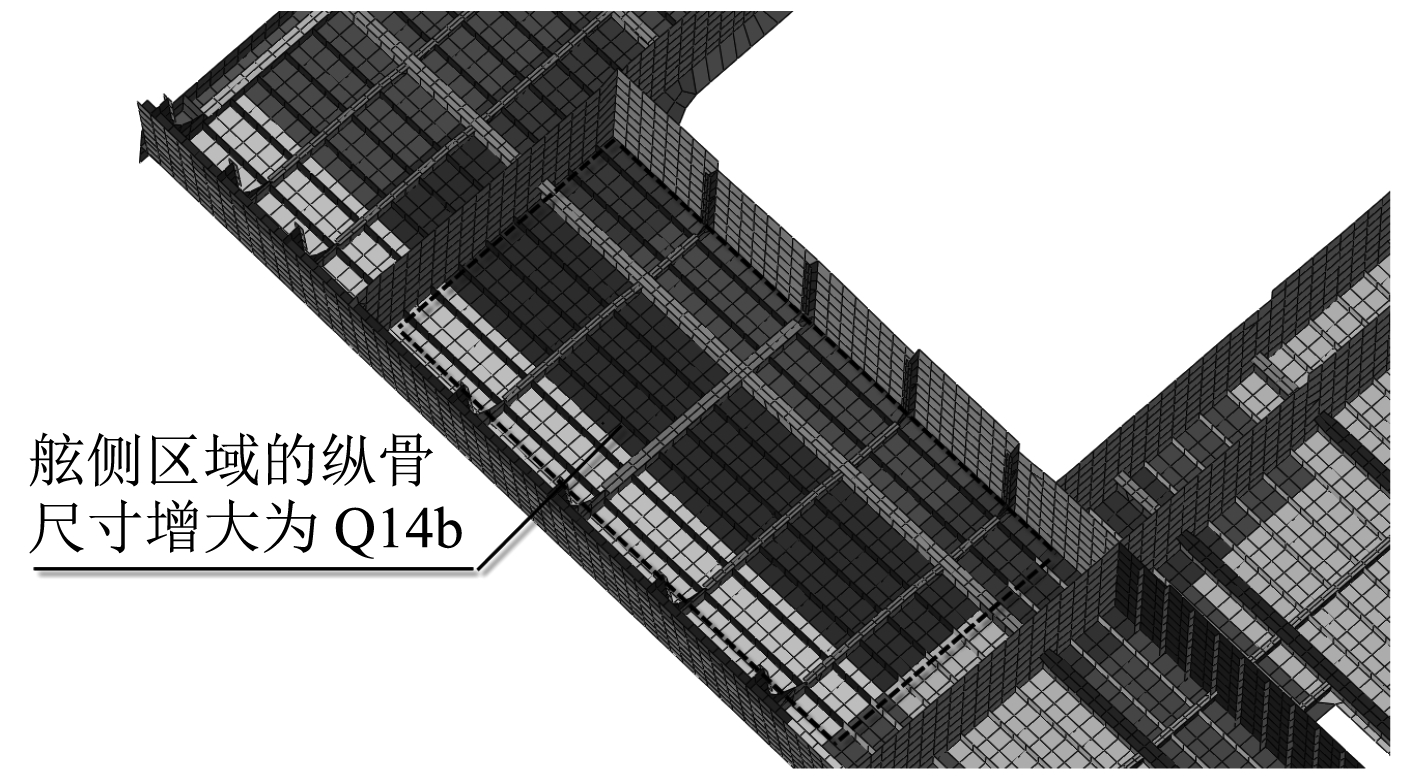
2.2 稳定性改进设计方法根据上文分析确定影响具有甲板大开口的板架结构轴压稳定性的关键因素,针对薄弱结构,本文提出如表4所示的5种改进方案(方案1~方案4见图8~图11)。
|
|
表 4 5种改进方案 Tab.4 5 kinds of improvements |
|
图 8 方案1 Fig. 8 Case 1 |

|
图 9 方案2 Fig. 9 Case 2 |

|
图 10 方案3 Fig. 10 Case 3 |
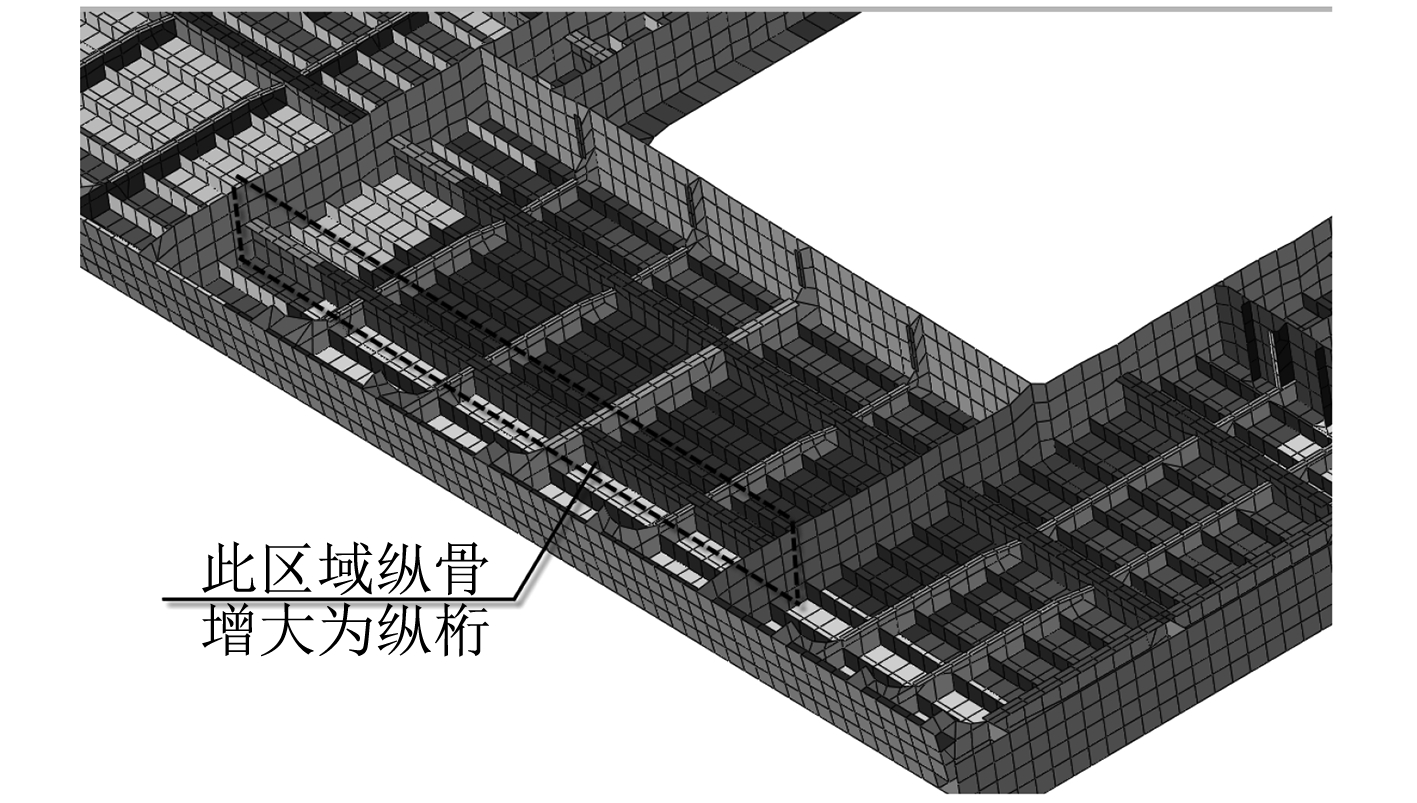
|
图 11 方案4 Fig. 11 Case 4 |
本文1.7节通过对比双层板架结构试验与仿真的结果,验证了本文所采用的非线性有限元方法的准确性。在此基础上,应用非线性有限元方法,对原始板架及5种改进方案进行非线性有限元分析计算,得到各方案双层板架在轴向压力载荷下的极限承载能力,如表5所示。
|
|
表 5 各种方案对比分析 Tab.5 Comparison of various cases |
原始板架和5种改进方案在轴压载荷下的载荷-位移曲线如图12所示。
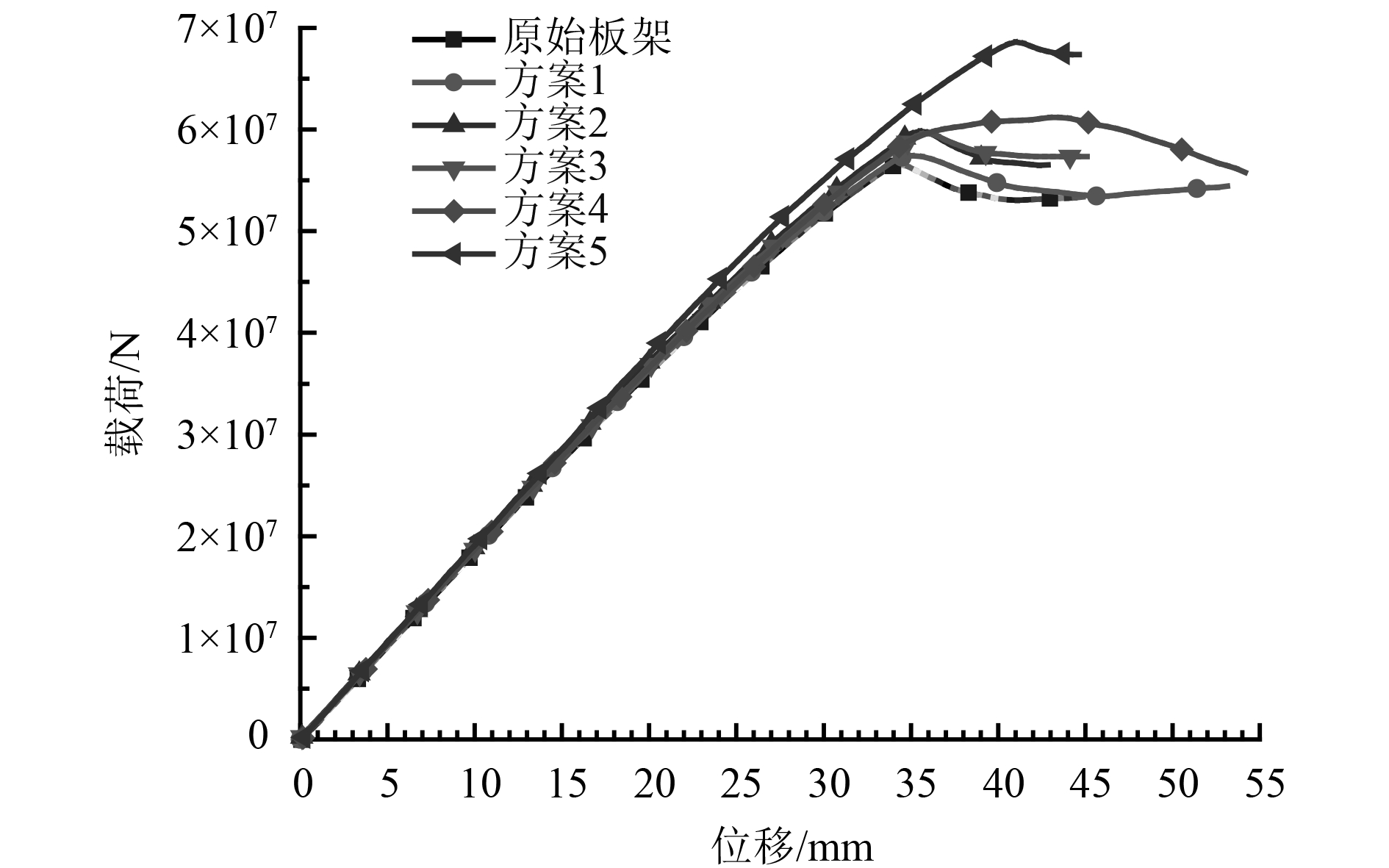
|
图 12 原始板架和改进方案的载荷-位移曲线 Fig. 12 Load - displacement curve of original plate and improved scheme |
与原始板架相比,方案1重量增加0.01 t,极限承载能力提高1.08%;方案2重量增加0.53 t,极限承载能力提高5.67%;方案3重量增加2.53 t,极限承载能力提高5.41%;方案4重量增加0.57 t,极限承载能力提高7.79%。从极限承载能力分析,方案2、方案3改进效果相当,但是方案3增加了更多的重量;从增加的重量上分析,方案2、方案4增加的重量相当,但方案4对极限承载力的提高更为明显。因此单独改进一种构件的方案里,方案4的改进效果最好。方案5综合了方案2、方案3、方案4,其对极限承载力的提高高于3种方案之和,说明改进的构件之间存在耦合效应,能够相互影响。
3 结 语本文通过试验观测到了含有大开口的甲板板架结构轴向受压过程中从线弹性小变形到弹性屈曲直至完全崩溃失效的全过程。并且使用试验结果对非线性有限元计算方法进行验证。对原始板架结构提出5种改进方案,并使用非线性有限元计算方法进行计算分析。可得到以下几点结论。
1)大开口处的甲板局部屈曲以及纵骨的侧向失稳为整个结构失效的主要诱因。设计过程中,若甲板上布置有大开口,应将大开口外侧甲板及纵骨适当加强。
2)同时改进增强不同的纵向承力构件对极限承载力的提高效果优于分别单独改进某种纵向构件的效果之和,说明不同构件之间相互影响,存在耦合效应。
3)非线性有限元方法能够较为准确地模拟含有大开口的甲板板架结构的稳定性。
| [1] | ENDO H, TANAKA Y, AOKI G, et al. Longitudinal Strength of The Fore Body of Ships Suffering from Slamming[J]. Journal of the Society of Naval Architects of Japan, 1988, 1988(163): 322–333. |
| [2] | YAO T, FUJIKUBO M, YANAGIHARA D, et al. Buckling Collapse Strength of Chip Carrier under Longitudinal Bending (1st Report): Collapse test on 1/10-scale hull girder model under pure bendung[J]. Journal of the Society of Naval Architects of Japan, 2002, 2002(191): 255–264. |
| [3] | DOW R S. Testing and Analysis of a 1/3-Scale Welded Steel Frigate Model[J]. Structural Analysis, 1991. |
| [4] | 王佳颖, 张世联. 纵向箱型梁舱段极限强度试验研究[J]. 中国造船, 2011, 52(2): 47–54. https://www.wenkuxiazai.com/doc/2645877ca417866fb84a8e77.html |
| [5] | KWON Y B, PARK H S. Compression tests of longitudinally stiffened plates undergoing distortional buckling[J]. Journal of Constructional Steel Research, 2011, 67(8): 1212–1224. |
| [6] | 吴梵, 朱晓军, 黄晓明, 等. 平台支撑的潜艇内部平面舱壁极限强度的模型试验研究[J]. 船舶力学, 2007(05): 773–779. |
| [7] | PAIK J K, THAYAMBALLI A K, LEE J M. Effect of Initial Deflection Shape on the Ultimate Strength Behavior of Welded Steel Plates Under Biaxial Compressive Loads[J]. Journal of Ship Research, 2004, 48(1): 45–60. |
 2018, Vol. 40
2018, Vol. 40
