2. 中国船舶科学研究中心,江苏 无锡 214082
2. China Ship Scientific Research Center, Wuxi 214082, China
极地具有重要的战略价值,尤其是近年来,随着全球气候变暖、海冰加速融化,极地蕴藏的丰富资源和极具价值的北极航道已进一步将极地的潜在价值推到现实的高度。
北极问题实质上是资源和航线问题,近年来,北半球的许多国家纷纷明确表示北极地区是该国战略利益中至关重要的区域,并表示将采取一切必要手段来维护本国在这一地区的利益。对于中国来说,奉行防御型国策的前提下,无论从极地运输战略角度考虑,还是从增强我国国际地位和发言权角度来考虑,设计并建造我国自己的极地水面舰船势在必行。与此同时,为了保证极地水面舰船的安全,需要制定和实施相应的极地水面舰船冰级规范。
为了确保民用极地船舶安全性,北极周边国家纷纷制定和实施了相应的冰级规范,根据不同冰级给出了冰载荷的大小、作用范围和作用形式。冰级规范里面最重要的是芬兰-瑞典冰级规范和国际船级社协会极地冰级规范(IACS PC),世界上主要船级社(ABS,BV,DNV,LR,GL)也制定了各自冰级规范,中国船级社基于国际船级社协会极地冰级规范,在《钢质海船入级规范》中针对冰区船体加强给出了相应规定。
本文基于国际船级社协会极地冰级规范研究设计冰载荷计算的理论基础,分析目前规范存在的不足,研究民用极地船舶规范对于极地水面舰船的适用性,分析开展极地水面舰船冰级规范研究的必要性,并指出其对应的发展方向。
1 国际船级社协会极地冰级规范国际船级社协会发布了《IACS unified requirements for polar ships》,即极地冰级规范,对全球的海冰情况进行了比较全面的描述,将船舶分为PC1-PC7七个冰级,并给出了详细的计算冰载荷的公式[1]。
1.1 船体分区划分极地船舶的船体区域,以反映预期作用在这些区域上的载荷大小。在纵向上分为4个区域:首部区、首部过渡区、船中区和尾部区。首部过渡区、船中区和尾部区在垂向上进一步分为底部区、下部区和冰带区。
1.2 设计冰载设计冰载由均匀分布在一长方形载荷作用板(高b和宽w)上的平均压力Pavg表征。
所有极地船舶的首部区,以及极地船级PC6和PC7船舶的首部过渡区中的冰带区范围内,冰载荷参数为实际首部形状的函数。为确定冰载荷参数(Pavg,b和w),应要求对首部区分区之中下列冰载荷特征参数:形状参数fai,总的碰擦力Fi,线载荷Qi以及压力Pi进行计算。
式(1)–式(8)计算所得的设计冰作用力适用于首柱处纵剖面角
定义碰擦载荷特征的参数反映在船级因子之中,且列于表1。
|
|
表 1 船级因子 Tab.1 Class factors |
在首部区,与浮冰碰擦载荷情况有关的力F,线载荷Q,压力P以及载荷板的长宽比AR是冰区高位水线处量得的船体角的函数。船体角的影响通过对首部形状系数fa的计算得到,船体角的定义如图1所示。

|
图 1 船体角的定义 Fig. 1 Definition of hull angles |
首部区的水线长度通常分成4个等长度的分区。应对每个分区长度当中位置处的力F、线载荷Q、压力P以及载荷板的长宽比AR进行计算(在计算冰载荷参数Pavg,b和w时,应取F,Q和P的最大值)。
1)首部区载荷特征参数确定如下:
形状系数
| $f{a_i} = \min \left( {f{a_{i,1}},f{a_{i,2}},f{a_{i,3}}} \right)\text{,}$ | (1) |
式中:
| $\begin{aligned}&f{a_{i,1}} = \frac{{\left[ {0.097 - 0.68{{\left( {\frac{x}{L} - 0.15} \right)}^2}} \right]{\alpha _i}}}{{{{(\beta _i')}^{0.5}}}}\text{,}\\&f{a_{i,2}} = \left[ {\frac{{1.2C{F_F}}}{{{\rm{sin}}(\beta _{}') \cdot C{F_C} \cdot {D^{0.64}}}}} \right]\text{,}\\&f{a_{i,3}} = 0.60\text{。}\end{aligned}$ |
力
| ${F_i} = f{a_i} \cdot C{F_C} \cdot {D^{0.64}}{\text{,}}\;\;\;\;\;\;\;\;{\rm{MN}}\text{;}$ | (2) |
载荷板的长宽比
| $A{R_i} = 7.46{\rm{sin}}(\beta _{}') \geqslant 1.3\text{;}$ | (3) |
线载荷
| ${Q_i} = {F_i}^{0.61} \cdot \frac{{C{F_D}}}{{AR_i^{0.35}}}\text{,}\;\;\;\;\;\;\;\;\;{\rm{MN}}/{\rm{m}}\text{;}$ | (4) |
压力
| ${P_i} = F_i^{0.22} \cdot CF_D^2 \cdot AR_i^{0.3}{\text{,}}\;\;\;\;\;\;{\rm{MPa}}\text{。}$ | (5) |
2)船舶首部区,以及对于具有船级附加标志为PC6和PC7船舶的首部过渡区的冰带区,设计载荷板的宽度wBow以及高度bBow的尺寸如下:
| ${w_{Bow}} = {F_{Bow}}/{Q_{Bow}}\text{,}$ | (6) |
| ${b_{Bow}} = {Q_{Bow}}/{P_{Bow}}\text{。}$ | (7) |
式中:FBow为首部区的最大力Fi,MN;QBow为首部区的最大线载荷Qi,MN/m;PBow为首部区的最大压力Pi,MPa。
3)设计载荷板范围内的平均压力Pavg按下式确定:
| ${P_{avg}} = F/\left( {b \cdot w} \right)\text{。}$ | (8) |
4)船体区因子
与各个船体区有关的区域因子反映了该区预期承受载荷的相对大小。各个船体区因子AF见表2,如果某一结构件越过船体区的边界,则应使用最大的船体区因子确定构件的尺寸。
|
|
表 2 船体区因子 Tab.2 Hull area factors (AF) |
针对国际船级社协会极地冰级规范,研究设计冰载荷计算、船级因子及船体区因子的理论基础。
2.1 挤压力分析本文式(2)是基于快速碰撞的船冰作用工况得到的,其理论基础为基于能量平衡原理的冰载荷理论模型[2]。
能量平衡方法认为运动体的有效动能耗散于浮冰的挤压破碎和势能。
| $K{E_e} = IE + PE\text{,}$ | (9) |
其中:KEe为有效动能;IE为浮冰挤压能;PE为势能。
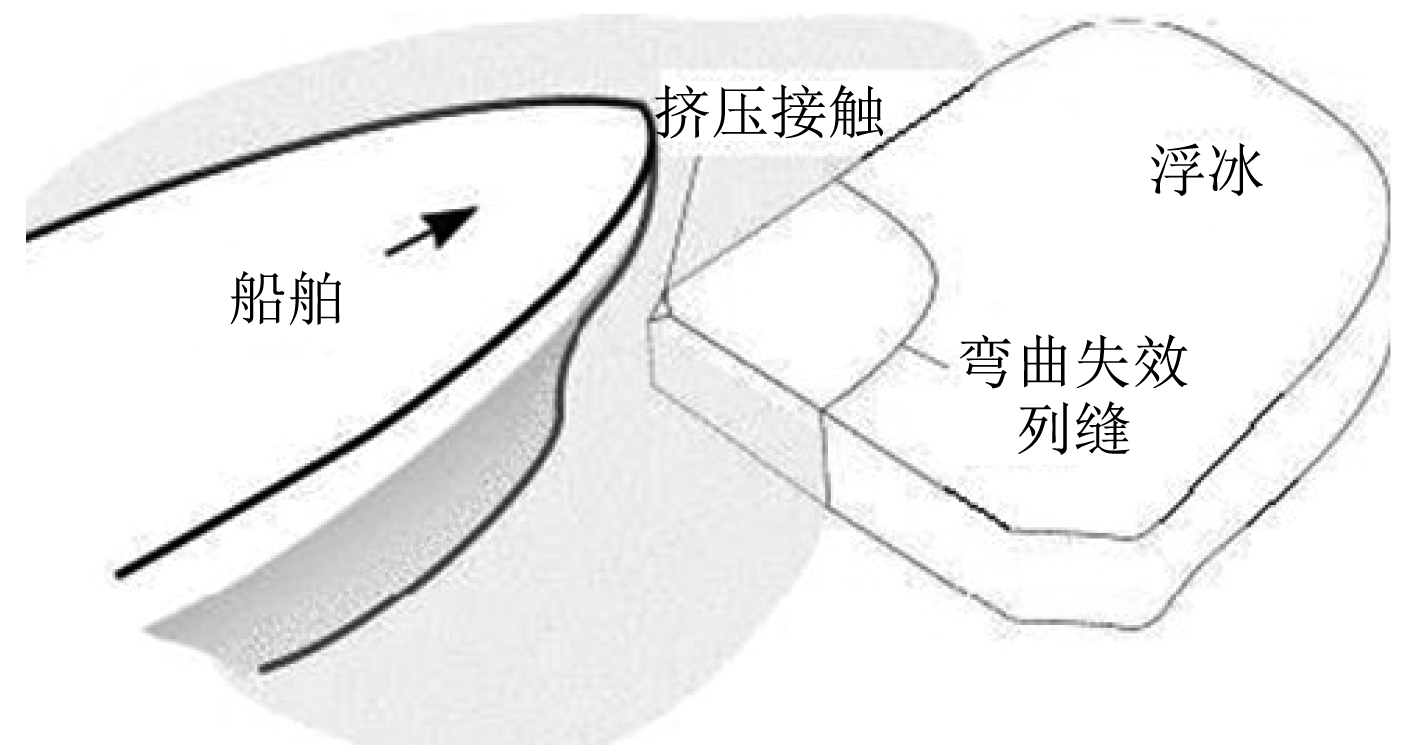
|
图 2 快速碰撞作用示意 Fig. 2 Design scenario for the general glancing impact collision |
浮冰挤压能IE等于法向挤压力Fn对法向挤压位移δ所做的功,KEe与碰撞位置的有效质量Me和法向速度Vn有关。势能是耗散在可恢复过程中的能量,此处不考虑势能,则有:
| $\frac{1}{2}{M_e}V_n^2 = \mathop \int \nolimits_0^{{\delta _m}} {F_n}{\rm d}\delta\text{。} $ | (10) |
其中:δ为浮冰法向挤压位移;Fn为法向挤压力;Me为有效质量(Me=Mship/C0);C0为质量折减系数;Vn为法向速度(Vn=Vshipl );l为方向余弦值。
针对快速碰撞的情况,给出简化的碰撞接触示意图,如图3所示。浮冰受挤压后与船首接触区域形状近似为等腰三角形,定义该接触区域的面积为A,该接触区域的宽度W和高度H可以通过浮冰法向挤压位移δ、法向剖面角β′和冰缘角φ等计算获得:
| $W = \frac{{2\delta \tan\frac{\varphi }{2}}}{{{\rm{cos}}\left( {{\rm{\beta '}}} \right)}}\text{,}$ | (11) |
| $H = \frac{\delta }{{{\rm{sin}}\left( {{\rm{\beta '}}} \right){\rm{cos}}\left( {{\rm{\beta '}}} \right)}}\text{,}$ | (12) |
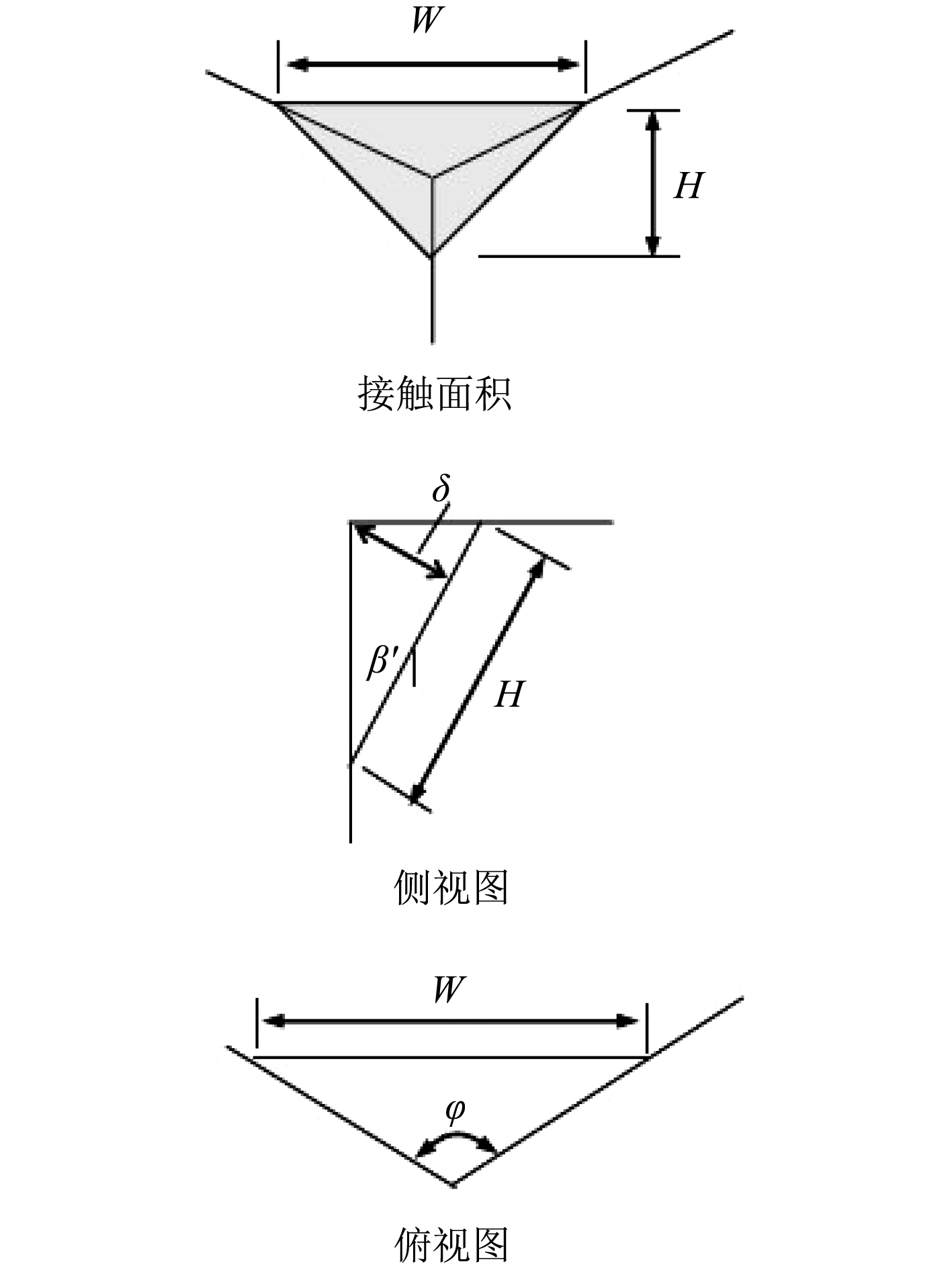
|
图 3 接触区域 Fig. 3 Nominal contact geometry |
根据冰压力-面积关系[3],平均压力为:
| $P = {P_0}{A^{ex}}\text{,}$ | (13) |
挤压力Fn为:
| ${F_n} = {\rm{PA}} = {P_0}{A^{1 + ex}}\text{,}$ | (14) |
定义角度系数
| $\frac{1}{2}{M_e}V_n^2 = {P_0} \cdot {k^{1 + ex}} \cdot \mathop \int \nolimits_0^{{\delta _m}} {\delta ^{2 + 2ex}}{\rm d}\delta \text{,}$ | (15) |
求得最大法向位移δm为:
| ${\delta _m} = {\left( {\frac{{\frac{1}{2}\left( {3 + 2ex} \right){M_e}V_n^2}}{{{P_0} \cdot {k^{1 + ex}}}}} \right)^{\frac{1}{{3 + 2ex}}}}\text{,}$ | (16) |
简化为:
| ${F_n} = {P_0}^{\frac{1}{{3 + 2ex}}} \cdot {k^{\frac{{1 + ex}}{{3 + 2ex}}}} \cdot {\Biggr(\frac{1}{2}\left( {3 + 2ex} \right){M_e}V_n^2\Biggr)^{\frac{{2 + 2ex}}{{3 + 2ex}}}}\text{。}$ | (17) |
用船的质量Mship和船速Vship代替有效质量Me和法向速度Vn则可以得到:
| ${F_n} = {P_0}^{\frac{1}{{3 + 2ex}}} \cdot {k^{\frac{{1 + ex}}{{3 + 2ex}}}} \cdot {\left( {\frac{{{l^2}}}{{2{C_0}}}} \right)^{\frac{{2 + 2ex}}{{3 + 2ex}}}} \cdot {\Bigr(\left( {3 + 2ex} \right){M_{ship}}V_{ship}^2\Bigr)^{\frac{{2 + 2ex}}{{3 + 2ex}}}}\text{,}$ | (18) |
定义参数fa
| $fa = {(3 + 2ex)^{\frac{{2 + 2ex}}{{3 + 2ex}}}} \cdot {\left( {\frac{{tan\frac{\varphi }{2}}}{{{\rm{sin}}\left( {{\rm{\beta '}}} \right){\rm{co}}{{\rm{s}}^2}\left( {{\rm{\beta '}}} \right)}}} \right)^{\frac{{1 + ex}}{{3 + 2ex}}}} \cdot {\left( {\frac{{{l^2}}}{{2{C_0}}}} \right)^{\frac{{2 + 2ex}}{{3 + 2ex}}}}\text{,}$ | (19) |
挤压力可以表示为:
| ${F_n} = fa \cdot {P_0}^{\frac{1}{{3 + 2ex}}} \cdot {M_{ship}}^{\frac{{2 + 2ex}}{{3 + 2ex}}} \cdot V_{ship}^{\frac{{4 + 4ex}}{{3 + 2ex}}}\text{,}$ | (20) |
考虑常数ex取值为–0.1,同时考虑接触区域的形状,取冰缘角φ=150°,则可以推导得到:
| ${F_n} = fa \cdot {P_0}^{0.36} \cdot V_{ship}^{1.28} \cdot {M_{ship}}^{0.64}\text{。}$ | (21) |
本文表1的船级因子为计算设计冰载荷非常重要的参数。对比式(2)和式(21),可以得到:
| $C{F_C} = {P_0}^{0.36} \cdot V_{ship}^{1.28}\text{,}$ | (22) |
同样基于能量模型进行推导分析,还可以得到:
| $C{F_F} = {\sigma _f} \cdot h_{ice}^2\text{,}$ | (23) |
| $C{F_D} = {P_0}^{0.389}\text{。}$ | (24) |
式中:P0为冰的压溃强度;σf为弯曲破坏强度。说明船级因子的值和冰的破碎强度、冰的弯曲强度、冰的厚度、船舶的载重量、撞击速度等有关系。针对不同的冰级,船级因子是基于上述这些参数典型值计算得到,如表3所示[4]。
|
|
表 3 典型参数和对应的船级因子 Tab.3 Class parameters and factors |
针对表2开展研究。
船体区因子反映了某船体区域预期承受载荷的相对大小,也一定意义上反映了区域要求的结构加强水平。基于详细的船舶破损数据,加拿大和俄罗斯均对船体区因子开展了研究。
基于统计资料,可以确定在冰载荷作用下船舶首部、船中、尾部等不同位置区域发生破损事故的情况。同时根据一定的船舶尺度数据进行计算,确定某一冰级条件下船体各个区域位置必需的板厚,将首部位置的板厚视作1,其他位置区域的板厚均除以首部区域的板厚转换为一个比例系数。船体区因子正是基于事故统计数据和计算得到比例系数来确定的。在船体区因子研究方面,首先加拿大提出了船体区因子的建议值(见表4),而后俄罗斯也提出了建议值(见表5)。
|
|
表 4 加拿大提出的船体区因子(**表示不要加强)[5] Tab.4 Canadian proposed hull area factors |
|
|
表 5 俄罗斯提出的船体区因子(**表示不要加强)[6] Tab.5 Russian proposed hull area factors |
同时,加拿大和俄罗斯共同创建了研究性的团体组织,针对船舶定义、船体分区、冰区航行规则等进行讨论以求达到一致的结果,尽管在一些方面获得了统一的意见,但是并没有获得关于船体区因子的一致结果。对应相同的冰级和相同的船体区域,两者给出的值不完全相同。
1998年,加拿大和俄罗斯先后将各自提出的建议值提交IACS讨论。1999年,在蒙特利尔会议上,IACS最终确定针对两国提出的建议值若不相同则取平均值,同时要求所有的值为0.5的倍数,进行适当的修正,得到表6所示结果[7]。表6是确定表2对应船体区因子的基础。
|
|
表 6 提出的船体区因子(**表示不要加强) Tab.6 Proposed hull area factors |
针对国际船级社协会极地冰级规范,本文重点从设计冰载荷计算、船级因子和船体区因子3个方面分析了规范的理论基础,在此基础上进一步研究现有规范存在的不足。
1)船冰作用工况的局限性
国际船级社协会极地冰级规范在研究冰载荷计算公式时主要针对船首部和船肩部的快速碰撞工况,对于其他船体区域的冰载荷(例如,船中部和船尾部),国际船级社协会IACS 极地冰级规范将其取为基于经验和已有损坏测量数据的船首/肩部快速碰撞工况冰载荷的一定百分数[1]。
实际上,除了快速碰撞外,船冰作用工况还主要有:船肩部发生反弹碰撞,船肩部发生楔形碰撞,船中部发生快速碰撞,船中部受到封闭挤压,浮冰撞击船中部产生压力。不同的船舶与冰作用工况,船体受到的冰载荷可能不同。特别地,对于冰区双向作业船舶来说,需要特别关注尾部破冰向前航行时遭受的冰载荷。
可以看出,目前规范考虑的船冰作用工况较少,存在一定的局限性。
2)冰压力与面积关系分析
式(13)表征了冰压力和面积之间的关系。
Kujala和Arughadhoss[8]基于试验结果研究获得了包络曲线,反映了接触面积和冰压力之间的关系,公式中取P0=0.42,ex=–0.52,在DNV规范中取ex=–0.5,国际船级社协会极地冰级规范中取ex=–0.1,不同取值对应的曲线存在差异[9],本文给出如图4所示结果。
不同的ex取值,计算得到的压力偏差较大。国际船级社协会极地冰级规范,在分析冰载荷计算公式时,P0的取值取决于不同的冰级要求,与Kujala和Arughadhoss基于试验分析得到的结果有一定的不同。
同时在进行挤压力计算时,式(19)中的冰缘角假定为定值,取φ=150°,则式(19)可以简化为:
| $fa = 1.94 \cdot {\left( {\frac{{3.732}}{{{\rm{sin}}\left( {{\rm{\beta '}}} \right){\rm{co}}{{\rm{s}}^2}\left( {{\rm{\beta '}}} \right)}}} \right)^{0.32}} \cdot {\left( {\frac{{{l^2}}}{{2{C_0}}}} \right)^{0.64}}\text{。}$ | (25) |
可以发现式(25)和式(1)有较大差别,这是因为C0在实际计算时相对较复杂,所以规范采用了简化公式。
经过分析,可以发现规范给出的设计冰载荷计算公式一定意义上反映了结构承受的载荷特性,但是其中一些参数的取值尚需要进一步研究,特别是需要在基于冰力学特性研究的基础上获得准确的冰压力-面积关系。
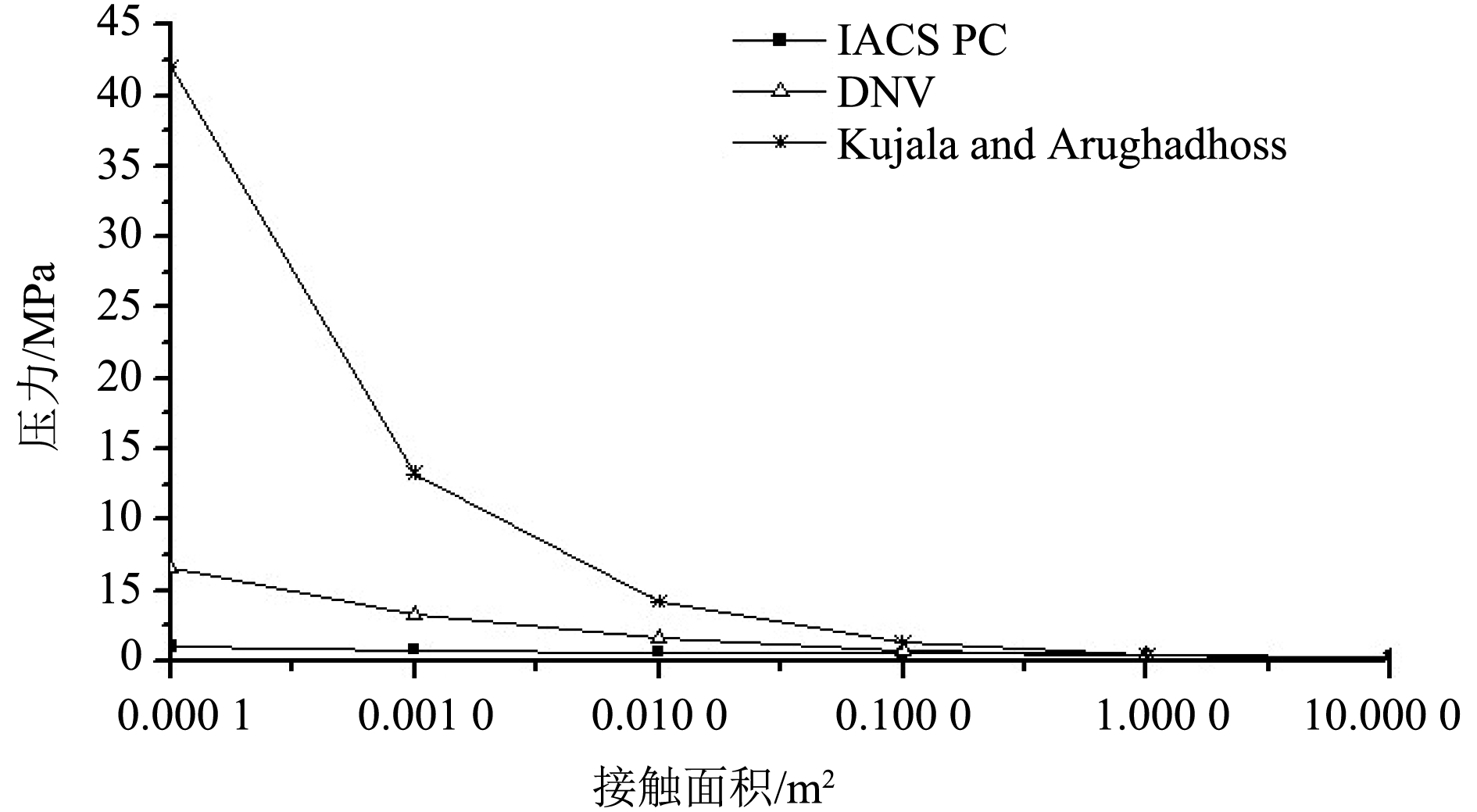
|
图 4 压力-面积关系 Fig. 4 Pressure-area curves |
3)船级因子修正
船级因子主要通过式(22)~式(24)计算得到。计算时,针对不同的冰级,航速、海冰特征冰厚等取典型值,计算获得的船级因子如表3所示。对比表3和规范中表1的船级因子,可以发现存在不同,说明规范是基于公式的计算结果进行修正得到。
考虑到极地环境的复杂性、冰载荷可能造成的船体严重破坏等因素,船级因子对于准确计算冰载荷非常重要,所以需要进一步开展研究,获得准确的计算船级因子的方法或者相应的修正船级因子的数据资料。
4)船体区因子修正
本文2.3节对规范中船体区因子进行研究分析。
将表2和表6对应的船体区因子进行对比分析。表2中*对应的数值为1.00,表6实际得到的值为0.80,进行数值的修正主要基于两方面原因:1)进一步考虑了船舶破损方面的历史资料;2)所有极地船舶的首部区,以及极地船级PC6 和PC7 船舶的首部过渡区中的冰带区范围内,冰载荷参数为实际首部形状的函数,实际上在PC6 和PC7冰级下,船舶高速航行时,冰带区承受较大的冰载荷冲击。
通过分析可以发现,加拿大和俄罗斯提出的船体区因子主要是基于极地船舶的历史破损数据资料,同时考虑了航行实践经验、相关的极地航行规则及极地船舶加强要求。而国际船级社协会极地冰级规范是在加拿大和俄罗斯提出的船体区因子基础上进行修正获得的,船体区因子的研究需要不断深化,以获得准确的确定船体区因子的方法或者相应的修正方法。
4 极地水面舰船冰级规范研究方向目前国际上BV船级社和LR船级社已经形成了针对极地水面舰船的冰级规范。
1)差异性分析
基于BV船级社的民船规范《Rules for the classification of steel ships》[10]和军船规范《Rules for the classification of military ships》[11],开展规范的差异性分析。
2种规范在冰级定义上相同,均使用IAS,IA,IB,IC,ID的冰级划分;在计算推进器输出功率时,2种规范给出了不同的公式,军船规范针对IB和IC冰级要求给出了计算最小许用功率的公式,同时针对IAS和IA的冰级要求给出了不同的计算最小许用功率的公式,而民船规范仅给出一种计算公式;计算设计冰压力的公式相同,但是在具体参数的定义方面2种规范存在差异;2种规范在计算冰带区内舷侧纵桁及冰带外舷侧纵桁对应的剖面模数和截面面积时给出了不同的计算公式。
同时基于LR船级社的规范《Rules and regulations for the classification of ships》[12]和《Rules and regulations for the classification of naval ships》[13]开展规范的差异性分析。
军船规范定义的冰级划分为Ice Class 1AS,Ice Class 1A,Ice Class 1B,Ice Class 1C,且该4种冰级均为当年冰的冰况,在民船规范中给出了更详细的划分并定义冰级符号,针对非常轻微的冰况定义了Ice Class 1D和Ice Class 1E冰级,针对当年冰的冰况考虑了一般功率输出的情况和增强的功率输出以提高破冰能力的情况,针对多年冰况,规范主要使用国际船级社协会冰级规范的公式来计算冰载荷;军船规范和民船规范在船体区域划分上存在不同,同时针对浮冰带区域板厚、骨材剖面模数等的计算公式也存在不同。
2)极地军船冰级规范发展分析
通过分析可以发现,由于实际用途和结构布置方面等的差异,极地一般民用船舶和军船在冰区加强要求、设计冰压力、推进器输出功率等方面存在差异,所以在设计与建造极地水面舰船之前需要首先形成相应的标准规范。
虽然我国已建造完成了极地科考船,同时基于国际船级社协会极地冰级规范,相应地也形成了针对极地船舶的相关加强规定,但是到目前为止没有形成针对极地水面舰船的冰级规范,需要在现有民船极地冰级规范基础上,积极开展极地水面舰船冰级规范研究。具体到冰载荷计算与结构加强方面,主要考虑以下内容:
1)基于极地水面舰船快速性、灵活性、极限承载能力、结构破损后剩余强度要求及结构加强的要求等,考虑极地海冰、低温等环境因素,研究目前冰载荷规范理论对于极地舰船结构的适用性;
2)通过本文分析,可以发现现有的民船冰级规范在考虑船冰作用工况、挤压力计算、船级因子及船体区因子等方面尚存在不足,在开展极地水面舰船冰级规范研究时,需要在这些方面继续不断深化研究;
3)极地双向作业是很重要的发展方向,通过开展冰载荷计算、结构加强、船体结构分区等研究,形成针对极地双向作业水面舰船的规范。
5 结 语本文重点对现有的国际船级社协会极地冰级规范进行研究,分析了目前规范的不足之处,同时研究了民船规范和军船规范之间存在的差异,考虑到目前我国没有形成完整的针对极地水面舰船的冰级规范,现有的民船规范仍然有非常重要的借鉴意义,在开展极地水面舰船冰级规范研究时,首先针对性地解决现有民船极地冰级规范存在的问题,在充分研究极地环境条件、水面舰船作战要求及水面舰船航行性能基础上,研究获得针对极地水面舰船的冰级规范。
| [1] | IACS Unified Requirements UR-Ⅱ, Requirements Concerning Polar Class [S], 2016. |
| [2] | DALEY C G. Oblique ice collision loads on ships based on energy methods [J]. Oceanic Engineering International, 2001, 5(2): 67-72. https://www.researchgate.net/profile/Claude_Daley/publication/287831071_Oblique_Ice_Collision_Loads_On_Ships_Based_On_Energy_Methods/links/56dd9be808ae628f2d24a5dd.pdf?origin=publication_detail |
| [3] | DALEY C G. Re-analysis of polar sea ice pressure-area relationship [J]. Marine Technology, 2007, 44(4): 234-244. |
| [4] | DALEY C G. Background notes to design ice loads-IACS unified requirements for polar ships. IACS Ad-hoc group on polar class ships transport Canada, 2000. http://www.engr.mun.ca/~cdaley/9093/PC_Ship-Ice Loads.pdf |
| [5] | BOND J E. Structural design requirements for polar ships-proposed. MIL systems report # 1875-0005-02B, 1998. |
| [6] | Draft. The fourth edition of the IACS unified rules (Harmonized Rules) for polar ships, material son the contract " Technical Support to the Canada-Russian Bilateral Project on polar rules Harmonnization”, 1998. |
| [7] | BOND J. Background notes to hull area definition, extents and factors-IACS unified requirements for polar ships. IACS Ad-hoc group on polar class ships, 2000. http://www.engr.mun.ca/~cdaley/9093/PC_Ship-Ice Loads.pdf |
| [8] | KUJALA P, ARUGHADHOSS S. Statistical analysis of ice crushing pressures on a ship’s hull during hull-ice interaction[J]. Cold Regions Science and Technology, 2012, 70: 1-11. |
| [9] | TIAN Xi-min, ZOU Zao-jian, YU Ji-jun, WANG Fu-hua. Review on advances in research of ice loads on ice-going ships. Journal of Ship Mechanics, 2015, 19(3): 337-348. |
| [10] | Bureau Veritas. Rules for the classification of steel ships[S]. 2005. |
| [11] | Bureau Veritas. Rules for the classification of military ships[S]. 2003. |
| [12] | Lloyd’s Register. Rules and regulations for the classification of ships[S]. 2013. |
| [13] | Lloyd’s Register. Rules and regulations for the classification of naval ships[S]. 2013. |
 2018, Vol. 40
2018, Vol. 40
