2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China
筒盖电液系统是一个典型的非线性时变系统,存在流量/压力非线性、液体可压缩性、电液转换、摩擦特性、阀的工作死区等非线性及阻尼系数、流量系数、油液温度等时变性[1],所以筒盖开关盖动作在传统控制方式下存在稳定性不高、控制精度差等缺点。因此,借助Simulink仿真技术建立精确的系统模型,实现筒盖角速度/时间曲线与角度/时间曲线的反步跟踪控制,可以有效提升筒盖动作的控制精度。
1 筒盖开盖动力学分析
|
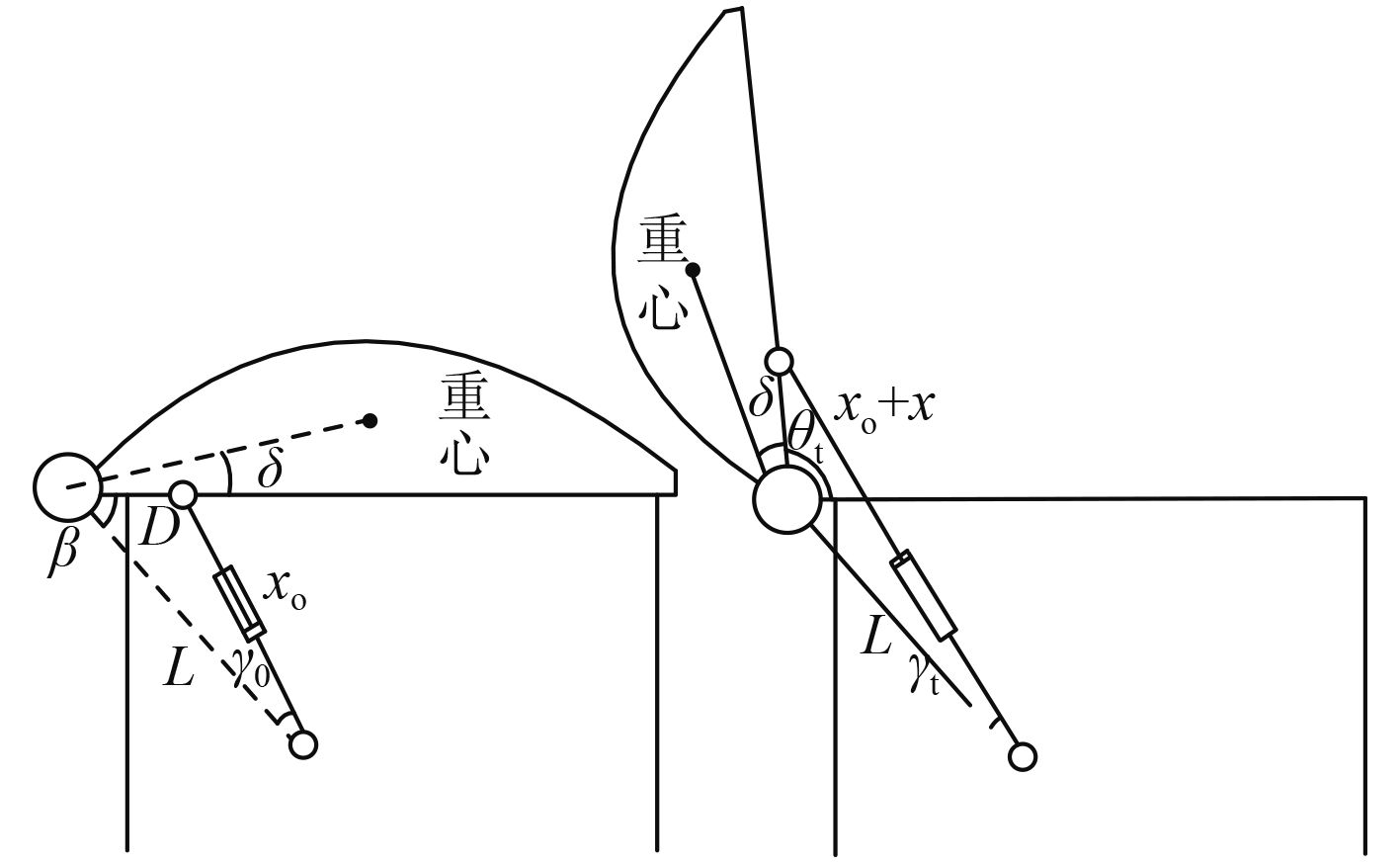
图 1 典型筒盖开盖结构原理图 Fig. 1 Typical launcher cover structure schematic |
筒盖跟踪目标曲线通常为角速度/时间曲线或角度/时间曲线,而精确的液压缸输入为直线位移,因此,根据机构模型,推导筒盖角度与液压缸位移的变换关系。
开盖液压推杆一端固定于某处支撑点,另一端连接在筒盖上,推动筒盖使筒盖绕转轴转动。其中筒盖转轴与支撑点的距离为固定值
| ${({x_o} + {x_t})^2} = {L^2} + {D^2} - 2LD\cos (\beta + {\theta _t}){\text{。}}$ | (1) |
从而得到角度/位移变换为:
| $x_t=\sqrt {{L^2} + {D^2} - 2LD\cos (\beta + {\theta _t})} - {x_o}{\text{,}}$ | (2) |
位移/角度变换为:
| ${\theta _t} = arc\cos (\frac{{{L^2} + {D^2} - {{({x_o} + {x_t})}^2}}}{{2LD}}) - \beta {\text{。}}$ | (3) |
筒盖运动过程中,筒盖重力随开盖角度变换而变换,为了准确分析筒盖电液系统的变负载特性,推导筒盖对液压缸作用力与筒盖角度的变化关系:
将筒盖质心到转轴的距离用
| $ J\alpha = F \cdot D\sin \phi - mg\cos \left( {\delta + {\theta _t}} \right) {\text{,}}$ | (4) |
对于
| $ \cos \phi = \frac{{{{\left( {{x_o} + {x_t}} \right)}^2} + {D^2} - {L^2}}}{{2D\left( {{x_o} + {x_t}} \right)}} {\text{,}}$ | (5) |
综上得到液压缸负载力为:
| $ F = \frac{{J\alpha + mg\cos (\alpha + {\theta _t})l}}{{D\sin \left( {arc\cos \left( {\displaystyle\frac{{{{\left( {{x_o} + {x_t}} \right)}^2} + {D^2} - {L^2}}}{{2D\left( {{x_o} + {x_t}} \right)}}} \right)} \right)}} {\text{。}}$ | (6) |
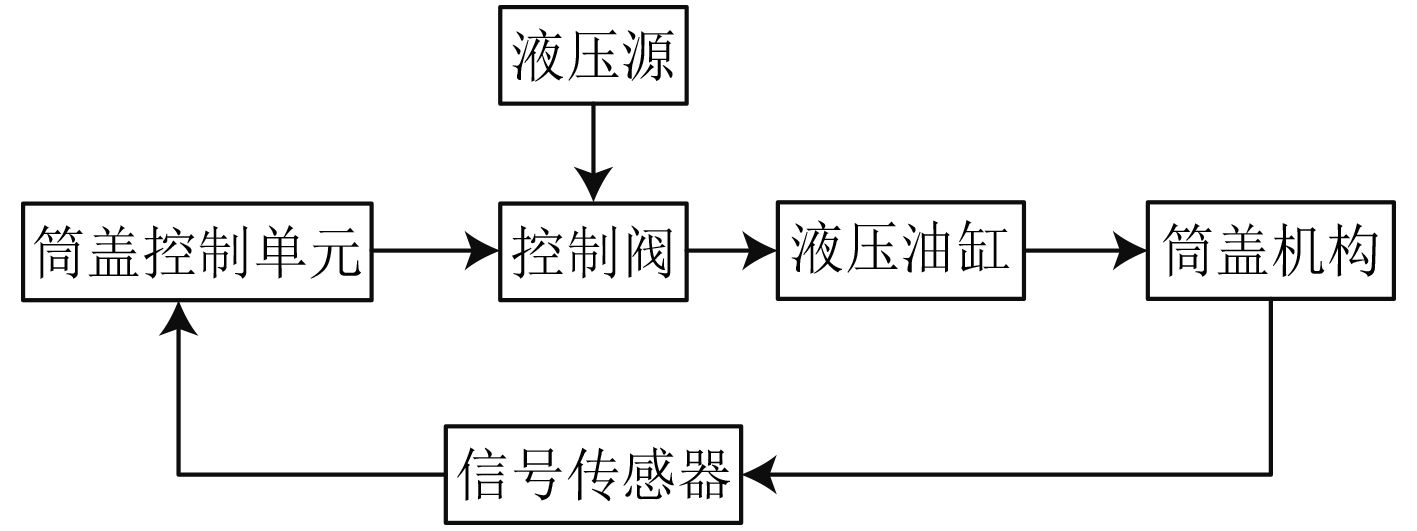
筒盖电液系统原理如图2所示。
|
图 2 筒盖电液系统原理图 Fig. 2 Typical launcher cover electro-hydraulic system schematic |
筒盖电液系统可以等效为经典的阀控液压缸模型[3]。当系统伺服阀的阀芯位移为
| $ {Q_{dA}} \!=\! \left\{ \begin{array}{l}\!\!\!\!\!\!{C_{dd}}{\omega _{dv}}{x_{dv}}\sqrt {2\left( {{P_{ds}} - {P_{dA}}} \right)/\rho},{x_{dv}} \geqslant 0 {\text{,}}\\\!\!\!\!\!\!{C_{dd}}{\omega _{dv}}{x_{dv}}\sqrt {2{P_{dA}}/\rho},{x_{dv}} < 0{\text{。}}\end{array} \right.$ | (7) |
| $ {Q_{dB}} \!=\! \left\{ \begin{array}{l}\!\!\!\!\!\!{C_{dd}}{\omega _{dv}}{x_{dv}}\sqrt {2{P_{dB}}/\rho}, {x_{dv}} \geqslant 0{\text{;}}\\\!\!\!\!\!\!{C_{dd}}{\omega _{dv}}{x_{dv}}\sqrt {2\left( {{P_{ds}} - {P_{dB}}} \right)/\rho}, {x_{dv}} \!< 0{\text{。}}\end{array} \right.$ | (8) |
其中
| ${Q_{dL}} = {C_{dd}}{\omega _{dv}}{x_{dv}}\sqrt {\frac{{{P_{ds}} - \operatorname{sgn} \left( {{x_{dv}}} \right){P_{dL}}}}{\rho }} {\text{,}}$ | (9) |
其中
根据液压流量连续,考虑液压缸内外漏以及液压油压缩特性,将流入液压缸2个腔体的流量分别表示为:
| $ {Q_{dA}} \!\!=\!\! \left\{ \begin{aligned} & \frac{{{V_{dA}}}}{{{\beta _e}}}\frac{{{\rm d}{P_{dA}}}}{{{\rm d}t}} \!\!+\!\! {C_{dip}}{P_{dL}} \!\!+\!\! {C_{dep}}{P_{dA}} + {A_{dp}}\frac{{{\rm d}{x_{dp}}}}{{{\rm d}t}}{\text{,}} \\& \!\!-\!\! \frac{{{V_{dB}}}}{{{\beta _e}}}\frac{{{\rm d}{P_{dB}}}}{{{\rm d}t}} \!\!+\!\! {C_{dip}}{P_{dL}}{\rm{ - }}{C_{dep}}{P_{dB}} \!\!+\!\! {A_{dp}}\frac{{{\rm d}{x_{dp}}}}{{{\rm d}t}} {\text{。}} \\ \end{aligned} \right.$ | (10) |
其中:
由于活塞杆一般在中间位置附近做小幅度位移运动,因此可以认为
| ${Q_{dL}} = {A_{dp}}\frac{{{\rm d}{x_{dp}}}}{{{\rm d}t}} + {C_{dtp}}{P_{dL}} + \frac{{{V_{dt}}}}{{4{\beta _e}}}\frac{{{\rm d}{P_{dL}}}}{{{\rm d}t}}{\text{,}}$ | (11) |
其中:
结合得到的液压负载力方程可以得到:
| $ \frac{{J\alpha + mg\cos (\alpha + {\theta _t})l}}{{D\sin \left( {\arccos \left( {\displaystyle\frac{{{{\left( {{x_o} \!\!+\!\! {x_t}} \right)}^2} + {D^2} \!\!-\!\! {L^2}}}{{2D\left( {{x_o} \!\!+\!\! {x_t}} \right)}}} \right)} \right)}} \!\!=\!\! {P_{dA}}{A_{dP}} \!\!-\!\! {P_{dB}}{A_{dP}} \text{,} $ | (12) |
令
| $m\frac{{{{\rm d}^2}{x_{dp}}}}{{{\rm d}{t^2}}} = {A_p}{P_{dL}} - {B_p}\frac{{{\rm d}{x_{dp}}}}{{{\rm d}t}} + F{\text{,}}$ | (13) |
在此基础上,设计筒盖系统动作的反步控制器。
3 筒盖系统反步控制器设计在现有的筒盖控制环节中,仅采用角度时间/时间曲线作为控制量,导致最终筒盖开盖时间控制精度不高,同时筒盖动作过程中动作平稳性不佳,为了实现筒盖动作曲线对预设曲线良好的跟踪效果,设计了对液压缸位移/时间曲线和液压缸速度/时间曲线同时跟踪的反步控制器[4]。
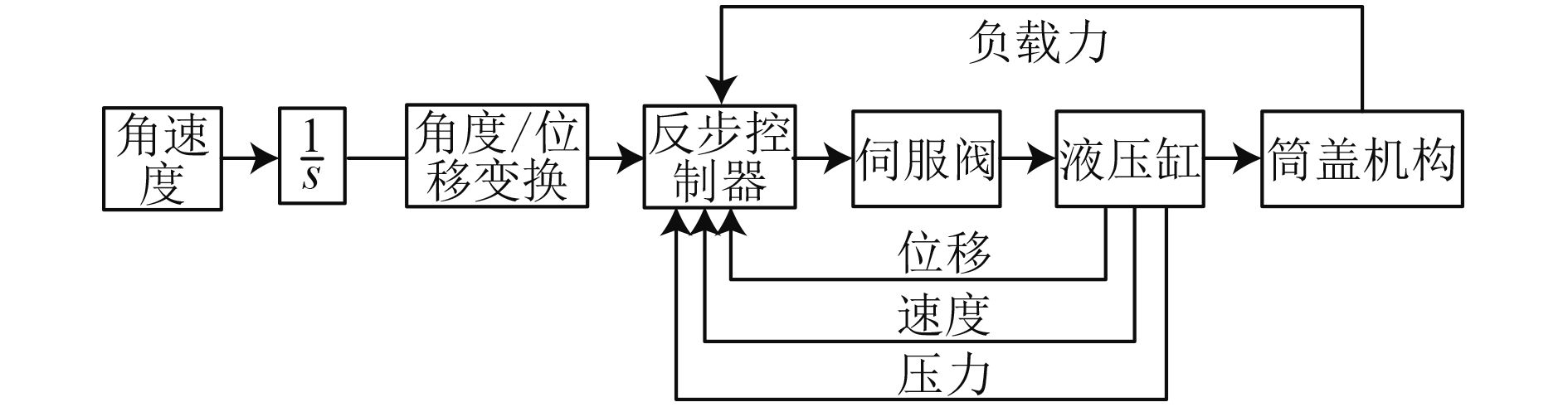
从筒盖系统的角度,预先设置筒盖开关盖角速度/时间曲线,通过角度/位移转换模块得到液压缸位移/时间曲线和液压缸速度/时间曲线,将其与实时采集到的液压缸实际位移、速度、液压缸压力等数据送入反步控制器,生成最终的电流控制量完成对伺服阀的控制,控制原理如图3所示。
|
图 3 反步环控制原理图 Fig. 3 Backstepping ring control schematic |
为了采用反步法对电液系统进行控制[5],首先需要将其写成系统状态方程,系统的非线性方程写成反步法所需的严格反馈形式,选取状态变量为
| $\left\{ \begin{aligned}& {{\dot x}_1} = {x_2} {\text{,}} \\& {{\dot x}_2} = {\theta _1}{x_3} - {\theta _2}{x_2} - F/m {\text{,}} \\& {{\dot x}_3} = - {\theta _3}{x_2} - {\theta _4}{x_3} + {\theta _5}u {\text{。}} \\ \end{aligned} \right.$ | (14) |
其中:
| $\left\{ \begin{aligned} &{\theta _1} = {A_p}/m {\text{,}} \\ & {\theta _2} = {B_p}/m {\text{,}} \\ &{\theta _3} = 4{\beta _e}{A_p}/{V_t} {\text{,}} \\ &{\theta _4} = 4{\beta _e}{C_{tp}}/{V_t} {\text{,}} \\ &{\theta _5} = 4{\beta _e}/{V_t} {\text{,}} \\ & u = {Q_L} {\text{。}} \\ \end{aligned} \right.$ | (15) |
对系统进行反步控制器的设计,其中
| $\left\{ \begin{gathered} {e_1} = {x_1} - {x_{1d}} {\text{,}} \\ {e_2} = {x_2} - {\alpha _1} {\text{,}} \\ {e_3} = {x_3} - {\alpha _2} {\text{。}} \\ \end{gathered} \right.$ | (16) |
步骤1
为了使跟踪误差
| ${V_1} = \frac{1}{2}e_1^2{\text{。}}$ | (17) |
对函数两端进行求导,并将系统的状态方程代入:
| $\begin{gathered} {{\dot V}_1} = \dot e{}_1 \cdot {e_1} = e{}_1({{\dot x}_1} - {{\dot x}_{1d}}) = e{}_1({x_2} - {{\dot x}_{1d}}) \\ = e{}_1({e_2} + {\alpha _1} - {{\dot x}_{1d}}) {\text{,}} \\ \end{gathered} $ | (18) |
可使虚拟控制量为:
所以
步骤2
为了使
| ${V_2} = \frac{1}{2}e_2^2 + {V_1}{\text{。}}$ | (19) |
对函数两端进行求导,并将系统的状态方程代入:
| $\begin{gathered} {{\dot V}_2} = e{}_2{{\dot e}_2} - {k_1}e_1^2 + e{}_1{e_2} \\ = e{}_2({\theta _1}({e_3} + {\alpha _2}) - {\theta _2}{x_2} - F/m \\ + {k_1}({x_2} - {{\dot x}_{1d}}) - {{\ddot x}_{1d}}) - {k_1}e_1^2 + e{}_1{e_2} {\text{,}}\\ \end{gathered} $ | (20) |
可使虚拟控制量为:
| ${\alpha _2} = - \frac{1}{{{\theta _1}}}(e{}_1 - {\theta _2}{x_2} - F/m + {k_1}({x_2} - {\dot x_{1d}}) - {\ddot x_{1d}} + {k_2}{e_2}){\text{,}}$ | (21) |
其中
所以
步骤3
为了使
| ${V_3} = \frac{1}{2}e_3^2 + {V_2}{\text{。}}$ | (22) |
对函数两端进行求导,并将系统的状态方程代入:
| $\begin{gathered} {{\dot V}_3} = e{}_3{{\dot e}_3} - {k_1}e_1^2 - {k_2}e_2^2 + {\theta _1}e{}_2{e_3} \\ = e{}_3( - {\theta _3}{x_2} - {\theta _4}{x_3} + {\theta _5}u - {{\dot \alpha }_2}) \\ - {k_1}e_1^2 - {k_2}e_2^2 + {\theta _1}e{}_2{e_3} {\text{,}}\\ \end{gathered} $ | (23) |
| $得 $u = - \frac{1}{{{\theta _5}}}({\theta _1}e{}_2 - {\theta _3}{x_2} - {\theta _4}{x_3} - {\dot \alpha _2} + {k_3}{e_3})\text{,}$ | (24) |
此时,
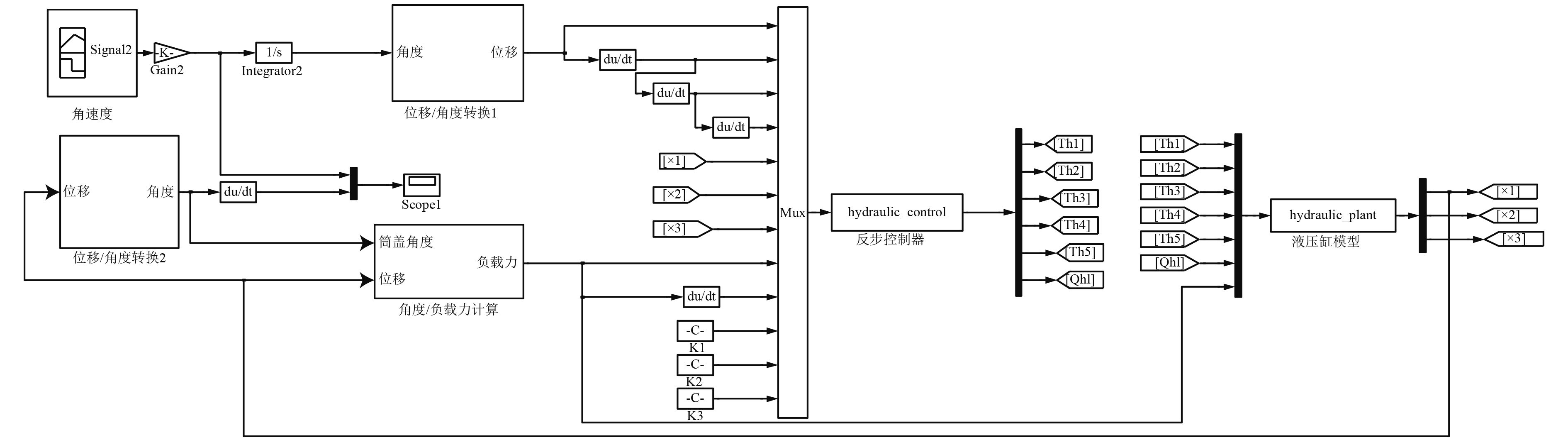
根据2筒盖动力学分析与3筒盖电液系统模型分析,在Matlab/Simulink中分别搭建了液压缸模型、位移/角度转换模块、负载力计算模块,并将反步控制器在控制模型中实现,最终完成电液系统仿真模型[6]。
筒盖电液系统仿真模型如图4所示。
|
图 4 电液系统Simulink仿真模型 Fig. 4 Electro-hydraulic system Simulation model |
根据实际数据,设置仿真模型中参数如表1所示。
|
|
表 1 仿真模型主要参数 Tab.1 The main parameters of the simulation model |
通过合理调整仿真模型中位移曲线跟踪环节中的参数,达到了良好的控制效果,具体结果如图5~图8所示。
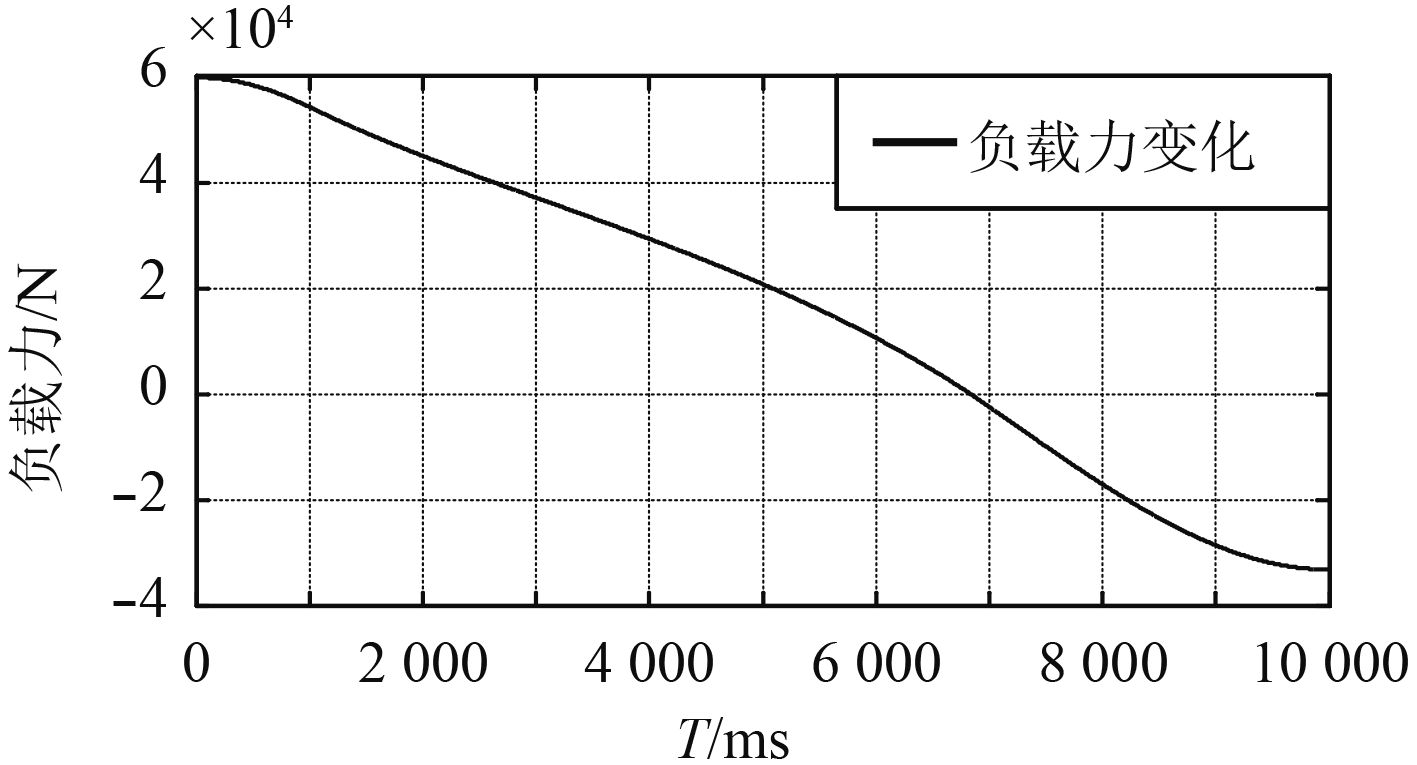
|
图 5 负载力变化曲线 Fig. 5 Load force curve |
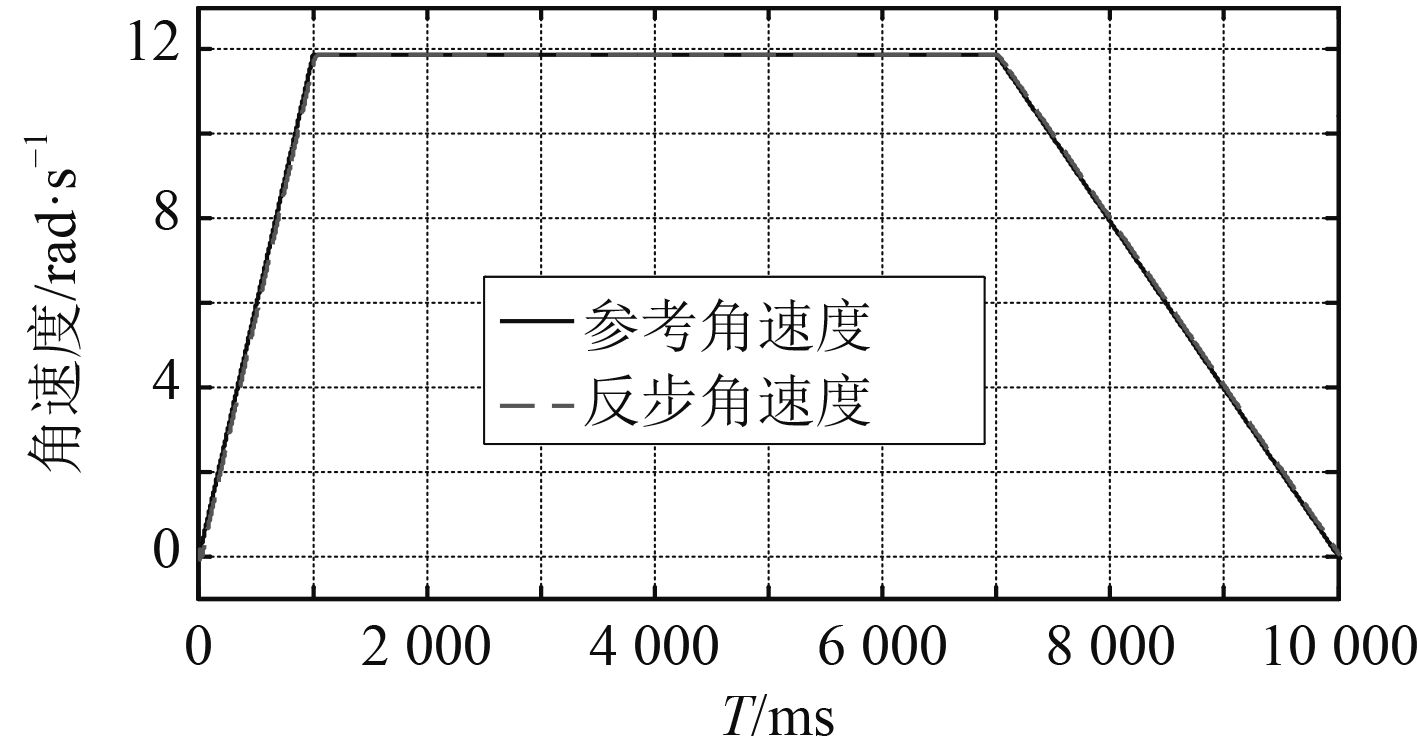
|
图 6 角速度跟踪曲线 Fig. 6 Angular speed tracking curve |
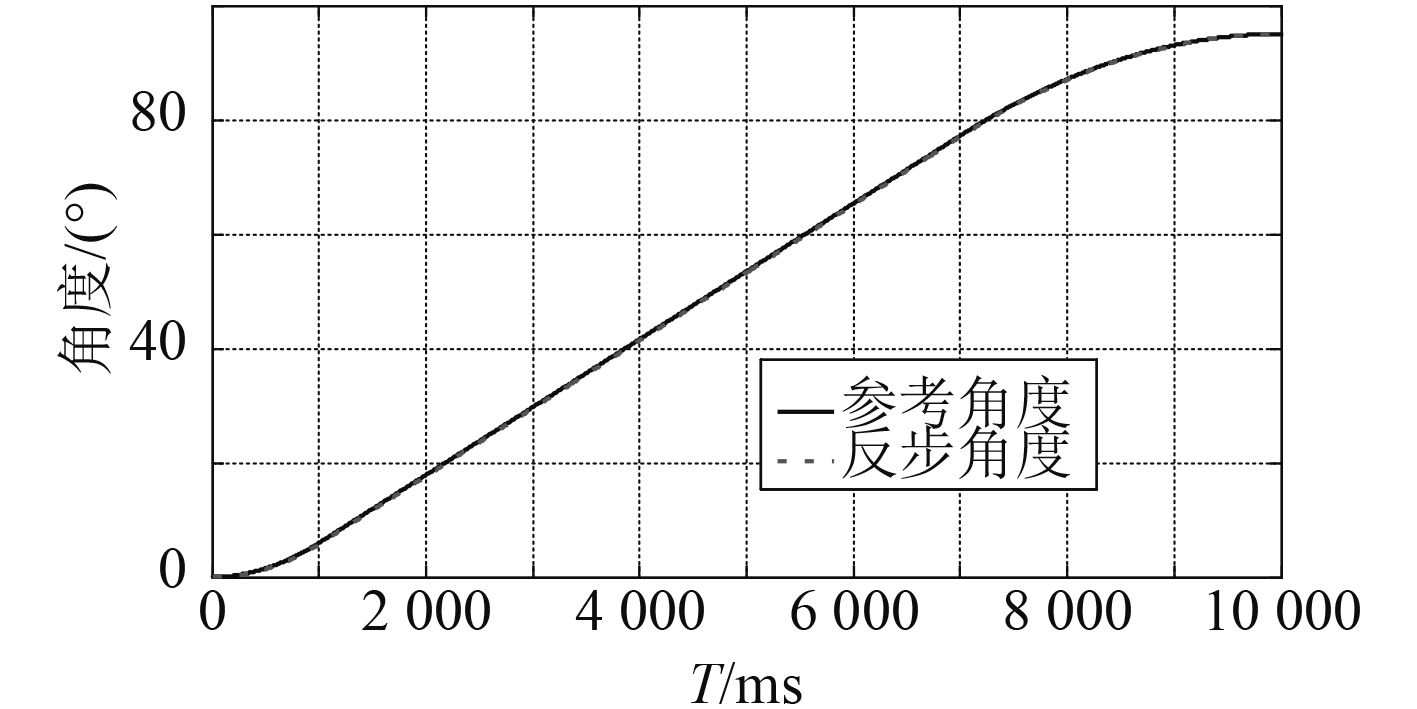
|
图 7 角度跟踪曲线 Fig. 7 Angular tracking curve |
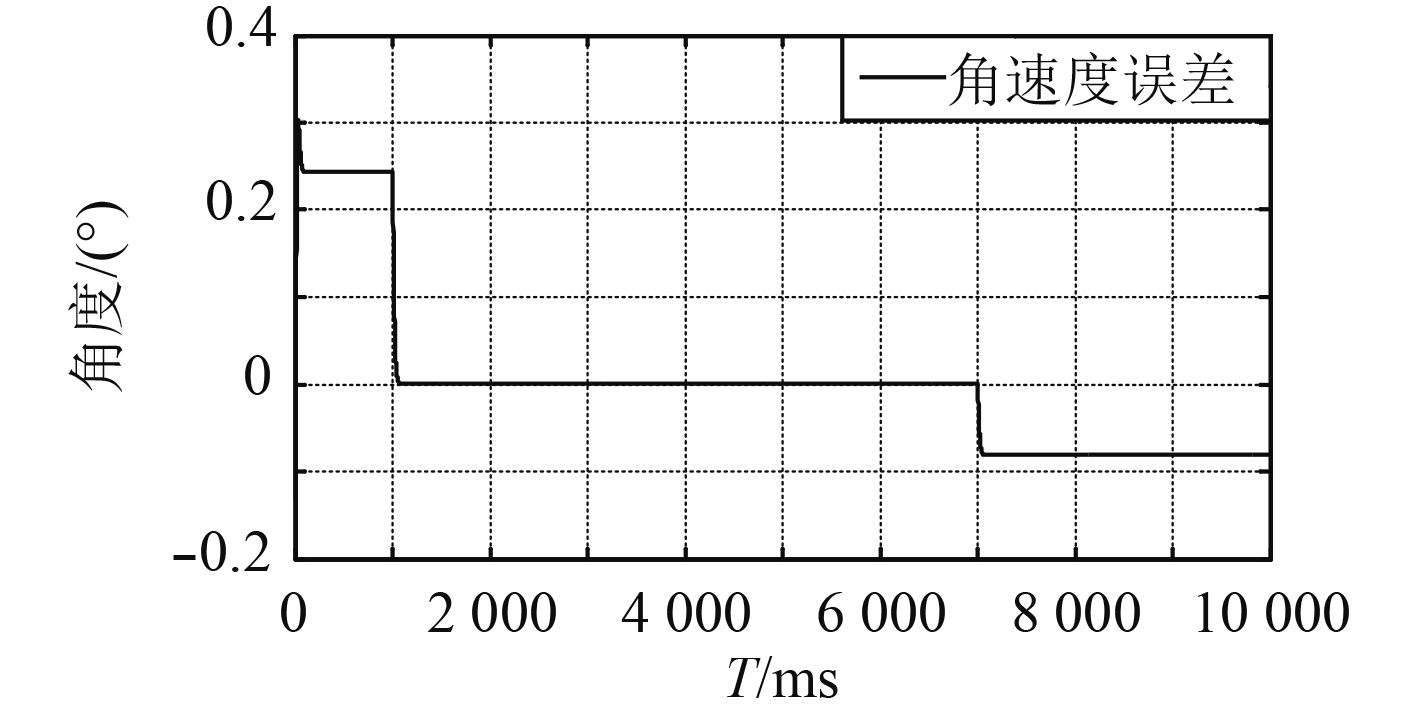
|
图 8 角速度跟踪误差曲线 Fig. 8 Angular speed tracking error curve |
从仿真结果可以看出,相比于原筒盖单闭环角度控制,所设计的具有速度补偿功能的反步控制器对角速度/时间曲线和角度/时间曲线的跟踪误差明显减小,最大误差减小到了0.30°,说明将反步控制算法应用到筒盖控制中能够有效提升筒盖动作控制精度。
| [1] | 田凡, 靳宝全, 程珩. 基于联合仿真的电液系统模糊PID控制研究[J]. 液压气动与密封, 2010, 6(5): 27–31. http://www.cqvip.com/QK/95681A/201006/34228965.html |
| [2] | 倪火才. 潜地导弹发射装置构造[M]. 哈尔滨:哈尔滨工程大学出版社, 1998. |
| [3] | 宋志安, 等. Matlab/simulink与液压控制系统仿真[M]. 北京:国防工业出版社, 2012. |
| [4] | 袁朝辉, 袁鸣. 电液系统中新型反步自适应控制器设计[J]. 机电工程, 2013, 07. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jdgc201307001 |
| [5] | 石胜利, 李建雄, 方一鸣. 具有输入饱和的电液伺服系统反步位置跟踪控制[J]. 中南大学学报: 自然科学版, 2016, 47(10): 3369–3374. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zzjsyjc201112029 |
| [6] | 胡良谋, 李景超, 曹克强. 基于MATLAB/SIMULINK的电液伺服控制系统的建模与仿真研究[J]. 机床与液压, 2003(3): 230–231. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zbzzjs200706026 |
 2018, Vol. 40
2018, Vol. 40
