航速指目标单位时间内运动的距离,是描述目标运动的基本要素之一。在实际应用中,除了多普勒雷达等少数雷达之外,绝大多数雷达不能提供目标航速的直接测量信息,而是通过航迹滤波间接获取。因此,航速精度主要取决于目标位置测量精度,与目标本身航速大小基本没有关系。低速水面目标由于在雷达扫描周期内运动距离较小,受雷达测量精度的限制,导致通过航迹滤波输出的航速误差相对目标航速而言往往较大。而且对于同样的航速误差,目标航速越小航速误差比越大,以至于当目标航速较小时,滤波输出的航速几乎不可用。
针对低速水面目标航速解算问题,袁桂生[1]在介绍了海空目标相对和绝对航速解算方法的基础上,探讨了几种提高航速解算精度的途经,但不够深入;黄孟俊等[2]提出一种海上目标航向航速解算新方法,利用雷达载体的精确GPS信息实现海上目标航向航速的高精度解算;韩孟孟等[3]研究了一种多站模式下舰船航向航速快速解算方法,提高了航向航速解算速率,并未提高解算精度。因此为了提高低速水面目标航速解算精度,本文在分析航速精度影响因素的基础上,提出一种基于两级策略的航速精确解算方法,并通过仿真试验验证了算法的有效性。
1 航速精度分析假设
| $\left\{ \begin{array}{l}{x_i} = {r_i}\cos {\eta _i}\sin {\theta _i}{\text{,}}\\{y_i} = {r_i}\cos {\eta _i}\cos {\theta _i}{\text{,}}\\{z_i} = {r_i}\sin {\eta _i}{\text{。}}\end{array} \right.$ | (1) |
依据目标航速的定义,有
| $\left\{ \begin{array}{l}{v_{{x_i}}} = {{\left( {{x_i} - {x_{i - 1}}} \right)} / {{T_i}}}{\text{,}}\\{v_{{y_i}}} = {{\left( {{y_i} - {y_{i - 1}}} \right)} / {{T_i}}}{\text{,}}\\{v_{{z_i}}} = {{\left( {{z_i} - {z_{i - 1}}} \right)} / {{T_i}}}{\text{。}}\end{array} \right.$ | (2) |
其中
进而目标航速
| ${V_i} = \sqrt {v_{{x_i}}^2 + v_{{y_i}}^2 + v_{{z_i}}^2} {\text{。}}$ | (3) |
由于雷达测量存在误差,获得的目标位置参数实际应为
| $\left\{ \begin{array}{l}{{\bar r}_i} = {r_i} + \Delta {r_i}{\text{,}}\\{{\bar \theta }_i} = {\theta _i} + \Delta {\theta _i}{\text{,}}\\{{\bar \eta }_i} = {\eta _i} + \Delta {\eta _i}{\text{。}}\end{array} \right.$ | (4) |
其中
因此,实际获得的航速为
| ${\bar V_i} = \frac{{\sqrt {{{\left( {{{\bar r}_i}\cos {{\bar \eta }_i}\sin {{\bar \theta }_i} - {{\bar r}_{i - 1}}\cos {{\bar \eta }_{i - 1}}\sin {{\bar \theta }_{i - 1}}} \right)}^2} + {{\left( {{{\bar r}_i}\cos {{\bar \eta }_i}\cos {{\bar \theta }_i} - {{\bar r}_{i - 1}}\cos {{\bar \eta }_{i - 1}}\cos {{\bar \theta }_{i - 1}}} \right)}^2} + {{\left( {{{\bar r}_i}\sin {{\bar \eta }_i} - {{\bar r}_{i - 1}}\sin {{\bar \eta }_{i - 1}}} \right)}^2}} }}{{{T_i}}}{\text{,}}$ | (5) |
于是航速误差为
| $\Delta {V_i} = {\bar V_i} - {V_i}{\text{。}}$ | (6) |
将
| $\begin{split}{\bar V_i} = {V_i} + \frac{{\partial \bar V}}{{\partial \Delta {r_i}}}\Delta {r_i} + \frac{{\partial \bar V}}{{\partial \Delta {r_{i - 1}}}}\Delta {r_{i - 1}} + \frac{{\partial \bar V}}{{\partial \Delta {\theta _i}}}\Delta {\theta _i} +\\ \frac{{\partial \bar V}}{{\partial \Delta {\theta _{i - 1}}}}\Delta {\theta _{i - 1}} + \frac{{\partial \bar V}}{{\partial \Delta {\eta _i}}}\Delta {\eta _i} + \frac{{\partial \bar V}}{{\partial \Delta {\eta _{i - 1}}}}\Delta {\eta _{i - 1}}\end{split}{\text{,}}$ | (7) |
其中
| $\frac{{\partial \bar V}}{{\partial \Delta {r_i}}} = \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}\cos {\eta _i}\sin {\theta _i} + \frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}\cos {\eta _i}\cos {\theta _i} + \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}\sin {\eta _i}{\text{,}}$ |
| $\begin{split}\frac{{\partial \bar V}}{{\partial \Delta {r_{i - 1}}}} = - \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}\cos {\eta _{i - 1}}\sin {\theta _{i - 1}}-\\\frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}\cos {\eta _{i - 1}}\cos {\theta _{i - 1}} - \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}\sin {\eta _{i - 1}}\end{split}{\text{,}}$ |
| $\frac{{\partial \bar V}}{{\partial \Delta {\theta _i}}} = \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}{y_i} - \frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}{x_i}{\text{,}}$ |
| $\frac{{\partial \bar V}}{{\partial \Delta {\theta _{i - 1}}}} = \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}{y_{i - 1}} - \frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}{x_{i - 1}}{\text{,}}$ |
| $\begin{split}\frac{{\partial \bar V}}{{\partial \Delta {\eta _i}}} = - \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}{r_i}\sin {\eta _i}\sin {\theta _i} -\\\frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}{r_i}\sin {\eta _i}\cos {\theta _i} + \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}{r_i}\cos {\eta _i}\end{split}{\text{,}}$ |
| $\begin{split}\frac{{\partial \bar V}}{{\partial \Delta {\eta _{i - 1}}}} = \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}{r_{i - 1}}\sin {\eta _{i - 1}}\sin {\theta _i} +\\\frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}{r_{i - 1}}\sin {\eta _{i - 1}}\cos {\theta _{i - 1}} - \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}{r_{i - 1}}\cos {\eta _{i - 1}}{\text{,}}\end{split}$ |
因此航速误差为
| $\begin{split}\Delta {V_i} = \frac{{\partial \bar V}}{{\partial \Delta {r_i}}}\Delta {r_i} + \frac{{\partial \bar V}}{{\partial \Delta {r_{i - 1}}}}\Delta {r_{i - 1}} + \frac{{\partial \bar V}}{{\partial \Delta {\theta _i}}}\Delta {\theta _i} + \\\frac{{\partial \bar V}}{{\partial \Delta {\theta _{i - 1}}}}\Delta {\theta _{i - 1}} + \frac{{\partial \bar V}}{{\partial \Delta {\eta _i}}}\Delta {\eta _i} + \frac{{\partial \bar V}}{{\partial \Delta {\eta _{i - 1}}}}\Delta {\eta _{i - 1}}\end{split}{\text{。}}$ | (8) |
下面依次分析距离、方位、俯仰各测量误差对航速精度的影响。
1.1 距离误差影响距离误差往往时刻变化,不失一般性,假设距离误差从
| $d\left( {\Delta {r_i}} \right) = \Delta {r_i} - \Delta {r_{i - 1}}{\text{,}}$ | (9) |
从而可得距离误差对航速精度的影响为
| $\begin{split}\!\!\Delta {V_{ri}} =& \left[ {\frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}\left( {\cos {\eta _i}\sin {\theta _i} - \cos {\eta _{i - 1}}\sin {\theta _{i - 1}}} \right) + } \right.\\&\left[ {\frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}\left( {\cos {\eta _i}\cos {\theta _i} - \cos {\eta _{i - 1}}\cos {\theta _{i - 1}}} \right) + } \right.\\&\left. {\frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}\left( {\sin {\eta _i} - \sin {\eta _{i - 1}}} \right)} \right]\Delta {r_i} + \left( {\frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}\cos {\eta _{i - 1}}\sin {\theta _{i - 1}} + } \right.\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\\&\left. {\frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}\cos {\eta _{i - 1}}\cos {\theta _{i - 1}} + \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}\sin {\eta _{i - 1}}} \right)d\left( {\Delta {r_i}} \right){\text{。}}\!\!\!\!\!\!\end{split}$ | (10) |
对低速水面目标而言,在相邻2个周期内,
| $\begin{split}\Delta {V_{ri}} \approx & \left( {\frac{{{v_{{x_i}}}}}{{{V_i}}}\cos {\eta _{i - 1}}\sin {\theta _{i - 1}} + \frac{{{v_{{y_i}}}}}{{{V_i}}}\cos {\eta _{i - 1}}\cos {\theta _{i - 1}} + } \right.\\&\left. {\frac{{{v_{{z_i}}}}}{{{V_i}}}\sin {\eta _{i - 1}}} \right)\frac{{{\rm d}\left( {\Delta {r_i}} \right)}}{{{T_i}}}{\text{。}}\end{split}$ | (11) |
定义
| $\Delta {V_{ri}} = \cos \phi \frac{{{\rm ds}\left( {\Delta {r_i}} \right)}}{{{T_i}}}{\text{,}}$ | (12) |
其中
从式(12)可以看出,距离误差中的固定部分
类似地,假设方位误差从
| $d\left( {\Delta {\theta _i}} \right) = \Delta {\theta _i} - \Delta {\theta _{i - 1}},$ | (13) |
从而可得到方位误差对航速精度的影响为
| $\begin{split}\Delta {V_{\theta i}} = &\left( {\frac{{{v_{{x_i}}}{v_{{y_i}}}}}{{{V_i}}} - \frac{{{v_{{y_i}}}{v_{{x_i}}}}}{{{V_i}}}} \right)\Delta {\theta _i} + \left( {\frac{{{v_{{x_i}}}{y_{i - 1}}}}{{{V_i}{T_i}}} - \frac{{{v_{{y_i}}}{x_{i - 1}}}}{{{V_i}{T_i}}}} \right)d\left( {\Delta {\theta _i}} \right) =\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \\&\left( {\frac{{{v_{{x_i}}}{y_{i - 1}}}}{{{V_i}}} - \frac{{{v_{{y_i}}}{x_{i - 1}}}}{{{V_i}}}} \right)\frac{{d\left( {\Delta {\theta _i}} \right)}}{{{T_i}}}{\text{。}}\end{split}$ | (14) |
定义
| $\Delta {V_{\theta i}} = {r_{i - 1}}\left( {\cos \phi ' - \frac{{{v_{zi}}{z_{i - 1}}}}{{{r_{i - 1}}}}} \right)\frac{{d\left( {\Delta {\theta _i}} \right)}}{{{T_i}}}{\text{,}}$ | (15) |
其中
对水面目标而言
| $\Delta {V_{\theta i}} = {r_{i - 1}}\cos \phi '\frac{{d\left( {\Delta {\theta _i}} \right)}}{{{T_i}}}{\text{。}}$ | (16) |
从式(16)可以看出,方位误差中的固定部分
类似地,假设俯仰误差从
| $d\left( {\Delta {\eta _i}} \right) = \Delta {\eta _i} - \Delta {\eta _{i - 1}}{\text{,}}$ | (17) |
从而可得俯仰误差对航速精度的影响为
| $\!\!\!\!\!\!\!\!\begin{split}& \Delta {V_{\eta i}} = \left[ { - \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}\left( {{r_i}\sin {\eta _i}\sin {\theta _i} - {r_{i - 1}}\sin {\eta _{i - 1}}\sin {\theta _{i - 1}}} \right) - } \right.\\& \frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}\left( {{r_i}\sin {\eta _i}\cos {\theta _i} - {r_{i - 1}}\sin {\eta _{i - 1}}\cos {\theta _{i - 1}}} \right) + \\& \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}\left. {\left( {{r_i}\cos {\eta _i} \!-\! {r_{i - 1}}\cos {\eta _{i - 1}}} \right)} \right]\Delta {\eta _i} \!+\! \left( { \!-\! \frac{{{v_{{x_i}}}}}{{{V_i}{T_i}}}{r_{i - 1}}\sin {\eta _{i - 1}}\sin {\theta _i} - } \right. \\& \left. {\frac{{{v_{{y_i}}}}}{{{V_i}{T_i}}}{r_{i - 1}}\sin {\eta _{i - 1}}\cos {\theta _{i - 1}} + \frac{{{v_{{z_i}}}}}{{{V_i}{T_i}}}{r_{i - 1}}\cos {\eta _{i - 1}}} \right)d\left( {\Delta {\eta _i}} \right){\text{。}}(18)\end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!$ |
对低速水面目标而言,在相邻2个周期内,
| $\begin{split}\Delta {V_{\eta i}} \approx & {r_{i - 1}}\left( { - \frac{{{v_{{x_i}}}}}{{{V_i}}}\sin {\eta _{i - 1}}\sin {\theta _i} - \frac{{{v_{{y_i}}}}}{{{V_i}}}\sin {\eta _{i - 1}}\cos {\theta _{i - 1}} + } \right.\\&\left. {\frac{{{v_{{z_i}}}}}{{{V_i}_i}}\cos {\eta _{i - 1}}} \right)\frac{{d\left( {\Delta {\eta _i}} \right)}}{{{T_i}}}{\text{。}}\end{split}$ | (19) |
定义
| $\Delta {V_{\eta i}} \approx {r_{i - 1}}\cos \phi ''\frac{{d\left( {\Delta {\eta _i}} \right)}}{{{T_i}}}{\text{,}}$ | (20) |
其中
从式(20)可以看出,俯仰误差中的固定部分
通过以上分析可得,欲减小距离、方位、俯仰各测量误差对航速精度的影响,均需要增加
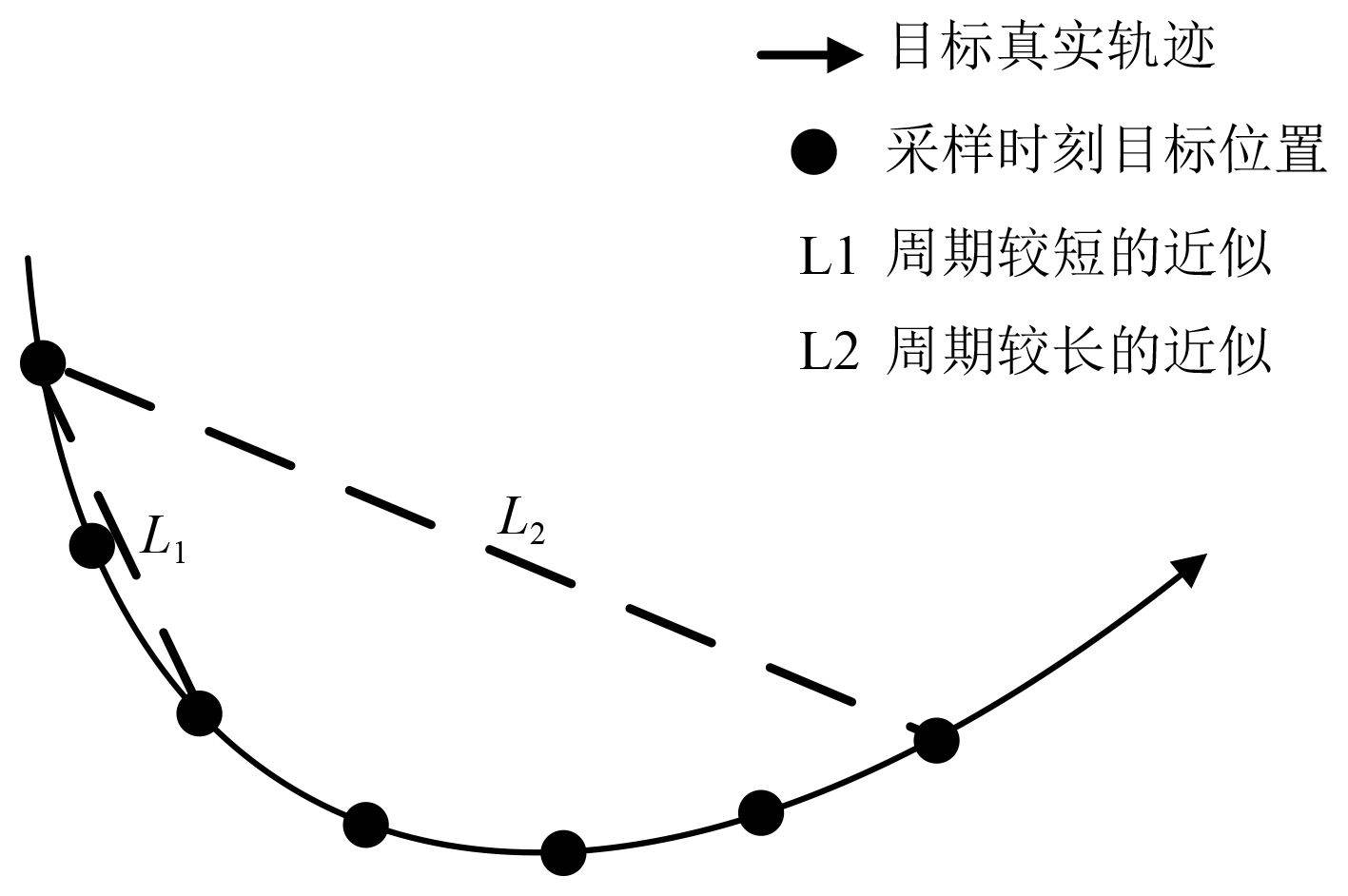
|
图 1 周期大小对直线近似的影响 Fig. 1 The effect of the periodic size on the linear approximation |
为了克服这个困难,本文采用两级解算策略。如图2所示,首先选取较小的
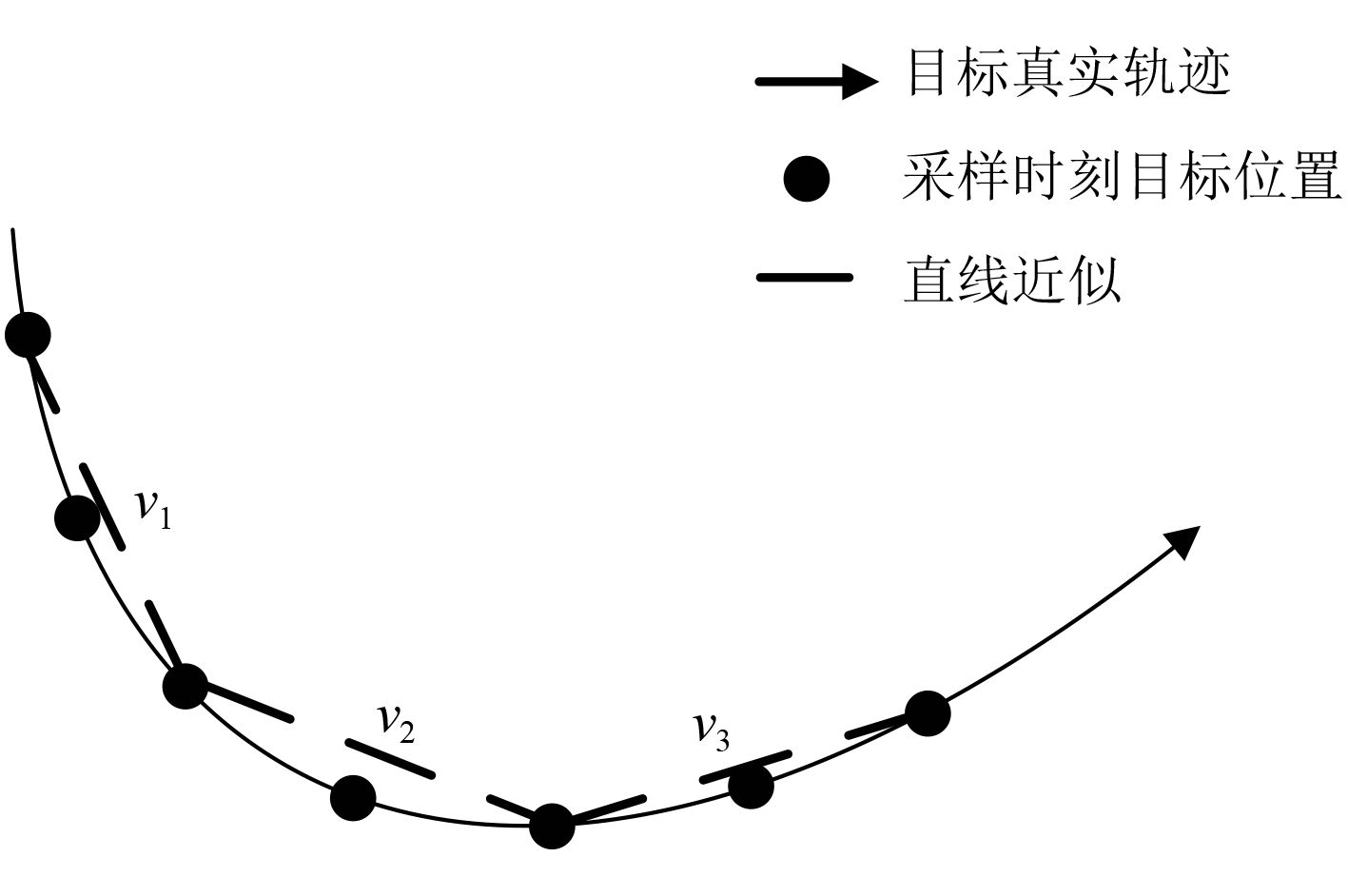
|
图 2 基于两级策略的航速精确解算示意图 Fig. 2 Accurate calculation of speed based on two-level strategy |
均值漂移(Mean Shift)算法是一种在一组数据的概率密度分布中寻找局部极值稳定的方法,具有良好的平滑效果,同时还能适应一定的变化[4 – 6]。因此采用mean shift算法对
① 初始化
②计算核函数
| ${G_{hi}} = \sum\limits_{i = 1}^m {\exp \left[ { - {{\left( {\frac{{{v_i} - {{\tilde v}_k}}}{h}} \right)}^2}} \right]} \begin{array}{*{20}{c}} ,&{} \end{array}i = 1, \cdots ,m{\text{。}}$ | (21) |
其中
③计算mean shift值
| ${\tilde v_{k + 1}} = \frac{{\sum\limits_{i = 1}^m {{G_{hi}}{w_i}} {v_i}}}{{\sum\limits_{i = 1}^m {{G_{hi}}{w_i}} }}{\text{,}}$ | (22) |
其中
④判断
下面设置3个典型的场景对算法进行仿真验证。仿真中,雷达探测周期为2 s,距离探测精度为100 m,方位探测精度为0.3°。
场景1:平台以6 m/s的航速向正北运动,目标初始相距平台约30 km,以10 m/s的航速匀速直线向正东运动。
场景2:平台以6 m/s的航速向正北运动,目标初始相距平台约30 km,开始以10 m/s的航速匀速直线向正东运动,期间一段时间减速运动。
场景3:平台以6 m/s的航速向正北运动,目标初始相距平台约30 km,开始做转弯运动,之后以10 m/s的航速匀速直线向正东运动。
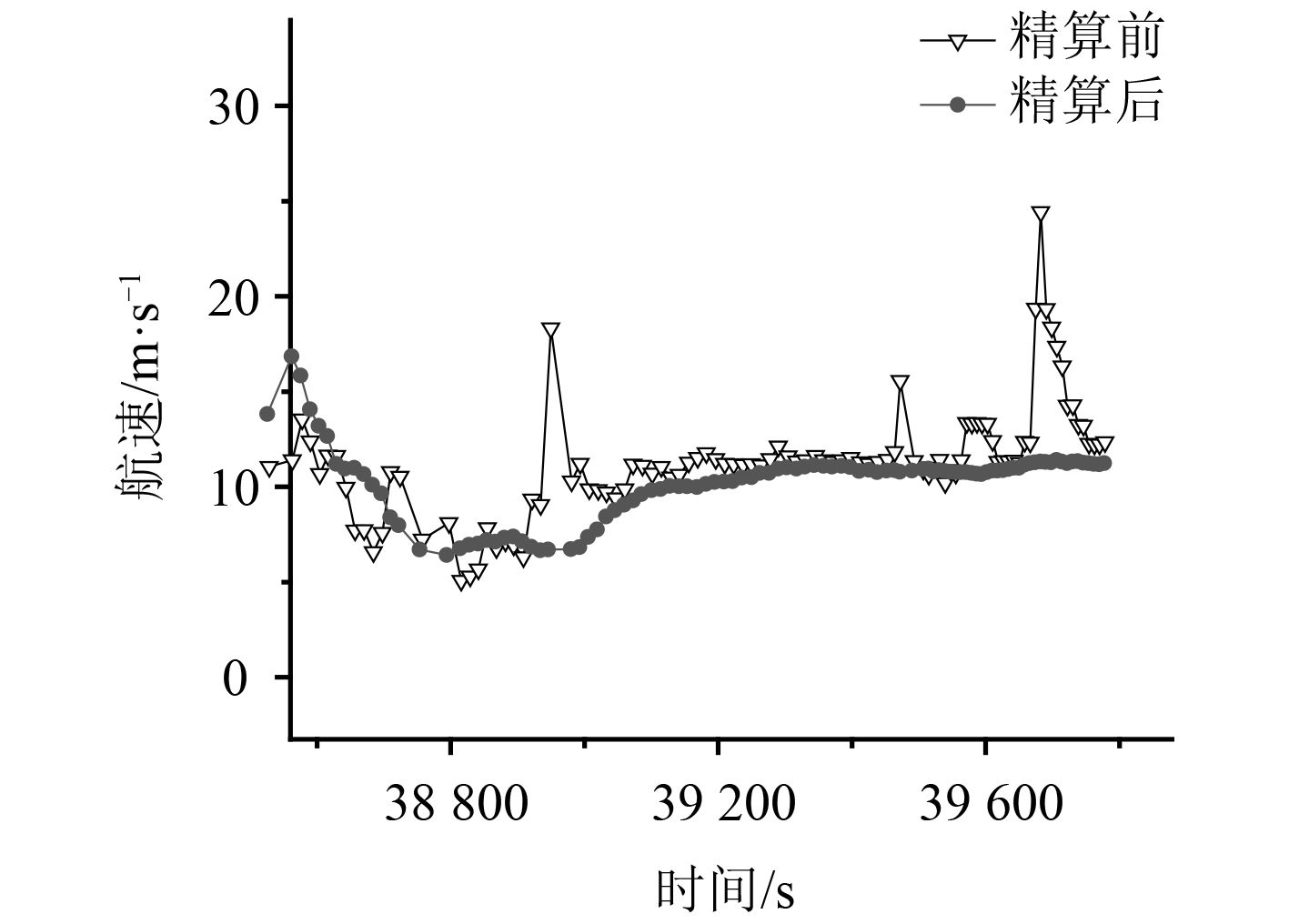
通过航速精确解算得到精算前后航速对比结果,分别如图3、图4和图5所示。精算前航速指雷达上报的航速,精算后航速指采用本文算法精确解算得到的航速。
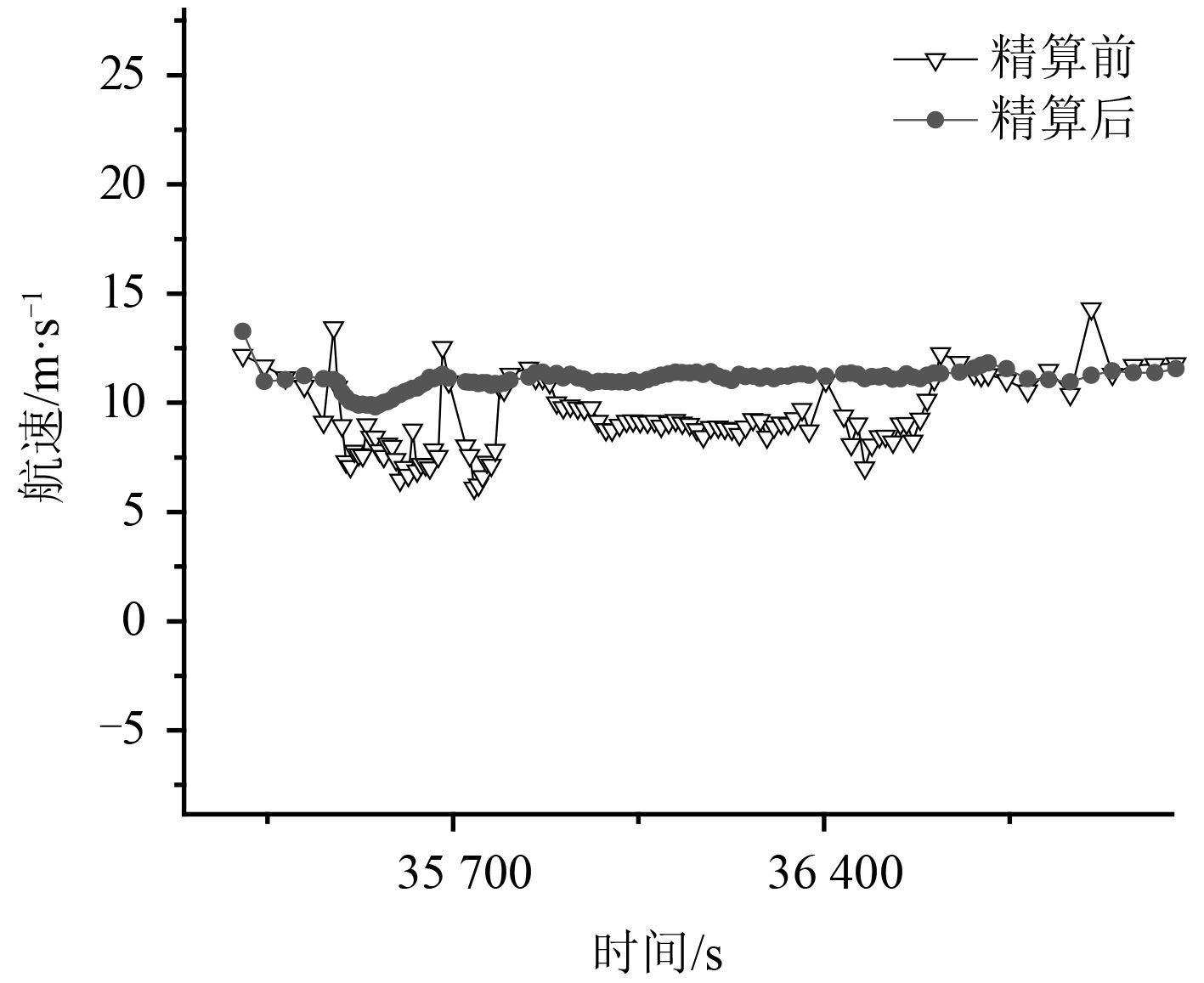
|
图 3 目标1精算前后航速对比结果 Fig. 3 Speed comparison result before and after the accurate calculation of target 1 |
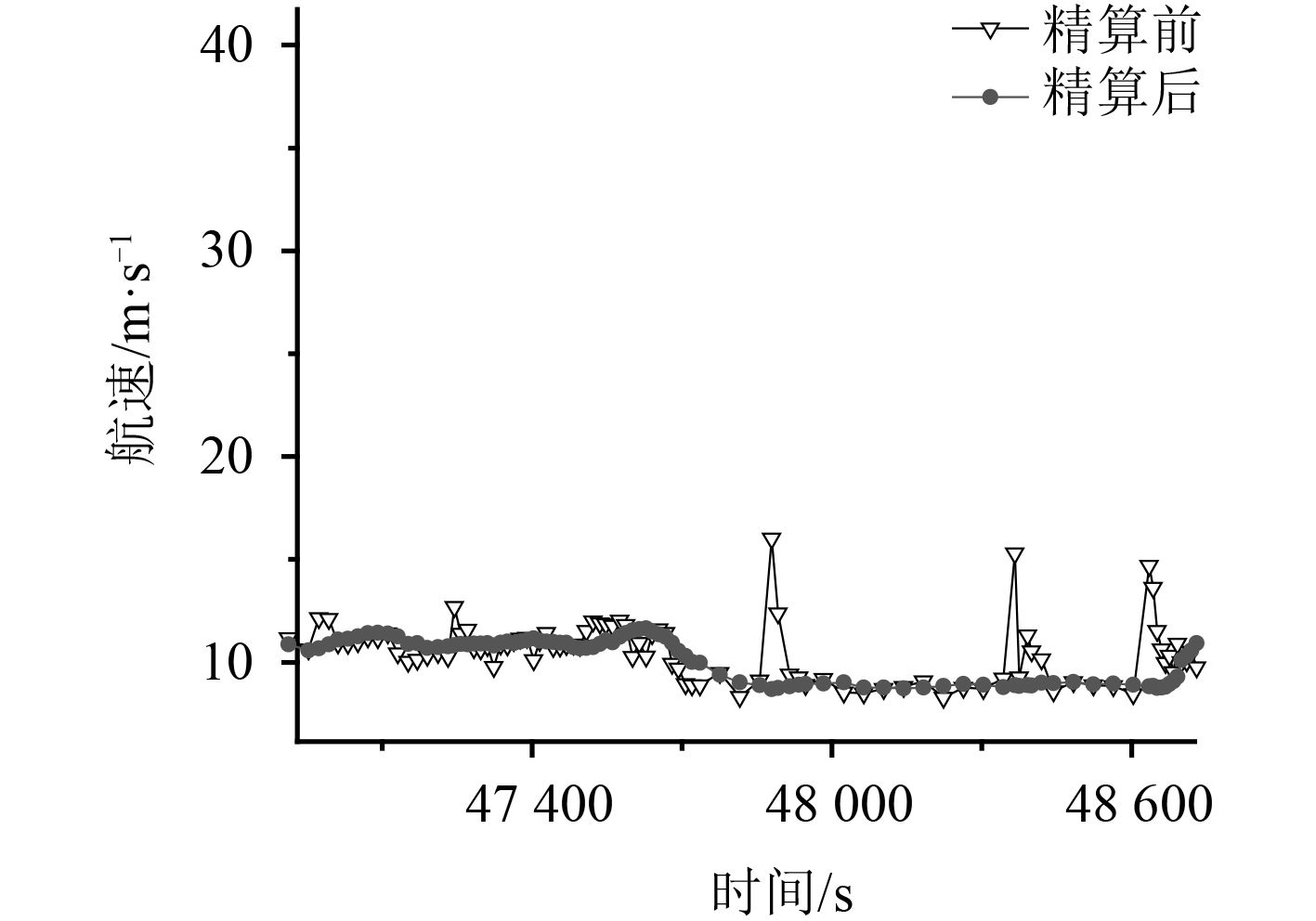
|
图 4 目标2精算前后航速对比结果 Fig. 4 Speed comparison result before and after the accurate calculation of target 2 |
|
图 5 目标3精算前后航速对比结果 Fig. 5 Speed comparison result before and after the accurate calculation of target 3 |
统计精算前后的航速误差,如表1所示。
|
|
表 1 精算前后航速误差 Tab.1 Speed error before and after accurate calculation |
从仿真验证结果可以看出:该算法能够大幅提高航速精度(见表1),并且有效抑制原航速信息中存在的毛刺现象(如图3~图5所示)。
4 结 语针对低速水面目标航速解算问题,本文首先从理论角度分析了航速精度的影响因素,发现距离、方位、俯仰测量误差中的变化部分是影响航速精度的主要因素,要降低其影响需要增大解算周期。然后根据分析结果设计了基于两级策略的航速精确解算方法,单次解算时适度增大解算周期,以取得较好的直线近似性能,在此基础上对多个单次解算结果进行平滑处理,以达到进一步增大解算周期的效果。最后通过仿真试验对算法进行验证,结果表明本文算法在提高航速精度等方面具有明显效果。
| [1] | 袁桂生. 目标航向航速解算及验证方法研究[J]. 雷达与对抗, 2009, 1: 26–29. |
| [2] | 黄孟俊, 陈建军, 赵宏钟. 海上目标航向航速解算新方法[J]. 信号处理, 2011, 27(7): 1035–1038. http://mall.cnki.net/magazine/Article/XXCN201107018.htm |
| [3] | 韩孟孟, 池庆玺, 裴虎城. 一种多站模式下舰船航向航速快速解算方法[J]. 战术导弹技术, 2015, 1: 69–72. http://www.cnki.com.cn/Article/CJFDTotal-ZSDD201501014.htm |
| [4] | COMANICIU C, RAMESH V, MEER P. Real-time tracking of non-rigid objects using mean shift[C].// Proceedings IEEE Conference on Computer Vision and Pattern Recognition, 2000, 2: 142–149. |
| [5] | 江二华. 基于改进Mean Shift的运动目标跟踪算法研究[D]. 济南: 山东大学, 2014. |
| [6] | 肖江, 陈想, 丁亮. 一种改进的Mean shift运动目标跟踪算法[J]. 信息技术, 2017, 1: 127–130. http://www.cqvip.com/QK/92337A/201303/44793287.html |
 2018, Vol. 40
2018, Vol. 40
