2. 海军工程大学 科研部,湖北 武汉 430033
2. Research Department, Naval University of Engineering, Wuhan 430033, China
20世纪80 年代初,美国学者E.G williams等提出了近场声全息(NAH)的概念[1- 2]。NAH考虑了倏逝波的影响,突破了瑞利判据对重建分辨率的限制,近年来得到广泛应用。NAH与远场声全息不同,在被测声源的近表面的全息面上记录测量数据,然后通过傅里叶变换技术重建三维声场的声压、声强、粒子振速。由于二维傅里叶变换算法本身的限制,平面NAH要求测量面必须和声源面共形[3],为了使NAH能够应用于任意形状的声源面,边界元方法[4]被提出来。陈心昭等对边界元方法进行改进,提出了分布源边界点法[5],进一步简化了边界元方法中对系数矩阵的繁琐计算。
根据格林公式,近场声全息中重构面声压的数据与全息面声压的数据以及二者之间的距离三者之间在波数域内是比较简单的代数关系。但是只有当全息面大于声源的4倍以上时,常规近场声全息算法重构的三维声场空间的参数才有效。在实际工程中,尤其是对飞机、舰船等大型设备而言,考虑到经济性等因素的影响,全息面很难大于声源的4倍。为了解决这个问题,有学者提出了Patch近场声全息的概念,并提出了多种算法,并对每种算法进行了深入研究。其中基于FFT的数据外推算法、基于PGA数据外推算法和SONAH算法是解决Patch近场声全息问题最经典的算法。
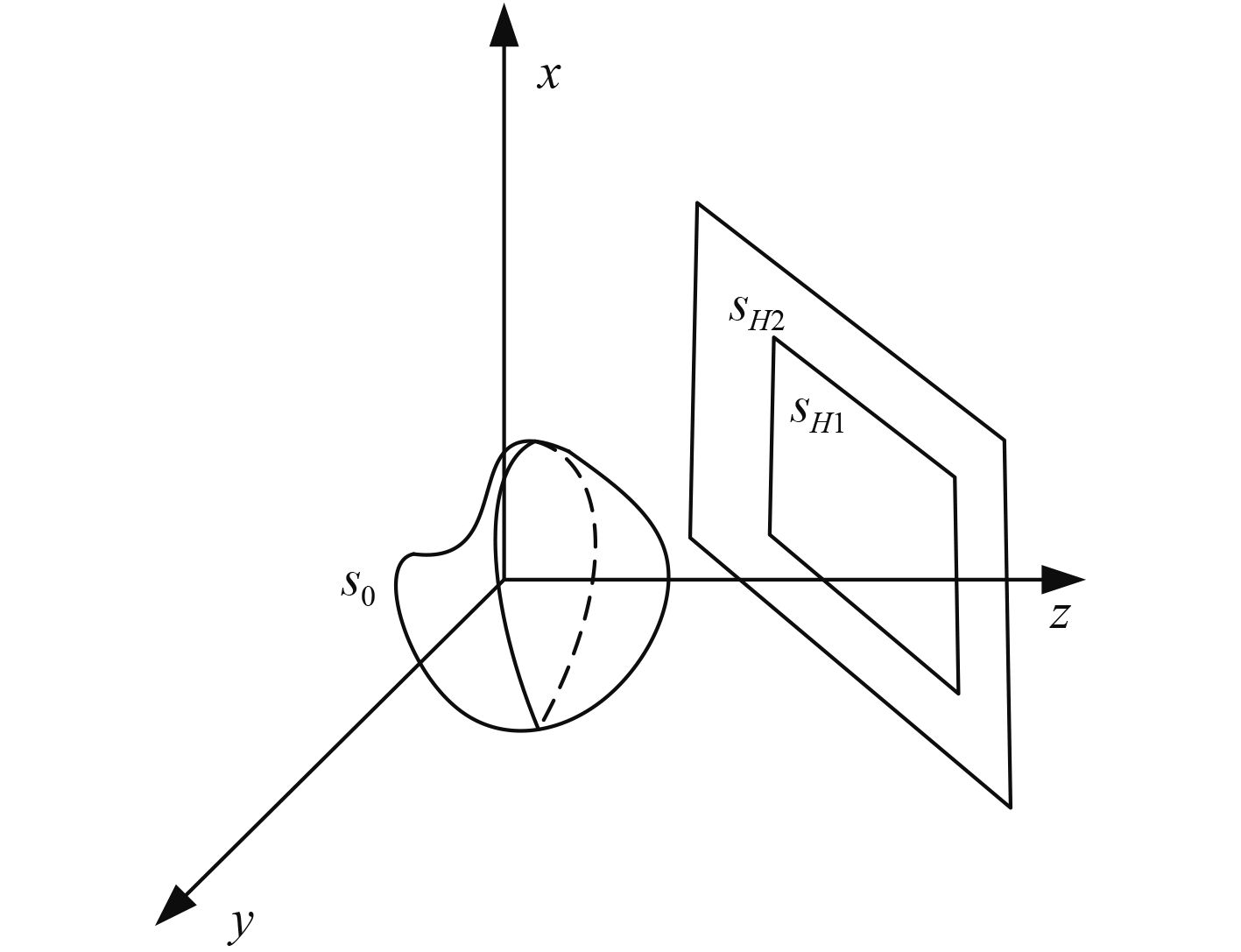
1 Patch近场声全息的算法Patch近场声全息的算法[6–10]可以分为2类,第1类算法以全息面数据外推为主要特征,其基础是一般的近场声全息。具有代表性的是基于快速傅里叶变换(FFT)的Patch近场声全息和基于能量带限(PGA)的Patch近场声全息。第2类算法以借助空域变换重构声源为主要特征。此类算法不存在空间域和波数域的转换,也就不存在“卷绕误差”。具有代表性的是统计最优(SONAH)近场声全息算法。如图1所示,以声源体形心为原点建立坐标轴。
|
图 1 全息面声压外推示意图 Fig. 1 Schematic diagram of holographic surface acoustic pressure extrapolation |
基于FFT进行数据外推其过程比较简单,分为数据补零、二维傅里叶变换、滤波、二维傅里叶逆变换、真实孔径数据替换、重建声源等6个步骤。具体来说,步骤如下:
1) 补零
对
| $p_{H2}^0(x,y,{z_H}) = \left\{ \begin{gathered} {p_{H1}}(x,y,{z_H}),(x,y) \in {S_{H1}}\text{;} \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,(x,y) \in {S_{H2}}\text{。}\\ \end{gathered} \right.$ | (1) |
2) 二维傅里叶变换
| $\tilde p_{H2}^i(x,y,{z_H}) = F[p_{H2}^i(x,y,{z_H})]\text{。}$ | (2) |
3) 滤波
| $\tilde p_{H2}^i(x,y,{z_H}) = \Pi ({a^i})\tilde p_{H2}^i(x,y,{z_H})\text{。}$ | (3) |
4) 二维傅里叶逆变换
| $p_{H2}^{i + 1}(x,y,{z_H}) = {F^{ - 1}}(p_{H2}^i(x,y,{z_H}))\text{。}$ | (4) |
5) 真实孔径数据替换
| $p_{H2}^{i + 1}(x,y,{z_H}) = \left\{ \begin{gathered} {p_{H1}}(x,y,{z_H}),(x,y) \in {S_{H1}}\text{;} \\ p_{H2}^{i + 1}(x,y,{z_H}),(x,y) \notin {S_{H2}} \text{。} \\ \end{gathered} \right.$ | (5) |
计算滤波器因子变化率
6) 重建声源
利用外推得到的扩展的全息面声压数据采用常规的近场声全息方法进行重建。
1.2 基于PGA的Patch近场声全息声源体辐射的声波可以分为传播波和倏逝波,倏逝波随着传播距离的增大成指数倍衰减。因此全息面声压在某种意义上可以看做是一种波数域带限或近似带限的信号。利用全息面声压的波数域带限特性,采用带限外推算法可以实现全息面声压数据的外推。计算过程分为补零、二维傅里叶变换、根据能量带限法则滤波、二维傅里叶逆变换、真实孔径数据替换和重建声源6步。具体来说,计算步骤如下:
1) 补零
对
| $p_{H2}^0(x,y,{z_H}) = \left\{ \begin{gathered} {p_{H1}}(x,y,{z_H}),(x,y) \in {S_{H1}} \text{;} \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,(x,y) \in {S_{H2}} \text{。} \\ \end{gathered} \right.$ | (6) |
2) 二维傅里叶变换
| $\tilde p_{H2}^i(x,y,{z_H}) = F[p_{H2}^i(x,y,{z_H})]\text{。}$ | (7) |
3) 滤波
| $\tilde p_{H2}^i(x,y,{z_H}) = L({k_c})\tilde p_{H2}^i(x,y,{z_H})\text{。}$ | (8) |
根据能量带限的法则滤波,
4) 二维傅里叶逆变换
| $p_{H2}^{i + 1}(x,y,{z_H}) = {F^{ - 1}}(p_{H2}^i(x,y,{z_H}))\text{。}$ | (9) |
5) 真实孔径数据替换
| $p_{H2}^{i + 1}(x,y,{z_H}) = \left\{ \begin{gathered} {p_{H1}}(x,y,{z_H}),(x,y) \in {S_{H1}} \text{;} \\ p_{H2}^{i + 1}(x,y,{z_H}),(x,y) \notin {S_{H1}} \text{。} \\ \end{gathered} \right.$ | (10) |
判断是否达到指定迭代次数,如果已经达到指定次数停止迭代,否则,转到步骤2继续迭代。
6) 重建声源
利用外推得到的扩展的全息面声压数据采用常规的近场声全息方法进行重建。
1.3 统计最优近场声全息(SONAH)统计最优近场声全息方法不涉及空间傅里叶变换,整个计算过程都是在空间域中进行的,在计算过程中不存在数据的卷绕误差,但是在应用统计最优近场声全息方法计算时,矩阵求逆的方法对计算的结果影响较大。
根据波场叠加原理,空间中任一点处的声压可以表示为全息面上所有测量点声压的线性叠加,并且这一权重系数和声场分布相互独立。即
| $p(r) = p_H^{\rm T}c(r)\text{,}$ | (11) |
其中:
1) 求取权重系数
根据权重系数独立于声场分布这一原理,计算重构面声压矩阵与全息面声压矩阵之间的权重系数。
| $a(r) = Ac(r)\text{,}$ | (12) |
其中
2) 计算重构面声压
根据式(2)计算重构面声压。
2 仿真分析本文采用点声源进行仿真分析,仿真球位置x0=y0=z0=0,空气密度
为了对比每种算法重建声场后的误差,定义声压幅值误差和声压相位误差如下:
| $erro{r_{am}} = \frac{{{{\left\| {\left| {{p_{re}}} \right| - \left| {{p_{th}}} \right|} \right\|}_2}}}{{{{\left\| {{p_{th}}} \right\|}_2}}} \times 100\text{\%} \text{,}$ | (13) |
| $erro{r_{ph}} = \frac{{{{\left\| {{{\left| {{p_{re}}} \right|}_{ph}} - {{\left| {{p_{th}}} \right|}_{ph}}} \right\|}_2}}}{{{{\left\| {{{\left| {{p_{th}}} \right|}_{ph}}} \right\|}_2}}} \times 100\text{\%} \text{。}$ | (14) |
其中
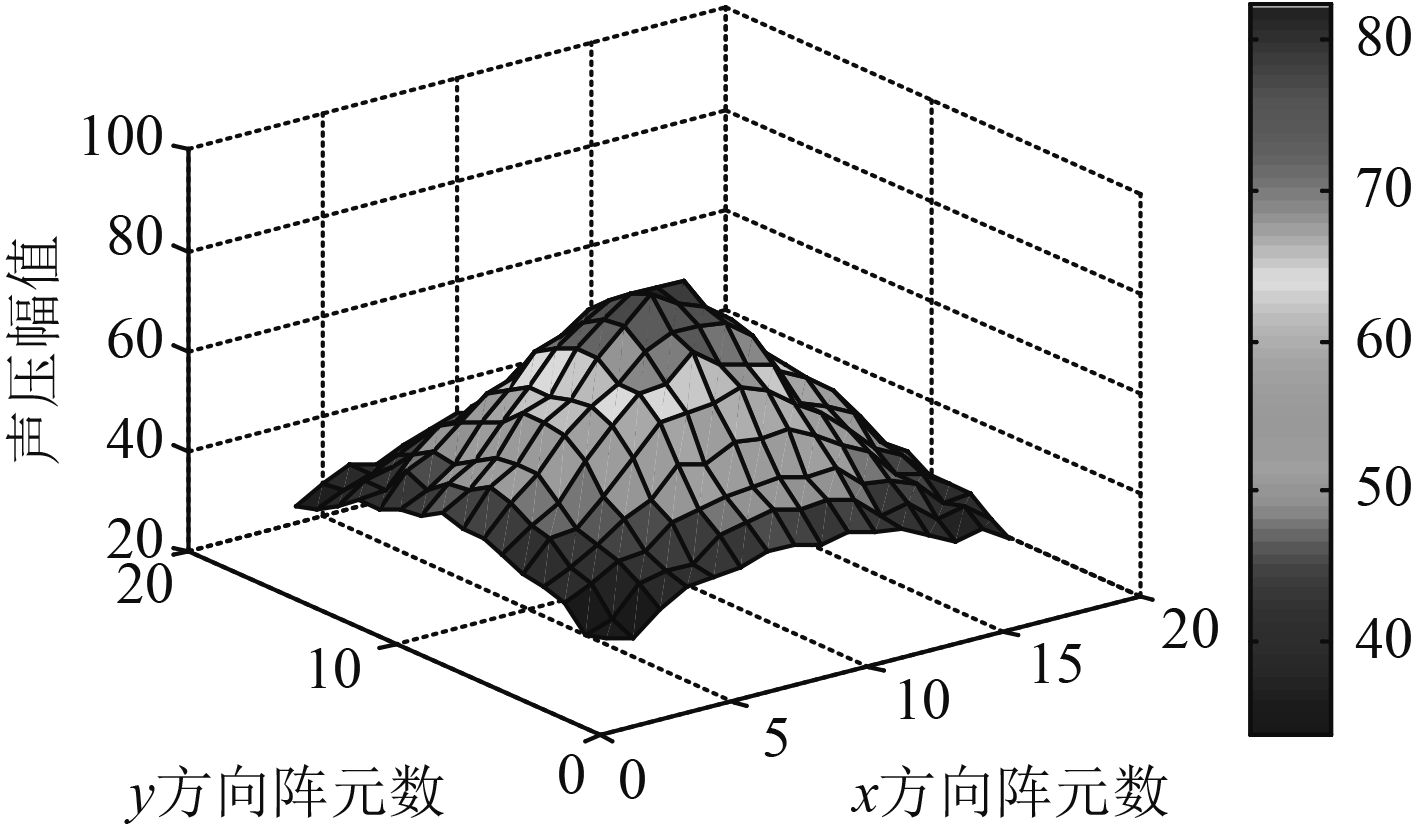
|
Fig. 2 Theory sound pressure of the square holographic surface |
图2表示在自由场内,方形全息面上各阵元的声压幅值。图3表示在重构面处理论的声压幅值。由于全息面的面积较小,必须将全息面面积外推至4倍声源面积才能满足一般意义上的近场声全息的条件,本文采用FFT数据外推算法、PGA数据外推算法、SONAH算法这3种方法对全息面数据外推并重构声源。
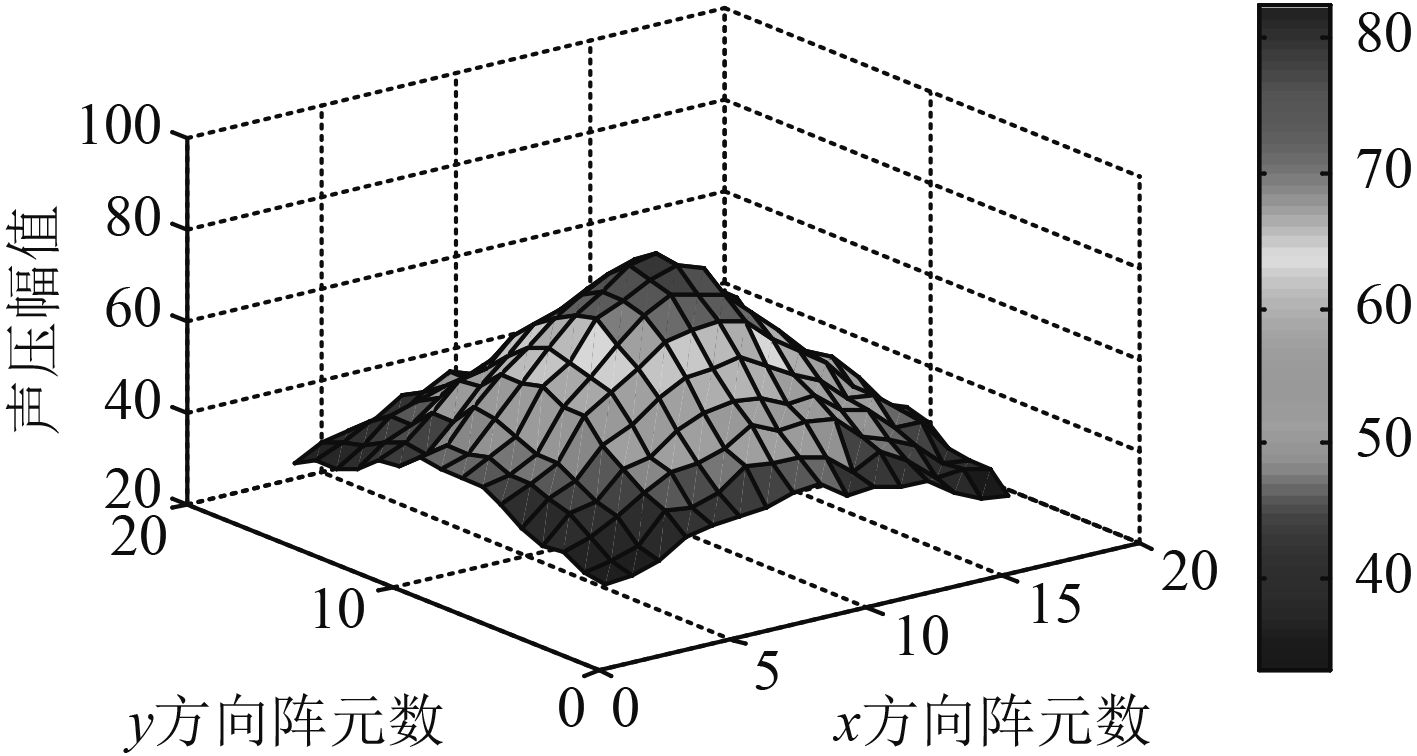
|
Fig. 3 Theory sound pressure of the reconstructed surface |
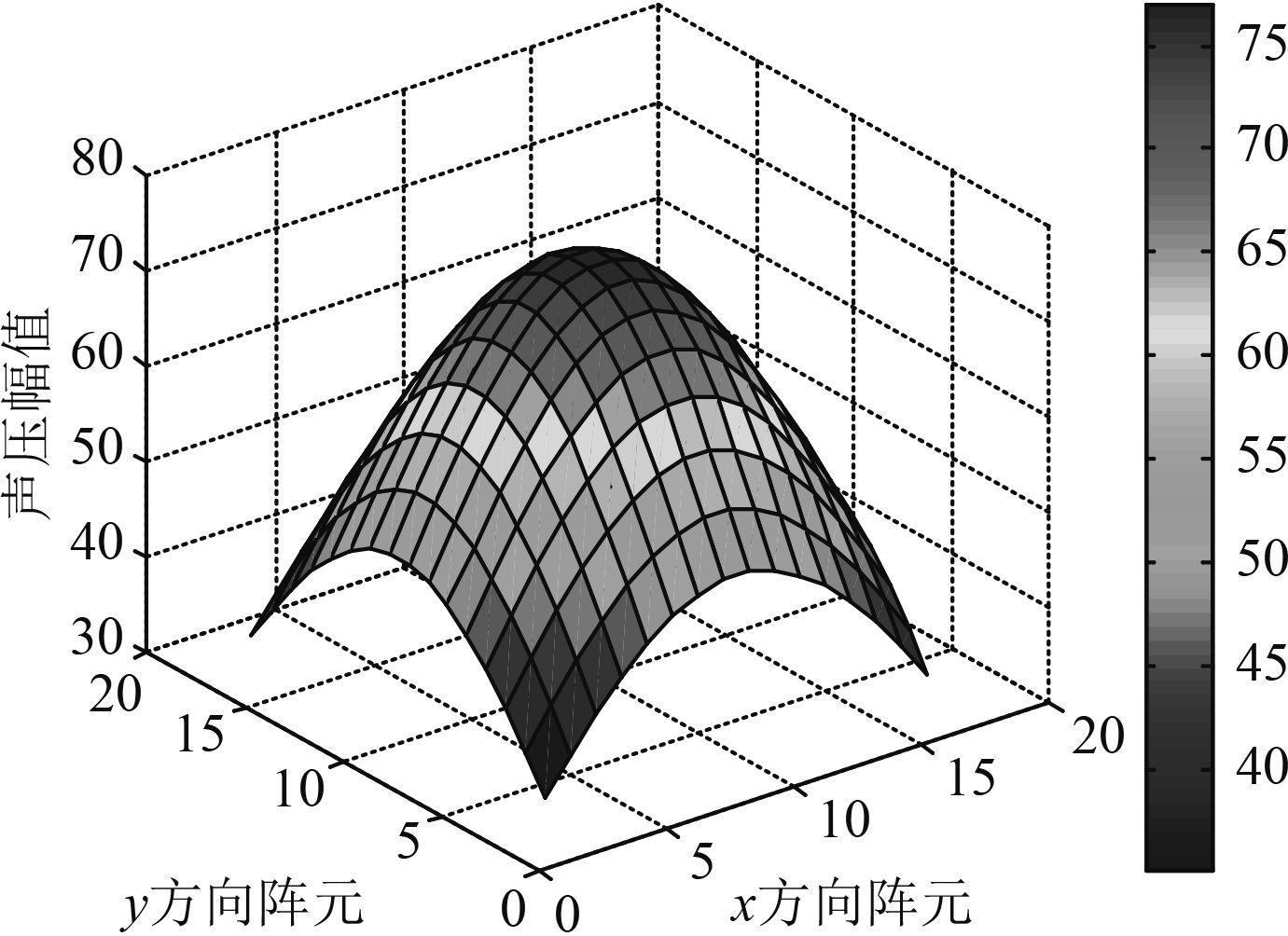
|
Fig. 4 Reconstructed surface sound pressure based on Fourier extrapolation |
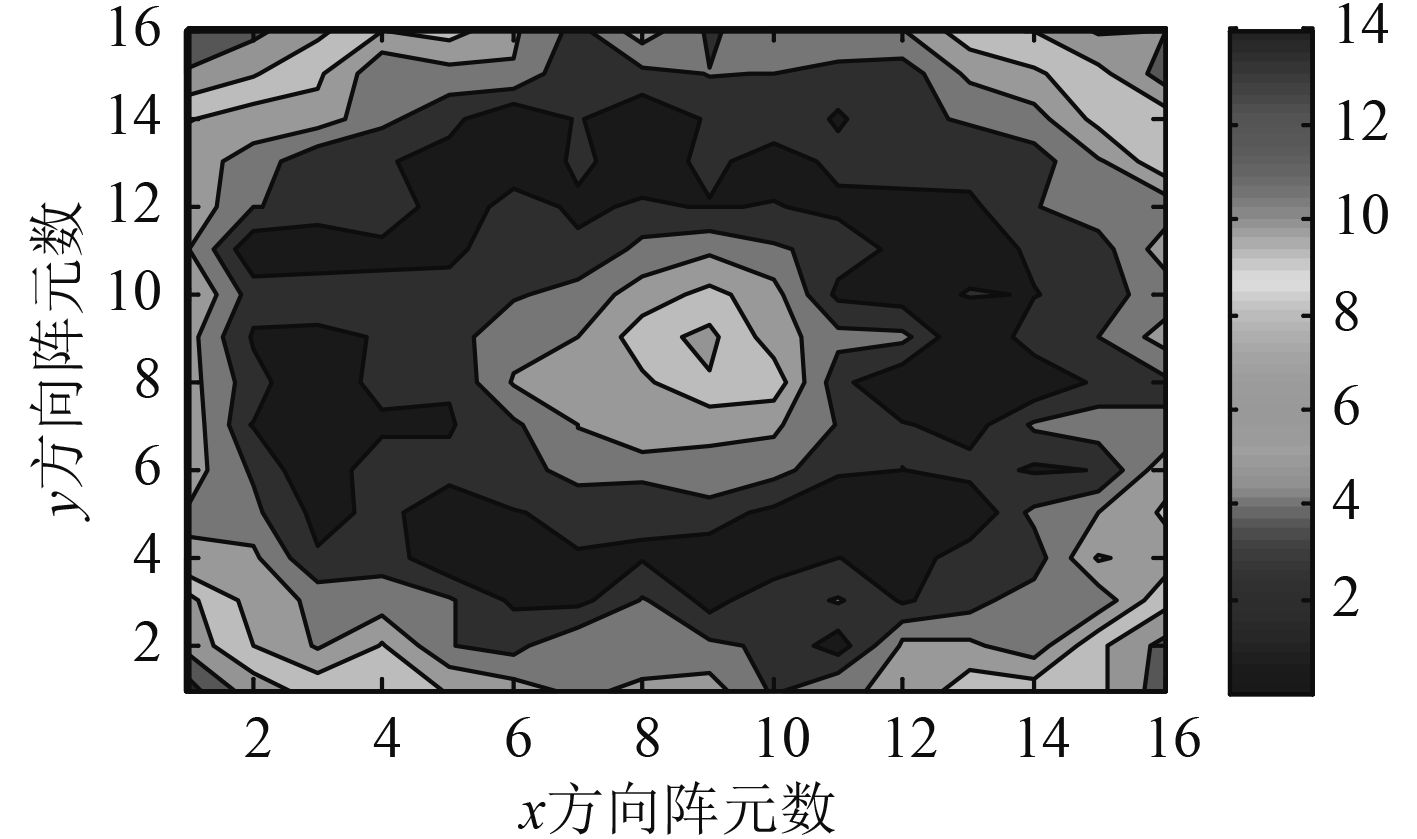
|
Fig. 5 Error distribution of sound pressure amplitude of reconstructed surface based on Fourier extrapolation method |

|
Fig. 6 Error distribution of sound pressure phase of reconstructed surface based on Fourier extrapolation method |
图4是基于FFT数据外推方法获得的重构面声压,图5是声压幅值误差,图6是声压相位误差,通过计算得出采用基于FFT数据外推方法重构声源后其声压幅值误差为10%,声压相位误差为0.16%。在重构面中心声源处和重构面边缘处声压幅值误差和声压相位误差都较大(声压幅值误差位于6%~14%之间),这是由于声压变化的梯度过大,导致算法误差较大,深色的环形区域显示重构的声源声压几乎和理论值相等。说明采用此算法能较好的重构声源。
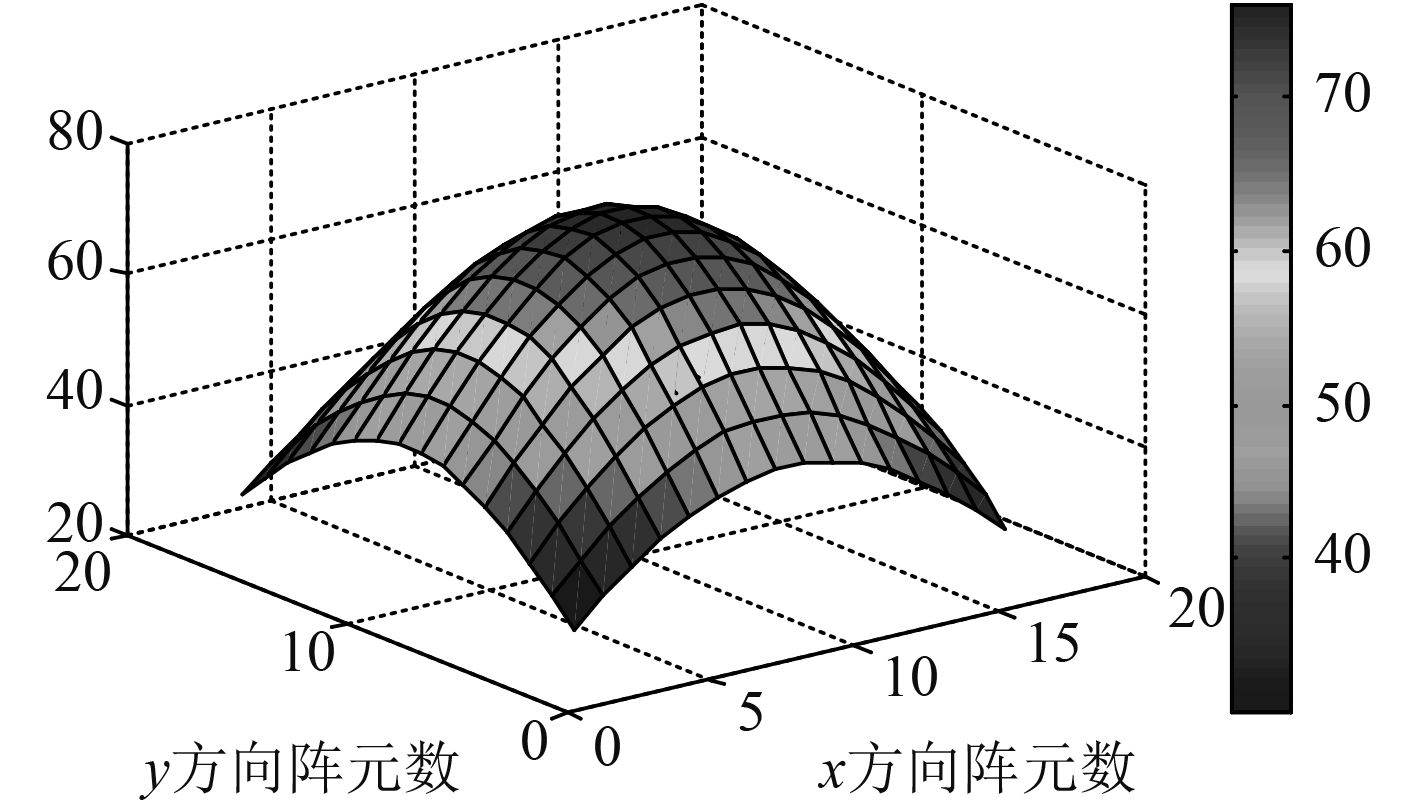
|
Fig. 7 Reconstructed surface sound pressure based on energy band extrapolation method |
图7是基于能量带限外推方法获得的重构面声压,图8是声压幅值误差,图9是声压相位误差,通过计算得出采用基于能量带限外推方法重构声源后其声压幅值误差为7%,声压相位误差为0.12%。重构声源的误差小于7%,说明采用能量带限外推的方法能较为准确的重构出声源。

|
图 8 基于能量带限外推方法的重构面声压幅值误差分布 Fig. 8 Error distribution of sound pressure amplitude of reconstructed surface based on energy band extrapolation method |

|
图 9 基于能量带限外推方法的重构面声压相位误差分布 Fig. 9 Error distribution of sound pressure phase of reconstructed surface based on energy band extrapolation method |
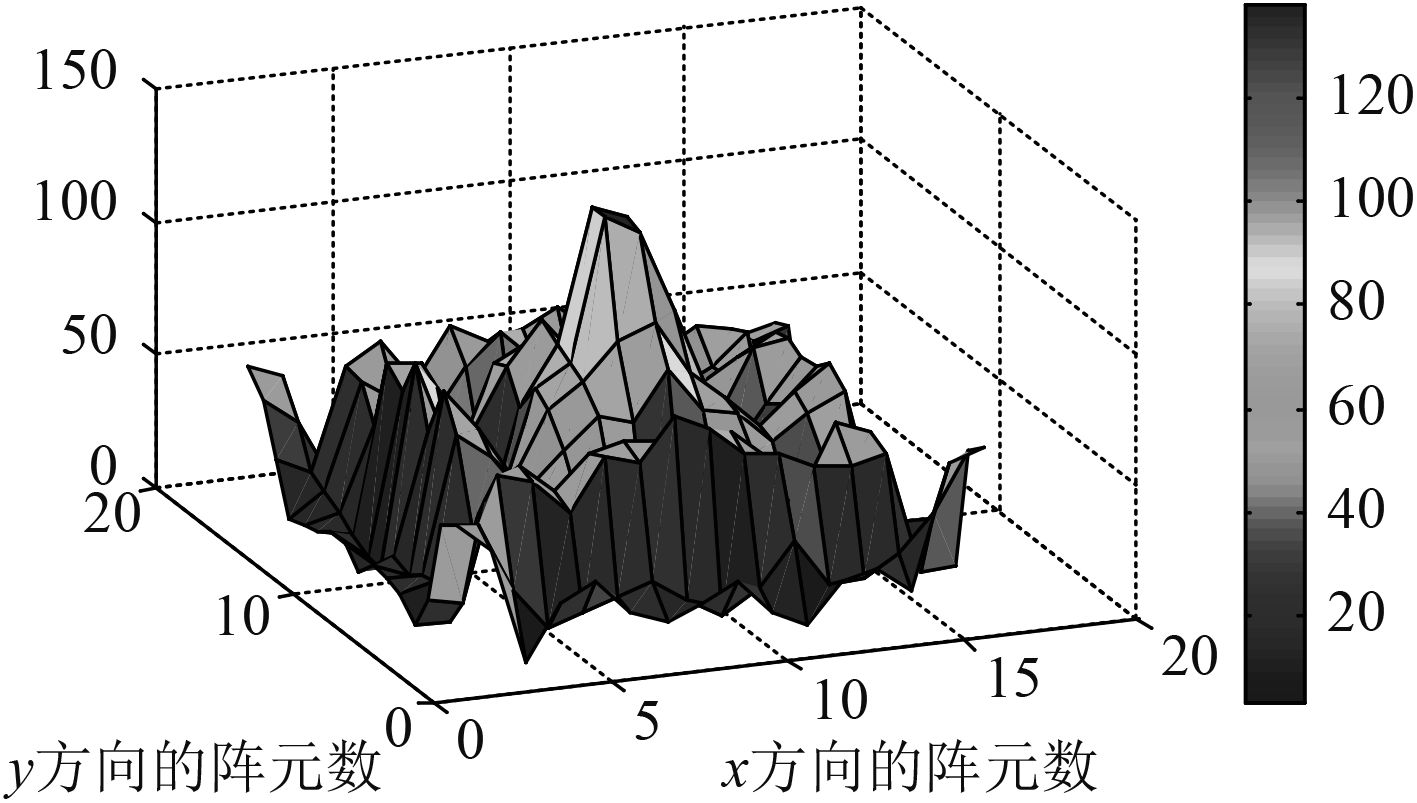
|
Fig. 10 Reconstructed surface sound pressure based on statistical optimal near-field acoustic holography |

|
图 11 基于统计最优近场声全息方法的重构面声压幅值误差分布 Fig. 11 Error distribution of sound pressure amplitude of reconstructed surface based on statistical optimal near-field acoustic holography |

|
图 12 基于统计最优近场声全息方法的重构面声压相位误差分布 Fig. 12 Error distribution of sound pressure phase of reconstructed surface based on statistical optimal near-field acoustic holography |
图10是基于统计最优近场声全息方法获得的重构面声压,图11是声压幅值误差,图12是声压相位误差,通过计算得出采用基于统计最优近场声全息方法重构声源后其声压幅值误差为40%。声压幅值误差最大处出现在声源中心处,达到50%,从图10可以看出,重构的声源失真比较严重。因为统计最优近场声全息方法中需要对矩阵求逆,本算例采用标准tikhonov方法求逆,对于矩阵奇异值较小项对应的区域其计算误差不可避免会增大,以至于计算结果不能用。
3 结 语Patch近场声全息的计算方法主要有基于快速傅里叶变换的数据外推算法、基于能量带限的数据外推算法和统计最优近场声全息算法。前2种算法的本质是首先将全息面获得的数据外推,满足全息面大于4倍声源的条件,然后采用一般的近场声全息的方法重构声源,关键在于数据外推的准确性。统计最优近场声全息算法将全息面、重构面采用矩阵的方法联系起来,计算的过程中需要对矩阵求逆,矩阵求逆的准确性关系着重建结果的有效性。通过改善矩阵求逆的结果能大大提高重建结果的准确性。
本文通过建立点声源声辐射模型,分析了FFT数据外推算法、PGA数据外推算法以及统计最优近场声全息算法在重构声源后的误差,并将几种算法的重建误差进行对比,结果表明当全息面小于4倍声源时基于能量带限外推的方法能较为准确的重构出声源的各项参数。
| [1] | MAYNARD J D, WILLIAMS E G, LEE Y. Nearfield acoustic holography I: Theory of generalized holography and the development of NAH[J]. Acoustical Society of America, 1985, 78(4): 1395–1413. |
| [2] | VERONESI W A, MAYNARD J D. Nearfield acoustic holography (NAH) II: Holographic reconstruction algorithms and computer implementation[J]. Acoustical Society of America, 1987, 81(5): 1307–1322. |
| [3] | 陈心昭, 毕传兴. 近场声全息技术及其应用[M]. 北京: 科学出版社, 2013. |
| [4] | VERONESI W A, MAYNARD J D. Digital holography reconstruction of sources with arbitrarily shaped surface[J]. Acoustical Society of America, 1989, 85(2): 588–598. |
| [5] | 毕传兴, 陈剑, 周广林, 等. 分布源边界点法在声场全息重建和预测中的应用[J]. 机械工程学报, 2003, 39(8): 81–85. http://www.cqvip.com/QK/90288X/2003008/8290409.html |
| [6] | WILLIAMS E G, HOUSTON B H, HERDIC P C. Fast Fourier transform and singular value decomposition formulations for patch nearfield acoustical holography. J. Acoust. Soc. Am., 2003, 114(3): 1322–1333. |
| [7] | SAIJYOU K, YOSHIKAWA S. Reduction methods of the reconstruction error for large-scale implementation of near-field acoustical holography. J. Acoust. Soc. Am., 2001, 110(4): 2007–2023. |
| [8] | SAIJYOU K. Regularization method of patch near-field acoustical holography for planar geometry. Proceedings of Inter-Noise, Jeju, 2003: 2195–2202. |
| [9] | LEE M Y, BOLTON J S. Patch near-field acoustical holography in cylindrical geometry. J. Acoust. Soc. Am., 2005, 118(6): 3721–3732. |
| [10] | LEE M Y, BOLTON J S. A one-step patch near-field acoustical holography. J. Acoust. Soc. Am., 2007, 122(3): 1662–1670. |
 2018, Vol. 40
2018, Vol. 40
