2. 中国人民解放军91977部队,北京 100036
2. No.91977 Unit of PLA, Beijing 100036, China
水下声学传感器网络是新兴的海洋技术热点,通过在目标水域大量布放传感器节点,以水声无线通信方式形成的一个多跳的自组织网络系统,协作地感知、采集和处理网络覆盖区域中的信息,并发送给接收者[1]。主要应用于海洋环境监测、海洋资源开发、灾难预防,辅助导航、战术监视、水雷侦察等方面[2]。
大规模水下声传感器网络通常用于监测部署区域的各种环境参数,比如温度,盐度等,而这些信息只有在与网络中的节点的位置绑定时才是有意义的[1]。此外,在有效利用节点能源、提高网络的吞吐量等方面,基于位置信息的地理路由算法比单纯的广播方法往往更有效,相当数量的MAC协议也需要节点的位置信息。因此大范围水下声传感器网络中的精确定位技术是一个亟待研究的关键技术。
目前的水下声传感器网络定位方法主要分为两大类:基于测距的定位方法和不基于测距定位算法[3]。基于测距的定位算法,节点首先测量到锚节点之间的距离和角度,然后利用三边测量法或三角测量法进行目标的定位解算,测距方式主要有RSSI,TOA,TDOA,角度测量主要有AOA等。不基于测距的定位方法,主要包括质心定位算法(Centroid scheme)、DV-hop定位算法、APIT定位算法、ALS定位算法、Amorphous定位算法等。基于测距的定位算法具有较高的精度,但精确测距需要额外的硬件装置支持,有些测距方法依赖精确的时间同步。不基于测距的定位算法普遍定位精度不高,应用面有限,需要较大的通信消耗。在水下传感器网络中,总体来说基于距离测量的、有精度能力保障的定位技术是研究与应用的主流。
文献[4]中,作者提出了一种水下GPS系统,用可以与卫星通信得到自己的精确位置的水面浮标充当水下的GPS卫星节点,为浮标通信范围内的节点提供位置信息,供其进行定位解算,但是这种方法需要时间同步,且只适用于单跳网络。文献[5]提出了一种基于无线传感器网络的水下定位系统,使用大量的装有水听器和GPS的标准站,采用声功率水平测距,利用发送和接受的电压差来计算距离,提出了新的方法,但是该方法是接收信号强度指示(RSSI)的水声测距应用,定位精度一般。文献[6]中,针对在稀疏网络中三维定位的问题,设计了USP分布式定位框架,将3D定位问题通过平面投影技术转化成对应的2D问题,通过迭代改善精度,有更低的数据存储量和更低的数据计算要求,但该方法由于网络中采用的锚节点数量很少,在稀疏网络中网络定位覆盖率较低,网络定位时间长。文献[7]中,作者提出了一种AUV辅助的水下传感器网络定位方法,AUV上浮到海面时接收GPS信号,然后以设定的轨迹下降到特定的深度,在巡航过程中唤醒节点,节点利用请求/应答的方式进行测距,实现自己的定位解算,但是AUV是非常昂贵的。而且这些方法都是适用于小规模水下声传感器网络定位的技术,对于大规模声传感器网络并不适用。
迭代定位算法首先由Joe Albowicz等提出并应用于密集的无线电传感器网络[8],作者提出了一种位置传播算法,在密集网络中布放少量的锚节点,提出了一种基于残差的定位精度评价方法评价成功定位的普通节点的定位精度,将精度高的节点升级为锚节点,从而使得系统的定位覆盖率迭代地增加,实现了大范围传感器网络较高的定位覆盖率和较小的定位误差。
本文研究水下传感器网络中的迭代定位方法,研究了节点定位过程中锚节点共线度的选取方式,并将一种新的三维欧几里得距离估计方法应用到网络中研究了普通的定位方法、三维欧几里得方法、迭代定位方法、联合三维欧几里得距离估计的迭代方法的定位覆盖率和定位误差。
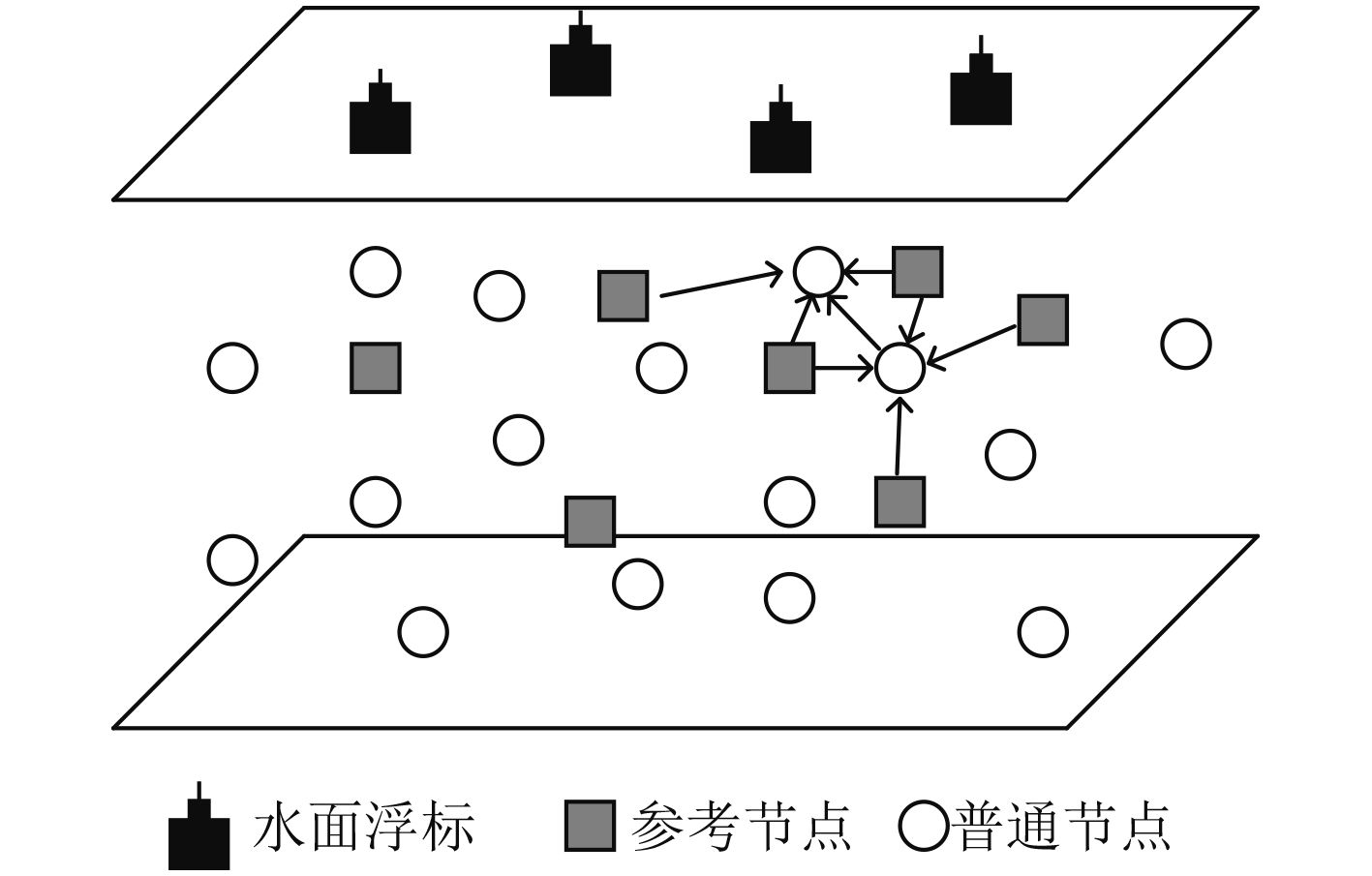
1 迭代定位机制 1.1 网络结构迭代定位的原理如图1所示,节点部署在三维水下区域中,共有水面浮标、锚节点和普通节点3种。
|
图 1 迭代定位网络结构图 Fig. 1 The structure diagram of iterative location network |
其中,水面浮标部署在水面,可以通过与GPS卫星或地面站进行无线电通信获得自己的精确位置供锚节点进行精确的位置解算。锚节点是水下节点中一类数量较少但是通信能力较强的节点,它与水面浮标进行通信可以获得自身的精确位置,并广播自己的位置信息供通信范围内的普通节点进行定位解算。普通节点主要通过与自己周围的邻居锚节点通信进行测距和自身的位置解算。
1.2 定位步骤水下声传感器网络中迭代定位方法主要分成4个阶段:
1)锚节点获得自身位置并泛洪广播定位信息的阶段
锚节点在定位过程中周期性与水面浮标进行通信,当节点接收到4个以上满足条件的浮标的位置和距离信息之后,进行自身定位解算,并泛洪广播定位信息(包含锚节点的ID,时间戳和节点坐标)。
2)普通节点定位解算的阶段
普通节点周期性发送信标信息(包含自己的节点ID和时间戳)供邻居节点进行测距,并且接收邻居节点的信标信息对邻居节点进行测距并在邻居节点链表中保存邻居节点的节点ID和距离信息,同时节点接收锚节点的定位信息,并在锚节点信息链表中添加得到的锚节点的节点ID,距离,坐标。当普通节点接收到满足条件的4个以上锚节点的定位信息之后就可以利用球面交汇的方法进行定位解算。球面交汇定位解算的基本方程如下:
| $\left\{ {\begin{array}{*{20}{c}} {{{(x - {x_1})}^2} + {{(y - {y_1})}^2} + {{(z - {z_1})}^2} = {r_1}^2} {\text{,}}\\ {{{(x - {x_2})}^2} + {{(y - {y_2})}^2} + {{(z - {z_2})}^2} = {r_2}^2} {\text{,}}\\ {{{(x - {x_3})}^2} + {{(y - {y_3})}^2} + {{(z - {z_3})}^2} = {r_3}^2} {\text{,}}\\ {{{(x - {x_4})}^2} + {{(y - {y_4})}^2} + {{(z - {z_4})}^2} = {r_4}^2}{\text{。}} \end{array}} \right.$ | (1) |
经过降次处理,得到三元一次方程组:
| $\begin{split}&\left[ {\begin{array}{*{20}{c}} {\left( {{x_2} - {x_1}} \right)}&{\left( {{y_2} - {y_1}} \right)}&{\left( {{z_2} - {z_1}} \right)} \\ {\left( {{x_3} - {x_2}} \right)}&{\left( {{y_3} - {y_2}} \right)}&{\left( {{z_3} - {z_2}} \right)} \\ {\left( {{x_4} - {x_3}} \right)}&{\left( {{y_4} - {y_3}} \right)}&{\left( {{z_4} - {z_3}} \right)} \\ {\left( {{x_1} - {x_4}} \right)}&{\left( {{y_1} - {y_4}} \right)}&{\left( {{z_1} - {z_4}} \right)} \end{array}} \right]*\left[ \begin{gathered} x \hfill \\ y \hfill \\ z \hfill \\ \end{gathered} \right] = \\&\left[ {\begin{array}{*{20}{c}} {\left( {r_1^2 - r_2^2 + d_2^2 - d_1^2} \right)/2} \\ {\left( {r_2^2 - r_3^2 + d_3^2 - d_2^2} \right)/2} \\ {\left( {r_3^2 - r_4^2 + d_4^2 - d_3^2} \right)/2} \\ {\left( {r_4^2 - r_1^2 + d_1^2 - d_4^2} \right)/2} \end{array}} \right]{\text{。}}\end{split}$ | (2) |
式中:锚节点坐标为
3)普通节点定位结果自评价阶段
迭代定位算法,普通节点位置估计成功之后,利用已估计的位置信息和测距信息利用式(3)计算置信值[9],评价自己的定位结果。
| $ \eta = \left\{ {\begin{array}{*{20}{c}}1{\text{,}}\\{1 - \frac{{\sum\limits_i {\left| {{{(u - {x_i})}^2} + {{(v - y{}_i)}^2} + {{(w - {z_i})}^2} - {l^2}_i} \right|} }}{{\sum\limits_i {{{(u - {x_i})}^2} + {{(v - y{}_i)}^2} + {{(w - {z_i})}^2}} }}}{\text{。}}\end{array}} \right.\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{}{\{ {\text{初始参考节点}}\} }\\{\{ {\text{普通节点}}\} }\end{array}}\\\end{array} $ | (3) |
式中:
4)迭代定位阶段
普通节点计算置信值之后,如果置信值大于提前设定的门限,则该普通节点升级为锚节点,广播自己的定位信息供其他邻居普通节点进行位置解算。随着定位过程的进行,将会有越来越多的普通节点通过评价定位质量的机制升级为锚节点,这样节点部署区域的定位覆盖率就会迭代地增加。
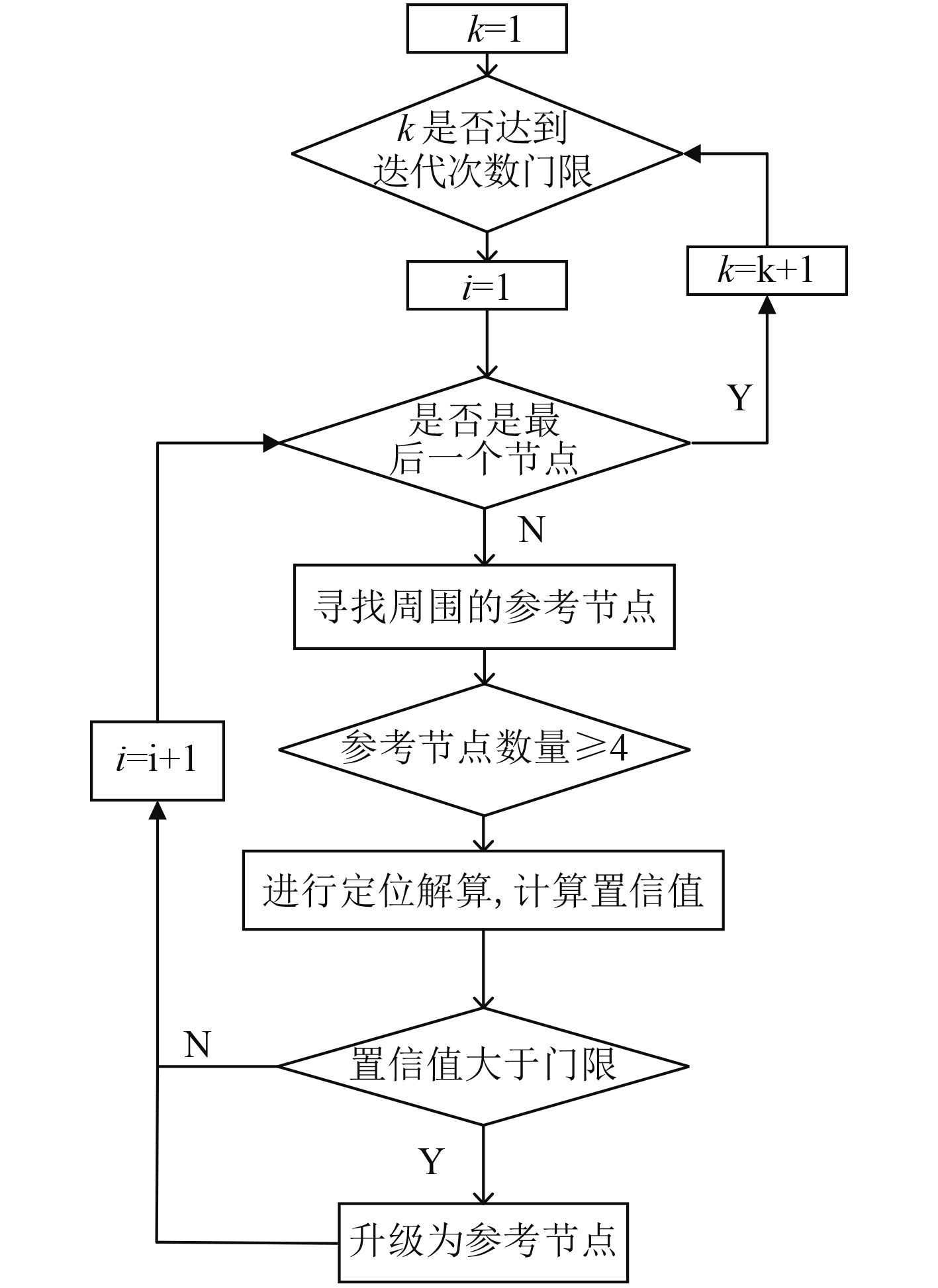
1.3 迭代算法流程
|
图 2 迭代算法流程图 Fig. 2 The flow chart of iterative algorithm |
在三维无线传感器网络空间中,未知节点只要获得至少4个锚节点的位置信息便可以应用三维最小二乘定位算法来实现其定位。但当未知节点通信范围内锚节点数目少于4个时,未知节点将无法定位[10]。Euclidean定位算法是由美国路特葛斯大学(Rutgers University)的Niculescu等提出的,它的定位是利用已知平面几何原理来估测与锚节点距离两跳的未知节点的所在位置。文献[9]中将二维欧几里得距离估计扩展到了三维。当锚节点数量不足时,普通节点可以通过三维欧几里得距离估计计算到一跳范围之外的锚节点距离信息。这样,待定位节点可以利用一跳范围之外的锚节点参与定位解算,增加定位成功率。
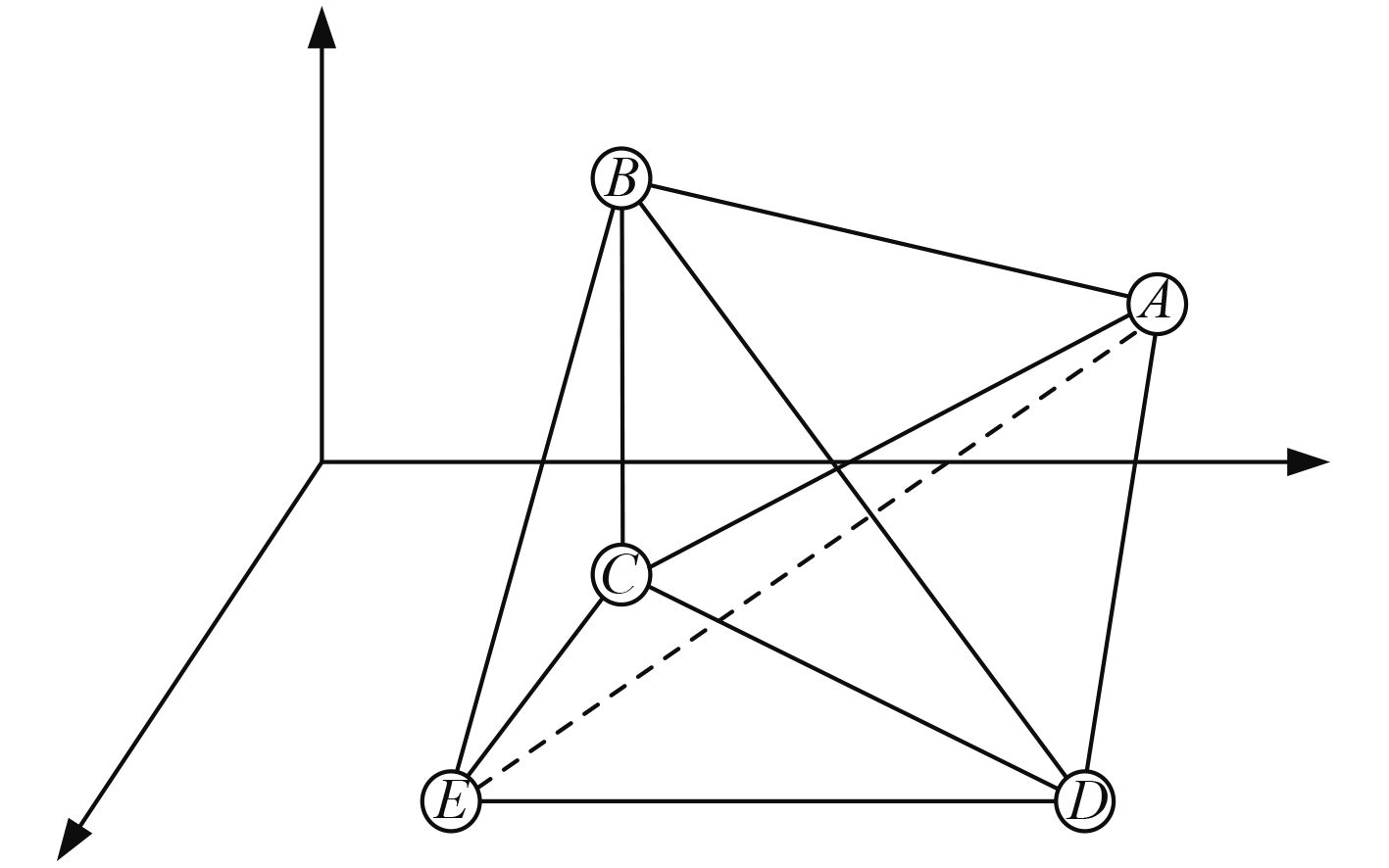
基本原理如图3所示,待定位节点E和参考节A的不相邻,并且有2个邻居锚节点BC,节点E想要计算到节点A的距离,如果存在D点使得节点E已知节点对AB,AC,AD,BD,BC,CD,EB,EC,ED之间的距离信息,则节点E利用ABC基本平面解算两个D位置,再利用BCD求解出4个E的位置,再找一个与D相异的W点求出另外4个E的位置,即可筛选出E的位置求出AE距离。
|
图 3 三维欧几里得距离估计示意图 Fig. 3 The schematic figure of 3D Euclidean distance estimation |
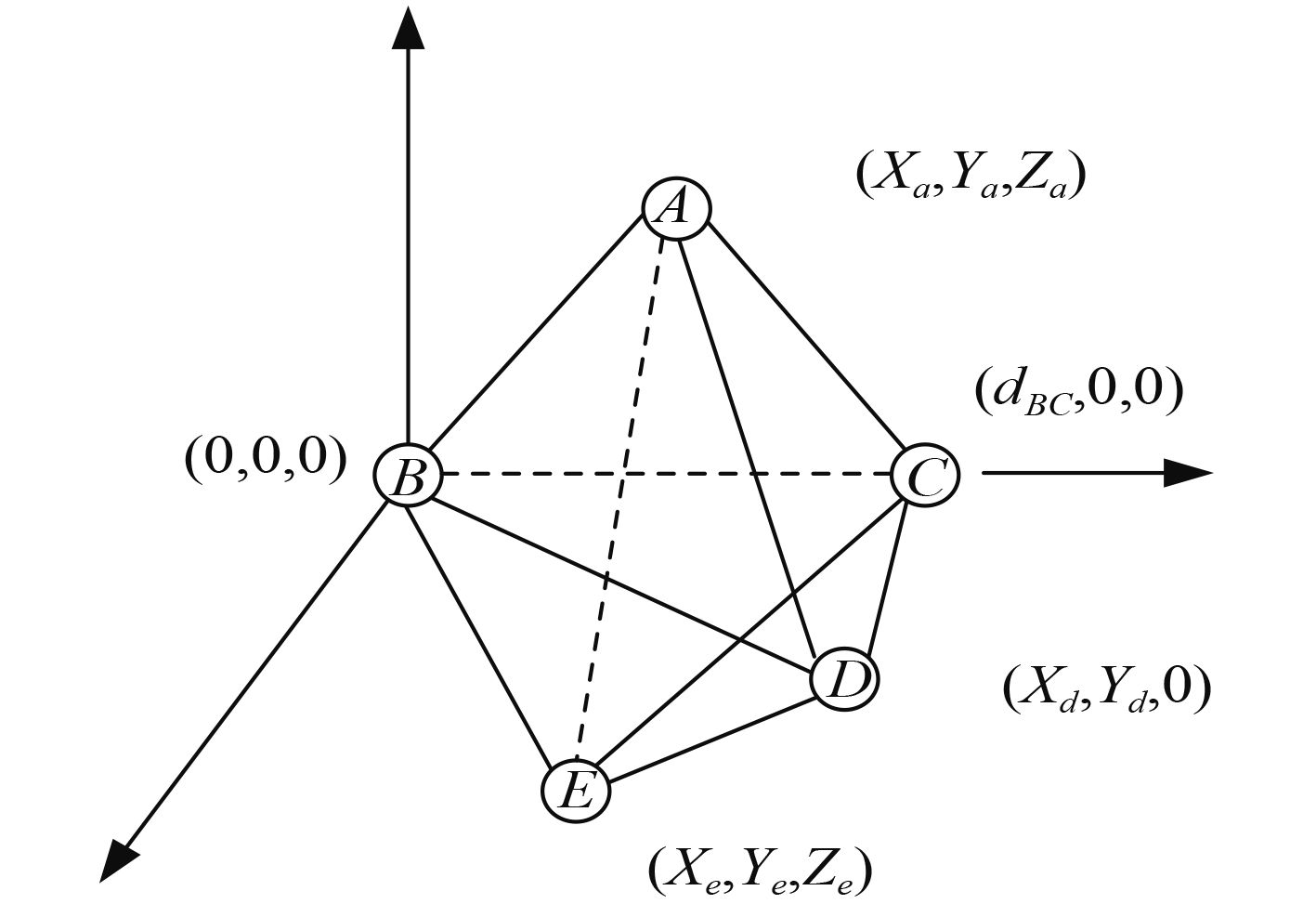
文献[11]提出了一种利用坐标法解决三维欧几里得距离估计的问题,大大减小了算法的计算量,对算法中BCD平面的锚节点没有数量要求,是解决三维欧几里得距离估计的一种较好的方法。其原理如图4所示。
|
图 4 相对坐标法三维欧几里得距离估计原理图 Fig. 4 The schematic diagram of 3D Euclidean distance estimation in |
利用BC为x轴与BC垂直的轴为y轴,与BCD所在平面垂直的轴为z轴,建立坐标系,可利用方程(4)求得D点的坐标
| $\left\{ \begin{gathered} {({x_d} - {\rm{ }}{d_{BC}})^2} + {\rm{ }}y_d^2 = {\rm{ }}d_{CD}^2 \hfill {\text{,}}\\ x_d^2 + {\rm{ }}y_d^2 = {\rm{ }}d_{BD}^2 {\text{,}}\hfill \\ \end{gathered} \right.$ | (4) |
关于BC轴对称,选定一个D点,
| $\left\{ \begin{gathered} x_a^2 + {\rm{ }}y_a^2 + {\rm{ }}z_a^2 = {\rm{ }}d_{AB}^2{\text{,}} \hfill \\ ({x_a} - {\rm{ }}{d_{BC}})2 + {\rm{ }}y_a^2 + {\rm{ }}z_a^2 = {\rm{ }}d_{AC}^2 {\text{,}}\hfill \\ {({x_a} - {\rm{ }}{x_d})^2} + {({y_a} - {\rm{ }}{y_d})^2} + {\rm{ }}z_a^2 = {\rm{ }}d_{AD}^2 {\text{。}}\hfill \\ \end{gathered} \right.$ | (5) |
解得2个A点
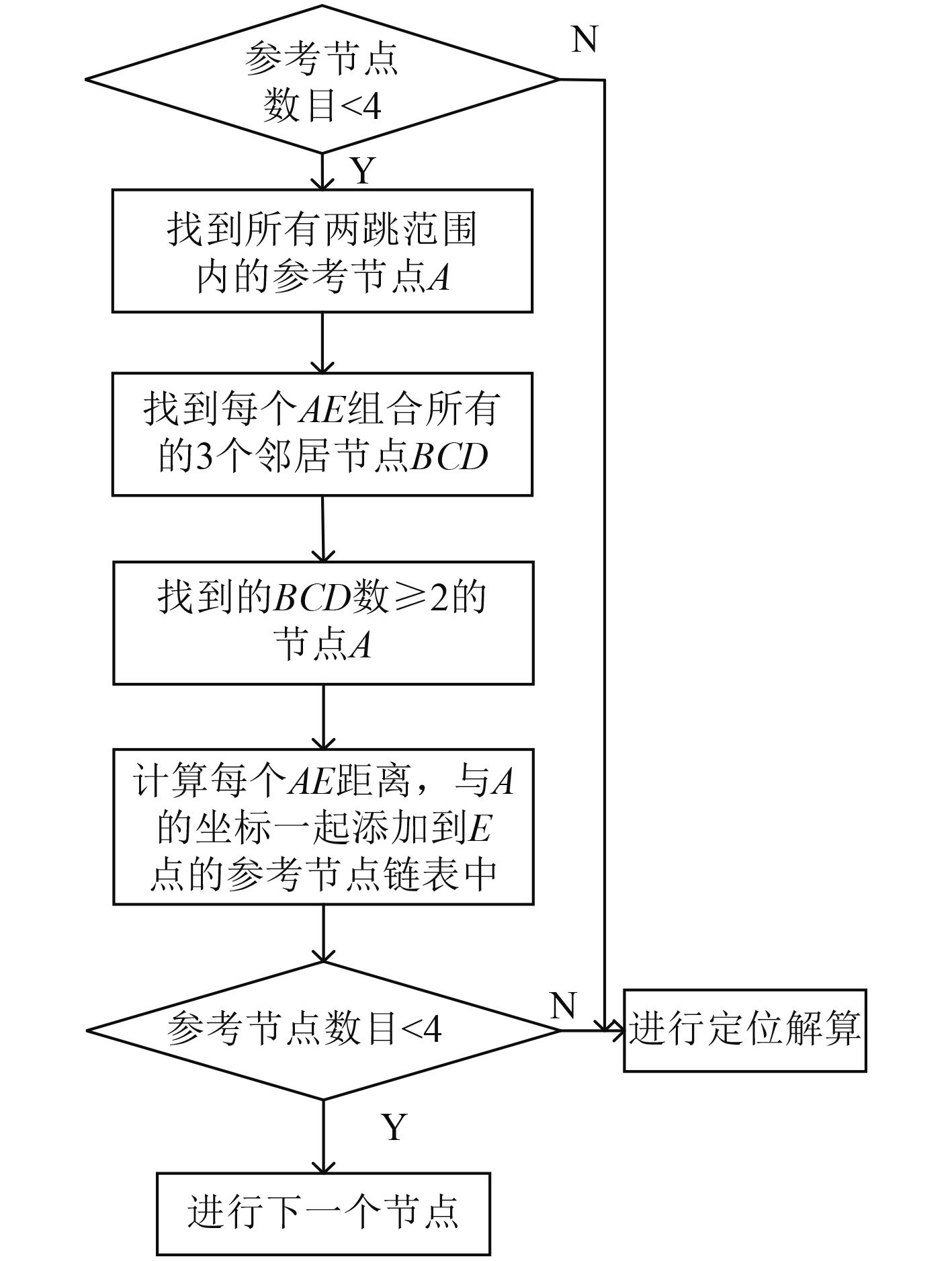
算法流程如图5所示。
|
图 5 3DEculidean算法流程 Fig. 5 The flow of 3D Euclidean algorithm |
本文的仿真过程中,节点布放在20 km×20 km×4 km的区域中。节点的通信距离为2 km。距离测量值符合均值为真值,标准差为1 m的正态分布。节点数量从以步长值为50,从500到900变化,锚节点占20%。普通节点升级为锚节点的置信值为0.98。每个节点密度(节点数量对应)运行100次,每次运行所有节点进行5次迭代。
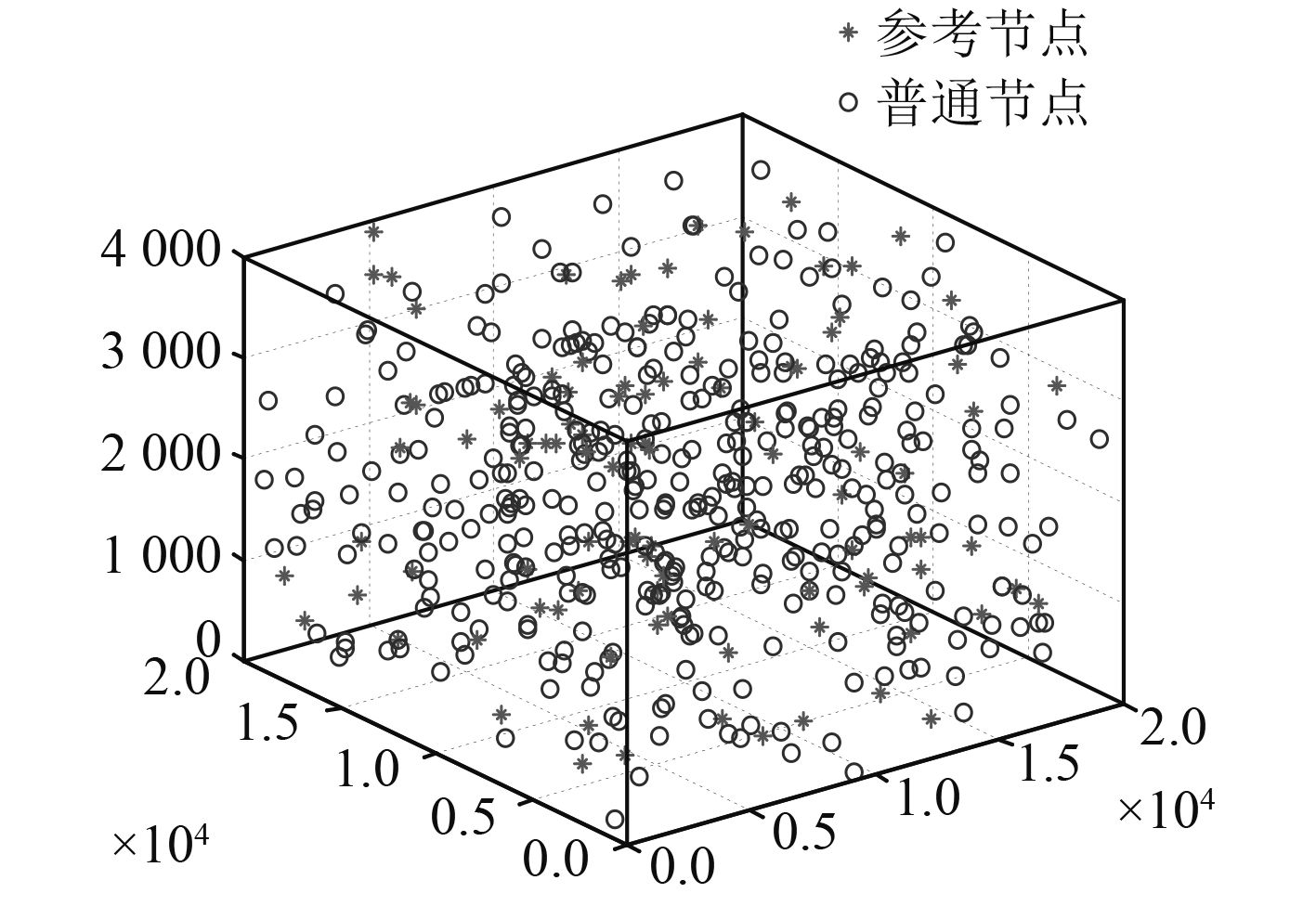
3.1 节点部署情况图6代表仿真区域中有500个节点,锚节点占20%的情况下一次运行所产生的节点部署情况示意图。
|
图 6 传感器节点分布图示例 Fig. 6 Example of sensor node distribution diagram |
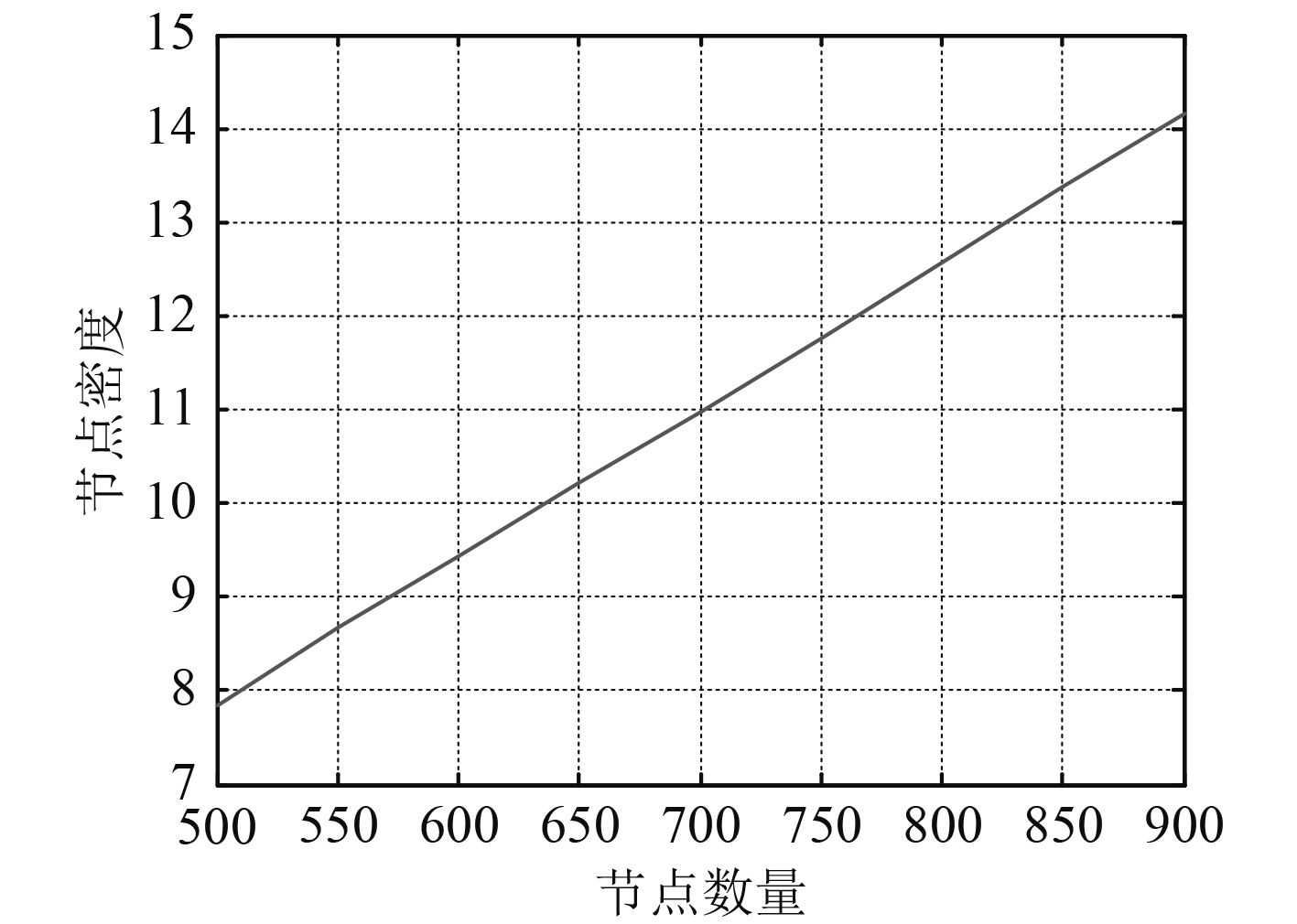
节点密度定义为区域中当前节点数量下每个节点通信范围内的平均节点数量。在部署区域中网络中的节点数量与节点密度的关系如图7所示。
|
图 7 节点密度与节点数量关系 Fig. 7 The relationship between node density and number of node |
由于节点定位过程中节点共线会导致较大误差,所以在定位解算过程中需要避免3个节点或者4个节点共线的情况。
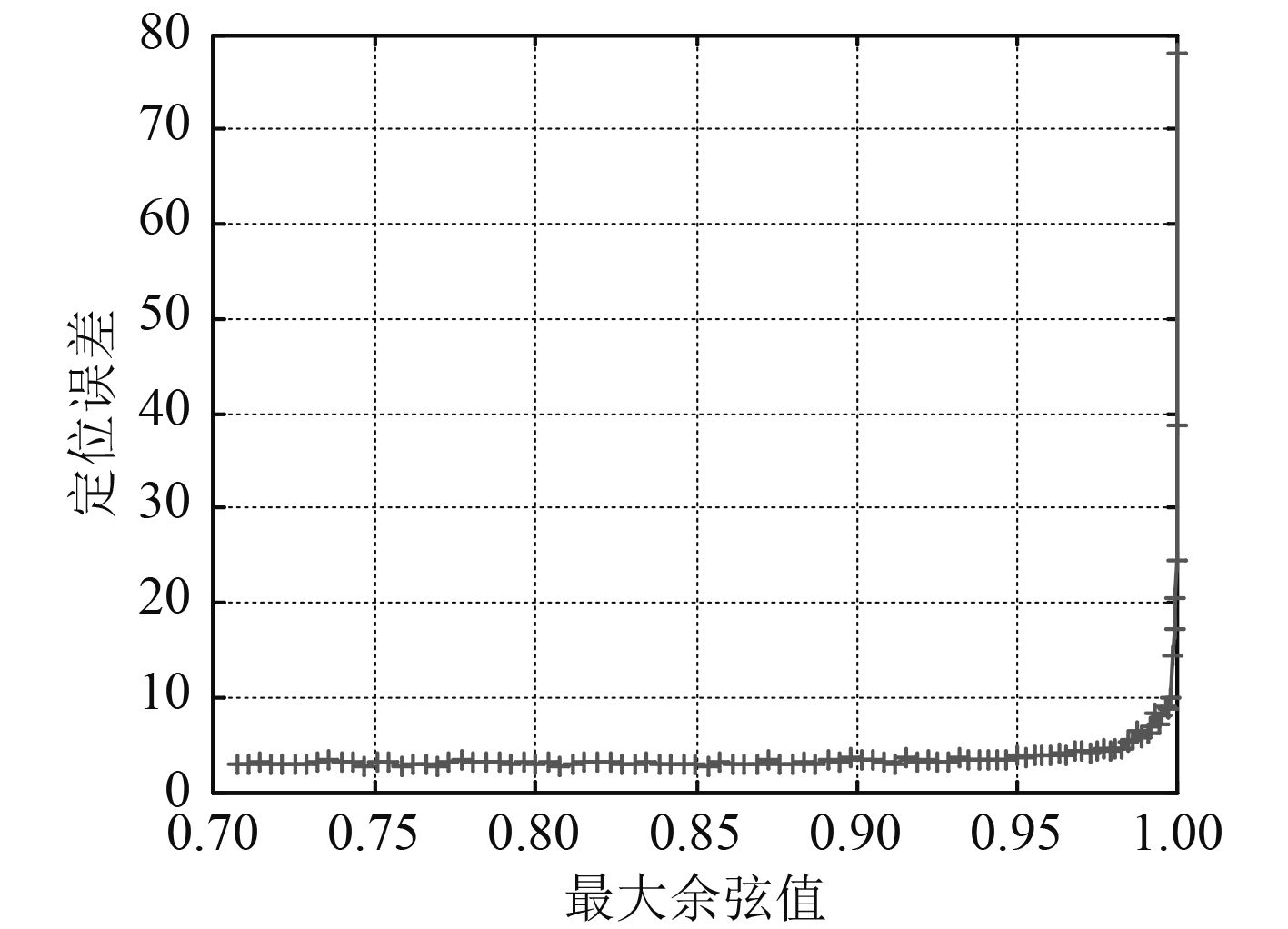
|
图 8 最大余弦值与定位误差关系图 Fig. 8 Relation diagram of maximum cosine value and positioning error |
用于解算的锚节点每3个组成1个组合,共线度的定义为任意3个锚节点组成的三角形内角余弦值的最大值。图7仿真了节点位置为[0,0,0],锚节点位置为,
|
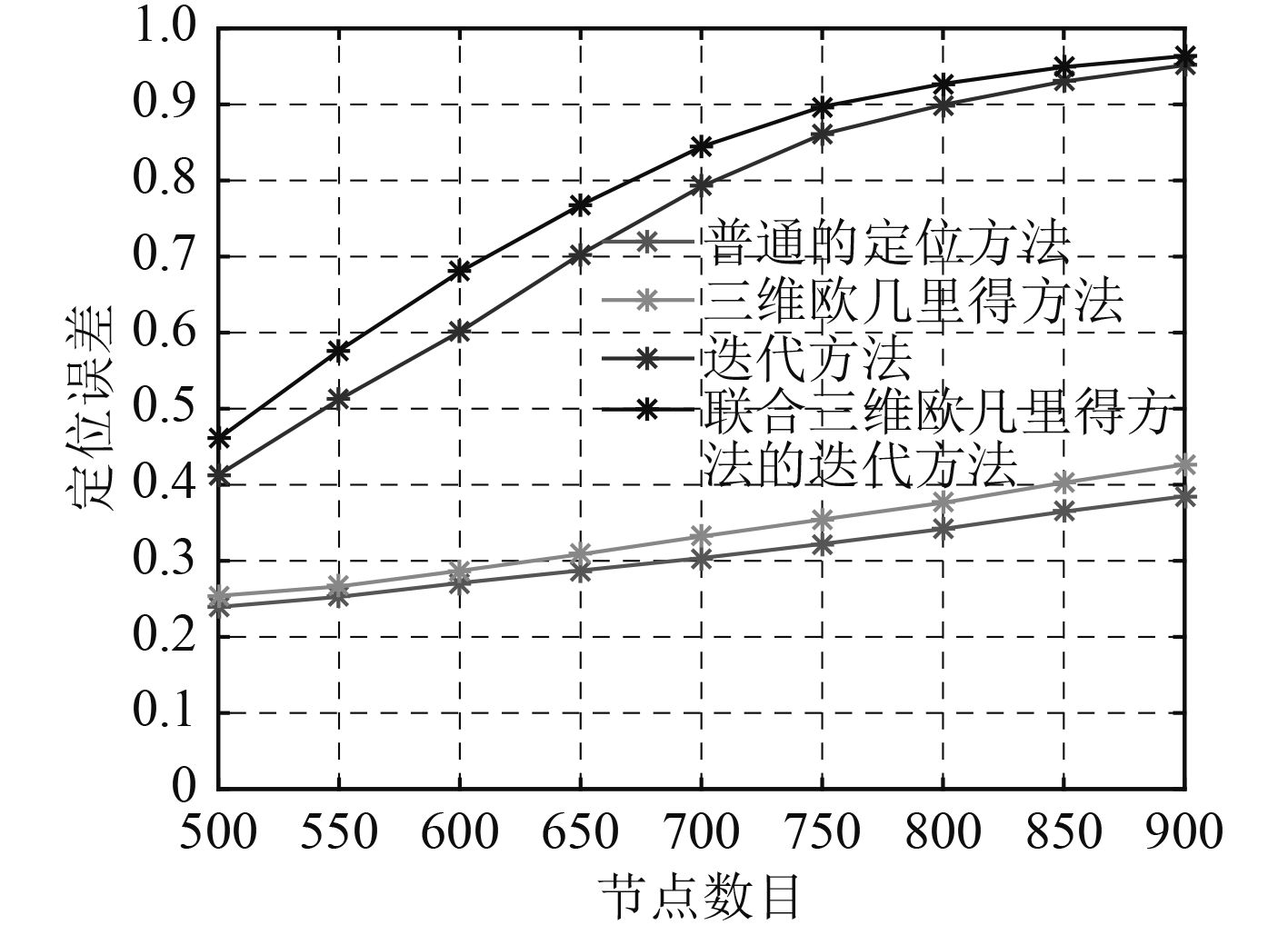
图 9 节点数量与定位覆盖率关系图 Fig. 9 Relation diagram of node number and location coverage |
定位覆盖率定义为:定位过程结束后所有节点中已知位置的节点数量与总节点数量的比值。此处普通定位方法指节点仅用1跳范围内的锚节点进行定位,不进行评价升级的定位方法。图9中可以看出,普通的定位方法定位覆盖率很低,而单纯的三维欧几里得方法对普通定位方法的结果有所改善但是效果并不明显。这是由于节点密度较低,锚节点数量较少时,节点两跳范围内的锚节点数量也较少,即使应用3DEculidean方法节点也较难找到足够数量的锚节点,导致定位覆盖率改善不大,随着节点密度的升高定位结果有所改善。迭代定位方法的定位覆盖率要明显高于前两者,是因为随着迭代过程的进行,锚节点数目迭代地增加,导致系统定位覆盖率迭代地升高。带三维欧几里得距离估计方法的迭代定算法的定位覆盖率要比单纯的迭代算法的定位覆盖率高,是因为节点在运行过程中在参解算的锚节点数目不足时,会寻找一跳范围以外的锚节点参与定位解算,随着节点数量增加,节点密度升高,大部分节点只通过迭代作用就能找到足够的锚节点进行定位解算,三维欧几里得的作用将降低。
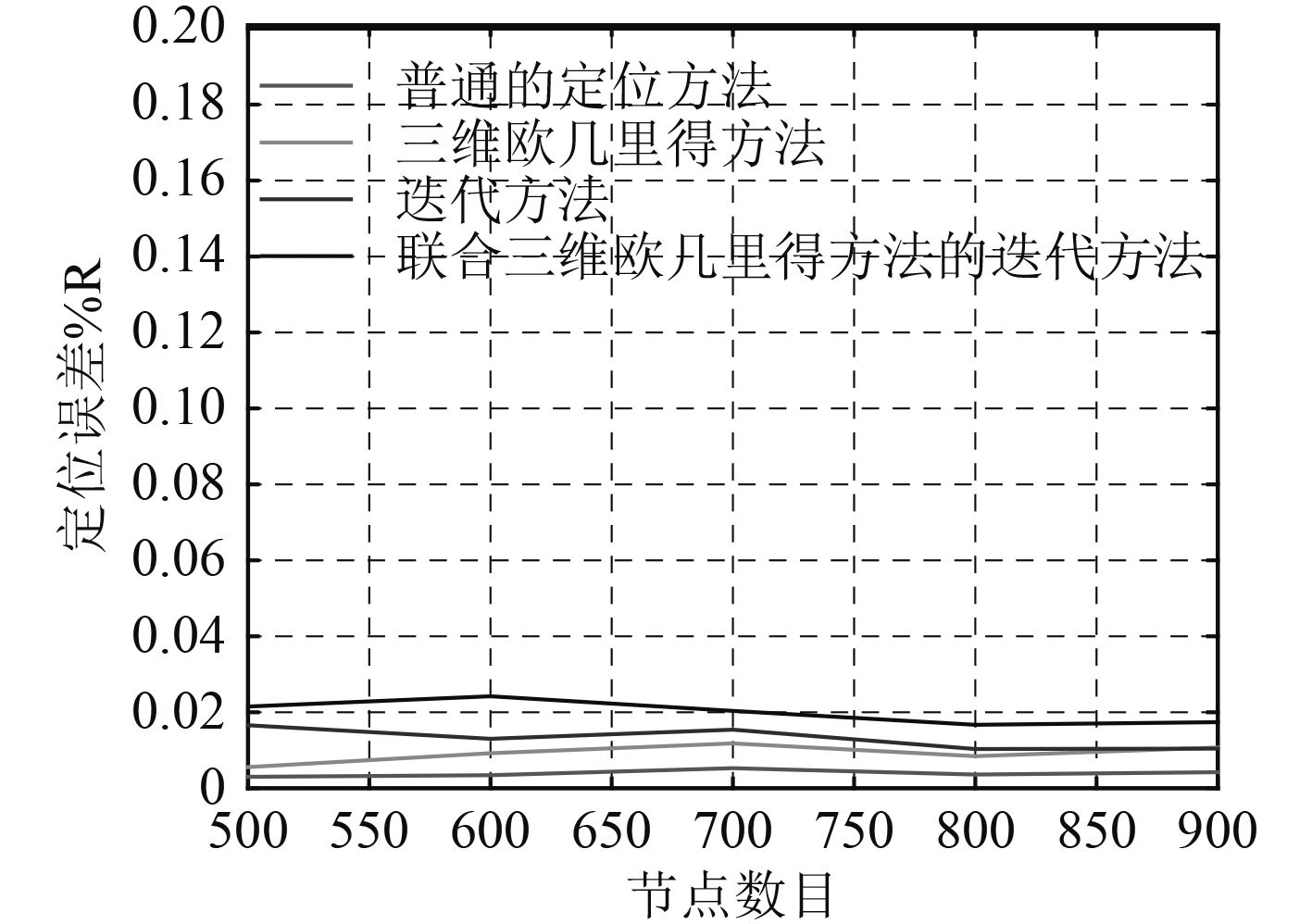
3.5 定位误差定位误差定义为所有节点的平均定位误差与通信距离的比值。
|
图 10 节点数量与定位误差关系图 Fig. 10 Relation diagram of node number and positioning error |
从图10中可以看出,常规定位方法的定位精度最高,三维欧几里得方法定位误差高于常规方法,这是因为三维欧几里是基于测距信息进行AE距离计算,其中计算节点D相对位置,计算节点A相对位置,计算节点E的相对位置,各个步骤都有误差,由于误差积累,最后的距离值比真实测距的误差高,所以三维欧几里得方法的定位误差高于常规方法。迭代方法中由于有的锚节点是普通节点升级而来,本身就存在定位误差,随着迭代的进行会产生误差的积累,导致平均定位误差最高。联合三维欧几里得距离估计的迭代方法的定位误差最高,一方面是待定位节点找到的两跳范围内的锚节点可能是普通节点升级之后的锚节点本身具有一定误差,另一方面是由于之前提到的三维欧几里得算法的误差积累导致距离估计误差较大。
4 结 语本文研究了大规模水下传感器网络中的迭代定位方法,通过少量初始锚节点定位普通节点,评估定位成功节点的精度保持情况,升级定位精度高的普通节点为锚节点参与定位余下的普通节点,使网络的定位覆盖率迭代地升高。利用一种相对坐标三维欧几里得距离估计方法去估计1跳范围外的锚节点,提高定位成功率。给出了网络定位中节点不共线的选择方法,比较了普通定位方法,单纯的三维欧几里得方法、迭代定位方法,联合三维欧几里得的迭代定位方法的定位误差和定位覆盖率。结果表明,以一定的精度损失为代价,迭代定位方法显著提高了定位覆盖率,而联合三维欧几里得距离估计的迭代方法可进一步提升定位覆盖率。
| [1] | 齐赛. 水下传感器网络拓扑控制与节点定位技术研究[D]. 北京: 中国科学院声学研究所, 2008. |
| [2] | AKYILDIZ I F, POMPILI D, MELODIA T. Underwater acoustic sensor networks: research challenges[J]. Ad Hoc Networks, 2010, 3(3):257–279. |
| [3] | CHEN K, ZHOU Y, HE J. A localization scheme for underwater wireless sensor networks[C]// Advances in Data & Web Management, Joint International Conferences, Apweb/waim, Suzhou, China, April. 2009:550–555. |
| [4] | BECHAZ, C. THOMAS, H. GIB system: the underwater GPS solution, in: Proceedings of the 5th Europe Conference on Underwater Acoustics, 2000. |
| [5] | B FU,F ZHANG,M ITO,Y WATANABE,T AOKI .Development of a new underwater positioning system based on sensor network[J]. Artificial Life & Robotics. 2008, 13(1):45–49. |
| [6] | CHENG, W. TEYMORIAN, A. Y. MA, L. et al.Underwater localization in sparse 3D acoustic sensor networks[J], in: Proceedings of the IEEE INFOCOM, 2008: 236–240. |
| [7] | EROL, M. VIERIRA, L. F. M. GERLA, M. AUV-Aided localization forunderwater sensor networks[J]. in: Proceedings of the International Conference on Wireless Algorithms, Systems and Applications(WASA), 2007: 44–51. |
| [8] | ALBOWICZ J, CHEN A, ZHANG L. Recursive position estimation in sensor networks[C]// Network Protocols, 2001. Ninth International Conference on. IEEE, 2001: 0035. |
| [9] | ZHOU Z, CUI J H, ZHOU S. Efficient localization for large-scale underwater sensor networks ☆[J]. Ad Hoc Networks, 2010, 8(3):267–279. |
| [10] | 张居成. 深水长基线定位导航技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. |
| [11] | 唐良瑞, 宫月, 罗艺婷,等. 一种基于Euclidean的无线传感器网络三维定位算法[J]. 电子学报, 2012, 40(4):821–825. http://www.cqvip.com/QK/90131X/201204/42028629.html |
 2018, Vol. 40
2018, Vol. 40
