随着电力电子装置的飞速发展,船舶电力推进逐渐显示出其无可比拟的优越性,电力推进逐渐成为船舶动力装置的发展方向。但是随着船舶电力推进的应用,船舶上的用电装置正在不断增加,一些较大功率的负载越来越多的出现在船舶上。这些大功率负载的应用,给船舶带来巨大便利的同时,也给船舶带来了很大的危害。比如:在轻载状态下,船舶电网的频率和功率波动较小。但是相比于陆地电网,船舶电站容量较小,电网输电线短且船舶工作环境较为恶劣,当船舶电网中有大功率负载变化时,就会使船舶电网的频率和功率产生较大的波动,这些波动除了可能会对电网中其他负载的运行产生显著的影响,增加原动机的机械应力和热应力,增加船舶燃料的消耗;还有可能造成整个船舶电网断电,整个船舶无法运行。
针对这一问题,本文创新性的采用能量储存技术。这些年来,能量储存技术在国内外得到了飞快的发展,特别是锂电池和超大容量电容技术发展十分迅猛,并且已经很好的应用到汽车领域(比如特斯拉和比亚迪)。这种能量存储技术同样也适用于船舶电力系统,利用储能装置(超级电容和锂电池)补偿电网中能量波动,即当系统轻载时,储能装置吸收能量减小这些能量对系统的冲击;当系统重载或过载时,储能装置释放能量,满足系统的需求。
本文以某1 500 m作业水深钻井船为模型,利用Matlab对船舶电力推进系统进行建模,运用粒子群算法对混合储能单元容量进行优化,精确地控制了混合储能单元的充放电,并研究了混合储能技术对船舶功率波动和频率波动的影响。
1 船舶电站的建模船舶电站系统一般由原动机、发电机、附属设备和配电板组成。柴油机具有结构简单、热效率高、经济性好等特点,因而在船舶电站系统大部分采用柴油机作为原动机拖动同步发电机进行发电,下面对柴油机调速系统、发电机励磁系统进行建模。
1.1 柴油机调速系统当柴油机所加负载增大时,柴油机转速就会相应增加,使输入输出转矩达到新的平衡。反之,当柴油机所加负载减小时,柴油机转速就会相应减小,使输入输出转矩达到新的平衡。但是在船舶上要求柴油机的转速是一个定值,因而调速系统必须将转速恢复到设定值。柴油机调速系统的原理框图如图1所示。
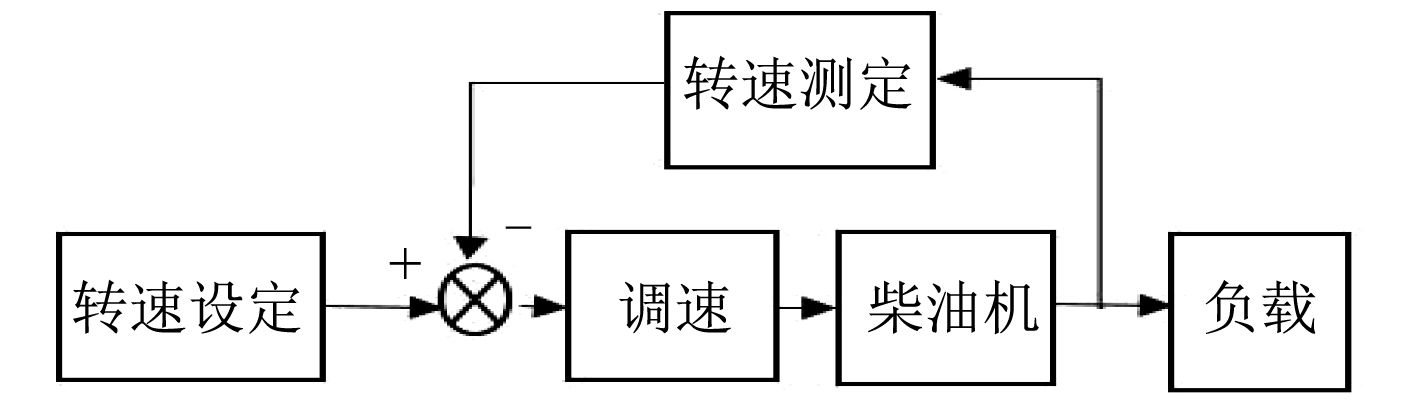
|
图 1 柴油机调速系统的原理框图 Fig. 1 Schematic diagram of speed control system in the diesel engine |
根据柴油机调速器数学模型和原理框图,用Matlab/Simulink构建出柴油机调速系统的仿真模型如图2所示。
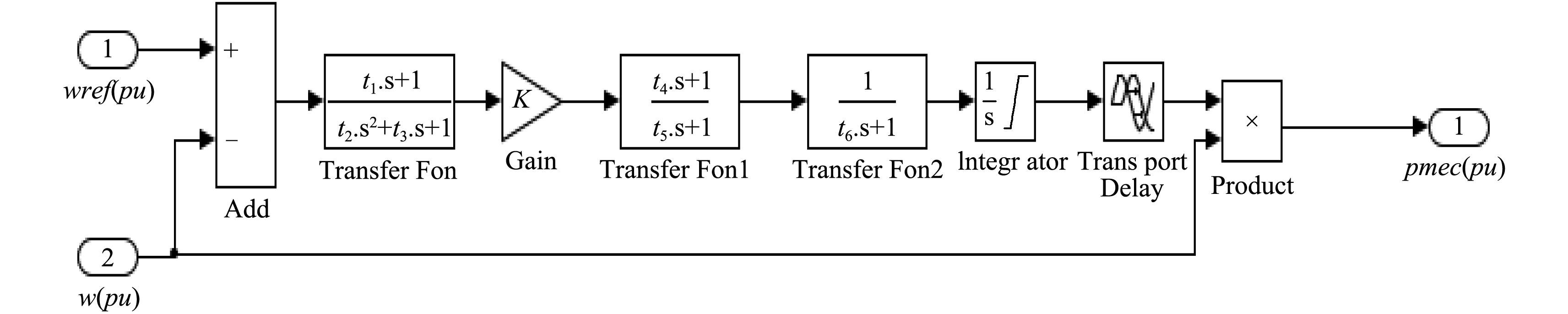
|
图 2 柴油机调速系统的仿真模型 Fig. 2 Simulation model of diesel engine speed regulation system |
调速控制系统通过油门执行器动作,调节柴油机的喷油量,从而达到调节柴油机转速的目的。图2以柴油机的转速为控制对象,采用比较典型的PID控制的闭环反馈控制系统。K为控制器放大系数,t1,t2,t3为控制器时间常数,t4,t5,t6为执行器时间常数。wref(pu)为设定转速,w(pu)为检测模块测得的发电机转子的实际转速。将wref(pu)和w(pu)进行对比,接着通过调速器对柴油机速度进行控制,最后得到机械转矩,将得到的机械转矩与测得的柴油机实际转速w(pu)相乘,就可以得到同步发电机的机械功率pmec(pu)。同步发电机在此功率的驱动下进行运转。
1.2 发电机励磁系统当船舶上的负载发生变化时,同步发电机输出端电压的也随之发生变化,偏离额定值,使得电网中的用电设备不能正常工作,更为严重的是可能导致船舶发电机解列、电网崩溃导致整个船舶停电。因此需要采用控制系统对发电机进行调节,使得同步发电机端电压返回到额定的状态。而能够实现这种功能的是同步发电机的励磁系统。励磁系统的基本功能是给同步发电机磁场绕组提供直流电流。除此之外,励磁系统还能通过控制励磁电压控制励磁电流,完成控制功能(电压调节、无功功率分配和电力系统稳定性的提高)和保护功能(发电机、励磁机和其他设备不超过自身容量上限)。故同步发电机励磁系统是保证船舶电力系统具有良好工作性能的重要部分。同步发电机励磁系统原理框图如图3所示。
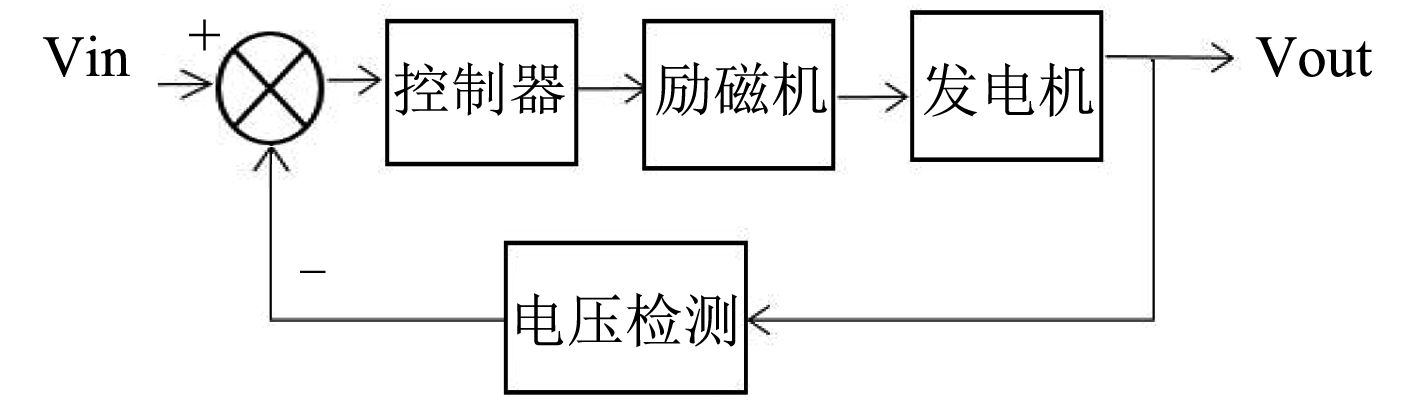
|
图 3 柴油机调速系统的仿真模型 Fig. 3 Simulation model of diesel engine speed regulation system |
根据图3发电机励磁系统原理框图和发电机励磁系统的数学模型,利用Matlab/Simulink建立同步发电机相复励交流励磁系统的仿真模型,如图4所示。

|
图 4 相复励交流励磁系统simulink仿真模型 Fig. 4 Simulink simulation model of phase compound excitation syste |
在图4中,采用一个典型PID控制的闭环反馈励磁系统,补偿器和主调节器共同构成一个组控制回路。一个微分环节构成了系统的反馈回路,该微分环节对整个控制系统起到阻尼和稳定的作用。在图4中,交流励磁系统有4个输入量Uref,Ud,Uq,Ustab和一个输出量Vf。Uref是同步发电机的设定电压,Ud是同步发电机d轴上的电压分量,Uq是同步发电机q轴上的电压分量,Ustab是同步发电机的接地零电压,Vf是励磁电压。电压分量Ud,Uq通过d-q轴电压与功率投影计算后通过低通滤波器的作用,产生一个相复励的电压信号。该电压信号一部分被送到主控制回路和比例饱和环节进行处理,一部分直接送到比例饱和环节,经过选择后输出到励磁机。
2 混合储能单元 2.1 混合储能单元充放电电路为了实现对超级电容和锂电池的充放电控制,本文采用如图5所示的DC-DC变换器。DC-DC变换器实质上就是BUCK-BOOST电路,也被称为反号变换器。DC-DC变换器与经过变频器整流过后的直流电流直接相连。DC-DC变换器主要有IGBT、电感、二极管等原件组成,这个电路能够使能量的双向流动。
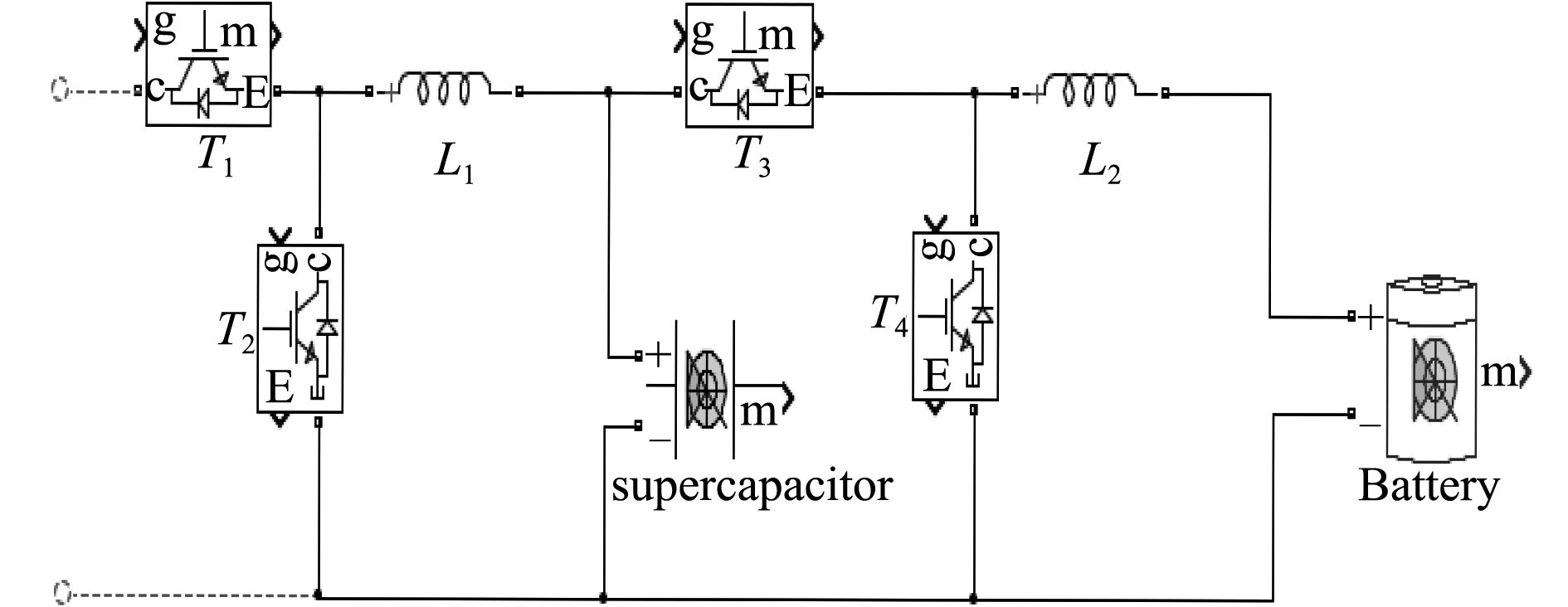
|
图 5 DC-DC变换器 Fig. 5 DC-DC converter |
超级电容器的充放电工作原理:当开关管T1导通,T2截止,此时电路运行在BUCK模式下,能量通过T1和电感L1向超级电容器充电;当开关管T2导通,T1截止时,电路工作在BOOST模式下,超级电容器通过T2,L1释放能量。特别注意的是开关管T1和T2不能同时导通,一旦同时导通,系统将会发生短路。对于锂电池来说,其充放电工作原理和超级电容器的充放电原理一样,开关管T3和T4也不能同时导通。
超级电容器和锂电池组成的混合储能单元的能量值的大小和方向是由半导体器件的周期决定的。当系统中有大功率负载突加时,开关管T2,T4导通,开关管T1,T3截止,即混合储能单元工作在BOOST模式下,它和同步发电机一起放电,提供负载所需要的能量,用公式表示如下:
| ${P_G} + {P_B} + {P_S} = {P_L}\text{,}$ |
式中:
| ${P_G} = {P_B} + {P_L} + {P_S}\text{。}$ |
超级电容器有时被称为电双层电容器,是一种拥有高能量密度的电化学容器。其具有高电流容量、使用寿命长、温度范围广、环境友好、维护保养容易、状态容易监控等优点。超级电容器能量存储量由以下公式确定:
| $E = \frac{1}{2}C{U^2}\text{。}$ |
考虑到超级电容器的端电压有一个工作范围
| ${E_{\max }} = 0.5nC{U_{\max }}/3.6 \times {10^9}\text{,}$ |
| ${E_{\min }} = 0.5nC{U_{\min }}/3.6 \times {10^9}\text{。}$ |
锂电池是一种可逆电池,既可以放电也可以充电。主要靠锂离子在正负极之间移动来工作。其具有高能量密度、单体电压高、自放电率小、输出功率大、工作温度范围广等优点。单个锂电池的端电压可以用下列公式确定:
| ${V_{cell}} = {V_e} + k \cdot \ln (\frac{{0.9 \times SOC}}{{1 - 0.9 \times SOC}})\text{。}$ |
式中:
假设给出锂电池的最大放电程度DOC,那么锂电池中剩余能量的最小值为:
| ${E_{{\rm{min}}}} = mC{V_{cell}}(1 - DOC)/{10^6}\text{,}$ |
式中
混合储能单元有超级电容器和锂电池组合而成,而超级电容器和锂电池具有不同的功率密度、能量密度和循环寿命。与单个超级电容器和锂电池相比,如何通过这两者有效组合,使系统获得最佳的功率和能量密度就变得尤为重要。本文创新性使用粒子群算法,很好地解决了这一问题。
3.1 目标函数的建立考虑到混合储能单元能量准确的分配、超级电容器和锂电池操作特性互补、系统中发电机状态的优化、系统功率的波动、多余能量存储时多余成本等因数,选取如下目标函数:
| ${{\min }}F({X_1},{X_2}) = {X_1} \cdot {C_1} + {X_2} \cdot {C_2}$ |
式中:
考虑到船舶电力系统的安全运行,以下2个限制条件需要考虑:1)同步发电机的输出功率限制,2)同步发电机的运行功率限制。具体公式如下:
| $\frac{{{P_{gi}}(k) - {P_{gi}}(k - 1)}}{{\Delta t}} \leqslant m\text{,}$ |
| $P_{cont,gi}^{\min }(k,{N_f}) \leqslant {{\rm{P}}_{gi}}(k) \leqslant {P_{start}}(k) \leqslant P_{cont,gi}^{\max }(k,{N_f})\text{。}$ |
式中:
考虑到整个系统的安全运行,下面的限制条件需要考虑:
| $0 \leqslant {n_i}{C_i} \leqslant {C_{\max }},i = 1,2\text{,}$ |
| ${P_B} + {P_S} \geqslant \Delta P\text{,}$ |
| $20\% \leqslant SO{C_B} \leqslant 90\% \text{,}$ |
| $30\% \leqslant SO{C_S} \leqslant 99\% \text{,}$ |
| ${I_{{\rm{min}}1}} \leqslant {I_B} \leqslant {I_{\max 1}}\text{,}$ |
| ${I_{{\rm{min}}2}} \leqslant {I_s} \leqslant {I_{\max 2}}\text{。}$ |
在上面的一些限制条件中,
粒子群算法也称粒子群优化算法,是J. Kennedy和R. C. Eberhart等对鸟儿捕食行为的研究后提出的一种算法,其基本思想是通过群体中个体的协作和信息共享来寻找最优解。与遗传算法相比,粒子群算法的优势在于简单容易实现并且没有许多参数需要调整。粒子群算法能够很好地解决非线性系统优化问题,因此目前已被广泛的应用到神经网络的训练、模糊系统的控制、函数的优化等领域。
把超级电容器和锂电池的数量看成一个粒子,那么基于粒子群算法的混合储能单元容量优化的步骤如下:
1)根据3.1中的目标函数和3.2中的限制条件,写出需要优化的函数
2)初始化随机生成的N个二维粒子粒子群。根据混合存储单元容量的能量跨度,每个随机粒子获得初始值。因此第i个粒子的位置和速度可以通过下列公式获取:
| ${x^i} = ({x_{i,1}},{x_{i,2}})\text{,}$ |
| ${v^i} = ({v_{i,1}},{v_{i,2}})\text{。}$ |
3)设每个粒子的局部最优位置和全局最优位置如下:
| $P_{\rm{i}}^t = {(P_{i1}^t,P_{i2}^t)^{\rm T}},i = 1,2.....N\text{。}$ |
| $P_G^{t} = {(P_{g1}^t,P_{g2}^t)^{\rm T}}\text{。}$ |
那么在t+1时刻,粒子的位置更新由以下公式决定:
| $v_{id}^{t + 1} = v_{id}^t + {c_1}{r_1}(P_{id}^t - x_{id}^t) + {c_2}{r_2}(P_{gd}^t - X_{id}^t)\text{。}$ |
式中
粒子移动的下一个位置,可用下式确定:
| $x_{id}^{t + 1} = x_{id}^t + v_{id}^{t + 1} \;\; (d = 1,2)\text{。}$ |
4)每一个粒子计算混合储能单元的产生的最大功率和系统功率的损失率,当达到这些要求时,计算目标函数,求出粒子的适应度值,并将求出的适应度值和全局最优比较,如果效果更优,则替换局部最优和全局最优值。
5)判断目标函数
本文以某1 500 m作业水深钻井船为模型,利用Matlab/Simulink搭建含有混合储能单元船舶电力系统。仿真系统主要模块的主要参数如表1所示。
|
|
表 1 主要模块主要参数 Tab.1 The main model parameters |
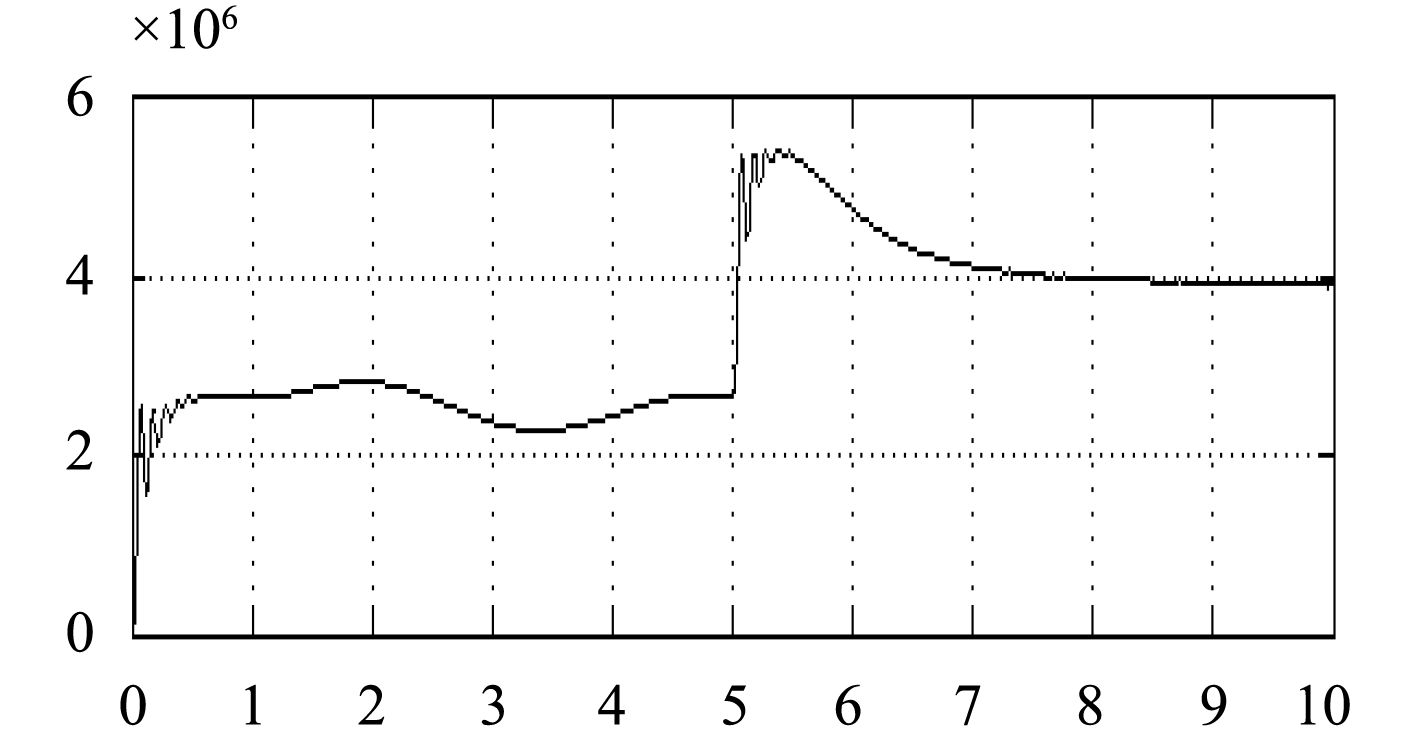
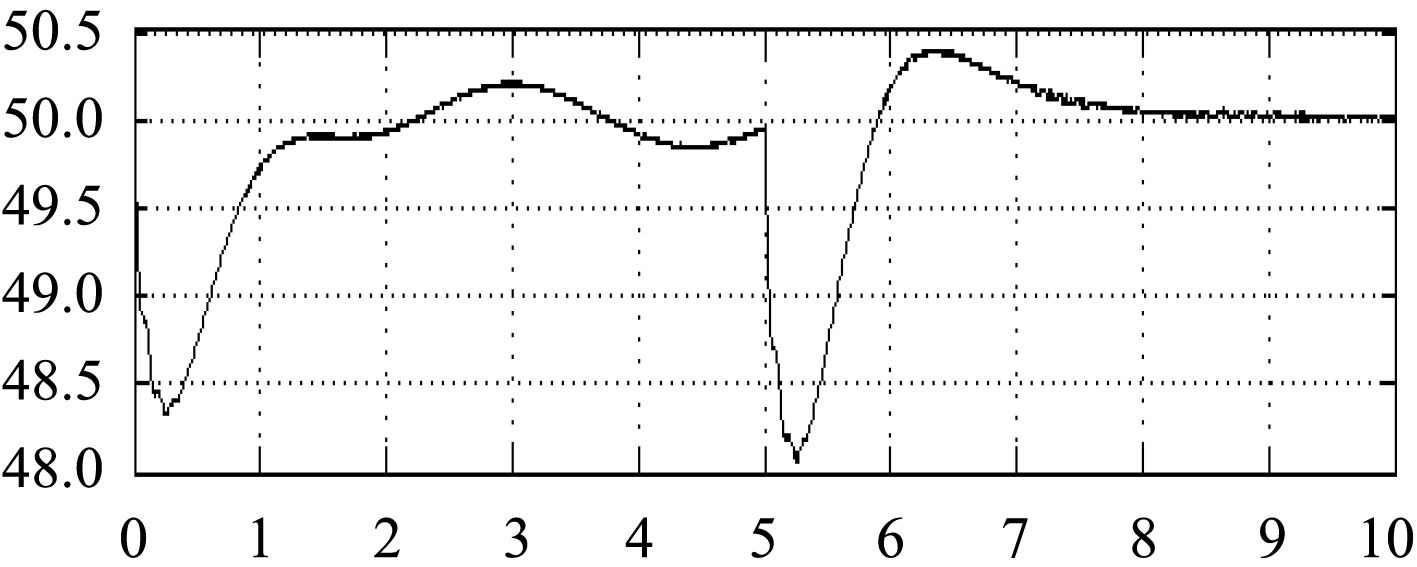
图6和图7为未加混合储能单元时,系统稳定后在5 s时突加负载,系统功率和频率的曲线。
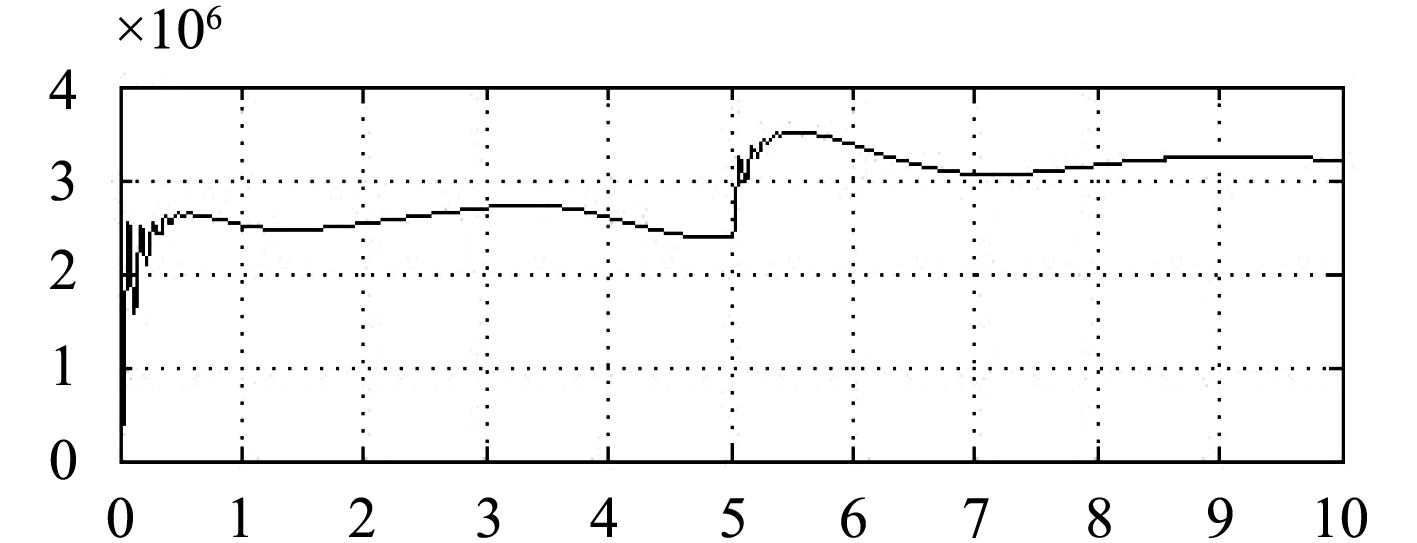
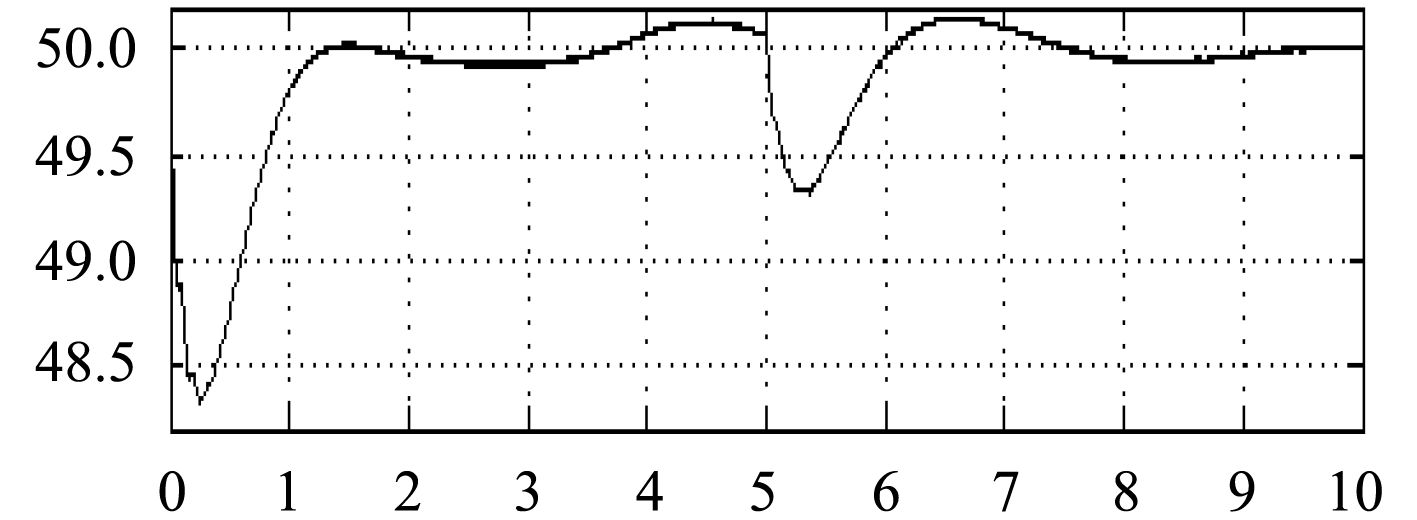
图8和图9为加混合储能单元时,系统稳定后在5 s时突加负载,系统功率和频率的曲线。
通过比较图6和图8、图7和图9,可以发现添加混合储能单元时,在系统突加大功率负载时,混合储能单元释放能量,这样系统的功率和频率的波动减少。
|
图 6 未加混合储能单元时系统功率 Fig. 6 Power without energy storage unit |
|
图 7 未加混合储能单元时系统频率 Fig. 7 Frequency without energy storage unit |
|
图 8 加混合储能单元时系统功率 Fig. 8 Power with energy storage unit |
|
图 9 加混合储能单元时系统频率 Fig. 9 Frequency with energy storage unit |
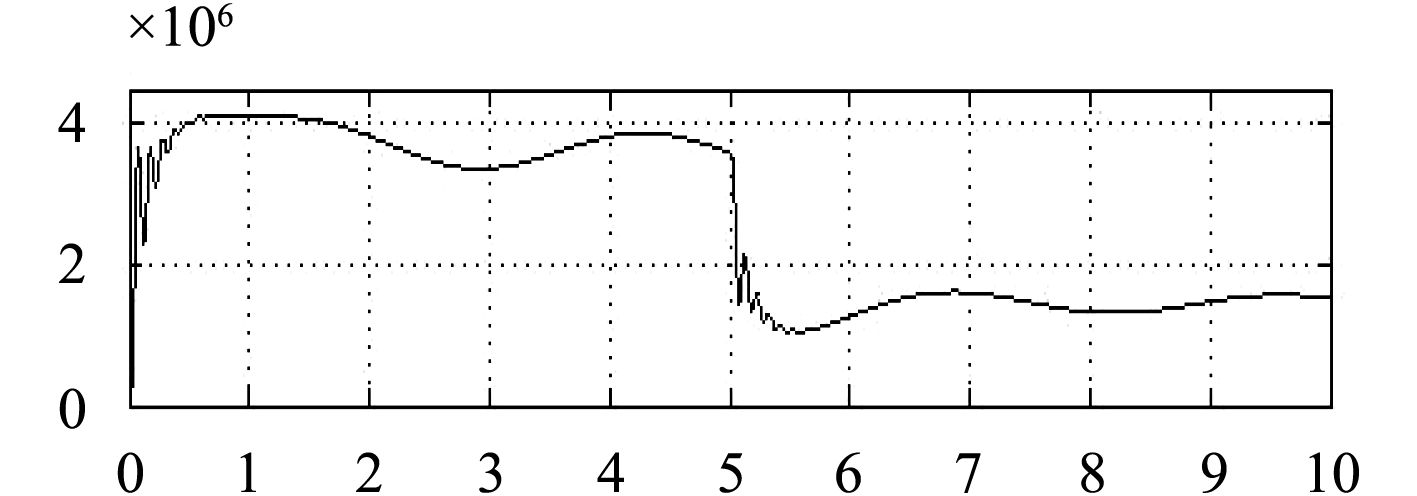
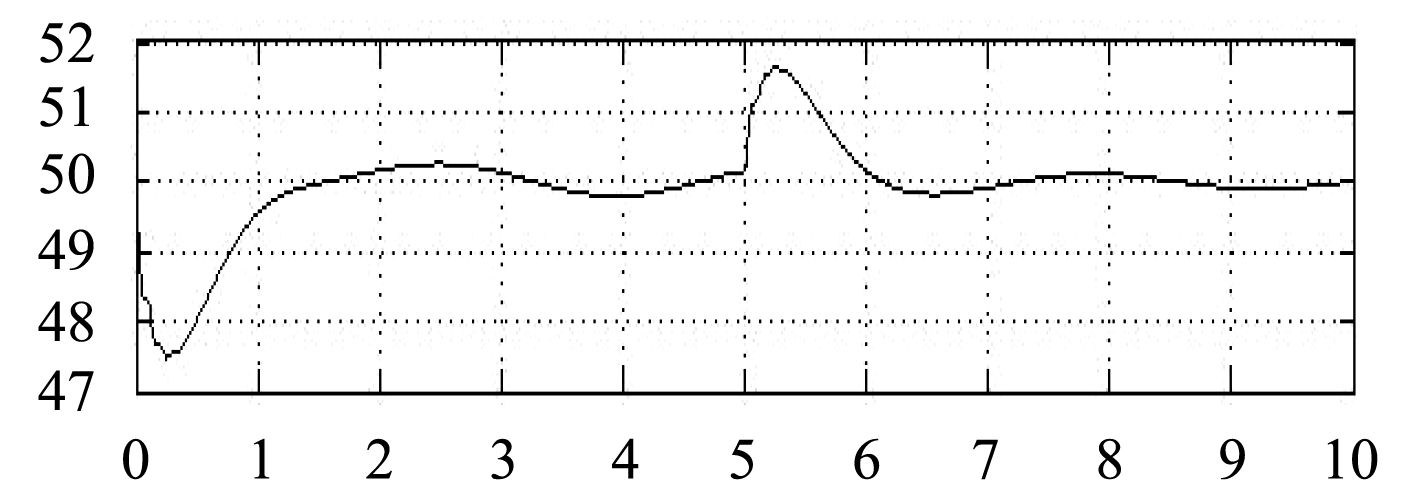
图10和图11为未加混合储能单元时,系统稳定后在5 s时突卸负载,系统功率和频率的曲线。
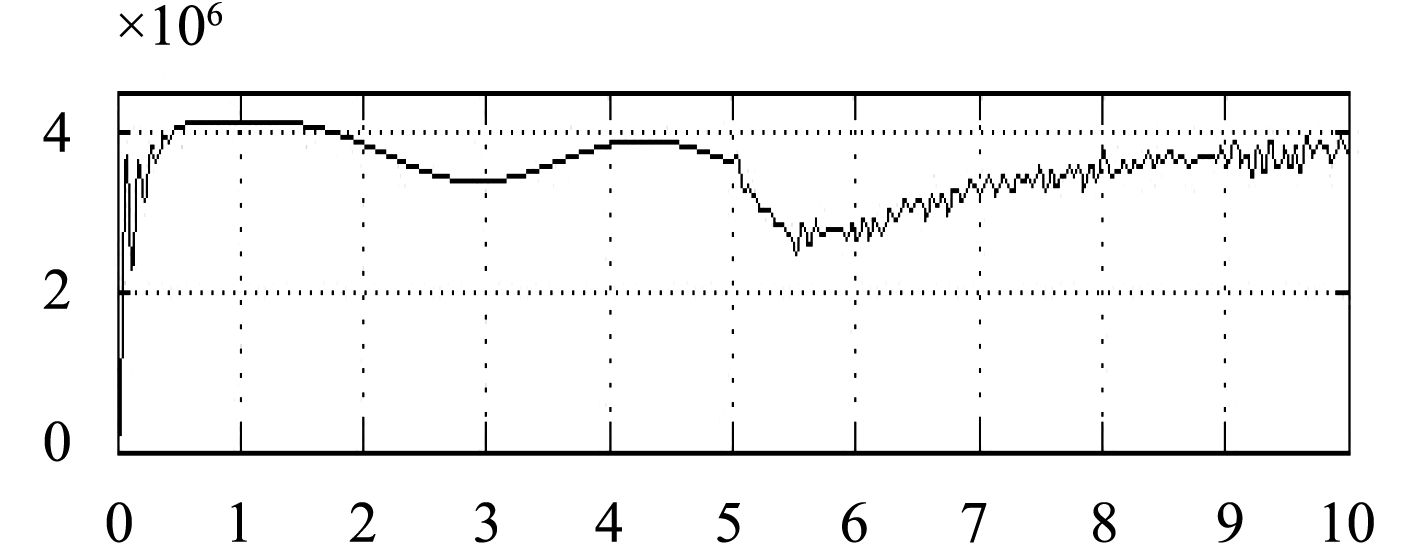
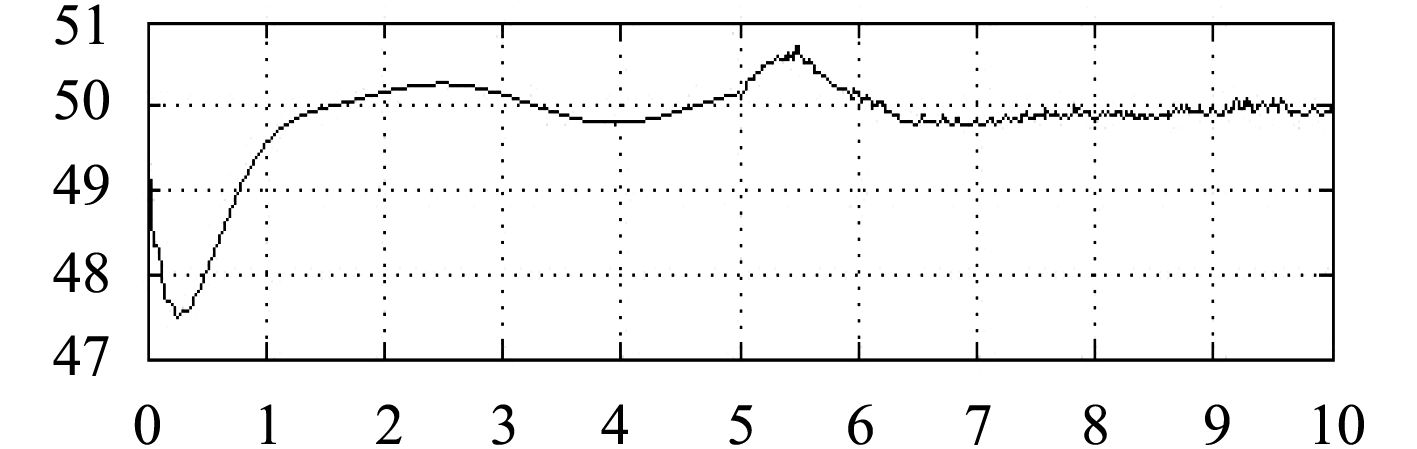
图12和图13为加混合储能单元时,系统稳定后在5 s时突卸负载,系统功率和频率的曲线。
通过比较图10和图12、图11和图13,可以发现添加混合储能单元时,在系统突卸大功率负载时,混合储能单元吸收能量,这样系统的功率和频率的波动减小。
|
图 10 未加混合储能单元时系统功率 Fig. 10 Power without energy storage unit |
|
图 11 未加混合储能单元时系统频率 Fig. 11 Frequency without energy storage unit |
|
图 12 加混合储能单元时系统功率 Fig. 12 Power with energy storage unit |
|
图 13 加混合储能单元时系统频率 Fig. 13 Frequency with energy storage unit |
针对船舶电力系统大功率负载突变,造成船舶电力系统波动问题,本文创新性采用混合储能技术;针对混合储能单元容量,本文创新性采用粒子群算法。运用Matlab对系统船舶电力系统建模,仿真大功率负载的突加和突减。仿真结果表明,这种方法能够明显地减少系统的波动,增强系统的稳定性。
| [1] | 林安平. 船舶电力推进系统中PMSM模糊矢量控制仿真研究[D]. 大连: 大连海事大学, 2007 |
| [2] | HOU Jun, SUN Jing HOFMANN He . Mitigating power fluctuations in electrical ship propulsion using model predictive control with hybrid energy storage system[C]// American Control Conference, Port land, Oregon, 2014: 4366–4371. |
| [3] | 陈刚, 张思全. 超级电容和锂电池技术在船舶电力推进系统中的应用研究概述[J]. 工业控制计算机, 2015, 8(28): 157-158. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gykzjsj201508072 |
| [4] | 陈晨, 王锡淮, 肖健梅. 含储能单元的船舶电力推进系统仿真[J]. 计算机仿真 , 2015, 1(32): 388-391. http://www.cqvip.com/QK/92897X/201501/663500874.html |
| [5] | RL HAUPT, SE HAUPT. Practical genetic algorithms[M]. John Wiley & Sons, 2004. |
 2018, Vol. 40
2018, Vol. 40
