2. 高新船舶和深海开发协同创新中心,上海200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
随着人类对海洋油气资源的开发逐渐向深海转移,海洋平台的作业水深不断增加,这对浮式海洋结构物的定位技术提出了更高的要求[1]。传统的浮式海洋结构物定位方法主要为锚泊定位和动力定位。锚泊定位主要应用于一般水深的情况下,随着水深的不断增加,锚泊定位的应用将会受限。动力定位则可以实现较高的定位精度,且定位成本与水深无关[2]。
锚泊辅助动力定位是一种结合了前2种定位方式特点的新型定位方式[3]。相较于传统的锚泊定位,在同等级海况下,由于推进器的作用,锚链的受力将得到改善和优化,可以防止锚链断裂失效,且提高了定位精度;相较于单独的动力定位系统,锚链的存在将减小推进器功率的消耗,并且使得系统更加稳定[4 – 5]。
近些年来,国内外都对锚泊辅助动力定位系统开展了较多的研究。Aamo[6]提出一种锚链张力反馈系统,将锚链张力的实时测量值作为信号加入动力定位控制系统,以减小锚链负载,避免锚链失效,从而提高了锚泊系统的安全性。Chris Jenman[7]分析了锚泊辅助动力定位系统需要考虑的主要问题。Nguyen[8]提供了一种根据环境载荷自动变换定位位置的方法,可以提高定位精度并减小功率消耗。Sue Wang[9]提出在推力器存在的情况下,可以减少纯锚泊定位时锚链的数量并减小锚链的重量和尺寸。张峰[10]研究了单缆失效对锚泊辅助动力定位系统的影响,王洪超[11]则对锚泊辅助动力定位系统在推进器失效情况下的定位情况进行研究,并提出了几种系统优化的方法。
本文以1艘半潜式海洋平台为对象,在锚泊辅助动力定位系统数学模型的基础上,建立锚泊辅助动力定位时域模拟程序,并在给定的海况条件下,对锚链和推力器复合失效的情况进行时域模拟,得到了一些有益结论,可在工程应用中提供一定的参考价值。
1 锚泊辅助动力定位系统数学模型 1.1 坐标系及坐标变换在锚泊辅助动力定位系统数学模型中,常用下列3个坐标系描述运动和受力:
1)大地坐标系(XGYGZG):大地坐标系固结在地球表面,平面XGOGYG与静水面重合,坐标原点即为定位的目标点,结构物的位置及首向在该坐标系下表示。
2)动坐标系(XYZ):动坐标系与结构物相固结并随其运动。坐标系原点与结构物重心重合,X轴正方向指向船首,Y轴正方向指向左舷,Z轴正方向竖直向上。船舶的运动学方程即在该坐标系中求解。
3)参考平行坐标系(XVYVZV):参考平行坐标系的原点固定在结构物的定位目标点上,且XV轴的正方向指向结构物的目标首向。
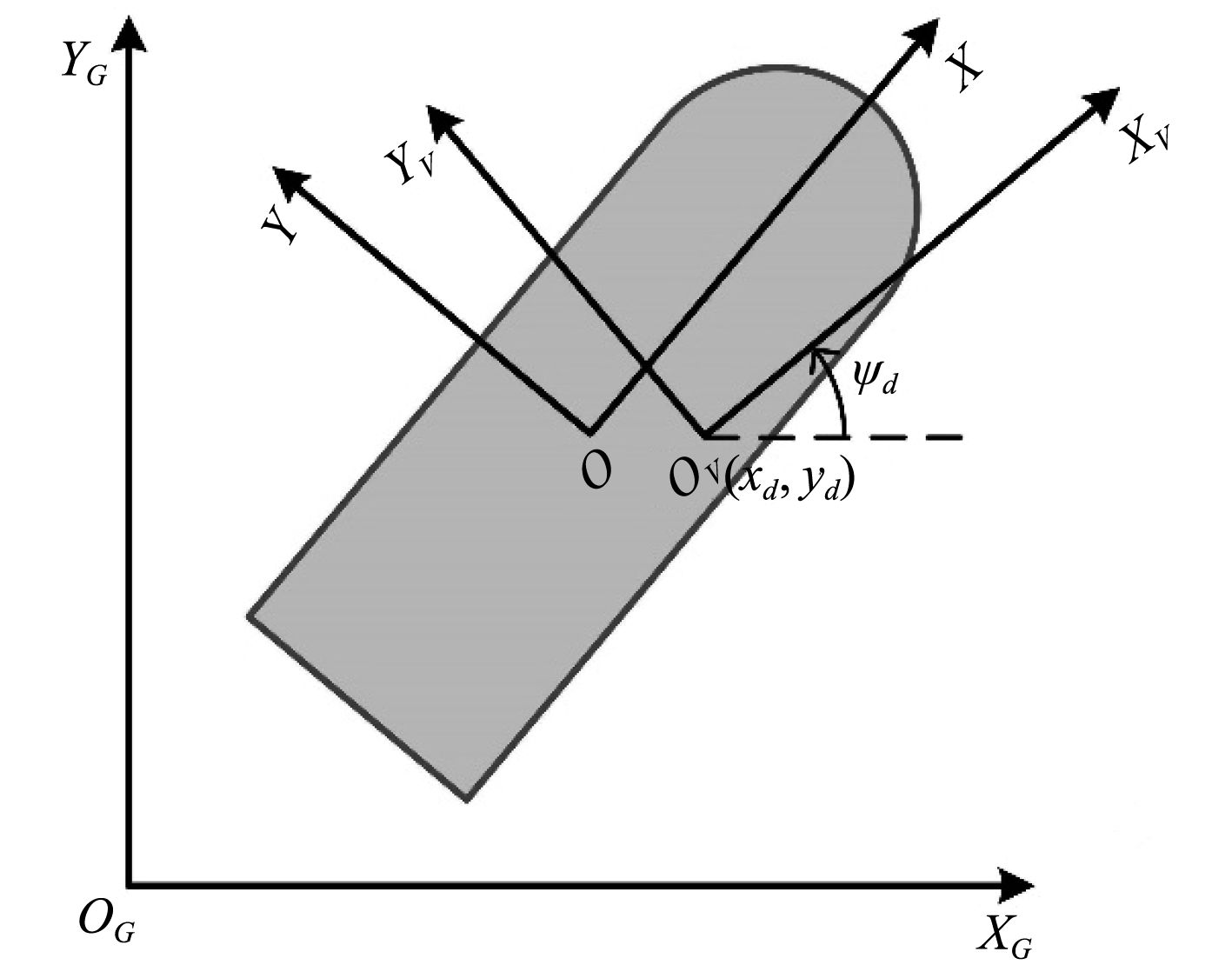
|
图 1 坐标系定义 Fig. 1 Definition of coordinate |
动力定位系统通常只处理结构物在水平面内3个自由度上的运动,结构物在大地坐标中的位置和首向可表示为:
| $\vec \eta = {\left[ {x,y,\psi } \right]^{\rm T}}{\text{,}}$ | (1) |
大地坐标系中船舶的位置和首向与动坐标系中船舶的运动速度通过转化矩阵相联系:
| $\dot {\vec \eta } = { R}(\psi )\vec v{\text{,}}$ | (2) |
其中:
在动力定位时域模拟中,通常将结构物的线性波频运动和非线性低频运动进行分离。波频运动是结构物在一阶波浪力激励下的线性往复运动,可写为:
| ${ M}(w){\ddot \eta _w} + { D}(w){\dot \eta _w} + { G}{\eta _w} = {\tau _{wave1}}{\text{,}}$ | (3) |
其中:
低频运动是指结构物在风力、二阶波浪力、流力、推进器推力、锚泊系统回复力等定常或缓变载荷作用下产生的运动,可写为:
| $\begin{split}[{{ M}_{RB}} + {{ M}_A}]\dot v + [{{ C}_{RB}}(v) + {{ C}_A}(v)]v + {{ D}_p}v = {\tau _{wind}} + {\tau _{current}} + {\tau _{wave2}} + {\tau _{moor}} + {\tau _{thruster}}\end{split}{\text{。}}$ | (4) |
其中:
二阶波浪力包含差频、合频及平均3部分。动力定位系统主要关注的是差频及平均部分,即波浪慢漂力和平均波浪力。假设入射不规则波可以表示为谐波的叠加组合:
| $\zeta (t) = \sum\limits_{i = 1}^N {{\zeta _i}\cos ({\omega _i}t + {\varepsilon _i})} {{\text{。}}}$ | (5) |
则海洋结构物上作用的二阶波浪力(忽略合频部分)可用二次传递函数QTF表示:
| $\begin{aligned} & {F^{(2)}} \!\!=\!\! \sum\limits_{i = 1}^N {{\zeta _i}^2} {P_{ii}} \!\!+\!\! 2\sum\limits_{i = 1}^N {\sum\limits_{j > i}^N {{\zeta _i}{\zeta _j}} } {P_{ij}}\cos \left\{ {({\omega _i} \!\!-\!\! {\omega _j})t \!\!+\!\! ({\varepsilon _i} \!\!-\!\! {\varepsilon _j})} \right\} \!\!+\!\! \\ & \;\;\;\;\;\;\;\;\; 2\sum\limits_{i = 1}^N {\sum\limits_{j > i}^N {{\zeta _i}{\zeta _j}} {Q_{ij}}\sin \left\{ {({\omega _i} \!\!-\!\! {\omega _j})t \!\!+\!\! ({\varepsilon _i} \!\!-\!\! {\varepsilon _j})} \right\}}{\text{。}}\quad \quad \quad \quad \; (6) \end{aligned}$ |
其中:
锚泊系统一般由一组通过转塔连接或直接连接浮式结构物的锚泊线组成,在锚泊辅助动力定位系统中,锚泊系统的作用通常在结构物低频运动模型中进行考虑。由于在锚泊辅助动力定位系统中,锚泊系统起到的是辅助作用,且平台偏移较小,可以对锚泊系统进行简化,忽略锚链的动态效应,采用求解锚泊线悬链线方程的方法进行锚链张力的计算,多段成分锚泊线的悬链线方程为[12]:
| ${\rm{tan}}{\theta _k} = \frac{{\left[ {\sum\limits_{i = 1}^{n + 1 - k} {{W_{n + 1 - i}}{L_{n + 1 - i}}} } \right]}}{Q}{\text{,}}$ | (7) |
| $H = \sum\limits_{i = 1}^n {{h_k}} = \sum\limits_{i = 1}^n {\frac{Q}{{{W_k}}}} \left[ {\sqrt {{{\tan }^2}{\theta _k} + 1} - \sqrt {{{\tan }^2}{\theta _{k + 1}} + 1} } \right]{\text{,}}$ | (8) |
| $S = \sum\limits_{i = 1}^n {{S_k}} = \sum\limits_{i = 1}^n {\frac{Q}{{{W_k}}}} \left[ {s{h^{ - 1}}(tan{\theta _k}) - s{h^{ - 1}}(tan{\theta _{k + 1}})} \right]{\text{,}}$ | (9) |
| $T = \sqrt {{{\left[ {\sum\limits_{k = 1}^n {{W_k}{L_k}} } \right]}^2} + {Q^2}} {\text{。}}$ | (10) |
其中:
得到单根锚泊线的水平回复力后,则整个锚泊系统回复力向量可写为:
| $\begin{array}{l}{\bf{ }}{\tau _{moor}} = - {{ R}^{\rm T}}(\psi ){g_{mo}} = \\ - {{ R}^{\rm T}}(\psi )\sum\limits_{i = 1}^m {\left[ {\begin{array}{*{20}{c}}{{Q_i}\cos {\beta _i}}\\{{Q_i}\sin {\beta _i}}\\{{Q_i}{{\bar x}_i}\sin {\beta _i} - {Q_i}{{\bar y}_i}\cos {\beta _i}}\end{array}} \right]} {\text{。}}\end{array}$ | (12) |
其中:
本文中,动力定位系统控制器中采用的是比例积分微分(Proportional-Integral-Derivative,PID)控制,动力定位系统水平面内三自由度PID控制方法可写成下式:
| ${\tau _{con}} = - {K_p}\Delta x - {K_d}\dot x - {K_i}\int_0^t {\Delta x(\tau ){\rm d}} \tau {\text{。}}$ | (13) |
其中,
推力分配是将前述控制器计算得到的总推力合理分配到各个推进器上,要求消耗功率最小以及实际推力和目标推力误差最小。本文的推力分配即求解下列最优化问题:
| $\begin{split} \min J(\Delta \alpha ,\Delta T,s) = {({T_0} + \Delta T)^{\rm T}}W({T_0} + \Delta T) + {s^{\rm T}}Qs + \\ \Delta {\alpha ^{\rm T}}\varOmega \Delta \alpha + \frac{{\rm d}}{{{\rm d}\alpha }}{\left( {\frac{\rho }{{\varepsilon + \det (B(\alpha ){B^{\rm T}}(\alpha ))}}} \right)_{\alpha = {\alpha _0}}}\Delta \alpha {\text{。}}\end{split} $ | (14) |
其中,目标函数的第1项代表总功率消耗;第2项为实际推力与目标推力间误差的罚函数;第3项的目的是减小全回转推进器的回转速度,以减小机构间的磨损;最后1项是为了避免推进器方向的奇异位置出现。
计算得到每个推进器的转角以及产生的推力后,各个推进器消耗的功率可通过下式计算:
| $P = \frac{{2\pi {K_Q}}}{{K_T^{{3 / 2}}{\rho ^{{1 / 2}}}D}}{T^{\frac{3}{2}}}{\text{。}}$ | (15) |
其中:
本文以1艘半潜平台为对象,其主要结构包括:下浮体2个、立柱4根、主甲板、箱型甲板、居住舱楼、井架、井架台、起重机、直升机平台等。平台的主要参数见表1。
|
|
表 1 半潜平台主要参数 Tab.1 Main parameters of the semi-submersible platform |
如图2所示,该平台动力定位系统采用8个全回转推进器并配备导管,编号依次为T1~T8。其中1,4,5,8号推进器分别距横向及纵向中心线15.70 m和35.50 m,2,3,6,7号推进器分别距横向及纵向中心线47.02 m和24.58 m。8个全回转推进器由4个配电板供电,连接同一配电板的2个推进器均采用对角布置。推进器参数见表2。
|
|
表 2 推进器参数 Tab.2 Main parameters of thrusters |
平台采用分布式悬链线系泊,如图3所示。锚泊系统由8根3段复合式锚链组成,从导缆孔至海底锚点各段材料及其长度分别为:顶部锚链150 m、中段聚酯纤维缆2 650 m、底部锚链1 500 m。系泊缆的预张力为1 185.6 kN,各系泊缆导缆孔位置及海底锚点位置见表3。
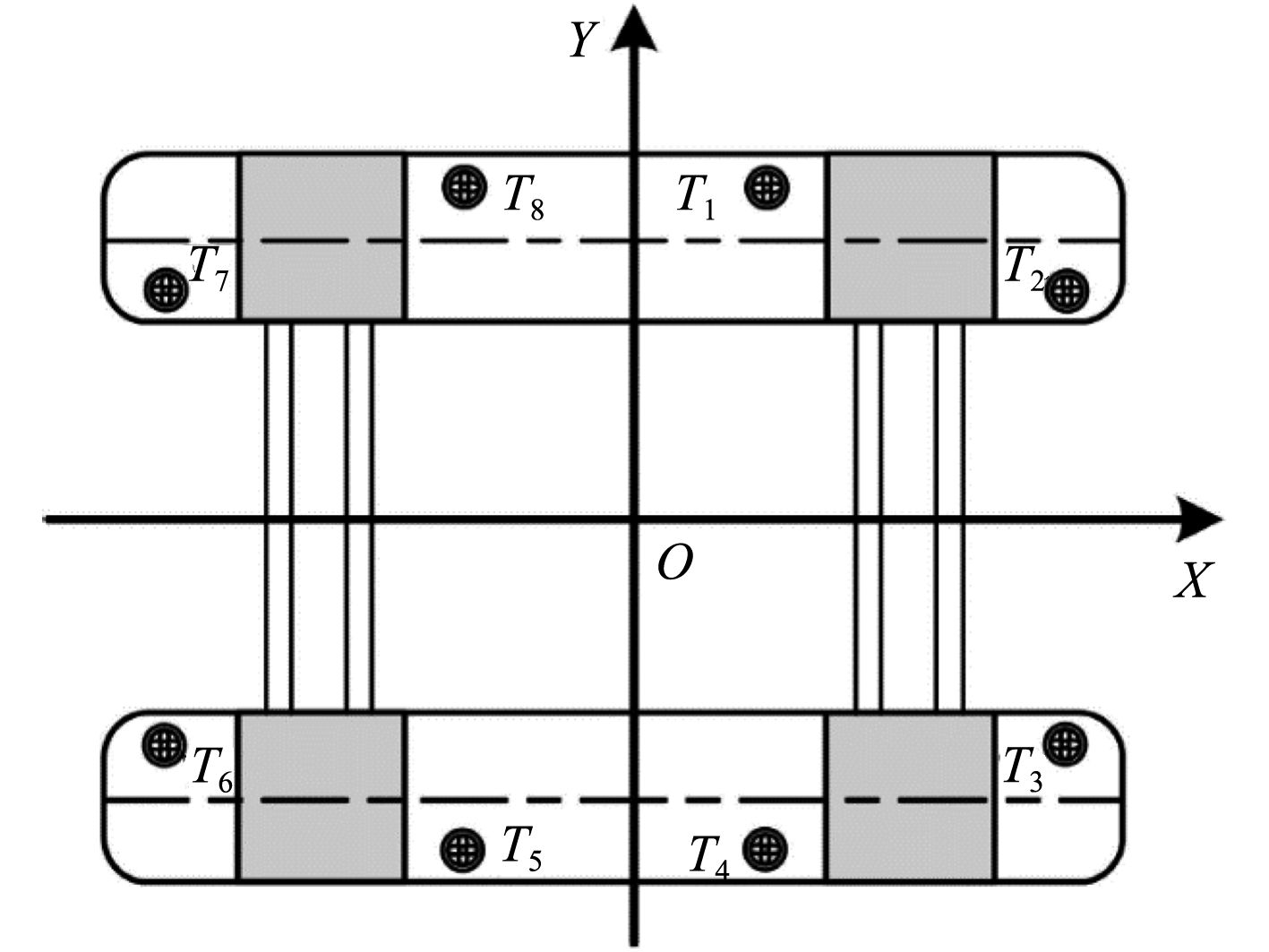
|
图 2 推进器布置 Fig. 2 Layout of the thrusters |

|
图 3 锚泊系统布置 Fig. 3 Layout of the mooring lines |
|
|
表 3 导缆孔及海底锚点坐标 Tab.3 Coordinates of the mooring lines position |
本文风浪流为同向联合作用,参数见表4。环境载荷方向为180°和135°,计算水深为1 500 m。
|
|
表 4 海洋环境条件 Tab.4 Environmental condition |
本文分别对完整模式、单缆失效模式以及锚链推力器复合失效模式下的锚泊辅助动力定位系统进行时域模拟。首先对180°和135°风浪流方向下完整模式的锚泊辅助动力定位系统进行时域模拟,进而将完整模式下,时域模拟中出现最大张力的锚链设为后续研究的失效缆;推力器失效则选取同一配电板上2个推力器同时失效的情况。所有计算工况列于表5。
|
|
表 5 计算工况 Tab.5 Calculation cases |
通过时域模拟得到了半潜平台的运动情况以及锚泊辅助动力定位系统的功率消耗。半潜平台偏移距离的时历曲线如图4和图6所示,半潜平台的功率消耗曲线时历如图5和图7所示,此处仅列出工况1、工况3、工况7、工况9的时历曲线。半潜平台运动及锚泊辅助动力定位系统功率消耗的统计数据列于表6和表8,各推进器的功率消耗统计数据列于表7和表9。
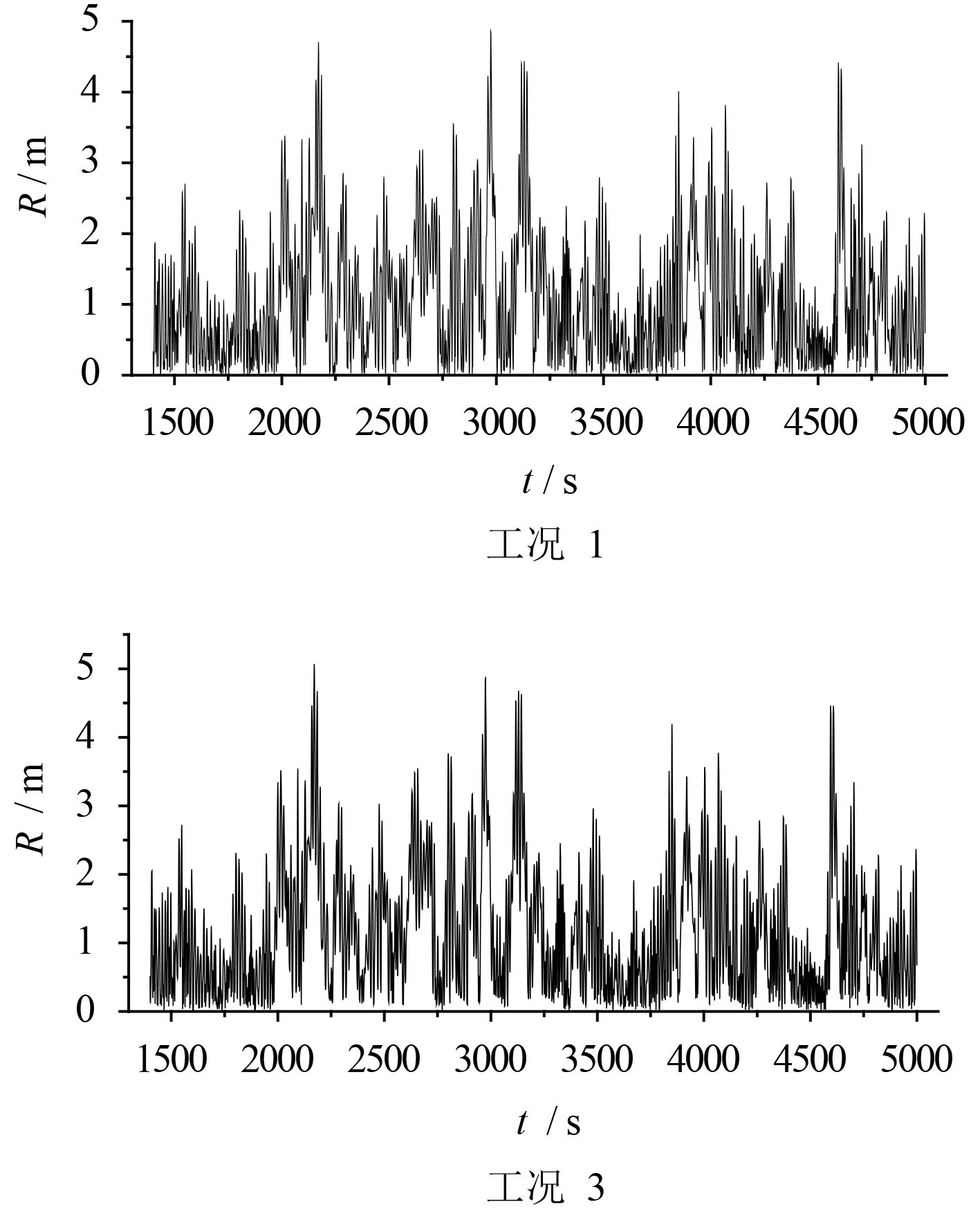
|
图 4 180°环境载荷各失效模式下平台偏移距离时历曲线 Fig. 4 Offset of the platform under different failure mode in 180° direction |
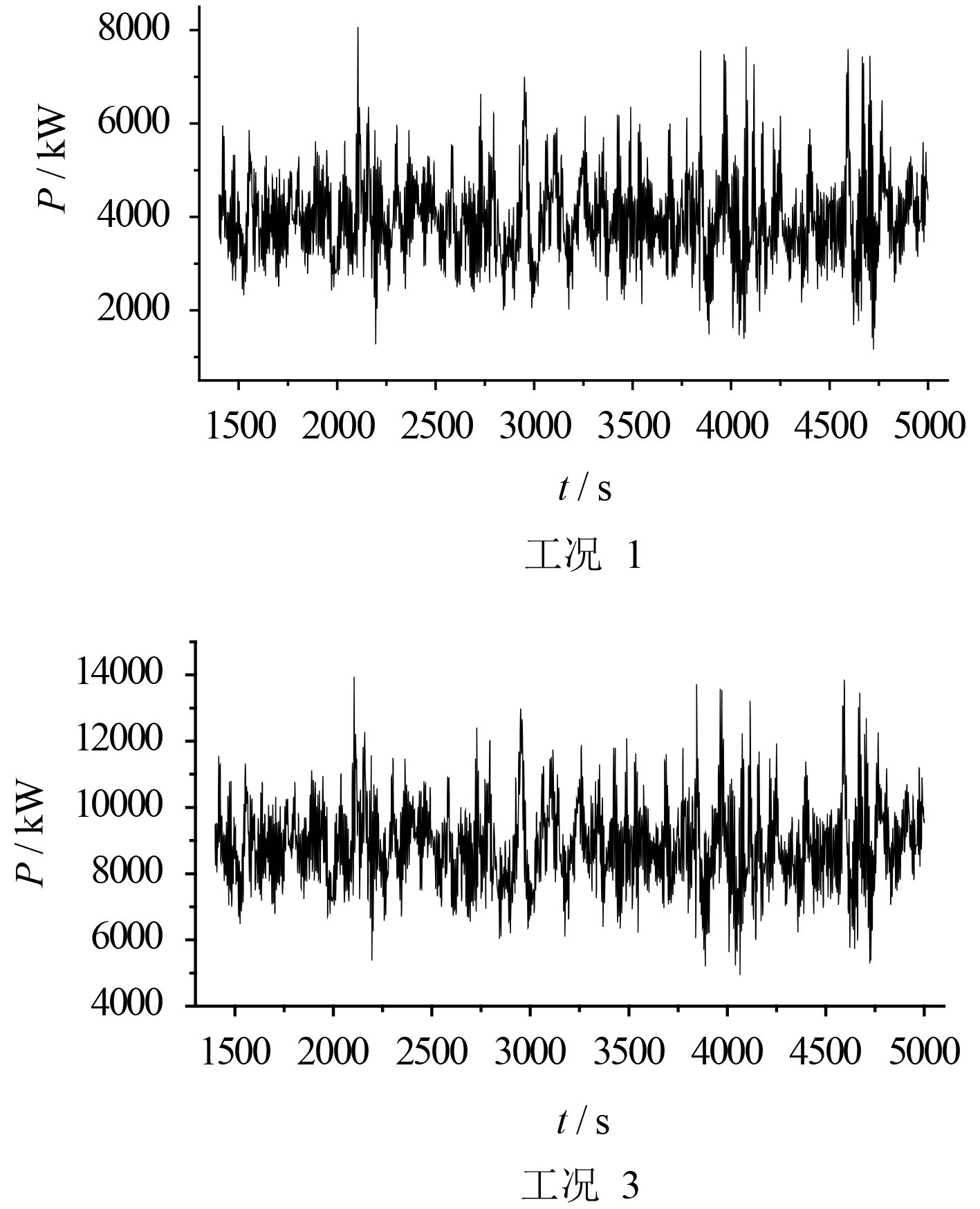
|
图 5 180°环境载荷各失效模式下功率消耗时历 Fig. 5 Power consumption of the platform under different failure mode in 180° direction |
|
|
表 6 180°环境载荷方向平台运动及总功率消耗统计值 Tab.6 The statistic values of the platform motion and platform utilized power in 180° direction |
|
|
表 7 180°环境载荷方向各推力器功率消耗统计值 Tab.7 The statistic values of the thrusters in 180° direction |
由表6可知,在180°环境载荷下,单缆失效以及锚链及推力器复合失效均会导致定位精度的降低,但影响程度较小。其中,锚泊系统单缆失效下最大偏移半径增加了4.2%,复合失效模式下(工况3)最大偏移半径增加了4.5%。这是由于在单缆失效模式下,动力定位系统在定位中起到主要作用,保证了平台的定位精度。而推力器失效主要影响的是动力定位系统的推力分配,对平台定位精度影响较小。所以在锚链及推力器复合失效的模式下,平台仍能保持较高的定位精度。
同样,由表6可知,在180°环境载荷下,单缆失效以及锚链及推力器复合失效模式下,平台的总功率消耗相比于完整模式将出现大幅度增长。其中,单缆失效模式下,平台平均功率消耗增加94.1%;锚链推进器复合失效模式下(工况3),平台平均功率消耗增加123.8%。这是由于当平台处于目标定位位置时,存在单缆失效情况的锚泊系统作用在平台上的力并不平衡,存在着使平台偏离定位位置和目标首向的力和力矩,此时动力定位系统需要提供额外的力和力矩来抵抗这部分载荷。进一步的,推进器的失效使得推力分配的求解可行域减小了,推力分配没有达到最优解,且推进器数目减少,剩余6个工作的推进器每个都需要提供更大的推力,来达到无推力器失效情况时8个推进器提供的合力及力矩,造成功率又进一步增加。
由表7可知,在180°环境载荷下,完整模式下每个推力器消耗的功率较为均匀,此时推力系统的功率储备较大,系统的安全性高。单缆失效模式下各推进器消耗的功率出现差异,处于平台左舷的4个推进器T1,T2,T7和T8消耗的功率更大,这是由于平台在目标定位位置和目标首向时,受到锚泊系统作用的方向为z轴正方向的力矩,所以左舷的推进器要比右舷的推进器提供更大的推力,以此抵抗锚泊系统的力矩;在锚链及推力器复合失效的模式下,各个推进器的功率消耗差距进一步扩大,如在工况4中,T8的平均功率达到1 773.38 kW,最大功率更是达到2 678.77 kW,此时该推进器处于高负荷工作状态,推进器的磨损加大,使得推进器寿命降低。
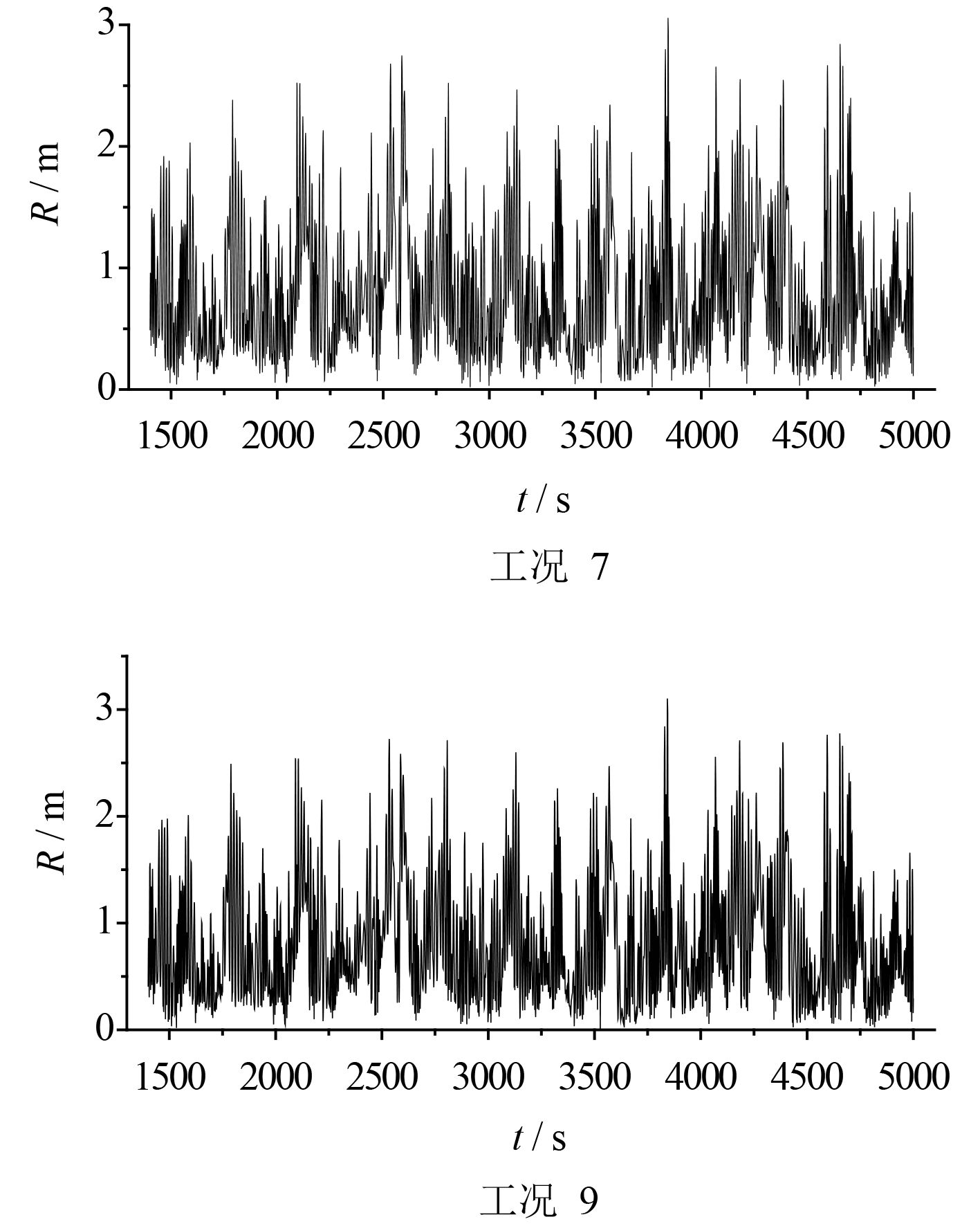
|
图 6 135°环境载荷各失效模式下平台偏移距离时历曲线 Fig. 6 Offset of the platform under different failure mode in 135° direction |
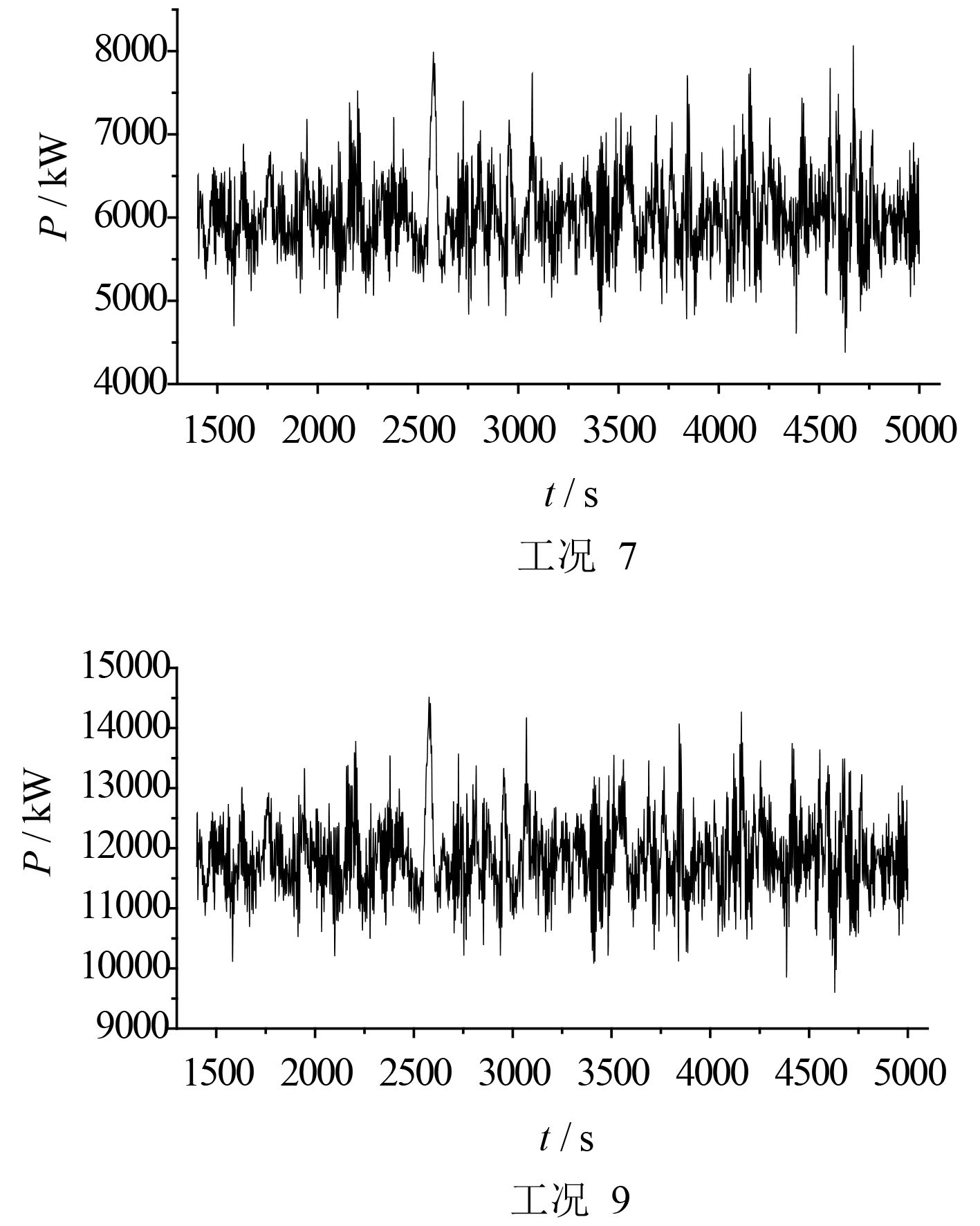
|
图 7 135°环境载荷各失效模式下功率消耗时历 Fig. 7 Power consumption of the platform under different failure mode in 135° direction |
|
|
表 8 135°环境载荷方向平台运动及总功率消耗统计值 Tab.8 The statistic values of the platform motion and platform utilized power in 135° direction |
|
|
表 9 135°环境载荷方向各推力器功率消耗统计值 Tab.9 The statistic values of the thrusters in 135° direction |
由表8可知,在135°环境载荷下,单缆失效及锚链推进器复合失效同样将造成平台定位精度的降低,但影响非常小。其中单缆失效模式下最大偏移半径增加了1.5%,复合失效模式下(工况9)最大偏移半径增加了1.6%。而且在135°环境载荷下,平台在3个模式下的定位精度要整体好于180°环境载荷下的定位精度,这是因为平台在180°环境载荷条件下,其附加质量较小,所以更容易在二阶波浪力的作用下,产生大规模的往复运动。总的来说,在135°环境载荷下,平台在复合失效模式下仍能保持较高的定位精度。
由表8可知,在135°环境载荷下,单缆失效及复合失效同样将导致平台的总功率消耗出现大幅度增长。其中单缆失效模式平台平均功率消耗增加70.7%,复合失效模式(工况9)平台平均功率消耗增加96.9%。而且在135°环境载荷下,平台在3种模式下的功率消耗要整体高于180°环境载荷下平台的功率消耗,这是因为平台处于135°环境载荷条件时,平台的有效受载荷面积更大,所受外载荷要大于180°环境载荷下的外载荷。尤其是在首摇方向上,存在着很大的力矩,需要动力定位系统进行抵抗。
由表9可知,在135°环境载荷下,完整模式及各失效模式下各推进器平均功率消耗都较为均匀,但在锚链及推进器复合失效的工况9、工况10及工况11中,存在推进器的瞬时最大功率接近推进器额定功率4 200 kW的情况。此时推进器的负载非常大,且与之相连的配电板负载同样很大,非常容易出现新的推进器失效,从而进一步恶化推力分配结果和功率消耗情况,最终致使平台失位。
4 结 语本文通过对半潜平台锚泊辅助动力定位系统锚链及推进器复合失效模式的时域模拟,得到了平台完整模式以及不同失效模式下的定位精度以及功率消耗,通过分析复合失效模式对锚泊辅助动力定位系统的影响,可以得到下列几个结论:
1)总体来说,锚泊辅助动力定位系统的安全冗余度较高,在平台单缆失效和锚链及推进器复合失效的情况下,仍然能保持较高的定位精度,保证作业的安全。
2)在平台总的功率消耗方面,锚链及推进器复合失效情况下,功率消耗相较于单缆失效时会进一步增加,使得油耗增加,整个系统的经济性下降。
3)在单个推进器工作情况上,在锚链及推进器复合失效模式中,180°外载荷工况下,各个推进器的工作状态会出现较大差别,推力系统中将会出现单个推进器功率消耗特别大的情况。而在135°外载荷工况下,将会出现个别推进器功率达到额定功率的情况,这种单个推进器功率消耗剧增的情况将使得整个推力系统的功率储备大幅降低,系统安全性降低,且容易出现新的推进器失效的情况,造成整个系统的情况进一步恶化,最终可能导致平台失位。所以在实际工程中,要密切关注这种单个推进器功率消耗剧增的情况。
| [1] | 金秋, 张国忠. 世界海洋油气开发现状及前景展望[J]. 国际石油经济, 2005, 13(3) : 43-44. http://www.cnki.com.cn/Article/CJFDTotal-SKYK201506002.htm |
| [2] | 赵志高, 杨建民, 王磊, 等. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002, 20(1) : 91-97. http://www.cnki.com.cn/Article/CJFDTOTAL-CANB200105000.htm |
| [3] | ASGEIR J S, JANN P S, et al. Thruster assisted position mooring system for turret-anchored FPSOs[C]//International Conference on Control Applications, 1999. |
| [4] | 孙攀. 深海半潜式钻井平台锚泊辅助动力定位系统研究[D]. 上海: 上海交通大学, 2011. |
| [5] | WICHERS J, VAN DIJK R. Benefits of using assisted DP for Deepwater Mooring Systems[C]//Offshore Technology Conference, 1999. |
| [6] | AAMO O M, FOSSEN T. Controlling line tension in thruster assisted mooring systems[C]//Proceedings of IEEE International Conference on Control Applications, 1999, 2: 1104-1109. |
| [7] | CHRIS Jenman. Mixing dynamic positioning with moorings[C]//Dynamic Positioning Conference, 2005. |
| [8] | NGUYEN D T, Sorensen A J. Setpoint chasing for thruster-assisted position mooring[J]. Oceanic Engineering, 2009, 34(4): 548-558. |
| [9] | SUE Wang. On the assessment of thruster assisted mooring[J]. Offshore Technology Conference, 2010. |
| [10] | 张峰, 王磊, 李勇跃. 锚泊辅助动力定位系统单缆失效影响研究[J]. 海洋工程, 2012, 30(3): 29-34. http://mall.cnki.net/magazine/Article/HYGC201203005.htm |
| [11] | 王洪超, 王磊, 张峰. 锚泊辅助动力定位系统推力器故障模式影响分析[J]. 海洋工程, 2013, 31(1): 26-31. http://www.cqvip.com/QK/90248X/201301/44860682.html |
| [12] | 余龙, 谭家华. 基于准静定方法的多成分锚泊线优化[J]. 海洋工程, 2005, 23(1): 69-73. http://mall.cnki.net/magazine/Article/HYGC200501011.htm |
 2018, Vol. 40
2018, Vol. 40

