2. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
在海洋资源竞争日益激烈、海洋环境复杂多变的形势下,大力开发新式海洋装备已成为提升国家海洋综合实力的最迫切需求。水下张力腿平台[1]是一种新型专用水下并联试验设施,通过8台液压绞车实现平台上浮、下潜及调平控制。考虑到平台的大惯性、大迟滞、并联驱动特性、强交叉耦合、复杂试验环境,及液压驱动系统的变负载、长管路、非线性特性,液压驱动系统建模及运动控制非常具有挑战性。
并联机器人常用的建模方法有牛顿-欧拉(Newton-Euler)法、拉格朗日(Lagrange)法、虚功原理法、凯恩(Kane)法[2 – 5]等。文献[6]针对一种3-PSS机器人,应用拉格朗日方程建立了其动力学模型,且在给定动平台运动轨迹和负载的情况下,求出了所需驱动力。张国伟等[7]以Kane方程为基础,分析并联机器人各个驱动杆件及运动平台质心点的速度、加速度关系,选取运动平台中心点的速度和角速度分量为广义速率,推导出机器人的动力学方程。文献[8]采用旋量键合图建立了球面2-DOF过约束并联机器人的并存系统动力学模型,相对于传统建模方法,该方法的建模过程更加规则化,能够得到适合于现代控制理论的空间并联机构动力学模型。
张力腿平台液压驱动系统包含非线性及不确定性,针对这类复杂控制对象,常用控制算法包括:H∞控制[9]、自适应控制[10]、滑模控制[11]、模糊控制[12]、反演控制[13]、神经网络控制[14]等。文献[15]针对一种六自由度欠约束柔性并联机器人,分别采用计算力矩控制器和PD控制器对其进行动力学控制。文献[16]借鉴具有多目标协同调节特性的生物网络机制,对并联机器人的一些多目标协同智能控制问题进行研究。牛雪梅[17]为了解决所建动力学模型用于并联机构控制计算量大、实时性差等问题,提出了一种基于RBF神经网络进行误差补偿的动力学模型补偿方案及解耦非奇异终端滑模控制方法。
本文结合水下张力腿平台驱动系统特性,开展建模及控制技术研究。在建模过程中,利用牛顿欧拉法建立了平台的动力学模型,并推导出驱动空间的外负载力矩方程,之后结合液压驱动系统模型及系统不确定分析,最终建立了包含综合不确定性且上界未知的系统控制模型。在控制技术研究过程中,针对系统综合不确定性上界未知特性,完成了自适应反演滑模控制器设计。最终,通过仿真验证了本文研究内容的正确性与有效性。
1 水下张力腿平台液压驱动系统 1.1 水下张力腿平台结构分析水下张力腿平台结构如图1所示,4台张力绞车和4台锚泊绞车分别通过张力缆和锚泊缆与4个重力锚相连。图中,垂向钢缆为张力缆,上端通过张力角点Ai与对应的张力绞车相连,下端固定在锚桩点Mi上。斜拉钢缆为锚泊缆,下端固定在锚桩点Mi,其上端通过锚泊角点Ci及Di与同侧对角的锚泊绞车相连。

|
图 1 水下张力腿平台 Fig. 1 Underwater tension leg platform |
平台采用八缆内置式布置方案,所有缆索均布置在平台的垂向投影面积内,其优点在于:
1)一组垂向索和斜拉索共用一个重力锚,比外拉斜索方案减少了4个锚桩;
2)可以限制并联平台在水平面内的移动及转动;
3)避免了大对角斜拉缆方案4缆交叉于一点的不利干扰。
1.2 液压驱动系统组成水下张力腿平台液压驱动系统由油箱、泵站、阀件、管路及液压绞车组成,液压绞车外形如图2所示。

|
图 2 水下液压绞车 Fig. 2 Underwater hydraulic winch |
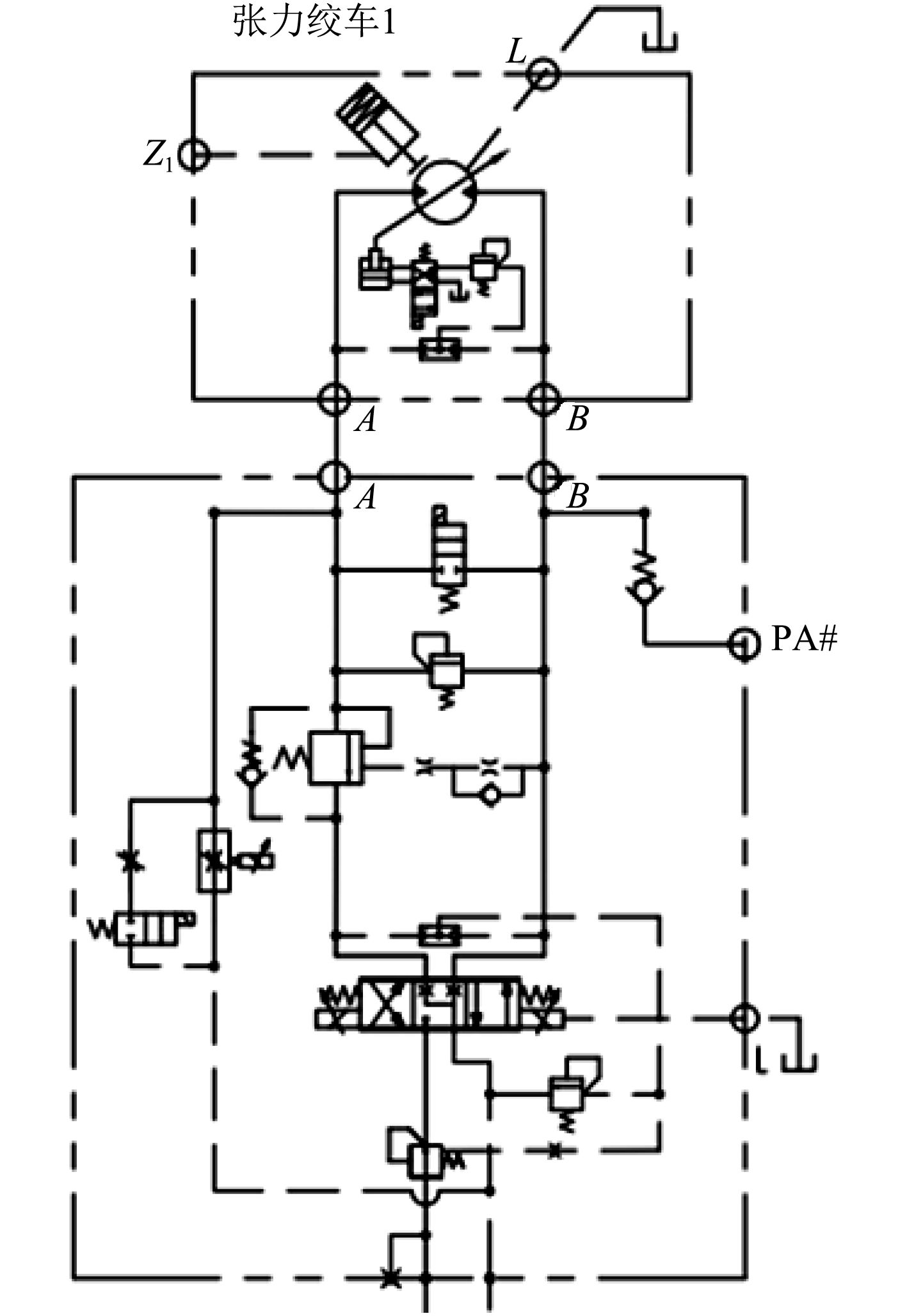
平台右舷耐压浮筒内部安装了1个液压泵站,向4台张力绞车、4台锚泊绞车主油路和控制油路提供压力油,液压驱动系统主回路工作原理如图3所示,其核心为三位四通电液比例换向阀,通过改变比例阀换向及阀芯开度调整,实现液压马达的正反转及转速控制。
|
图 3 液压驱动主回路 Fig. 3 Hydraulic drive main circuit |
另外,为满足平台下潜控制及调平控制中的不同要求,液压马达设计了大排量和小排量2种工作模式,分别对应绞车的行程控制及速度控制,本文主要研究绞车的速度控制模式。
2 系统建模 2.1 液压驱动系统动力学建模液压驱动系统可简化为阀控液压马达,其原理如图4所示。

|
图 4 阀控液压马达 Fig. 4 Valve-controlled hydraulic motor |
假设阀为理想的阀,且忽略摩擦损失、泄漏、流体质量和管道动态影响,其动力学模型可由下列4个基本方程构成[18]。
1)阀芯位移控制方程
| ${x_v} = Ku{\text{,}}$ | (1) |
式中:
2)液压阀流量方程
| ${Q_L} = {c_d}\omega {x_v}\sqrt {\tfrac{1}{\rho }({p_s} - {p_L}\operatorname{sgn} ({x_v}))} {\text{,}}$ | (2) |
式中:
3)液压马达流量连续性方程
| ${Q_L} = {D_m}\frac{{\rm d}{\theta _m}}{{\rm d}t} + {C_{tm}}{p_L} + \frac{{{V_m}}}{{4{\beta _e}}}\frac{{\rm d}{p_L}}{{\rm d}t}{\text{,}}$ | (3) |
式中:
4)液压马达力矩平衡方程
| ${T_s} = {p_L}{D_m} = {J_m}\frac{{{\rm d}^2}{\theta _m}}{{\rm d}{t^2}} + {B_m}\frac{{\rm d}{\theta _m}}{{\rm d}t} + {G_m}{\theta _m} + {T_L}{\text{。}}$ | (4) |
式中:
假设平台为质量均匀分布的刚体,且忽略缆绳弹性形变,其受力分析如图5所示。

|
图 5 受力分析 Fig. 5 Force analysis |
图中,
由于平台采用八缆内置式同侧耦合布缆方式,使得张力缆与同组锚泊缆之间存在相互作用,从很大程度上可以限制平台在水平面内的移动及转动;且平台本身为大尺寸、大惯性的结构体,在环境相对简单的湖泊中,受水中暗流影响,平台在水平面内的移动距离很小;因此,在平台控制过程中,更关注平台的垂向运动及纵横倾姿态。
假设平台垂向位置为
| $\begin{split} & {F_1} + {F_2} + {F_3} + {F_4} + {F_1}^\prime \cos {\sigma _1}^\prime + {F_2}^\prime \cos {\sigma _2}^\prime + \\ & {F_3}^\prime \cos {\sigma _3}^\prime + {F_4}^\prime \cos {\sigma _4}^\prime \!+\! {G_1} \!-\! {F_d} \!-\! {F_b} \!=\! ({m_1} \!+\! \Delta m)\ddot z {\text{。}}\end{split} $ | (5) |
横倾欧拉方程:
| $\begin{split} {F_1}\frac{{b'}}{2} \!+\! {F_4}^\prime \frac{{b''}}{2}\cos {\sigma _4}^\prime + {F_4}\frac{{b'}}{2} \!+\! {F_1}^\prime \frac{{b'}}{2}\cos {\sigma _1}^\prime \!-\! {F_2}\frac{{b'}}{2} - \\ \!\!\!\!\! {F_3}^\prime \frac{{b''}}{2}\cos {\sigma _3}^\prime \!\!-\! {F_3}\frac{{b'}}{2} \!-\! {F_2}^\prime \frac{{b''}}{2}\cos {\sigma _2}^\prime \!\!=\! ({I_x} \!+\! \Delta {I_x})\ddot \alpha{\text{。}} \end{split} $ | (6) |
式中:
纵倾欧拉方程:
| $\begin{split}& {F_3}\frac{{a'}}{2} \!+\! {F_2}^\prime \frac{{a''}}{2}\cos {\sigma _3}^\prime \!+\! {F_4}\frac{{a'}}{2} \!+\! {F_1}^\prime \frac{{a''}}{2}\cos {\sigma _4}^\prime \!- \!{F_1}\frac{{a'}}{2} \times \\& {F_4}^\prime \frac{{a''}}{2}\cos {\sigma _1}^\prime \!-\! {F_2}\frac{{a'}}{2} \!-\! {F_3}\frac{{a''}}{2}\cos {\sigma _2}^\prime \!=\! ({I_y} \!+\! \Delta {I_y})\ddot \beta{\text{。}} \! \!\!\end{split} $ | (7) |
由于平台在受到暗流作用时,水平方向几乎没有移动,为简化平台控制流程,平台运动控制以张力绞车为主,锚泊绞车随动,则锚泊缆张力
平台动力学模型可简化为:
| ${{{L}}_{{f}}}{\rm{\cdot}}{{F}}{\rm{ + }}{{{M}}_{{g}}} = {{{M}}_{{L}}}{\mathbf{\ddot \eta }}{\text{。}}$ | (8) |
式中:
| ${{{L}}_{{f}}} = \left[ {\begin{array}{*{20}{c}} 1&1&1&1 {\displaystyle\frac{{b'}}{2}}&{ - \displaystyle\frac{{b'}}{2}}&{ - \displaystyle\frac{{b'}}{2}}&{\displaystyle\frac{{b'}}{2}} { - \displaystyle\frac{{a'}}{2}}&{ - \displaystyle\frac{{a'}}{2}}&{\displaystyle\frac{{a'}}{2}}&{\displaystyle\frac{{a'}}{2}} \end{array}} \right];$ |
由式(8)可得:
| ${\mathbf{\ddot \eta }} = {{{M}}_{{L}}}^{ - 1}{{{L}}_{{f}}}{\rm{\cdot}}{{F}}{\rm{ + }}{{{M}}_{{L}}}^{ - 1}{{{M}}_{{g}}}{\text{,}}$ | (9) |
利用雅克比矩阵将任务空间动力学模型转化至关节空间可得:
| ${{{L}}} = {J_\eta }{{{M}}_{{L}}}^{ - 1}{{{L}}_{{f}}}{\rm{\cdot}}{{F}}{\rm{ + }}{J_\eta }{{{M}}_{{L}}}^{ - 1}{{{M}}_{{g}}}{\text{。}}$ | (10) |
式中:
由液压绞车机械传动关系可得:
| ${{L}} = \frac{R}{n}{\rm{\cdot}}{{\mathbf{\theta }}_{\mathbf{m}}}{\text{。}}$ | (11) |
式中:
由式(10)和式(11),可得:
| $\frac{R}{n}{{\mathbf{\ddot \theta }}_{\mathbf{m}}} = {J_\eta }{{{M}}_{{L}}}^{ - 1}{{{L}}_{{f}}}{\rm{\cdot}}{{F}}{\rm{ + }}{J_\eta }{{{M}}_{{L}}}^{ - 1}{{{M}}_{{g}}}{\text{,}}$ | (12) |
则张力腿驱动力方程为:
| ${{F}} = {({J_\eta }{{{M}}_{{L}}}^{ - 1}{{{L}}_{{f}}})^{ - 1}}\left(\frac{R}{n}{{\mathbf{\ddot \theta }}_{\mathbf{m}}} - {J_\eta }{{{M}}_{{L}}}^{ - 1}{{{M}}_{{g}}}\right){\text{。}}$ | (13) |
由力矩计算公式
| ${{{T}}_{{L}}} = \frac{R}{n}{({J_\eta }{{{M}}_{{L}}}^{ - 1}{{{L}}_{{f}}})^{ - 1}}\left(\frac{R}{n}{{\mathbf{\ddot \theta }}_{\mathbf{m}}} - {J_\eta }{{{M}}_{{L}}}^{ - 1}{{{M}}_{{g}}}\right){\text{。}}$ | (14) |
式中:
将式(14)代入式(4),可得新的力矩平衡方程如下:
| $\begin{split}{T_s} = {p_L}{D_m} = {J_m}\displaystyle\frac{{{\rm d}^2}{\theta _m}}{{\rm d}{t^2}} + {B_m}\displaystyle\frac{{\rm d{\theta _m}}}{{\rm d}t} + {G_m}{\theta _m} + \displaystyle\frac{R}{n}{({J_\eta }{M_L}^{ - 1}{L_f})^{ - 1}}\left(\displaystyle\frac{R}{n}{{\ddot \theta }_m} - {J_\eta }{M_L}^{ - 1}{M_g}\right){\text{,}}\end{split}$ | (15) |
则张力腿平台液压驱动控制模型如下:
| $\left\{ {\begin{array}{*{20}{l}}{{x_v} = Ku}{\text{,}}{{Q_L} = {c_d}\omega {x_v}\sqrt {{\displaystyle{1 \over \rho }}({p_s} - {p_L}{\mathop{\rm sgn}} ({x_v}))} }{\text{,}}{{Q_L} = {D_m}\displaystyle\frac{{\rm d}{\theta _m}}{{\rm d}t} + {C_{tm}}{p_L} + \displaystyle\frac{{{V_m}}}{{4{\beta _e}}}\displaystyle\frac{{\rm d}{p_L}}{{\rm d}t}}{\text{,}}\begin{array}{l}{T_s} = {p_L}{D_m} = {J_m}\displaystyle\frac{{{\rm d^2}{\theta _m}}}{{\rm d}{t^2}} + {B_m}\displaystyle\frac{{\rm d{\theta _m}}}{{\rm d}t} + {G_m}{\theta _m} + \displaystyle\frac{R}{n}{({J_\eta }{M_L}^{ - 1}{L_f})^{ - 1}}\left(\displaystyle\frac{R}{n}{{\ddot \theta }_m} - {J_\eta }{M_L}^{ - 1}{M_g}\right){\text{。}}\end{array}\end{array}} \right.$ | (16) |
经过转化可得:
| $\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}\left({J_m} + {({J_\eta }{M_L}^{ - 1}{L_f})^{ - 1}}\displaystyle\frac{{{R^2}}}{{{n^2}}}\right){{\ddot \theta }_m} = \!\! \!\! \!\!\!\!-\! {B_m}{{\dot \theta }_m} \!\!-\!\! {G_m}{\theta _m} \!+\! \displaystyle\frac{R}{n}{\left({J_\eta }{M_L}^{ - 1}{L_f}\right)^{ - 1}}{J_\eta }{M_L}^{ - 1}{M_g} \!\!+\! {T_s}{\text{,}}\!\!\!\!\!\!\!\!\end{array}\begin{array}{l}\displaystyle\frac{{{V_m}}}{{4{\beta _e}{D_m}}}{{\dot T}_s} = - {D_m}{{\dot \theta }_m} - \displaystyle\frac{{{C_{tm}}{T_s}}}{{{D_m}}} + {c_d}\omega Ku\sqrt {{\displaystyle{1 \over \rho }}({p_s} - {p_L}{\mathop{\rm sgn}} (u))} {\text{。}}\end{array}\end{array}} \right.$ | (17) |
假设
| $\left\{ {\begin{array}{*{20}{l}} {{{\ddot \theta }_m} = {a_1}{{\dot \theta }_m} + {a_2}{T_s} + {a_3}}{\text{,}} {{{\dot T}_s} = {b_1}{{\dot \theta }_m} + {b_2}{T_s} + {b_3}u} {\text{。}}\end{array}} \right.$ | (18) |
式中:
| ${a_1} = \frac{{ - {B_m}}}{{{J_m} + {{({J_\eta }{M_L}^{ - 1}{L_f})}^{ - 1}}\displaystyle\frac{{{R^2}}}{{{n^2}}}}}{\text{,}}$ |
| ${a_2} = \frac{1}{{{J_m} + {{({J_\eta }{M_L}^{ - 1}{L_f})}^{ - 1}}\displaystyle\frac{{{R^2}}}{{{n^2}}}}}{\text{,}}$ |
| ${a_3} = \frac{1}{{{J_m} + {{({J_\eta }{M_L}^{ - 1}{L_f})}^{ - 1}}\displaystyle\frac{{{R^2}}}{{{n^2}}}}}\displaystyle\frac{R}{n}{({J_\eta }{M_L}^{ - 1}{L_f})^{ - 1}}{J_\eta }{M_L}^{ - 1}{M_g}{\text{,}}$ |
| ${b_1} = \frac{{ - 4{\beta _e}{D_m}^2}}{{{V_m}}}{\text{,}}$ |
| ${b_2} = \frac{{ - 4{\beta _e}{C_{tm}}}}{{{V_m}}}{\text{,}}$ |
| ${b_3} = \frac{{ - 4{\beta _e}{D_m}}}{{{V_m}}}{c_d}\omega K\sqrt {\displaystyle\frac{1}{\rho }({p_s} - {p_L}\operatorname{sgn} (u))} {\text{。}}$ |
上述驱动控制模型是在一系列假设条件下得到的理想模型,与实际系统有一定出入。为使模型能够更加贴合实际,必须对驱动控制模型进行修正。系统的不确定来源主要包括:
1)平台自身不确定性
张力缆形变、平台形变及非对称性等;
2)液压系统不确定性
长期大负载工作影响、长管路影响等;
3)外界环境不确定性
外界水动力变化、其他干扰等。
定义包含了参数不确定性及未建模不确定性的综合不确定性因子分别为
| $\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = {a_1} + {a_2}{x_2} + {a_3} + {\lambda _1}} {\text{,}} {{{\dot x}_2} = {b_1}{x_1} + {b_2}{x_2} + {b_3}{u_s} + {\lambda _2}} {\text{,}} {{y_s} = {x_1}} {\text{。}}\end{array}} \right.$ | (19) |
式中,
针对水下张力腿平台包含综合不确定性且上界未知的驱动控制模型特性,本文采用自适应反演滑模控制:算法主体框架采用反演设计,将复杂非线性系统分解为不超过系统阶数的子系统[19],然后为每个子系统分别设计李雅普诺夫函数和中间虚拟控制量,一直后退到整个系统,直到完成整个控制律的设计,从而保证控制算法的渐进稳定性;在反演设计最后一步,引入滑模控制,提高了系统的鲁棒性[20];为了抑制滑模算法抖动,针对系统综合不确定性上界未知的特性,引入自适应算法,以补偿系统综合不确定性影响,从而提高控制系统在参数不确定性及随机干扰下的鲁棒性。
3.2 控制器设计步骤 1 设计虚拟控制律
定义
定义误差状态变量为
| $\left\{ {\begin{array}{*{20}{c}} {{z_{s1}} = {x_1} - {x_{1d}}} {\text{,}}\\ {{z_{s2}} = {x_2} - {x_{2d}}} {\text{。}}\end{array}} \right.$ | (20) |
式中,
由式(19)和试(20)可得:
| ${\dot z_{s1}} = {a_1}{x_1} + {a_2}{x_2} + {a_3} + {\lambda _1} - {\dot x_{1d}}{\text{,}}$ | (21) |
设计虚拟控制律为
| ${x_{2d}} = \frac{1}{{{a_2}}}\left( - {a_1}{x_1} - {a_3} + {\dot x_{1d}} - \frac{{\hat \varphi _1^2{z_{s1}}}}{{{{\hat \varphi }_1}\left| {{z_{s1}}} \right| + {\tau _{s1}}{e^{ - {a_s}t}}}} - {k_{s1}}{z_{s1}}\right){\text{。}}$ | (22) |
式中,
| ${\dot {\hat \varphi} _1} = {r_{s1}}\left| {{z_{s1}}} \right|,{r_{s1}} > 0{\text{,}}$ | (23) |
设计Lyapunov方程
| ${V_1} = \frac{1}{2}z_{s1}^T{z_{s1}} + \frac{1}{{2{r_{s1}}}}\tilde \varphi _1^2 + \frac{{{\tau _{s1}}}}{{{a_s}}}{e^{ - {a_s}t}}{\text{。}}$ | (24) |
式中,
对
| $ \begin{split} {{\dot V}_1} =& z_{s1}^{\rm T}{{\dot z}_{s1}} + \frac{1}{{{r_{s1}}}}{{\tilde \varphi }_1}{{\dot {\tilde \varphi} }_1} - {\tau _{s1}}{e^{ - {a_s}t}} = \\ & z_{s1}^{\rm T}({a_1}{x_1} + {a_2}{z_{s2}} + {a_2}{x_{2d}} + {a_3} + {\lambda _1} - {{\dot x}_{1d}}) + \frac{1}{{{r_{s1}}}}{{\tilde \varphi }_1}{{\dot {\tilde \varphi} }_1} - \\ &{\tau _{s1}}{e^{ - {a_s}t}} = z_{s1}^{\rm T}({a_1}{x_1} + {a_2}{z_{s2}} + {a_3} + {\lambda _1} - {{\dot x}_{1d}} - {a_1}{x_1} - {a_3} +\\ & {{\dot x}_{1d}} - \frac{{\hat \varphi _1^2{z_{s1}}}}{{{{\hat \varphi }_1}\left| {{z_{s1}}} \right| + {\tau _{s1}}{e^{ - {a_s}t}}}} - {k_{s1}}{z_{s1}}) + \frac{1}{{{r_{s1}}}}{{\tilde \varphi }_1}{{\dot {\tilde \varphi} }_1} - {\tau _{s1}}{e^{ - {a_s}t}} = \\ &z_{s1}^{\rm T}({a_2}{z_{s2}} -{k_{s1}}{z_{s1}} + {\lambda _1} - \frac{{\hat \varphi _1^2{z_{s1}}}}{{{{\hat \varphi }_1}\left| {{z_{s1}}} \right| +{\tau _{s1}}{e^{ - {a_s}t}}}}) + \\ & \frac{1}{{{r_{s1}}}}{{\tilde \varphi }_1}{{\dot {\tilde \varphi }}_1} - {\tau _{s1}}{e^{ - {a_s}t}} {\text{。}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ \ \ (25)\end{split} $ |
考虑到
| $\frac{1}{{{r_{s1}}}}{\tilde \varphi _1}{\dot {\tilde \varphi} _1} = \frac{1}{{{r_{s1}}}}({\hat \varphi _1} - {\varphi _1}){\dot {\hat \varphi} _1} = \left| {{z_{s1}}} \right|({\hat \varphi _1} - {\varphi _1}){\text{,}}$ | (26) |
则
| $ \begin{split} {{\dot V}_1} = &z_{s1}^{\rm{T}}({a_2}{z_{s2}} - {k_{s1}}{z_{s1}} + {\lambda _1} - \frac{{\hat \varphi _1^2{z_{s1}}}}{{{{\hat \varphi }_1}\left| {{z_{s1}}} \right| + {\tau _{s1}}{e^{ - {a_s}t}}}}) + \left| {{z_{s1}}} \right|({{\hat \varphi }_1} - \\ &{\varphi _1}) - {\tau _{s1}}{e^{ - {a_s}t}} \leqslant z_{s1}^{\rm T}({a_2}{z_{s2}} - {k_{s1}}{z_{s1}} - \frac{{\hat \varphi _1^2{z_{s1}}}}{{{{\hat \varphi }_1}\left| {{z_{s1}}} \right| + {\tau _{s1}}{e^{ - {a_s}t}}}}) + \\ & {{\hat \varphi }_1}\left| {{z_{s1}}} \right| \!-\!{\tau _{s1}}{e^{ - {a_s}t}} \!\!= \!\! z_{s1}^{\rm T}({a_2}{z_{s2}} \!-\! {k_{s1}}{z_{s1}})\! -\!\! \frac{{\tau _{s1}^2{e^{ - 2{a_s}t}}}}{{{{\hat \varphi }_1}\left| {{z_{s1}}} \right| \!+\! {\tau _{s1}}{e^{ - {a_s}t}}}}\!\! \leqslant \\ & {a_2}z_{s1}^{\rm T}{z_{s2}} - {k_{s1}}z_{s1}^{\rm T}{z_{s1}} {\text{。}}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ \ (27)\end{split} $ |
若
步骤 2 设计控制律
由式(20)和试(22)得:
| ${\dot z_{s2}} = {\dot x_2} - {\dot x_{2d}} = {b_1}{x_1} + {b_2}{x_2} + {b_3}{u_s} + {\lambda _2} - {\dot x_{2d}}{\text{,}}$ | (28) |
设计滑模面为
| $s = {z_{s2}} + {\lambda _s}\int {{z_{s2}}{ {\rm d}t}}{\text{,}} $ | (29) |
式中,
设计控制律为
| ${u_s} = {u_{eq}} + {u_{vss}}{\text{,}}$ | (30) |
式中:
设计等效控制律为
| ${u_{eq}} = - \frac{1}{{{b_3}}}\left[ {{b_1}{x_1} + {b_2}{x_2} - {{\dot x}_{2d}} + {\lambda _s}{z_{s2}}} \right]{\text{,}}$ | (31) |
切换控制律为
| ${u_{vss}} = - \frac{1}{{{b_3}}}\left[ {({{\hat \varphi }_2}{\rm{ + }}{\eta _s})\operatorname{sgn} (s)} \right]{\text{,}}$ | (32) |
式中,
结合式(29)–式(32),可得
| $\dot s = {\lambda _2} - ({\hat \varphi _2} + {\eta _s})\operatorname{sgn} (s){\text{。}}$ | (33) |
设计Lyapunov方程为
| ${V_2} = \frac{1}{2}{s^{\rm T}}s + \frac{1}{{2{r_{s2}}}}\tilde \varphi _2^2{\text{。}}$ | (34) |
式中:
对
| $\begin{align} & {{\dot V}_2} = {s^{\rm T}}\dot s + \frac{1}{{{r_{s2}}}}({{\hat \varphi }_2} - {\varphi _2}){{\dot {\hat \varphi }}_2} = \\ & {s^{\rm T}}\left[ {{\lambda _2} - ({{\hat \varphi }_2} + {\eta _s})\operatorname{sgn} (s)} \right] + \frac{1}{{{r_{s2}}}}({{\hat \varphi }_2} - {\varphi _2}){{\dot {\hat \varphi }}_2} {\text{。}}\end{align} $ | (35) |
设计
| ${\dot {\hat \varphi} _2} = {r_{s2}}\left| s \right|{\text{,}}$ | (36) |
式中,
将式(36)代入式(35)得
| $\begin{split} {{\dot V}_2} = &{s^{\rm T}}\left[ {{\lambda _2} - ({{\hat \varphi }_2} + {\eta _s})\operatorname{sgn} (s)} \right] + {{\hat \varphi }_2}\left| s \right| - {\varphi _2}\left| s \right| \leqslant & {{\hat \varphi }_2}\left| s \right| - ({{\hat \varphi }_2} + {\eta _s}){s\rm ^ T}\operatorname{sgn} (s) \leqslant & - {\eta _s}\left| s \right| \leqslant 0 \end{split} $ | (37) |
采用自适应反演滑模控制律后,误差
利用Matlab开展水下张力腿平台驱动控制仿真,模型参数为:
1)系统负载存在常规变化干扰
设计系统综合不确定性为:

|
图 6 系统负载存在常规变化干扰下正弦速度跟踪控制仿真 Fig. 6 Sine speed tracking control simulation under regularly changed disturbance |

|
图 7 系统负载存在常规变化干扰下斜坡速度跟踪控制仿真 Fig. 7 Ramp speed tracking control simulation under regularly changed disturbance |
|
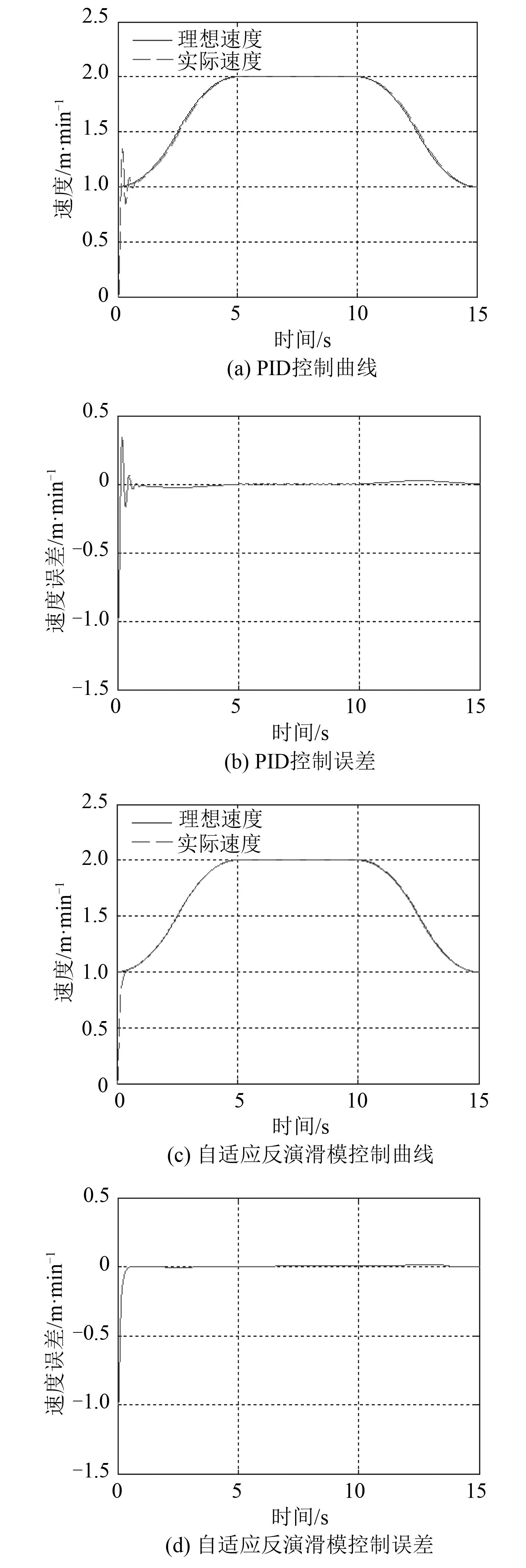
图 8 系统负载存在常规变化干扰时下潜速度跟踪控制仿真 Fig. 8 Dive speed tracking control simulation under regularly changed disturbance |
由上述结果可以看出,系统负载存在常规变化干扰时,自适应反演滑模控制和PID控制算法均可以完成常规速度曲线跟踪及下潜速度控制任务,但是自适应反演滑模控制算法的稳态速度误差更小且更平稳。
2)系统负载兼具常规及突变干扰
在仿真第10 s时,使干扰项发生突变,即

|
图 9 系统负载兼具常规及突变干扰时的正弦速度跟踪控制仿真 Fig. 9 Sine speed tracking control simulation under regularly and suddenly changed disturbance |
|
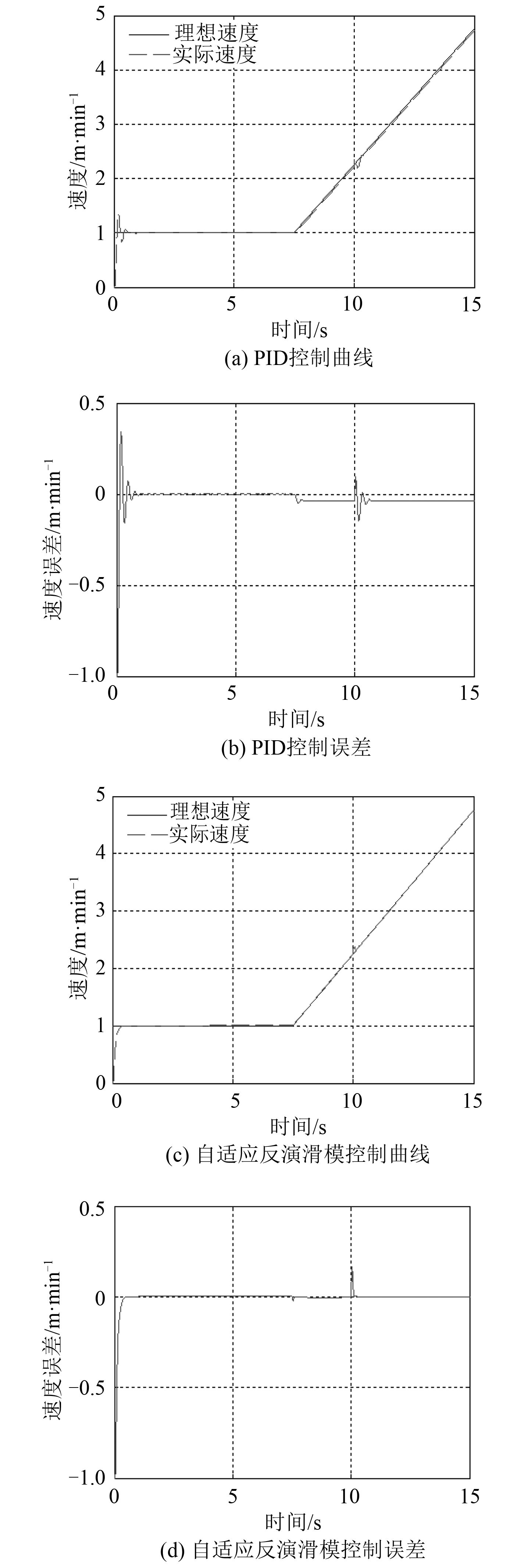
图 10 系统负载兼具常规变化及突变干扰时的斜坡速度跟踪控制仿真 Fig. 10 Ramp speed tracking control simulation under regularly and suddenly changed disturbance |
|
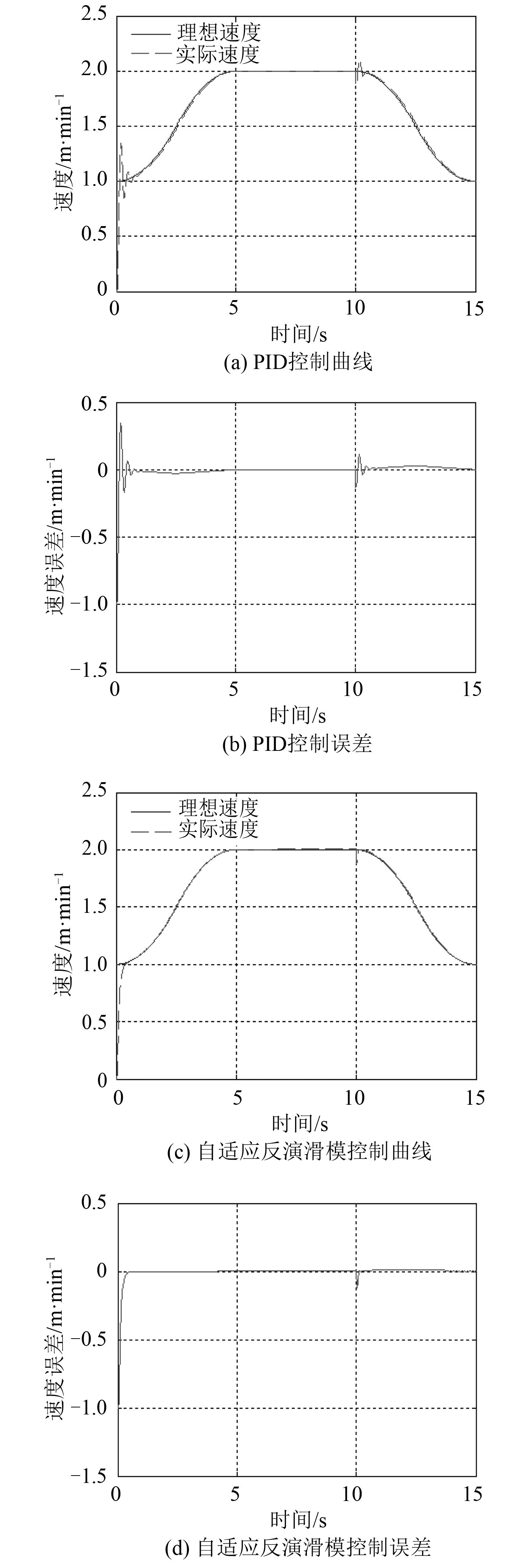
图 11 系统负载兼具常规变化及突变干扰时的下潜速度跟踪控制仿真 Fig. 11 Dive speed tracking control simulation under regularly and suddenly changed disturbance |
由上述仿真结果不难看出:在施加突变干扰后,自适应反演滑模控制和PID控制均出现一定的速度偏差,但这2种算法都能将突变干扰带来的偏差消除,只是PID控制算法在施加突变干扰后,会存在速度抖动现象,因而,相比较而言,自适应反演滑模控制算法的抗突变干扰能力更强,速度控制效果更好。
综合2种情况下的仿真结果可以得出:与PID控制算法相比,自适应反演滑模控制算法的稳态误差更小,且抗突变干扰能力更强。实际上,在平台控制中,对8台绞车的同步度要求很高,如果稳态偏差过大或因突然的干扰出现抖动,将不利于绞车的同步控制,因而,自适应反演滑模控制算法更适用于绞车速度控制。
5 结 语本文以一种新型专用水下张力腿平台的研制为背景,调研分析了国内外的研究现状,结合对象特性,开展了液压驱动系统建模及控制技术研究。
在建模过程中,通过工作原理分析及简化,建立了液压系统动力学模型;基于牛顿欧拉法建立了水下张力腿平台动力学模型,并推导出张力腿驱动外负载力矩;结合液压系统动力学模型及水下张力腿平台动力学模型,推导出包含综合不确定性且上界未知的关节空间驱动控制模型。在控制技术研究过程中,基于反演设计、滑模控制及自适应控制思想,设计了一种自适应反演滑模控制器,提高了系统的鲁棒性及抗干扰能力。
由于测量手段有限,在现阶段尚不能对系统的各种不确定因素进行详细分析甚至量化,只能通过综合不确定因素对其进行概括,在后续研究中,将对系统不确定性开展进一步分析,在此基础上,完善系统模型及控制算法设计。
| [1] | XIA Y K, XU G H, XU K, et al. Dynamics and control of underwater tension leg platform for diving and leveling[J]. Ocean Engineering, 2015(109): 454–478. |
| [2] | ABDELLATIF H, HEIMANN B. Computational Efficient Inverse Dynamics of 6-DOF Fully Parallel Manipulators by Using the Lagrangian Formalism[J]. Mechanism and Machine Theory, 2009, 44(1): 192–207. |
| [3] | ZHANG C D, SONG S M. An Efficient Method for Inverse Dynamics of Manipulators based on the Virtual Work Principle[J]. Journal of Robotic Systems, 2007, 10(5): 605–627. |
| [4] | AZIZI M R, NADERI D. Dynamic modeling and trajectory planning for a mobile spherical robot with a 3D of inner mechanism[J]. Mechanism and machine theory, 2013, 64(1): 251–261. https://link.springer.com/chapter/10.1007/978-81-322-2740-3_50 |
| [5] | GHERMAN B, PISLA D, VAIDA C, et al. Development of inverse dynamic model for a surgical hybrid parallel robot with equivalent lumped masses[J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(3): 402–415. |
| [6] | 张虎, 郭志飞, 徐安林. 3-PSS并联机构动力学分析与仿真[J]. 机床与液压, 2016, 44(21): 21–25. |
| [7] | 张国伟, 宋伟刚. 并联机器人动力学问题的Kane方法[J]. 系统仿真学报, 2004, 16(7): 1386–1391. http://www.cqvip.com/QK/92944X/200107/5372812.html |
| [8] | 李永泉, 宋肇经, 郭菲等. 多能域过约束并联机器人系统动力学建模方法[J]. 机械工程学报, 2016, 52(21): 17–25. http://www.cqvip.com/QK/91060X/2004007/10181724.html |
| [9] | 周洪. 6PUS-UPU冗余驱动并联机器人控制技术研究[D].秦皇岛: 燕山大学, 2014. |
| [10] | ZHANG X Y, HAN Y T, BAI T, et al. H∞ controller design using LMIs for high-speed underwater vehicles in presence of uncertainties and disturbances[J]. Ocean Engineering, 2015(104): 359–369. |
| [11] | 徐超, 刘刚, 徐国华, 等. 基于泵控液压舵机的潜艇深度及纵倾控制[J]. 中国舰船研究, 2017, 12(2): 116–123. https://www.wenkuxiazai.com/word/9a13b986102de2bd96058894-1.doc |
| [12] | CHEN Y, ZHANG R M, ZHAO X Y, et al. Adaptive fuzzy inverse trajectory tracking control of underactuated underwater vehicle with uncertainties[J]. Ocean Engineering, 2016(121): 123–133. |
| [13] | FAYZE F S. Adaptive hybrid control system using a recurrent RBFN-based self-evolving fuzzy-neural-network for PMSM servo drives[J]. Appl. Soft Comput, 2014(21): 509–532. |
| [14] | LI Y, WEI C, WU Q, et al. Study of 3 dimension trajectory tracking of underactuated autonomous underwater vehicle[J]. Ocean Engineering, 2015(105): 270–274. |
| [15] | 颜玉娇. 绳索牵引并联机器人的动力学建模与控制研究[D].合肥: 中国科学技术大学, 2015. |
| [16] | 郭崇滨. 并联机器人多目标协同智能控制研究[D].上海: 东华大学, 2013. |
| [17] | 牛雪梅. 新型3-DOF驱动冗余并联机构动力学建模及其滑模控制研究[D]. 镇江: 江苏大学, 2014. |
| [18] | 常同立. 液压控制系统[M]. 北京: 清华大学出版社, 2014. |
| [19] | 乔继红. 反演控制方法与实现[M]. 北京: 机械工业出版社, 2012. |
| [20] | 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005. |
 2018, Vol. 40
2018, Vol. 40

