管路系统的振动噪声主要有3种原因产生,分别是支撑基础和与管道相连的动力设备的振动、管内流体压力脉动引起的振动以及管内流体涡流共振引起的振动。其中,设备振动通常认为是管路系统最为主要的扰动源之一,由于设备与管路系统直接相连,设备(如泵)在运转时,自身不可避免的产生周期性振动,从而引起管路系统的振动,若设计不合理,甚至会引起管路系统的共振,其危害程度更大。
针对管路系统的振动可通过优化管路系统布置、优化管路马脚固定位置、更换低噪声设备及阀件、增加消声器、增加管路弹性连接件、管道敷设阻尼材料等方式降低管路系统的振动[1],尽管上述方法可以最大化降低管路系统的振动噪声,但其通常需要付出较高的代价,尤其对于普通民用船舶的管路系统振动控制,则会很少使用上述的减振降噪方法。基于此,本文设计一款调谐质量阻尼器,该设计具有针对性强、成本低、占用空间小、安装简便等优点,并且通过优化设计,还可针对某一频段进行被动振动控制[2]。
1 基本理论 1.1 数学模型由于管路系统自身可以被看做为一个单自由度系统,而调谐质量阻尼器本身仍可被看做为一个单自由度系统,因此,当将调谐质量阻尼器安装于主结构之上时,二者即构成了1个两自由度的振系[3 – 6]。其系统示意图如图1所示。
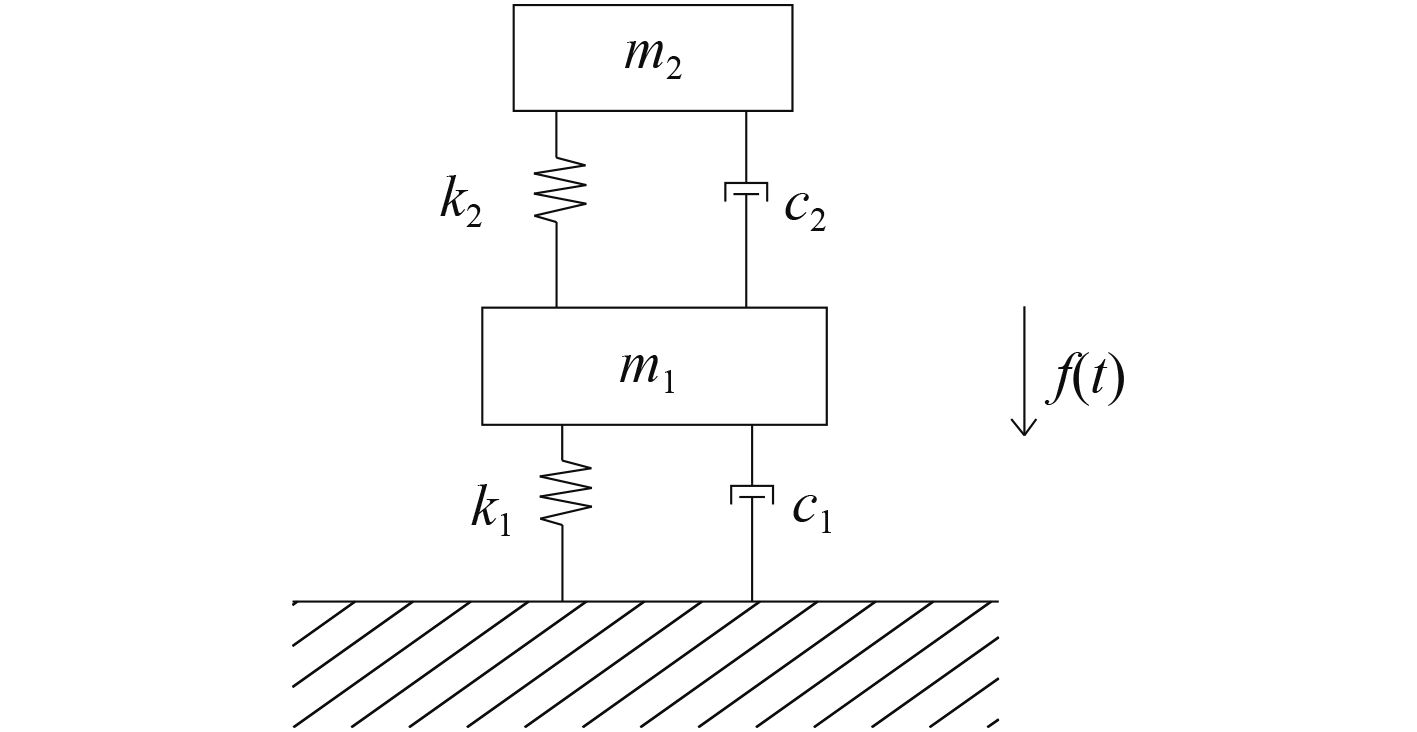
|
图 1 单调谐质量阻尼器示意图 Fig. 1 The schematic diagram of single TMD |
对于两自由度系统,其中m1为管路的等效质量,k1为其安装刚度,c1为其阻尼系数。设管路上受到不平衡质量的激励或外加激励
| $\left\{ \!\!\!\!\begin{array}{l}{m_1}{{\ddot x}_1} \!\!+\! ({c_1} \!\!+\! {c_2}){{\dot x}_1} \!-\! {c_2}{{\dot x}_2} \!+\! ({k_1} \!+\! {k_2}){x_1} \!-\! {k_2}{x_2} \!\!=\!\! {F_1}\sin \omega t{\text{,}}\\{m_2}{{\ddot x}_2}\! \!+\! {c_2}{{\dot x}_2} \!-\! {c_2}{{\dot x}_1} \!\!+\! {k_2}{x_2} \!-\! {k_2}{x_1} \!\!=\!\! 0{\text{。}}\end{array} \right.$ | (1) |
设式(1)的解为
考虑到F1为实数,而X1,X2为复数,为降低管路系统的振动,即使主结构的振幅
| $\left| {{X_1}} \right| = {F_1}\frac{{{{({{({k_2} - {\omega ^2}{m_2})}^2} + {\omega ^2}{c_2}^2)}^{\frac{1}{2}}}}}{{{{\left\{ {{{[({k_1} - {\omega ^2}{m_1})({k_2} - {\omega ^2}{m_2}) - {\omega ^2}{m_2}{k_2} - {\omega ^2}{c_1}{c_2}]}^2} + {\omega ^2}{{[({k_1} - {\omega ^2}{m_1}){c_2} + {c_1}({k_2} - {\omega ^2}{m_2}) - {\omega ^2}{m_2}{c_2}]}^2}} \right\}}^{\frac{1}{2}}}}}\text{,}$ | (2) |
设
令
| $\frac{{\left| {{X_1}} \right|}}{{{x_{st}}}} = \frac{{{{[{{({\lambda ^2} - {f^2})}^2} + {{(2{\xi _2}f\lambda )}^2}]}^{\frac{1}{2}}}}}{{{{\left\{ {{{[(1 - {f^2})({\lambda ^2} - {f^2}) - \mu {f^2}{\lambda ^2} - 4{\xi _1}{\xi _2}\lambda {f^2}]}^2} + {f^2}{{[2{\xi _2}(1 - {f^2})\lambda + 2{\xi _1}({\lambda ^2} - {f^2}) - 2{\xi _2}\mu {f^2}\lambda ]}^2}} \right\}}^{\frac{1}{2}}}}}\text{。}$ | (3) |
但在实船之中,为充分降低船舶管路系统的振动噪声,在对管路系统进行振动控制时,会在管路外表面包覆阻尼材料,进一步增加了管路自身的阻尼比。因此,为提高计算结果的准确性,主系统的阻尼比 不可忽略。设
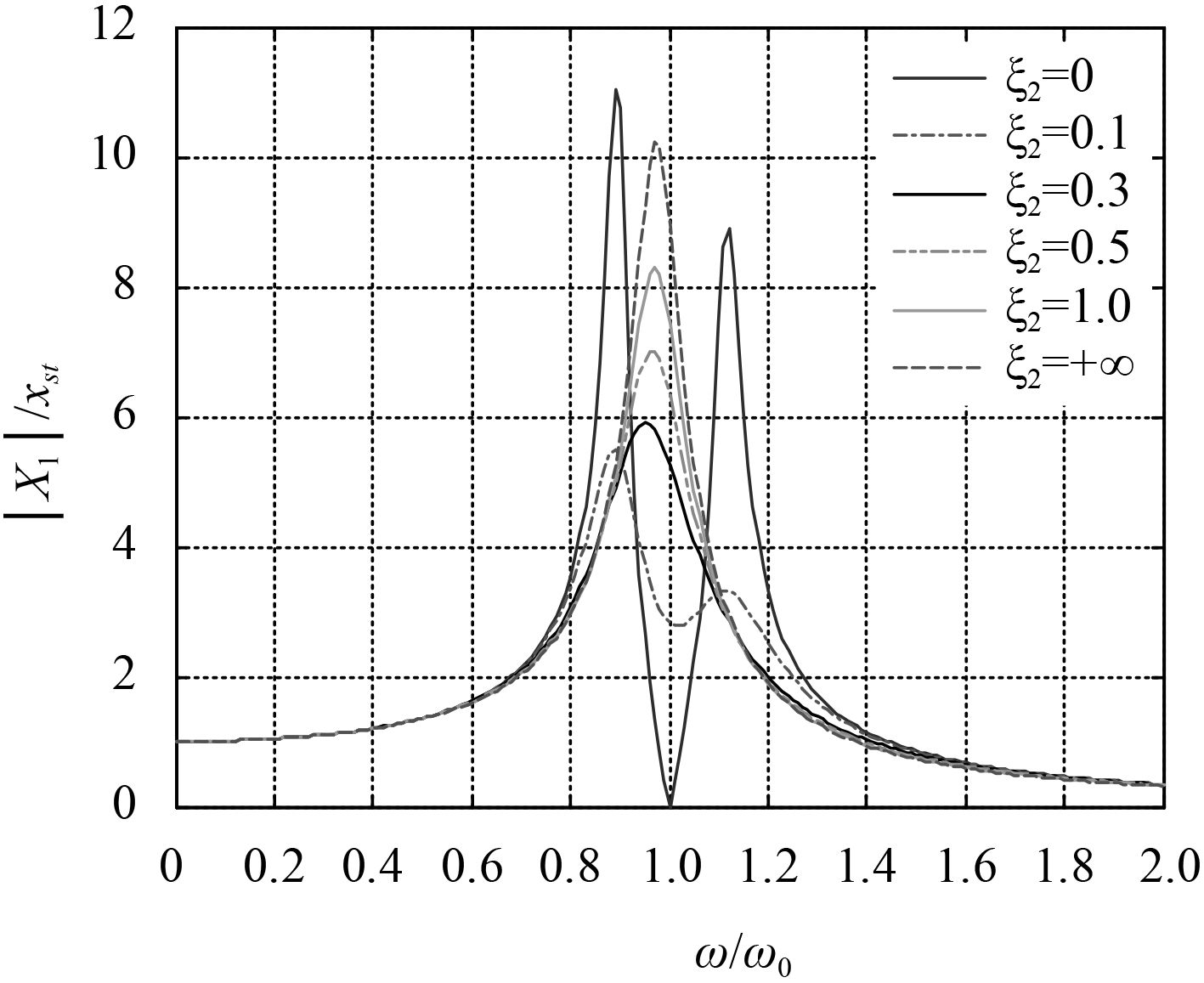
|
图 2 主系统有阻尼,调谐质量阻尼器不同阻尼比下主系统的幅频响应曲线图 Fig. 2 The amplitude-frequency response curve of different damping ratio on main system about TMD when the main system has damping |
从图2可以看出,当
为研究调谐质量阻尼器的不同质量对调谐质量阻尼器系统特性的影响,将主、次系统的各参数设置如表1所示。
|
|
表 1 调谐质量阻尼器质量对系统幅频特性影响参数设定 Tab.1 The parameter setting of the mass about TMD influence on the amplitude frequency characteristics |
依据上述各参数,对主系统的幅频响应进行仿真计算,经计算得到如图3所示曲线。
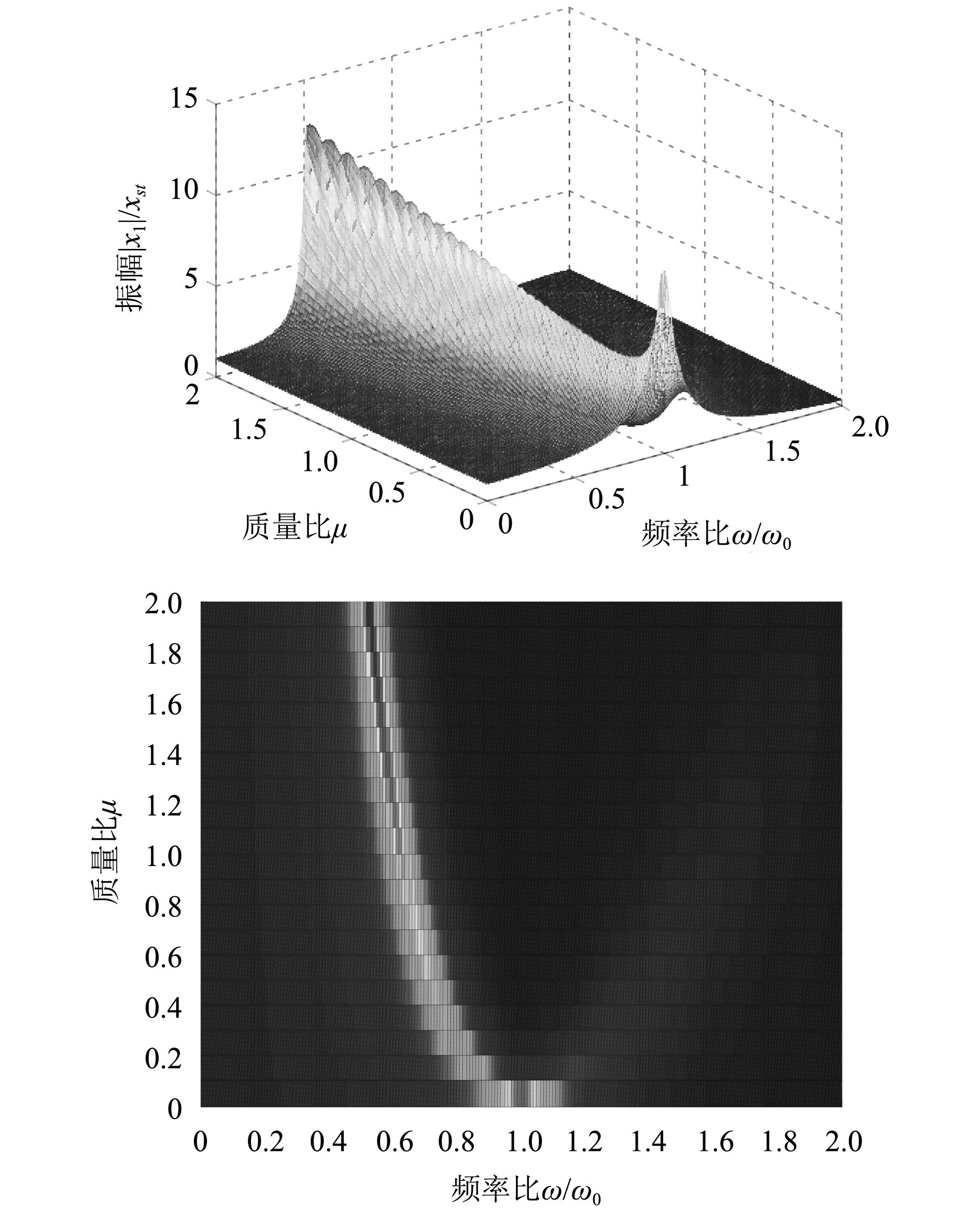
|
图 3 不同质量比对主系统振动特性影响图 Fig. 3 The influence diagram of main system’s vibration on different mass ratio |
通过图3可以看出,当质量比为0时,系统只有1个共振峰,即无调谐质量阻尼器时,主系统的振幅较大。随着质量比的增大,系统出现2个峰值。此时,主系统的振幅表现为左侧峰值先减小,后增大的特性,右侧峰值逐渐减小。主要是由于调谐质量阻尼器的质量变大,影响到了主系统自身的特性,且调谐质量阻尼器的质量变大,意味着占用了更多的空间,影响了主系统的稳定性,因此,在进行阻尼比的选择时,应通过计算,选择合适的质量比,达到最优的控制目的。
1.3 调谐质量阻尼器频率比对主系统振动特性的影响为研究调谐质量阻尼器的固有频率与主系统的调谐频率比对调谐质量阻尼器系统特性的影响,将主次系统的各参数设置为如表2所示。
|
|
表 2 调谐质量阻尼器频率比对系统幅频特性影响参数设定 Tab.2 The parameter setting of the frequency ratio about TMD in-fluence on the amplitude frequency characteristics |
依据上述各参数,对主系统的幅频响应进行仿真计算,经计算得到如图4所示曲线。
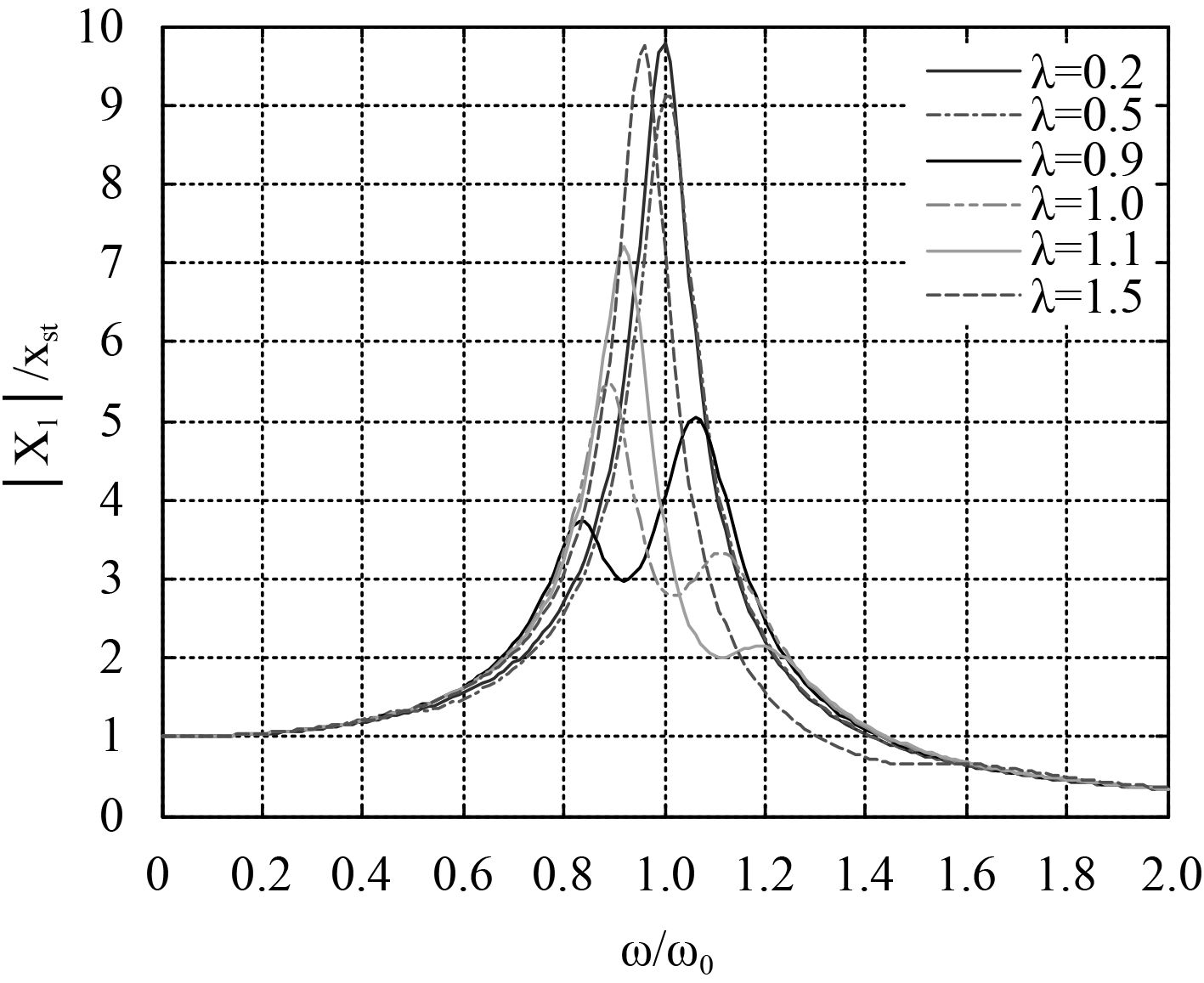
|
图 4 调谐质量阻尼器的调谐频率比对主系统幅频响应的影响对比图 Fig. 4 The influence diagram of the frequency ratio about TMD on main system’s amplitude frequency response |
从图4可以看出,随着调谐质量阻尼器调谐比的增大,主系统的振幅逐渐降低,当达到0.9时,幅值峰值达到最小,随着调谐频率比的继续增大,幅值开始变大。综上,可以看出,在调谐质量阻尼器存在阻尼时,调谐质量阻尼器的调谐频率比应小于1时才具有较好的减振效果。
2 控制模型的建立在进行调谐质量阻尼器的设计时,需要已知被控对象的控制频率、质量以及阻尼因子3个物理量。对于一般的海水泵而言,通常特征频率出现在轴频、倍频、叶频以及倍叶频处[7]。因此,本研究以试验室的管路系统台架的消声器输出端为假想控制对象,根据以往的测试结果,选取292 Hz的叶频为重点控制频率,估算被控对象的总质量为829.9 kg,阻尼因子为0.05。
2.1 调谐质量阻尼器参数的优化设计 2.1.1 吸振质量在进行管路系统的调谐质量阻尼器设计时,因为管路系统的特点,一般不适合悬挂过重的调谐质量,因此,为了既具有良好的调谐效果,又同时能够最小限制影响原管路系统的支撑结构,在进行调谐质量阻尼器质量选取时,通常选取调谐质量为被控管路系统质量的1/30~1/10[8]。
在确定最优参数时,本文拟通过在常规质量比的设置范围内,先设定一个质量比,据此计算出此质量比下的最优调谐频率比和副系统的阻尼因子,并以此构建一个完整的调谐质量阻尼器参数设计方案。在进行质量比的选择时,选取副系统与主系统的质量比为1/20,即副系统的质量为41.5 kg。
2.1.2 阻尼因子在进行阻尼因子的计算时,拟采用循环迭代法进行计算。即首先设定质量比、主系统的阻尼因子、副系统的阻尼因子范围和最优调谐频率比。通过迭代计算出在分析范围内的各最优参数,并以此作为副系统的最优阻尼因子和最优调谐频率比。
在参数的选择时,拟设置副系统的阻尼因子范围为0.001~0.999。最优调谐频率比的参数范围为0.001~0.999。
将上述各参数代入式(3)进行迭代计算,得到副系统的最优阻尼因子为0.158,副系统与主系统的最优频率比为0.936。
2.1.3 调谐质量阻尼器的最优频率比及最优阻尼比的校验为验证计算结果的准确性,在文献[9 – 10]中,利用曲线拟合法得到了调谐质量阻尼器的最优调谐频率比
| $\begin{split}\lambda = [1/(1 + \mu )] + (\sqrt {1 - 2{\xi _1}^2} - 1) - (1.398 + 0.126\sqrt \mu - \\2.004\mu )\sqrt \mu {\xi _2} - (0.362 - 5.897\sqrt \mu + 8.553\mu )\sqrt \mu {\xi _1}^2\text{,}\end{split}$ |
调谐质量阻尼器的最优阻尼因子
| ${\xi _2} = \sqrt {\frac{{3\mu }}{{8\left( {1 + \mu } \right)}}} + 0.157{\xi _1} - 0.321{\xi _1}^2 + 0.195{\xi _1}\mu \text{。}$ |
将主系统的阻尼因子、质量比代入以上两式,经计算,调谐质量阻尼器的最优阻尼因子为0.141,最优调谐频率比为0.908。
通过将上式与本文的迭代计算方法进行对比,可知副系统的最优阻尼因子和最优调谐频率比具备一定的准确性。
2.1.4 调谐质量阻尼器的刚度在进行阻尼器的刚度选择时,可依据下式进行计算:
| $\lambda = {\omega _2}/{\omega _1} = \sqrt {{{\rm{k}}_2}/{m_2}} /{\omega _1}\text{。}$ |
式中:
将各参数代入上式得
对于管路系统,当流体流过时,其自身受到各方向的激励,因此,表现出周向运动的特性,且随着频率的改变,控制对象的周向运动状态也会发生改变。为此,本文设计一种具有各向振动特性的调谐质量阻尼器,其设计如图5所示。

|
图 5 调谐质量阻尼器设计图 Fig. 5 The design drawing of TMD |
可以看出,该调谐质量阻尼器总共由可调质量环、气囊隔振器、固定卡环3部分组成。
1)可调质量环
该可调质量环主要由凹槽型的环形质量体和充液囊体组成。环形刚体质量41.5 kg,选用铅作为质量环的主材,液囊内的液体可根据实际情况进行选择,为安全起见,本文以水为例进行计算。取铅的密度为11.34 g/cm3,水的密度为1.0 g/cm3。经计算,可调质量环的尺寸见图5。
从图中可以看出,可调质量环有一条凹槽和水袋组成,通过调节液囊的充液程度,进而调节质量环的总体质量,由
2)气囊隔振器
由于气囊隔振器由橡胶、内部钢丝及气体组成,橡胶具有一定的阻尼比,钢丝则具有一定的刚度,此外,通过改变气囊隔振器的充气气压,还可以改变隔振器整体的刚度,因此,利用其刚度可调的性质,也是为了增加调谐质量阻尼器的可控频率,使其适应性增强。
4 吸振性能的仿真验证整个被控单元由消声器、手动蝶阀及几段管子组成,调谐质量阻尼器的布放位置为消声器后部的手动蝶阀附近。而首尾2段管子的端部均布置有马脚。因此,在仿真计算时,拟将首尾两端简化为固定约束条件,便于后续计算。
计算过程中,认为消声器与管子为同种材质,设置其密度为8.8 g/cm3,杨氏模量1.02×105 MPa,阻尼因子0.05,泊松比0.3;环密度11.34 g/cm3,泊松比0.3;分析中,实体单元利用四节点四面体单元solid285,共划分45 700个单元,其具体网格模型如图7所示。

|
图 7 调谐质量阻尼器加装前后被控管路单元在控制频点处的位移分布图 Fig. 7 The displacement distribution map of pipe element when adding TMD before and after on control frequency point |
图中环与管子之间用4根弹簧单元连接,赋予其刚度值和阻尼因子,以此来模拟气囊隔振器,设其阻尼因子为0.158,每根弹簧的刚度为4.5×104 kN/m;模型两端处固定约束。
考虑到实测试验时,在消声器的排水口和手动蝶阀附近均产生较大的振动,因此,为模拟该种情况下的被控单元振动情况,本文在消声器的排水口处施加一个方向向下的谐和力,并设定加载力的方向为坐标系中Z轴负向,幅值500 N,仿真计算频率为292 Hz处被控管路单元的位移分布情况。通过计算,得到被控管路单元在目标频率处的位移分布如图8(a)所示。

|
图 8 调谐质量阻尼器加装前后被控管路单元控制断面处的位移分布图 Fig. 8 The displacement distribution map of pipe element when adding TMD before and after on control section |
通过分析可知,在控制频点处,当未布放调谐质量阻尼器时,被控单元的整体最大位移为0.539×10–3m ,而布放调谐质量阻尼器后的整体最大位移为0.419×10–3 m,位移降幅为2.2 dB。而调谐质量阻尼器控制部分的振幅抑制效果更为明显,从图中可以看出,未布放时,被控单元局部的位移幅值约为0.275×10–3m,布放后,局部位移幅值约为0.718×10–3m,位移降幅约为11.7 dB,降噪效果明显。另外,从图中也可以看出,调谐质量阻尼器的振幅明显大于周边管路单元的振幅,这是由于管路的能量有效的转移到了调谐质量阻尼器之上,从而使得阻尼器的振幅变大而被控单元的振幅变小。
为更好地观察被控断面的振幅抑制效果,绘制布放调谐质量阻尼器前后的控制断面的位移分布图,见图8(b)。
可以看出,未布放调谐质量阻尼器时,控制断面的最大幅值为0.379×10–3 m,而布放调谐质量阻尼器后,控制断面的最大幅值为0.179×10–3 m,位移降幅为6.5 dB。整体上,取得了较好的降噪效果。
5 结 语综合上述各项分析可知,针对文中所提到的控制单元,当填加合适参数的调谐质量阻尼器后,在目标频点处,管路系统的振动得到了明显的抑制,无论是整体的振幅抑制还是局部的振幅抑制,均取得了较好的效果。该调谐质量阻尼器还具有体积小,易于安装、降噪效果明显等诸多特点。
| [1] |
程广福, 张文平, 柳贡民, 等. 船舶水管路噪声及其控制研究[J]. 噪声与振动控制, 2003, 31(2): 31–33.
CHENG Guang-fu, ZHANG Wen-ping, LIU Gong-min, et al. The Liquid-born noise and its control in water pipelines of ships [J]. Nosie and Vibration Control, 2003, 31(2): 31–33. http://www.cqvip.com/QK/94984X/201602/668259870.html |
| [2] |
洪荣晶, 姚慧珠. 控制管道振动用耦合阻尼器的动柔度优化设计方法[J]. 机械科学与技术, 1998, 27(1): 14–16.
HONG Rong-jing, YAO Hui-zhu. Method for optimum designing dynamic flexibility of coupled damper for controlling pipe vibration[J]. Mechanical Science and Technology for Aerospace Engineering, 1998, 27(1): 14–16. http://mall.cnki.net/magazine/article/JXZZ199801023.htm |
| [3] |
曾胜, 任意, 程涛涛, 等. 利用调谐质量阻尼器进行管路系统减振[J]. 振动、测试与诊断, 2012, 32(5): 823–826.
ZENG Sheng, REN Yi, CHENG Tao-tao, et al. Vibration suppression of pipe system with tuned mass damper[J]. Journal of Vibration, Measurement and Diagnosis, 2012, 32(5): 823–826. http://www.cqvip.com/QK/97495X/201205/43704936.html |
| [4] |
季文美. 机械振动[M]. 北京: 科学出版社. 1985. 6.
JI Wen-mei. Mechanical vibration[M]. Beijing: China Science Publishing. 1985. |
| [5] | J. M. HOWARD, M. P. NORTON and B. J. STONE. A coincidence damper for reducing pipe wall vibration in piping systems with disturbed internal turbulent flow[J]. Journal of Sound and Vibration, 1987, 113(2): 377–393. |
| [6] | K. W. NG. Ring damper for structureborne noise suppression in piping systems[J]. US, 1994, 32(4B): 27–41. |
| [7] |
吴英友, 邢维升, 朱显明, 等. 某型离心水泵振动特性分析[J]. 中国舰船研究, 2008, 3(1): 51–54.
WU Ying-you, XING Wei-jun, ZHU Xian-ming, et al. Study on vibration characteristic of centrifugal pump[J]. Chinese Journal of Ship Research, 2008, 3(1): 51–54. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=dltdxyxb200903010 |
| [8] |
同长虹, 张小栋. 调谐质量阻尼器参数优化及其应用[J]. 振动、测试与诊断, 2007, 27(2): 146–149.
TONG Chang-hong, ZHANG Xiao-dong. Parameter optimization of toned mass dampers and its application to bridge vibration[J]. Journal of Vibration, Measurement and Diagnosis, 2007, 27(2): 146–149. http://www.oalib.com/paper/4191465 |
| [9] |
李俊, 金咸定, 王宏. 减小船体艉部振动的调谐质量阻尼器研究[J]. 中国造船, 2001, 42(2): 69–74.
LI Jun, JIN Xian-ding, WANG Hong. Research on dynamic absorber for reducing vibration of ship stern[J]. Shipbuilding of China, 2001, 42(2): 69–74. http://www.doc88.com/p-2721292454399.html |
| [10] | TSAI H C, LIN G C. Explicit formulae for optimum absorber parameters for force excited and viscously damped systems[J]. Journal of Sound and Vibration, 1994, 176(5): 585–596. |
 2018, Vol. 40
2018, Vol. 40
