刚架结构由于出色的力学性能和良好的可设计性,被广泛应用船舶、桥梁、建筑等多种领域。大型刚架结构,在加工制造过程中,容易产生焊接和切削变形,形成初始几何缺陷;在运输、安装和使用过程中,受环境不确定因素,特别是海洋作业环境的影响,也会导致结构产生几何缺陷。几何缺陷在制造到安装过程中不可避免,它影响结构的失稳模式和承载能力[1]。这也是导致结构理论和实际力学性能差异的重要因素之一。当缺陷超过一定程度时,会破坏结构在正常工况下的使用精度,严重时会造成安全隐患。
刚架结构的失稳变形和极限承载分析是结构设计中的一项重要工作。目前结构的稳定性计算,一般采用非线性有限元理论获得结构载荷-位移的全过程,主要求解方法有弧长法、牛顿-拉斐逊法、位移增量法等。含几何缺陷的结构分析方法主要包括:临界缺陷模态法、随机缺陷模态法和一致缺陷模态法等。临界缺陷模态法认为非完善结构的平衡路径可看作完善结构在缺陷作用下发生的微小扰动,难以用于大位移的情况[2]。文献[3]从概率统计学角度,用正态分布近似地模拟结构的几何缺陷分布,分析讨论了考虑缺陷结构的临界载荷。文献[1 – 4]建立了含缺陷的结构概率模型,采用Monte Carlo法对含随机缺陷的结构进行稳定承载力分析。随机缺陷法需要对不同缺陷分布进行多次非线性计算,对于大型复杂结构进行计算时,工作量大,实现困难。
一致缺陷模态法,取最低阶屈曲模态模拟为结构的最不利几何缺陷分布,使用少量的非线性计算,求解出缺陷结构的最小临界载荷。文献[5]通过对比刚体结构一致缺陷模态法和随机缺陷模态法的计算分析结果,证明一致缺陷法在结构分析中的可行性。文献[6]利用一阶特征值屈曲模态表征结构的缺陷,考虑加筋圆柱壳结构的缺陷敏感性。文献[7]引入屈曲模态作分布的几何缺陷,对完全约束、部分约束和无约束的大跨度结构承载力进行计算分析。一致屈曲模态法虽然计算便捷,实用性强,但是其理论的可靠性有待证实。
对含有几何缺陷的结构研究不足还体现在如下几个方面:数值仿真模型大多停留在较为抽象的宏观层面,忽略有限元模型的局部细节特性,影响仿真效果;对结构进行非线性计算时,大多数仅考虑了几何或者材料非线性,没有全面考虑结构特性。为了提高计算精度,本文在不降低计算效率的情况下,建立多单元混合的局部精细化有限元模型,通过计算分析确定几何缺陷分布,克服一致缺陷模态法的不足。在非线性分析中,充分考虑结构双重非线性,即材料非线性和几何非线性。本文首先介绍几何和材料的非线性,然后确定刚架焊接结构仿真模型的关键参数,建立精细化有限元模型,在结构中引入几何缺陷分布,对结构进行双重非线性分析计算,最后验证方法的有效性和可靠性。
1 刚架结构本文研究对象为节点焊接连接刚架结构,主体结构完全固定在基座上,在连接处通过增大连接截面加强连接。其刚架结构特点如下:该结构顶部为承载部位,刚架通过顶部支撑某设备的重量,架体上分布的杆件通过焊接方式进行连接,将重量均匀传递到基座;为了便于制造,该框架结构的各支杆均采用方钢,竖直杆(VER)、水平杆(HOR)和倾斜方向杆件(SLO)采用3种不同的截面积尺寸,其规格如表1所示。
|
|
表 1 杆件截面规格表 Tab.1 Section areas of components |
采用有限元分析软件Ansys对模型进行仿真分析,为了最大限度的模拟结构实际状态,理论上应该精确构建出模型的每一个细节。对于大型复杂结构来说,这种策略对建模和计算来说都是一种考验,难以取得理想的效果。因此针对大型框架结构模型,应在保证计算效率的情况下,最大限度的保留结构细节特性,构建多单元混合的局部精细化有限元模型。
在同一个有限元模型中,同时建立大尺度和小尺度单元,必须针对不同区域采用不同的建模策略。在架体结构中杆件众多,承受拉、压、弯、扭等载荷作用。Ansys中的beam189三维有限应变梁单元能全面反应出杆件的轴力、弯曲、扭转和位移等状态,不仅可以减少计算量,而且计算精度不受影响[8]。因此,这里采用大尺度下的梁单元建立架体杆件模型。
杆件间通过焊接的方式刚性连接。连接点为水平、竖直和倾斜杆件焊接交汇处,且设计有加强板。连接点是架体损伤的起始处,是架体需重点关注的区域。为了能够准确表现出杆件连接点处的情况,对连接点区域采用小尺度单元精细化建模策略,连接点用实体单元Solid186构建,加强板采用壳单元Shell181构建。在有限元分析中,不同单元的自由度不相同,直接连接会造成变形不连续,利用多点约束(MPC)方法,通过不同类型单元之间的节点自由度耦合,将不同类型的单元进行连接,从而建立某种约束关系或者进行载荷传递。有限元模型如图1所示。
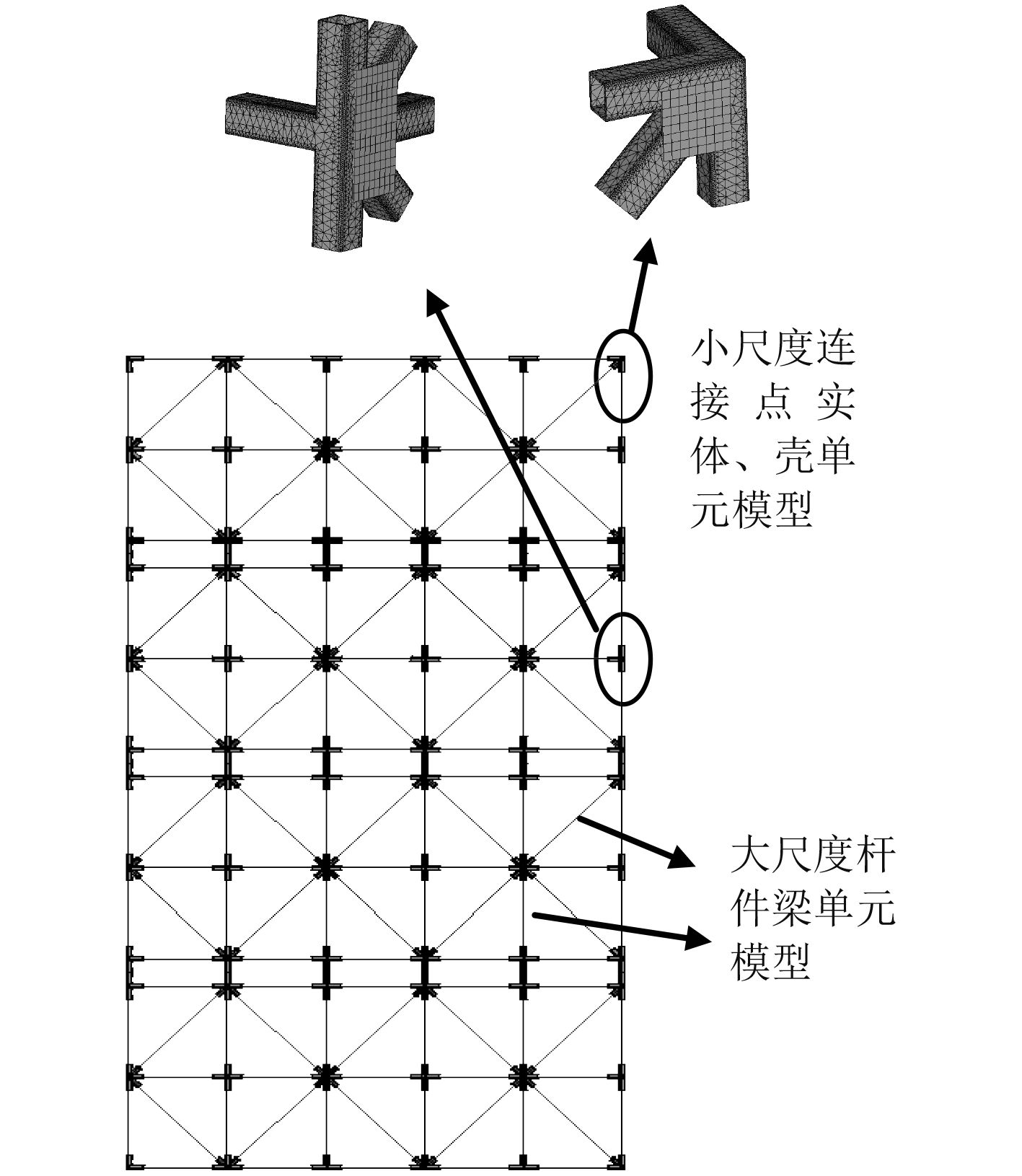
|
图 1 混合单元模型 Fig. 1 Mixed finite element model |
当架体承受小载荷小变形时,结构应力-应变表现为线弹性特性。但当对框架结构进行极限状态分析时,局部区域可能进入塑性状态,线弹性理论不再适用。在极限状态时,由变形引起的P-Delta效应以及材料的非线性特性等因素影响,结构会呈现出几何非线性和材料非线性状态,即双重非线性。
对于几何非线性,考虑大变形效应。首先假设材料处于线弹性状态,使用虚位移原理建立几何非线性单元增量平衡方程[9,10]:
| ${\Delta f} = \left( {{{{ K}_0}} + {{{ K}_\sigma }} +{{{ K}_L}} } \right) \cdot {\Delta u} {\text{。}}$ | (1) |
式中:△f为外载荷增量;K0小位移线性刚度矩阵;Kσ为初应力矩阵(几何刚度矩阵);KL为称为初始位移矩阵或大位移矩阵;{△u}为节点的位移增量。
考虑材料非线性,材料的屈服遵循von-mises屈服准则及和Prandt-Reuss塑性流动增量理论,位移增量包含弹性部分和塑性部分。材料的塑性状态,塑性变形沿屈曲面的法线方向平移。当截面内力满足屈曲面方程时,可以近似等效认为截面整体均进入屈服状态,则单元增量平衡方程可以表述为如下形式:
| ${\Delta f} = \left( { {{{ K}_0}} +{{{ K}_\sigma }} + {{{ K}_L}} - {{{ K}_R}}} \right) \cdot {\Delta u}\text{,}$ | (2) |
其中,KR为载荷矫正矩阵。
2.3 模型计算材料的本构关系用多线性随动强化模型表征,弹性模量为2.06×105 N/mm2,屈服强度345 N/mm2,泊松比为0.3,密度为7.83×10–3 g/mm3。应力-应变关系如图2所示。竖直坐标为应力(单位Pa),横坐标为应变。
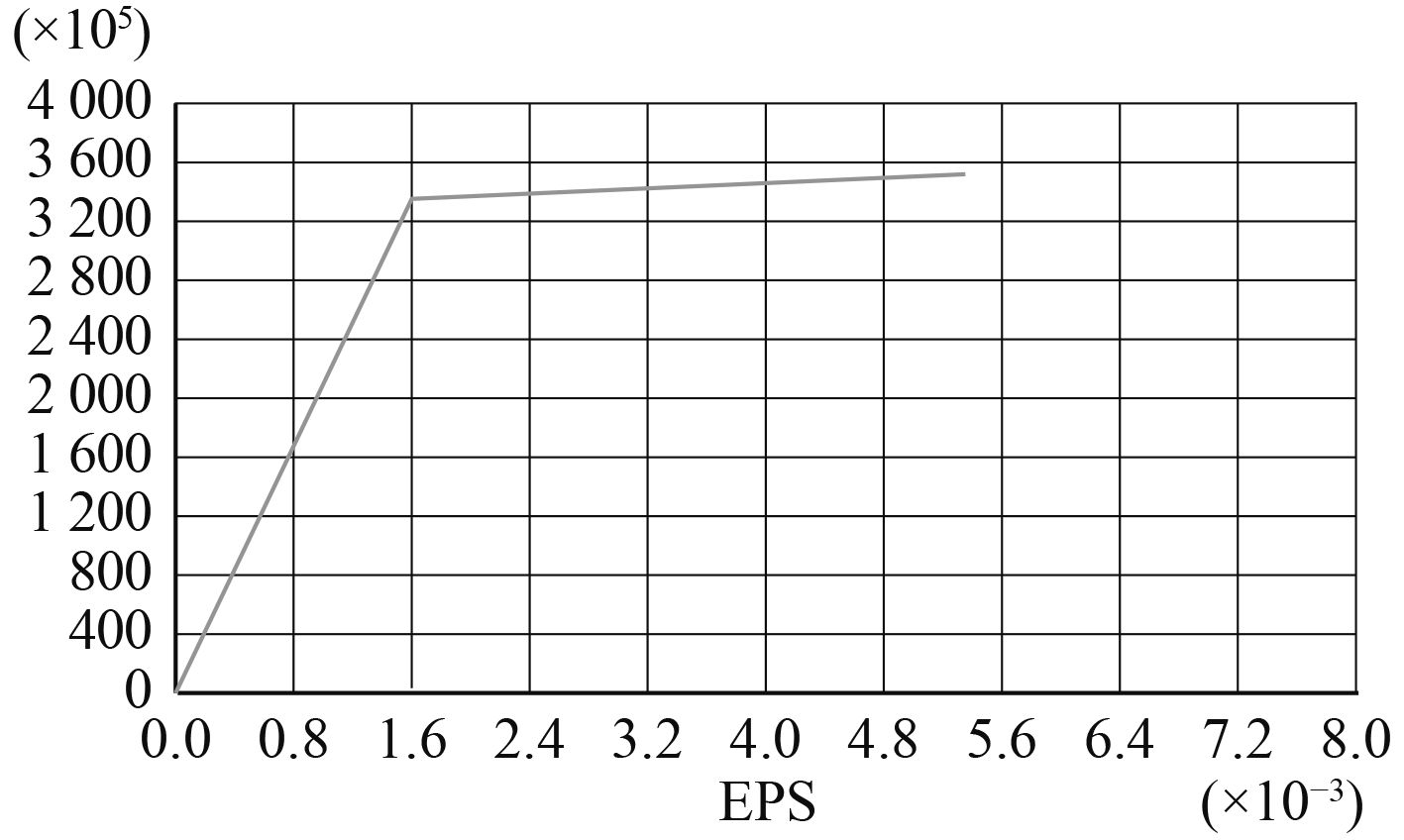
|
图 2 材料应力-应变曲线 Fig. 2 stress-strain curve of material |
在Ansys中,建立全梁单元模型、全体单元模型以及多单元混合模型进行对比分析。为了保证单元数量基本一致,划分单元时设定长度为10 mm,边界条件为架体底部梁单元完全固定。
本结构采用全实体模型时,计算量非常大,一般PC机难以胜任。为了减少计算时间,在架体线弹性范围内,选取有限的加载点,施加小载荷。混合单元模型在加载值处的位移载荷关系介于全梁单元模型和全实体单元模型之间,然而求解时间略高于全梁单元模型,远远低于全实体单元模型所需时间。综合分析,混合单元模型兼顾计算成本和计算精度要求,采用混合单元模型进行仿真较为合理。
3 缺陷模态分析 3.1 结构几何缺陷框架结构中的几何缺陷,即在生产制造、运输和安装调试过程中产生的安装偏差、弯曲和偏心等,无法消除且不可预知。框架结构的有限元模型,必须要考虑缺陷的影响。缺陷的处理方法很多,文献[1]使用凸集概率模型,文献[3]使用随机方法模拟初始缺陷。采用概率模型进行概率假设,计算量大;概念设计阶段,几何缺陷的形状和大小未知,概率假设依赖设计人员的经验,有很强的主观性。
比较流行的有一致缺陷模态法,其使用最少的非线性计算量,求解出缺陷结构的最小临界载荷,计算便捷,实用性强。一致缺陷模态,取最低阶屈曲模态模拟为结构最不利几何缺陷分布。其理论依据是结构按其模态变形时势能最小,有沿该模态变形的趋势,当结构缺陷分布形式为最低阶屈曲模态时,将对结构的性能影响最不利。利用一致缺陷模态法考虑结构初始几何缺陷时,首先要对结构进行特征屈曲分析,选取屈曲模态来模拟结构的初始几何缺陷分布,并将屈曲模态引入到非线性分析中。
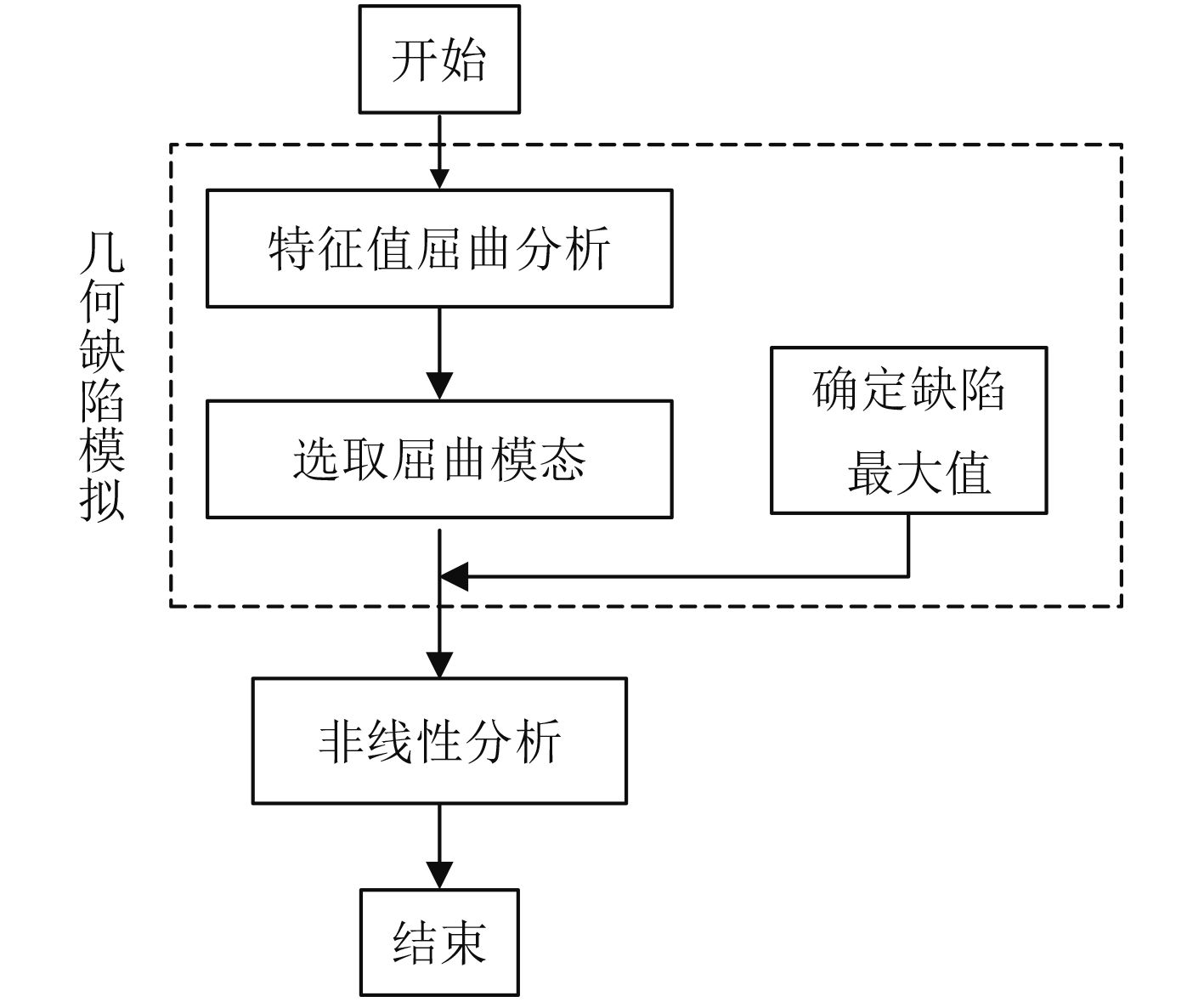
|
图 3 非线性分析流程 Fig. 3 Nonlinear analysis flowchart |
如图3所示,对结构进行特征屈曲分析,在Ansys中使用分块兰索斯法(Block-Lanczos)法获得结构的屈曲模态和特征值;选取低阶屈曲模态作为结构初始几何缺陷模式,结合初始几何缺陷最大值,确定构件节点的位移,模拟结构的初始缺陷状态。最后采用牛顿-拉斐逊法或弧长法对含缺陷结构进行非线性分析。
3.2 结构特征值屈曲根据以上分析,对刚架结构模型进行了线弹性特征值屈曲分析,结构顶部为受力区域,承受竖直向下的工作载荷。提取前15阶特征值和对应的模态,结构的前15阶线性特征屈曲模态如图4所示。
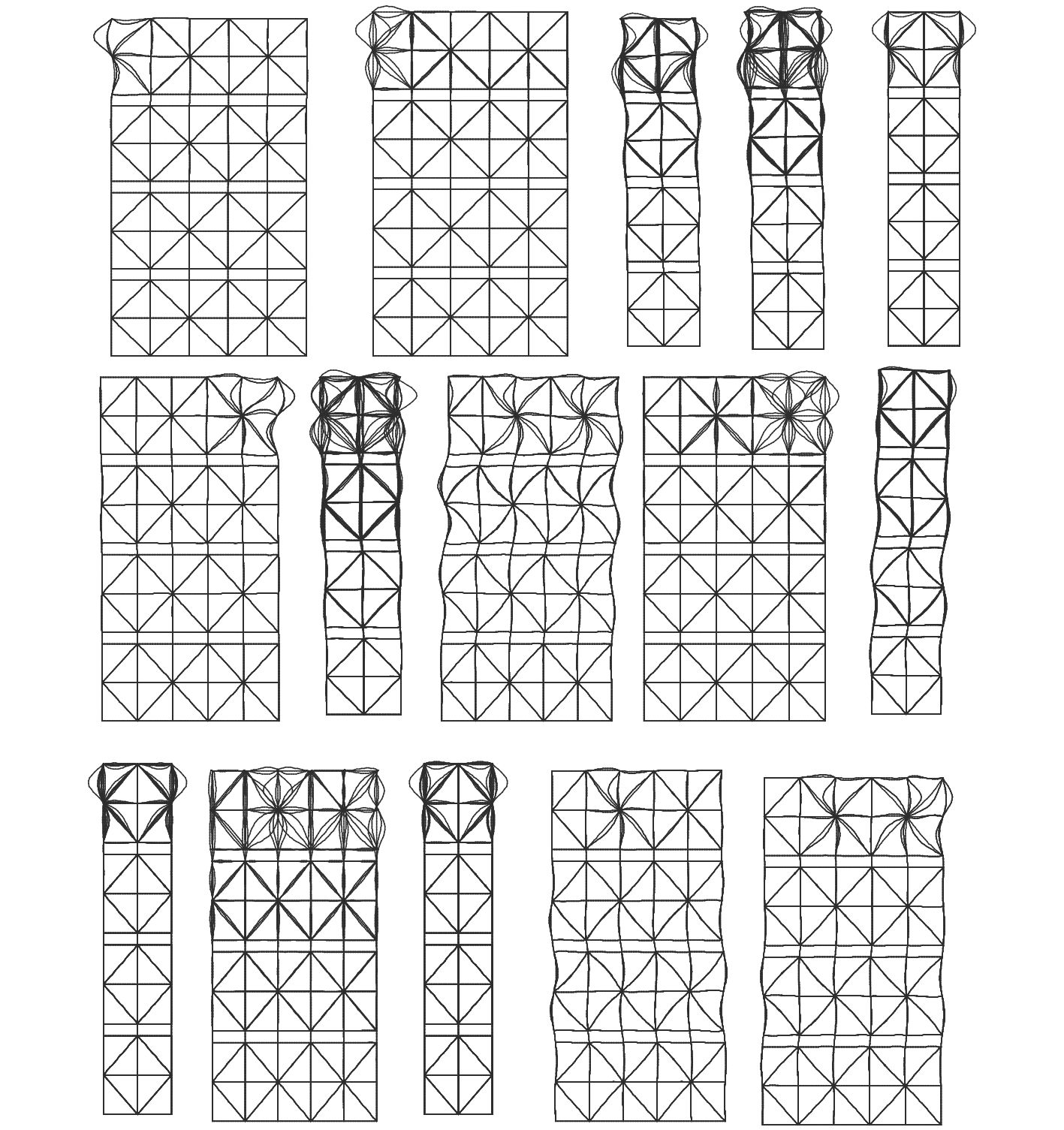
|
图 4 第1~15阶屈曲模态 Fig. 4 1st–15th failure mode of frame structure |
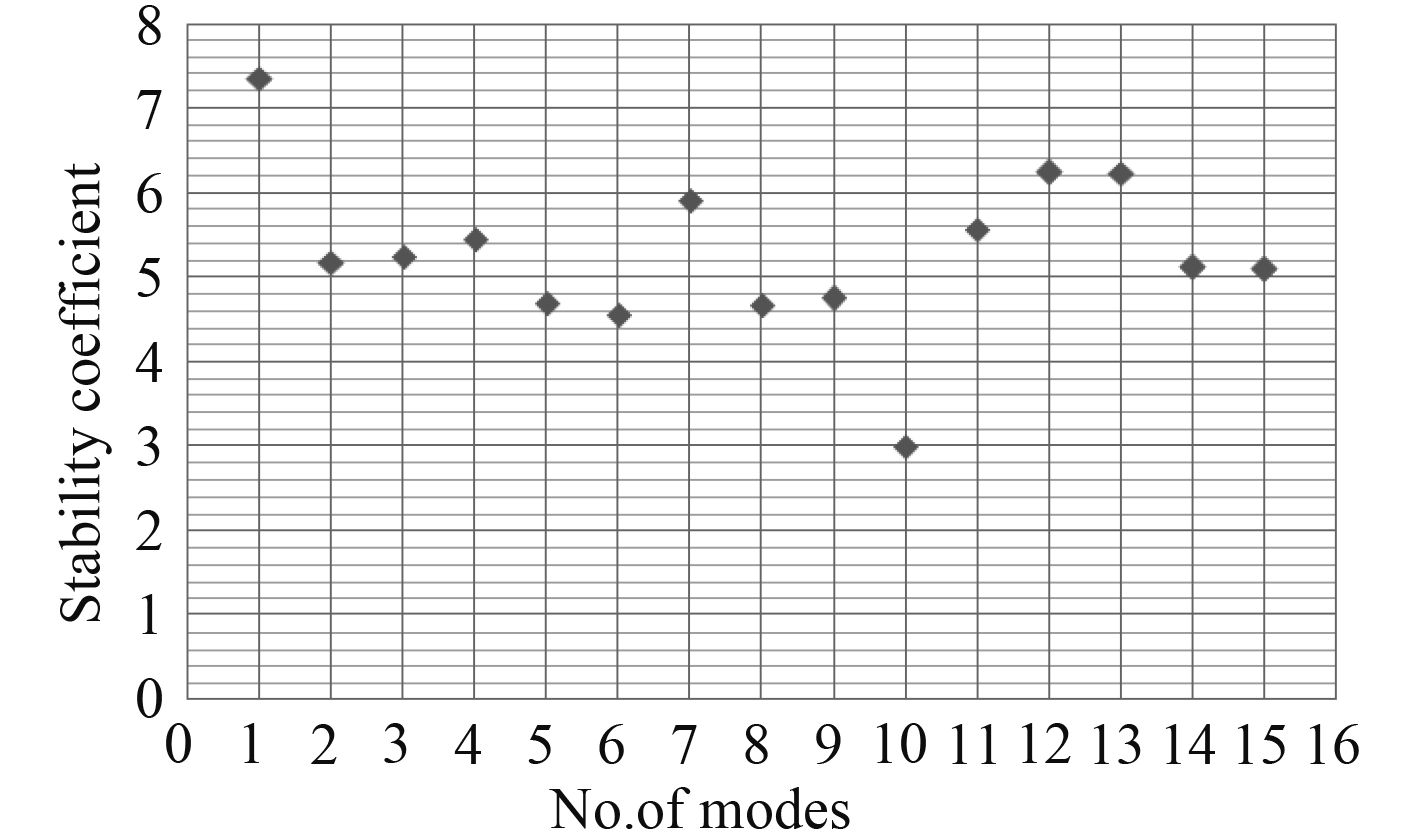
上述15阶特征屈曲模态,其中第1,2,6,8,9和14,15阶正面屈曲变形较为明显,在侧平面屈曲变形较小。其他屈曲变形模态正好相反。在给定工况下,第1阶模态表现为正面局部屈曲变形。不考虑几何缺陷的完整架体结构稳定系数λ=10.17,将上述15阶特征屈曲模态作为结构几何缺陷分布形式,引入到混合模型进行非线性分析,结果如图5所示。可以看不同的缺陷分布,稳定系数差异明显,结构对缺陷分布较为敏感。第1阶屈曲模态作为初始几何缺陷分布,得到结构的整体稳定性系数为λ1=7.36,为计算结果中最大值;第10阶屈曲模态作为初始几何缺陷分布,得到结构的整体稳定性系数为λ10=3.00,为最小值。按照结构最不利初始几何缺陷,第10阶屈曲模态刚度最差,应将其作为最不利初始几何缺陷施加到结构上,这样评估得到的结果结构稳定性好,安全可靠。
|
图 5 各阶模态稳定系数 Fig. 5 Stability coefficient under different geometrical imperfection |
在刚架焊接制造中,为了验证结构的可靠性,根据对刚架的检验验收要求,结构的安装误差最大值不能超过R,即
| $\left| {X' - X} \right| \leqslant R{\text{,}}$ | (3) |
其中:X'为实际坐标,X为理想坐标值。结构节点安装误差可以假设为近似服从正态分布,故节点坐标值也符合正态分布,令其均值为μ,方差为σ,则各节点坐标满足如下方程:
| $f(x') = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(x' - \mu )}^2}}}{{2{\sigma ^2}}}}} = \frac{1}{{\sqrt {2\pi } \sigma }}{e^{ - \frac{{{{(x' - x)}^2}}}{{2{\sigma ^2}}}}}{\text{。}}$ | (4) |
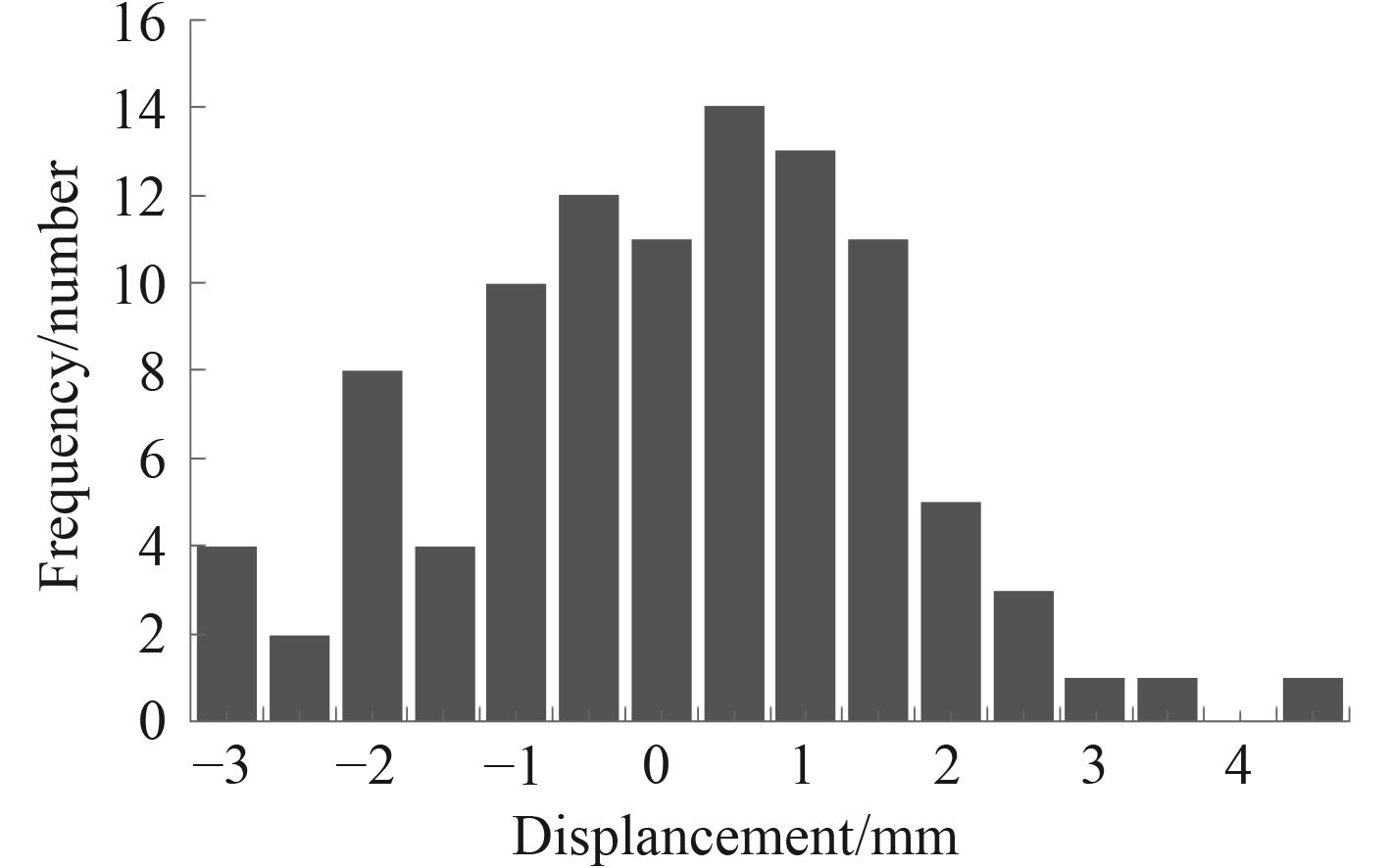
结构中所有节点位置偏差为多维独立随机变量,每一个样本点表示刚架的一种初始缺陷分布。为了获得足够的分析数据,取样本数N=100对含随机缺陷结构进行双非线性分析,节点缺陷分布如图6所示。
|
图 6 架体节点缺陷分布 Fig. 6 Node imperfection distribution of frame structure |
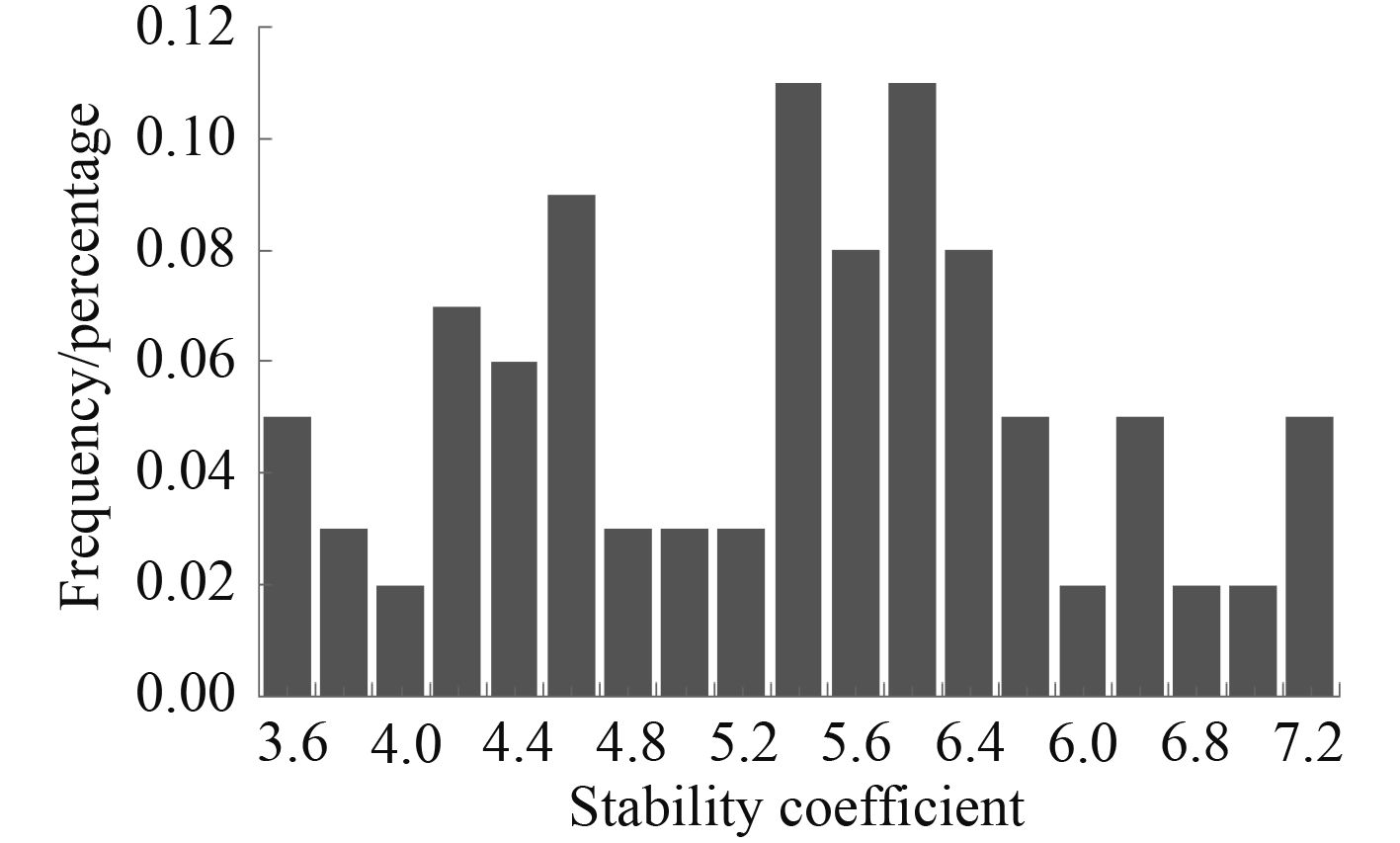
从图6中可以发现,其缺陷分布呈现中间高两端低的趋势,符合正态的假设。根据节点误差分布情况更新刚架数值仿真模型,将其引入到混合模型中,对含缺陷的刚架模型进行双非线性分析,得到相应的结构稳定性系数分布情况如图7所示。
|
图 7 结构稳定系数分布 Fig. 7 Stability coefficient distribution |
其中,稳定系数主要集中在5和6之间,稳定系数平均值为
|
|
表 2 不同稳定系数概率可靠度 Tab.2 Probality confidence level of each stability coefficient |
当按照“3西格玛”原则确定结构稳定系数,即当结构有99.87%的保证率时,其稳定系数λ=
对结构特征值屈曲模态计算,通过计算分析获得结构最不利缺陷,以第10阶屈曲模态作为初始缺陷分布模态时,即结构稳定系数λ=3,计算结果在保证安全可靠的同时,避免了过度保守的设计。
4 总 结本文采用有限元分析中采用单元混合的局部精细化有限元模型,在保证计算效率的前提下,又反应出了结构的细节特征,可获得更为精确的仿真模型。通过对刚架进行特征值屈曲分析,表明最低特征屈曲模态并非结构的最不利几何缺陷,为了获取结构的最不利几何缺陷模态,需要计算分析前几阶甚至十几阶特征值屈曲模态,这样得到计算结果才更为安全和合理。
| [1] |
卢家森,张其林.球面网壳最不利几何缺陷的凸集和概率模型[J],工程力学, 2013, 30(7): 100–104.
LU Jia-sen, ZHANG Qi-lin. Convex and probabilistic models of uncertainties in initial geometric imperfections of latticed shells[J]. Engineering Mechanics,2013,30(7):100–104. http://www.oalib.com/paper/4185708 |
| [2] | 敖鸿斐. 临界缺陷模态法在网壳缺陷敏感性分析中的应用[D]. 上海: 同济大学土木工程学院, 2005. |
| [3] |
郭佳民,董石麟,袁行飞.随机缺陷模态法在弦支穹顶稳定性计算中的应用[J],工程力学,2011,28(11):178–183.
GUO Jia-min,DONG Shi-lin,YUAN Xing-fei. Application of random imperfection mode method in stablity calculation of suspen-dome[J]. Engineering Mechanics[J], 2011, 28(11): 178–183. https://www.researchgate.net/profile/Jiamin_Guo/publication/288808524_Application_of_random_imperfection_mode_method_in_stability_calculation_of_suspen-dome/links/57e34a1308aedde5f365a1ad.pdf?origin=publication_detail |
| [4] |
刘慧娟,罗永峰,杨绿峰,等.单层网壳结构稳定性分析的随机缺陷模态迭加法[J].同济大学学报(自然科学版), 2012, 40(9): 1294–1299.
LIU Hui juan,LUO Yong feng,YANG Lu feng, etal. Stochastic imperfection mode superposition method for stability analysis of single-layer lattice domes[J].Journal of Tongji University (Natural Science),2012,40(9):1294–1299. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_tjdxxb201209003 |
| [5] |
王兵,胡长明,葛召深,等.考虑初始缺陷的扣件式钢管模板支架极限承载力研究[J].西安建筑科技大学学报(自然科学版), 2012, 44(6): 792–798.
WANG Bing, HU Chang-ming, GE Zhao-shen, et al. Study on ultimate bearing capacity of fastener-style tubular steel falsework with initial imperfection[J]. Jounal of Xi'an University of Architecture & Technology (Natural Science Edition),2012,44(6):792–798. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D192907 |
| [6] |
郝鹏,王博,李刚,等.基于缺陷敏感性分析的加筋圆柱壳结构设计[J].应用力学学报,2013,30(3):344–349.
HAO Peng,WANG Bo,LI Gang,etc.Structural design of stiffened shells based on imperfection sensitivity analysis[J].Chinese Journal of Applied Mechanics, 2013,30(3): 344–349. |
| [7] |
熊仲明,韦俊,曹欣,等.46.5 m大跨度弧形钢拱结构的稳定及其缺陷影响分析[J].工程力学,2009,26(11):172–178.
XIONG Zhong-ming,WEI Jun,CAO Xin,etc.Anlyses of stability and imperfection effect of 46.5m long-span steel arch structure with arch[J]. Engineering Mechanics[J], 2009, 26(11):172–178. http://www.cnki.com.cn/Article/CJFDTotal-JZSX200803058.htm |
| [8] | 高耀东, 刘学杰, 何建霞.ANSYS机械工程应用精选50例[M]. 北京: 电子工业出版社,2011:216–338. |
| [9] | KITIPORNCHAI S, CHAN S L. Nonlinear finite element analysis of angle and tee beam columns[J]. J Struct Engng ASCE, 1987, 113(4): 721–739. |
| [10] | ALBERMANI F G A, KITIPORNCHAI S. Nonlinear analysis of thinwalled structures using least element/member[J].J Struct Engng ASCE,1990,116(1):215–234. |
 2018, Vol. 40
2018, Vol. 40
