2. 中国舰船研究设计中心,湖北 武汉 430064;
3. 武汉理工大学 高性能舰船技术教育重点实验室,湖北 武汉 430063
2. China Ship Development and Design Center, Wuhan 430064, China;
3. Departments of Naval Architecture, Ocean and Structural Engineering, School of Transportation, Wuhan University of Technology, Wuhan 430063, China
在大开口甲板结构的设计中,大开口区域的甲板屈曲失效模式与极限承载能力一直是设计者关注的问题。由于甲板结构的失稳破坏是一个渐进的过程,同时涉及到几何非线性和材料非线性问题,且加筋板结构的多种失效模式使其屈曲失效过程十分复杂[1]。Paik等[2 – 5]研究了双轴向压缩载荷和侧向压应力作用下,加筋板结构的极限状态。并采用有限元计算方法对不同模型范围、初始缺陷、边界条件下,加筋板的结构响应进行分析。Fujikubo等[6, 7]采用有限元方法,对横向压缩载荷和侧向压力联合作用下加筋板的极限强度进行研究,开展了一系列板的有限元分析,得到了板的连续性对其屈曲和极限强度的影响规律。Xu等[8 – 10]通过模型试验与有限元数值计算的方法,确定了周期性边界条件在分析加筋板受轴向压缩载荷和侧向压力联合作用下的破坏特性和极限强度有更大的适用性。
针对大开口甲板结构的稳定性问题,张宇力等[11]对开口和不开口的甲板板架结构进行了特征值屈曲分析和极限承压屈曲分析。计算结果表明,开口附近板的屈曲模式对甲板板架稳定性的影响较大。周于程等[12]采用有限元方法对比分析了单层板架、双层板架和立体舱段3种模型甲板纵骨轴向应力分布的差异性,提出了基于稳定性要求合理设计甲板纵骨的方法。
上述文献或是对单一的加筋板结构失稳破坏进行了详细的理论、试验分析,或是对甲板板架结构整体的屈曲失效模式及应力分布进行研究。然而,对于大开口板架结构的失效诱因以及从加筋板屈曲破坏的角度来分析其对板架整体的失稳路径影响等方面的研究工作较少。鉴于此,本文设计了甲板大开口双层板架模型,开展了轴向受压极限强度模型试验,并对实验模型的受轴压破坏过程进行了数值计算分析,发现了导致整个板架失稳破坏的诱因。在此基础上,本文对原双层板架结构进行简化,通过对比分析简化后的模型与原双层板架模型的屈曲失效模式及极限承载能力,提出了大开口甲板板架稳定性试验及数值计算的简化方法,为此类型板架结构稳定性分析提供了新思路。
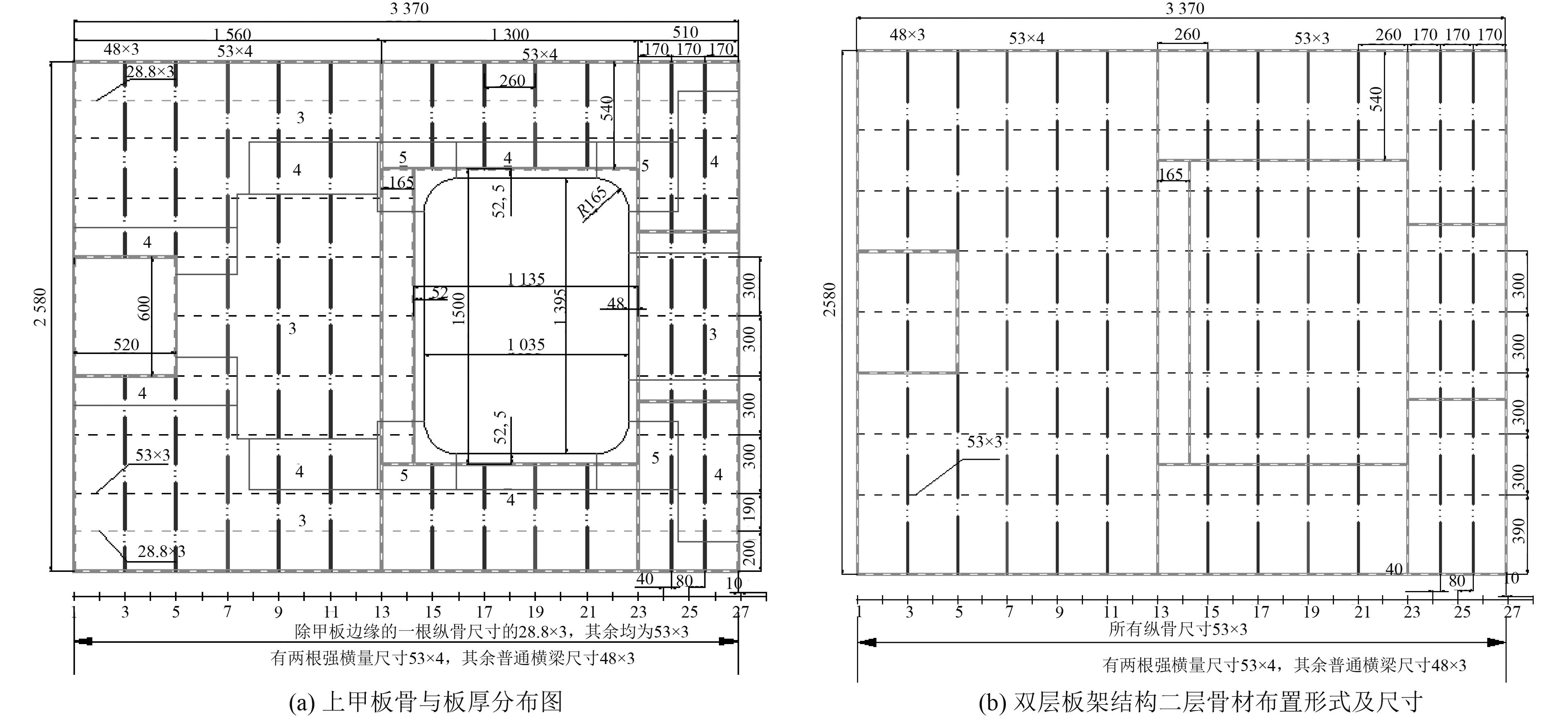
1 双层板架结构轴压稳定性试验及数值仿真分析 1.1 双层板架结构模型试验 1.1.1 大开口双层板架模型结构设计图1为该大开口双层板架模型CAD图,模型长度为3.37 m,宽度为2.58 m,高度为0.465 m。模型采用Q345B钢建造。
|
图 1 双层板架结构CAD图 Fig. 1 The CAD diagram of double deck frame structure |
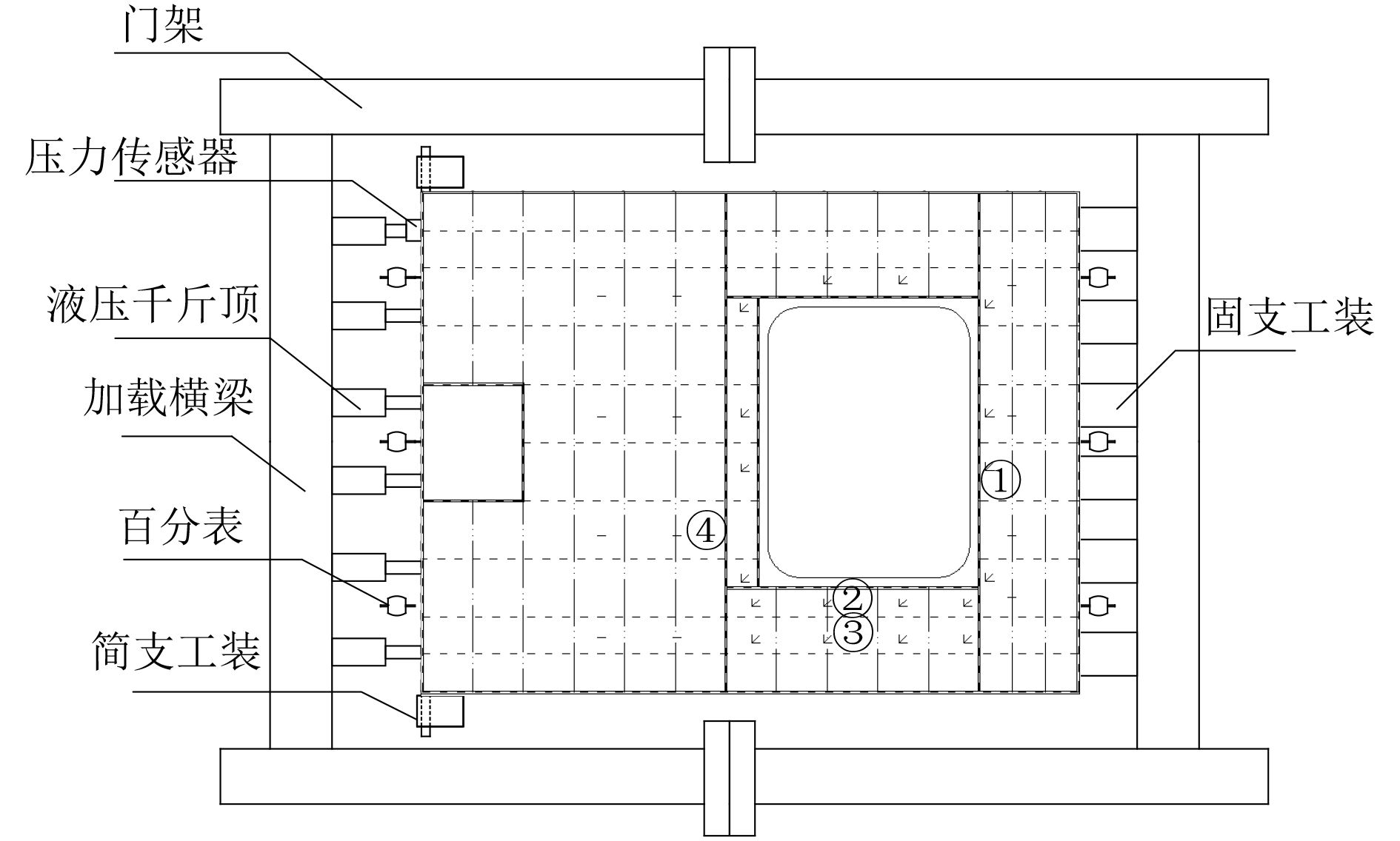
针对该双层板架结构模型的结构特点以及轴向压缩载荷的施加形式,本试验采用一端固支、一端简支的边界条件[13]。简支端与固支端具体工装形式如图2所示。

|
图 2 模型边界条件 Fig. 2 The boundary condition of the model |
将该双层板架试验模型固定在门架之中。其中,右侧刚性固定端与门架通过螺栓连接的形式固定,左侧板架端部与门架之间均匀布置6台液压千斤顶,以便轴向压缩载荷的施加。在双层板架结构的左端与右端分别布置3个百分表位移计,模型两端百分表读数的3个差值的平均值即为轴向压缩位移,如图3所示。
|
图 3 试验加载示意图 Fig. 3 Schematic diagram of the test load |
模型轴向压缩试验中,首先在线弹性范围内进行载荷的预加载与卸载,以减小焊接残余应力的影响[1]。预加载过程如表1所示。
|
|
表 1 线弹性范围内预加载过程(kN) Tab.1 Preloading process within the linear elastic scope(kN) |
经过以上轴压载荷工况下的弹性范围内的预加、卸载之后,通过查看模型各处应力测点的数据来排除和修复坏点,进一步调试加载和测试系统,为后续的加载至崩溃阶段做好准备。
|
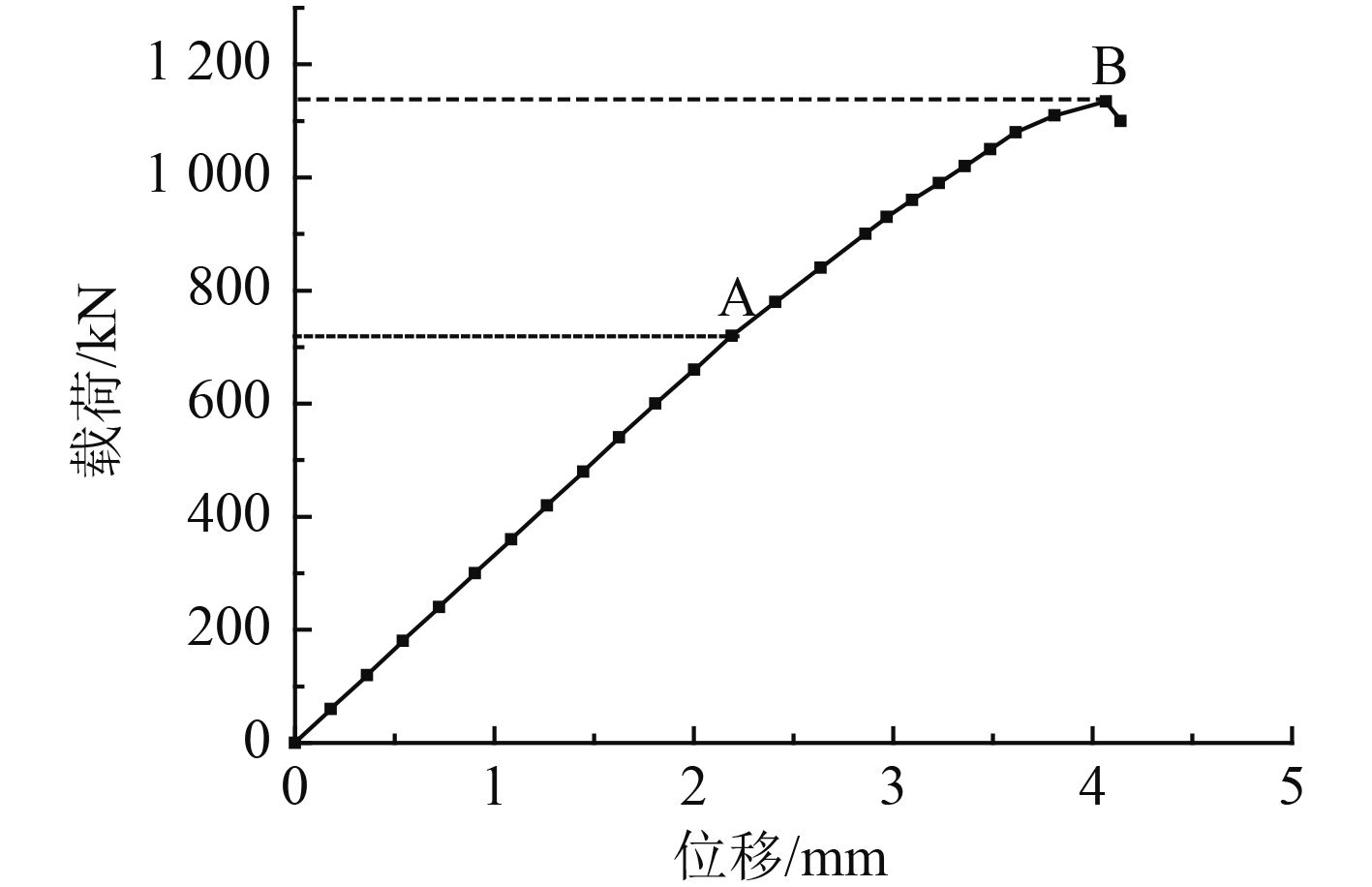
图 4 破坏试验结构载荷位移曲线 Fig. 4 The load-displacement curve of structure in destructive testing |
破坏试验中,随着轴向载荷的逐渐增大,百分表位移计示数持续增加。当所施加的载荷增加至1 134.6 kN时,双层板架结构发生屈曲破坏。破坏试验中结构的位移载荷曲线如图4所示。从图4可以看出,当轴向压缩载荷未到达A点之前时,即小于720 kN时,结构载荷位移曲线呈线性增长关系。当载荷超过B点后,随着载荷的进一步增大,结构大开口甲板处发生明显的褶皱现象,表明此时结构已经发生屈曲破坏,其破坏形式如图5所示。

|
图 5 甲板大开口双层板架屈曲破坏形式 Fig. 5 Buckling failure of double deck plates with large openings on deck |
与模型试验中的边界条件保持一致,为了同时满足加载端的简支边界条件及固定端的固支边界条件。在有限元模型中,取沿板架长度方向为x,宽度方向为y,高度方向为z,对固定端所有自由度进行约束、加载端z方向的位移和x和z方向的转角也进行约束。
1.2.2 初始缺陷处理为了使双层板架有限元模型更符合实际情况,在进行非线性有限元计算过程中,应当考虑甲板与骨材的初始缺陷。由于结构的低阶模态相比高阶模态具有更小的应变能,其变形模式更有可能由低阶模态主导[14]。因此本文采用结构的一阶模态作为初始变形,比例因子按照经验公式选取[15]:
| $\frac{{{w_{opl}}}}{t} = 0.1{\beta ^2},$ | (1) |
其中,
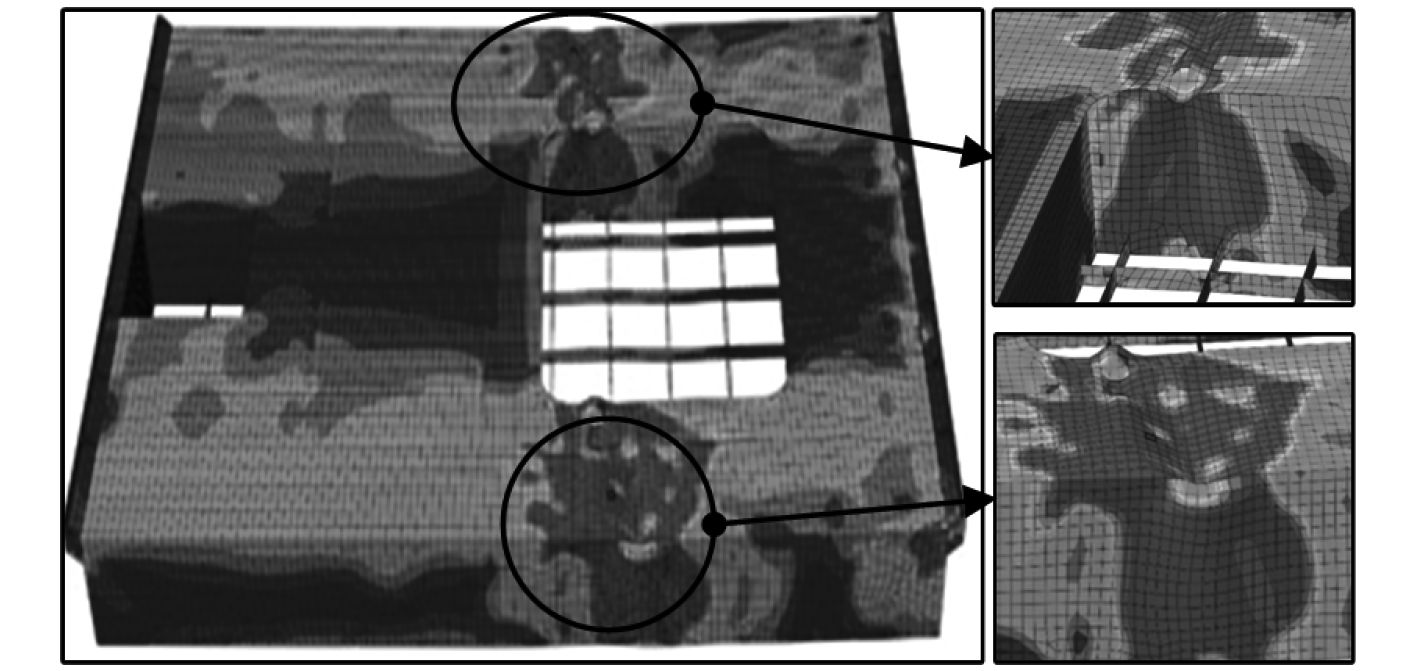
通过以上边界条件的设定与初始缺陷的处理方法,考虑到加载过程中局部结构大变形引起的几何非线性效应,应用ABAQUS/Standard对甲板大开口双层板架结构进行非线性有限元分析,数值计算结果如图6所示。通过对数值计算结果进行分析可知,双层板架结构大开口结构两侧甲板首先发生局部屈曲,同时甲板纵骨发生侧向失稳,纵舱壁和舷侧板均屈曲失效,最终导致了结构的整体失效。
|
图 6 有限元模型屈曲失效模式 Fig. 6 Buckling failure mode of finite element model |
通过对模型试验与数值仿真计算结构的对比分析可知,甲板大开口双层板架结构在大开口区域两侧的甲板局部屈曲最终导致了结构的整体失效。通过对加载过程中筋与板的失效模式的观测,发现大开口结构两侧甲板板首先发生下凹或隆起现象,甲板纵骨进而发生侧向失稳,纵舱壁和舷侧板也均屈曲失效。
1.3.2 极限承载力对比对比模型试验的极限载荷和数值计算的极限载荷,如表2所示。模型试验中测得双层板架结构极限承载力为1 134.6 kN,数值计算结果所得结构极限承载力为1 189.54 kN,两者误差仅为4.84%。
|
|
表 2 极限载荷对比 Tab.2 Comparison of ultimate loads |
通过以上的对比分析可知,本文所采用的非线性有限元计算方法较为可靠,对于结构屈曲失效模式以及极限承载能力的模拟精度较高。
2 有限元简化模型数值计算分析 2.1 单层板架简化模型 2.1.1 单层板架简化模型范围选取通过观察图5中双层板架模型的屈曲失效模式,分析其失稳破坏路径,发现甲板大开口两侧甲板在加载过程中挠度变化最为明显,该区域随着轴向压缩载荷的增大至最后发生褶皱坍塌时,整个双层板架达到极限承载能力。基于以上分析,对大开口双层板架模型进行简化处理,选取大开口区域附近介于2道强横梁之间的单层板架结构,研究其在轴压载荷作用下的失稳路径及极限承载能力。单层板架简化模型如图7所示。
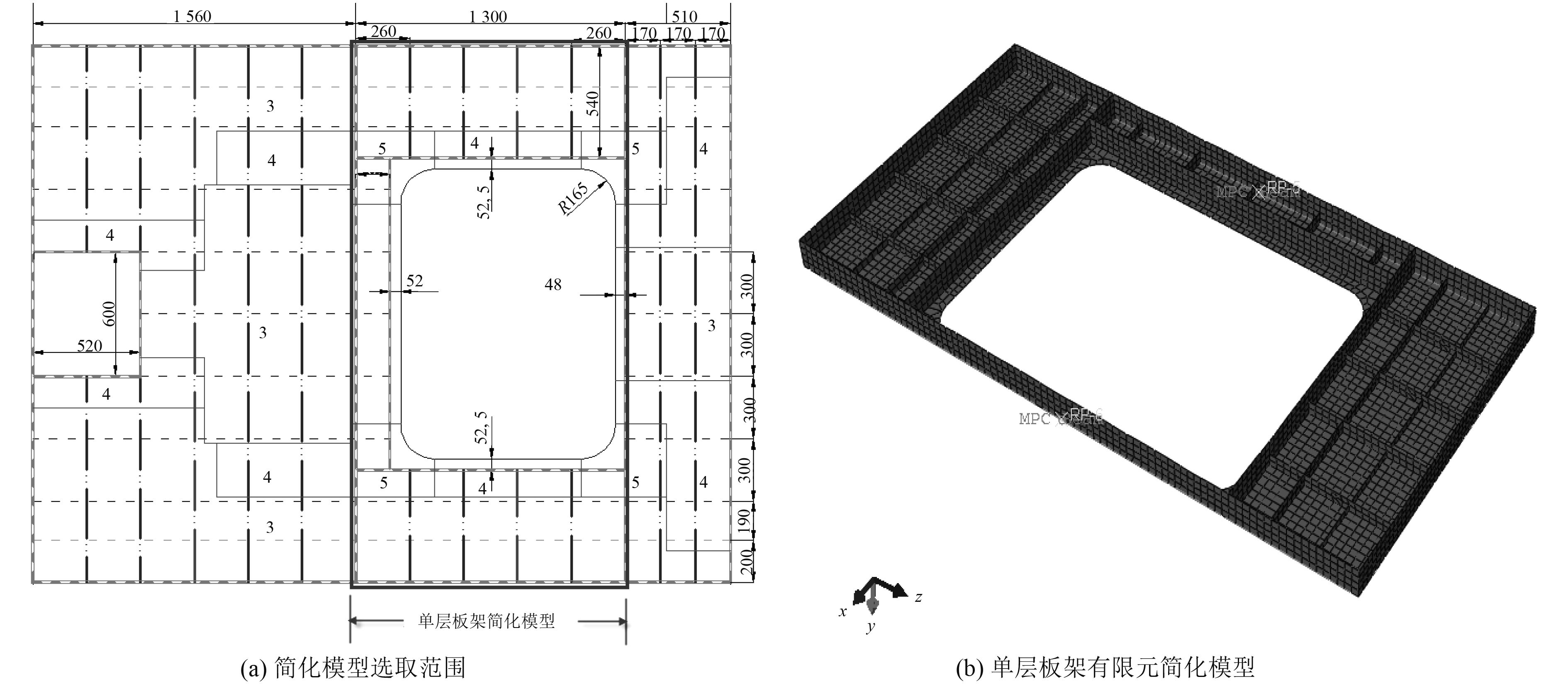
|
图 7 单层板架简化模型 Fig. 7 Simplified model of single-layer frame |
按照1.2.1节设置边界条件,坐标系的选取原则与双层板架模型一致。分别对两端强横梁设置刚性面约束,独立点位于中纵剖面与两横梁中和轴的交点位置。加载端及固定端的边界条件及加载点均在两端的独立点上进行设置。
通过分析该单层板架简化模型的屈曲模态,然后将屈曲模态的变形引入到计算模型之中,初始缺陷的比例系数按照式(1)选取。通过局部低阶屈曲模态叠加,合成结构的初始缺陷[16],引入的2种屈曲模态如图8所示。
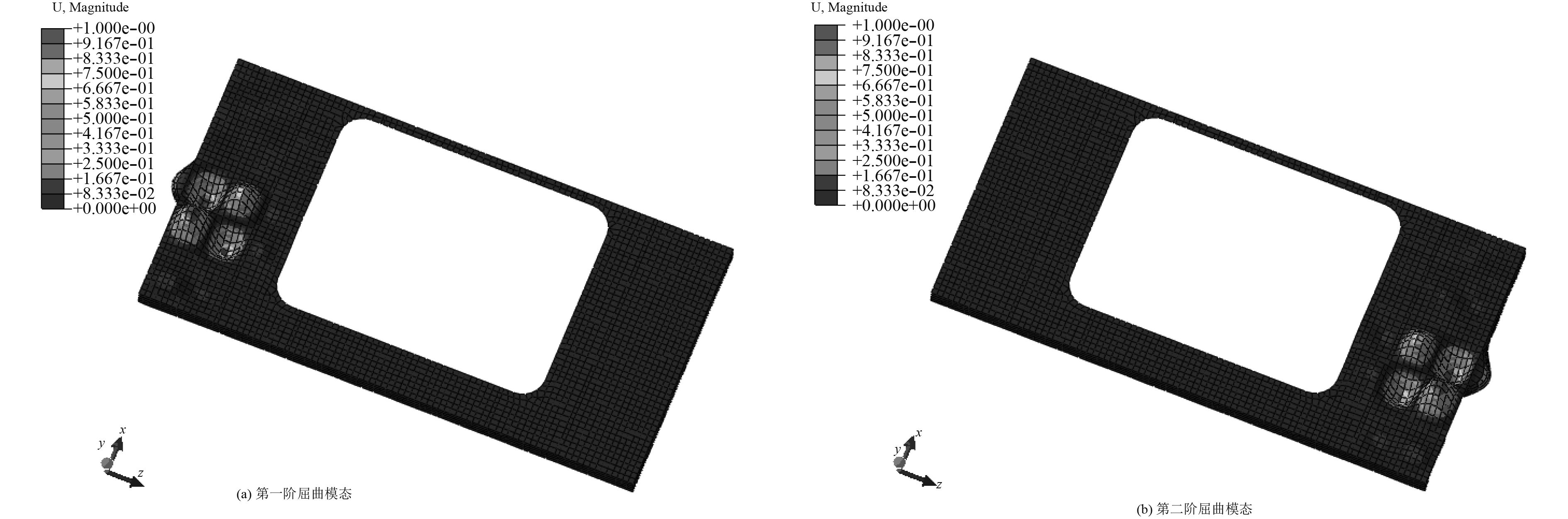
|
图 8 初始缺陷屈曲模态 Fig. 8 Buckling mode of initial imperfection |
通过上述方法设定有限元模型的边界条件与初始缺陷后,进行非线性有限元计算。大开口单侧筋与板Mises应力分布如图9所示。该单层板架简化模型整体破坏模式如图10所示。
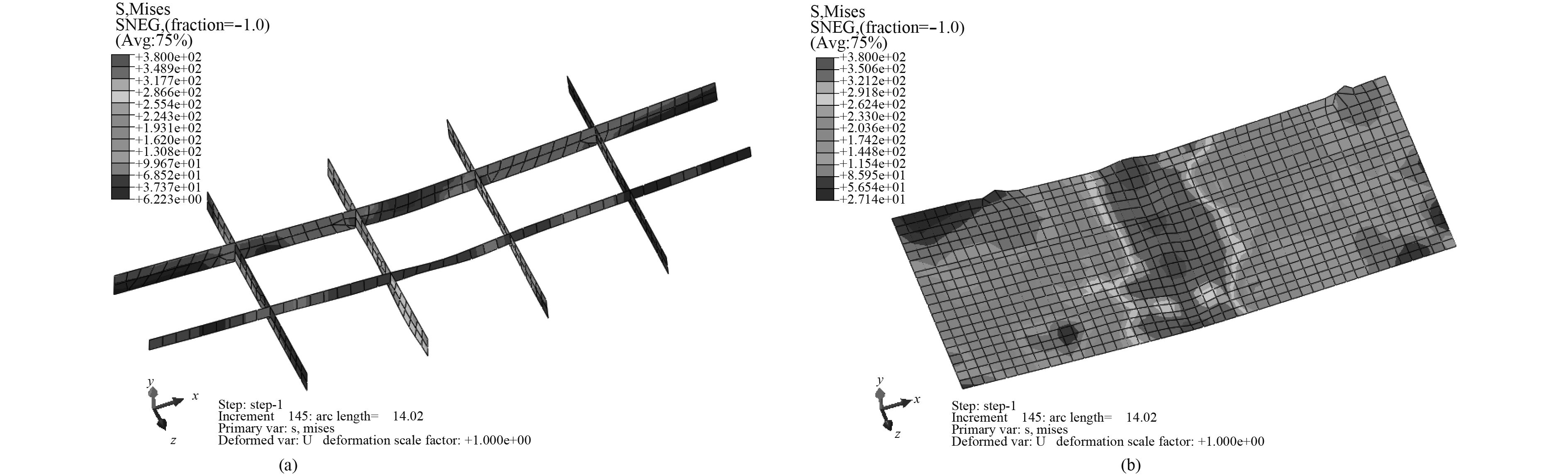
|
图 9 大开口单侧筋与板应力分布 Fig. 9 Stress distribution of stiffeners and plate of large opening |
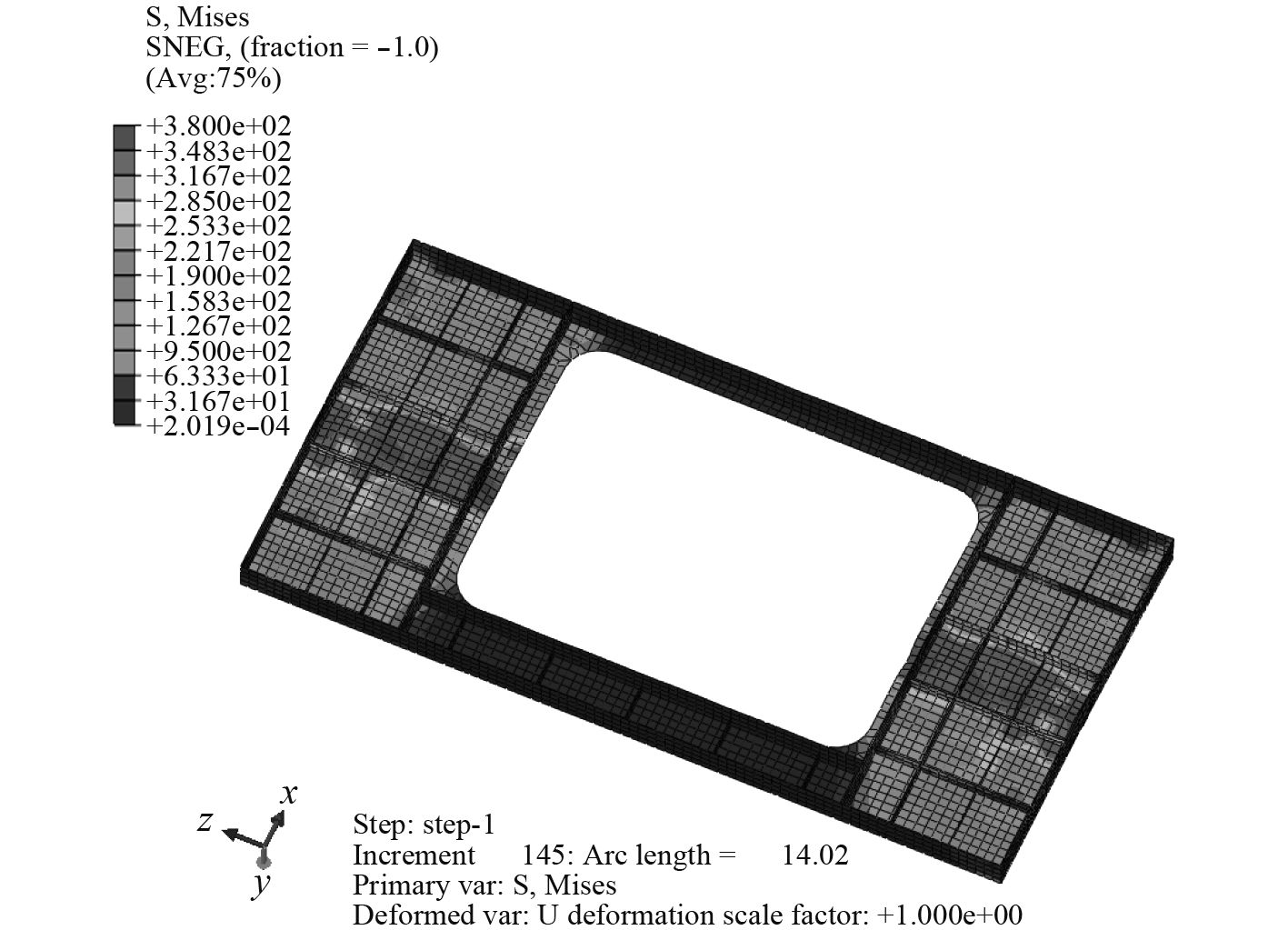
|
图 10 单层板架有限元简化模型破坏模式 Fig. 10 Failure mode of single-layer frame simplified model |
由单层甲板板架模型有限元计算结果可知,尽管对甲板大开口双层板架模型进行了大量的简化,但从数值计算结果来看,简化后的大开口单层板架结构屈曲失效模式与原双层板架结构高度一致。其失效诱因仍为大开口结构两侧的甲板板与甲板骨材的局部失稳导致。基于以上分析,进一步对单层甲板板架模型进行简化处理,仅选取大开口区域单侧加筋板结构为研究对象,其模型选取范围如图11所示。
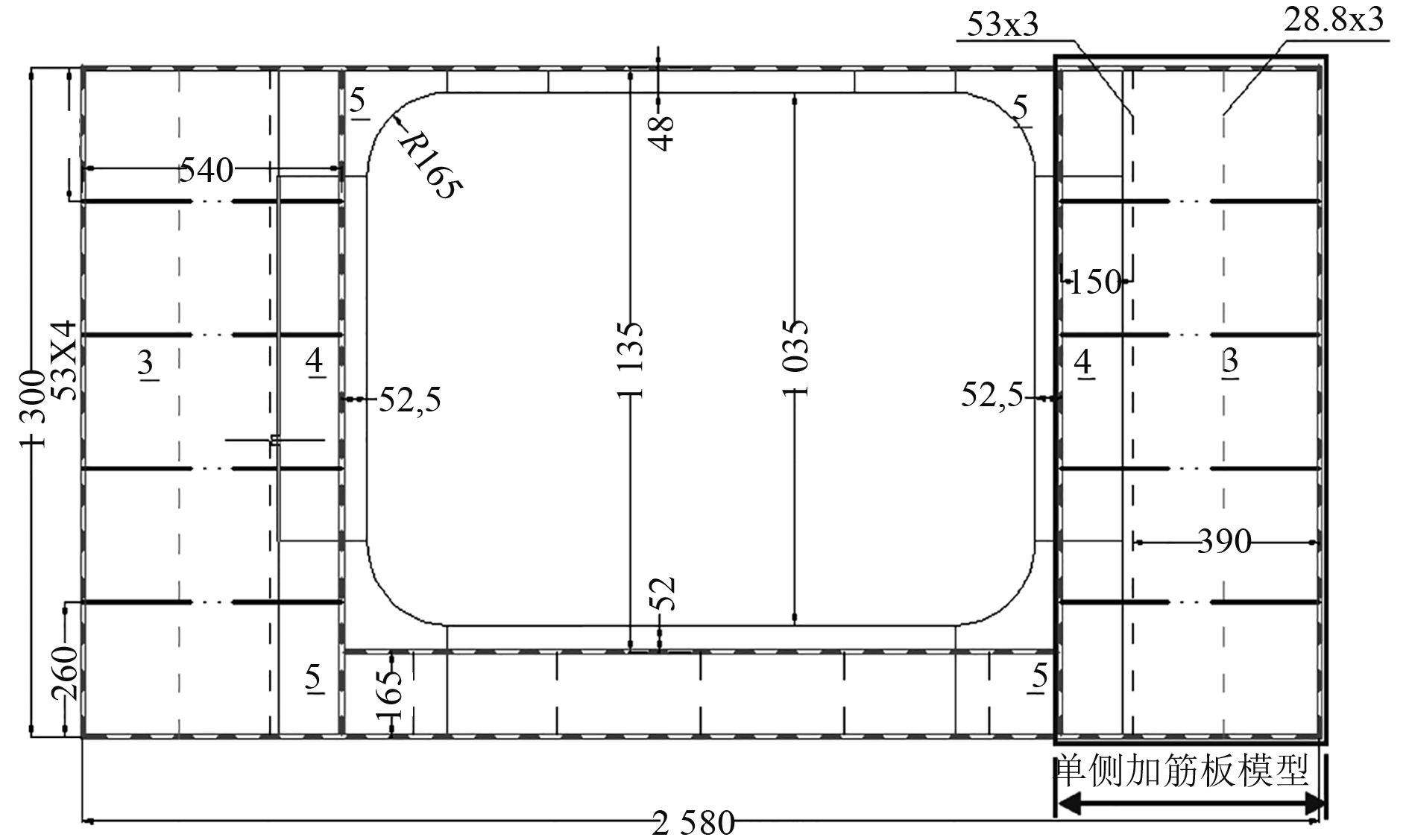
|
图 11 大开口结构单侧模型选取范围 Fig. 11 Selection range of open structure unilateral model |
通过设定与单层甲板板架相同的边界条件与初始缺陷,对简化加筋板模型进行数值计算。其中,简化加筋板结构筋与板Mises应力分布见图9。加筋板结构失稳区域集中在甲板中部,相应区域的加强筋发生明显侧倾现象。简化加筋板结构整体屈曲失效模式与单层板架有限元简化模型单侧结构的失效模式相似程度较高。
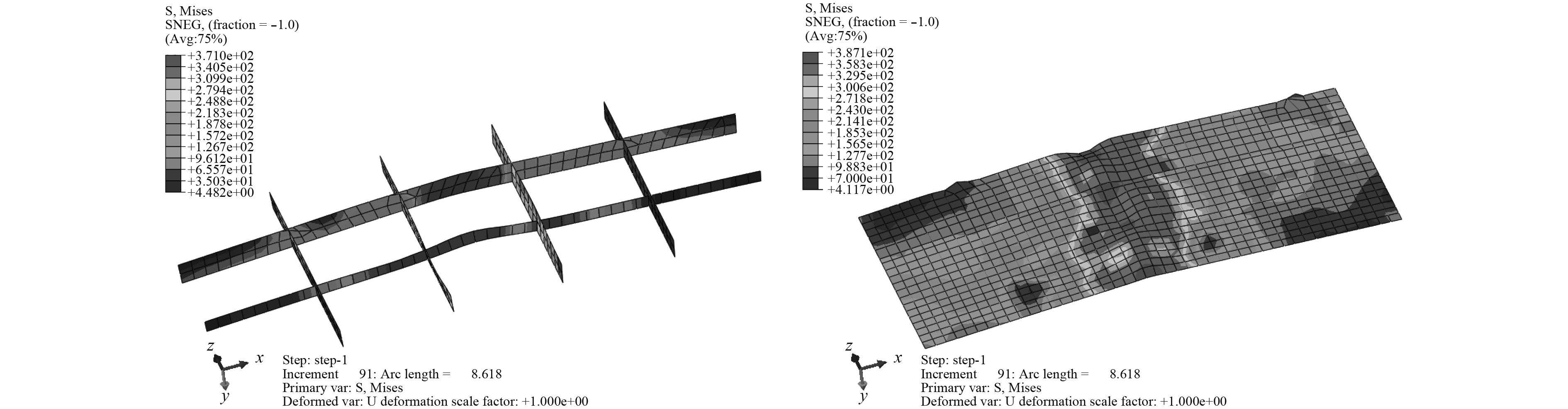
|
图 12 简化加筋板结构筋与板应力分布 Fig. 12 Stress distribution in simplified stiffened plate structure |
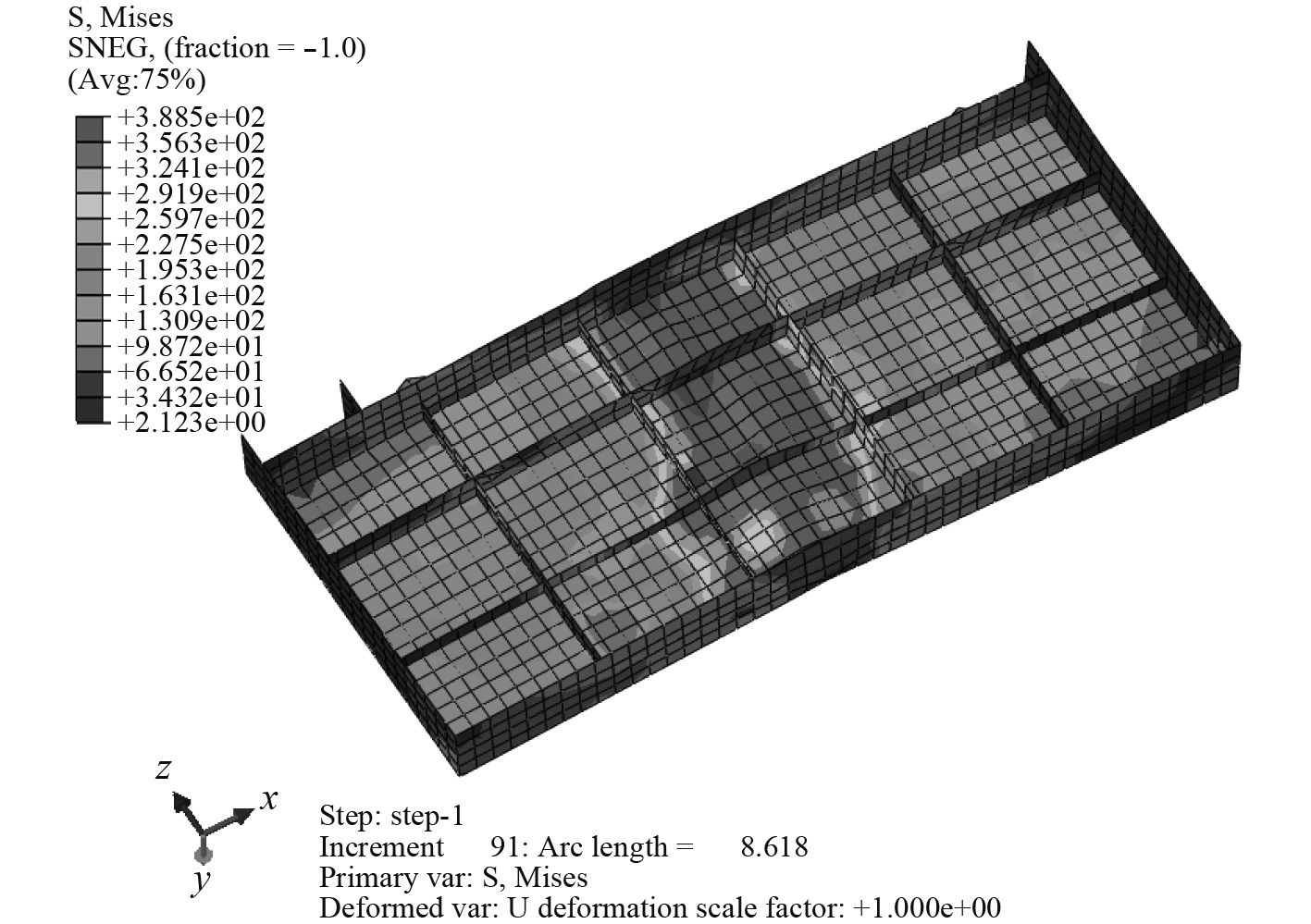
|
图 13 简化加筋板结构有限元模型失效模式 Fig. 13 Failure mode of simplified stiffened plate structure |
将3种模型有限元数值计算结果进行对比分析,如图14所示。其中,图14(a)为大开口双层板架结构数值计算结果,为了方便对比分析,隐藏其他构件,仅显示位于2道强横梁之间的单层板架结构。图14(b)和(c)分别为简化后的单层板架模型与加筋板模型的破坏模式。
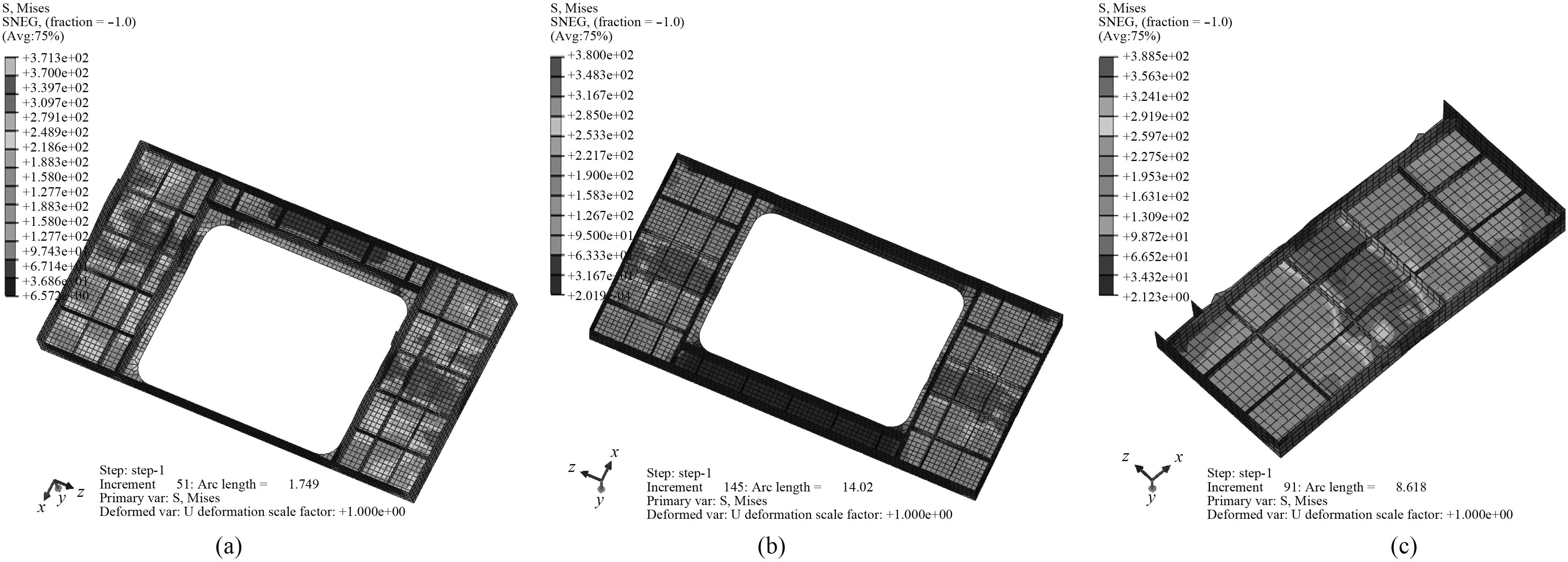
|
图 14 三种有限元模式失效模式对比 Fig. 14 Comparison of failure modes between three kinds of finite element models |
通过对3种结构失效模式的分析,发现甲板大开口双层板架失效诱因与2种简化后的局部结构失效原因一致。由于大开口区域的纵骨尺寸与甲板厚度同其他区域相比没有明显加强,而此处大开口结构的存在导致在此板架结构中,甲板大开口区域附近的结构强度最弱。当受到轴向载荷作用时,对于整个板架结构而言,主要的承力构件为大开口两侧的加筋板结构。由此可见,大开口两侧的加筋板结构面板的厚度不足及纵骨的尺寸较小为整个结构屈曲失效的主要诱因。
2.3.2 三种结构极限承载力对比分析对比3种类型结构数值计算得到的载荷位移曲线与试验所得载荷位移曲线,如图15所示。从结构极限承载力来看,3种结构在轴向压缩载荷作用下发生失稳破坏的极限载荷相差不大。但由于单层板架简化结构和简化加筋板结构均在原始双层板架基础上进行了一定的简化处理,在结构发生屈曲破坏时,3种结构的轴向位移有所不同。
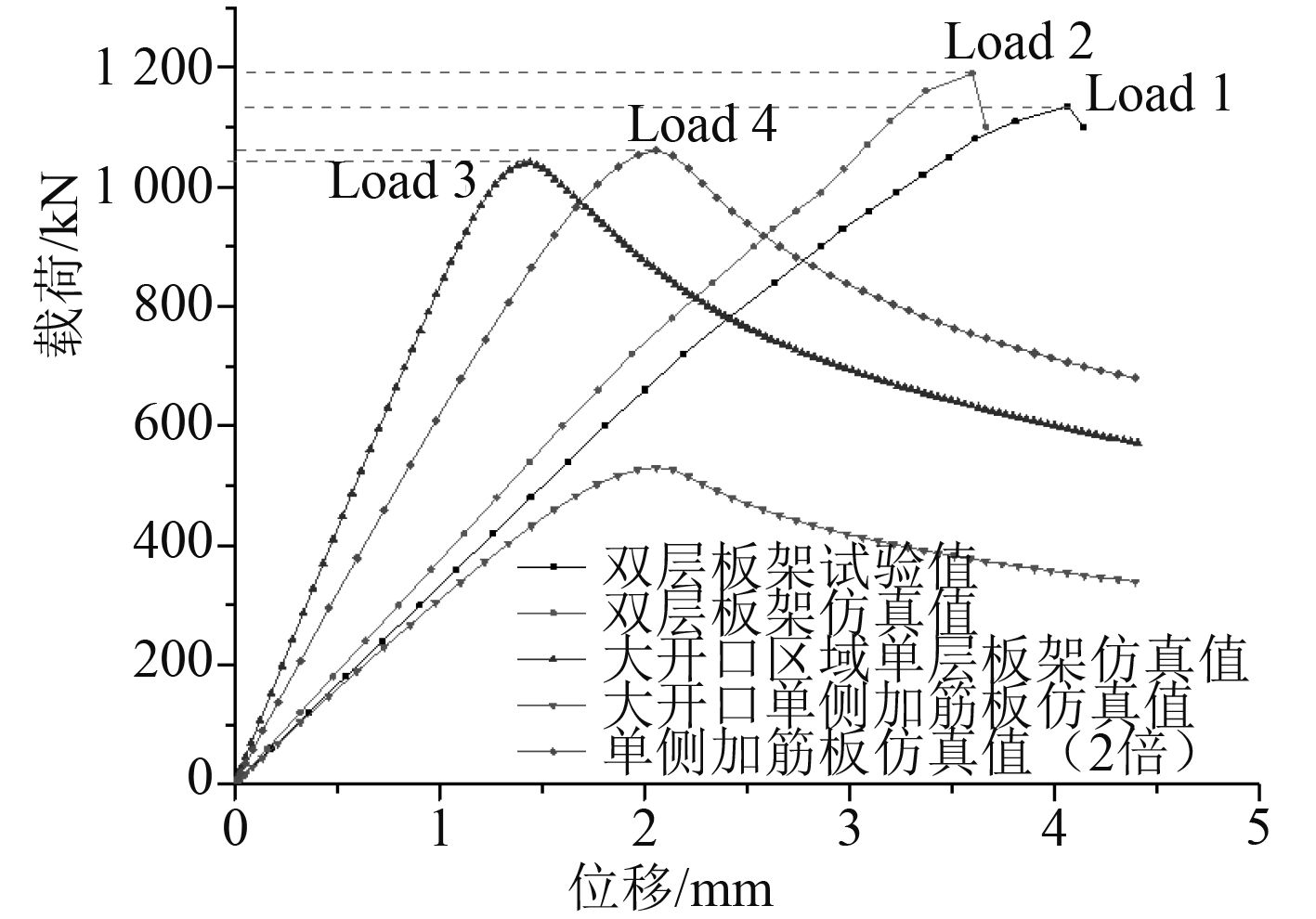
|
图 15 试验与仿真载荷位移曲线对比 Fig. 15 Comparison of test and simulation failure paths |
将双层板架模型试验的极限承载力与3种结构有限元数值计算结果进行对比,如表3所示。通过数据对比可见,本文采用的有限元计算方法与对双层板架的简化处理方式所得结果与试验得到的极限载荷误差均在10%以内。由此可见,简化后的加筋板结构可以很好地对原型双层板架结构在轴向压缩载荷作用下的屈曲失效模式和极限承载能力进行预测。同时,可节约大量的试验成本,减小试验与数值仿真的工作量。
|
|
表 3 三种板架结构极限承载力对比 Tab.3 Comparison of ultimate bearing capacity of three kinds of structures |
本文以大开口双层板架模型为研究对象,采用试验与数值仿真对比分析的方法,得到了其在轴向压缩载荷作用下的屈曲失效模式与极限承载能力,验证了本文所采用的非线性有限元方法的可靠性。在此基础上,根据该双层板架的结构特点与屈曲失效模式,提出了结构简化计算方法,可得到以下几点结论。
1)大开口板架结构试验模型、有限元模型、单层板架简化模型以及加筋板简化模型的计算结果均表明,大开口结构两侧纵骨的侧倾以及甲板局部屈曲导致了整体结构的失稳破坏。因此,在实际的设计过程中,应对甲板上布置有大开口区域的两侧甲板及纵骨适当加强。
2)本文简化的加筋板结构在轴向压缩载荷作用下,屈曲失效模式与双层板架模型相似程度较高,极限承载能力与试验值对比,误差为6.49%。在今后类似研究中可采用简化的加筋板结构进行大开口甲板结构的轴压极限强度的计算与校核。
3)本文以大开口双层板架结构为研究对象,但简化加筋板模型范围的选取、边界条件的设定对轴压极限强度计算结果的影响规律可推广到船底板架、舷侧板架等结构。
| [1] | 吴卫国, 袁天, 孔祥韶. 船舶甲板结构稳定性实验与数值仿真研究 [J]. 船舶力学, 2017, z(1): 472–479. http://cdmd.cnki.com.cn/Article/CDMD-10248-2008052247.htm |
| [2] | PAIK J K, SEO J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions-Part I: Plate elements [J]. Thin-Walled Structures, 2009, 47(8-9): 1008–1017. |
| [3] | PAIK J K, SEO J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions-Part II: Stiffened panels [J]. Thin-Walled Structures, 2009, 47(8-9): 998–1007. |
| [4] | PAIK J K, KIM B J, SEO J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part I—Unstiffened plates [J]. Ocean Engineering, 2008, 35(2): 261–270. |
| [5] | PAIK J K, KIM B J, SEO J K. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part II stiffened panels [J]. Ocean Engineering, 2008, 35(2): 271–280. |
| [6] | FUJIKUBO M, YAO T, KHEDMATI M R, et al. Estimation of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure Part 1: Continuous plate [J]. Marine Structures, 2005, 18(5-6): 383–410. |
| [7] | FUJIKUBO M, HARADA M, YAO T, et al. Estimation of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure Part 2: Continuous stiffened panel [J]. Marine Structures, 2005, 18(5-6): 411–427. |
| [8] | XU M C, SOARES C G. Comparisons of calculations with experiments on the ultimate strength of wide stiffened panels [J]. Marine Structures, 2013, 31(Supplement C): 82–101. |
| [9] | XU M C, YANAGIHARA D, FUJIKUBO M, et al. Influence of boundary conditions on the collapse behaviour of stiffened panels under combined loads [J]. Marine structures, 2013, 34: 205-225. |
| [10] | XU M, SOARES C G. Assessment of the ultimate strength of narrow stiffened panel test specimens [J]. Thin-Walled Structures, 2012, 55: 11-21. |
| [11] | 张宇力, 曾广武, 段洪, 等. 大开口对船舶板架稳定性和极限承载力的影响 [J]. 华中科技大学学报(自然科学版), 2002(5): 56–64. http://mall.cnki.net/magazine/Article/CBLX201210010.htm |
| [12] | 周于程, 郑绍文, 刘均, 等. 基于舱段模型的大开口甲板结构稳定性分析与设计 [J]. 中国舰船研究, 2014(2): 37–41, 54. http://www.cnki.com.cn/Article/CJFDTOTAL-JCZG201402007.htm |
| [13] | KWON Y B, PARK H S. Compression tests of longitudinally stiffened plates undergoing distortional buckling [J]. Journal of Constructional Steel Research, 2011, 67(8): 1212–1224. |
| [14] | 王保森, 董胜, 冯亮, 等. 加筋板极限强度数值计算影响因素及敏感分析 [J]. 中国海洋大学学报(自然科学版), 2018(2): 105–112. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1685466 |
| [15] | PAIK J K, THAYAMBALLI A K, LEE J M. Effect of initial deflection shape on the ultimate strength behavior of welded steel plates under biaxial compressive loads [J]. Journal of ship research, 2004, 48(1): 45–60. |
| [16] | 初艳玲. 考虑初始缺陷的结构非线性屈曲分析与应用 [J]. 中国造船, 2010(3): 119–127. http://mall.cnki.net/magazine/Article/GLJK201305008.htm |
 2018, Vol. 40
2018, Vol. 40
