0 引　言

IMO正在制定包括参数横摇、纯稳性丧失、骑浪/横甩、瘫船稳性和过度加速度这5种稳性失效模式的第2代完整稳性规则^[1]。具有传统意义的瘫船稳性是指船舶处于失去动力无法推进或操舵状态下，当船自由漂移时在风浪联合作用下发生共振横摇甚至倾覆^[2]。IMO目前正在制定的瘫船稳性薄弱性衡准草案主要以意大利和日本的提案为基础，分为第1层衡准和第2层衡准^[3–4]。针对第1层衡准方法基本已达成一致，对于第2层衡准方法的确定预计2018年左右才能完成^[5]。

瘫船稳性失效中基于危险性评估的倾覆概率方法成为近年来研究的热点，针对随机激励下复原力矩的非线性一直是处理该问题的主要难点^[6]。国内外学者针对横浪状态下的船舶大幅横摇运动的稳性进行过许多研究，包括线性化理论和线性化处理方法、非线性动力学的应用以及直接数值模拟方法^[7]。自从1953年Denis和Pierson首次将随机过程理论引入到线性耐波性领域的研究中，船舶在随机风浪中的倾覆概率研究也引起了各国学者的重视。

IMO草案中日本和意大利分别基于分段线性和局部线性方法，各自提出较为完善的概率计算方法。52届SLF会议上，意大利代表建议将2008 IS Code中气候衡准作为瘫船稳性的第1层衡准^[8]，并提出了基于局部线性化方法的横摇倾覆概率模型作为瘫船稳性的第2层薄弱性衡准或直接评估方法^[3]；日本代表提议利用基于Froude-Krylov假设的简化公式求解有效波倾系数^[9]，利用简化的Ikeda方法求解横摇阻尼系数^[10]，同时将基于GZ曲线分段线性化处理的横摇倾覆概率模型作为瘫船稳性的第2层衡准方法^[4]。Belenky^[11]在1993年提出了船舶横摇运动的分段线性化理论，通过对回复力矩的分段线性处理，求解得到单自由度横摇运动方程的解析解，并以此评估倾覆概率。之后基于该方法，Iskandar^[12]，Umeda^[13]，Paroka^[14–15]等日本学者进行了大量实船评估计算和方法上的改进。

本文基于瘫船稳性第2层衡准，针对C11和CEHIPAR 2792两艘集装箱船，利用分段线性化方法得到横摇运动方程的解析解，并据此计算倾覆概率。在样船计算的基础上同局部线性化结果进行对比，并重点探讨暴露时间、波浪谱以及分段分界点的选取等敏感性因素对倾覆概率的影响。

1 瘫船稳性分段线性化数值计算模型 1.1 单自由度横摇运动方程

船舶在横浪下运动，一般采用横摇和横荡耦合的运动模型，并且考虑波浪辐射力和绕射力的影响。田才福造等^[16]已经证明单自由度横摇方程也可以近似表达横摇运动。因此，日本方法采用1-DOF非耦合运动方程，波浪激励力只考虑Froude-Krylov力，方程无因次化后表示如下：

$\ddot \varphi + d\left( {\dot \varphi } \right) + \omega _0^2 \cdot k{f_i}\left( \varphi \right) = \omega _0^2 \cdot \left[ {{m_{{\rm{wind}}}}\left( t \right) + {m_{{\rm{wave}}}}\left( t \right)} \right]{\text{。}}$

(1)

式中：ω₀为横摇固有频率；GM为初稳性高； $d\left( {\dot \varphi } \right) = \displaystyle\frac{{D\left( {\dot \varphi } \right)}}{{{J_{xx}} + \Delta {J_{xx}}}}$ ； ${\omega _0} = \sqrt {\frac{{W \cdot GM}}{{{J_{xx}} + \Delta {J_{xx}}}}} $ ； $k{f_i}\left( \varphi \right) = \displaystyle\frac{{GZ\left( \varphi \right)}}{{GM}}$ ； ${m_{{\rm{wind}}}}\left( t \right) = \displaystyle\frac{{{M_{{\rm{wind}}}}\left( t \right)}}{{W \cdot GM}}$ 为风作用的无因次瞬时力矩； ${m_{{\rm{wave}}}}\left( t \right) = \displaystyle\frac{{{M_{{\rm{wave}}}}\left( t \right)}}{{W \cdot GM}}$ 为波浪作用的无因次瞬时力矩。

无因次的Froude-Krylov波浪激励力矩可由有效波倾系数计算得到。在线性假设下，将不同振幅和相位的规则波进行叠加，研究船舶在不规则波中的摇荡运动特性。波浪谱采用第15届ITTC会议推荐的双参数谱：

${S_{{\rm{wave}}}}\left( {{\omega _i}} \right) = \frac{A}{{\omega _i^5}}\exp \left( {\frac{{ - B}}{{\omega _i^4}}} \right), $

(2)

式中：

$\left\{ \begin{array}{l}A = 172.75\frac{{H_{1/3}^2}}{{T_m^4}}, \\B = \frac{{691}}{{T_m^4}}{\text{。}}\end{array} \right.$

(3)

其中：H_1/3为有义波高，m；T_m为不规则波的平均周期，s。

风倾力矩可以分为阵风成分 ${m_a}\left( t \right)$ 和定常风成分m₀，表示如下：

${m_{{\rm{wind}}}}\left( t \right) = {m_0} + {m_a}\left( t \right), $

(4)

其中：

${m_0} = \frac{{0.5{\rho _{{\rm{air}}}}{C_m}U_m^2{A_L}{H_C}}}{{W \cdot GM}}, $

(5)

${m_a}\left( t \right) = \frac{{{\rho _{{\rm{air}}}}{C_m}{U_m}{A_L}{H_C}}}{{W \cdot GM}}U\left( t \right)\text{。}$

(6)

式中： ${\rho _{{\rm{air}}}}{\rm{ = }}1.222$ kg/m³为空气密度；C_m为空气阻尼系数；U_m为定常风的平均风速； $U\left( t \right)$ 为随时间变化的阵风风速；A_L船舶横向受风面积；H_C为从风作用中心到波浪作用中心的距离。

阵风谱函数采用Davenport谱，表示如下：

${S_{{\rm{wind}}}}\left( {{\omega _i}} \right) = 4K \cdot \frac{{U_m^2}}{{{\omega _i}}} \cdot \frac{{X_D^2}}{{{{\left( {1 + X_D^2} \right)}^{\frac{4}{3}}}}}\text{。} $

(7)

其中： $K = 0.003$ ， ${X_D} = 600\frac{{{\omega _i}}}{{{{\pi }}{U_m}}}$ 。

图1（a）和图1（b）所示分别为风速 ${U_m} = 25$ m/s时波浪谱与阵风谱函数图像。

非线性阻尼一般用随机等效线性方法近似，横摇阻尼系数α的取值按下式进行：

$\alpha \left( {{\sigma _{\dot \varphi }}} \right){\rm{ = }}\mu {\rm{ + }}\sqrt {\frac{2}{{{\pi }}}} \beta {\sigma _{\dot \varphi }}\text{。}$

(8)

式中： ${\sigma _{\dot \varphi }}$ 为横摇运动角速度的标准差，μ和β为一、三次项的阻尼系数。

1.2 复原力矩项分段线性处理

分段线性化方法最早由Belenky^[11]在1993年提出，使得船舶在波浪中的倾覆概率可以通过解析解进行研究。

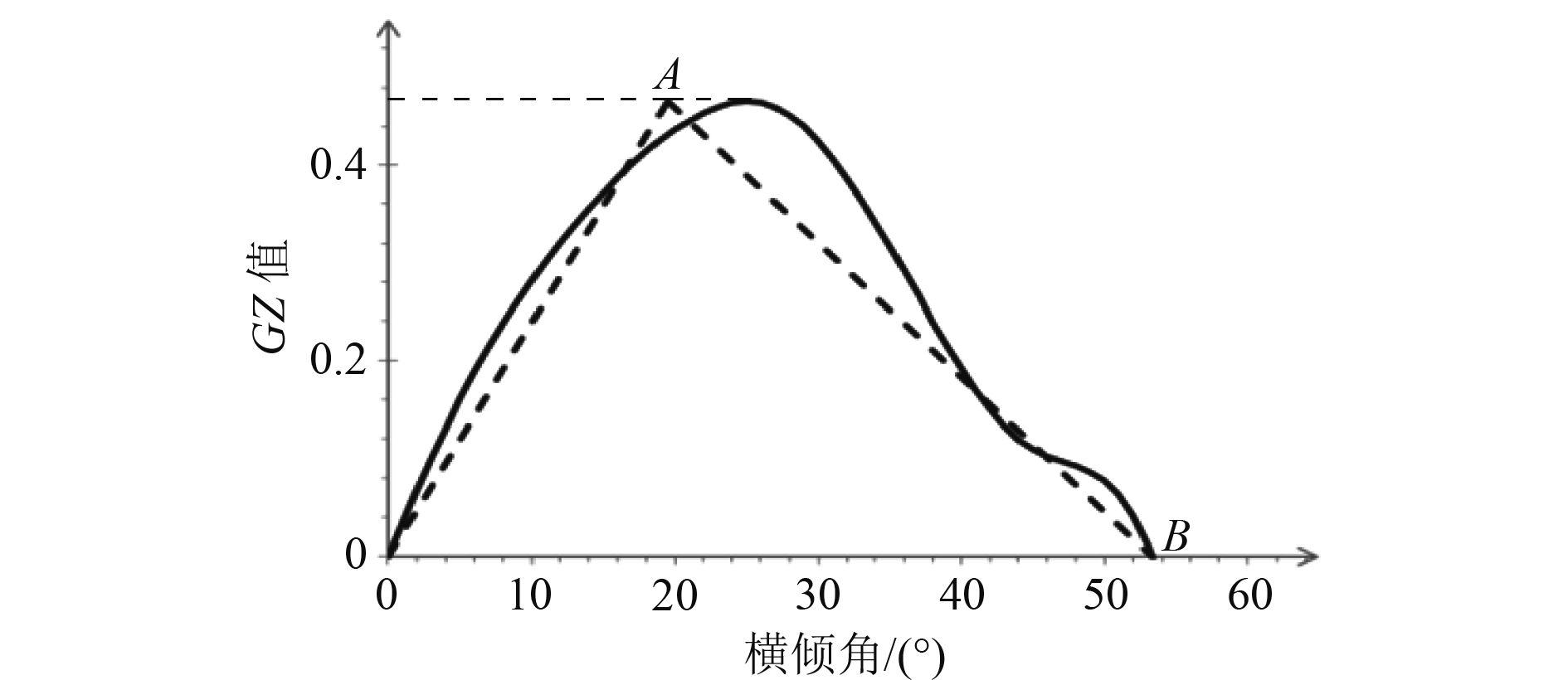
GZ曲线的分段线性按照如下原则^[6]进行计算：分段线性三角形的高与原始GZ曲线的最大复原力臂 $G{Z_{\max }}$ 保持一致，三角形的底边长等于静稳性曲线的稳距，三角形与坐标轴所围成的面积与静稳性曲线下的面积（倾斜后船舶具有的位能）近似相等，如图2所示。

等效的稳性高计算式如下：

$G{M^*} = \frac{2}{{\varphi _{m0}^2}}\int_0^{{\varphi _{m0}}} {GZ(\varphi )} {\rm{d}}\varphi \text{。}$

(9)

将复原力臂曲线分段线性近似后，无因次的复原力臂曲线 $k{f_i}\left( \varphi \right)$ 即被分成2个区间。横倾角从0°到 ${\varphi _{m0}}$ 之间的区间，称之为Range 0；从 ${\varphi _{m0}}$ 到稳性消失角 ${\varphi _V}$ 之间的区间，称之为Range 1，如图3所示。

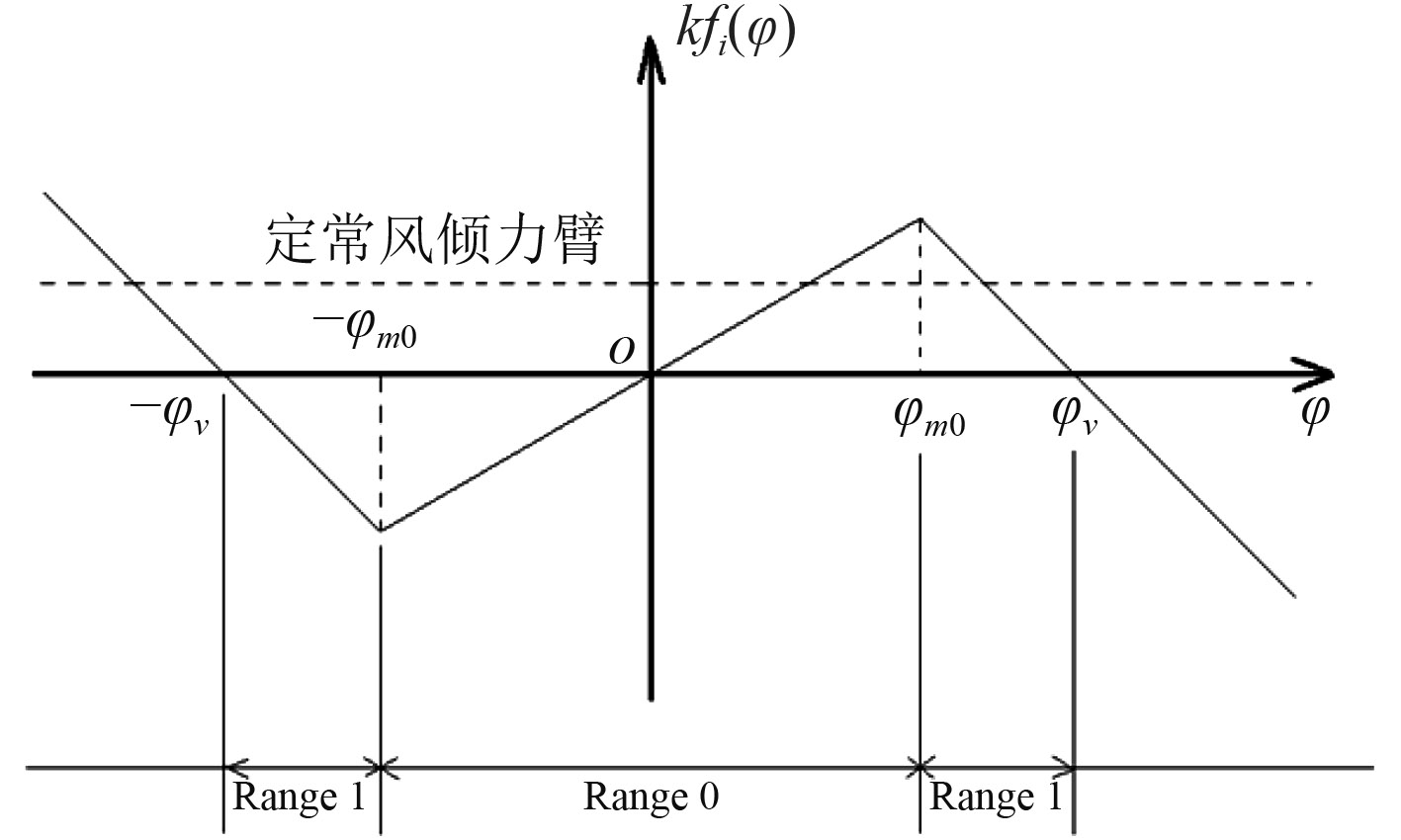
经过分段线性后，复原力矩系数 $k{f_i}\left( \varphi \right)$ 可表示如下：

$k{f_i}\left( \varphi \right) = \left\{ \begin{array}{l}k{f_0} \cdot \varphi \begin{array}{*{20}{c}}{}&{}&{,0 < \varphi \leqslant {\varphi _{m0}}},\end{array}\\k{f_1} \cdot \left( {{\varphi _V} - \varphi } \right),{\varphi _{m0}} < \varphi \leqslant {\varphi _V},\end{array} \right.\begin{array}{*{20}{c}}{{\rm{Range}}0}\\{{\rm{Range}}1}\end{array}{\text{顺风}} ;$

(10)

$k{f_i}\left( \varphi \right) = \left\{\!\!\! \begin{array}{l}k{f_0} \cdot \varphi \begin{array}{*{20}{c}}{}&{, - {\varphi _{m0}} \leqslant \varphi < 0},\end{array}\\k{f_1} \cdot \left( { - {\varphi _V} - \varphi } \right), - {\varphi _V} \leqslant \varphi < - {\varphi _{m0}},\end{array} \right.\begin{array}{*{20}{c}}\!\!\!\! {{\rm{Range}}0}\\\!\!\!\! {{\rm{Range}}1}\end{array}{\text{逆风}}\text{。}$

(11)

1.3 横摇运动方程解析解

将1-DOF无因次化的横摇运动方程（1）的各非线性系数线性近似后，将简化为关于横摇角 $\varphi $ 的2阶常系数线性非齐次微分方程。经过计算，得到方程（1）在每个阶段的 $\varphi \left( t \right)$ 解析解如下（式中各参数表达式详见文献[17]）：

1）Range 0阶段

${\varphi _0}\left( t \right) \!=\! \frac{{{{\dot \varphi }_0}}}{{{k_1}}}{{\rm{e}}^{ - \alpha t}}\sin \left( {{k_1}t} \right) \!+\! \sum\limits_{i = 1}^{{N_W}} {{q_{ai}}\sin \left( {{\omega _i}t + {\psi _i} \!+\! {\delta _{0i}}} \right)} \!+\! {\varphi _D}, $

(12)

其中： ${k_1} = \sqrt {\omega _0^2k{f_0} - {\alpha ^2}} $ 为振荡衰减项的圆频率； ${\dot \varphi _0}$ 为初始横摇角速度； ${\varphi _D}$ 为定常风倾力矩引起的固定横摇角； ${q_{ai}}$ 为横摇稳态响应项的幅值； ${\delta _{0i}}$ 为相频响应函数； ${\psi _i}$ 为 $0 \sim 2{\rm{\pi }}$ 随机变化的初相角。

2）Range 1阶段

${\varphi _1}\left( t \right) = A{{\rm{e}}^{{\lambda _1}t}} + B{{\rm{e}}^{{\lambda _2}t}} + \sum\limits_{i = 1}^{{N_W}} {{p_{ai}}\sin \left( {{\omega _i}t + {\psi _i} + {\delta _{1i}}} \right)} + {\varphi '_D}, $

(13)

其中， ${\lambda _{1,2}} = - \alpha \pm \sqrt {{\alpha ^2} + \omega _0^2k{f_1}} $ 为齐次方程的特征根；A，B为微分方程通解的系数； ${\varphi '_D}$ 为定常风倾力矩引起的固定横摇角； ${p_{ai}}$ 为稳态响应项的幅值； ${\delta _{1i}}$ 为相频响应函数。

2 倾覆概率计算模型 2.1 倾覆条件

分段线性化方法将船舶的横摇运动分为2个区间进行考虑：

对于Range 0阶段的解析式（12），可以看出自由横摇运动幅值 $\displaystyle\frac{{{{\dot \varphi }_0}}}{{{k_1}}}{{\rm{e}}^{ - \alpha t}}$ 随时间推移逐渐收敛，C₁₁船横摇角时历如图4所示，即认为这种情况不属于引起船舶倾覆的危险事件。

对于Range 1阶段，式（13）右端中 $A{{\rm{e}}^{{\lambda _1}t}}$ 是一个不收敛的项，即会随着时间推移出现横摇角度发散的情况。A的定义具体如下：

$A = \frac{1}{{{\lambda _1} - {\lambda _2}}}\left[ {\left( {{{\dot \varphi }_1} - {{\dot p}_1}} \right) - {\lambda _2}\left( {{\varphi _{m0}} - {{\varphi '}_D} - {p_1}} \right)} \right], $

(14)

$\left\{ \begin{array}{l}A > 0{\rm{ }}\mathop {\lim }\limits_{t \to \infty } \varphi \left( t \right) = + \infty, \\A < 0{\rm{ }}\mathop {\lim }\limits_{t \to \infty } \varphi \left( t \right) = - \infty, \\A = 0{\rm{ }}\left| {\varphi \left( t \right)} \right| < p + {\varphi _V}{\text{。}}\end{array} \right.$

(15)

顺风条件下，A>0为当横摇角从Range 0增大进入Range 1后，横摇运动幅值会随着时间推移继续增大，直至船舶倾覆。A<0和A=0为当横摇角从Range 0增大进入Range 1后，横摇运动幅值会逐渐减小直至返回Range 0，这种情况安全。

逆风条件下，A>0和A=0趋于安全，A<0代表船舶发生倾覆。

这样船舶倾覆概率问题就转换为求解横摇运动解析解中的参数A的取值范围。如果定义单位时间内船舶倾覆为事件F，船舶横摇进入顺风Range 1阶段为事件L，船舶横摇进入逆风Range 1阶段为事件W，A>0为事件A₊，A<0为事件A_-，则事件F发生概率可以写成：

$\begin{split}& P(F) = P({A_ + }L + {A_ - }W) = P(L) \cdot P\left( {{A_ + }\left| L \right.} \right) +\\ & P(W) \cdot P\left( {{A_ - }\left| W \right.} \right),\end{split}$

(16)

定义顺风和逆风状态下单位时间内横摇角从Range 0增大到Range 1的概率分别为 ${u_l}$ 和 ${u_w}$ ，由于在Range 1阶段的横摇运动符合高斯过程(Gaussian Process)，所以 ${u_l}$ 与 ${u_w}$ 分别由以下2个公式确定(Price & Bishop, 1974) ^[18]：

${u_l} = \frac{1}{{2{\rm{\pi }}}}\sqrt {\frac{{{V_{\dot q}}}}{{{V_q}}}} \exp \left[ { - \frac{{{{\left( {{\varphi _{m0}} - {\varphi _{Dl}}} \right)}^2}}}{{2{V_q}}}} \right],$

(17)

${u_w} = \frac{1}{{2{\rm{\pi }}}}\sqrt {\frac{{{V_{\dot q}}}}{{{V_q}}}} \exp \left[ { - \frac{{{{\left( { - {\varphi _{m0}} - {\varphi _{Dw}}} \right)}^2}}}{{2{V_q}}}} \right], $

(18)

其中： ${\varphi _{Dl}}$ 和 ${\varphi _{Dw}}$ 分别为船舶在Range 0阶段顺风侧和逆风侧的静倾角； ${V_{\dot q}}$ 和 ${V_q}$ 分别为船舶在Range 0阶段的横摇角和横摇角速度方差。

对于参数A取值范围的概率问题，本文采用IMO推荐的简化计算方法^[17]，认为横摇运动进入Range 1时的初始横摇运动是一个小量，即 ${p_1}$ , ${\dot p_1}$ 等于0。此时参数A的概率密度函数可表达为：

$\left\{ \begin{array}{l}f\left( A \right) = \frac{{{{\left( {{\lambda _1} - {\lambda _2}} \right)}^2}\left( {A - {C_4}} \right)}}{{{V_{\dot q}}}}\exp \left[ {\frac{{{{\left( {{\lambda _1} - {\lambda _2}} \right)}^2}{{\left( {A - {C_4}} \right)}^2}}}{{2{V_{\dot q}}}}} \right],\\{C_4} = - \frac{{{\lambda _2}}}{{{\lambda _1} - {\lambda _2}}}\left( { - \frac{{{K_0}}}{{\omega _0^2k{f_1}}} - {\varphi _{m0}} + {\varphi _V}} \right),\end{array} \right.{\text{顺风}};$

(19)

$\left\{\!\!\!\! \begin{array}{l}f\left( A \right) = \frac{{{{\left( {{\lambda _1} - {\lambda _2}} \right)}^2}\left( {A - {C_4}} \right)}}{{{V_{\dot q}}}}\exp \left[ {\frac{{{{\left( {{\lambda _1} - {\lambda _2}} \right)}^2}{{\left( {A - {C_4}} \right)}^2}}}{{2{V_{\dot q}}}}} \right],\\{C_4} = - \frac{{{\lambda _2}}}{{{\lambda _1} - {\lambda _2}}}\left( { - \frac{{{K_0}}}{{\omega _0^2k{f_1}}} + {\varphi _{m0}} - {\varphi _V}} \right),\end{array} \right.{\text{逆风}}{\text{。}}\!\!\!\!\! $

(20)

最终通过计算：

$\left\{ \begin{array}{l}P\left( {{A_ + }\left| L \right.} \right) = \int_0^\infty {f\left( A \right)} {\rm{d}}A,\\P\left( {{A_ - }\left| W \right.} \right) = \int_{ - \infty }^0 {f\left( A \right)} {\rm{d}}A{\text{。}}\end{array} \right.$

(21)

即可得到参数A取值范围的概率。由以上各式即可求解单位时间内船舶的倾覆概率：

$\begin{split}{u_F} = &{u_{{\rm{cap}}l}} + {u_{{\rm{cap}}w}}=\\ &{u_l} \cdot P\left( {{A_ + }\left| L \right.} \right) + {u_w} \cdot P\left( {{A_ - }\left| W \right.} \right){\text{。}}\end{split}$

(22)

2.2 倾覆概率计算

经过2.1节的公式推导，得到了单位时间倾覆概率计算表达式，假设船舶的倾覆事件符合泊松分布，可得到给定暴露时间T内的倾覆概率：

$P\left( T \right) = 1 - {{\mathop{\rm e}\nolimits} ^{ - {u_{{\rm{cap}}}} \cdot T}}{\text{。}}$

(23)

3 样船计算与敏感性因素分析 3.1 样船模型

以C₁₁集装箱船（APL China号）和IMO稳性工作组提供的研究船型CEHIPAR 2792集装箱船为例，进行分析与计算。2艘样船的基本参数见表1与表2。取空气阻尼系数C_m=1.0，线性阻尼系数为0.003 81 v/s^–1。

3.2 GZ曲线分段线性化结果

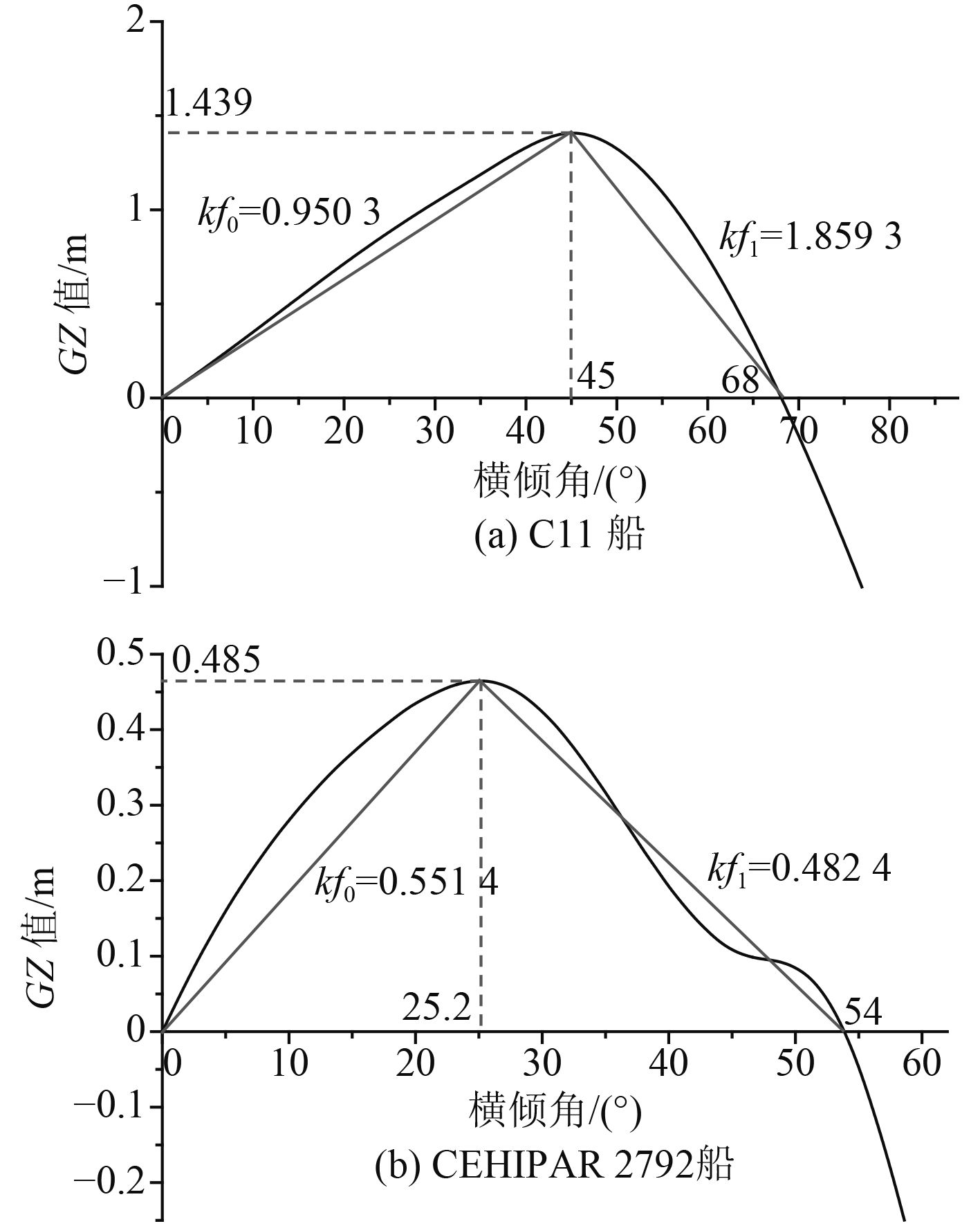
分别对C₁₁船与CEHIPAR 2792船在各自设计吃水下的GZ曲线进行分段线性近似，如图5所示。

3.3 倾覆概率敏感性因素分析 3.3.1 暴露时间

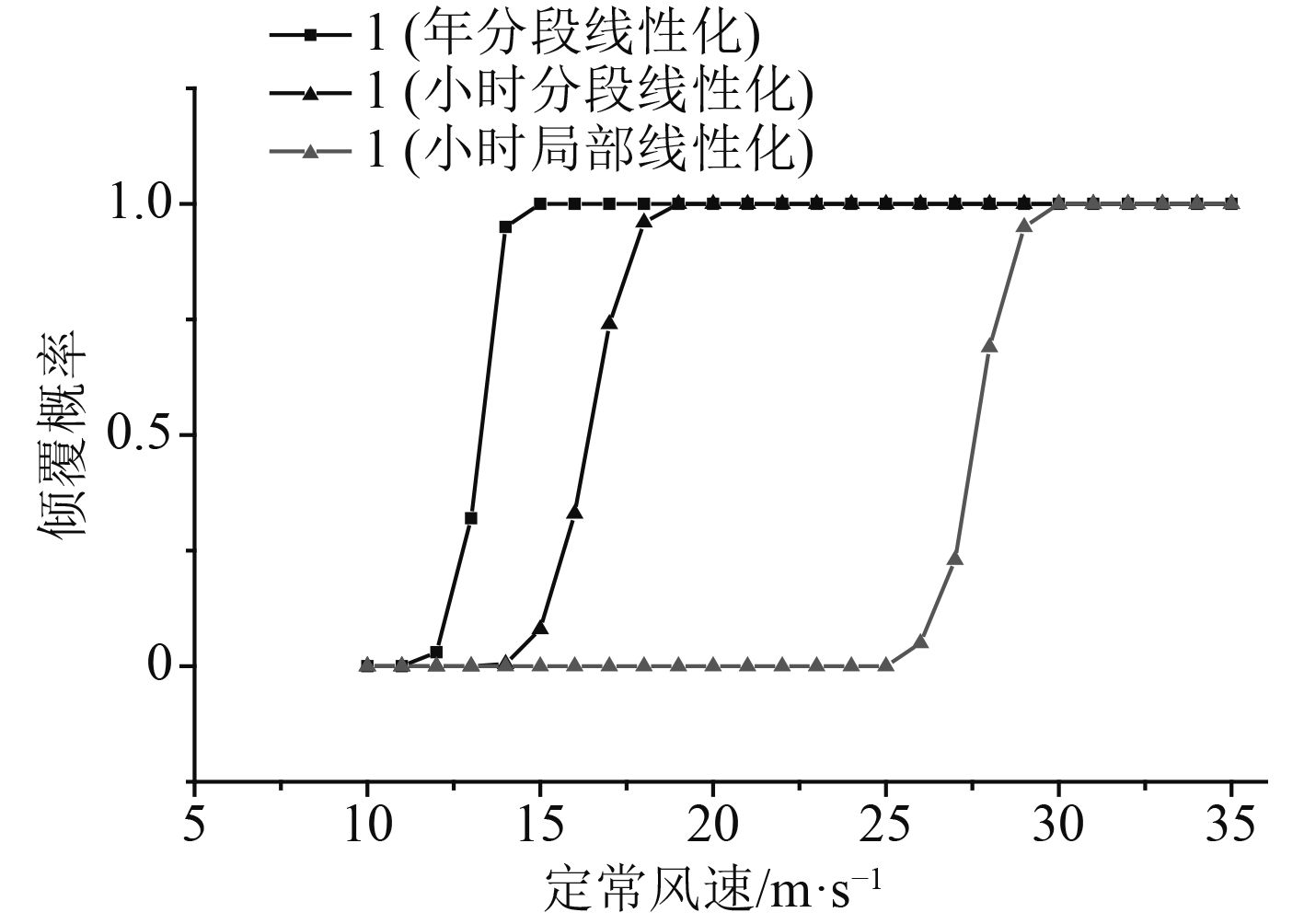
本节基于分段线性化方法，利用Matlab编制了相应的计算程序，计算了CEHIPAR 2792船在设计吃水载况下，暴露时间 ${T_{\exp 1}} = 1$ h和 ${T_{\exp 2}} = 1$ 年，定常风速取 $10 \sim 35\;{\rm{m}}/{\rm{s}}$ 范围内的倾覆概率。同时，将暴露时间为1 h的计算结果同局部线性化（具体计算过程见文献[3]）结果进行对比，如图6所示。

通过分段线性化和局部线性化方法计算CEHIPAR 2792船的倾覆概率，都能够得到一条具有当定常风速超过一定阈值后，船舶倾覆概率出现急剧上升特征的曲线。 ${T_{\exp 1}} = 1$ h的倾覆概率大幅增长对应的风速区间要大于 ${T_{\exp 2}} = 1$ 年，局部线性化方法计算所得的倾覆概率突增对应的风速区间要远大于分段线性化结果，这可能与分段线性化处理后船舶倾斜位能（GZ曲线下的面积）的减小有关。

3.3.2 波浪谱

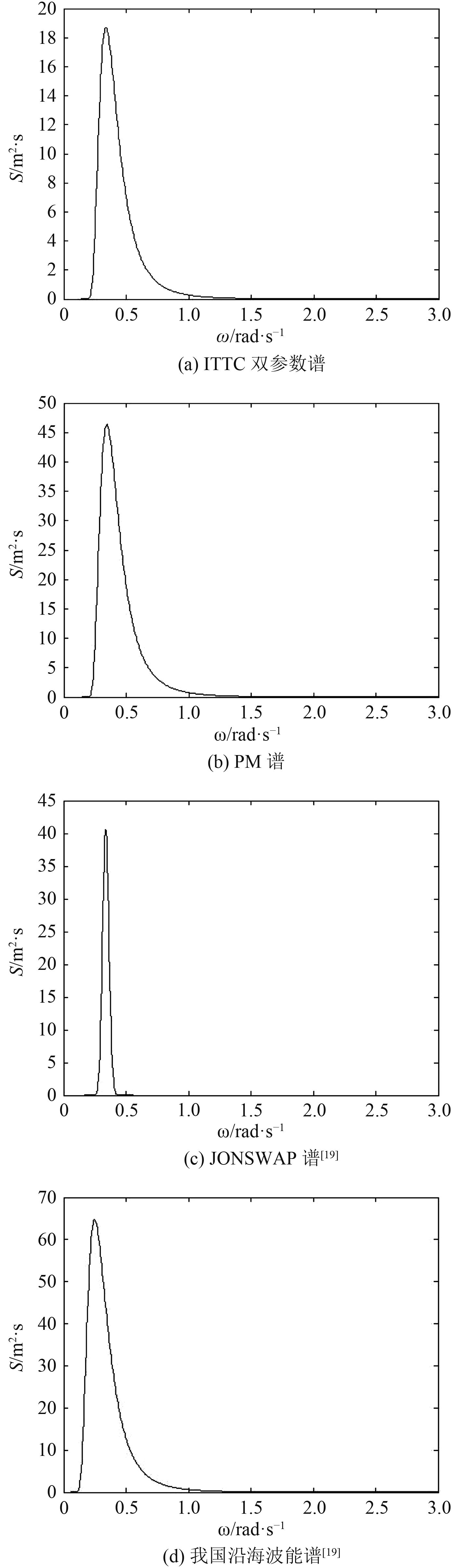
图7（a）~图7（d）所示为在定常风速均为U_m=25 m/s时4种常用的波浪谱函数图像。

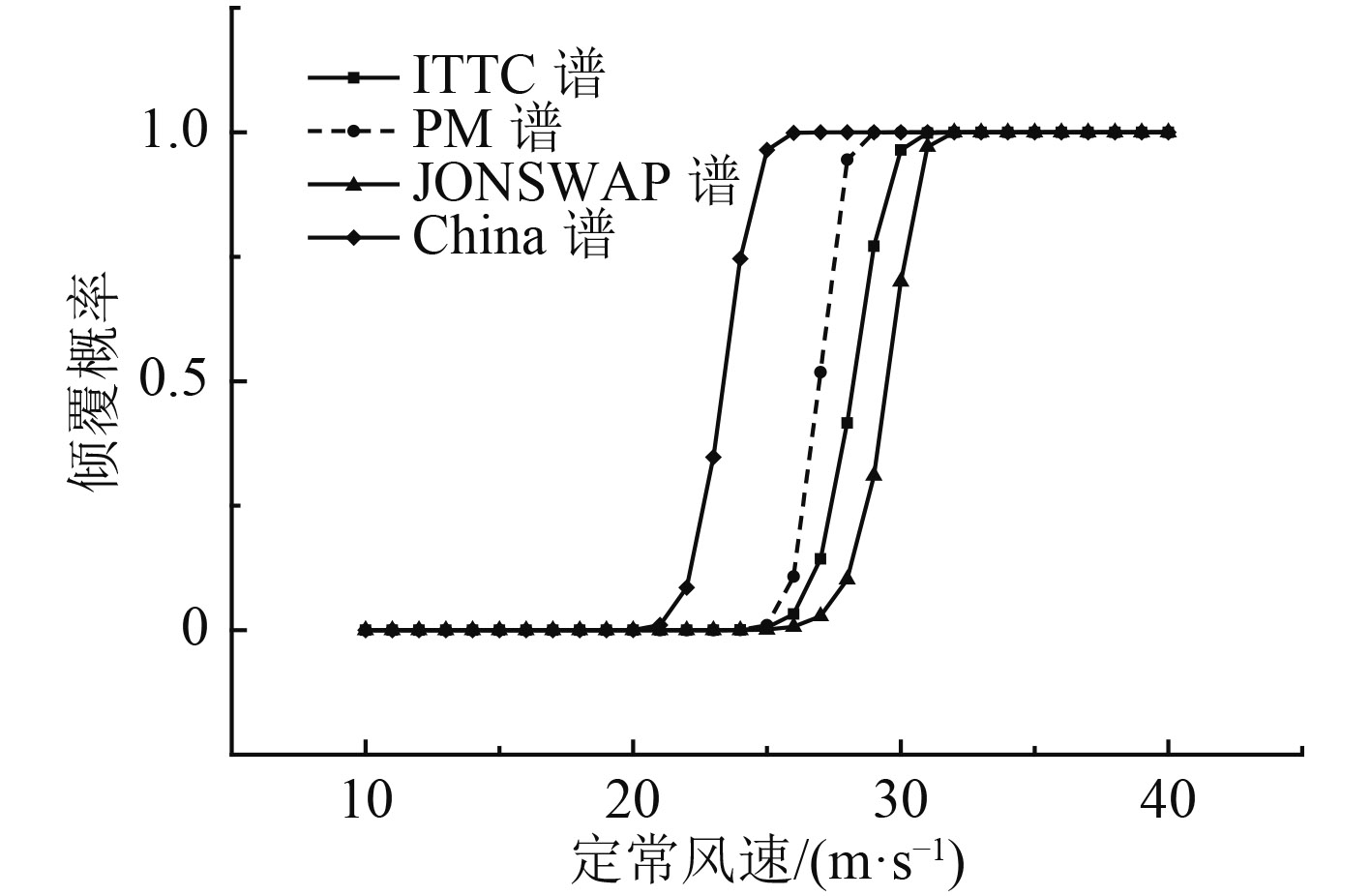
图8所示为分别采用这4种波浪谱计算C₁₁船在正常吃水下的倾覆概率。我国沿海波能谱的计算结果和其他3种谱的差别比较大，而且最为危险。应用JONSWAP谱的计算结果对船舶抵抗倾覆能力的评估最为乐观，ITTC双参数谱和PM谱则介于中间。对于我国沿海波能谱、PM谱、ITTC双参数谱，从三者波浪谱函数图像来看，其形态相近，我国沿海波能谱波峰幅值最大，因此波浪激励力矩也较大，相同定常风速下倾覆概率计算结果最大；JONSWAP谱虽然波能谱峰值很高，但波浪频率跨度很窄，波能很低，相同定常风速下倾覆概率计算结果最小。

3.3.3 GZ曲线分段点位置

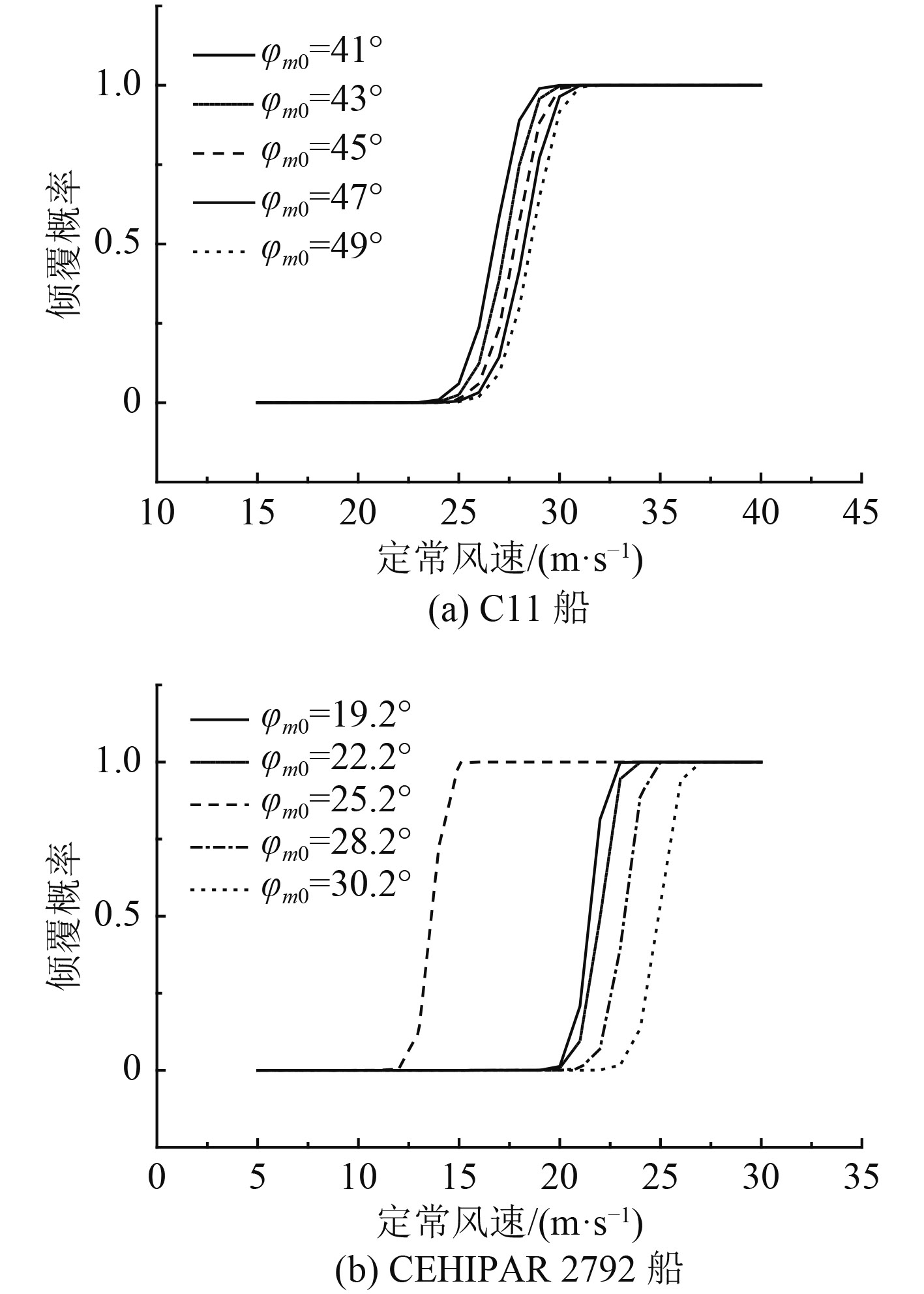
在1.2节中已经简要介绍了GZ曲线分段线性拟合的方式，但是对于分段三角形中回复力臂最大处横倾角 ${\varphi _{m0}}$ （即Range 0和Range 1的分界点）取法并没有做出规定。计算表明， ${\varphi _{m0}}$ 取值不同会影响倾覆概率的数值。图9（a）和图9（b）所示，分别为C₁₁船和CEHIPAR 2792船在正常吃水下通过适当平移分界点 ${\varphi _{m0}}$ 横坐标位置后得到的若干条倾覆概率曲线。

如图9（a）所示，随着 ${\varphi _{m0}}$ 取值的减小，计算结果趋于危险。但是总体来说，在曲线急剧上升区域内变化 ${\varphi _{m0}}$ 对C₁₁船倾覆概率的影响不是非常显著。

如图9（b）所示，改变 ${\varphi _{m0}}$ 的取值对CEHIPAR 2792船倾覆概率的影响要远大于C₁₁船。当 ${\varphi _{m0}}{\rm{ = }}25.2^\circ $ 时，曲线明显偏离总体变化趋势，向左突变，而25.2°正好是该船回复力臂最大值处的横倾角。

4 结　语

本文针对船舶在横风横浪中瘫船状态的大幅横摇运动，主要是基于IMO最新制定的瘫船稳性第2层衡准开展分析，利用分段线性化方法得到横摇运动方程的解析解，并据此进行倾覆概率的计算。可以得到以下结论：

1）GZ曲线分段线性近似法简化了横摇运动方程的非线性系数项，使得微分方程解析解的求解成为可能，且可以有效地计算船舶在横风横浪下的倾覆概率，计算结果相比局部线性化方法偏于危险。

2）对于分段线性化的计算，暴露时间越长，倾覆概率的计算结果越危险。

3）不同的波浪谱对倾覆概率的计算影响是存在的，应当根据海区特征选取适当的波浪谱。

4）对某些具有凹凸变化的GZ曲线的船型（如CEHIPAR 2792船），分段线性化分界点的取法对其倾覆概率的评估影响较大，从提高稳性衡准安全裕度的角度，建议将其取在GZ曲线顶点位置处。