环肋圆柱壳是典型的深海耐压结构,在结构设计时,在一定容积下减轻结构重量,提高结构装载重量,是深海耐压结构设计常常关心的问题。高强度钢材料屈服强度、抗拉强度比普通钢要高,在满足同样的结构强度、使用容积的情况下,结构设计中采用高强度钢材料,可以减少钢材使用量,进而减小结构的单位容积重量,故高强度钢在深海耐压结构中被广泛应用。
为了减轻环肋圆柱壳重量,需要对其进行优化设计。国内外学者对环肋圆柱壳优化方法进行了广泛的研究。Liang 等[1]提出了在稳定性和屈服强度约束条件下,受静水压力的潜艇耐压壳体结构重量最轻的优化设计方案。由于该设计问题属于离散变量多模态约束最小值问题,作者采用回溯程序设计方法进行求解,获得的优化设计方案的重量比原有模型重量减轻6.65%。Bagheri 等[2]采用遗传算法对环肋圆柱壳进行多目标优化设计,以最大固有频率和最小结构重量为目标函数,采用权重法将多目标转化为单目标,研究了权重系数、加强筋结构形式和设计变量的取值范围对优化结果的影响。
国内丁海旭等[3]对潜艇耐压船体进行优化设计,以结构重量和满应力设计为目标,建立单目标非线性约束优化的目标规划模型,求解连续与离散混合变量的最优解,并进行规整,获得了关于满应力设计和结构重量较轻的耐压船体设计方案。杨卓懿等[4]对环肋圆柱壳进行了优化,建立了强度计算的响应面模型,并采用罚函数法进行优化,获得了结构重量最轻的优化解。王燕[5]对潜艇耐压结构优化设计方法进行探索,采用有限元法对系列潜艇环肋骨圆柱壳进行强度和稳定性分析,分别建立了分析的二次响应面模型和Kringing近似模型,然后以重量为目标,采用混合整型优化方法对环肋圆柱壳进行优化设计,并进行了对比。
目前国内外环肋圆柱壳结构优化研究均是针对具体模型的优化,主要研究优化算法和优化过程,优化结果只适用于具体的设计模型,缺少对高强度钢材料通用性的优化成果,以指导环肋圆柱壳结构设计。本文首先建立了600 MPa级高强度钢环肋圆柱壳结构优化计算方法。以多学科优化软件Isight为平台,联合利用多岛遗传算法(MIGA)和序列二次规划法(NLPQL)对高强度钢环肋圆柱壳单位容积重量进行优化,得到了最小环肋圆柱壳单位容积重量、最优的半径厚度比与最大工作压力的关系曲线和拟合公式。
1 环肋圆柱壳无量纲化的强度稳定性计算方法适用于600 MPa级高强度钢环肋圆柱壳无量纲化的强度和稳定性计算方法,主要依据GJB/Z 21A-2001潜艇结构设计计算方法[6]和现代潜艇结构强度理论与试验[7]进行计算。计算时选用以下几个无量纲的变量
| $u = \frac{{\sqrt[4]{{3(1 - {v^2})}}}}{2}\frac{l}{{\sqrt {Rt} }}{\text{,}}$ | (1) |
| $\beta = \frac{{lt}}{A} = \frac{{lt}}{{(h{t_1} + b{t_2})}}{\text{。}}$ | (2) |
其中
| ${P_j} = K{P_{jx}}{\text{,}}$ | (3) |
式中:
计算下列参数:
| $\gamma = 0.5\sqrt {3(1 - {v^2})} {P_j}/E(R/t){\text{,}}$ | (4) |
其中
| ${u_1} = u\sqrt {1 - \gamma } {\text{,}}$ | (5) |
| ${u_2} = u\sqrt {1 + \gamma } {\text{,}}$ | (6) |
| ${F_5} = {u_2}sh2{u_1} + {u_1}sh2{u_2}{\text{,}}$ | (7) |
| ${F_1} = \sqrt {1 - {\gamma ^2}} (ch2{u_1} - \cos 2{u_2})/F_5{\text{,}}$ | (8) |
| ${F_4} = 2(1 - 0.5v)({u_1}ch{u_1}\sin {u_2} + {u_2}sh{u_1}\cos {u_2})/{F_5}{\text{,}}$ | (9) |
| ${K_2} = 1 - {F_4}/(1 + \beta {F_1}){\text{,}}$ | (10) |
| ${K_1} = 0.5 + {F_2}/(1 + \beta {F_1}){\text{,}}$ | (11) |
| ${K_f} = (1 - v/2)\beta {F_1}/(1 + \beta {F_1}){\text{,}}$ | (12) |
肋骨根部壳板内表面的纵向应力:
| ${\sigma _1} = {K_1}{P_j}(R/t)/{\sigma _s}{\text{,}}$ | (13) |
其中
跨中壳板的中面周向应力:
| $\sigma _{_2}^0 = {K_2}{P_j}(R/t)/{\sigma _s}{\text{,}}$ | (14) |
肋骨平均应力:
| ${\sigma _f} = {K_f}{P_j}(R/t)/{\sigma _s}{\text{。}}$ | (15) |
相邻肋骨壳板欧拉失稳压力:
| ${P_{e1}} = \left\{ \begin{array}{l}0.6E/{(R/t)^2}/(u - 0.37){\text{,}}\;\;\;\;u \geqslant 1{\text{,}}\\1.21E{(R/t)^2} {\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < u < 1{\text{,}}\end{array} \right.$ | (16) |
| ${\sigma _{e1}} = {P_{e1}}R/t{\text{,}}$ | (17) |
| ${\tau _1} = {\sigma _{e1}}/{\sigma _s}{\text{。}}$ | (18) |
当为600 MPa级高强度钢时,系数
| ${C_{s1}} = \left\{ \begin{aligned}{l}0.044\,42\tau _1^5 - 0.476\,5\tau _1^4 + 1.985\tau _1^3 - 3.905\tau _1^2 +\\ 3.214{\tau _1} + 0.084\,22,\;\;0.75 \leqslant {\tau _1} \leqslant 3{\text{,}}\\1{\text{,}}\;\;\;\;\;\;\;\;\;\;0 < {\tau _1} < 0.75{\text{。}}\end{aligned} \right.$ | (19) |
系数
| ${C_{g1}} = \left\{ \begin{array}{l}1{\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < u \leqslant 1{\text{,}}\\0.75{\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1 < u \leqslant 2{\text{,}}\\1.25 - 0.25u{\text{,}}\;\;\;\;\;\;\;\;\;u > 2{\text{。}}\end{array} \right.$ | (20) |
肋间壳板失稳临界压力:
| ${P_{cr1}} = {C_{g1}}{C_{s1}}{P_{e1}}{\text{,}}$ | (21) |
| $\alpha = \pi /(L/R){\text{,}}$ | (22) |
其中本例优化中
| $b/l = \frac{{0.5(b/t)\sqrt[4]{{3(1 - {v^2})}}}}{{u(R/t)}}{\text{,}}$ | (23) |
| ${t_1}/l = \frac{{0.5{t_1}/{t_0}\sqrt[4]{{3(1 - {v^2})}}}}{{u(R/t)}}{\text{。}}$ | (24) |
肋骨型心具体壳板表面高度与厚度之比:
| $\begin{align}{y_0}/t = \frac{\begin{array}{l}(b/t)({t_2}/t)(0.5{t_2}/t + h/t + 0.5) + \\(h/t)({t_1}/t)(0.5h/t + 0.5)\end{array}}{{(h/t)({t_1}/t) + (b/t)({t_2}/t)}}{\text{,}}\end{align}$ | (25) |
| $\begin{split}&I/{R^3}l = \displaystyle\frac{{{I_0} + {{({y_0} + 0.5t)}^2}ltA/(lt + A) + l{t^3}/12}}{{{R^3}l}}=\\&\displaystyle\frac{b}{{12l}}\displaystyle\frac{{{{({t_2}/t)}^3}}}{{{{(R/t)}^3}}} + \displaystyle\frac{{{t_1}}}{{12l}}\displaystyle\frac{{{{(h/t)}^3}}}{{{{(R/t)}^3}}} + \displaystyle\frac{{{{({y_0}/t + 0.5)}^2}}}{{(1 + \beta ){{(R/t)}^3}}} + \displaystyle\frac{1}{{12{{(R/t)}^3}}}{\text{。}}\!\!\!\end{split}$ | (26) |
其中
| $\begin{array}{l}U = \displaystyle\frac{{0.535{t^3}L}}{{I/l\sqrt {R(t + A/l)} }}=\\\;\;\; \!\! \displaystyle\frac{{0.535\sqrt {R/t} L/R}}{{[\displaystyle\frac{b}{{12l}}{{(\displaystyle\frac{{{t_2}}}{t})}^3} \!\!+\!\! \displaystyle\frac{{{t_1}}}{{12l}}{{(\displaystyle\frac{h}{t})}^3} \!\!+\!\! {{(\displaystyle\frac{{{y_0}}}{t} \!+\! 0.5)}^2}/(1 \!+\! \beta ) \!+\! 1/12]\sqrt {1 \!\!+\!\! 1/\beta } }}{\text{。}}\end{array}$ | (27) |
舱段间总体失稳欧拉力
| ${P_{e2}} = \displaystyle\frac{E}{{{n^2} - 1 + 0.5{\alpha ^2}}}[\displaystyle\frac{{{\alpha ^4}}}{{{{({\alpha ^2} + {n^2})}^2}\displaystyle\frac{R}{t}}} + \displaystyle\frac{I}{{{R^3}l}}{({n^2} - 1)^2}]{\text{,}}$ | (28) |
可以看出,
| ${\tau _2} = \frac{{{\sigma _2}}}{{{\sigma _s}}} = \frac{{0.95{P_{e2}}R}}{{(t + A/l)}} = \frac{{0.95{P_{e2}}(R/t)\beta }}{{(1 + \beta ){\sigma _s}}}{\text{。}}$ | (29) |
当为600 MPa级高强度钢时,系数
| ${C_{s2}} = \left\{ \begin{split}(0.04442\tau _2^5 - 0.4765\tau _2^4 + 1.985\tau _2^3 - 3.905\tau _2^2 + \\ 3.214{\tau _2} + 0.08422) \times 0.9{\text{,}}\;\;\;0.75 \leqslant {\tau _2} \leqslant 3{\text{,}}\\0.9{\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < {\tau _2} < 0.75{\text{。}}\!\!\!\end{split} \right.$ | (30) |
| ${C_{g2}} = \left\{ \begin{array}{l}1 - 0.14U{\text{,}}\;\;\;\;\;\;\;\;0 < U < 1.2{\text{,}}\\0.83{\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;U \geqslant 1.2{\text{。}}\end{array} \right.$ | (31) |
舱段间失稳临界压力:
| ${P_{cr2}} = {C_{g2}}{C_{s2}}{P_{e2}}{\text{。}}$ | (32) |
选取7个无量纲的设计变量
查阅相关资料,设计变量取值范围如下:
| $\begin{array}{l}0 < R/t < 150{\text{,}}1 < b/t < 5{\text{,}}0 < \beta < 5{\text{,}}2 < h/t < 15{\text{,}}\\0 < {t_1}/t < 1{\text{,}}0 < {t_2}/t < 3{\text{,}}0 < u < 3{\text{。}}\end{array}$ |
单位容积重量为目标函数:
| $\min f = \min \{ 2\delta \left( {1 + \frac{1}{\beta }} \right)/(R/t)\}{\text{,}} $ | (33) |
其中
1)强度约束
跨中壳板中面周向应力:
| $\sigma _2^0 \leqslant {k_1}{\sigma _s} {\text{或}} {g_1} = \sigma _2^0 - {k_1}{\sigma _s} \leqslant 0{\text{,}} $ | (34) |
对于600 MPa级高强度钢
肋骨根部壳板内表面纵向应力:
| ${\sigma _1} \leqslant 1.15{\sigma _s} {\text{或}} {g_2} = {\sigma _1} - 1.15{\sigma _s} \leqslant 0{\text{,}} $ | (35) |
肋骨平均应力:
| ${\sigma _f} \leqslant 0.6{\sigma _s} {\text{或}} {g_3} = {\sigma _f} - 0.6{\sigma _s} \leqslant 0{\text{。}} $ | (36) |
2)稳定性约束
肋间壳板失稳临界压力:
| ${P_{cr1}} \geqslant {P_j} {\text{或}}{g_4} = {P_j} - {P_{cr1}} \leqslant 0{\text{,}} $ | (37) |
舱段总体失稳临界压力:
| ${P_{cr2}} \geqslant 1.2{P_j} {\text{或}} {g_5} = 1.2{P_j} - {P_{cr2}} \leqslant 0{\text{,}} $ | (38) |
3)几何约束
肋骨高度与壳板半径之比:
| $\frac{h}{R} \leqslant 0.12 {\text{或}} {g_6} = \frac{h}{R} - 0.12 \leqslant 0{\text{。}} $ | (39) |
该优化问题属于连续型变量约束优化问题,联合运用多岛遗传算法(MIGA)和序列二次规划法(NLPQL)进行优化,采用多岛遗传算法进行全局搜索,得到一个最优解,然后在该最优解基础上采用进一步局部寻优,从而得到满足约束条件单位容积重量最轻的设计方案。
多岛遗传算法是全局优化算法的一种,它能求解全局最优解,避免了在局部区域搜索;同时它只评价设计点,不计算任何函数的梯度,适合处理离散型和连续性设计变量。相比传统遗传算法,它将每一代的种群划分为几个“岛”,每个“岛”都进行传统遗传算法操作,岛与岛之间有个体发生“迁移”,这使其具有更优良的全局求解能力。
序列二次规划法(NLPQL)能够处理设计变量实型问题。NLPQL算法将目标函数以二阶泰勒级数展开,并把约束条件线性化,通过解二次规划得到下一个设计点。该方法能够有效地探索初始设计点周围局部区域,如果设计空间是连续单峰的形态,能够沿最快下降方向快速搜索。
2.5 优化过程本文采用Isight软件对强度和稳定性计算模型进行集成,然后在Isight软件优化算法下进行驱动优化,图1为Isight对环肋圆柱壳进行确定性优化的流程图。

|
图 1 环肋圆柱壳确定性优化流程图 Fig. 1 Deterministic optimization process of ring-stiffened cylindrical shell |
表1列出了600 MPa级高强度钢环肋圆柱壳单位容积重量优化结果,从表1可以看出,
|
|
表 1 600 MPa级高强度钢环肋圆柱壳单位容积重量优化结果 Tab.1 Weight to Volume Optimization results of the 600 MPa ring-stiffened cylindrical high-strength steel shell |
为了研究600 MPa级高强度钢环肋圆柱壳
从统计学角度,一项试验中欲考察的变量称为因子或因素,因子被考察的范围称为试验范围,试验结果称为响应(Response)或输出(Output),在试验范围内,因素所取的值称为水平。常用的试验设计方法有全因子设计、正交设计、中心组合设计、拉丁方设计和最优拉丁方设计等。对于因子数目较大时,可以采用拉丁方设计或最优拉丁方设计[8],拉丁方设计中每个因子的设计空间等分
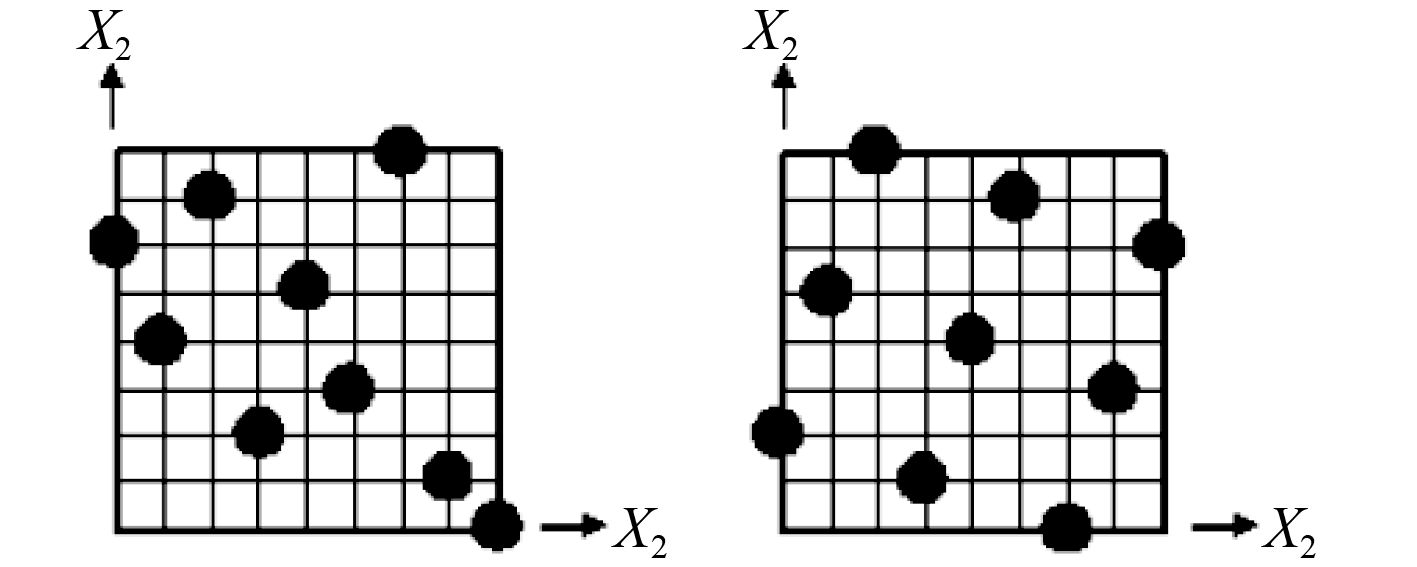
|
图 2 拉丁方设计(左)和最优拉丁方设计(右) Fig. 2 Latin square design (left) and optimal Latin square design (right) |
本文采用最优拉丁方进行试验设计,取500个取样点,对每个采样点进行单位容积重量计算,然后进行各变量之间的相关性分析,得到单位容积重量
从图3可以看出,单位容积重量与约束
从图4可以看出,
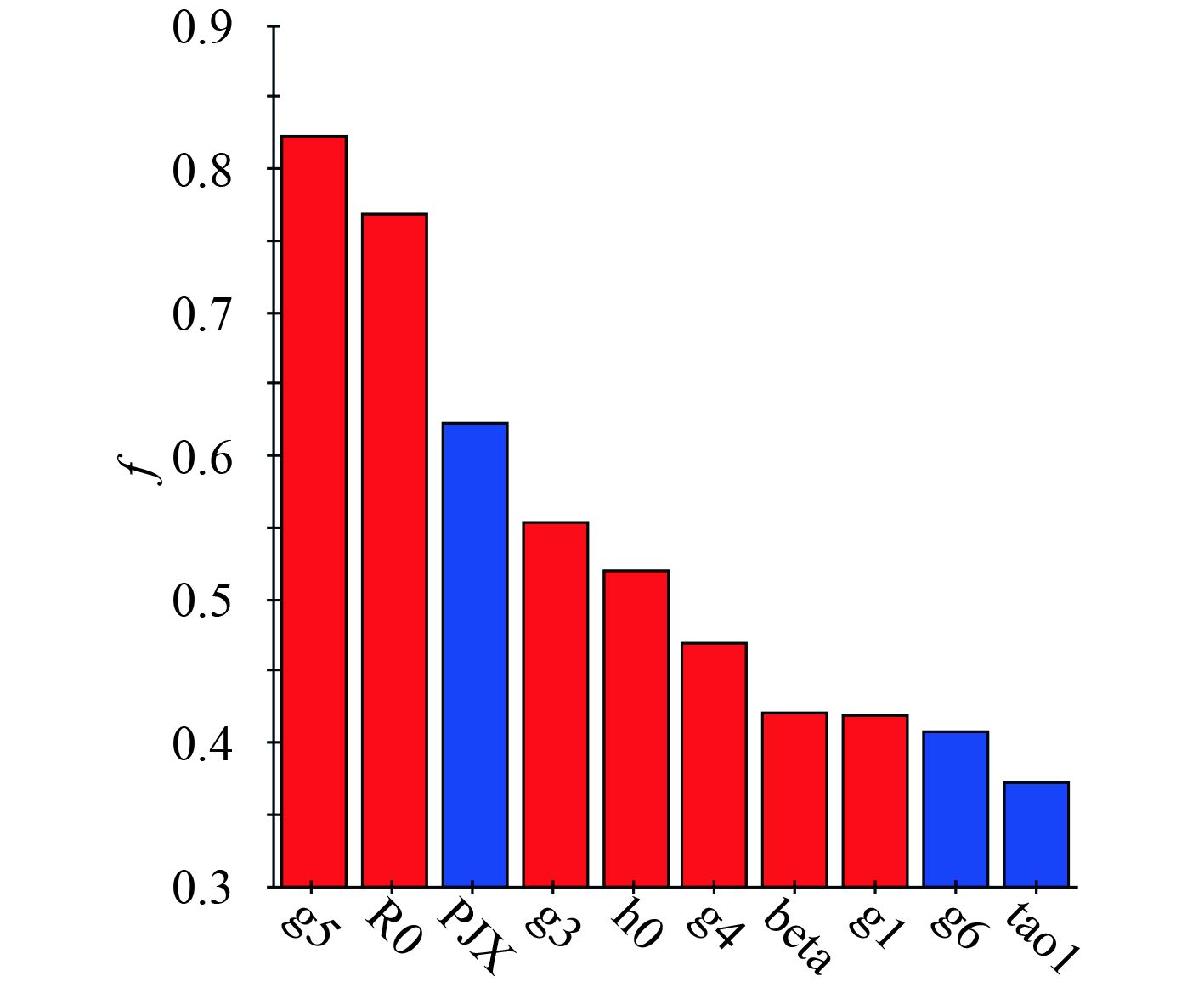
|
图 3
|
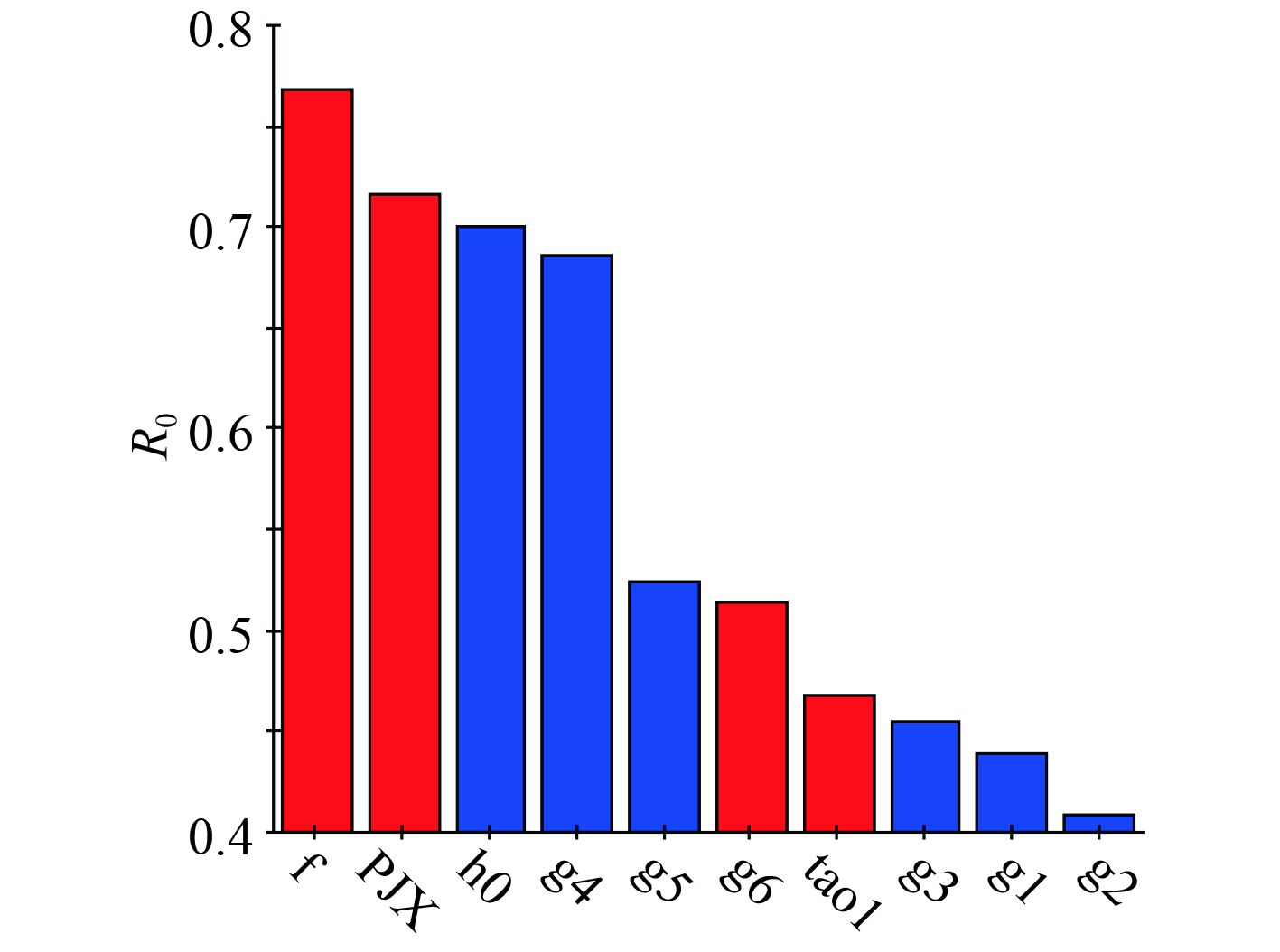
|
图 4
|
从图5可以看出,
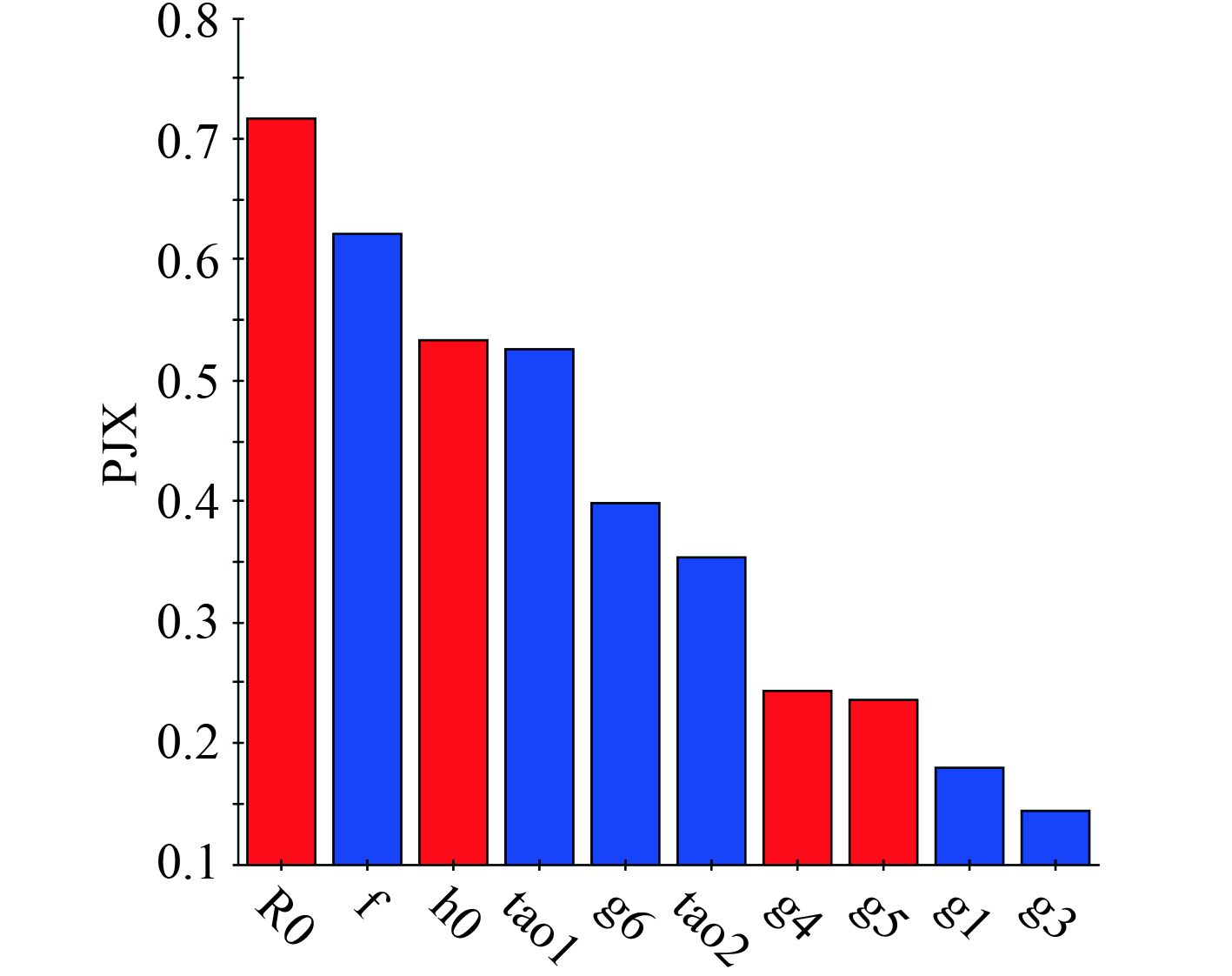
从图6可以看出,
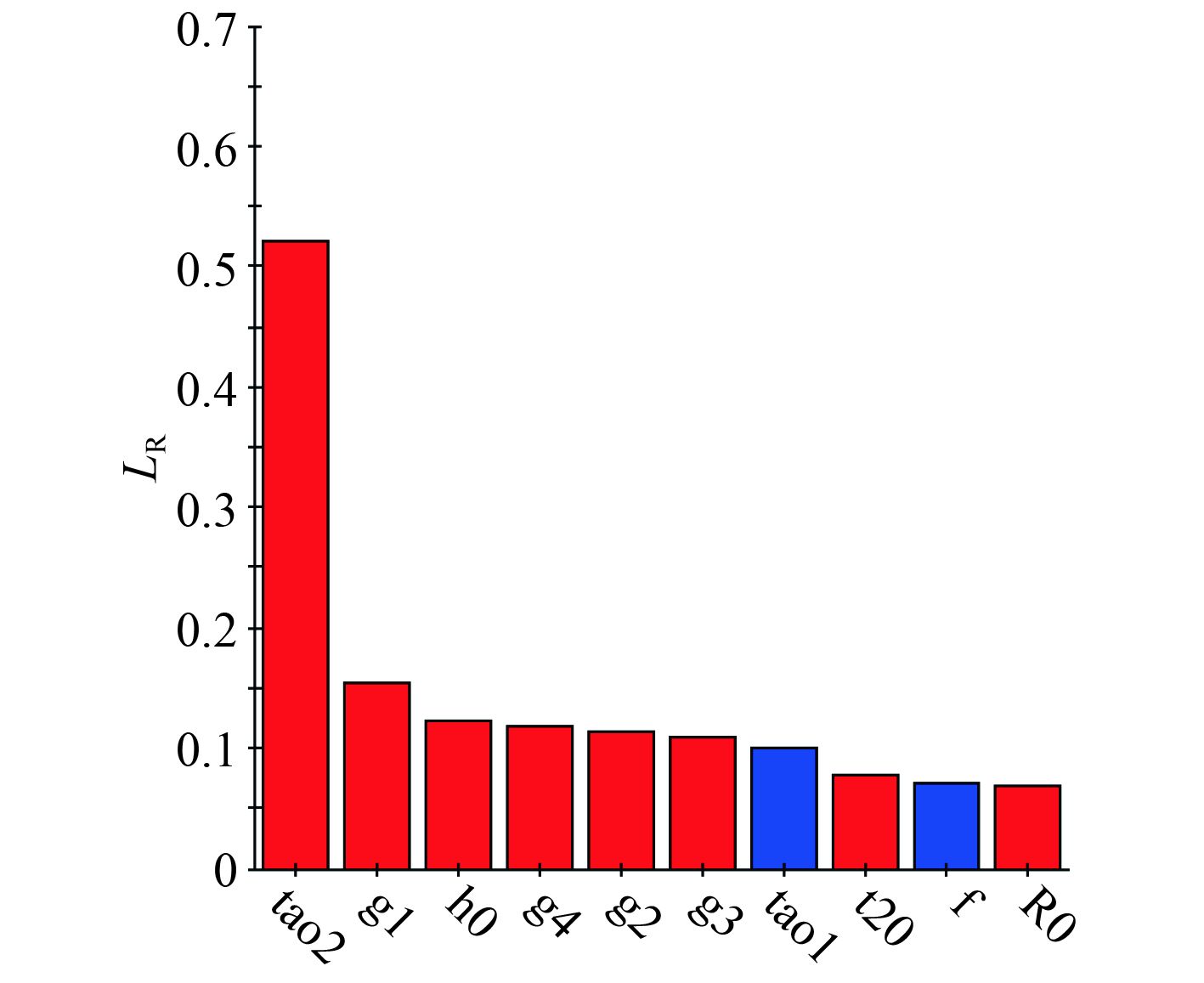
|
图 5
|
|
图 6
|
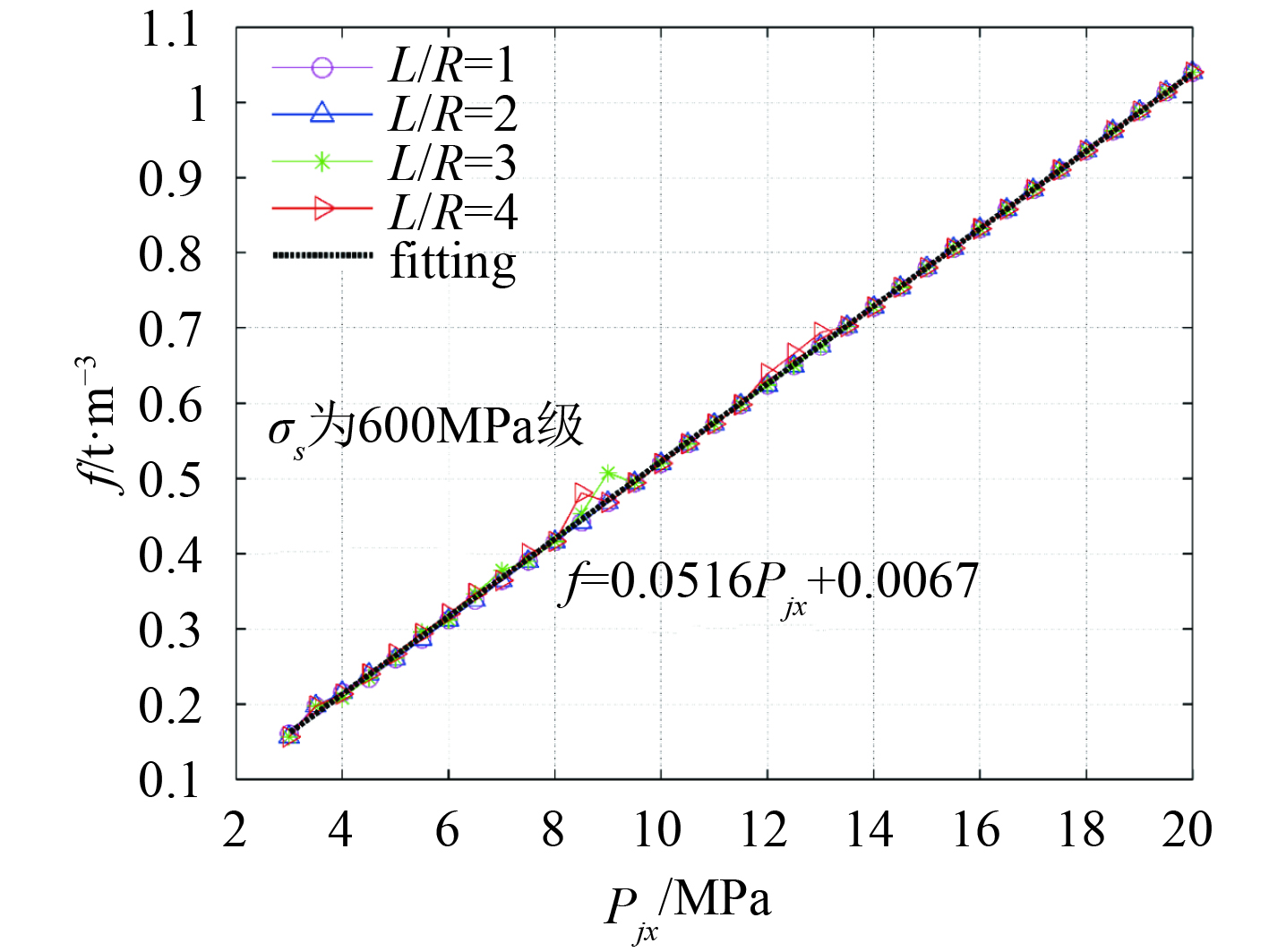
图7为不同的
| $f = 0.0516{P_{jx}} + 0.0067{\text{。}} $ | (40) |
图8为在不同的
| ${(\frac{R}{t})_{opt}} = 363.02P_{jx}^{ - 1.002}{\text{。}} $ | (41) |
|
图 7
600 MPa级高强度钢环肋圆柱壳
|

|
图 8
600 MPa级高强度钢环肋圆柱壳
|
1)本文依据GJB/Z 21A-2001潜艇结构设计计算方法建立了600 MPa级高强度钢环肋圆柱壳强度和稳定性无量纲的计算方法,该方法可用于环肋圆柱壳强度和稳定性校核和优化设计。
2)在上述计算方法的基础上对环肋圆柱壳单位体积重量进行优化,通过多岛遗传算法(MIGA)整体寻优和序列二次规划法(NLPQL)局部寻优,得到了在不同的圆柱壳长度半径比、不同的最大工作压力下,600 MPa级高强度钢环肋圆柱壳最小的单位容积重量和对应的最优的半径厚度比,在圆柱壳长度半径比为1,2,3,4情况下分别绘制了600 MPa级、高强度环肋圆柱壳最大工作压力与最小的单位容积重量关系曲线,最大工作压力与最优的半径厚度比关系曲线,并证明了最小的单位容积重量、最优的半径厚度比仅和材料、最大工作压力有关,和圆柱壳长度半径比关系不大。
3)根据上述优化结果,提出了计算600 MPa级高强度环肋圆柱壳最小的单位容积重量、最优的半径厚度比的拟合公式,该公式可以用于评估高强度钢环肋圆柱壳单位容积重量是否最优,可以计算单位容积重量最优情况下的半径厚度比,指导深海耐压环肋圆柱壳优化设计与评估。
| [1] | LIANG C C, HSU C Y, TSAI H R. Minimum weight design of submersible pressure hull under hydrostatic pressure[J]. Compurers & Structures, 1996, 63(2): 187–201. |
| [2] | BAGHERI M, JAFARI A A, SADEGHIFAR M. Multi-objective optimization of ring stiffened cylindrical shells using a genetic algorithm[J]. Journal of Sound and Vibration, 2011, 330: 374–384. |
| [3] |
丁海旭, 沈永春. 用逼近目标规划模型进行潜艇耐压船体最佳设计[J]. 船舶力学, 2004, 8(2): 79–85.
DING H X, SHEN Y C. Approximate goal programming model for optimization design of submarine pressure hull structure. Journal of ship mechanics, 2004, 8(2): 79–85. http://www.cnki.com.cn/Article/CJFDTOTAL-CBLX199801004.htm |
| [4] |
杨卓懿, 庞永杰. 响应面模型在耐压壳优化设计中的应用研究[J]. 哈尔滨工程大学学报, 2010, 31(6): 689–692.
YANG Z Y, PANG Y J. Application of the response surface model to optimize the design of a pressure shell. Journal of Harbin Engineering University, 2010, 31(6): 689–692. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hebgcdxxb201006002 |
| [5] | 王燕. 潜艇结构的优化设计方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010. |
| [6] | GJB/Z 21A-2001. 潜艇结构设计计算方法[S]. |
| [7] | 徐秉汉, 朱邦俊, 欧阳吕伟, 等. 现代潜艇结构强度的理论与试验[M]. 北京: 国防工业出版社, 2007: 45–59. |
| [8] | JIN R, CHEN W, SUDJIANTO A. An efficient algorithm for constructing optimal design of computer experiments[J]. Journal of Statistical Planning and Inference, 2005, 134(1): 268–287. |
 2018, Vol. 40
2018, Vol. 40
