随着反舰武器科学技术的发展,掠海飞行半穿甲导弹成为了目前各国主要使用的反舰武器,主要通过侵入舰船内部爆炸,产生爆炸冲击波和高速破片对水面舰艇产生破坏作用[1 – 2]。而现代的反舰导弹的设计中,更注重爆炸后破片的杀伤作用。
国内外目前已经有一些关于战斗部爆炸后的形成破片的速度计算方法,也做了相关的试验,Gurney[3]在早期的研究中就发现弹丸初速与壳体强度关系不大,并通过理论计算给出球体、圆柱壳、无限平板被炸药驱动后的破片速度分布计算方法;Arnolda等[4]通过实验得到了柱体战斗部爆炸后破片的形状和分布。
Hu等[5]通过AUTODYN对不同方向不同长径比的裸药在封闭环境内爆炸产生的压力分布规律,并与实验结果对比,验证了通过有限元方法对炸药爆炸计算的正确性;MOXNES等[6]通过使用并比较拉格朗日法、欧拉法、SPH法等3种不同的数值计算方法对带壳爆炸的情况进行仿真计算,同时也对壳体使用分离节点法的情况进行比较,结果证明SPH分离节点法与使用了分离节点法的拉格朗日方法与实验结果吻合较好;Kong等[7 – 8]通过实验方法测试两端封闭圆柱体战斗部端点起爆情况下,侧壁破片速度与端盖破片速度,并用SPH方法对战斗部爆炸过程进行仿真,得到了破片的质量分布情况,并发现带端盖的战斗部无法简单的通过Gurney计算;印立魁等[9]使用AUTODYN多层球形预制破片战斗部破片初速场,计算结果与实验结果吻合良好,并在此基础上,得到了多层球形预制破片战斗部破片初速的理论计算方法;Tanapornraweekit等[10]通过有限元方法研究了壳体材料性能与战斗部爆炸之后产生的破片之间的关系,发现低强度材料壳体爆炸后产生最多的破片数及最大的平均动能。
本文利用有限元仿真软件LS-DYNA对带壳圆柱体战斗部爆炸过程进行模拟,并在此基础分析有端盖的封闭圆柱体战斗部与无端盖战斗部侧壁破片速度分布的区别;同时,计算不同长径比的战斗部封闭圆柱体战斗部爆炸后,侧壁破片速度及端盖速度的变化规律及能量分配的区别。
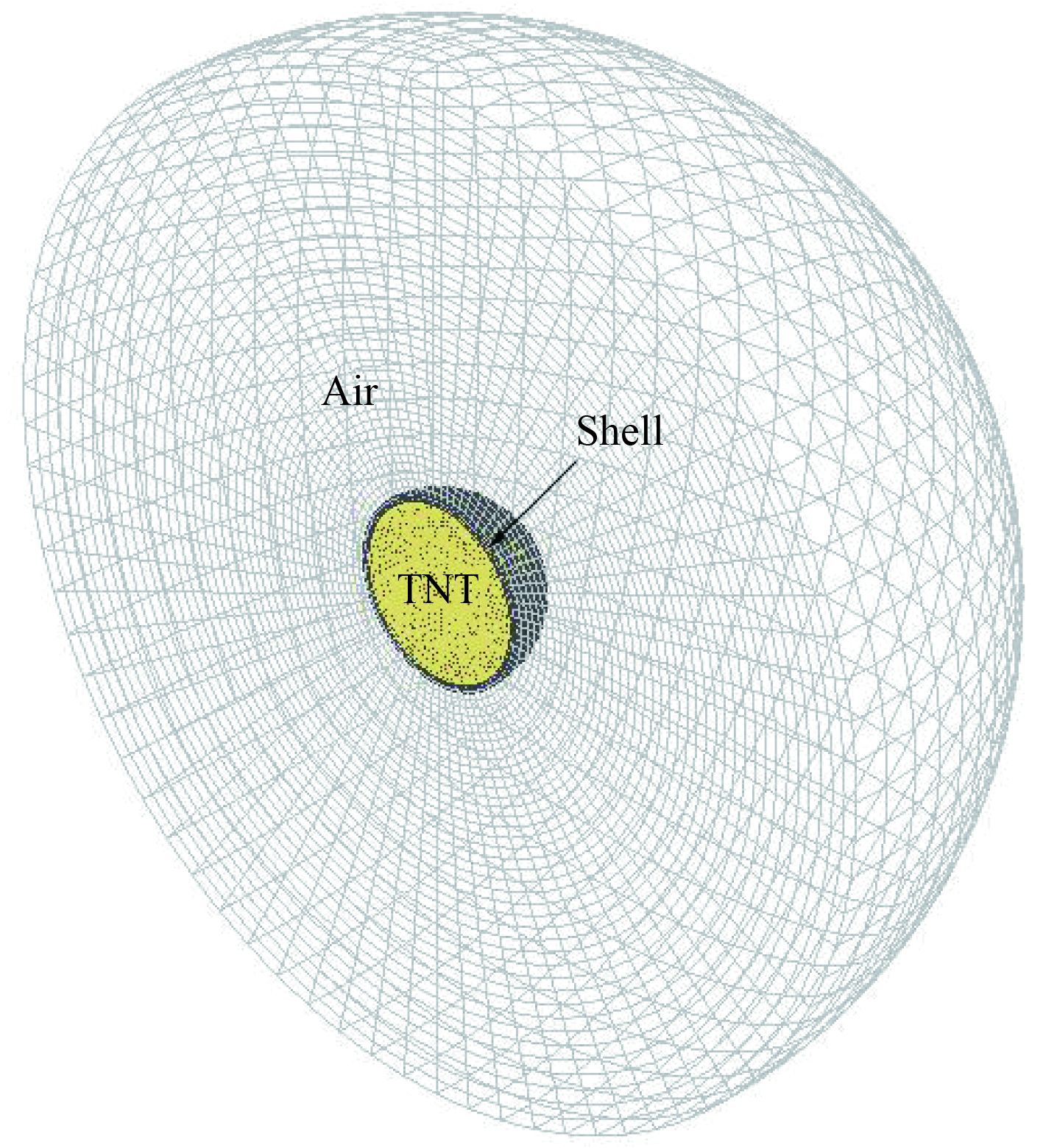
1 有限元计算方法 1.1 计算模型计算采用商用有限元计算软件Ansys/LS-DYNA建立结构模型,使用cm,g和μs为基本单位制,战斗部炸药、壳体及空气域均使用SOLID164实体单元。炸药单元位于空气单元正中心,炸药单元与空气单元之间通过共节点的方式相互作用;战斗部壳体单元内侧与炸药单元外侧共面,并使用*CONSTRAINED_LAGRANGE_IN_SOLID关键字定义战斗部壳体与炸药及空气之间的耦合作用。同时,采取随机生成方式,随机生成部分节点,稍微降低这些节点处的失效应变,使得战斗部壳体的破坏存在一定的非对称性。球体战斗部有限元模型剖视图如图1所示。
|
图 1 球体战斗部有限元模型图(剖视图) Fig. 1 The finite element model of sphere warhead (sectional view) |
有限元计算过程中主要涉及到TNT炸药、壳体30CrMnSiNi2A合金、空气3种材料,其中TNT炸药采用高爆炸药模型(*MAT_HIGH_EXPLOSIVE_BURN),状态方程使用JWL方程(*EOS_JWL),即
| $p = A(1 - \frac{{\omega \eta }}{{{R_1}}}){e^{{R_1}\eta }} + B(1 - \frac{{\omega \eta }}{{{R_2}}}){e^{{R_2}\eta }} + \omega \eta {\rho _0}e{\text{,}}$ |
|
|
表 1 TNT炸药参数 Tab.1 Parameters of TNT |
战斗部靠壳体材料采用的是30CrMnSiNi2A,使用的材料模型是考虑应变率的Cowper-Symonds模型[11] (*MAT_PLASTIC_KINEMATIC)描叙,即
| ${\sigma _d} = ({\sigma _0} + \frac{{E{E_h}{\varepsilon _f}}}{{E - {E_h}}})[1 + {(\frac{{\dot \varepsilon }}{D})^{\frac{1}{n}}}]{\text{。}}$ |
|
|
表 2 战斗部壳体材料参数(30CrMnSiNi2A) Tab.2 Parameters of 30CrMnSiNi2A |
空气采用空材料模型模拟(*MAT_NULL),状态方程使用线性多项式方程(*EOS_NONLINEAR_POLYNOMIAL)。
|
|
表 3 空气参数 Tab.3 Parameters of air |
多项式中C1=C2=C3=C4=0,其他材料参数如表3所示。
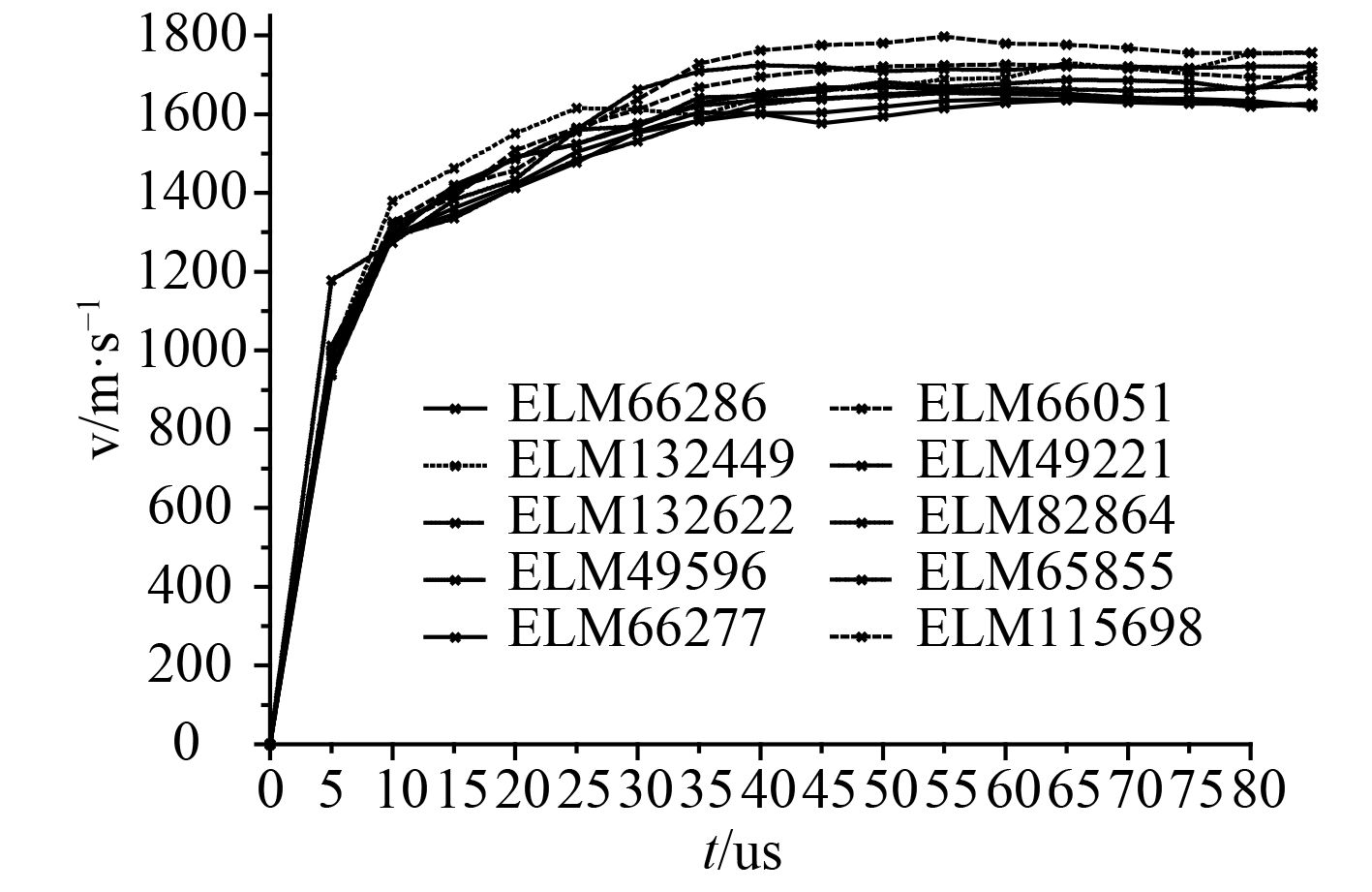
1.3 计算结果计算结果战斗部的破坏过程如图2所示,同时在战斗部壳体不同方向上选取10个单元(ELM66286,66051,132449,49221,132622,82864,49596,65855,66277,115698),并将前80 μs内速度变化曲线如图3所示。

|
图 2 球体战斗壳体破坏过程 Fig. 2 The failure process of spherical warhead shell |
|
图 3 壳体破片单元速度曲线图 Fig. 3 The velocity curve of shell fragment element |
取这些单元的平均初始速度作为壳体爆炸后形成破片的平均初始速度,可得v0'=1 680 m/s,同时根据Gurney公式[2]计算球体壳体破片初速公式:
| ${v_0} = \sqrt {2E} \sqrt {\frac{\beta }{{1 + 0.6\beta }}}{\text{。}} $ |
对于TNT:
通过以上的有限元建模方法,对以下带端盖柱形战斗部进行有限元仿真计算,战斗部装药全部为150 g,同时长径比包括1/2,2/3,3/4,1,4/3,3/2,2/1七种情况,战斗部的装填比均在0.83左右。战斗部的具体参数如表4所示。
不同长径比(L/D=1/2,1,2)的带端盖柱体战斗部的破坏模式如图4所示。

|
图 4 不同长径比的柱体战斗壳体破坏过程 Fig. 4 The failure process of cylindrical warhead shell with L/D variation |
从图4中可以看出,不同长径比的带壳战斗部爆炸后的破片飞散方式存在一定的区别:如图4(a),当L/D较大时,侧壁的破片飞散的角度较小,尤其是中部基本都沿着径向飞散,且破片的分布与文献[5]中的大小和形状吻合较好;而对于图4(b)和图4(c),即L/D较小时,战斗部的侧壁基本同时失效,破片的飞散角本部较大,飞散的形状基本类似于球形向外飞散;同时,“细长”型的战斗部端盖的变形弧度大;“短粗”型的战斗部端盖的变形弧度小。根据壳体的破坏过程来看,战斗部在破裂之前侧壁在长度方向的拉伸很小;从破片的大小来看,“细长”型战斗部的爆炸后形成的破片数量要多余“短粗”型的战斗部,战斗部越短粗,越容易形成较大的破片。
|
|
表 4 柱形战斗部尺寸及质量 Tab.4 The size and quality of cylindrical warhead |
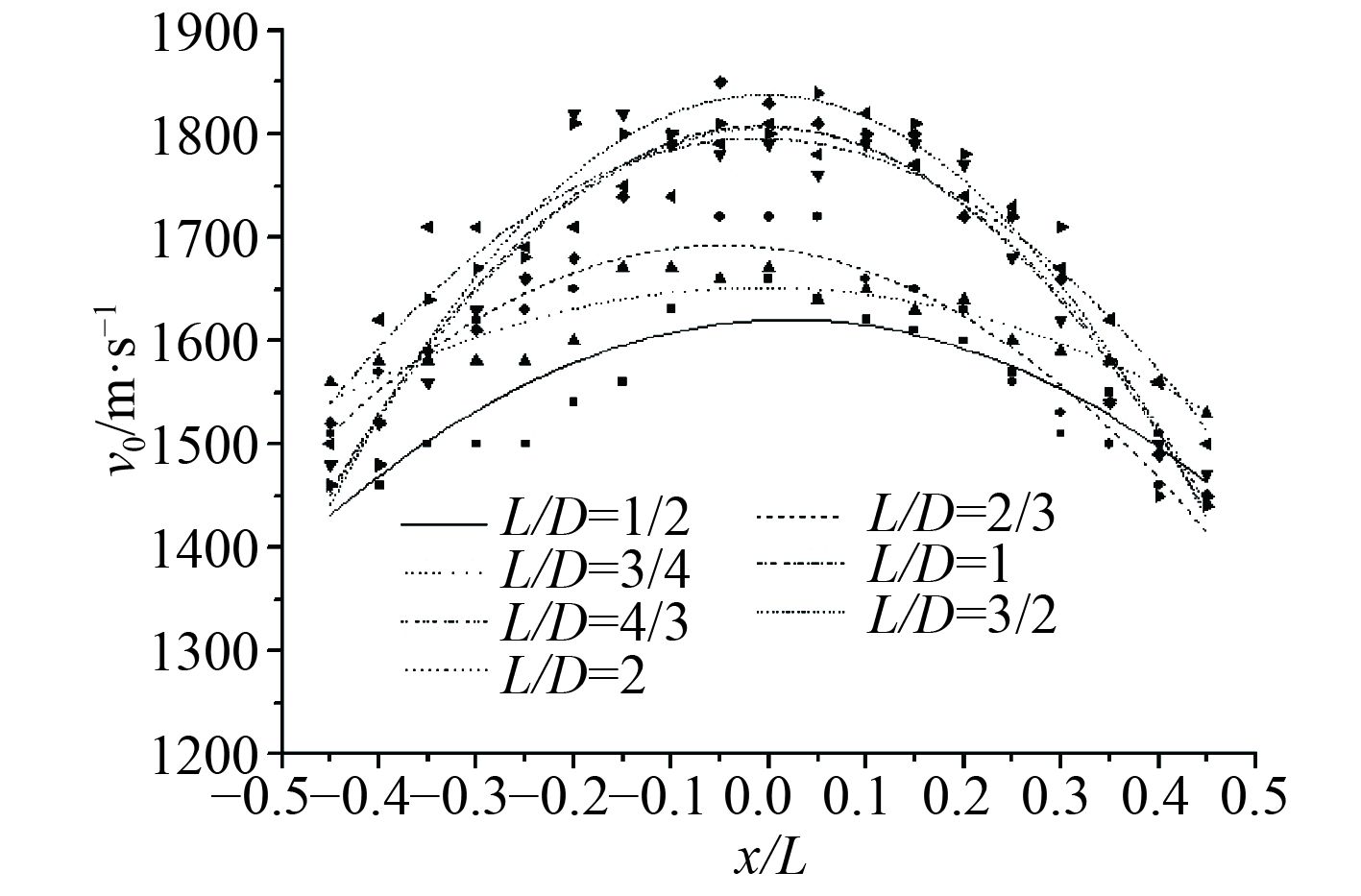
为了进一步研究破片飞散的规律,在不同工况下,根据距离壳体中部距离不同位置的单元速度,将侧壁形成的破片沿轴向的分布曲线绘制如图5所示。
从图5可以看出,虽然壳体在画网格时采用了随机的节点分离,但是破片的速度分布基本满足抛物线的分布规律。长径比不同的战斗部破片的最小速度,即距离端部最近的壳体的速度之间相差并不大,这些战斗部的共同点是C/M均在0.82~0.85之间。那么,可以认为圆柱壳体与端盖交界处的速度主要由C/M决定。
工况1~工况3的速度分布曲线的峰值,相对工况4~工况7的速度分布,明显中心的峰值比较小,而当L/D≥1时,抛物线的峰值则趋于稳定。这是由于,对于中心起爆,当长径比达到一定大小后,位于中间部分长度的圆柱壳可以近似认为是无限长圆柱壳起爆的情况,因此,这一部分的速度很大程度上取决于C/M的值。
|
图 5 战斗部破片轴向的速度分布曲线 Fig. 5 The distribution of fragment velocity along the axis of cylinder |
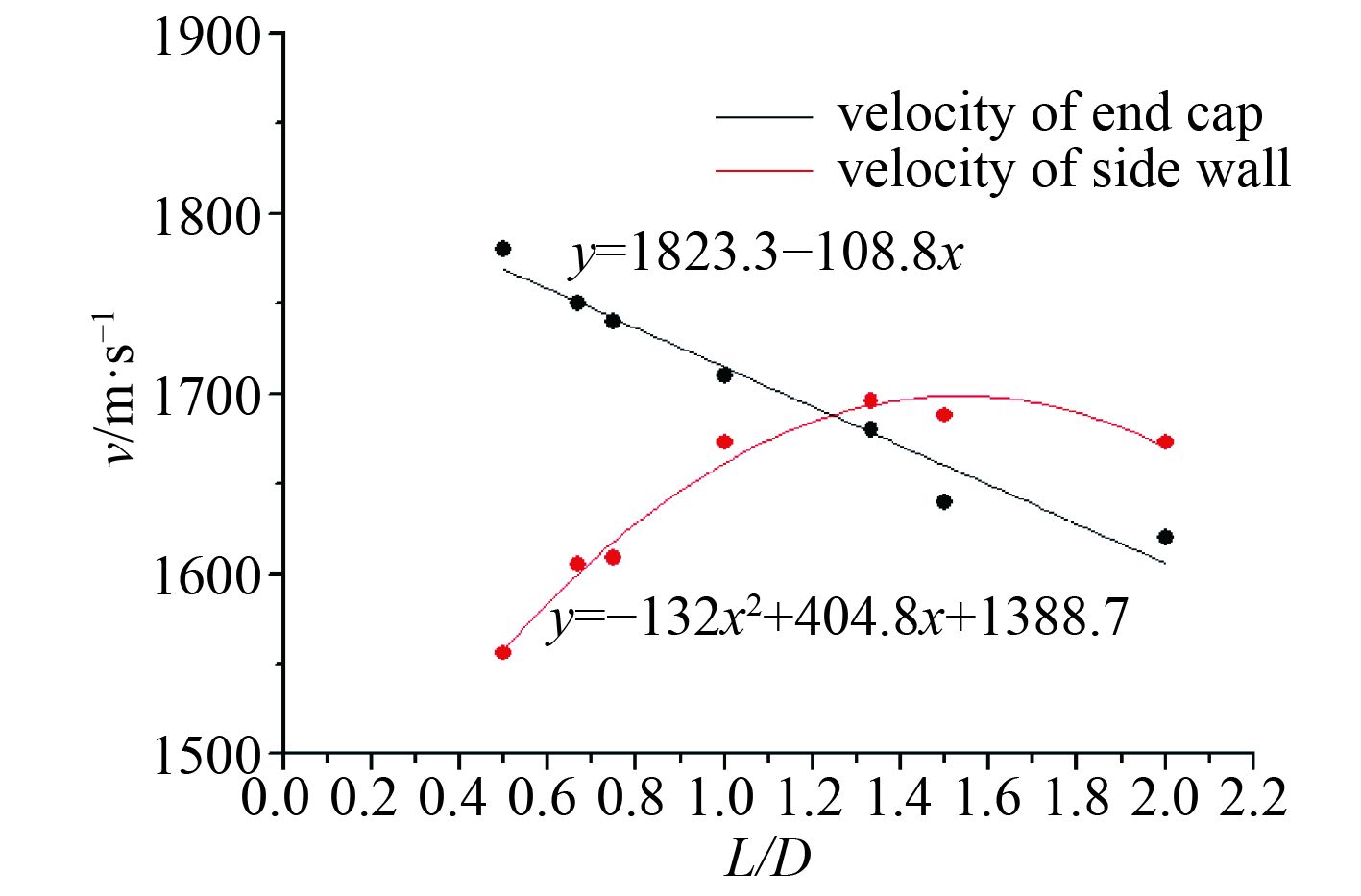
仿真端盖速度与侧壁的平均速度见表5。其中侧壁的平均速度时通过积分拟合曲线求出的平均速度。同时,将端部和侧壁的平均速度绘制如图6的曲线。
|
|
表 5 端盖及侧壁破片的平均速度 Tab.5 The average velocity of end caps and side wall |
|
图 6 端盖及侧壁破片平均速度随L/D变化图 Fig. 6 The average velocity of end caps and side wall with L/D variation |
从图6可以看出,当L/D在0.5~2范围内时,端盖破片速度的变化基本满足随着长径比的增大呈线性下降的趋势;侧壁破片的平均速度则随着长径比的增大而增长,但是存在一定极限。由于后期随着长径比的增加装填比的下降,导致侧壁的速度也会下降。已有的研究结论[1]也表明了长径比的增加侧壁的速度修正比例因子也随之增加,同时长径比降低还会导致炸药与侧壁的质量比下降,这才表现出在长径比较小时,破片的速度先增加后减小的变化特征。
3 结 语本文通过Ansys/LS-DYNA数值模拟带壳战斗部爆炸的过程进行计算,以球体战斗部的仿真计算结果与Gurney公式的计算结果进行对比,验证了通过分离节点法计算带壳战斗部破片分布的可行性,并对中心起爆情况下,不同长径比的带壳圆柱体战斗部的爆炸过程进行仿真计算,得到以下结论:
1)当L/D较大时,侧壁破片飞散的角度较小,中部基本都沿着径向飞散;L/D较小时,壳体破碎形式更趋近于球体。“细长”型战斗部端盖的变形分布弧度大;“短粗”型战斗部端盖的变形分布弧度小。从破片的大小来看,“细长”型战斗部爆炸后形成的破片数量要多于“短粗”型战斗部,且战斗部的长径比越小,越容易形成较大的破片。
2)可以看出侧壁速度分布基本满足抛物线的分布规律,对于中心起爆,当长径比达到一定大小后,位于中间部分长度的圆柱壳可以近似认为是无限长圆柱壳起爆的情况,抛物线的峰值趋于稳定。
3)端盖速度的变化基本满足随着长径比的增大呈线性下降的趋势,而侧壁的平均速度则是随着长径比的增大而增长,但是存在一定的极限。
| [1] | 惰树元, 王树山. 终点效应学[M]. 北京: 国防工业出版社, 2000. |
| [2] | KURKI T. Contained explosion inside a naval-vessele evaluation of the structure response[D]. Helsinki University of Technology, 2007. |
| [3] | GURNEY R W. The initial velocities of fragments from bombs, shell and grenades[R]. Aberdeen, MD, US: Ballistic Research Laboratory, 1943. |
| [4] | ARNOLD W, ROTTENKOLBER E. Fragment mass distribution of metal cased explosive charges[J]. International Journal of Impact Engineering, 2008, 35(12): 1393–1398. |
| [5] | HU Y, WU C, LUKASZEWICZ M, et al. Characteristics of Confined Blast Loading in Unvented Structures[J]. International Journal of Protective Structures, 2011, 2(1): 21–42. |
| [6] | MOXNES J F, PRYTZ A K, FRØYLAND Ø, et al. Experimental and numerical study of the fragmentation of expanding warhead casings by using different numerical codes and solution techniques[J]. Defense Technology, 2014, 10(2): 161–176. |
| [7] | KONG X, WU W, LI J, et al. Experimental and numerical investigation on a multi-layer protective structure under the synergistic effect of blast and fragment loadings[J]. International Journal of Impact Engineering, 2014, 65(2): 146–162. |
| [8] | KONG X, WU W, LI J, et al. A numerical investigation on explosive fragmentation of metal casing using Smoothed Particle Hydrodynamic method[J]. Materials and Design, 2013, 51(60): 729–741. |
| [9] |
印立魁, 蒋建伟. 多层球形预制破片战斗部破片初速场的计算模型[J]. 含能材料, 2014, 22(3): 300–305.
YIN L K, JIANG J W. Calculation Model of Initial Velocity Field on Multilayered Spherical Fragments Warhead[J]. Chinese Journal of Energetic Materials, 2014, 22(3): 300–305. http://www.cnki.com.cn/Article/CJFDTotal-BIGO201412005.htm |
| [10] | TANAPORNRAWEEKIT G, KULSIRIKASEM W. Effects of Material Properties of Warhead Casing on Natural Fragmentation Performance of High Explosive (HE) Warhead[J]. World Academy of Science, Engineering and Technology, 2013, 59(2): 1275–1280 |
| [11] |
吴林杰, 朱锡, 侯海量, 等. 空中近距爆炸下加筋板架的毁伤模式仿真研究[J]. 振动与冲击, 2013, 32(14): 77–81.
Lin-Jie W U, HOU H L, CHEN C H. Simulations for damage modes of a stiffened plate subjected to close-range air-blast loading[J]. Zhendong Yu Chongji/journal of Vibration & Shock, 2013, 32(14): 77–81+126. |
 2018, Vol. 40
2018, Vol. 40
