随着我国对海洋权益的日益重视,水下航行器在海洋资源的开发和探测应用上也越来越广泛。由于执行任务的多样性和海洋环境的复杂性,对水下航行器的性能也提出了较为苛刻的要求,因此对航行器推进电机的要求也更严格。由于永磁无刷直流电机电子换向代替了传统的电刷换向,转子励磁采用永磁体材料,因此成为广泛应用于水下航行器的推进电机之一。
电机尤其是在大功率长时间运行时,由于所处的空间有限,产生的损耗大部分转化为热量,功率密度大,导致电机温度升高,比如永磁体在高温下会发生退磁现象[1 – 2],导致电机的可靠性和工作点的性能产生很大的影响。所以对电机的温度场进行详细的研究是非常必要的,减少损耗,提高效率有着很重要的意义。
电机运行过程中产生的损耗主要由以下几部分组成[3]:1)由于气隙磁场的交变产生的定子铁心损耗,包括磁滞损耗、涡流损耗和异常损耗;2)定子绕组电流产生的铜损;3)定子电流中的谐波分量在转子永磁体中产生的涡流损耗;4)机械损耗,包括转子表面空气摩擦损耗、轴承磨损等。
目前对电机的温度场分析,主要有简化公式法、等效热路法、温度场法[4]等。简化公式法是一种粗略估计电机平均温升的方法,只能估计定子铁心或绕组的平均温升。等效热路法是一种将温度场的各种参数用“路”的方法来等效,从而对电机各主要部分进行温升计算。温度场法即对电机的温度求解区域离散,采用有限元法对其求解,具有较高的求解精度。
Motor-CAD软件由英国Motor Design公司开发,是全球唯一一款基于网络法与有限元法的电机热与电磁设计软件。Motor-CAD包括Therm电机热设计模块、Emag电机电磁设计模块及motor-LAB辅助后处理工具,可实现相互之间的耦合,其中电机热设计模块可参数化建模对电机各种条件下的稳态温度场进行求解。
本文以210 kW无刷直流电机为研究对象,计算了电机主要部分的导热系数,建立三维有限元分析模型,利用motor-CAD软件电磁计算模块对电机初始条件的损耗进行计算,然后将其计算结果导入热计算模块作为利用等效热路法计算温度场的初始条件进行磁热互耦迭代,直到对不同强制冷却方式下的电机稳态温度场计算达到要求的收敛精度。得出了电机负载工况下的温度分布,为电机初期设计阶段热力学分析提供一定的依据。
1 电机关键性能参数及几何模型的建立:本文研究的无刷直流电机应用场合为水下航行器推进电机,在此环境下电机设计为低转速,大扭矩,高比功率密度,工作环境在封闭狭窄空间中,外壳带强制冷却。
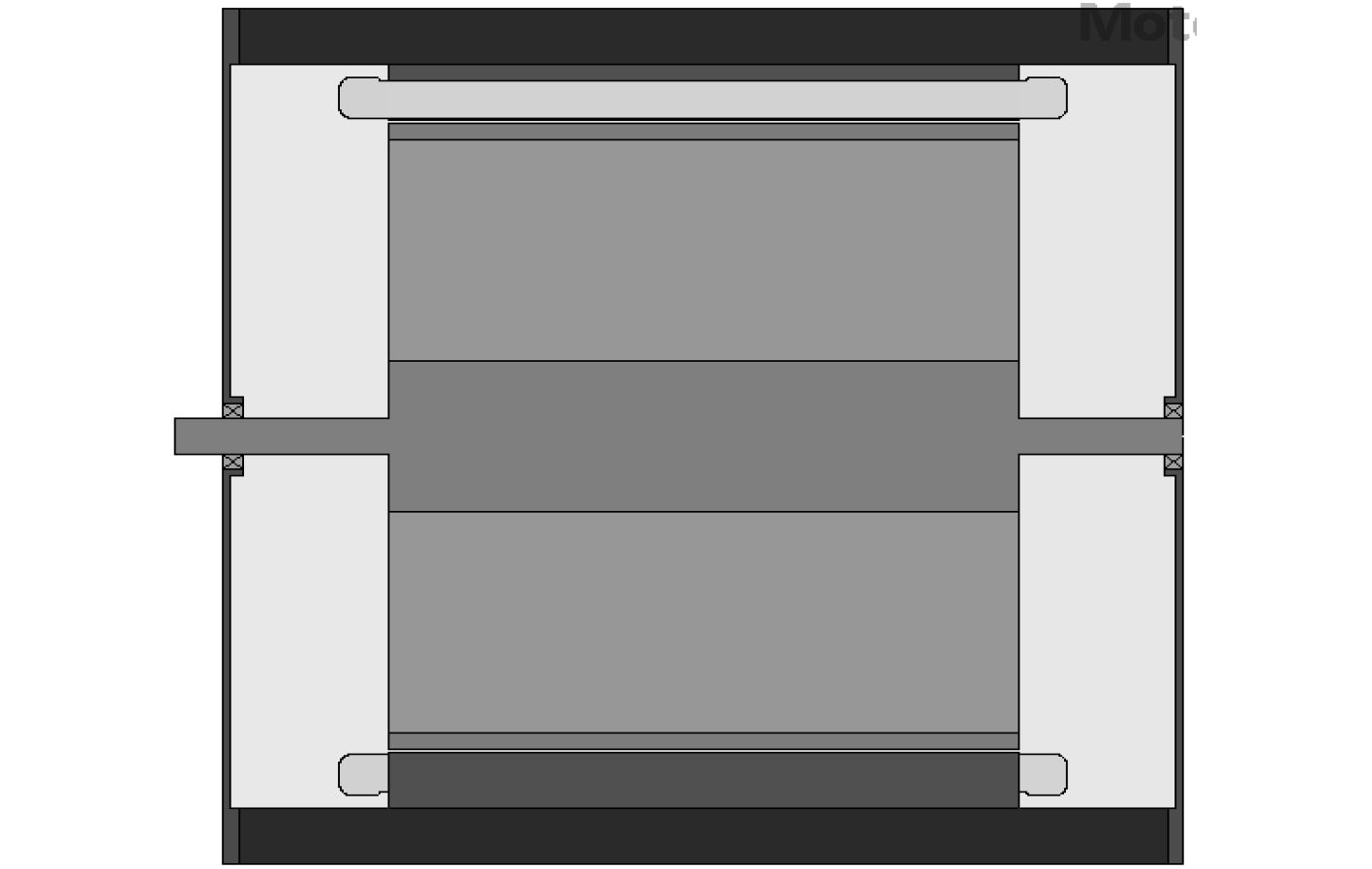
利用Motor-CAD软件对此电机的几何模型进行建立,针对32极96槽的无刷直流电机进行分析。如图1和图2所示。

|
图 1 电机径向结构 Fig. 1 Radial structure of motor |
|
图 2 电机轴向结构 Fig. 2 Axial structure of motor |
本文电机铁心材料为35DW270,永磁体材料为N38UH,机壳材料为高强度铝合金,绕组导线材料为铜。
2 传热理论及初始,边界条件设定 2.1 传热理论对于电机的温度场分析,内部损耗产生的热量通过热传导主要从壳体以对流换热的方式散出,由于壳体换热采用螺旋水道内冷却介质流动换热,所以辐射换热在温度场的分析中可以忽略不计。
热传导是指介质中由于存在温度梯度而产生的能量传输,导热规律由傅叶定律制约,傅里叶定律[5]可以表示为:
| $q_n^{''} = - k\frac{{\partial T}}{{\partial n}}\text{。}$ | (1) |
式中:
对流换热指流体整体运动而导致的换热,其规律由牛顿冷却公式决定:
| $q_n^{''} = h\left( {{T_s} - {T_\infty }} \right)\text{。}$ | (2) |
其中:h为对流换热系数,W/(m2·k),与边界条件有关;Ts为换热表面温度,℃;T∞为流体温度,℃。
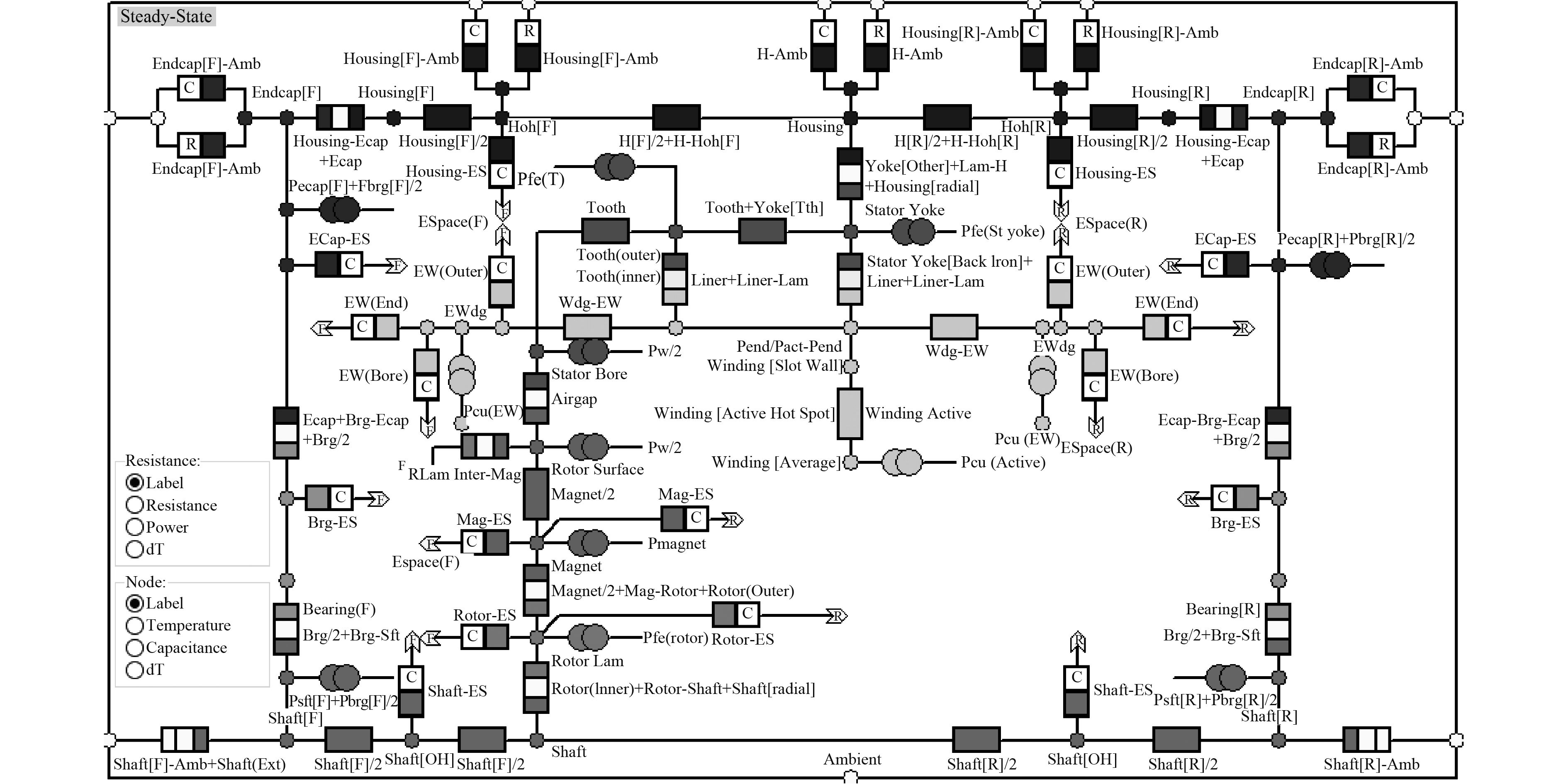
等效热路法是仿照电路学原理,将传热学中的温度T等效为电路中的电压V,热阻包括导热热阻、对流热阻。辐射热阻等效为电阻R,导热速率q等效为电流I。在对电机温度场进行分析的时候,定子铁心的损耗和铜损以及永磁体的涡流损耗作为热源,类似于电路中的电压源,然后结合电机各部分结构的传热特性将一个个传热路径中的热阻类比于电阻,最终形成一个电机整体热量传递的热网络“电路图”,利用电路学基尔霍夫定律列出全部的热平衡方程进行联立求解,从而得到电机各主要部分温升。
在电路学中,有欧姆定律U=IR,类似的,用T表示温度,Rt表示热阻,热阻中,导热热阻
式中:A为与热流方向相垂直的截面积,m2;L为截面厚度,m;h为对流换热系数,w/(m2·k);A为换热面积,m2。
设Pi为电机每个节点的损耗,C为热导,即热阻的倒数,
| ${ P} = { C} { T} \text{。}$ | (3) |
式中:P为电机各网络节点总损耗矩阵;C为节点间总热导矩阵;T热网络节点总温度矩阵。
求此线性方程,即可得到热网络法下电机各节点温度。
电机的等效热网络模型如图3所示。
|
图 3 电机等效热网络图 Fig. 3 Equivalent thermal network diagram of motor |
电机初始条件设定为环境温度20℃。
传热过程中3类边界条件:
1)对应于表面保持固定温度Ts的情况;
2)表面恒定热流密度
3)在表面上存在对流冷却或加热。
直流无刷电机的稳态温度场分析属于第3类边界条件,即
| $- k\frac{{\partial T}}{{\partial n}} = h\left( {T - {T_\infty }} \right)\text{,}$ | (4) |
由于电机壳体内流道是螺旋水道,设定冷却液体介质进口温度为20 ℃。
对于管内流动,雷诺数定义为:
| ${{\mathop{Re}\nolimits} _D} = \frac{{\rho {U_m}D}}{\mu }\text{,}$ | (5) |
其中:ρ为流体密度,kg/m3;Um为管道横截面上的平均流体速度,m/s;D为管道直径,m;μ为流体的动力粘性系数,N·s/m2.
管内流动由层流向湍流发展的临界雷诺数为
| ${{\mathop{Re}\nolimits} _{Dc}} \approx 2300\text{。}$ | (6) |
1)对于管内充分发展的层流,对流换热系数h:
均匀表面热流密度的圆管发展的层流,努塞尔数
| $h = \frac{{N{u_D}}}{D}k, $ | (7) |
式中,k为流体的导热系数,w/(m·k)。
2)管内充分发展的湍流(冷却情况,忽略管道内摩擦):
| $N{u_D} = 0.023{\mathop{Re}\nolimits} _D^{4/5}{Pr ^n}\text{,}$ | (8) |
| $Pr = \frac{{\mu {C_p}}}{k}\text{。}$ | (9) |
式中,Cp为流体的比定压热容,J/(kg·k),n取0.3。
3)电机两端面与20 ℃空气接触自然对流,此时空气热导率查表得为0.024 W/(m·k)。
表1为电机各主要部件材料的导热系数。
|
|
表 1 材料导热系数 Tab.1 Thermal conductivity of materials |
1)铁损:定子铁心损耗是由于气隙磁场的交变产生的损耗,目前对这一损耗的求解主流是采用基于Bertotti铁耗分离模型,主要由磁滞损耗,涡流损耗、异常损耗3部分组成。Bertotti铁耗分离模型[6]的计算公式:
单位体积(1 m3)铁心材料产生的铁耗:
| $\begin{split}& d\left( {{P_{fe}}} \right) = {k_f}\left[{k_h}B_m^2f + \frac{{\sigma {{\left( {\pi d} \right)}^2}}}{6}{{\left( {{B_m}f} \right)}^2} + \right.\\ &\left.8.67*{k_e}{{\left( {{B_m}f} \right)}^{1.5}} \right]\text{。}\end{split}$ | (10) |
式中:kf为叠片系数;kh为磁滞损耗系数;σ为材料电导率,s/m;d为叠片厚度,m;f为电频率,Hz;Bm为单元中磁密的幅值,T;ke为异常损耗系数。其中kf,d,σ由硅钢片材料给定。kh,ke由硅钢片材料的Bm(T)–P(W/kg)曲线数据插值得到。
2)铜损:铜损耗主要是由于定子绕组中通过电流时产生的损耗,由于采用逆变器两相导通,所以
绕组的集肤效应影响较小,可以忽略。
3)永磁体涡流损耗:永磁体的涡流损耗主要由气隙谐波磁势[7]产生。
| ${P_m} = \mathop \smallint \nolimits {J^2}/\sigma {\rm d}V\text{。}$ | (11) |
式中:Pm为转子永磁体涡流损耗,w/kg;J为涡流密度,m2/s;σ为永磁体的电导率,s/m。
在损耗空间进行积分可得总的损耗。
由于电机转速低,机械损耗占总损耗的比例很小,在本文分析中,忽略此项损耗,着重分析以上3个方面额定工况的损耗。
3.2 磁热互耦初始损耗值计算计算初始温度20 ℃时电机在额定工况下的损耗,作为后续进行磁热互耦迭代计算稳态温度场的初始值。计算结果如表2所示。
|
|
表 2 20 ℃电机损耗 Tab.2 Motor loss at 20 ℃ |
为考虑接触热阻对电机稳态温度场分析的影响,对电机主要接触部分,如壳体和定子铁心接触面等的接触热阻加以设定,接触间隙以接触平均值设定,详见表3。
|
|
表 3 电机主要部分接触热阻 Tab.3 Thermal contact resistance of main parts of motor |
通过3.2部分初始损耗的计算,将其结果导入热计算模块进行磁热互耦迭代,对稳态温度场分析,直到达到要求的收敛误差1%。
4.1 不同冷却介质温度场分别采用EGW50/50(乙二醇和水各50%的混合物)和DB-10(变压器油)作为冷却介质。螺旋流道进口温度20 ℃,流体流量0.6 L/s,8个冷却流道(见图4)为串联形式。

|
图 4 机壳螺旋水道 Fig. 4 Spiral channel of casing |
|
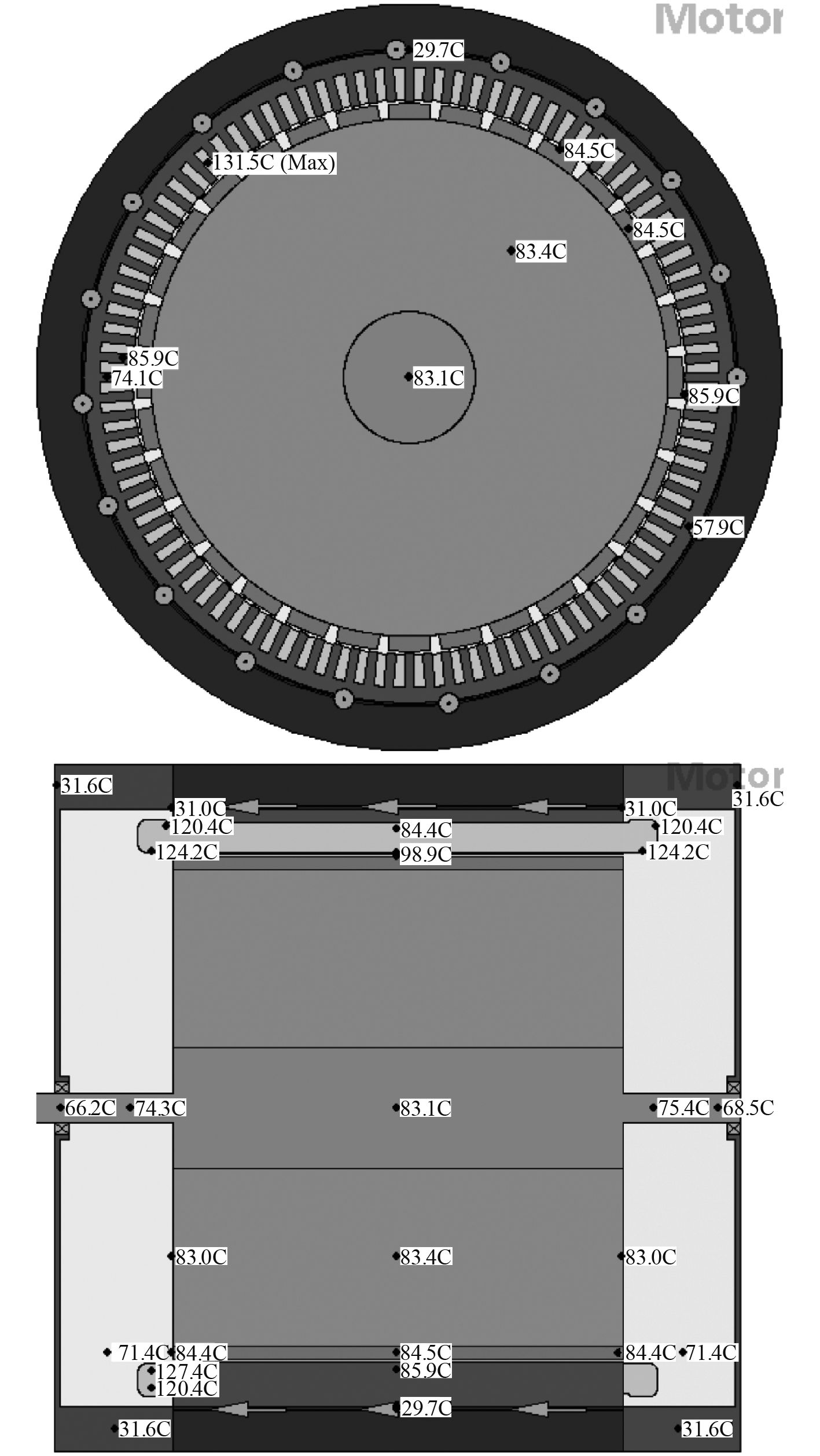
图 5 介质为EGW50/50时径向和轴向温度分布 Fig. 5 Radial and axial temperature distributions when the medium is EGW50/50 |
|
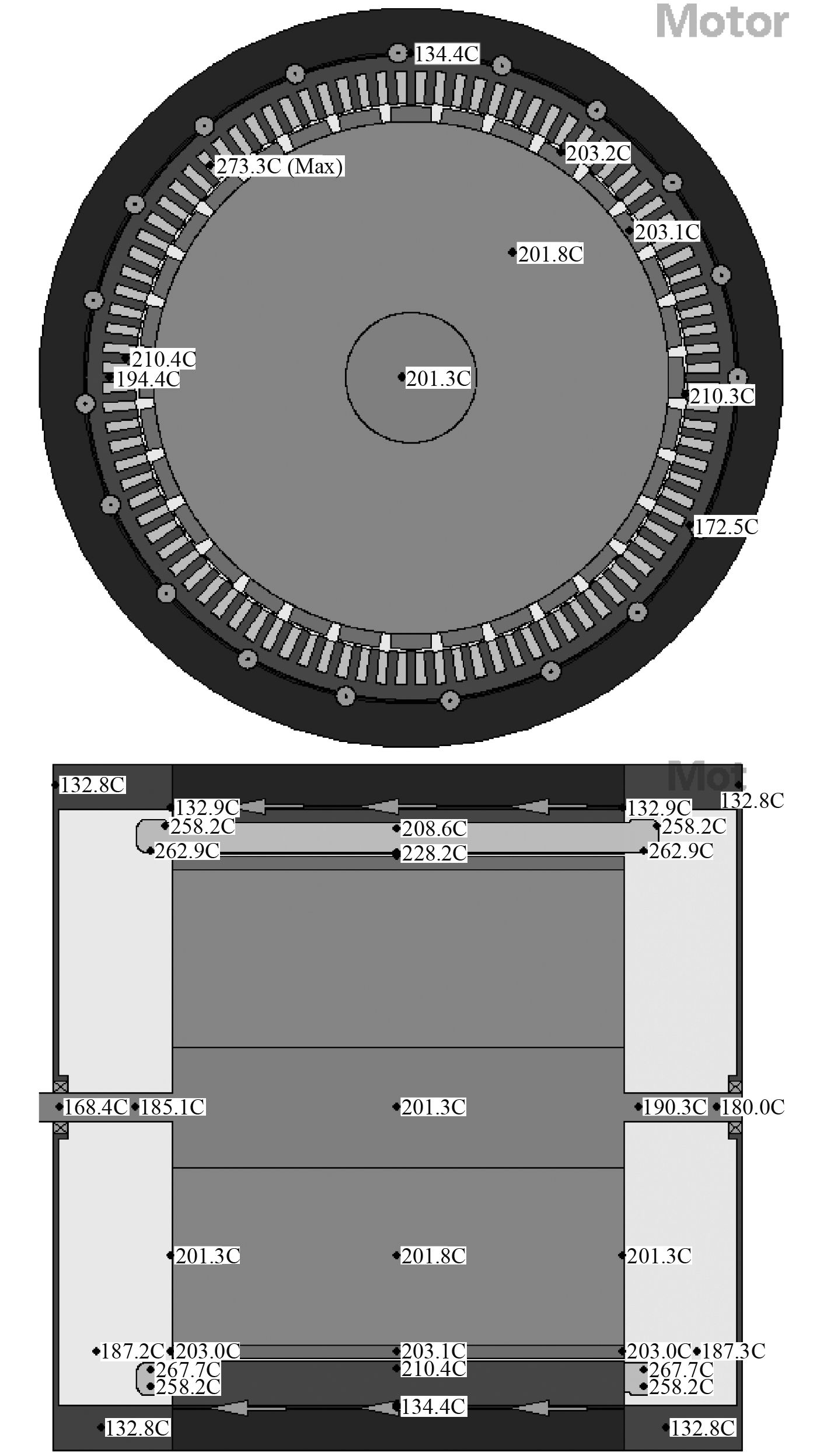
图 6 介质为DB-10时径向和轴向温度分布 Fig. 6 Radial and axial temperature distributions when the medium is DB-10 |
|
|
表 4 不同冷却介质稳态关键点温度 Tab.4 Critical point temperature at different cooling mediums |
螺旋流道进口温度20 ℃,8个冷却流道串联。冷却流体介质为EGW50/50(乙二醇和水各50%的混合物),流量分别为0.6 L/s,1.5 L/s。
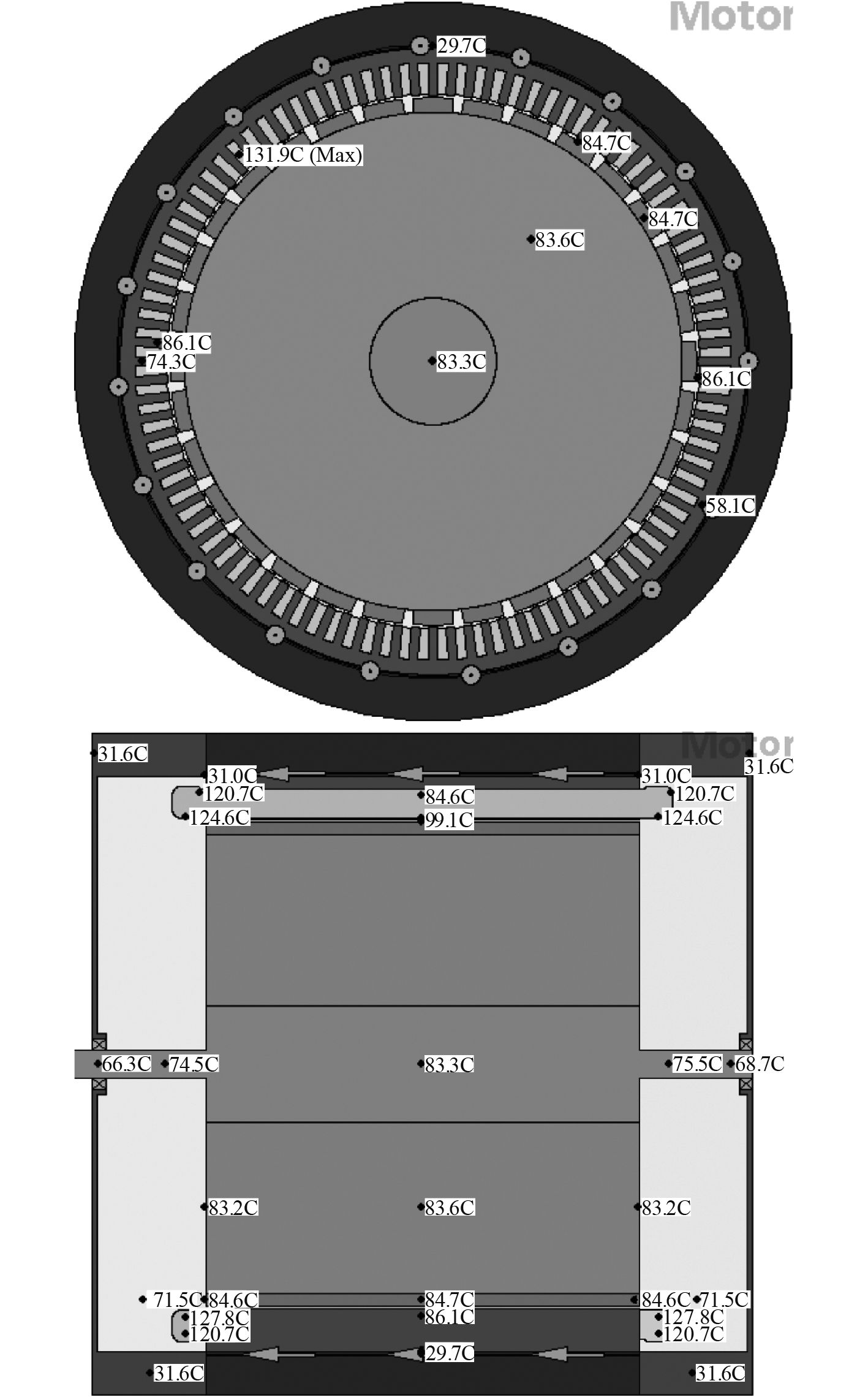
|
图 7 流量为0.6 L/s时径向和轴向温度分布 Fig. 7 Radial and axial temperature distributions at flow rates of 0.6 L/s |

|
图 8 流量为1.5 L/s时径向和轴向温度分布 Fig. 8 Radial and axial temperature distributions at flow rates of 1.5 L/s |
|
|
表 5 不同冷却流量稳态关键点温度 Tab.5 Critical point temperature at different cooling flow rates |
本文绕组导线为矩形导线,通过改变导线的截面高度来分析不同电流密度下温度场分布。螺旋流道进口温度20 ℃,8个冷却流道串联,冷却介质水,流量为0.6 L/s。
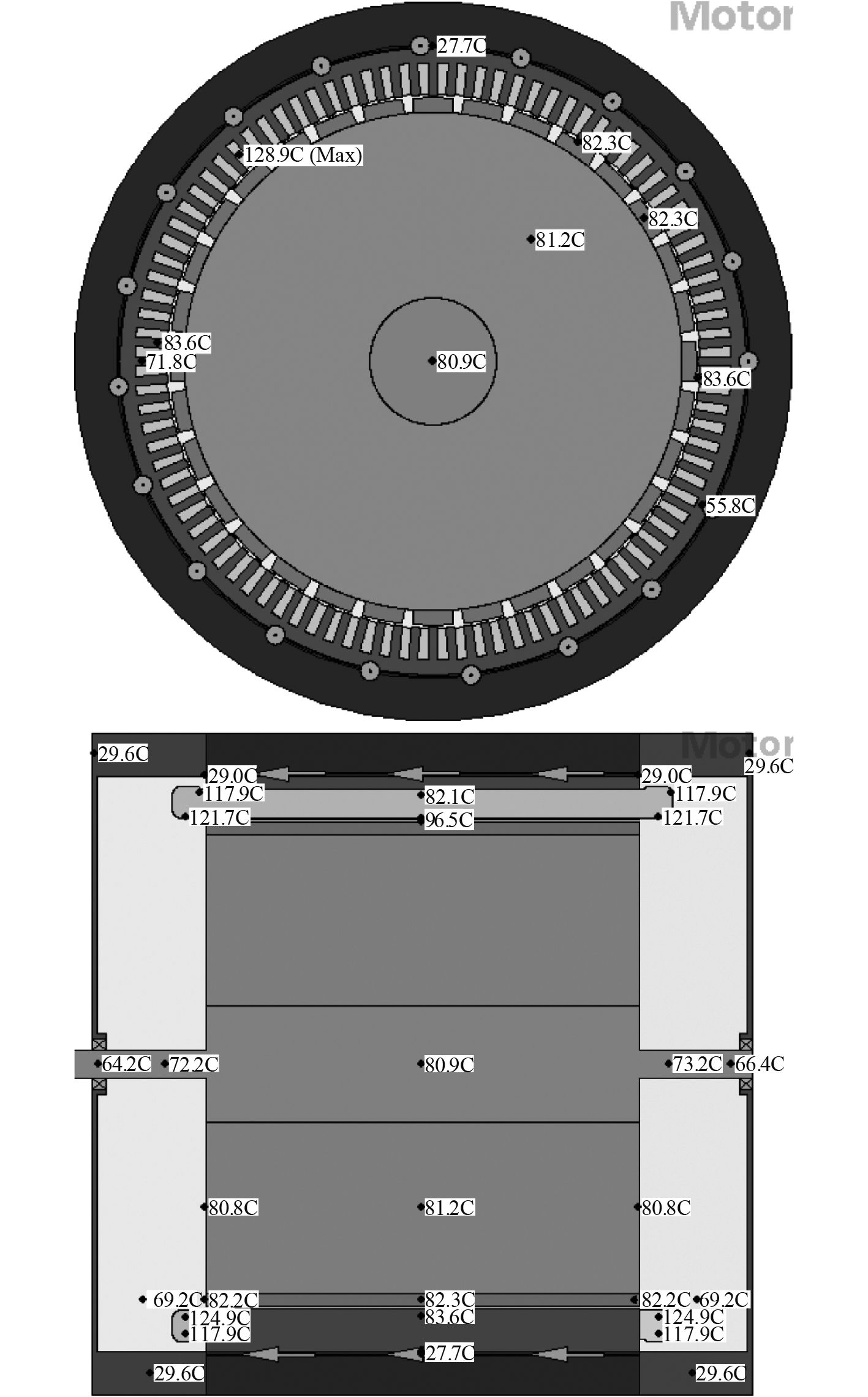
|
图 9 电流密度8.7 A/mm2时径向和轴向温度分布 Fig. 9 Radial and axial temperature distributions at current density 8.7 A/mm2 |
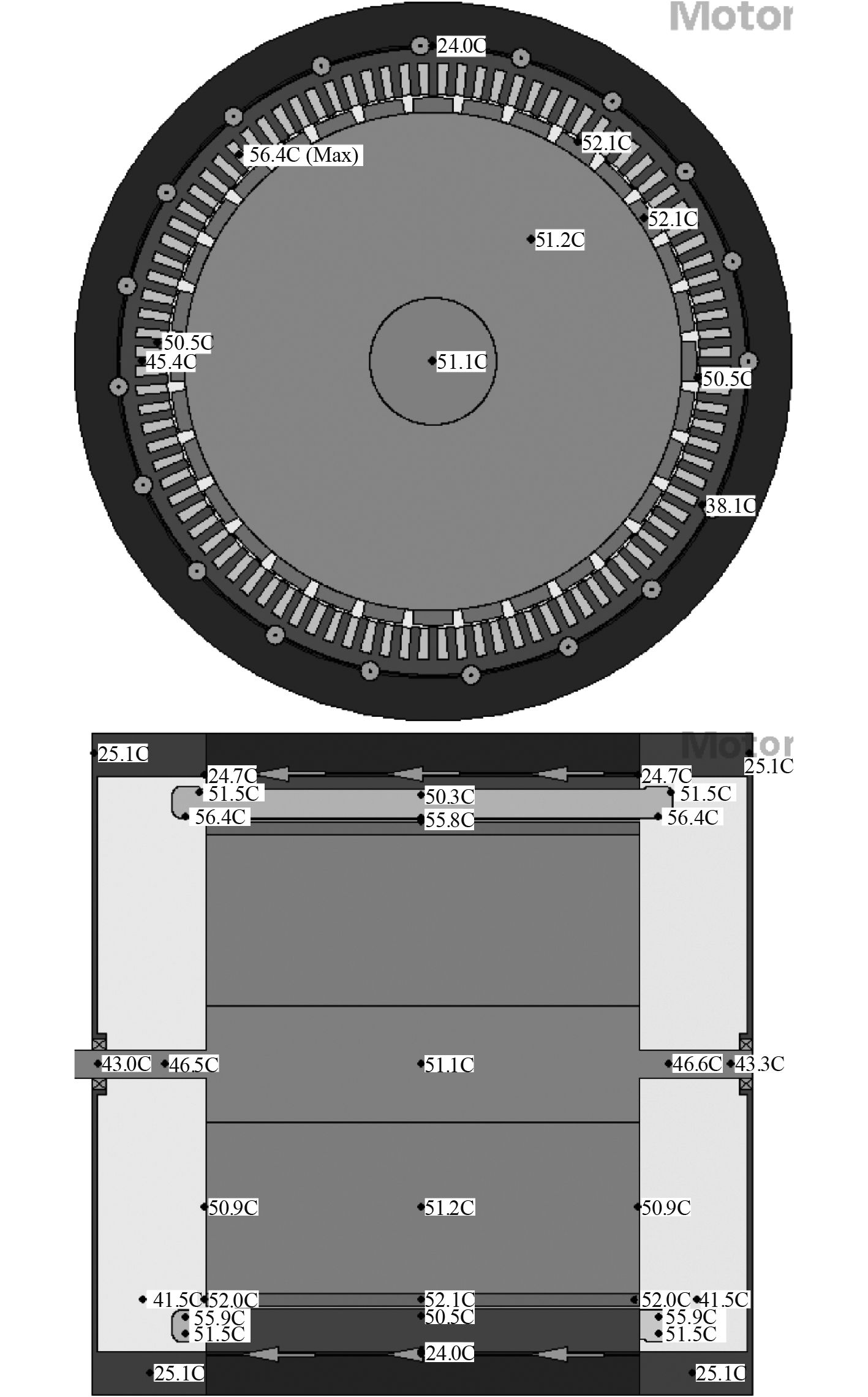
|
图 10 电流密度4.7 A/mm2时径向和轴向温度分布 Fig. 10 Radial and axial temperature distributions at current density 4.7 A/mm2 |
|
|
表 6 不同电流密度稳态关键点温度 Tab.6 Steady state critical point temperature at different current densities |
通过对同一条件下不同冷却介质、不同流量以及不同电流密度下的温度场求解,额定工况稳态时,最高温升出现在定子绕组中心,其次是绕组端部,由于绕组嵌线加工工艺的差别,除定子绕组外,温度在同一轴向上基本一致,温度梯度呈径向分布。改变电流密度对铜损的影响最大,减小电阻,提高电机效率,与此同时也增加了生产成本。
5.1 不同冷却介质温度场分析对比图5和图6分析,可知冷却介质为EGW50/50时,绕组最高温度为131.5 ℃,绕组端部为124.7 ℃;冷却介质为DB-10时,绕组最高温度为273.3 ℃,绕组端部为267.7 ℃,永磁体温度为203 ℃,永磁体可能会因为工作温度过高而产生退磁,影响电机的运行性能和效率。可见采用热导率和比热容比较大的EGW50/50在相同条件下要比DB-10的冷却效果好
5.2 冷却介质不同流量温度场分析对比图7和图8,冷却介质EGW50/50流量为0.6 L/s时,绕组最高温度为131.9 ℃,绕组端部127.8 ℃。流量1.5 L/s时,绕组最高温度为123.9 ℃,绕组端部119.9 ℃。永磁体温度分别为84.7 ℃,78.0 ℃。可见,加大螺旋流道的介质流量会显著降低电机主要部分的温度,例如绕组端部、永磁体等。
5.3 不同电流密度温度场分析|
|
表 7 不同电流密度电机主要损耗 Tab.7 Main loss of motor at different current density |
图9和图10对比分析,电流密度8.7 A/mm2时,绕组最高温度为128.9 ℃,绕组端部124.9 ℃;电流密度4.7 A/mm2时,绕组最高温度为56.4 ℃。通过减小电流密度,铜耗显著降低,永磁体和铁损变化不大,总损耗明显减少,关键部位温升明显降低,效率提高,但与此同时也增加了加工制作成本。
6 结 语本文利用Motor-CAD软件对3种不同强制冷却工况时额定工况下稳态温度场进行分析。结果表明,同条件下,虽然DB-10的稳态温升比EGW50/50大,但由于电机工作过程中产生的大电流对绝缘性能的要求更为严格,故在保证电机温升可控的情况下使用DB-10(变压器油)为冷却介质更加安全合理;增加冷却介质流量换热效果增强,稳态温升减小;减小电流密度,铜损减少,效率提高。电机主要部分接触热阻不可忽略。
| [1] | (美)乌曼(Umans, S.)著; 刘新正, 苏少平, 高琳译. 电机学: 第7版[M]. 北京: 电子工业出版社, 2014. 10. |
| [2] | 杜国华, 房建成, 刘西全, 等. 高速永磁无刷直流电机的热分析[J]. 北京航空航天大学学报, 2012, 38(8): 1101–1105. http://www.cnki.com.cn/Article/CJFDTotal-BJHK201208023.htm |
| [3] | 叶金虎. 现代无刷直流永磁电动机的原理和设计[M]. 北京: 科学出版社, 2007. |
| [4] | 叶雪荣, 苏博男, 由佳欣, 等. 基于有限元法的永磁直流电机三维稳态温度场分析[J]. 机电原件, 2012, 32(2). http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jidyj201202010 |
| [5] | (美)英克鲁佩勒(Incropera, F. P.)等著; 葛新石, 叶宏译. 传热和传质基本原理: 第六版[M]. 北京: 化学工业出版社, 2007. 4. |
| [6] | KAIS A, DAVID H, PHILIP H M, et al. Rotor loss in permanent-magnet brushless AC machines[C]// IEEE Ttansactions on Industry Applications. 2000, 36(6): 1612–1618. |
| [7] | ZHU Z Q, HOWE D. BIRCH T S. Calculation of winding inductances of brushless motors with surface-mounted permanent magnet[C]//IEE, EMD97. |
 2018, Vol. 40
2018, Vol. 40
