2. 海军航空大学 航空基础学院,山东 烟台 264001
2. Academy of Aeronautical Foundation, Naval Aeronautical University, Yantai 264001, China
自主水下航行器(Autonomous Underwater Vehicle,AUV)具有自主性高、机动性好、探测地域大、隐蔽性强等显著优势,在水下环境中得到广泛应用,而要实现AUV的这些优势,最关键的是要实现AUV的自主导航与探测。然而,精准的AUV自主导算法需要系统提供远距离、长时间的精准速度、位置和姿态信息,而这一技术主要利用SLAM算法完成AUV的自主定位与制图。该算法可以描述为[1]:AUV从初始的位置出发,在未知环境中运动,依靠自身所携带的传感器对未知环境进行感知,处理计算机对传感器数据进行处理并创建地图,同时依据此地图对AUV进行导航。
SLAM算法最先由国外学者提出[2],并在国外发展迅速,由于在机器人的自主定位中广泛应用,算法的种类也越来越多,技术较为成熟。国内SLAM算法研究起步较晚,目前已在地面机器人、空中无人机和水下航行器等领域展开应用。本文提出一种基于EKF的水下SLAM算法[3],通过对特征进行2次探测,提高了AUV和特征的定位精度,以便更好实现AUV的自主精确导航与探测。
1 水下航行器模型构建航行器的运动模型和环境探测模型是SLAM系统的关键部分,AUV在水下的运动状态由航行器系统的运动模型体现,AUV装载的声呐传感器由环境探测模型表示。模型的创建需要在一致的坐标系内,本文采用全局坐标系作为航行器系统模型的基础坐标系。
1.1 AUV水下运动模型AUV相对于全局坐标系的位置和姿态,均可以通过运动坐标系相对全局坐标系的坐标值
| $\begin{split} {{\dot x}_g} = & u\cos \psi \cos \theta + v\left( {\cos \psi \sin \theta \sin \varphi - \sin \psi \cos \varphi } \right) + \\& w\left( {\cos \psi \sin \theta \cos \varphi + \sin \psi \sin \varphi } \right) \text{,}\end{split} $ | (1) |
| $\begin{split} {{\dot y}_g} = & u\sin \psi \cos \theta + v\left( {\sin \psi \sin \theta \sin \varphi + \cos \psi \cos \varphi } \right) + \\&w\left( {\sin \psi \sin \theta \cos \varphi - \cos \psi \sin \varphi } \right) \text{,}\end{split} $ | (2) |
| ${\dot z_g} = - u\sin \theta + v\cos \theta \sin \varphi + w\cos \theta \cos \varphi \text{,}$ | (3) |
| $\dot \varphi = p + q\sin \varphi \tan \theta + r\cos \varphi \tan \theta\text{,} $ | (4) |
| $\dot \theta = q\cos \varphi - r\sin \varphi \text{,}$ | (5) |
| $\dot \psi = q\sin \varphi /\cos \theta + r\cos \varphi /\cos \theta \text{。}$ | (6) |
式中:
声呐的探测信息是AUV测量环境特征位置、方向的信息来源[4],特征模型在全局坐标系[5]中的表示,需要对特征模型在传感器坐标系中的位置和方向

|
图 1 AUV观测模型 Fig. 1 Measurement model for AUV |
则观测方程可以表示为:
| ${Z_s}\left( k \right) \!\!=\! \!\left[\!\!\!\! {\begin{array}{*{20}{c}} {\rho \left( k \right)} \\ {\psi \left( k \right)} \\ {\theta \left( k \right)} \end{array}} \!\!\!\!\right] \!\!=\!\! \left[\!\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\sqrt {{{\left( {{x_g} \!\!-\!\! {x_s}\left( k \right)} \right)}^2} \!\!+ \!\!{{\left( {{y_g} \!\!-\!\! {y_s}\left( k \right)} \right)}^2} \!\!+\!\! {{\left( {{z_g} \!\!-\!\! {z_s}\left( k \right)} \right)}^2}} } \\ {\arctan \left( {\frac{{{y_g} - {y_s}\left( k \right)}}{{{x_g} - {x_s}\left( k \right)}}} \right) - {\psi _s}} \\ {\arctan \left( {\frac{{{z_g} - {z_s}\left( k \right)}}{{\sqrt {{{\left( {{x_g} - {x_s}\left( k \right)} \right)}^2} + {{\left( {{y_g} - {y_s}\left( k \right)} \right)}^2}} }}} \right) - {\theta _s}} \end{array}} \!\!\!\!\!\!\right] \!\!+\!\! \nu \left( k \right)\text{。}$ | (7) |
其中,
在建立水下自主航行器(AUV)系统模型基础上,提出采用基于捷联惯导系统与声呐传感器的水下自主航行器同时定位与制图算法EKF-SLAM算法。捷联惯导的导航原理[6]是通过惯性器件测量水下自主航行器的角速度和3个敏感轴向的加速度,并通过四元数法解算出自主水下航行器的位姿和速度,但是计算所得到的是近似值,存在计算误差,随时间增长导航偏差会不断增大。基于捷联惯导系统与声呐传感器的水下自主航行器同时定位与制图技术的EKF-SLAM算法,利用捷联惯导的输出参数与声呐传感器探测的环境特征估计定位,通过算法的递推更新滤除误差,提高导航定位精度[7]。
2.1 状态方程AUV的位置、姿态信息是通过对惯性导航器件的输出进行积分运算得到的,惯导器件的输出参数含有随机误差,将会影响到AUV的定位精度,且随着时间的累积,误差的影响也明显,最终导致AUV迷失方向。本文解决这一问题的方法是通过在AUV的状态向量中引入惯导器件的高斯误差[8],通过滤波器消除这一误差。
水下自主航行器的状态方程可以表示成:
| ${X_v}\left( {k{\rm{ + }}1} \right){\rm{ = }}{F_v}\left[ {{X_v}\left( k \right),{U_v}\left( k \right),k + 1} \right] + \omega \left( k \right)\text{。}$ | (8) |
式中:
不考虑AUV的俯仰和滚转运动,即
| ${\left[\!\!\!\! {\begin{array}{*{20}{c}} {{x_g}} \\ {{y_g}} \\ {{z_g}} \\ \psi \\ u \\ v \\ w \\ r \end{array}} \!\!\!\!\right]_{\left( {k + 1} \right)}} = {\left[\!\!\! {\begin{array}{*{20}{c}} {{x_g} + \left( {uT + \frac{{{T^2}}}{2}} \right)\cos \psi - \left( {vT + \frac{{{T^2}}}{2}} \right)\sin \psi } {{y_g} + \left( {uT + \frac{{{T^2}}}{2}} \right)\sin \psi + \left( {vT + \frac{{{T^2}}}{2}} \right)\cos \psi } {{z_g} + wT + \frac{{{T^2}}}{2}} {\psi + rT + \frac{{{T^2}}}{2}} {u + T} {v + T} {w + T} {r + T} \end{array}} \!\!\right]_{\left( k \right)}} \!\!\!\!+ \omega \left( k \right)\text{。}$ | (9) |
其中,
AUV利用装载在机身上的主动声呐,观测环境信息从而获得特征模型和探测声呐之间的几何位置关系,并以此为参考校正AUV的坐标。声呐探测模型是通过构建声呐传感器同特征模型之间的距离和方向获得的,则第
| $Z\left( k \right) = {H_i}\left[ {{X_v}\left( k \right),{m_i},k} \right] + v\left( k \right)\text{。}$ | (10) |
其中:
已知
| ${Z_s}\left( k \right) \!\!=\!\! \left[\!\!\!\!\! {\begin{array}{*{20}{c}} {\rho \left( k \right)} \\ {\psi \left( k \right)} \\ {\theta \left( k \right)} \end{array}} \!\!\!\!\!\!\right] \!\!=\!\! \left[\!\!\!\!\!\! {\begin{array}{*{20}{c}} {\sqrt {{{\left( {{x_g}\!\! -\!\! {x_s}\left( k \right)} \right)}^2}\!\! +\!\! {{\left( {{y_g} \!\!-\!\! {y_s}\left( k \right)} \right)}^2} \!\!+\!\! {{\left( {{z_g}\!\! -\!\! {z_s}\left( k \right)} \right)}^2}} } \\ {\arctan \left( {\frac{{{y_g} - {y_s}\left( k \right)}}{{{x_g} - {x_s}\left( k \right)}}} \right) - {\psi _s}} \\ {\arctan \left( {\frac{{{z_g} - {z_s}\left( k \right)}}{{\sqrt {{{\left( {{x_g} - {x_s}\left( k \right)} \right)}^2} + {{\left( {{y_g} - {y_s}\left( k \right)} \right)}^2}} }}} \right) - {\theta _s}} \end{array}} \!\!\!\!\!\!\right] \!\!+\!\! \nu \left( k \right)\text{。}$ | (11) |
由于
| $H = \nabla h = \frac{{\partial h}}{{\partial {x_h}}}{|_{\left( {{x_k},{u_k}} \right)}}\text{,}$ | (12) |
便可实现观测方程的线性化,观测方程可写为:
| $\delta Z\left( {k + 1} \right) = H\delta X\left( k \right)\text{。}$ | (13) |
AUV工作环境为100 m×100 m水下模拟环境,以特征点表示水下信标、海丘、海岭等特征明显的海底地貌,仿真图用*表示特征点。AUV是以3±0.3 m/s的恒定航速做匀速运动,初始角为0°,最大转弯角30±3°,最大转弯角速度为20 rad/s。声呐探测的最远距离为30 m,测量误差为0.1 m,则状态方程的误差协方差
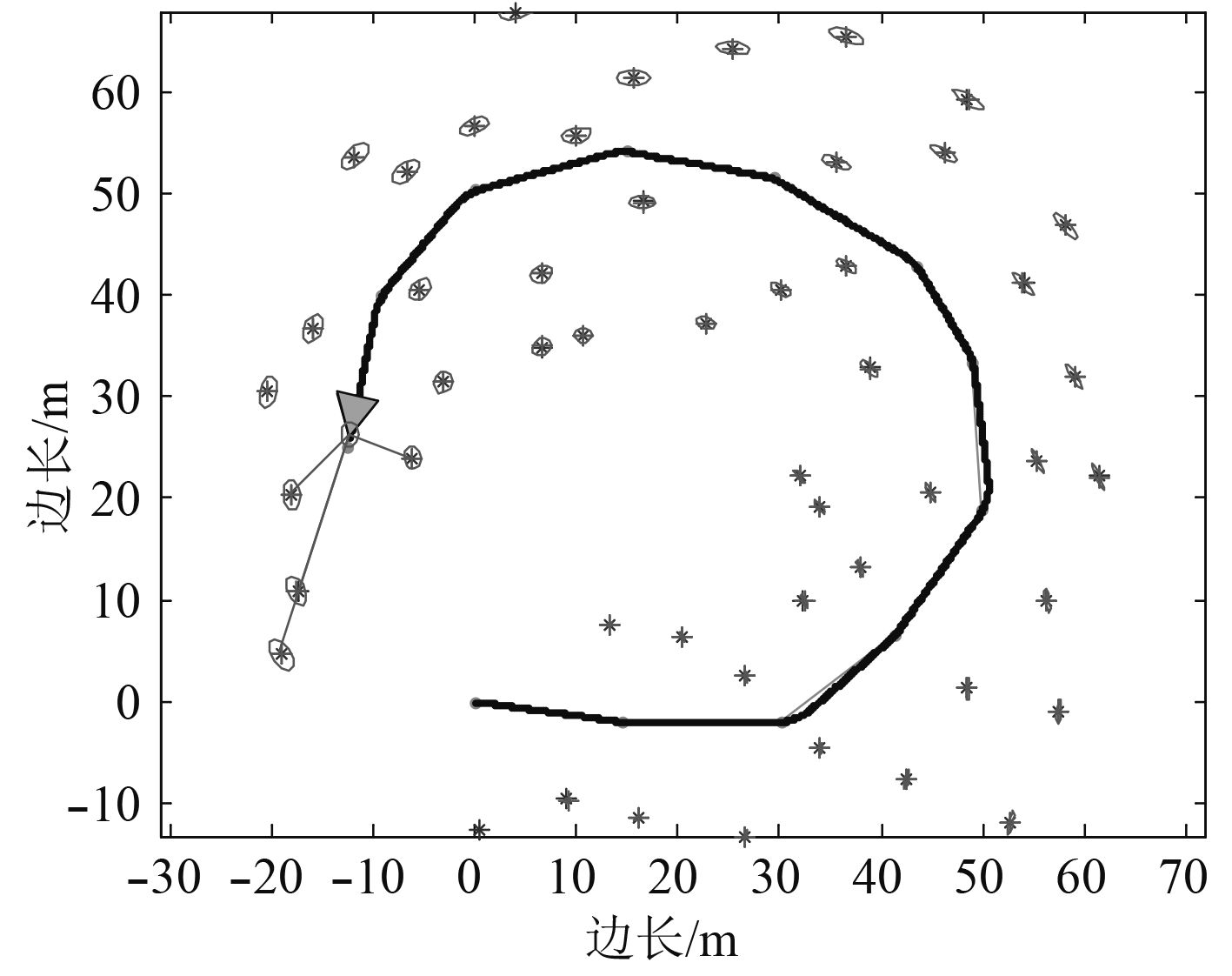
|
图 2 50个特征点时的EKF-SLAM算法仿真 Fig. 2 Simulation results of EKF-SLAM algorithm with 50 features |
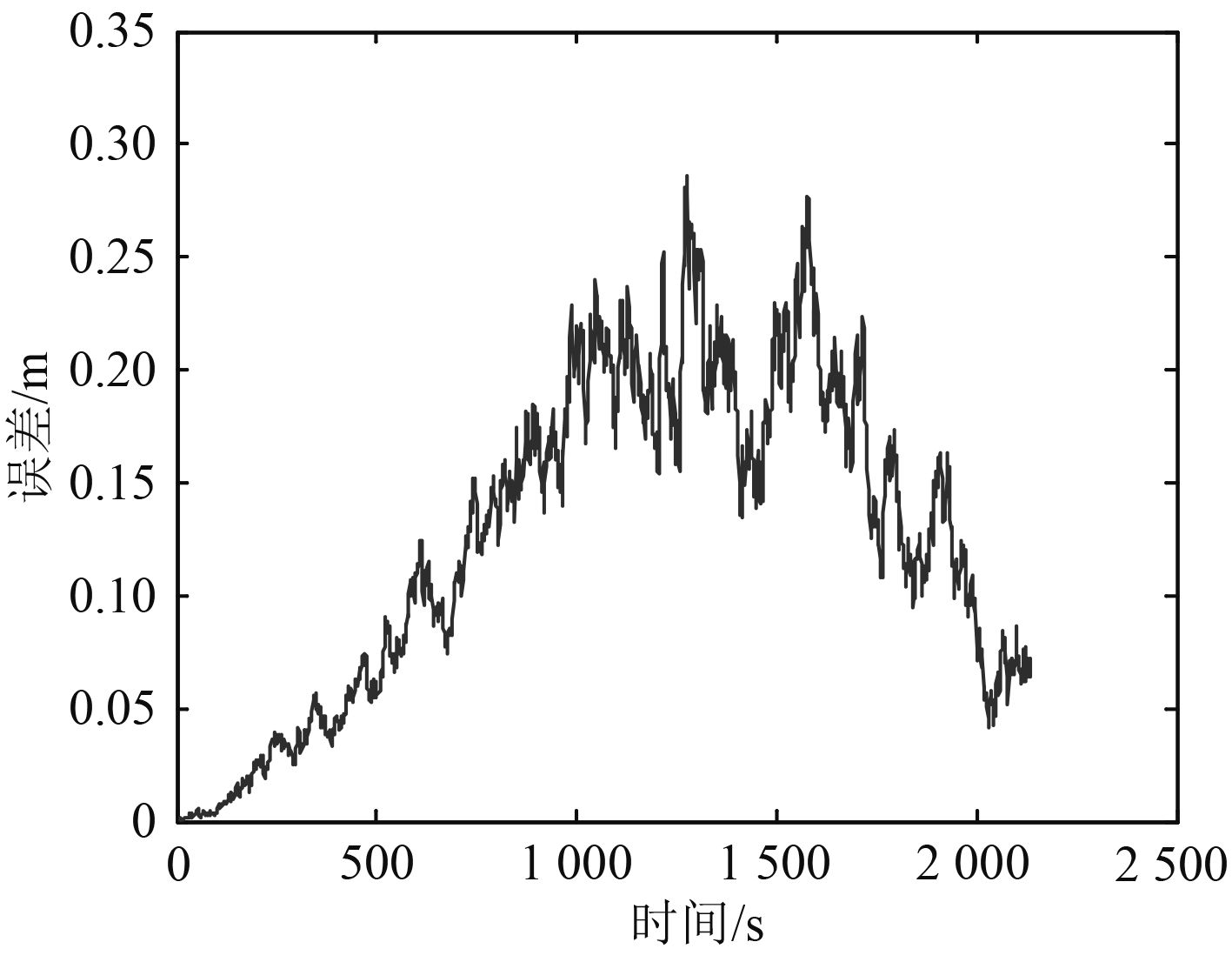
|
图 3 50个特征点的AUV定位误差 Fig. 3 Position errors for AUV with 50 features |
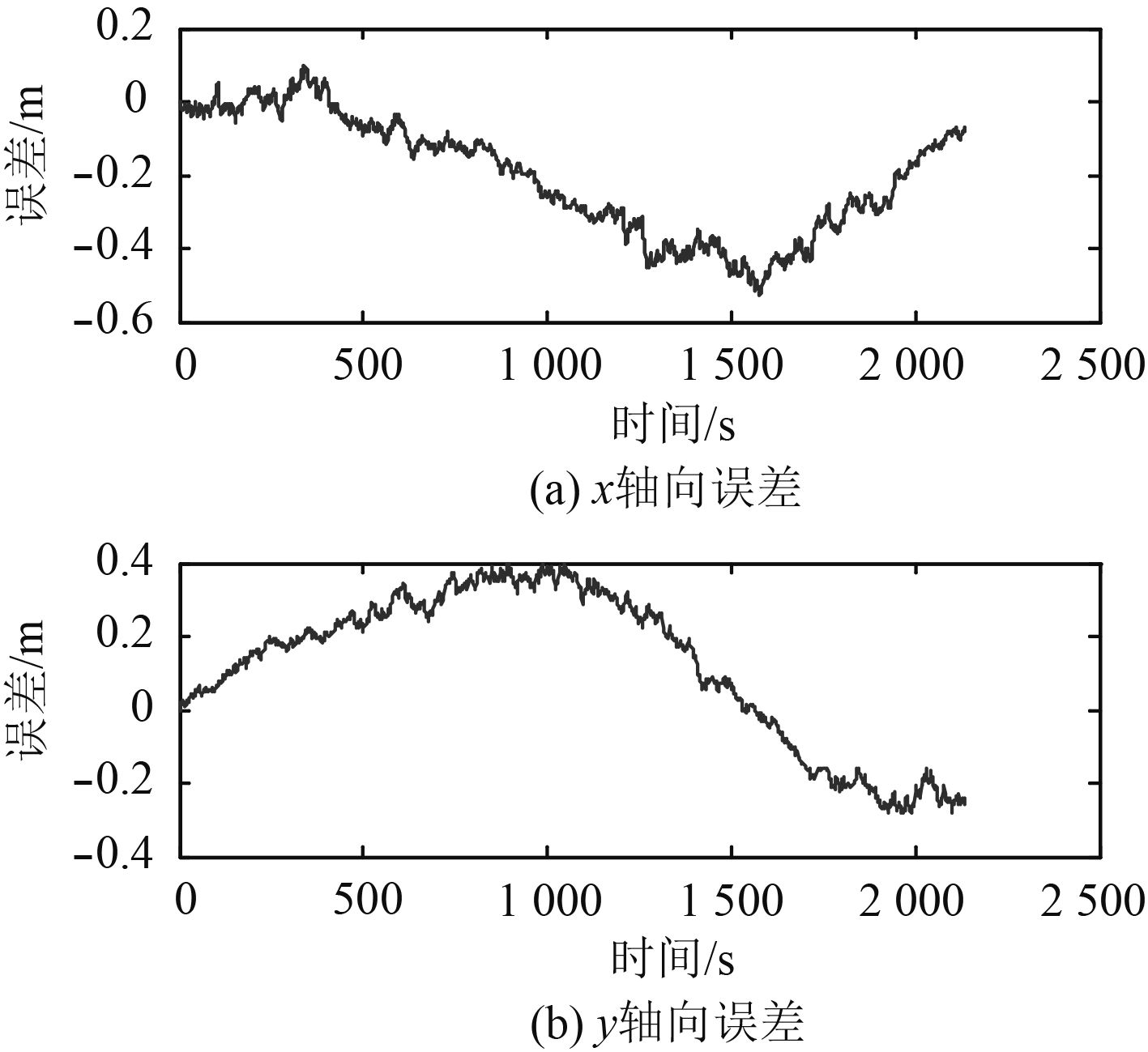
|
图 4 AUV在x轴与y轴向上的定位误差 Fig. 4 Position errors on x and y axis for AUV |
从图3和图4可以看出,在环境特征点为50个时,AUV的定位与制图精度较高,且呈收敛趋势,算法具有较好的稳定性。AUV在x轴向的定位误差在沿x轴向运动时误差较小,沿y轴向运动时误差较大;在y轴向的定位误差与x轴向的情况相反。
为检验算法的数据关联作用,在环境特征点为50个时做2次圆周运动的定位与制图精度,如图5所示。

|
图 5 二次圆周运动的EKF-SALM算法仿真 Fig. 5 Simulation results of EKF-SLAM algorithm with the second circular motion |

|
图 6 二次圆周运动的AUV定位误差 Fig. 6 Position errors for AUV with the second circular motion |
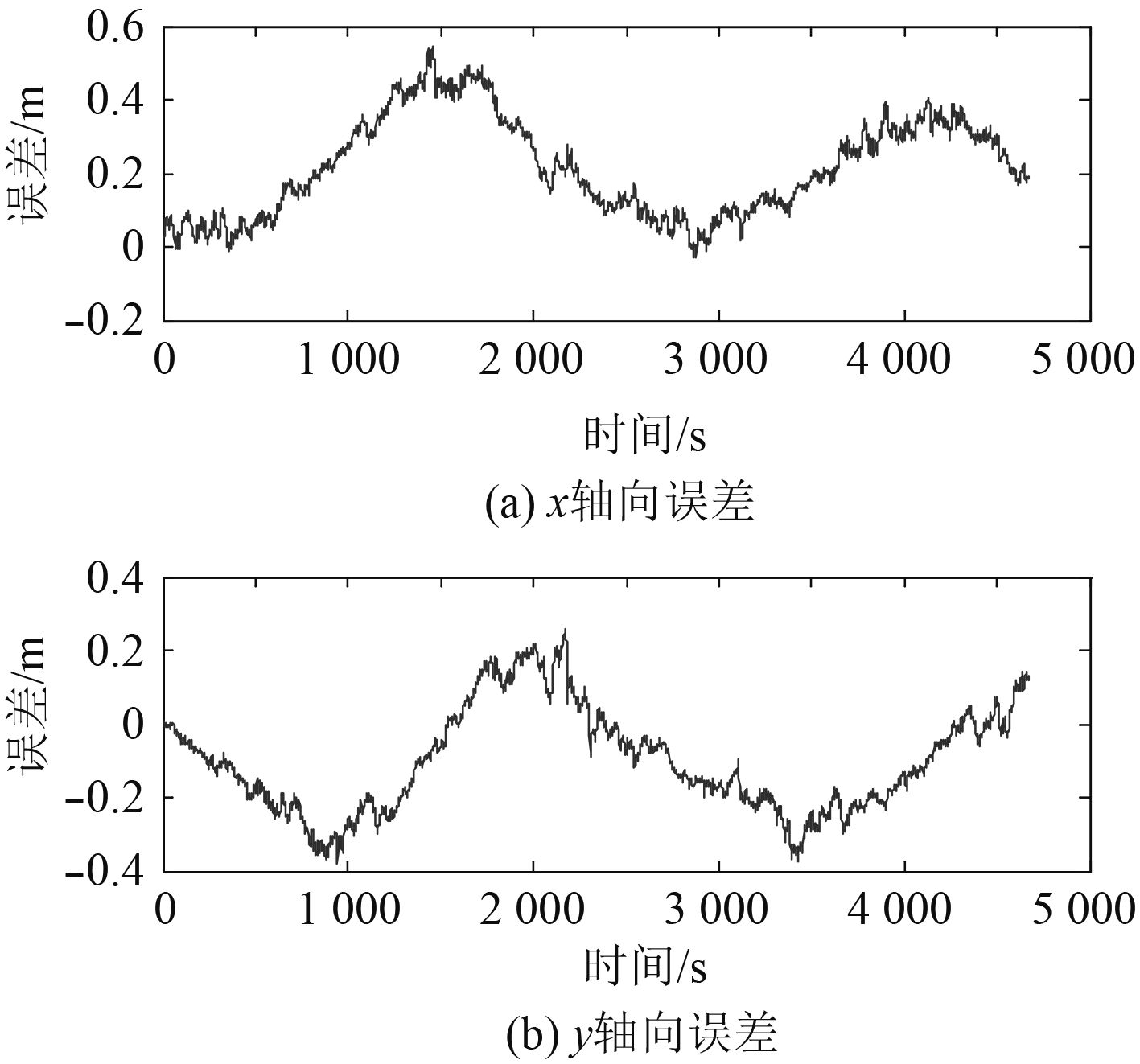
|
图 7 二次圆周运动的AUV在x轴与y轴向上的定位误差 Fig. 7 Position errors on x and y axis for AUV with the second circular motion |
从图6和图7可以看出,AUV采用2次探测路径运动时,定位误差明显降低,其主要原因是由于通过数据关联对特征点的重复关联匹配,使特征点位置更好地修正。在AUV的定位误差较大时,对已探测过的区域进行重复探测,可以提高AUV的定位与制图精度。
4 结 语本文在建立AUV运动模型与声呐模型的基础上,研究了基于EKF的SLAM算法,并采用数据关联方法优化了滤波算法,且提高算法定位精度。在环境特征点较多时,仿真验证了算法在圆形路径下的定位与制图精度,结果表明算法的精度符合实际要求;对比相同环境特征密度下,采用2次探测路径,结果表明该算法可有效提高AUV定位精度,从而验证了该算法的有效性和可行性。实际应用中,外界的三维环境非常复杂,可能还包含许多动态目标,对此还需进一步深入研究。
| [1] | 刘明雍, 赵涛, 周良荣. SLAM算法在AUV中的应用进展[J]. 鱼雷技术, 2010, 18(1): 41–48. http://mall.cnki.net/magazine/Article/YLJS201001010.htm |
| [2] | 张恒, 樊晓平. 移动机器人同步定位与地图构建过程中的轨迹规划研究[J]. 机器人. 2006, 28(3): 285–290. http://mall.cnki.net/magazine/Article/JQRR200603009.htm |
| [3] | FREDRIK O. Comparison of kalman filter estimation approaches for state space models with nonlinear measurements[C]//Proceedings of Scandinavian Conference on Simulation and Modeling, SIMS, 2005. |
| [4] | 曹军, 曾碧, 何元烈. 基于路标观测的改进 EKF-SLAM 算法[J]. 自动化与信息工程, 2014, 35(1): 21–31. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gdzdhyxxgc201401005 |
| [5] | 黄鲁粤. 基于惯性传感器与声纳的水下机器人定位与地图构建[D]. 青岛: 中国海洋大学, 2010. |
| [6] | 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2012. 198–211. |
| [7] | WEBB T, PRAZENICA R, KURDIAL A, et al. Vision based state estimation for autonomous micro air vehicles[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 816–826. |
| [8] | 蔡自兴, 贺汉根, 陈虹. 未知环境中移动机器人导航控制理论与方法[M]. 北京: 科学出版社, 2009. |
| [9] | 王希彬. 无人机视觉同时定位与地图构建技术[D]. 烟台: 海军航空工程学院, 2012. |
| [10] | 王永清. 同时定位与地图创建中的数据关联技术研究[D]. 青岛: 中国海洋大学, 2007. |
| [11] | 张碧丛, 李琳. 马氏距离在移动机器人导航中的应用[J]. 机械设计与制造, 2012, 5(6): 59–63. http://mall.cnki.net/magazine/Article/HEBG200402011.htm |
 2018, Vol. 40
2018, Vol. 40
