0 引　言

在实验室环境中，惯性系统仿真试验平台用来模拟船舶在海浪中的运动，可以用于研究船舶受风浪影响之后的变化情况，也可以用于对各种船用仪器设备进行陆地测试等。舰艇空间运动仿真通过对初始导航信息、海洋环境信息、舰艇运动模型和空间运动状态的设置完成，从而生成导航信息，完成惯导精度测试的工作。

对于连续运行时间很长的船用惯导系统，惯性指示位置和航向角的主要误差源是系统陀螺仪未被补偿的漂移误差，特别是随机漂移误差，为了保持希望的位置精度和航向精度，需要对系统进行综合校准^[1]，也就是重新装订导航系统运行的初始条件。高精度导航技术是惯性系统仿真试验平台的关键，而综合校准技术是高精度导航技术中需要重点研究的关键技术之一。

1 综合校准技术

惯性导航系统正常运行需要设定10个初始条件，为了缩短系统重调时间，通常来说，经纬度和位置误差直接由外部参考测量提供，同时依靠水平速度阻尼使北向和东向速度误差小到可以免去重调。剩下还有3个水平失准角和水平失准角速度^[2]，共计6个参数。

1.1 综合校准误差模型

对于在地球表面上运行的惯性导航系统，通常选择北-东-地本地水平指北坐标系NED（简记为n坐标系）作为导航解算坐标系。其中，N轴水平指北，E轴水平指东，D轴垂直向下。因为导航系统解算坐标系a和惯导系统测量参考坐标系m都与坐标系n重合，可以得到速度矢量微分方程和位置坐标矢量微分方程的导航解算方程组^[3]。

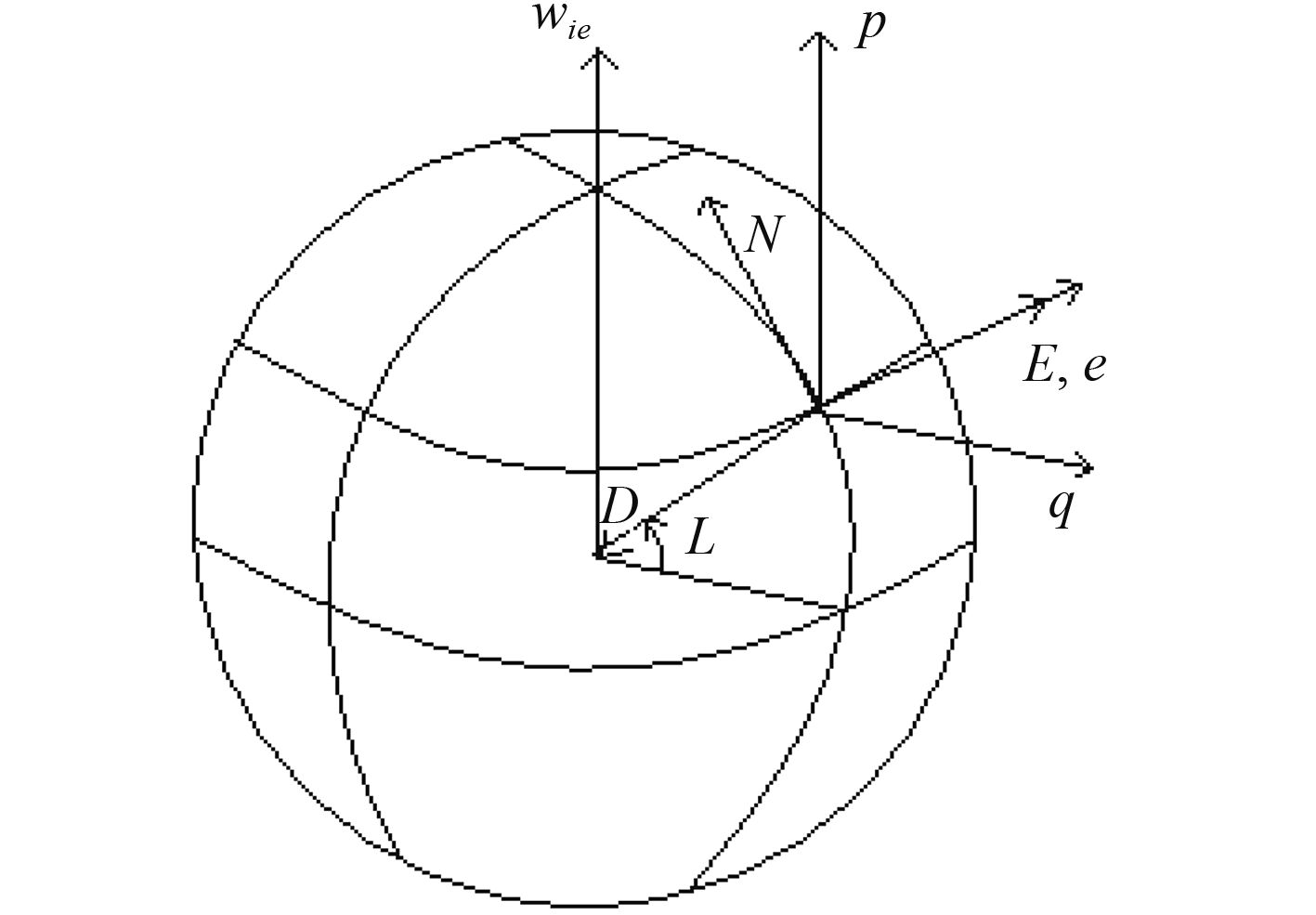
为了求解方便，定义与NED当地水平指北坐标系不同的另一个右手坐标系，即qep坐标系。船用惯导一般采用qep右手坐标系作为平台坐标系P^[4]，参考图1。坐标系qep的原点在运载体质心，各坐标轴定义如下：

q轴为赤道轴，平行于赤道平面与本地子午面的交线，由地轴指向外；

e轴为纬度轴，与等纬度圈相切，指向东；

p为极轴，平行于地球自转轴。

坐标系NED绕E轴旋转90°+L便得坐标系qep，2个坐标系之间的方向余弦矩阵可表示为：

${\bf C}_{NED}^{qep} = \left[ {\begin{array}{*{20}{c}}{ - \sin L} & 0 & { - \cos L}\\0 & 1 & 0\\{\cos L} & 0 & { - \sin L}\end{array}} \right]\text{。}$

(1)

平台坐标系P相对计算坐标系C的漂移角 ${\dot \psi ^p}$ 满足下列微分方程：

${\dot \psi ^p} = - [\omega _{ip}^p]{\psi ^p} + \delta \omega _d^p\text{，}$

(2)

式中： ${\dot \psi ^p}$ 为 $\psi $ 角在平台坐标系中的时间导数； $[ \omega _{ {ip}}^{ p}]$ 为P系相对惯性坐标系的角速度的反对称矩阵； $\delta \omega _d^p$ 为在P系中表示的未被补偿的平台漂移角速度误差矢量。

一般情况情况下，平台角速度 $\omega _{ip}^p$ 是时变的。当P系对准qep坐标系时，可以合理假设 $\omega _{ip}^p \approx \omega _{ie}^p$ 为常量。假设陀螺漂移角速度误差 $\delta \omega _d^p = {\left[ {\begin{array}{*{20}{c}} {{\varepsilon _q}}&{{\varepsilon _e}}&{{\varepsilon _p}} \end{array}} \right]^{\rm T}}$ 为常数，其ψ角误差方程如下：

$\begin{align}&{\psi _q}\left( t \right) = {\psi _q}\left( {{t_0}} \right)\cos {\omega _{ie}}\left( {t - {t_0}} \right) + {\psi _e}\left( {{t_0}} \right)\sin {\omega _{ie}}\left( {t - {t_0}} \right)+\\ & \frac{{{\varepsilon _q}}}{{{\omega _{ie}}}}\sin {\omega _{ie}}\left( {t - {t_0}} \right) + \frac{{{\varepsilon _e}}}{{{\omega _{ie}}}}\left( {1 - \cos {\omega _{ie}}\left( {t - {t_0}} \right)} \right)\text{，}\\[8pt] &{\psi _e}\left( t \right) = - {\psi _q}\left( {{t_0}} \right)\sin {\omega _{ie}}\left( {t - {t_0}} \right) + {\psi _e}\left( {{t_0}} \right)\cos {\omega _{ie}}\left( {t - {t_0}} \right)-\\ & \frac{{{\varepsilon _q}}}{{{\omega _{ie}}}}\left( {1 - \cos {\omega _{ie}}\left( {t - {t_0}} \right)} \right) + \frac{{{\varepsilon _e}}}{{{\omega _{ie}}}}\sin {\omega _{ie}}\left( {t - {t_0}} \right)\text{，}\\[8pt] &{\psi _p}\left( t \right) = {\psi _p}\left( {{t_0}} \right) + {\varepsilon _p}\left( {t - {t_0}} \right)\text{。}\end{align} $

(3)

式中：Ψ_q，Ψ_e，Ψ_p为3个坐标轴方向的漂移误差角，即平台坐标系相对计算坐标系的转角矢量；ε_q，ε_e，ε_p为3个坐标轴方向的陀螺常值漂移角速度ω_ie为地球自转角速度。

当船用惯导系统采用高度阻尼和水平速度阻尼时候，可以略去加速度计误差和参考速度误差，可得经纬度误差和方位角误差与ψ角的关系式为

$\left[ {\begin{array}{*{20}{c}} {\delta l} \\ {\delta L} \\ {{\varphi _d}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\tan L}&0&{ - 1} \\ 0&1&0 \\ { - 1/{\rm cos}L}&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _q}} \\ {{\psi _e}} \\ {{\psi _p}} \end{array}} \right]\text{。}$

(4)

式中：δ_l为经度误差；δ_L为纬度误差；ϕ_d为方位角误差。

1.2 GPS三点校方案

一般来说，要解决3个平台失准角和3个平台角速度（即陀螺漂移角速度）共计6个未知参数，需要建立包含这6个未知数的6个独立方程。若系统由GPS提供外部参考位置信息，采用GPS位置信息进行惯导系统的综合校准，至少需要进行3次独立观测。系统状态方程为：

${z_i} = {H_1}\Psi \left( {{t_i}} \right) + {v_i}\text{。}$

(5)

式中： ${H_1} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\tan L}\\ 0 \end{array}} & {\begin{array}{*{20}{c}} 0\\ 1 \end{array}} & {\begin{array}{*{20}{c}} { - 1}\\ 0 \end{array}} \end{array}} \right]$ ；v_i为观测噪声。

令t₁，t₂，t₃表示可以由GPS获得外部参考位置的时刻，假设在t₁时刻舰艇获得第1点参考位置， ${z_1} = {H_1}\varPsi \left( {{t_1}} \right)$ 。

在第2个参考位置：

${z_2} = {H_2}\varPsi \left( {{t_2}} \right)\text{。}$

(6)

式中： $\varPsi \left( {{t_2}} \right)$ 可表示为

$\varPsi \left( {{t_2}} \right) = {\varPhi} \left( {{t_2},{t_1}} \right)\varPsi \left( {{t_1}} \right) + { B}\left( {{t_2},{t_1}} \right)\varepsilon \left( {{t_1}} \right)\text{。}$

(7)

式中：Φ（t₂，t₁）为系统转移矩阵；B（t₂，t₁）为系统控制矩阵。

在第3点参考位置，观测方程为：

${z_3} = {H_3}\varPsi \left( {{t_3}} \right)\text{。}$

(8)

$\begin{align}& \varPsi \left( {{t_3}} \right) = {\varPhi} \left( {{t_3},{t_1}} \right)\varPsi \left( {{t_1}} \right) + {\varPhi} \left( {{t_3},{t_2}} \right){ B}\left( {{t_2},{t_1}} \right)\varepsilon \left( {{t_1}} \right) +\\ & { B}\left( {{t_3},{t_2}} \right)\varepsilon \left( {{t_2}} \right)\text{。}\end{align}$

(9)

在无噪声的情况下，可以利用上述3个方程来联合确定校正量。将联立方程展开后，可得6维矢量-矩阵代数方程如下：

$\begin{split}&\left[ {\begin{array}{*{10}{c}}{\tan L} \!\!\!&\!\!\! 0 \!\!\!& \!\!\!{ - 1} \!\!\!& \!\!\!0 \!\!\!&\!\!\! 0 \!\!\!& \!\!\!0\\0 \!\!\!& \!\!\!1 & \!\!\!0 &\!\!\! 0 \!\!\!& \!\!\!0 \!\!\!& \!\!\!0\\{\tan L\cos {\omega _{ie}}\left( {{t_2} - {t_1}} \right)}\!\!\! &\!\!\! {\tan L\sin {\omega _{ie}}\left( {{t_2} - {t_1}} \right)} \!\!\!&\!\!\! { - 1}\!\!\! &\!\!\! {\tan L\sin {\omega _{ie}}\left( {{t_2} - {t_1}} \right)}\!\!\! &\!\!\!{\tan L\left[ {1 - \cos {\omega _{ie}}\left( {{t_2} - {t_1}} \right)} \right]}\!\!\! & \!\!\!{ - {\omega _{ie}}\left( {{t_2} - {t_1}} \right)}\\{ - \sin {\omega _{ie}}\left( {{t_2} - {t_1}} \right)} \!\!\!& \!\!\!{\cos {\omega _{ie}}\left( {{t_2} - {t_1}} \right)} \!\!\!& \!\!\!0\!\!\! &\!\!\! { - 1 + \cos {\omega _{ie}}\left( {{t_2} - {t_1}} \right)} \!\!\!& \!\!\!{\sin {\omega _{ie}}\left( {{t_2} - {t_1}} \right)} \!\!\!&\!\!\! 0\\{\tan L\cos {\omega _{ie}}\left( {{t_3} - {t_1}} \right)} \!\!\!& \!\!\!{\tan L\sin {\omega _{ie}}\left( {{t_3} - {t_1}} \right)} \!\!\!&\!\!\! { - 1} \!\!\!& \!\!\!{\tan L\sin {\omega _{ie}}\left( {{t_3} - {t_1}} \right)} \!\!\!&\!\!\! {\tan L\left[ {1 - \cos {\omega _{ie}}\left( {{t_3} - {t_1}} \right)} \right]}\!\!\! &\!\!\! { - {\omega _{ie}}\left( {{t_3} - {t_1}} \right)}\\{ - \sin {\omega _{ie}}\left( {{t_3} - {t_1}} \right)} \!\!\!&\!\!\! {\cos {\omega _{ie}}\left( {{t_3} - {t_1}} \right)} \!\!\!& \!\!\!0 \!\!\!& \!\!\!{ - 1 + \cos {\omega _{ie}}\left( {{t_3} - t} \right)}\!\!\! &\!\!\! {\sin {\omega _{ie}}\left( {{t_3} - {t_1}} \right)}\!\!\! &\!\!\! 0\end{array}} \right] \times \\&\left[ {\begin{array}{*{20}{c}}{{\varPsi _q}\left( {{t_1}} \right)}\\{{\varPsi _e}\left( {{t_1}} \right)}\\{{\varPsi _p}\left( {{t_1}} \right)}\\{{\varepsilon _q}\left( {{t_1}} \right)/{\omega _{ie}}}\\{{\varepsilon _e}\left( {{t_1}} \right)/{\xi _{ie}}}\\{{\varepsilon _p}\left( {{t_1}} \right)/{\omega _{ie}}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}{\delta {l_1}}\\{\delta {l_1}}\\{\delta {l_2}}\\{\delta {l_2}}\\{\delta {l_3}}\\{\delta {l_3}}\end{array}} \right]\text{。}\end{split}$

(10)

上面的方程组是奇异的，产生奇异的原因是东向陀螺漂移偏置 ${\varepsilon _e}\left( {{t_1}} \right)$ 引起方位失准角 ${\varphi _D} = - {\varepsilon _e}/{\omega _{ie}}\cos L$ ，而东西陀螺漂移偏置和方位失准角传递到导航位置误差是等同的。根据式（10）可以由最小二乘法求得 ${\hat \varPsi _q}\left( {{t_1}} \right),{\hat \varPsi _e}\left( {{t_1}} \right),{\hat \varPsi _p}\left( {{t_1}} \right),{\hat \varepsilon _q},{\hat \varepsilon _e},{\hat \varepsilon _p}$ ，之后就可以按第2次标校和第3次标校作出最优估计，对系统进行综合校正。这种GPS三点校正的方法必须用有3点位置观测，综合校正应在观测时刻精确应用。

1.3 外参考速度校准方案

若依靠外部辅助测量装置能获得精确的参考速度信号，如多普勒速度仪等，可以采用外参考速度校准方案。空间稳定惯性导航系统在速度阻尼条件下的水平速度误差是位置误差的微分，随着时间t增长，忽略陀螺仪与g有关的漂移速度误差系数及加速度误差系数可得简化速度误差表达式为：

$\begin{align}& \delta {v_N} = - R{\omega _{ie}}\left[ {\left( {\varPsi _x^e\left( 0 \right) + \Delta {\varepsilon _{1x}}t} \right)\cos {\gamma _2}\left( t \right) + } \right.\\ &\left. {\left( {\varPsi _y^e\left( 0 \right) + {\Delta _{1y}}t} \right)\sin {\gamma _2}\left( t \right)} \right]\text{，}\\ &\delta {v_E} = R{\omega _{ie}}\sin L\left[ { - \left( {\varPsi _x^e\left( 0 \right) + \Delta {\varepsilon _{1x}}t} \right)\sin {\gamma _2}\left( t \right) + } \right.\\&\left. {\left( {\varPsi _y^e\left( 0 \right) + \Delta {\varepsilon _{1y}}t} \right)\cos {\gamma _2}(t)} \right] - R\Delta {\varepsilon _{2z}}\cos L\text{。}\end{align}$

(11)

式中：δ_VN为北向速度误差；δ_VE为东向速度误差；R为地球半径；Ψ_x，Ψ_y为载体坐标系变换到地球坐标系的平台失准角；γ₂为在绕Zp轴负方向的旋转角；ε_1x，ε_1y，ε_2z为空间稳定平台相对惯性坐标系的陀螺常值漂移角速度。

由式（11）可以得到：

$\begin{split}& \delta \left[ {\begin{array}{*{20}{c}}{\cos {\gamma _2}\left( {{t_1}} \right)} & {\sin {\gamma _2}\left( {{t_1}} \right)}\\ \vdots & \vdots \\{\cos {\gamma _2}\left( {{t_1} + n\Delta t} \right)} & {\sin {\gamma _2}\left( {{t_1} + n\Delta t} \right)}\end{array}} \right]\left[ {\begin{array}{*{20}{c}}{\varPsi _{x0}^e}\\{\varPsi _{y0}^e}\end{array}} \right] = \\ & \left[ {\begin{array}{*{20}{c}}{ - \frac{{\delta {v_N}\left( {{t_1}} \right)}}{{{R_{{w_{ie}}}}}}}\\ \vdots \\{ - \frac{{\delta {v_N}\left( {{t_1} + n\Delta t} \right)}}{{{R_{{\omega _{ie}}}}}}}\end{array}} \right]\text{。}\end{split}$

(12)

式中：Ψ_x0，Ψ_y0均为载体坐标系变换到地球坐标系的平台失准角估计值。

式（12）有最小二乘解：

$\begin{array}{l}\left[ {\begin{array}{*{20}{c}}{\overline {\varPsi _{x0}^e} }\\[8pt]{\overline {\varPsi _{y0}^e} }\end{array}} \right] = \left[\!\!\! {\begin{array}{*{20}{c}}{\displaystyle\sum\limits_{i = 0}^n {{{\cos }^2}{\gamma _2}\left( {{t_1} + i\Delta t} \right)} } & {\displaystyle\frac{1}{2}\sum\limits_{i = 0}^n {2{\gamma _2}\left( {{t_1} + i\Delta t} \right)} }\\ \vdots & \vdots \\{\displaystyle\frac{1}{2}\sum\limits_{i = 0}^n {\sin 2{\gamma _2}\left( {{t_1} + i\Delta t} \right)} } & {\displaystyle\sum\limits_{i = 0}^n {{{\sin }^2}{\gamma _2}\left( {{t_1} + i\Delta t} \right)} }\end{array}} \!\!\!\right]\times \\[10pt] \left[ {\begin{array}{*{20}{c}}{ - \displaystyle\sum\limits_{i = 0}^n {\displaystyle\frac{{\delta {v_N}\left( {{t_1} + i\Delta t} \right)\cos {\gamma _2}\left( {{t_1} + i\Delta t} \right)}}{{{R_{{w_{ie}}}}}}} }\\ \vdots \\{ - \displaystyle\sum\limits_{i = 0}^n {\displaystyle\frac{{\delta {v_N}\left( {{t_1} + i\Delta t} \right)\sin {\gamma _2}\left( {{t_1} + i\Delta t} \right)}}{{{R_{{\omega _{ie}}}}}}} }\end{array}} \right]\text{。}\quad\quad\quad\quad\ \ (13)\end{array}$

将最小二乘估计 $\overline {\varPsi _{x0}^e} $ 和 $\overline {\varPsi _{y0}^e} $ 分别除以（t₁+t₂）/2，可得 $\Delta {\hat \varepsilon _{1x}}$ 和 $\Delta {\hat \varepsilon _{1y}}$ 的近似值：

$\begin{array}{l}\Delta {{\hat \varepsilon }_{1x}} = 2\overline {\varPsi _{x0}^e} /\left( {{t_1} + {t_2}} \right)\text{，}\\[7pt]\Delta {{\hat \varepsilon }_{1y}} = 2\overline {\varPsi _{y0}^e} /\left( {{t_1} + {t_2}} \right)\text{。}\end{array}$

(14)

在将 $\varPsi _{x0}^e$ 和 $\varPsi _{y0}^e$ 代入速度误差表达式的第2项得：

$\begin{split}& \overline {\Delta {{\hat \varepsilon }_{2x}}} = - \displaystyle\frac{1}{{\left( {n + 1} \right)R\cos L}}\sum\limits_{i = 0}^n {\left[ {\delta {v_E}\left( {{t_1} + i\Delta t} \right) + {R{\omega _{ie}}\sin L}} \right.} \\[3pt]& \left. {\left( {\overline {\varPsi _{x0}^e} \sin {\gamma _2}\left( {{t_1} + i\Delta t} \right) - \overline {\varPsi _{y0}^e} \cos {\gamma _2}\left( {{t_1} + i\Delta t} \right)} \right)} \right]\text{。}\end{split}$

(15)

然而，由于速度信号比位置信号伴随较多的随机误差，因此，为了确保综合校准精度，在t_c时刻提供一点外参考位置是必要的。令

$\!\!\!\begin{array}{l}\left\{\begin{array}{l}\delta l\tilde L\left( {{t_c}} \right) = - \delta \tilde \varPsi _x^e\sin {\gamma _2}\left( {{t_c}} \right) + \delta \tilde \varPsi _y^e\cos {\gamma _2}\left( {{t_c}} \right)\text{，}\\[5pt]\delta \tilde l\left( {{t_c}} \right) = \tan L\left[ {\delta \tilde \varPsi _x^e\cos {\gamma _2}\left( {{t_c}} \right) + \delta \tilde \varPsi _y^e\sin {\gamma _2}\left( {{t_c}} \right)} \right] - \\ \Delta {{\hat \varepsilon }_{2z}}{t_c}\text{。}\end{array}\right.\end{array}$

(16)

结合外参考位置，可以得到综合校准修正量：

$\begin{array}{l}\left\{\begin{array}{l}\Delta {{\tilde \varepsilon }_{1x}} = \Delta {{\tilde \varepsilon }_{1Y}} = \displaystyle\frac{{\delta \tilde L\left( {{t_c}} \right)}}{{\left( {\cos {\gamma _2}\left( {{t_c}} \right) - \sin {\gamma _2}\left( {{t_c}} \right)} \right){t_c}}}\text{，}\\[8pt]\Delta {{\tilde \varepsilon }_{2x}} = \left\{ {\delta \tilde L\left( {{t_c}} \right)\tan L\left[ {\displaystyle\frac{{1 + \sin 2{\gamma _2}\left( {{t_c}} \right)}}{{\cos 2{\gamma _2}\left( {{t_c}} \right)}}} \right] - \delta \tilde l\left( {{t_c}} \right)/{t_c}} \right\}\text{。} (17)\end{array}\right.\end{array}$

2 结　语

上述综合校准方案与其他关键的高精度导航技术如初始对准技术、水平阻尼技术、各类组合导航技术等相融合，为导航系统运行提供精确的初始条件，为下一步惯性系统仿真试验平台研制奠定基础。该平台结合3轴模拟试验台模拟不同海况下舰船摇摆的情况，考核惯导系统的姿态指标，又可与模拟惯导解算生成的惯导信息进行比对，评估惯导系统技术指标的合理性。从而实现对惯导系统技战术指标的检测和鉴定，达到在实验室中测试各型导航设备的目的。