在舰船磁隐身设计中,为了预测新造舰艇的磁场特性,目前主要采用母型船修正和物理模型2种方法,在实际应用中均受到很大限制。母型船修正法依赖于此前曾经设计过的相近船型,且船体钢材也需接近。在缺乏母型船的情况下,此方法并无应用价值,特别是对于新船型设计。此方法周期比较长,且成本较高[1]。由此可见,传统的磁场预测方法难以满足现在高速、高质量的舰船设计与建造要求,特别是涉及新船型、新材料的舰船磁场分布问题及磁场目标值的优化问题,传统方法显得过于低效。
作为一种新的磁场特性预测方法,仿真法具有明显的优越性,可以极大提高舰船消磁系统的设计手段,既能快速、准确地预估舰船的感应磁场和绕组磁场,还能对消磁系统多种配置方案进行优化。
国外通常在舰船结构设计的同时利用强大的磁场分析软件对舰船进行仿真建模[2 – 5],以及消磁绕组建模,预测出舰船感应磁场及消磁绕组磁场的分布特征,提出消磁绕组配置的初步技术指标,为消磁系统设计提供技术依据。随着舰船各个阶段设计的逐步深入,相应地修改、调整数学模型,最终模拟出准确的感应磁场,并通过不同消磁绕组的位置及形状获取不同的消磁绕组磁场,进行消磁绕组优化设计,再利用物理模型或实船进行验证。
在舰船消磁系统设计中,法国、英国、德国等发达国家均使用仿真软件,采用有限元算法进行建模仿真计算。他们的设计技术具有通用性好、研究周期短、研制成本低等特点。
本文以基于有限元算法的通用电磁场仿真软件Flux为工具,对舰船磁场特性预测进行研究。
1 舰船磁场计算原理现代舰船一般用钢铁建造。在地球磁场的磁化作用下,在船体周围空间产生舰船磁场。该过程可视为弱磁场作用下铁磁物质的静态磁化,而其感应磁场部分可视为可逆磁化。此外,舰船磁场主要关注舰船外部区域的磁场。因此,舰船感应磁场计算可视为一个开域静磁场问题。
麦克斯韦方程是电磁场分析的基础,而静态磁场方程由麦克斯韦电磁方程简化而来,其基本方程式如下[6]:
| $\left\{ \begin{array}{l}div\overrightarrow B = 0\text{,}\\rot\overrightarrow H = \overrightarrow J \text{,}\\\overrightarrow B = \mu \overrightarrow H \text{。}\end{array} \right.$ | (1) |
其中:
为了求解方程(1),需引入矢量模型和标量模型。矢量模型一般适用于2D静磁问题,使用磁矢位,而标量模型则一般适用于3D静磁问题,使用磁标势。舰船感应磁场的计算属于3D静磁问题,因此使用的是磁标势。
在静磁问题的求解中引入磁标势
| $\overrightarrow H = - grad(\phi ) + \overrightarrow T\text{。} $ | (2) |
其中:
| $div([{\mu _r}]{\mu _0}( - grad(\phi ) + \overrightarrow T ) + {\overrightarrow B _r}) = 0\text{。}$ | (3) |
其中:
根据电流源的情况,式(3)可划分为3种标量磁位公式:
1)没有电流源
此时使用总磁标势
| $\overrightarrow H = - grad({\phi _{tot}})\text{,}$ | (4) |
求解方程为:
| $div([{\mu _r}]{\mu _0}( - grad({\phi _{tot}})) + {\overrightarrow B _r}) = 0\text{。}$ | (5) |
状态变量为总磁标势
2)电流源属于不需剖分(non-mesh)类型
此时使用简化磁标势
| $\overrightarrow H = - grad({\phi _{red{H_j}}}) + {\overrightarrow H _j}\text{,}$ | (6) |
求解方程为:
| $div([{\mu _r}]{\mu _0}( - grad({\phi _{red{H_j}}}) + {\overrightarrow H _j}) + {\overrightarrow B _r}) = 0\text{。}$ | (7) |
状态变量为简化磁标势
3)电流源属于需剖分(mesh)的类型
此时使用简化磁标势
| $\overrightarrow H = - grad({\phi _{red{T_0}}}) + {\overrightarrow T _0}\text{,}$ | (8) |
求解方程为:
| $div([{\mu _r}]{\mu _0}( - grad({\phi _{red{T_0}}}) + {\overrightarrow T _0}) + {\overrightarrow B _r}) = 0\text{。}$ | (9) |
状态变量为简化磁标势
以某船为研究对象,使用Flux软件对舰船磁场特性预测进行仿真研究。现将基于Flux软件的舰船磁场特性预测仿真流程和注意问题总结如下:
1)舰船三维模型构建
本文采用输入舰船特征点的方式进行建模。
首先,确定船体各个特征点的坐标位置,然后输入Flux软件中,通过连线、建面和建体完成舰船模型的构建。点的选取,应有取舍,选得太多,虽然计算结果的精度会有所提高,但建模难度会增大,而且导致计算占用大量内存,计算时间过长。选得太少,则不能准确反映舰船的特征,对结果也有影响。
典型的特征点,应包括各甲板面与水密隔壁、主要肋骨、尾封板和首尖部位的交点。对于形状变化较大的部位,如首尖部位,应适当增加定位点,才能较好模拟此处磁场。
对于一些特殊的舰船结构问题,应采取一定的简化措施,避免造成剖分的困难。
对于曲率较大的面,如球鼻首,在Flux软件中建面比较困难,需要大量的坐标点进行定位连接,耗费大量时间,而收效并不明显。这时,可以将曲面作方形面处理,以提高建模效率。
轴系穿过多个舱壁、甲板和船体外壳。如果每根轴系作统一处理,则轴系的线与舱壁面、甲板面和船体面均有交叉,在Flux软件中无法形成体。
这时,应将圆形截面的轴系视为长方体,并按舱壁面将其划分为数段,在每个舱壁面上找出轴的定位点,将轴的面和舱壁面分开,以形成不同的体。
2)模型的网格划分
鉴于舰船复杂的结构,为降低剖分难度,在舰船三维模型网格划分时尽量选用只有四面体单元的自动剖分器[7]。
Flux软件可以通过剖分单元尺寸对网格剖分进行控制和调整。剖分单元大小的设置,直接影响到剖分时间和剖分精度。设置过小,尽管剖分精度有一定的提高,但耗费大量计算时间,且占用过量内存,对计算机要求较高。成功实现满足计算精度要求的剖分的基本原则是保证边界盒有2~3层剖分单元(内、外边界盒之间)。
一般而言,面的剖分出错较少,体剖分出错相对较多,问题多位产生平的或负四面体,导致体剖分无法进行。这时候需对相关部位进行适当修改。
3)物理属性定义
物理属性定义包括对材料和环境磁场的定义。
本文研究对象由4种不同磁特性的钢材制造,在其舰船磁场模型中需定义4种不同磁导率的材料,磁化曲线为线性。在材料定义中,分别使用面域(surface regions)和体域(volume regions),并关联到相关的面和体。
一般而言,船体各个部位钢板厚度会有所不同。为了简化问题的处理,可以将船体钢板厚度取为船体大部分钢板实际的厚度。
在环境磁场定义方面,可根据舰船所在地或研究需要,设置某地的地磁场。为求取舰船某个方向的感应磁场,地磁场只需设置对应分量即可。如,为求取舰船纵向感应磁场,地磁场只需设置纵向分量。
4)求解与后处理
经过以上步骤,可对问题进行求解,得到相关物理量的曲线,或对此物理量进行三维显示,并以文本形式输出相关数据。
Flux软件还可以进行参数化求解。在求解过程中,可将各材料的相对磁导率设为变量,对每个变量赋多个值,则一次求解就可以得到多种不同磁导率组合的计算结果。
3 仿真算例以某船为研究对象,对某地地磁环境下此船在某一深度上的磁场分量Zix,Ziy,Ziz进行仿真计算,并与此船在该地同一深度的磁场测量结果进行比较。
以纵向感应磁场的垂向分量Zix量为例,其磁场比较情况见图1~图3。
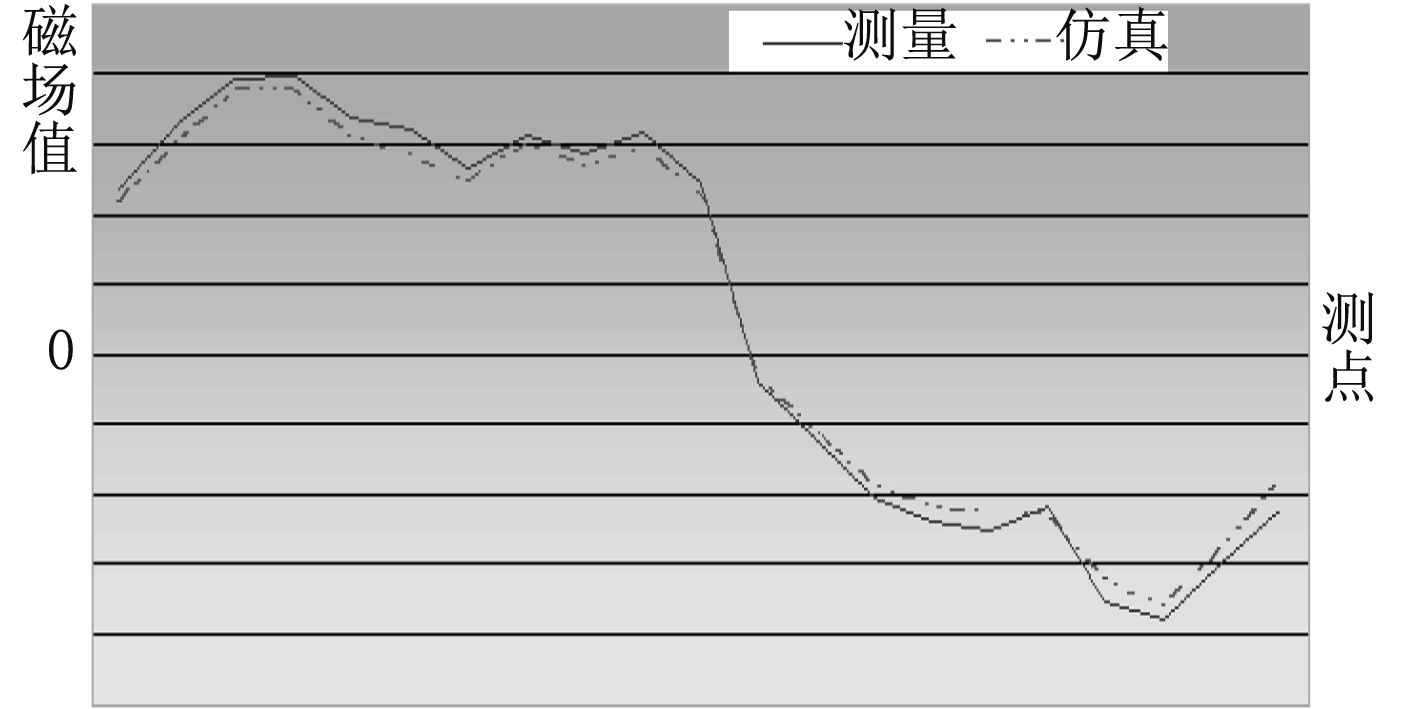
|
图 1 Zix(龙骨下) Fig. 1 Zix (Under the keel) |
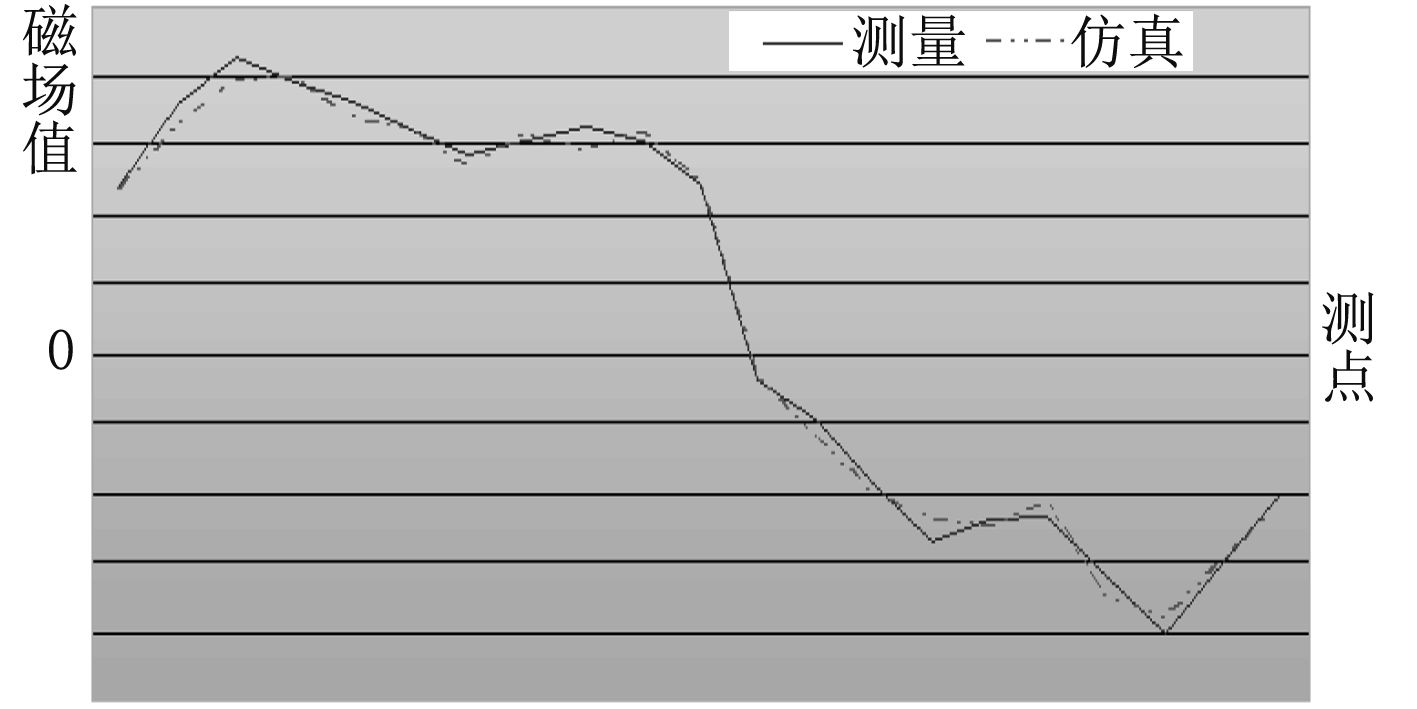
|
图 2 Zix(左舷) Fig. 2 Zix (Port side) |
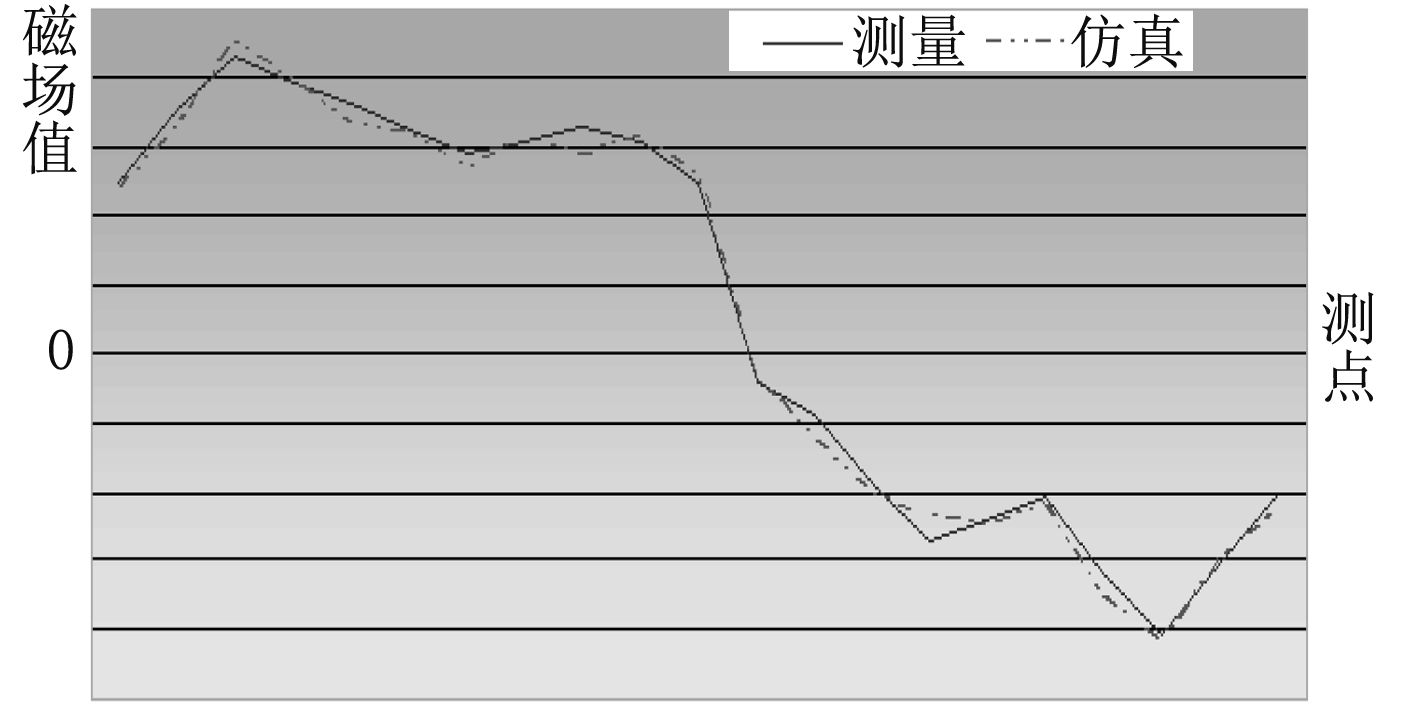
|
图 3 Zix(右舷) Fig. 3 Zix (Starboard) |
由图1~图3可见,仿真计算所得的Zix曲线与实测磁场曲线趋势基本一致。与测量值相比,仿真计算所得的Zix在各测点的相对误差均在15%以内,大部分测点的误差低于8%,少数测点大于10%。经分析,误差的产生主要由于以下原因:
1)建模过程中,舰船三维模型作了一定程度的简化。忽略较小的铁磁设备,一些特殊的舰船结构,如球鼻首和轴系,都作了简化处理。
2)船体肋骨的设置与实际有差别。尽管进行了等值换算,但与实际仍存在误差。
3)有限元数值分析方法存在计算误差。
4)受测量工具的影响,实测数据也存在一定误差。
4 结 语本文以通用电磁场仿真软件Flux为工具,结合舰船磁场的特点,对舰船磁场特性预测的方法进行研究。通过对仿真计算流程,包括舰船三维模型构建、网格剖分和物理属性定义等步骤的分析,完成了舰船磁场特性预测的仿真实现。仿真结果表明,与实测磁场值相对误差低于15%,对工程实践有重要参考价值。
| [1] | 舰船消磁理论与方法[M]. 北京: 国防工业出版社, 2011: 160–178. |
| [2] | PIERRE DALLET J. Ship magnetic modelization by finite element[J]. Marelec, 2001, 25: 5. |
| [3] | PAO-LA-OR P, KULWORAWANICHPONG T, SUJITJORN S, et al. Distribution of flux and electromagnetic force in induction motors: a finite element approach[J]. WSEAS Transaction on Systems, 2006, 5(3): 617–624. |
| [4] | JOAO P A B, NELSON S. Magnetic materials and 3D finite element modeling[M]. Boca Raton, FL: CRC Press Inc, 2013: 121–130. |
| [5] | BATHE K J. Finite element procedures. cambridge, MA: Klaus-Jurgen Bathe. 2006: 51–62. |
| [6] | Physical Application: Magnetic, Electric, Thermal [M]. FLUX 9.30 User's guide. 2005, 3: 15–40. |
| [7] | HOITHAM P, JEFFREY I, BOOKING B, et al. Electromagnetic signature modeling and reduction [C]//Conf Proc. UDT Europe, 1997: 97–100. |
 2018, Vol. 40
2018, Vol. 40
