在目标回声散射特征研究中,经常采用单频CW脉冲信号和宽带LFM线性调频信号作为声呐系统的声源信号,而接收系统则是由多元水听器构成的一系列基阵,阵信号的处理通常采用波束形成算法。
波束形成算法可采用时延波束形成或频域波束形成,频域波束形成方法主要适用于窄带系统,即信号带宽与中心频率的比很小的系统,对于目前主动声呐当中应用较热门的宽带LFM信号,一般采用时延波束形成,可以使系统工作于较宽频条件[1]。随着硬件DSP技术的发展,使得时延波束形成在工作频带位于几十千赫以下的阵处理信号中得到了广泛的应用。
为了获得足够的角度分辨精度,传统的时延波束形成都要对信号进行足够的升采样,然后再通过低通滤波器后求和,此法可以给出很高的精度,但一般输入的序列会很长,计算量也会随之大增,尤其占用了大量内存,对与内存有限的硬件系统要求模拟信号经过采样变为数字信号,则数字信号采样可移位的最小间隔为采样间隔
基于舰艇回声散射特征测试的实际情况,一般采用单频CW脉冲信号和宽带LFM线性调频信号作为测试信号,本文在数字内插波束形成的基础上,将对信号的升采样过程转变为对滤波器的升采样过程,采用跳点卷积和重叠保留法[2],从而提高计算速度和减少对硬件内存的苛刻要求。
1 快速时延波束形成原理 1.1 传统时延波束形成常规时延波束形成是将各阵元所接收的信号分别移动相应的采样间隔,求和便得到波束输出。所移动的采样间隔,是通过预成波束的角度计算得到的。由于所移动的位移必须是最小采样间隔的整数倍,所以预成的角度不能任意指定。传统的时延波束形成最常用的就是数字内插波束形成,内插滤波器主要有内插器和低通滤波器组成。
定理的条件下,通常为了节省存储空间和提高信号的传输和处理速度,采用升采样的方法缩短采样间隔,以便获得更为细致的波束分布。
| $\frac{{d\sin \theta }}{c} = n \cdot Ts, \; \theta = \arcsin \frac{{n \cdot Ts \cdot c}}{d}\text{。}$ | (1) |
式中:d为阵元间距;c为声速;TS为采样间隔;n为波束号。
在很多情况下,需要在某个固定的角度上形成波束,而这就需要确定最小波束控制角。传统的时延波束形成是通过阵列信号的升采样实现,这样会使得计算量和内存大增,不够经济,对于一些要求实时计算和显示的情况,较为困难。
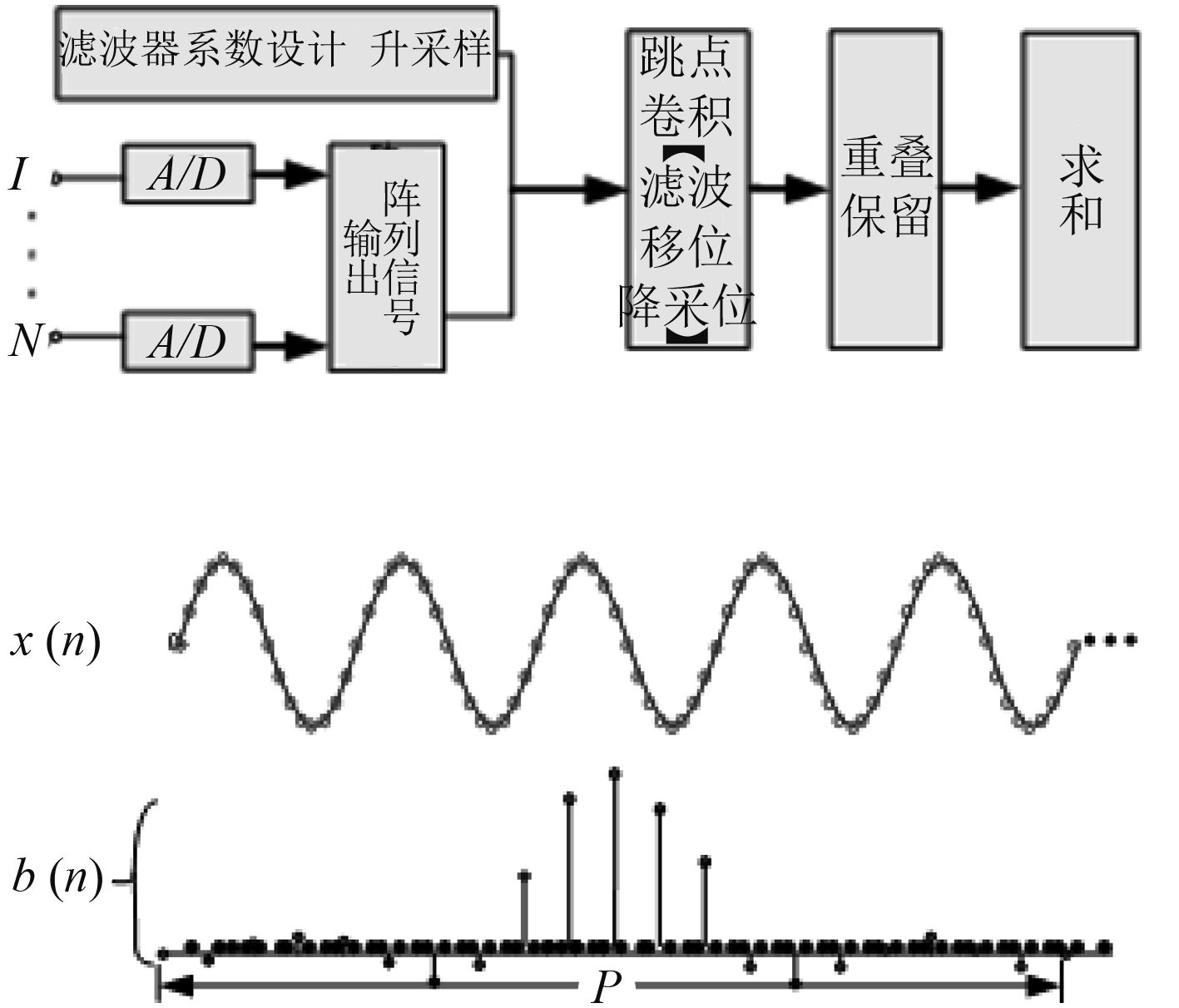
1.2 快速时延波束形成快速时延波束形成是将信号的升采样过程转变为对滤波器(系数)的升采样过程,采用跳点卷积和重叠保留法,从而提高计算速度和减少内存使用,图1是其原理框图和示意图。将信号分成若干段(本文中分成3段),采用重叠保留法;设计滤波器,系数为
|
图 1 快速时延波束形成算法框图及示意图 Fig. 1 Model of fast BF algorithm and abridged view |
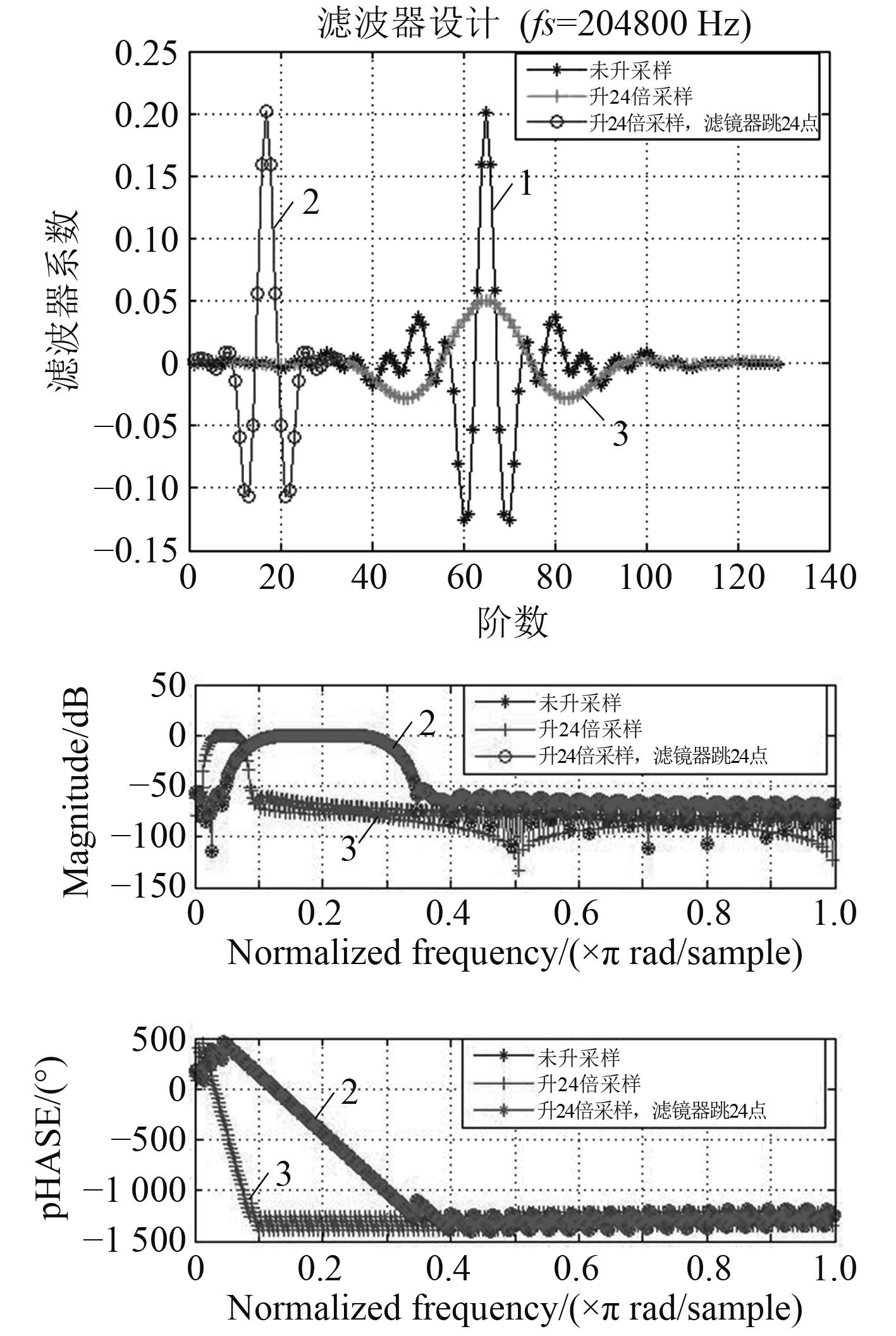
滤波器设计如图2所示,线1为未升采样滤波器幅频和相频特性,阶数为N(64)阶,绿线为升M倍采样后的滤波器幅频和相频特性,线2为第2种情况下,跳M点后的抽取值,其幅频、相频特性如图,从图中可知,其系数与升采样前的系数一致。根据每个通道要移的点数和跳点滤波器的长度,确定卷积运算的信号起始和截至点,这样既保证了该方位波束要求的各延迟不产生量化误差,又不会使计算量增加,同时,将信号分成若干段作处理,采用重叠保留法,又降低对硬件内存的要求。相对于传统的时延波束形成,理论上可以使计算量和内存降低到原来升采样的倍数,即仅为常规波束形成的
|
图 2 滤波器设计及其特性曲线 Fig. 2 Filter design and filter characteristic |
重叠保留法是快速时延波束形成原理中的关键点之一,它是一种块卷积的方法,实现一个P点脉冲响应
| ${y_r}(n) = {x_r}(n)*h(n)\text{,}$ | (2) |
式中:xr(n)为输入序列;h(n)为脉冲响应;yr(n)为输出序列。
这种分段的方法将
单频CW脉冲信号和线性调频LFM信号是水声试验和水声研究中经常被用到的信号,下面是2种信号不同算法的数值仿真结果,仿真是在普通的PC机上,利用Matlab程序[3]实现的,比较2种算法对阵列信号的波束形成,考察其在计算速度和内存占用两方面的性能。
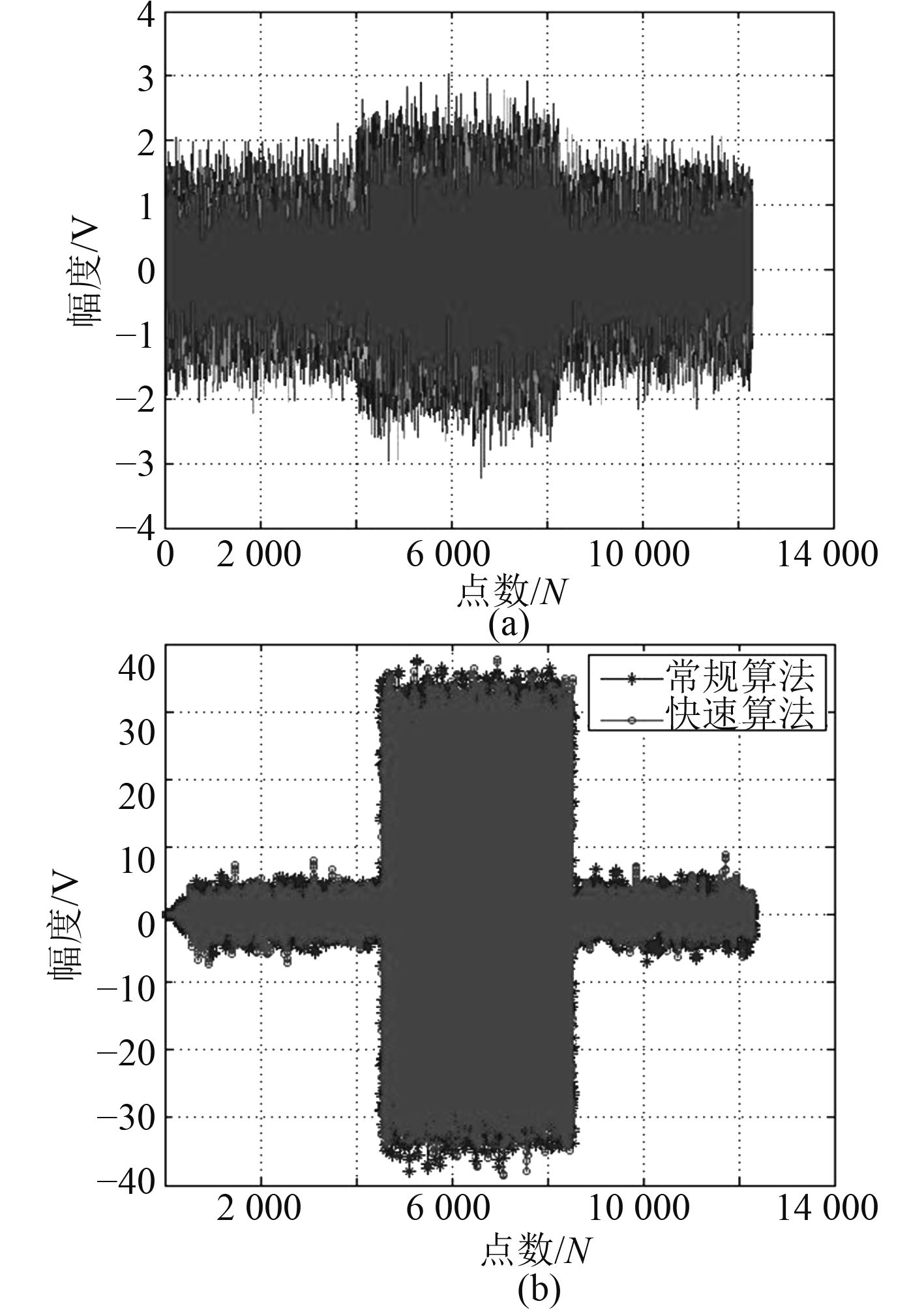
2.1 单频信号仿真结果单频CW脉冲信号设计频率为10 kHz,采样频率为200 kHz,脉宽为20 ms,信号长度60 ms,幅度为1V的正弦信号。图3是仿真单频阵输出信号和2种算法波束形成结果。表1是关于2种算法在普通计算机中的计算速度(计算量)和内存的对比。从图3和表1中可以看出,快速算法获得的结果与常规算法的输出结果与理论一致,说明快速算法的有效性,而在计算机的计算量和占用内存方面几乎都是常规算法的
|
图 3 仿真阵(32元)输出单频(CW)信号及2种波束形成结果 Fig. 3 Array signal (CW, N=32) and beamforming of two abridge |
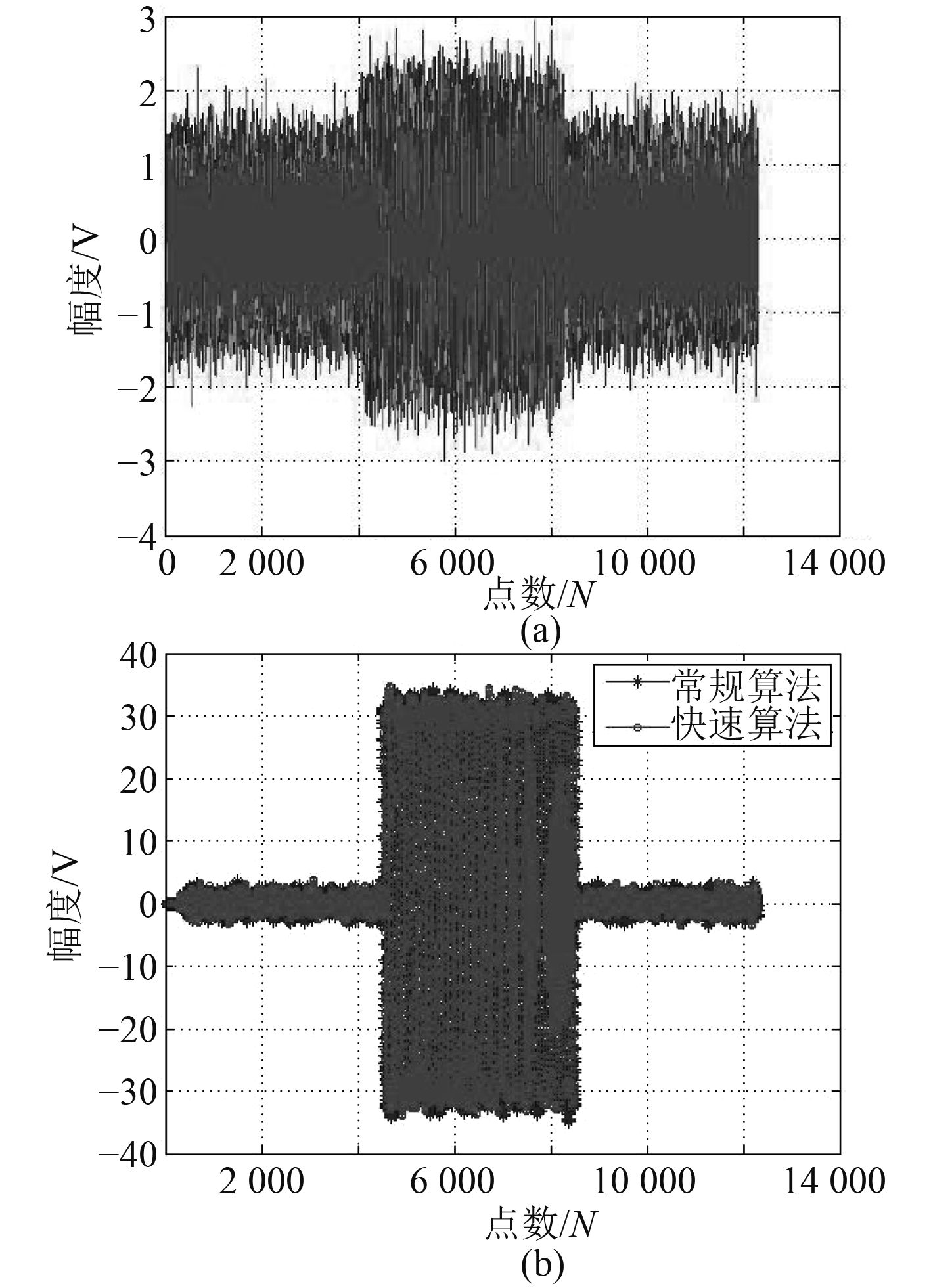
线性调频LFM信号设计中心频率5 kHz,带宽1 OCT,采样频率200 kHz,脉宽20 ms,信号长度60 ms,均为32元阵列信号,升采样
|
图 4 仿真阵(32元)输出宽带(LFM)信号及2种波束形成结果 Fig. 4 Array signal (LFM, N=32) and beamforming of two abridge |
|
|
表 1 两种算法仿真结果对比(CW,LFM) Tab.1 Contrast of two algorithm artificial result |
对单频CW脉冲信号和宽带LFM线性调频信号的仿真结果可以看出:基于2种水声测试常用的单频、宽带信号,快速时延波束形成算法可以大幅提高计算速度和减少内存使用,计算量和内存仅是常规算法的
海试中被测目标与收发合置测试系统位于水下10 m深度,测试距离300~600 m,处理信号为CW脉冲直达声信号和宽带LFM线性调频复杂目标的回波信号,接收为32元直线阵,阵元间距为中心频率30 kHz对应波长的0.8倍,下面是2种算法的处理结果。
3.1 单频信号处理结果处理信号为单频CW脉冲直达声信号,频率25 kHz,采样率200 kHz,脉宽为1 ms,测试距离350 m左右,升采样
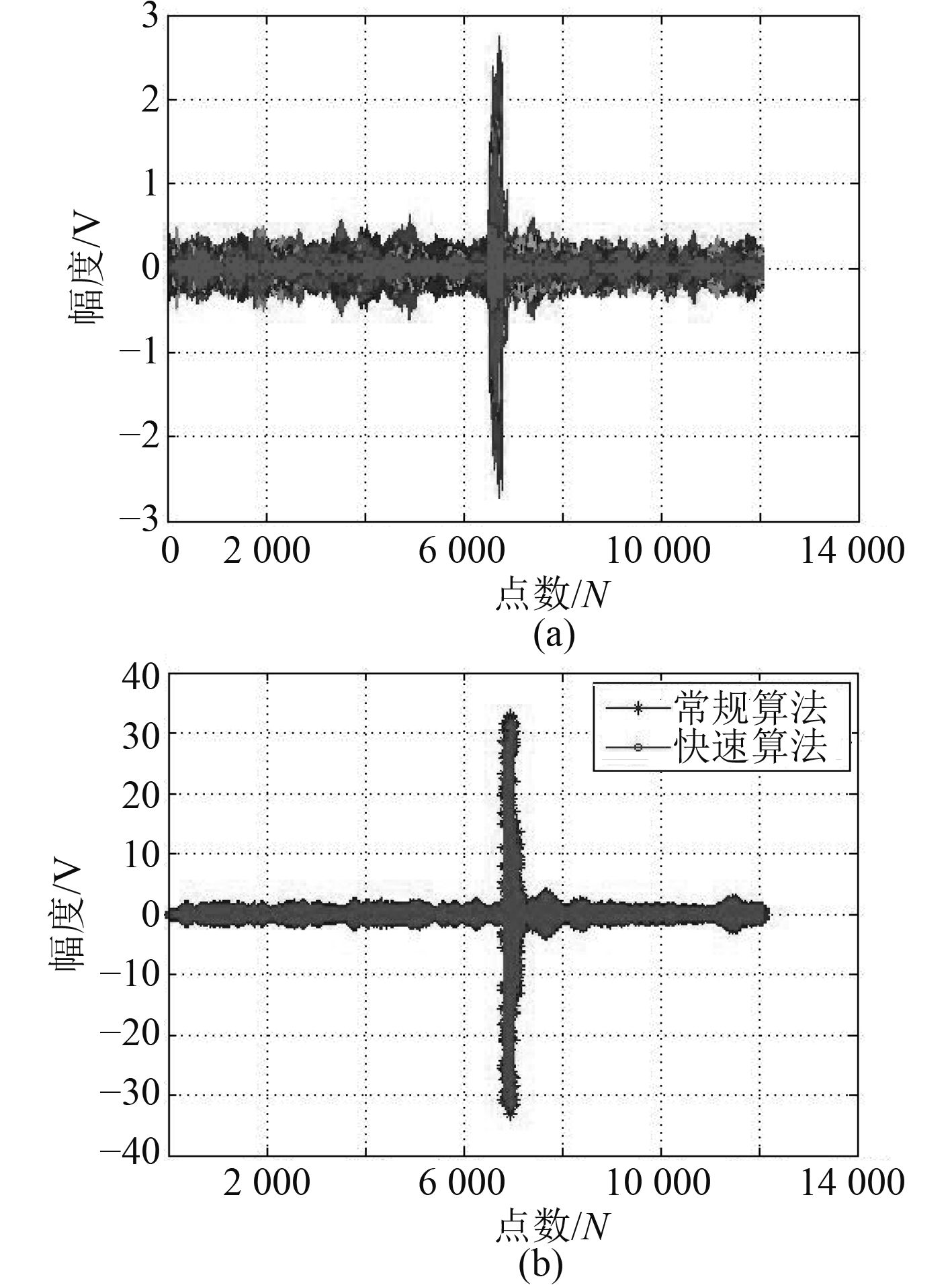
|
图 5 实测单频(CW)信号及2种波束形成结果 Fig. 5 Measured CW signal and beamforming of two algorithm |
处理信号为宽带线性调频信号复杂目标回波信号,中心频率为30 kHz,采样率200 kHz,脉宽10 ms,测试距离400 m左右,升采样
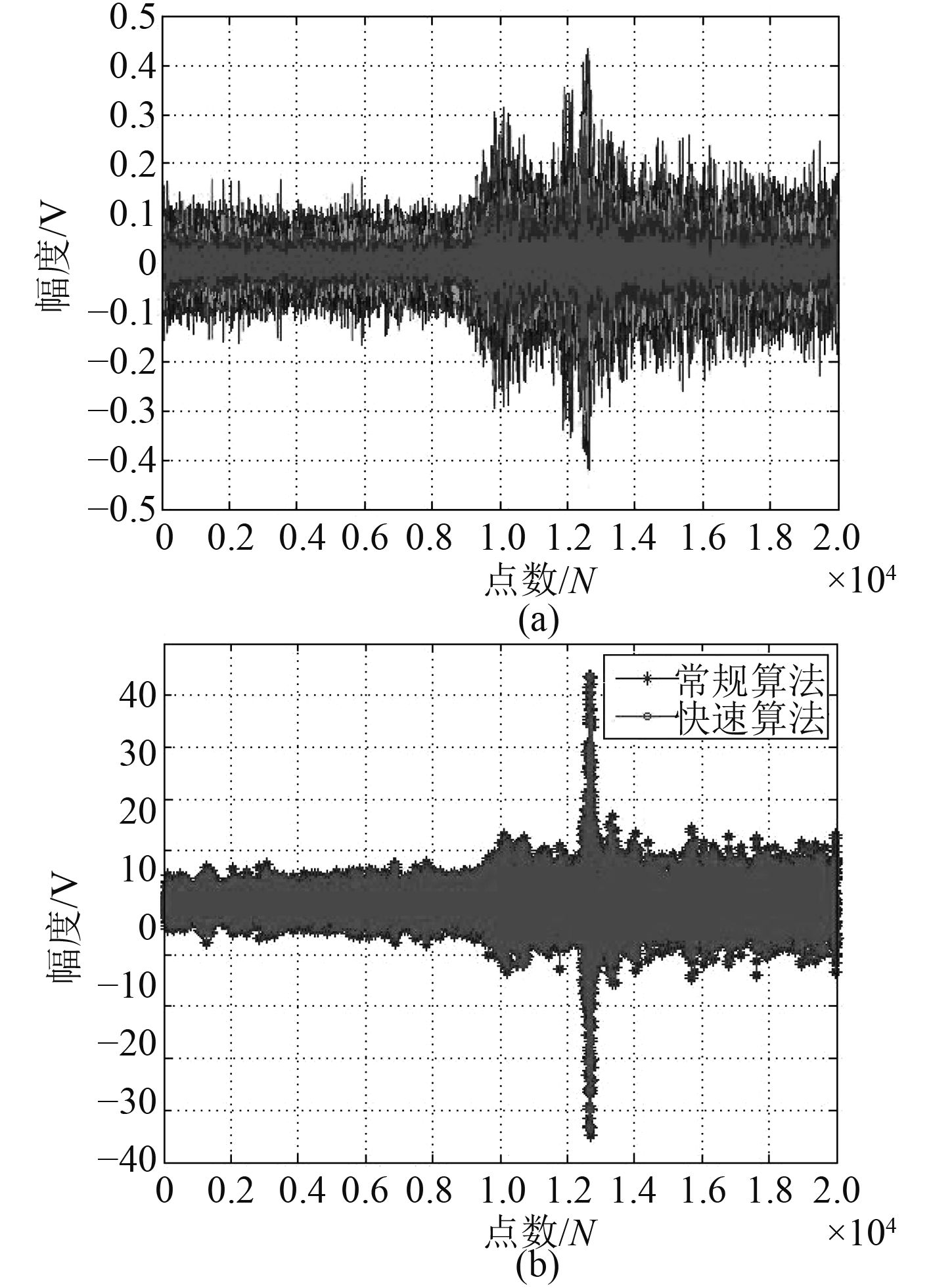
|
图 6 实测宽带(LFM)信号及2种波束形成结果 Fig. 6 Measured LFM signal and beamforming of two algorithm |
|
|
表 2 两种算法实测结果对比(CW,LFM) Tab.2 Contrast of two algorithm artificial result |
从上面数值仿真结果和海试数据的处理结果可以看出,对于单频CW脉冲信号和宽带线性调频信号,采用快速算法能够获得与常规算法一致的精度,同时还可以大幅提高计算速度和减少内存使用,计算量和内存仅是传统算法的
基于DSP硬件系统的快速时延波束形成算法研究具有现实的工程实际意义,理论仿真和实测数据处理结果表明,对于水声常用的CW脉冲信号和线性调频信号,快速算法与常规算法处理结果具有很好的一致性,同时又大幅提高了计算速度和减少了对硬件内存的使用,具有实际的工程应用价值。本文结论如下:
1)时延波束形成中将对信号的滤波过程转变为卷积过程,同时对数据的升采样转变为对滤波器的升采样,采用跳点卷积和重叠保留法,能够大幅提高波束形成的速度和减少对硬件内存的使用,计算量和内存仅是传统算法的
2)该算法有效提升了时延波束形成的计算速度,减少了对DSP等硬件测试系统内存的要求,为阵列信号的波束形成在DSP等硬件系统的实时处理和显示提供了一种方法。
| [1] | 田坦, 刘国枝, 孙大军, 等. 《声呐技术》[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000: 96–97. |
| [2] | A. V. 奥本汉姆, R. W. 谢费, J. R. 巴克等著. 刘树堂, 黄建国译. 《离散时间信号处理》[M]. 西安: 西安交通大学出版社, 2011: 464–475. |
| [3] | 罗军辉, 罗勇江, 等. 《Matlab7.0在数字信号处理中的应用》[M]. 北京: 机械工业出版社, 2005: 121–130. |
 2018, Vol. 40
2018, Vol. 40
