在深海环境中,会聚区是水声传播最显著的特点之一,当声源和接收器都位于海洋近表层时,海面声源发射的声波形成一个向下的波束,这一波束沿着深海折射路径传播后,重新出现在近海面,在距声源数十公里处产生一个声强较高的环带状区域,称为会聚区[1],该现象随着距离的增大反复出现。会聚区现象使得声呐作用距离可能增加至几十海里,甚至100余海里。因此在这些海区,无论是搜索和发现能力、隐蔽性能及其战术机动方法,与在浅海环境下相比,都会有很大的变化。很多学者对会聚区中的声传播特征及其应用进行了广泛的研究[2 – 9],但对于深海会聚区目标探测机动方法则相对较少。为此,在深海会聚区内,如何有效利用会聚区环境效应,采用合理的机动方法,提高目标探测能力,是充分利用会聚区环境效应实施作战的重要前提。
本文在介绍会聚区形成条件及会聚区态势判断方法基础上,建立了会聚区目标探测模型,研究了不同态势下会聚区目标机动探测过程,并通过数值仿真,定量分析了探测方与目标之间距离随时间的变化规律,并结合海上实验数据进行了验证分析。
1 深海会聚区声场 1.1 会聚区形成条件
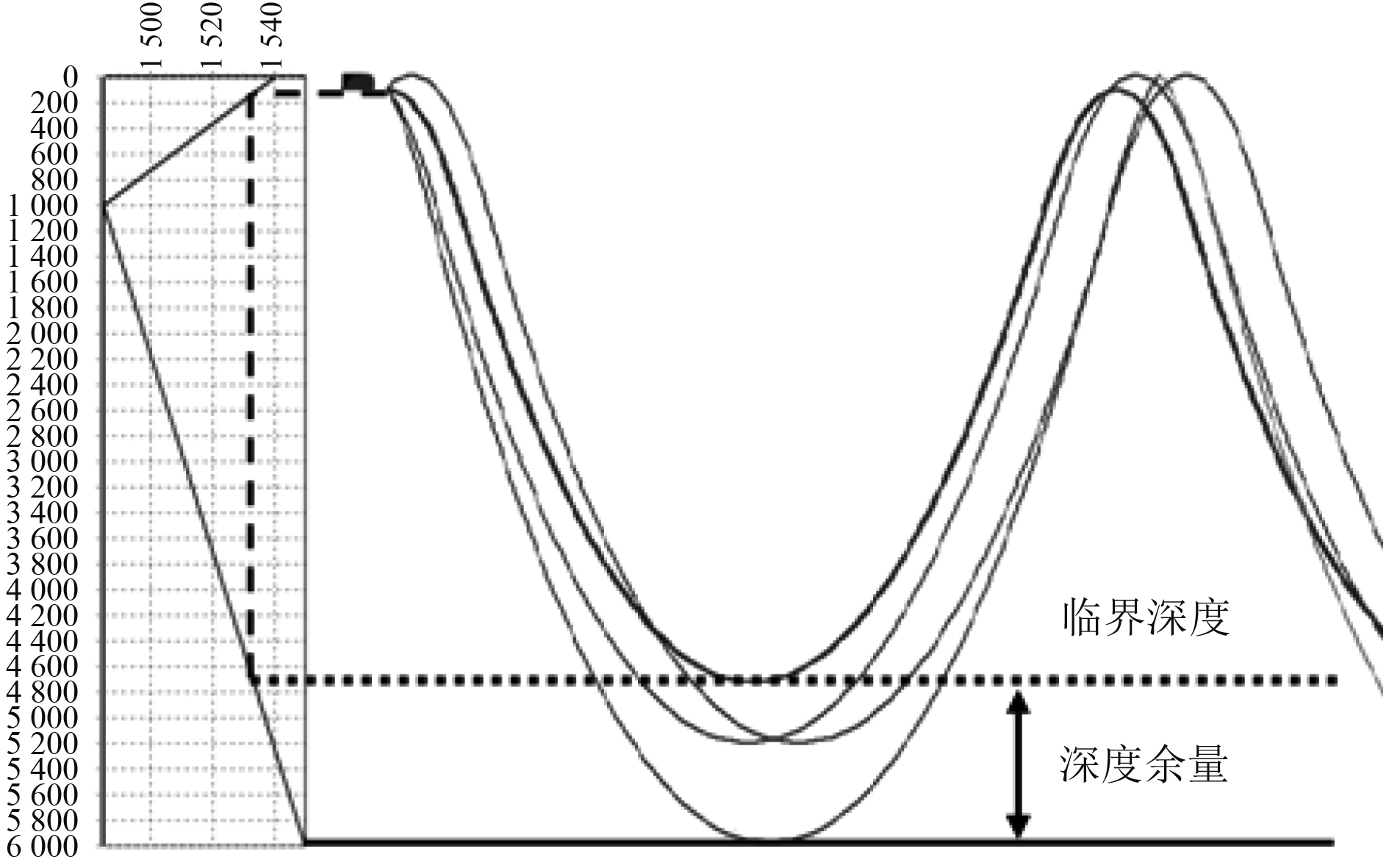
|
图 1 会聚区形成条件示意图 Fig. 1 Formation conditions of deep-ocean convergence zone |
当声源和接收器两者都置于声道内,并且海水的深度必须足够大是形成会聚区的2个必要条件。此时传播至海洋深处的声线发生折射,不触及海底而聚焦在一起。因此对于给定声速剖面存在一个产生会聚区的最小海水深度,即临界深度。临界深度以下到海底的深度距离称为深度余量,如图1所示。
1.2 深海会聚区目标态势判定对于深海会聚区目标,由于接收器距离声源较远,信号出现时间较短,方位变化率又比较慢,导致会聚区目标的判别以及目标运动态势判断都存在较大的困难,这也在一定程度上限制了会聚区环境应用。文献[10]中,提出了利用会聚区距离-频率干涉条纹特征,如图2所示,实施会聚区目标判定及目标运动态势判断的方法,通过仿真结果和海试数据初步验证了方法的有效性。
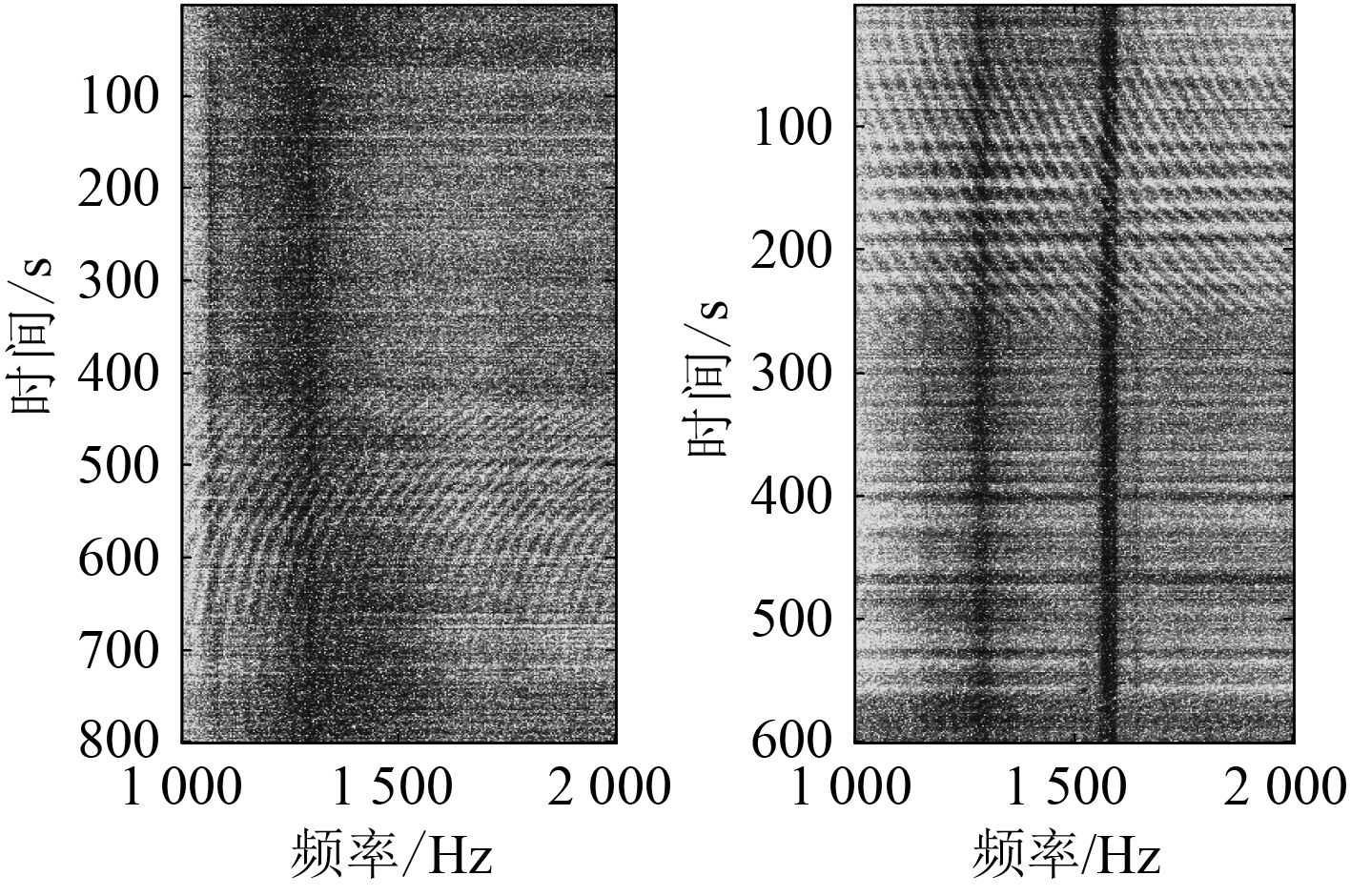
|
图 2 深海试验数据干涉条纹图 Fig. 2 Waveguide invariant striations from deep-ocean experimental data |
为了分析舰艇在会聚区探测过程的机动方式,首先建立坐标系,以便于描述舰艇和目标的海上运动,然后构建各要素的数学模型进行分析。在直角坐标系下,初始时刻,舰艇位于W0,坐标位置为原点,航向为Cw0,航速为Vw,目标初始方位为B0,距离为D0,目标位于M0,坐标位置(Xm0,Ym0),航向为Cm,航速为Vm;t时刻,舰艇位于W1,坐标位置(Xw,Yw),航向为Cw,航速为Vw,目标位于M1,坐标位置(Xm,Ym)。假设目标航向,航速保持不变;会聚区距离为R,会聚区宽度为W,会聚区探测机动示意图如图3所示。
初始时刻记为0时刻,舰艇初始位置为原点,t时刻舰艇位置可表示为
| ${X_w} = \int_0^t {{V_w}\left( t \right)\sin {C_w}\left( t \right)} {\rm d}t\text{,}$ | (1) |
| ${Y_w} = \int_0^t {{V_w}\left( t \right)\cos {C_w}\left( t \right)} {\rm d}t\text{。}$ | (2) |
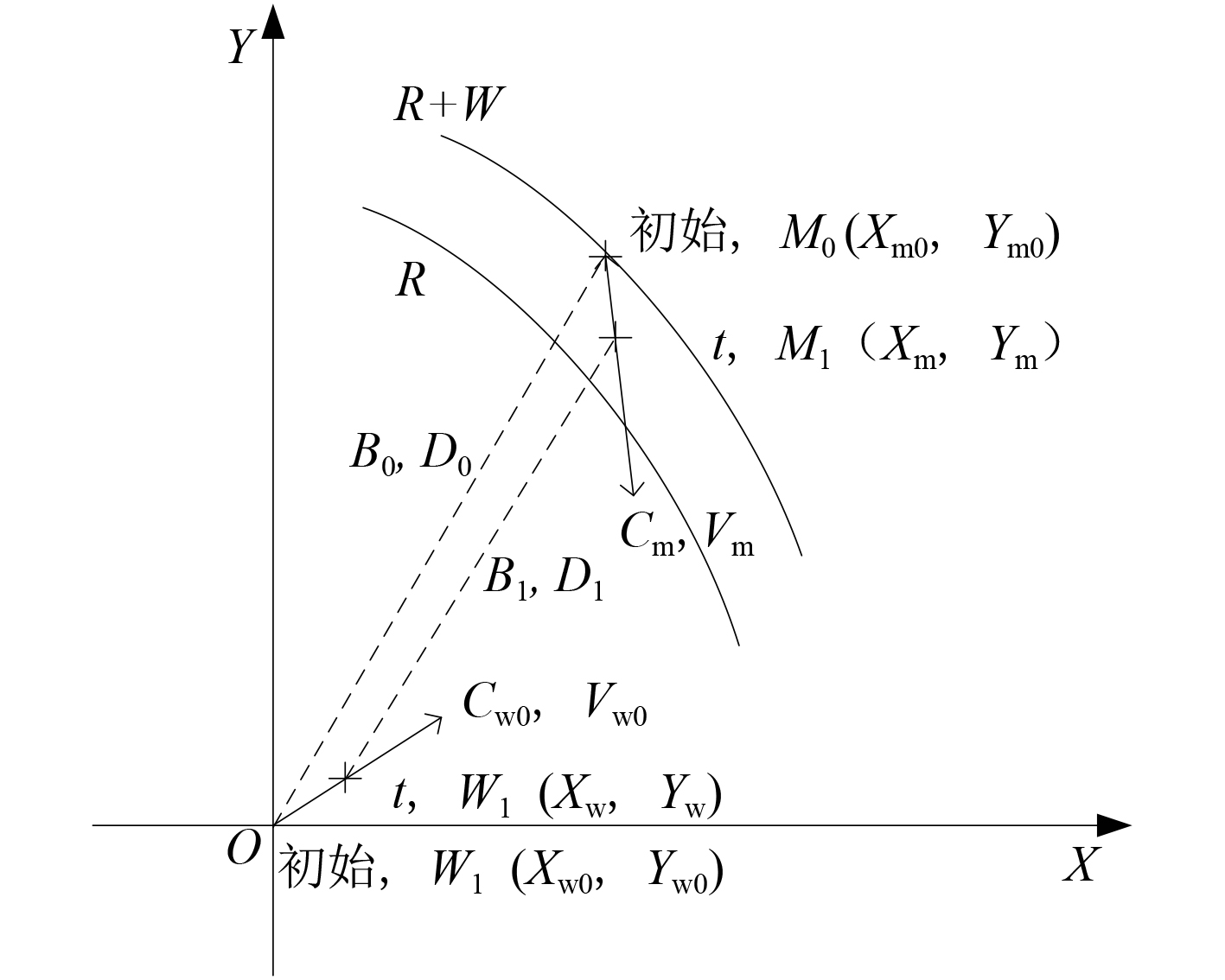
|
图 3 会聚区探测机动示意图 Fig. 3 Maneuvering to detect in convergence zone |
目标初始位置利用相对于舰艇的方位和距离进行描述,记为
| ${X_{m0}} = {D_0}\sin {\beta _0},$ | (3) |
| ${Y_{m0}} = {D_0}\cos {\beta _0}\text{。}$ | (4) |
则t时刻目标位置位于
| ${X_m} = {D_0}\sin {\beta _0} + {V_m}\sin {C_m}t,$ | (5) |
| ${Y_m} = {D_0}\cos {\beta _0} + {V_m}\cos {C_m}t\text{。}$ | (6) |
舰艇如何通过机动延长会聚区探测时间,其问题实质是舰艇通过机动,使舰艇与目标尽可能长时间的保持在会聚区范围内。因此,首先讨论机动过程中,舰艇与目标之间距离随探测时间的变化关系。
将舰艇与目标间距离记为时间函数
| $\begin{split}f\left( t \right) = & {D^2} = {\left( {{X_m} - {X_w}} \right)^2} + {\left( {{Y_m} - {Y_w}} \right)^2}{\rm{ = }}\\ & {\left( {{D_0}\sin {\beta _0} \!\!+\!\! {V_m}t\sin {C_m} \!\!-\!\! \int_0^t {{V_w}\left( t \right)\sin {C_w}\left( t \right)} {\rm d}t} \right)^2}\!\!+\!\! \\ & {\left( {{D_0}\cos {\beta _0} \!\!+\!\! {V_m}t\cos {C_m} \!\!-\!\! \int_0^t {{V_w}\left( t \right)\cos {C_w}\left( t \right)} {\rm d}t} \right)^2}\text{。}\end{split}\!\!\!\!$ | (7) |
为了分析舰艇与目标间距离随时间的变化,对初始态势进行一定假设。假设本艇速度不变,发现目标后保持初始航向Cw0,
| $\begin{split}f\left( t \right) =& {D^2} = {\left( {{X_m} - {X_w}} \right)^2} + {\left( {{Y_m} - {Y_w}} \right)^2}= \\& \left( {{D_0}\sin {\beta _0} + {V_m}t\sin {C_m} - } \right.\\& {\left. {\left( {{V_w}{t_0}\sin {C_w}_0{\rm{ + }}{V_w}\left( {t - {t_0}} \right)\sin {C_w}_1} \right)} \right)^2}+\\& \left( {{D_0}\cos {\beta _0} + {V_m}t\cos {C_m} - } \right.\\& {\left. {\left( {{V_w}{t_0}\cos {C_w}_0 + {V_w}\left( {t - {t_0}} \right)\cos {C_w}_1} \right)} \right)^2},\end{split}$ | (8) |
整理得
| $f\left( t \right){\rm{ = A}}{t^2} + Bt + C\text{。}$ | (9) |
其中:
| $A = {V_m}^2 - 2{V_m}{V_w}\cos \left( {{C_m} - {C_w}_1} \right) + {V_w}^2,$ |
| $\begin{split}B =& 2{D_0}\left( {{V_m}\cos \left( {{C_m} - {\beta _0}} \right) - {V_w}\cos \left( {{C_w}_1 - {\beta _0}} \right)} \right)+\\& 2{V_w}^2{t_0}\left( {\cos \left( {{C_w}_1 - {C_w}_0} \right) - 1} \right) - \\&2{V_m}{V_w}{t_0}\left( {\cos \left( {{C_m} - {C_w}_0} \right){\rm{ - }}\cos \left( {{C_m} - {C_w}_1} \right)} \right),\end{split}$ |
| $\begin{align}C{\rm{ = }}& {D_0}^2 - 2{D_0}{V_w}{t_0}\cos \left( {{C_w}_0 - {\beta _0}} \right) + 2{V_w}^2{t_0}^2-\\& 2{V_w}^2{t_0}^2\cos \left( {{C_w}_1 - {C_w}_0} \right) + 2{D_0}{V_w}{t_0}\cos \left( {{C_w}_1 - {\beta _0}} \right)\text{。}\end{align}$ |
对时间
| $\!\!\!\begin{split}\frac{{\partial f}}{{\partial t}}= & {\rm{ 2(}}{D_0}{V_m}\cos ({C_m} - {\beta _0}) - {D_0}{V_w}\cos ({C_{w1}} - {\beta _0})-\\& {V_m}{V_w}{t_0}\cos ({C_m} - {C_w}_0) + {V_m}{V_w}{t_0}\cos ({C_{w1}} - {C_m})+\\& {V_m}^2{t_0}\cos ({C_{w1}} - {C_w}_0) - {V_w}^2{t_0}) +\\& ({V_m}^2 - 2{V_m}{V_w}\cos ({C_w}_1 - {C_m}) + {V_w}^2)t,\quad\quad (10)\end{split}$ |
| $\frac{{{\partial ^2}f}}{{{\partial ^2}t}}{\rm{ = }}{V_m}^2 - 2{V_m}{V_w}\cos ({C_w}_1 - {C_m}) + {V_w}^2\text{。}$ | (11) |
下面针对不同参数组合,对舰艇与目标间距离随时间的变化关系进行讨论。
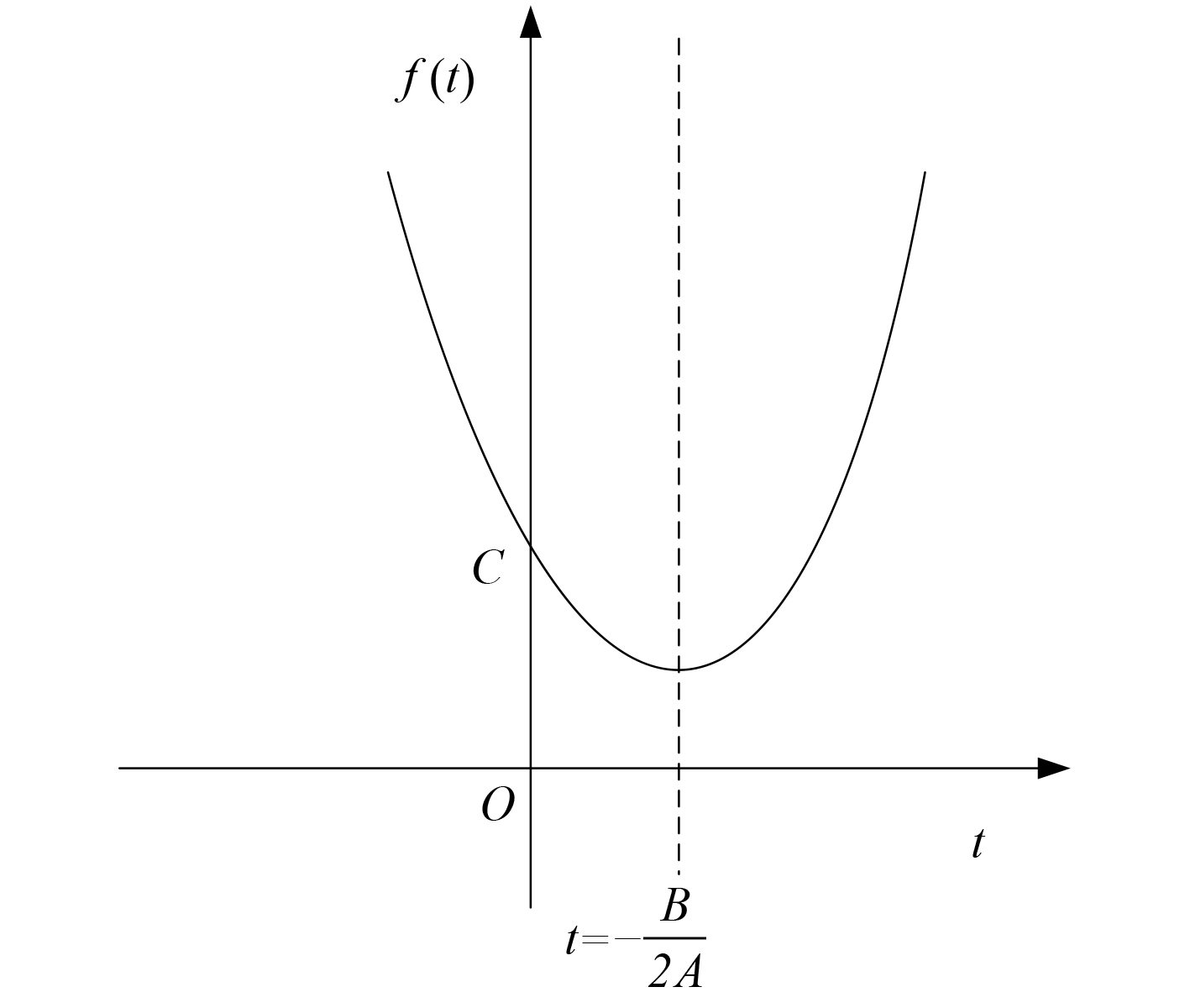
1)当
|
图 4
当
|
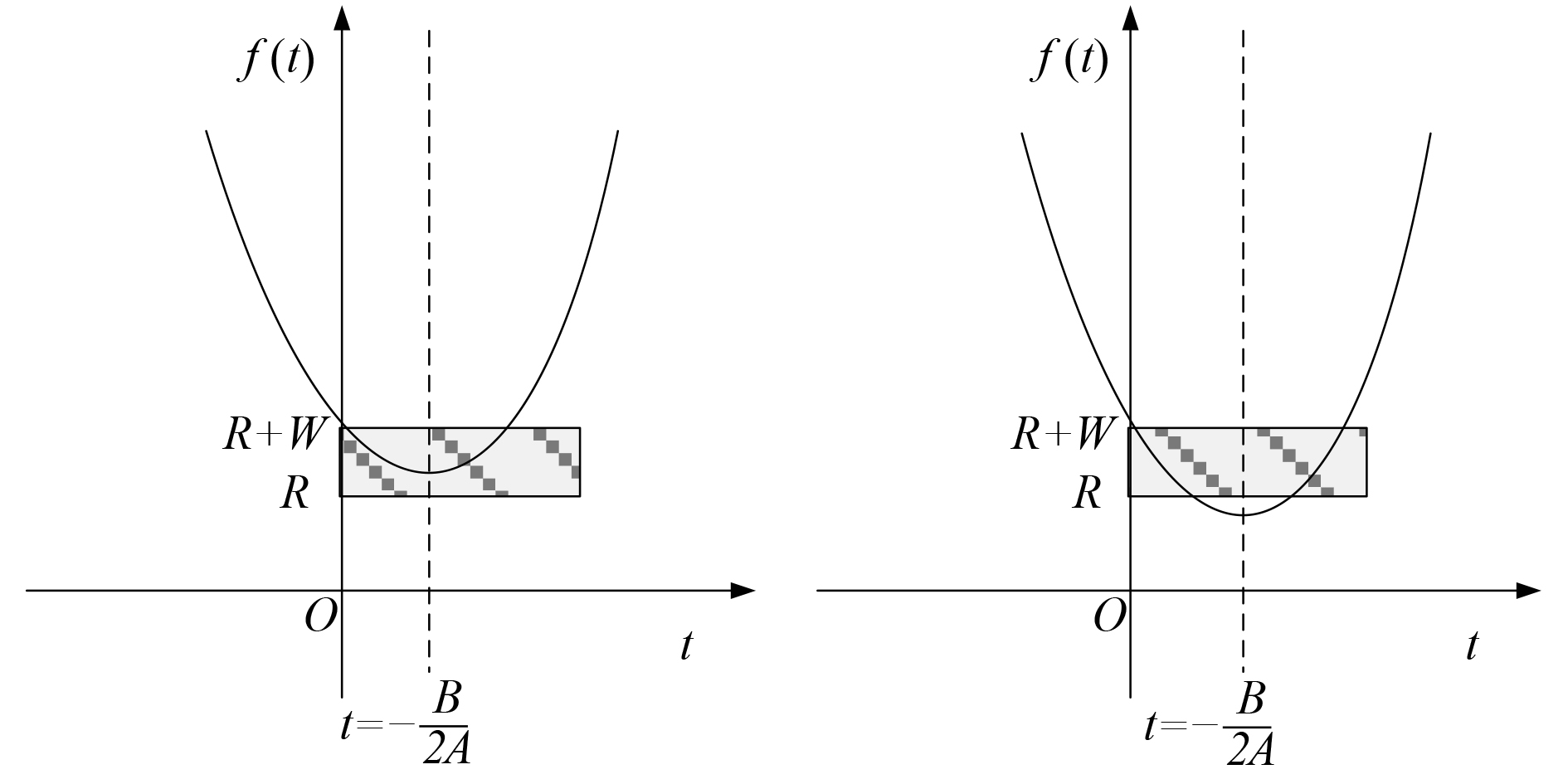
2)当
利用式(9)可以得到t时刻距离函数
| $\Delta f = f\left( t \right) - f\left( 0 \right) = {\rm{A}}{t^2} + Bt,$ | (12) |
在实际探测过程中,参数
| $t = \frac{{ - B \pm \sqrt {{B^2} + 4A\Delta f} }}{{2A}}\text{。}$ | (13) |
|
图 5
当
|
结合抛物线参数意义进一步对会聚区内舰艇与目标间距离变化特点进行分析。
1)抛物线开口方向
从参数A的表达式可以看出,
|
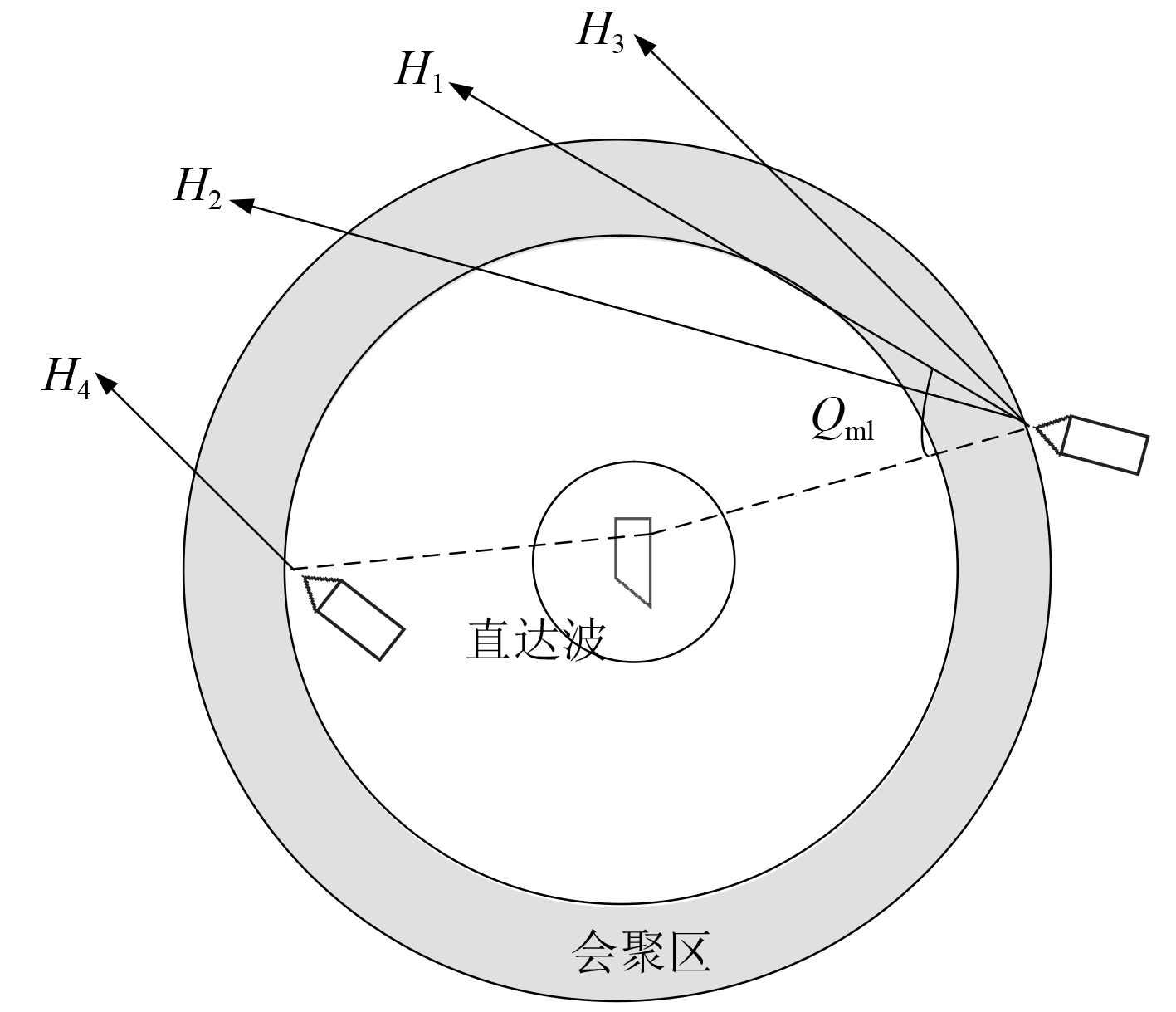
图 6 不同态势目标穿越会聚区示意图 Fig. 6 Traversing CZ of different situation targets |
第1类:当
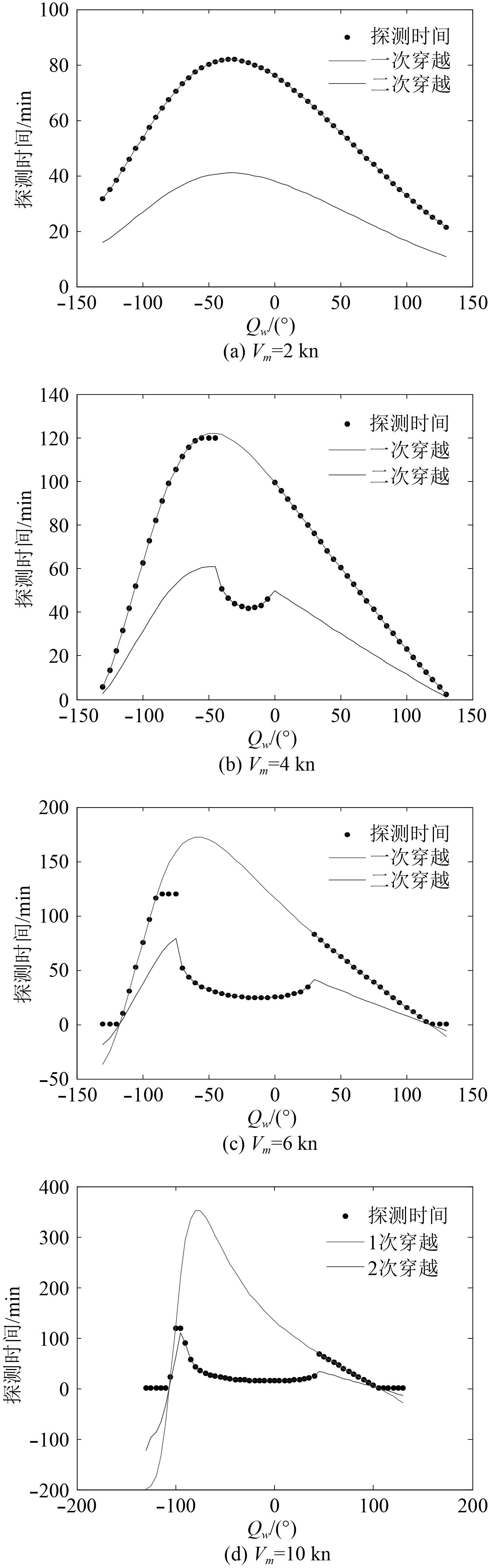
当目标舷角>Qml时,目标一次穿越会聚区,如图6中H2航向。目标一次穿越会聚区,是指目标与舰艇间的距离最小值Rmin>会聚区距离R,如图7(a)所示。当舰艇与目标距离减小到Rmin后,两者距离逐渐增大,处于远离态势,脱离会聚区范围,若两者运动要素保持不变,则目标不会再次穿越同一会聚区。
|
图 7 不同接近态势穿越会聚区,目标距离变化示意图 Fig. 7 The distance change for approach situation targets |
当目标舷角<Qml时,目标2次穿越会聚区,如图7中H3航向。目标2次穿越会聚区,是指目标与舰艇间的距离最小值Rmin<会聚区距离R,如图7(b)所示。当舰艇与目标距离减小到Rmin时,已经完成第1次穿越会聚区,然后两者距离增大,处于远离态势,目标将再次穿越同一会聚区。
第2类:当
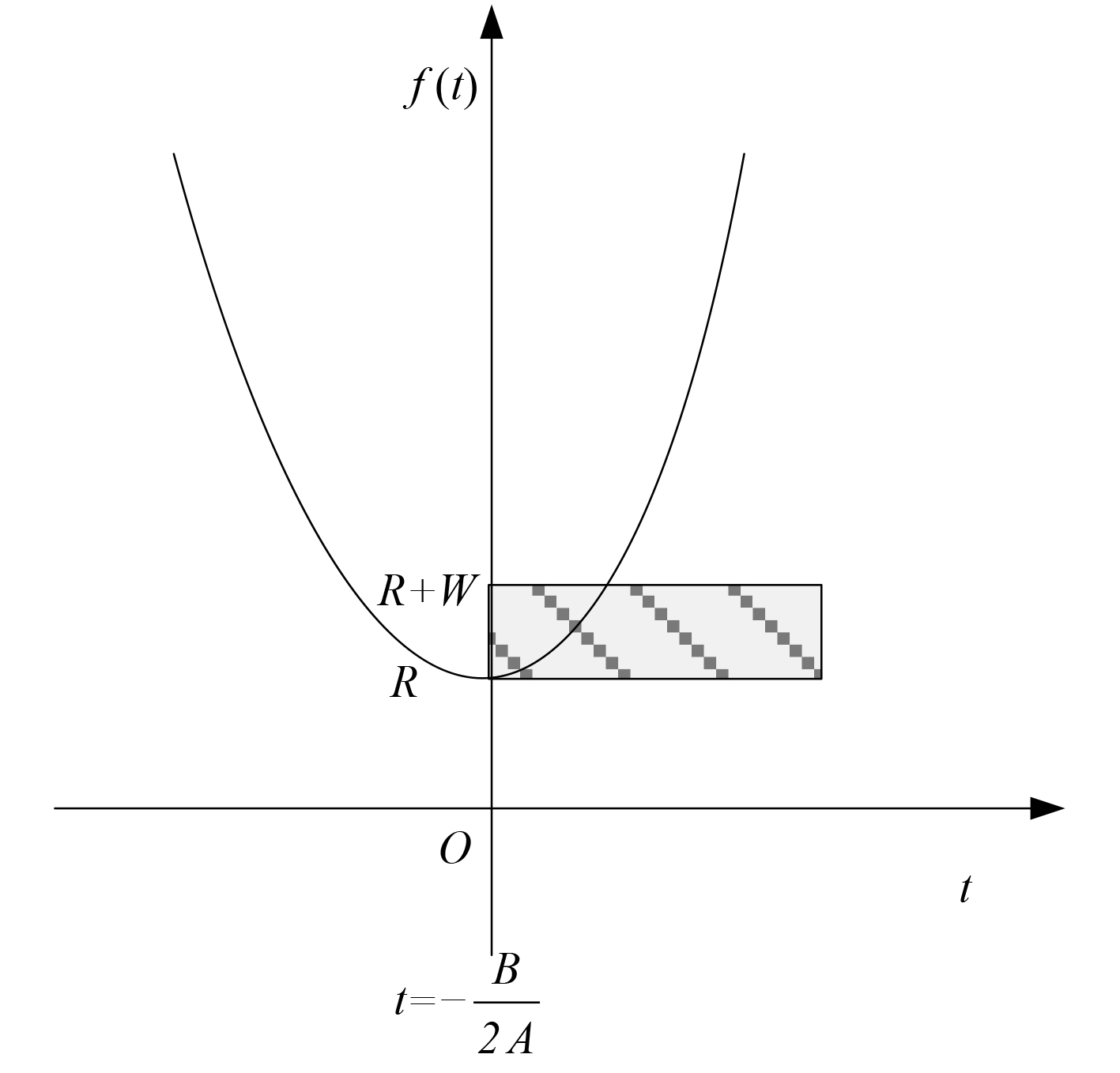
|
图 8 会聚区远离目标,目标距离变化示意图 Fig. 8 The distance change for far from situation targets |
2)抛物线开口大小
根据参数意义可知,参数
3)抛物线与坐标轴交点
根据参数意义可知,参数
仿真条件见表1。
|
|
表 1 仿真参数列表 Tab.1 Simulation parameter list |
1)会聚区目标处于接近运动态势
当目标航向变化角Qm较小时,即舰艇位于目标小舷角时,目标2次穿越会聚区的概率较高,此时目标与舰艇间的距离最小值Rmin<会聚区距离R,式(13)中,Δf=W,与初始态势无关,2个解分别对应目标第1次穿出会聚区时间和第2次进入会聚区的时间,此时,舰艇探测目标时间随舰艇舷角Qw增大而延长,即舰艇进行机动将目标置于声呐最大可听测舷角Qwmax进行跟踪,目标探测时间最长;大舷角机动的同时增加舰艇速度,可以进一步延长探测时间,当如图9(a)所示,舰艇速度Vw=2 kn时,将目标置于声呐最大可听测舷角进行机动,相对于将目标置于最小可听测航向进行跟踪探测时间延长2.2 min;舰艇速度Vw=10 kn时,将目标置于声呐最大可听测舷角Qwmax进行机动,相对于将目标置于目标最小可听测航向Qwmin进行跟踪探测时间延长12.4 min,可见,接近态势下,提高舰艇机动速度,更有利于舰艇通过机动延长目标跟踪时间。
当目标航向变化角Qm增大后,即舰艇位于目标大舷角时,目标穿越1次会聚区的概率较高,如图10所示。此时目标与舰艇间的距离最小值Rmin>会聚区距离R。当舰艇低速机动时,目标探测时间随舰艇舷角Qw增大而减小;舰艇将目标置于小舷角进行跟踪,速度越大,目标2次穿越会聚区的概率越高,探测时间越短;舰艇将目标置于大舷角Qwmax进行跟踪,速度越大,目标1次穿越会聚区的概率越低,探测时间越短,如图9(b)所示。
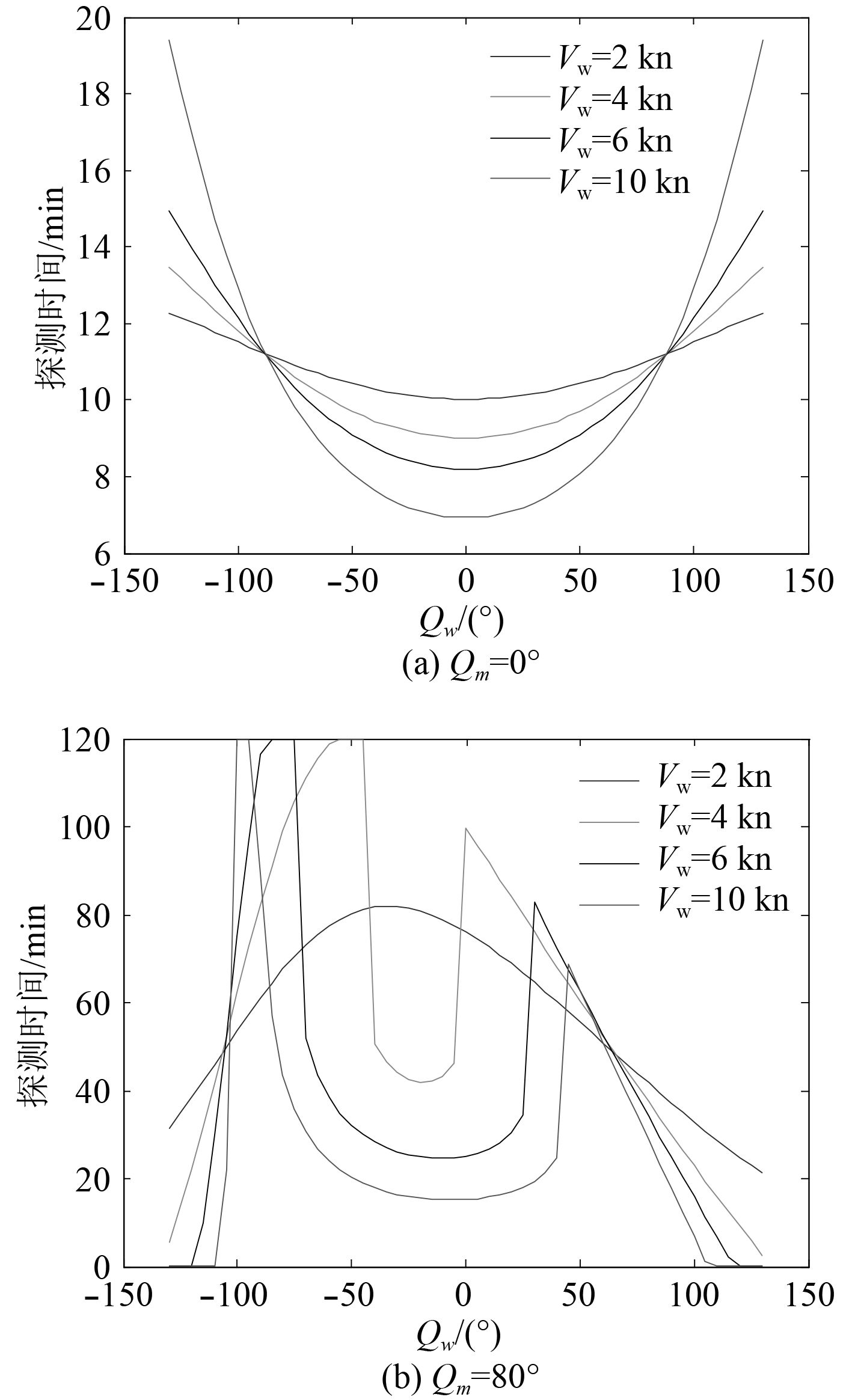
|
图 9 接近态势,舰艇不同速度时探测时间对比 Fig. 9 Contrast of detection time at different speed under for approach situation targets |
|
图 10 舰艇Qm=80°时,舰艇不同速度时探测时间 Fig. 10 When Qm=80°, detection time at different speed |
2)会聚区目标处于远离运动态势
通过仿真结果可得出以下结论:
当目标航向变化角Qm较小时,即舰艇位于目标大舷角时,即舰艇处于尾追目标态势,舰艇探测目标时间随舰艇舷角Qw增大而减小,即舰艇将目标置于最小可听测舷角Qwmin航向进行跟踪,目标探测时间最长;保持最小可听测舷角航向机动的同时增加舰艇速度,可以进一步延长探测时间,当如图11(a)所示,舰艇速度Vm=2 kn时,将目标置于最小可听测舷角Qwmin航向进行跟踪,相对于将目标置于最大可听测舷角跟踪时间延长2.4 min;舰艇速度Vm=10 kn时,将目标置于最小可听测舷角Qwmin航向进行跟踪,相对于将目标置于最大可听测舷角跟踪时间延长22 min,可见,远离态势下,提高舰艇机动速度,同样有利于舰艇通过机动延长目标跟踪时间。
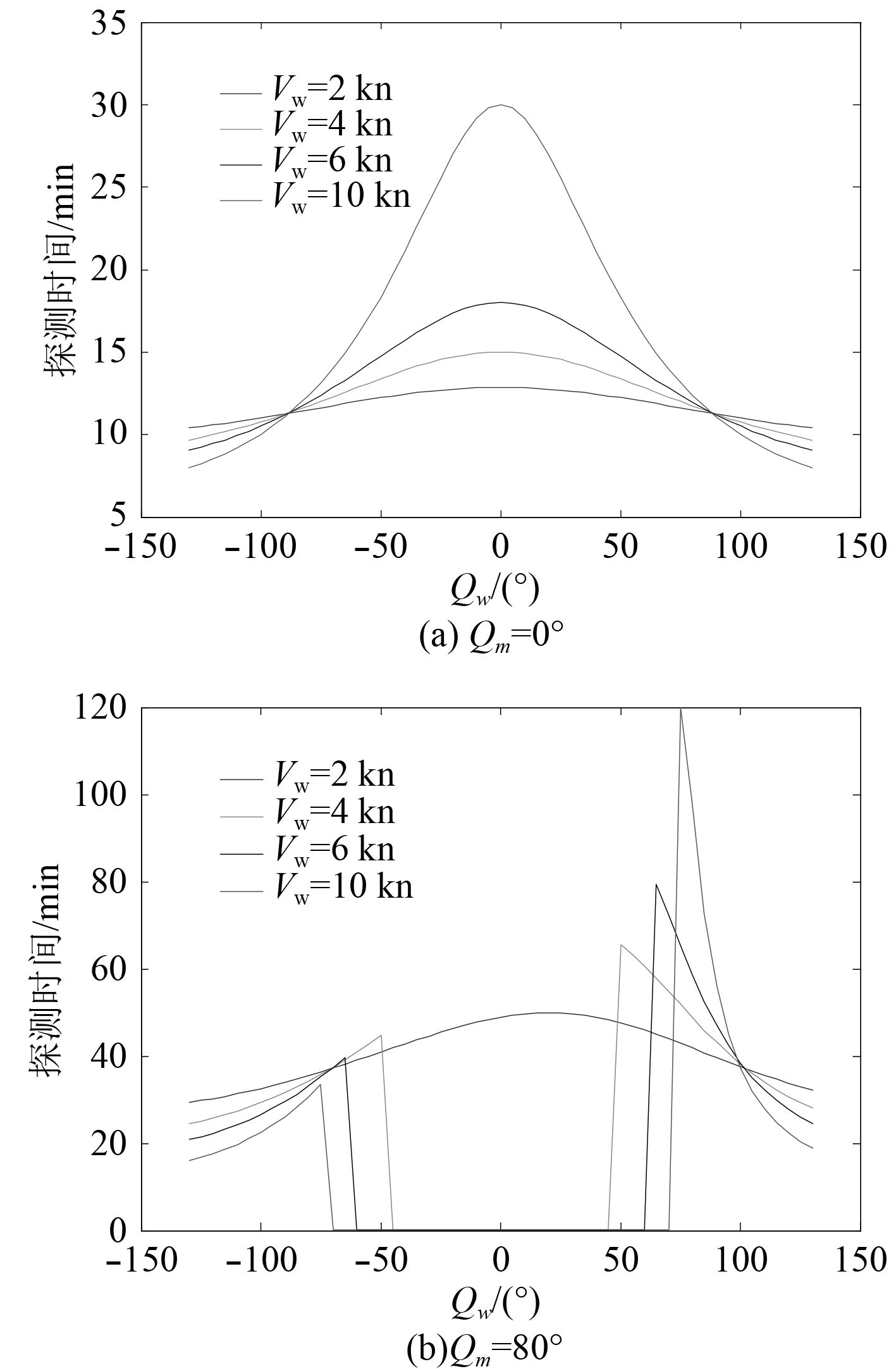
|
图 11 远离态势,舰艇不同速度时探测时间对比 Fig. 11 Contrast of detection time at different speed under for far from situation targets |
2)当目标航向变化角Qm增大后,即舰艇位于正横附近时,舰艇将目标置于最小可听测舷角Qwmin航向进行跟踪,目标探测时间最长,舰艇探测目标时间随舰艇舷角Qw增大而减小;随着舰艇速度的增加,目标最小可听测舷角Qwmin增大,当Qw<Qwmin时,舰艇与目标之间初始阶段不满足远离态势;当Qw>Qwmin时,舰艇与目标之间处于远离态势,将目标置于最小可听测舷角Qwmin航向进行跟踪,目标探测时间最长,如图11(b)所示。
图12给出了目标速度不同时,即Vm分别为10 kn或16 kn,会聚区远离目标,舰艇选择不同航速、航向时,潜艇探测目标时间对比图。通过对比可以看出,其他要素相同时,舰艇对低速目标的探测时间更长,通过机动延长探测时间的效果更为明显。
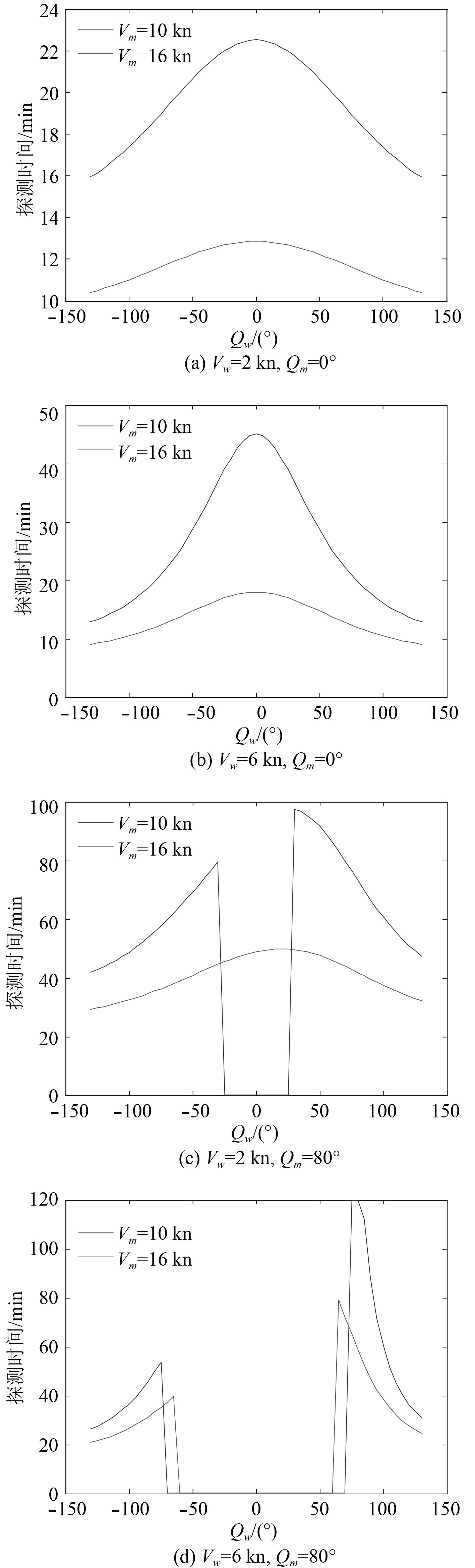
|
图 12 目标速度不同,舰艇不同运动要素时探测时间 Fig. 12 Detection time at different speed and course |
结合某次海上试验数据,对深海会聚区内目标机动方法进行检验。试验海区海深近6 000 m,为典型深海声速剖面,有足够深度余量,能够形成会聚区,第一会聚区距离为33 nmile左右,会聚区宽度3 nmile左右,满足试验验证条件。试验开始前,舰艇测量声速梯度,声速梯度测量完成后,开始机动;目标按试验方案机动,并记录航行要素及周围目标情况。具体舰艇与目标机动要素如表2所示。
|
|
表 2 海上试验验证结果 Tab.2 Marine test results |
第1航次,舰艇发现目标后,采用最小可听测舷角Qwmin航向,目标噪声持续10 min,第3航次,目标处于接近过程中,舰艇发现目标后,采用最大可听测舷角Qwmax航向,与目标舰接触时间为12 min,相对于第1航次延长2 min,试验结果与理论分析结果一致。
第2航次,舰艇发现目标后,采用最小可听测舷角Qwmin航向,目标噪声持续13 min,第4航次,舰艇发现目标后,采用较大可听测舷角航向,与目标舰接触时间为11 min,相对于第2航次缩短2 min,试验结果与理论分析结果一致。
4 结 语本文介绍了舰艇利用会聚区实施探测的条件及利用会聚区波导干涉条纹特征实施会聚区目标判定及目标运动态势判断的方法,研究了舰艇利用会聚区探测机动方法,分析了针对会聚区不同运动态势目标,舰艇搜索目标和摆脱跟踪的机动方法,在深海会聚区实际应用中,当发现目标,并判断为会聚区目标及目标运动态势后,机动方法应遵循以下原则:1)搜索目标:在接近态势下可采用最大可听测舷角航向并适当增速;在远离态势下,可转向最小可听测舷角航向,增速跟踪;2)摆脱跟踪:在接近态势下可采用最小可听测舷角航向并适当增速;在远离态势下,可转向最大可听测舷角航向,增速摆脱,并通过仿真和试验验证了方法的有效性。
| [1] | JENSEN B, KUPERMAN W A, PORTER M B, et al. Computational ocean acoustics(second edition) [M]. American Institute of Physics, 2011: 21-23. |
| [2] | KIMBERLY M F. Improving accuracy of acoustic prediction in the philippine sea through incorporation of mesoscale environmental effects[R]. AD Report. Naval Postgraduate School. 2008: 6. |
| [3] | TOBY E S. Improving underwater vehicle communication in the littoral zone through adaptive vehicle motion[J]. (A). J. Acoust. Soc. Am. 125, 2581, 2009. |
| [4] |
李玉阳, 笪良龙. 海洋锋对深海会聚区特征影响研究[J]. 声学技术, 2010, 6: 78–79.
LI yuyang, DA lianglong. Research on the effects of ocean front on characteristics of convergence zone [J]. Technical Acoustics, 2010, 6: 78–79. http://cdmd.cnki.com.cn/Article/CDMD-10217-2008029241.htm |
| [5] | STEPHEN D L. Dependence of the structure of the shallow convergence zone on deep ocean bathymetry[J]. (A). J. Acoust. Soc. Am. 127, 1962, 2010. |
| [6] | KEVIN D H. Detection performance modeling and measurements for convergence zone (CZ) propagation in deep water(A)[J]. J. Acoust. Soc. Am. 130, 2530, 2011. |
| [7] | STEPHEN D L. Investigating sources of variability of the range and structure of the low frequency shallow convergence zone (A)[J]. J. Acoust. Soc. Am. 130, 2555, 2011. |
| [8] | SONG H C. Diversity combining for long-range acoustic communication in deep water[J]. J. Acoust. Soc. Am. 132, EL68, 2012. |
| [9] | KEVIN D H. Towed array propagation measurements and modelling in the Philippine Sea (A)[J]. J. Acoust. Soc. Am. 131, 3353, 2012. |
| [10] |
唐帅, 笪良龙, 徐国军, 等. 深海会聚区波导不变量特征研究及应用[J]. 海洋科学, 2014, 7: 82–85.
TANG Shuai, DA Liang-long, XU Guo-jun. Research on waveguide invariant characters and application in deep-ocean convergence zone [J]. Marine sciences, 2014, 7: 82–85. |
 2018, Vol. 40
2018, Vol. 40
