0 引　言

动力定位系统的定位能力不仅能为动力定位系统的设计提供依据，也可作为在使用过程中的重要参考标准，对其研究的重要性不言而喻。依据IMAC规范，动力定位能力是船舶动力定位系统能够抵抗的极限海况，一般以定位能力曲线表示^[1]。定位能力计算过程中考虑的是推进器系统与环境外力是否平衡，其数学模型实质是求解带非线性约束的推力优化问题。传统上使用序列二次规划法、牛顿法等适用于单极值问题的算法来求解优化^[2,3]。但现代船舶一般都布置多个推进器且常含有回转推进器，增加了推力优化的复杂度，导致在定位能力计算中的优化问题很有可能出现多极值解，即有多个局部最优值。加上传统优化算法对初始值很敏感，如果初始值设置得不恰当就无法得出最优解，陷入局部最优^[4]。现代智能算法突破了传统算法的局限性，并因其快速有效而被广泛应用^[5]。文献[4]利用模拟退火算法进行了动力定位能力的优化计算，文献[6]以神经网络进行了训练并优化计算了动力定位能力，都得到了较好的结果。粒子群（PSO）是源于鸟群活动的全局优化算法，能够用来求解具有多极值的问题。综合学习粒子群（CLPSO）算法是PSO算法的一个变种，在多峰问题上有较好的应用，但由于CLPSO算法利用当前搜索速度和个体最优值来更新搜索速度，使得算法在迭代后期搜索速度值很小，从而导致收敛速度很慢，降低了计算效率^[7]。为改善CLPSO算法，研究者做了一些有益的工作。文献[8]提出了一种依据种群进化过程中的信息动态调整粒子的变异概率的自适应CLPSO算法，文献[9]引入克隆选择机制，提出了免疫综合学习粒子群算法。这些改进算法在解决复杂多峰问题上都发挥了较好的效果。基于多种群的改进也是优化算法的改进方向之一，可以得到良好的效果^[10-11]。本文基于CLPSO算法和多种群思想提出了多种群综合学习粒子群算法（MCLPSO），并利用所提算法计算了实际船舶的动力定位能力。

1 环境载荷的计算

要计算船舶的定位能力，首先要计算其所受的环境载荷。船舶所受的环境载荷主要是风力、流力、波浪力，本文只计算水平面上的力及力矩。假设风、浪、流同向，方向角都设为 $\alpha $ 。

风力与风速、风向、船舶构件的形状及高度等有密切相关，将这些因素整合成一个风力系数，风力计算公式为：

$\left\{ \begin{array}{l} {F_{wdx}}(\alpha ) = {C_{wdx}}(\alpha )V_{wd}^2, \\[5pt] {F_{wdy}}(\alpha ) = {C_{wdy}}(\alpha )V_{wd}^2, \\[5pt] {M_{wd}}(\alpha ) = {C_{wdM}}(\alpha )V_{wd}^2{\text{。}} \end{array} \right.$

(1)

式中， ${C_{wdx}}(\alpha )$ ， ${C_{wdy}}(\alpha )$ ， ${C_{wdM}}(\alpha )$ 均为在方向角下的风力系数。

流力的计算与风力相似，流力计算公式为：

$\left\{ \begin{array}{l} {F_{cx}}(\alpha ) = {C_{cx}}(\alpha )V_c^2, \\[5pt] {F_{cy}}(\alpha ) = {C_{cy}}(\alpha )V_c^2, \\[5pt] {M_c}(\alpha ) = {C_{cM}}(\alpha )V_c^2{\text{。}} \end{array} \right.$

(2)

式中， ${C_{wdx}}(\alpha )$ ， ${C_{wdy}}(\alpha )$ ， ${C_{wdM}}(\alpha )$ 均为在方向角下的流力系数。

波浪力中的一阶成分不会使船舶移动，对船舶动力定位的影响主要由二阶波浪力引起，二阶波浪力计算公式为：

$\left\{ \begin{array}{l} {F_{wvx}}(\alpha ) = \int_0^\infty {S(\omega ){C_{wvx}}(\omega ){\rm d}\omega }, \\[5pt] {F_{wvy}}(\alpha ) = \int_0^\infty {S(\omega ){C_{wvy}}(\omega ){\rm d}\omega }, \\[5pt] {M_{wv}}(\alpha ) = \int_0^\infty {S(\omega ){C_{wvM}}(\omega ){\rm d}\omega } {\text{。}}\end{array} \right.$

(3)

式中： $\omega $ 为波浪频率； ${C_{wvx}}(\omega )$ ， ${C_{wvy}}(\omega )$ ， ${C_{wvM}}(\omega )$ 均为二阶波浪力系数； $S(\omega )$ 为波能谱，本文采用JONSWAP谱。

2 动力定位系统定位能力

动力定位系统定位能力是衡量动力定位系统性能的重要指标，可以采用可抵抗最大风速来表示。可抵抗最大风速是指动力定位系统满足控制精度范围之内时，船舶各个方向上可以抵抗的最大风速。在分析定位能力的过程中，一般假设风、浪、流等环境力同方向，并可以叠加，且流速一定，进而考虑推进器的推力与外界环境力在水平面上的静态平衡。所以需要利用优化算法求解各推进器的推力大小及其方向以满足此静态平衡。本文以总推力最小为优化目标，建立推力求解的数学模型，如式（4）所示。

$\left\{ {\begin{array}{*{20}{l}} {\min g(T) = \sum\limits_{i = 1}^{num} {{T_i}} }, \\ {s.t. } \\ {\sum\limits_{i = 1}^{num} {{T_i}} \cos ({\theta _i}) = {F_{wdx}} + {F_{cx}} + {F_{wvx}} }, \\ {\sum\limits_{i = 1}^{num} {{T_i}} \sin ({\theta _i}) = {F_{wdy}} + {F_{cy}} + {F_{wvy}}}, \\ {\sum\limits_{i = 1}^{num} {{T_i}} ({x_i}\sin ({\theta _i}) - {y_i}\cos ({\theta _i})) = {M_{wd}} + {M_c} + {M_{wv}}} {\text{。}}\end{array}} \right.$

(4)

式中： $ i = 1,2,...,num$ ，num为推进器的个数； ${T_i}$ 为推力大小， ${T_{i\min }} \leqslant {T_i} \leqslant {T_{i\max }}$ ， ${T_{i\min }}$ 和 ${T_{i\max }}$ 是推力的上下限； ${\theta _i}$ 为推力角度， ${\theta _i} \in ([0,{\theta _{i\min }}] \cup [{\theta _{i\max }},2\pi ])$ ， ${\theta _{i\min }}$ 和 ${\theta _{i\max }}$ 为推力禁止角范围；（ ${x_i}$ , ${y_i}$ ）为各推进器的坐标； ${F_{wdx}}$ ， ${F_{cx}}$ ， ${F_{wvx}} $ ， ${F_{wdy}}$ ， ${F_{cy}}$ ， ${F_{wvy}}$ ， ${M_{wd}}$ ， ${M_c}$ ， ${M_{wv}}$ 分别是风、流、浪在横荡、纵荡、及首摇3个自由度上的力及力矩。

在实际求解过程中，需要对上述优化问题的约束条件进行处理。这里采用外点惩罚函数的方法将问题转化为无约束问题^[12]。惩罚函数可表述为：

$\begin{split} &\min {\text{ G}}(T) = \sum\limits_{i = 1}^{num} {{T_i}} {\text{ + }} \\& {\lambda _1}(\sum\limits_{i = 1}^{num} {{T_i}} \cos ({\theta _i}) - {F_{wdx}} - {F_{cx}} - {F_{wvx}})+ \\ &{\lambda _2}(\sum\limits_{i = 1}^{num} {{T_i}} \sin ({\theta _i}) - {F_{wdy}} - {F_{cy}} - {F_{wvy}}) + \\& {\lambda _3}(\sum\limits_{i = 1}^{num} {{T_i}} ({x_i}\sin ({\theta _i}) - {y_i}\cos ({\theta _i})) - {M_{wd}} - {M_c} - {M_{wv}})\text{。} \end{split} $

(5)

式中， ${\lambda _1}$ ， ${\lambda _2}$ ， ${\lambda _3}$ 均为惩罚因子。

计算船舶在不同角度下所能承受的最大风速过程中，设流速为固定值，首先风向角设为0°，采用二分法计算此风向下可抵抗的最大风速，接着方向角以一定的间隔（如10°）增加，继续计算最大风速，直至360°。最后为了直观表现，以各个角度上计算得到的最大风速在极坐标系上绘制出一条包络曲线，即定位能力曲线。在计算某个风向下的可抗最大风速时，需要设置一个合理风速上限和下限，以便求解。动力定位能力计算流程如图1所示。

动力定位能力计算关键在于推进器推力与环境力的平衡判定。平衡判定就是依据推力数学模型，采用优化算法对推力进行优化求解，有解则为能够平衡，反之，则不能。所以优化算法的性能十分重要。

3 多种群综合学习粒子群算法 3.1 综合学习粒子群算法

粒子群算法结构简单，参数少，收敛速度快，被广泛应用于各种领域中。对于某个优化问题，种群中的每个粒子的位置代表一个潜在解，并根据目标函数选择出各粒子个体最优值pb以及种群全局最优值pg，粒子通过速度V更新位置X，进而更新pb和pg。传统PSO在处理复杂多峰问题中易于陷入局部最优，为此Liang等提出了一种新的更新策略，并基于该策略提出了综合学习粒子群（Comprehensive Learning PSO，CLPSO）算法^[7]。传统PSO是以粒子自身的最优值和全局最优值来更新速度和位置，而新的更新策略的主要思路是利用种群中任意粒子的最优信息来更新某一粒子的速度，进而更新位置：每个粒子的每一维都以大小为 $Pc$ 的概率向群体中任意粒子的个体最优值的相应维学习，对于不同粒子， $Pc$ 值可以不同。粒子的速度及位置更新方式如下式：

$\left\{ \begin{array}{l} V_{jd}^{t + 1} = \omega V_{jd}^t + cr_{jd}^t(pb_{{f_j}(d)}^t - X_{jd}^t), \\ V_{jd}^{t + 1}{\text{ = }}\min ({V_{jd\max }},\max ({V_{jd\min }},V_{jd}^{t + 1})), \\ X_{jd}^{t + 1} = X_{jd}^t + V_{jd}^{t + 1}, \\ X_{jd}^{t + 1}{\text{ = }}\min ({X_{jd\max }},\max ({X_{jd\min }},X_{jd}^{t + 1})){\text{。}} \\ \end{array} \right.$

(6)

式中： $j = 1,2, \cdots ,ps$ ； $d = 1,2, \cdots ,D$ ；ps是种群的规模，D是搜索空间的维数； $X_j^t = [X_{j1}^t, \cdots ,X_{jd}^t, \cdots ,X_{jD}^t]$ 为粒子j的位置、 $V_j^t = [V_{j1}^t, \cdots ,V_{id}^t, \cdots ,V_{jD}^t]$ 是粒子j的速度； $[{X_{jd\min }},{X_{j\max }}]$ 是粒子j第d维的搜索范围， $[{V_{jd\min }},{V_{jd\max }}]$ 是速度范围； $\omega $ 是惯性权重； $c$ 是学习因子； $r_{jd}^t$ 是（0，1）间均匀分布的随机数。 ${f_j}(d)$ 表示粒子j在第d维需要学习的其他粒子， $pb_{fj}^t$ 可以是任意一个粒子的个体最优位置。

${f_j}(d)$ 的确定方法：对于粒子j的每一维，都生成一个随机概率，若这个随机概率大于学习概率 $P{c_j}$ ，则该粒子的这一维向其自身个体最优值的对应维学习；反之，则从群体中随机选出2个粒子，学习它们中较好的那个个体最优值。为了保证种群的多态性，CLPSO还设置了一个更新间隔代数m，即当粒子j的个体最优值 $p{b_j}$ 连续m代未得到更新，则重新生成 ${f_j}(d)$ 。

由于CLPSO算法仅使用粒子的个体最优信息来指导整个迭代过程，因此种群具有较高的多样性，扩大了搜索范围。这种变化使得算法更偏重于全局搜索能力而削弱了局部搜索能力。CLPSO算法的缺陷具体表现为：1）由于全局最优值未参与到粒子的速度和位置更新中，使得粒子速度在迭代后期过小，以致收敛速度较慢。2）由于缺乏跳出局部最优的措施，一旦大部分粒子的个体最优值陷入局部最优时，将导致算法开始收敛，无法搜寻到全局最优值。

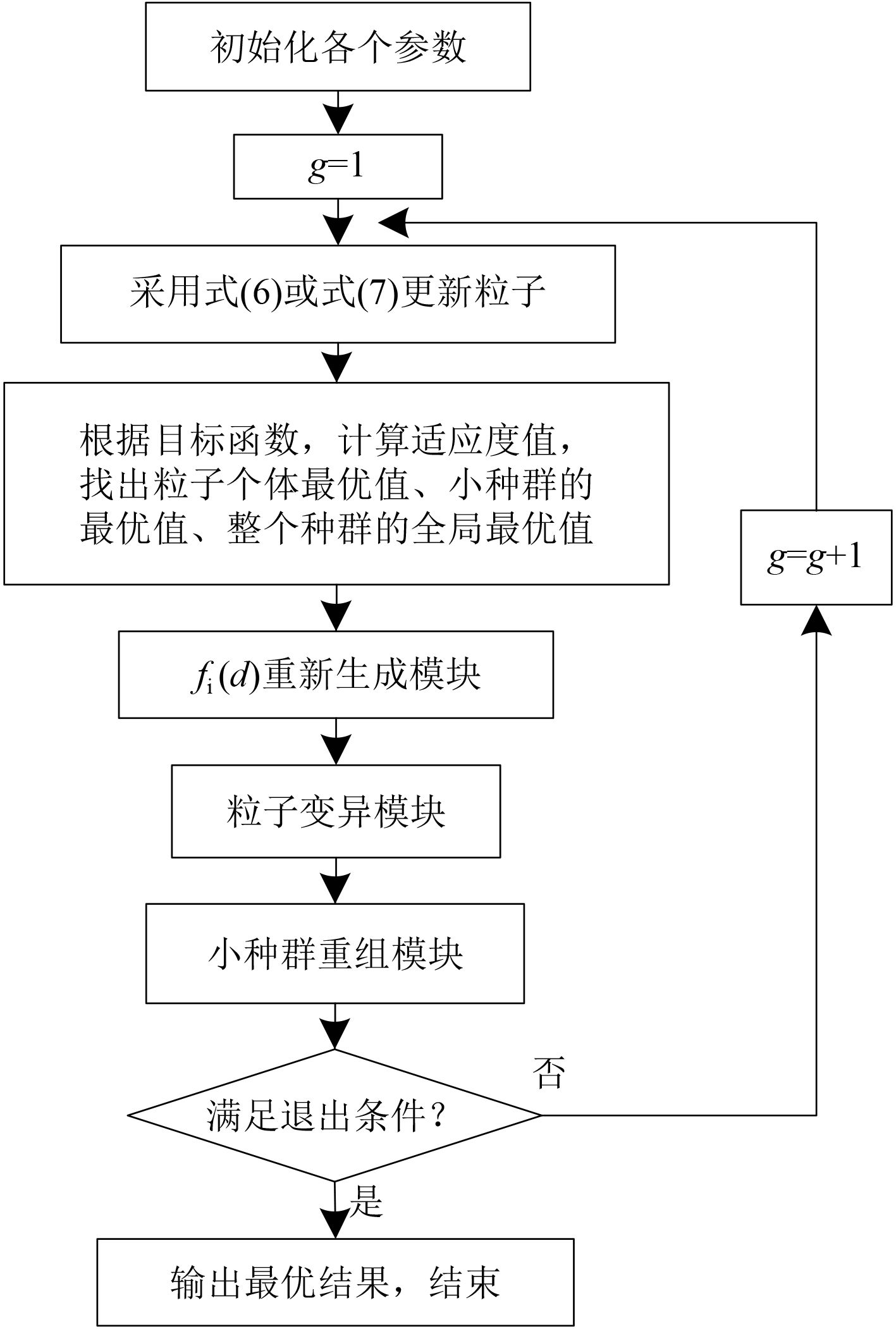
3.2 多种群综合学习粒子群算法

多种群思想是借鉴同一物种在不同地域进化所呈现的自然现象而来的。多种群算法是将多个小种群组成一个种群，通过小种群各自搜索最优值的方式提高全局算法搜索能力，并以整个种群最优值间接交流、动态重组种群等方式来增加种群多样性，同时加快算法的收敛速度。本文提出的多种群综合学习粒子群算法（MCLPSO）主要思路是：首先将整个种群分成N个小种群，然后分别进行迭代进化，并且在适当的条件下进行种群粒子交换和粒子变异，MCLPSO算法计算框架如图2所示。

MCLPSO算法主要步骤如下：

步骤1　将种群分成N个小种群，并初始化各个参数。

步骤2　各个小种群进行CLPSO算法迭代，并通过目标函数找出粒子个体最优值、小种群的最优值以及整个种群的全局最优值。为了保证算法在前期具有较高的全局搜索能力，在算法前期（可设为第 ${g_0}$ 代之前），各个小种群采用式（6）进行更新所有粒子状态；为了克服原来CLSPO算法在后期局部搜索能力的不足，在第 ${g_0}$ 代之后，给出一种新的更新策略。即将整个种群的全局最优值pg加入到速度更新中，如式（7）所示。

$\left\{\!\!\!\! \begin{array}{l} V_{jd}^{t + 1} = \omega V_{jd}^t + {c_1}r_{1jd}^t(pb_{{f_j}(d)}^t - X_{id}^t) + {c_2}r_{2jd}^t(pg_d^t - X_{jd}^t), \\ V_{id}^{t + 1}{\text{ = }}\min ({V_{id\max }},\max ({V_{id\min }},V_{id}^{t + 1})), \\ X_{jd}^{t + 1} = X_{jd}^t + V_{jd}^{t + 1}, \\ X_{jd}^{t + 1}{\text{ = }}\min ({X_{jd\max }},\max ({X_{jd\min }},X_{jd}^{t + 1})) {\text{。}}\end{array} \right.$

(7)

式中： ${c_1}$ ， ${c_2}$ 是学习因子； $p{g^t}$ 是各个小种群最优值 $\{ pg{1^t}, \cdots ,pg{n^t}, \cdots ,pg{N^t}\} $ 中的最优值； $r_{1jd}^t$ ， $r_{2jd}^t$ 是（0，1）间均匀分布的随机数。

步骤3 　若某个小种群连续 ${R_1}$ 代未更新其小种群最优值，则该种群有可能陷入局部最优。为了让该小种群尽可能跳出局部最优，采用变异策略：让该小种群中的每个粒子的每一维，以概率 $Pm$ 进行变异，变异方式为：

$X_{jd}^t = X_{jd}^t + randn({X_{jd\max }} - {X_{jd\min }})(G - g)/G\text{。} $

(8)

式中，randn为（–1，1）间的随机数，G为总的迭代代数，g为当前代数。

步骤4　在第 ${g_0}$ 代之后，为了加强种群多样性，每隔 ${R_2}$ 代，种群之间粒子随机交换，以重组小种群。重组种群的方法为：所有小种群随机选取自身种群50%的粒子和其他种群的粒子随机交换。值得说明的是，每一个待交换的粒子的交换对象粒子可以是任何一个其他种群中的任意一个粒子。

综上，MCLPSO算法的流程如图3所示。

4 实例仿真与分析

为了验证本文提出的多种群综合学习粒子群算法的有效性，采用该算法对一艘1 000 t起重船的动力定位系统的定位能力进行优化分析。

4.1 船舶相关参数

所研究的船舶为长江航道局三峡库区1 000 t应急抢险打捞起重船，该船的相关参数如表1所示。该船共布置有4个推进器，具体信息如表2所示，计算过程中所用坐标系及推进器布置位置如图4所示。

4.2 定位能力计算及结果分析

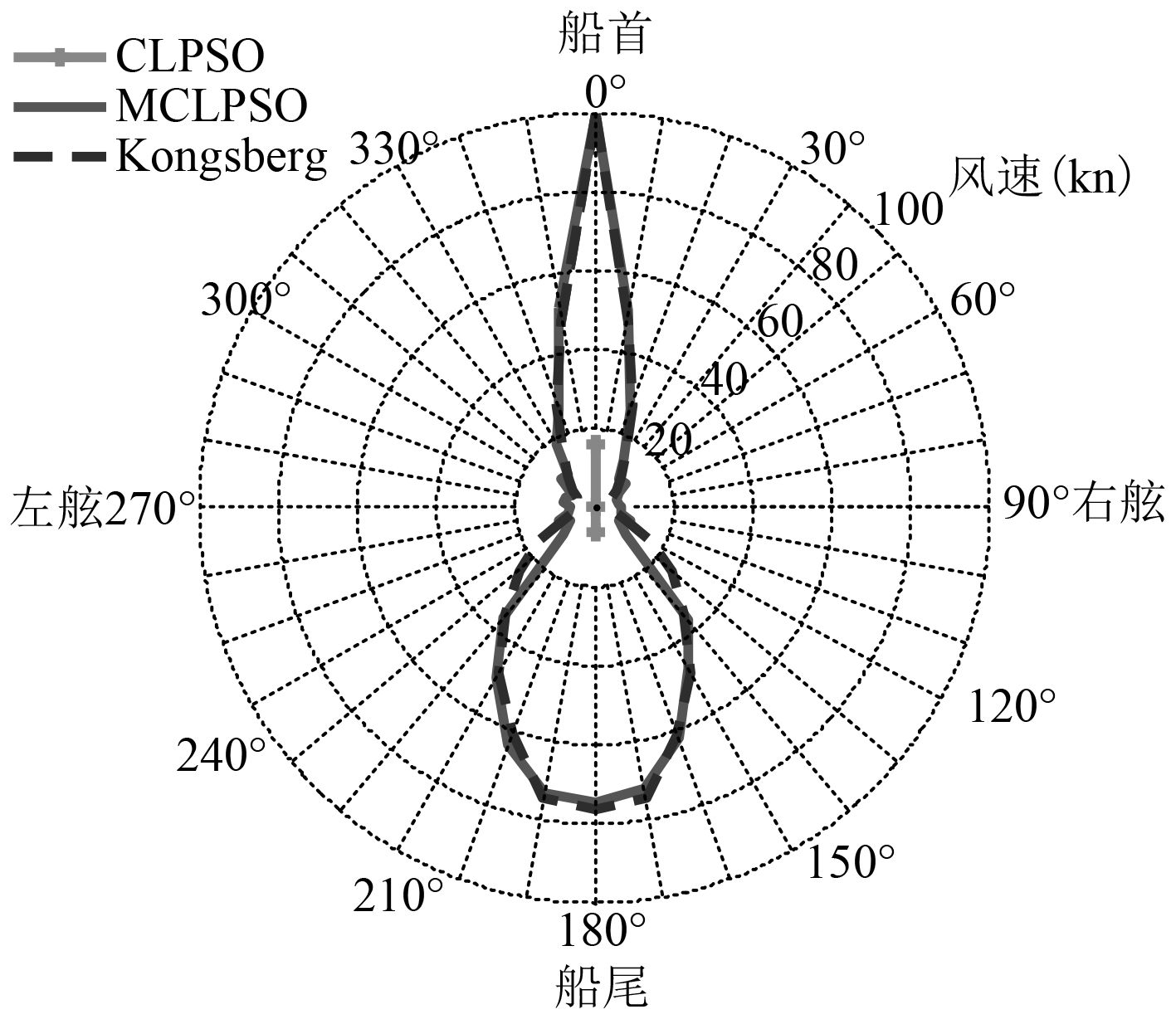
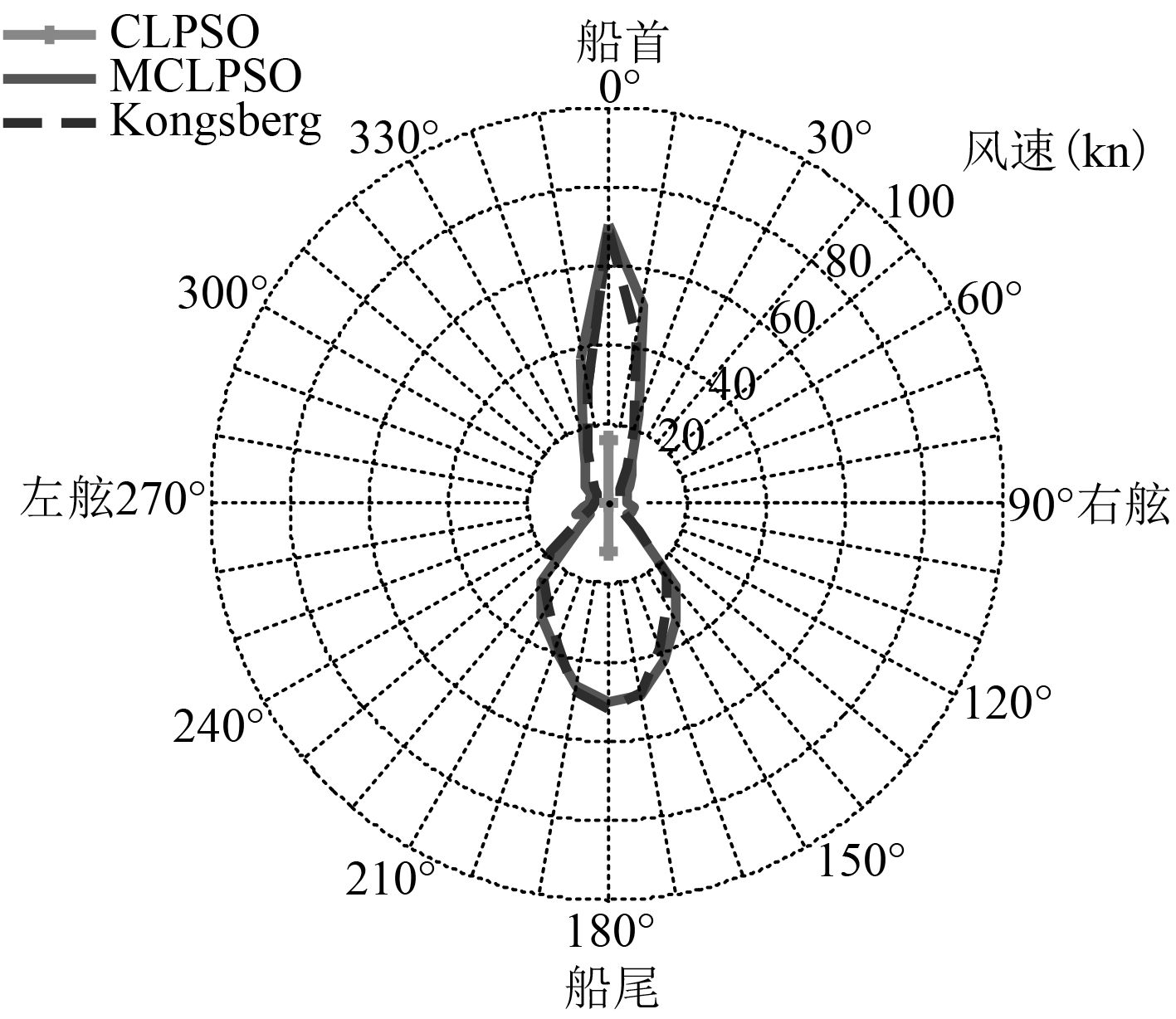
为了验证MCLPSO算法的有效性，设计了3种推进器工作模式。1）所有推进器正常工作；2）单推进器失效最好模式：推进器2失效；3）单推进器失效最坏模式：推进器4失效（推进器3和4对称布置）。分别利用CLPSO算法和MCLPSO算法来优化计算定位能力，并与Kongsberg公司计算结果比较。

算法参数设置：MCLPSO算法和CLPSO算法总种群规模都为75，最大迭代次数G都为300， $\omega $ 从0.9～0.3线性递减，m为6， $Pc$ 的设置参考文献[7]；MCLPSO算法的小种群数设为5，即每个小种群规模为15， ${g_0}$ 设为60；c为2， ${c_1}$ 和 ${c_2}$ 都为1.1； ${R_1}$ 为15， ${R_2}$ 为20。3个惩罚因子都设为10 000，变异概率设为0.1。

在计算过程中，流速大小设为1.5 kn，且当水平面3个自由度上的环境载荷与推进力的误差的绝对值之和小于0.1时，则认为推力有解。编写Matlab程序，计算结果如图5～图7所示。

从图5～图7可以看出利用本文提出的MCLPSO算法进行优化的定位能力曲线与Kongsberg公司的计算结果很吻合，说明MCLPSO算法有效。而利用CLPSO算法计算出的结果与之相差甚远，其主要原因是CLPSO算法在后期的收敛速度变慢以及陷入局部最优的概率较大，导致算法在总迭代次数较小的情况下难以收敛到最优值，以至于程序认为推力不能平衡环境载荷，无法得出正确结果。

另一方面可以看出，模式1的定位能力最好，模式2次之，模式3的定位能力最差。同时结果也表明该起重船的定位能力在风浪向角为 $0^\circ $ 时最好，在风浪向角为 $180^\circ $ 时稍差一点，在风浪向角为 $30^\circ \sim 120^\circ $ 和 $240^\circ \sim 330^\circ $ 时最差。很明显，该起重船无法全方位作业，应该避免船舷两侧受力作业，且当推进器3或推进器4失效时尽快维修。

5 结　语

本文针对动力定位能力分析问题，给出了定位能力计算流程，并针对性地提出了一种适用于动力定位能力优化计算的多种群综合学习粒子群算法。在算法中多个种群并行进化，为了提高算法的各项性能，在前后期采用了2种不同的更新策略，同时增加了粒子变异机制和种群重组机制。最后将算法应用到实际船舶的动力定位能力计算中，计算结果表明所提算法是一种有效的动力定位能力优化计算的方法。