高性能船舶中双体船和三体船由于其优越的性能受到了额外的关注[1]。双体船的 2 个片体尺寸相同,2 个片体的横向连接大大增加了其有效宽度,使得双体船的横向稳定性优良且相对细长的片体设计又增加了其快速性,三体船与双体船相比具有更加宽大的甲板面积,且2 个侧片体可以对主体进行保护增加了其抗沉性。目前这 2 种船型在民用、军事等领域获得了广泛的应用,还衍生出SWATH、穿浪双体船、频海战斗舰等一系列性能优化船型。
在具有如此多优点的同时,由于船型的限制,双体船的摩擦阻力比同排水体积单体船大,导致其在临界傅汝德数内必然存在不利的兴波干扰。而且双体船无法对 2 个片体之间的兴波干扰进行有效灵活的调节;三体船虽然可以利用片体错位进行调节但是其宽度过大加大了建造难度且航道会有所限制。所以既不会太宽而又可以通过主、侧体相互错位调节兴波的非对称双体船具有非常良好的发展前景。
对于非对称双体船船型,目前国内建造了一艘实船,如图1中的Asian Lady号。理论研究方面,贾静蓓等[2]对非对称双体船的初稳性公式进行推导,并编制程序计算了非对称双体船各船型参数对稳性高GM的影响;黄志敏[3]对其振动特性进行研究;李广年等[4]基于线性兴波理论采用混合遗传算法针对非对称双体船兴波阻力进行船型优化。目前大多研究集中在兴波阻力上,对于非对称双体船总阻力及航态的研究尚少。本文基于粘性流体力学理论,采用CFD技术模拟了非对称双体船在不同船型参数下的水动力性能,探讨了非对称双体船的运动特点,对非对称双体船从阻力及航行姿态的角度进行优选,以期可以为新型高性能船舶的研究提供参考。
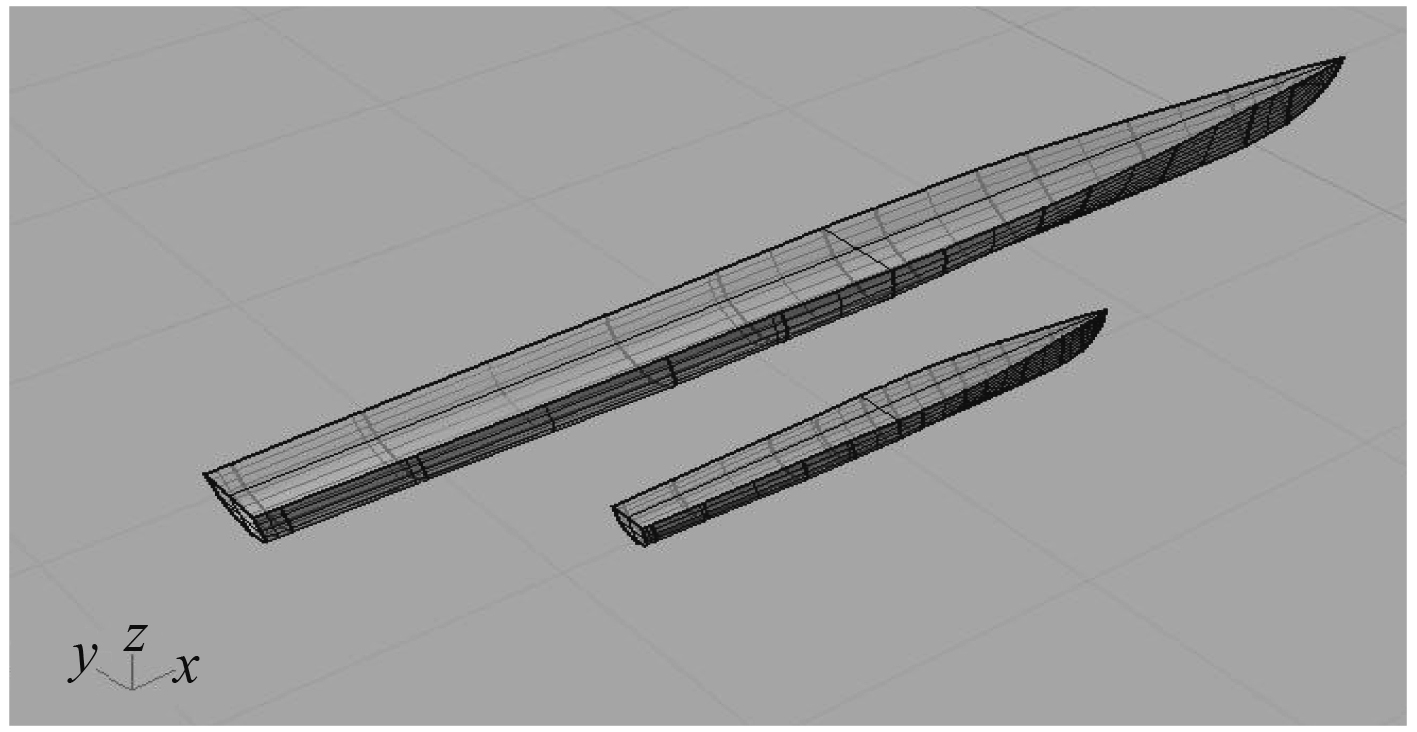
1 CFD数值模拟方法 1.1 船体模型建立计算模型的坐标系选取为:由船尾指向船首为x轴正方向;向主体左舷为y轴正方向;垂直向上为z轴正方向。建立的非对称船模型如图2所示。

|
图 1 “亚洲女士”号示意图 Fig. 1 Diagram of Asian Lady ship |
|
图 2 非对称双体船示意图 Fig. 2 Diagram of asymmetry catamaran |
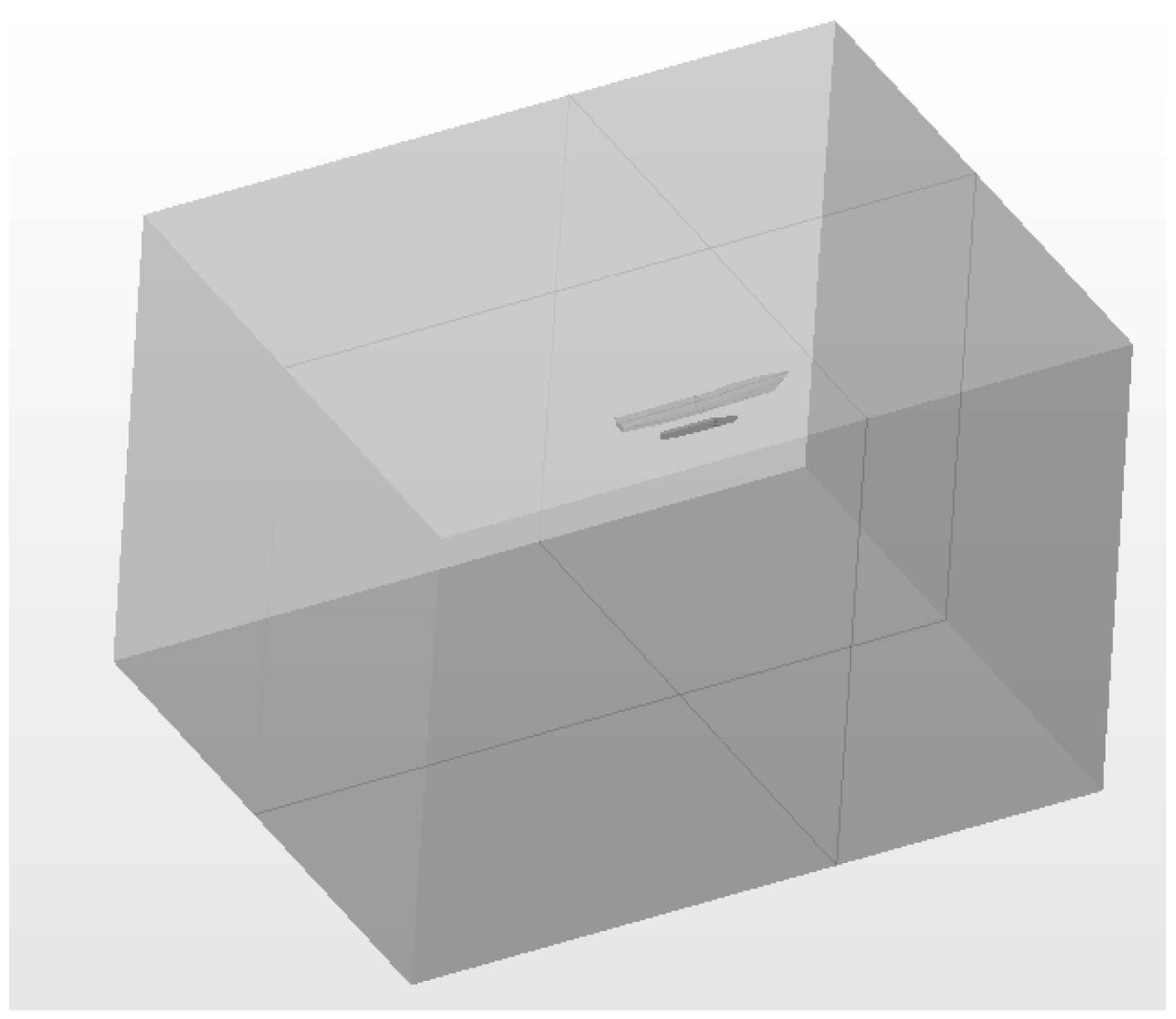
模拟计算域为4.5 L×3 L×3 L的长方体,L为船长。船在靠近来流端1.5 ~2.5 L的位置。高度方向:自由液面上方为1 L,水下为2 L。
|
图 3 计算域示意图 Fig. 3 Diagram of computing domain |
本文选择的是Realizable
| $\begin{split} \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}[(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_j}}}] + {G_k} - \rho \varepsilon,\end{split} \text{。}$ | (1) |
其中:
此外本文根据壁面函数法来解决近壁面处的粘性效应。大量研究表明,贴近船体表面的流体区域从内到外依次可以分为以层流为主的粘性底层、复杂的过渡层和湍流为主的对数层。过渡层流动较复杂,因其厚度极小,计算中常将其归入对数层。为了解决层流和湍流分界点的问题,引入无因次距离
船体表面第1层网格节点的无因次距离
| ${y^ + } = 0.172(\frac{y}{L}){Re ^{0.9}}\text{。}$ | (3) |
其中
本文模拟采用切割体与棱柱层网格生成器。网格基础尺寸0.047 5 m,船体表面网格设置为基础尺寸的30%。船体附近和尾部流场区域进行加密,加密处最小为基础尺寸的60%。对自由液面进行逐层加密,最密处网格z方向厚度为基础尺寸的15%,x,y方向为基础尺寸的200%。边界层总厚度为0.02 m,边界层层数设置为6层,棱柱层成长率为1.2。非对称船型无法进行对称面的简化设置,故只能2个船体共同计算,最终计算的网格数量约为304万。

|
图 4 非对称双体船船计算域网格 Fig. 4 Grid of asymmetry catamaran computing domain |
计算域的入口、顶部、底部和后方以及两侧的边界设置为速度入口,出口边界为压力出口,船体表面设置为无滑移壁面。模拟时间步采用的是隐式非定常形式,时间步长设置为0.005 s。模拟采用VOF多相流模型,欧拉相设置空气、水2项。模拟考虑重力。采用静水VOF波,水密度为997.561 kg/m3。空气密度为1.184 15 kg/m3。隐式不定常时间步为0.005 s,内部最大迭代次数为10。
2 非对称双体船船型布局研究应用前述方法模拟了非对称双体船在不同片体尺寸与布局下的运动响应,并进行分析,选取了性能优越的船型。设主体长为L,侧体长为l;主体宽为B,侧体宽为b;主侧体中横剖面距离为d,d为0表示主侧体中横剖面在同一水平线上,d为正表示侧体沿x轴向主体尾部移动。主侧体中纵剖面距离为K。侧体位于主体右侧,计算时保持主体尺度与位置不变,变换侧体的尺度与布局。主体船尺度如表1所示。
|
|
表 1 主船体尺度 Tab.1 Scale of main hull |
工况如表2所示。
|
|
表 2 工况 Tab.2 Working conditions |
计算时改变侧体与主体的长度比l/L,宽度比b/B取为0.5,中横剖面距离d/L取为0,K/B为1.5。阻力结果如图5所示。

|
图 5 总阻力随长度比的变化曲线 Fig. 5 Curve of the total resistance with length changing |
由图5可知,非对称型双体船的阻力随着侧片体与主片体长度比的不断加大,阻力值会不断增加,在长度比为0.33~0.4的范围内增加的速度明显加快,到0.5之后阻力增加放缓,从一个角度说明随着侧体的长度与主体长度越接近,整个船体的阻力值会不断增大,增加的速度逐渐趋于0,当l/L为1时,阻力稳定即为对称型双体船的阻力值。
图6为航行姿态的变化结果。
|
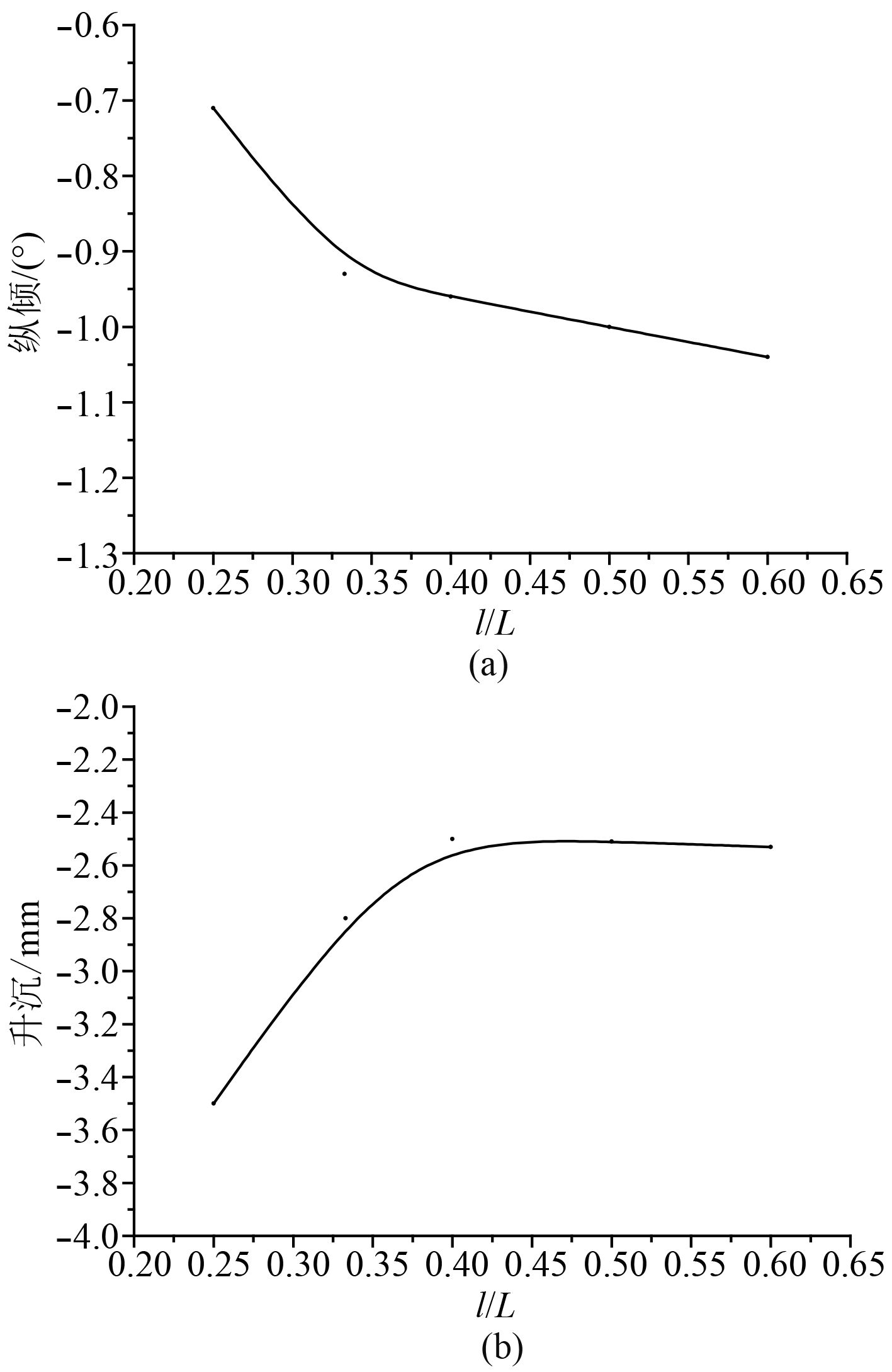
图 6 航行姿态随长度比的变化曲线 Fig. 6 Curve of the sailing gesture with length changing |
由图6可知,船处于尾倾状态,且尾倾幅度随着l/L的增加而增加,尤其在0.25~0.33之间增加的尤其迅速,过来0.35之后速度开始放缓。升沉曲线说明船体下沉,且升沉幅度随着l/L的增大逐渐放缓,0.25~0.4范围内升沉值不断减少,长度比l/L大于0.4后升沉值基本不变。
由上述分析可以得出,侧体与主体的长度比不宜取得过大,那样阻力会增大且船会比较倾斜,但考虑到片体长度如果选取过小船体的下沉幅度会比较大,故综合考虑选取l/L为0.5进行之后的计算分析。
2.2 主体尺度不变,侧体宽度变化改变侧体与主体的宽度比,此时l/L取0.5,K/B为1.5,d/L为0。具体工况见表3。阻力计算结果如图7所示。
|
|
表 3 工况 Tab.3 Working conditions |

|
图 7 总阻力随宽度比的变化曲线 Fig. 7 Curve of the total resistance with width changing |
由图7可知,船体的总阻力随着侧片体与主片体宽度比的增加会不断加大,在宽度比b/B达到0.5之后,阻力增加的幅度变大。原因是由于片体宽度的不断加大使两船体“靠近”,片体之间的兴波产生不利干扰。图8为航行姿态的结果分析。
|
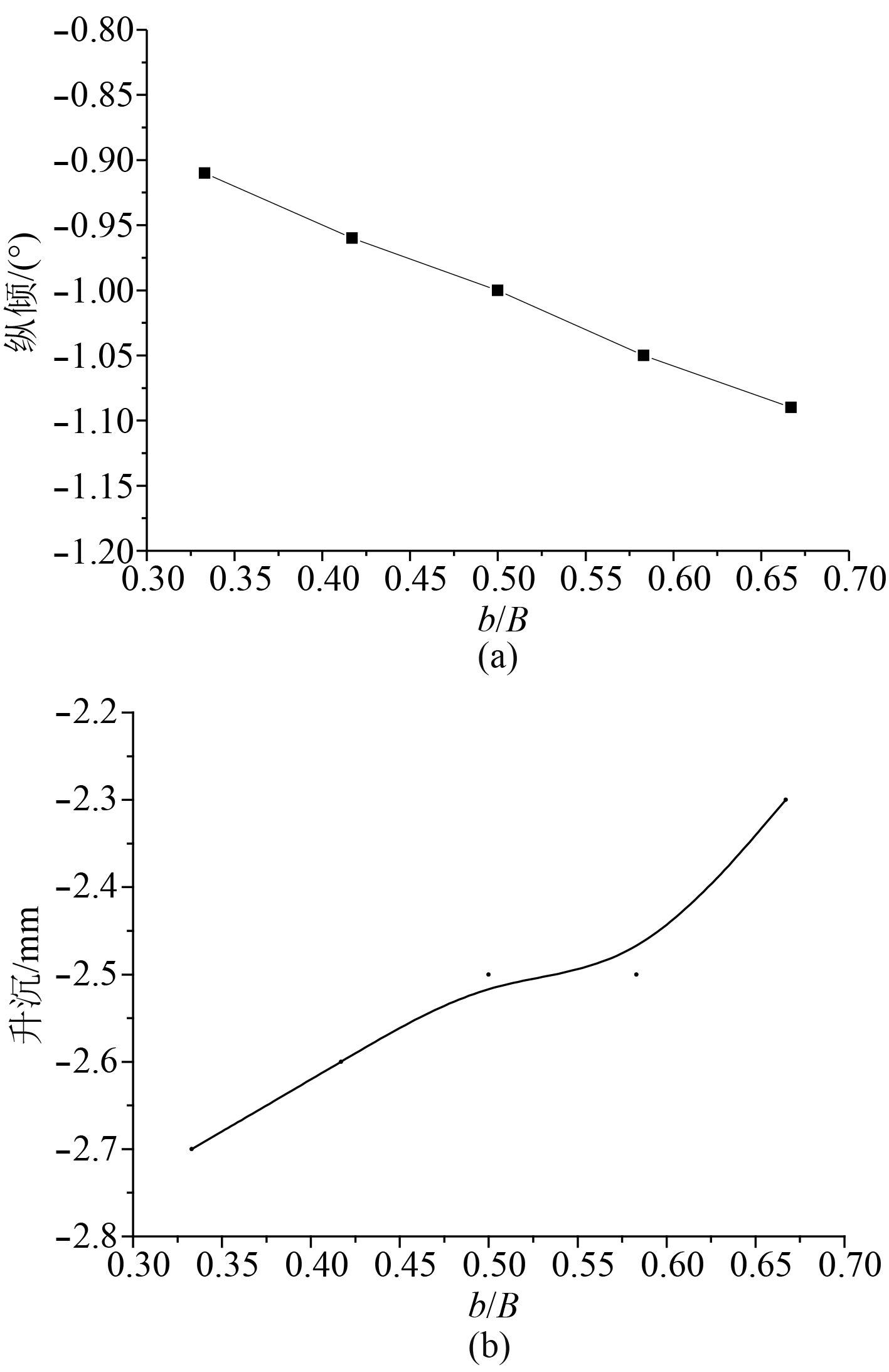
图 8 航行姿态随宽度比的变化曲线 Fig. 8 Curve of the sailing gesture with width changing |
纵倾角为负,说明船尾倾,且随着宽度比b/B的加大,尾倾幅度逐渐加大,基本上呈线性趋势。升沉为负值,船体下沉,随着侧体与主体宽度比加大,升沉数值减小,说明非对称双体船会逐渐趋于正浮状态。
综合上述分析,为了在获得好的航行姿态的同时使得总阻力不止过大,片体的宽度值取为主体的0.5倍。
2.3 改变主侧体中纵剖面距离此时保持主侧体的长宽不变,主体与侧体中横剖面距离不变,改变主侧体的中纵剖面距离。取l/L为0.5,b/B为0.5,d/L为0,改变K/B值。计算工况见表4,阻力结果如图9所示。
|
|
表 4 工况 Tab.4 Working conditions |
|
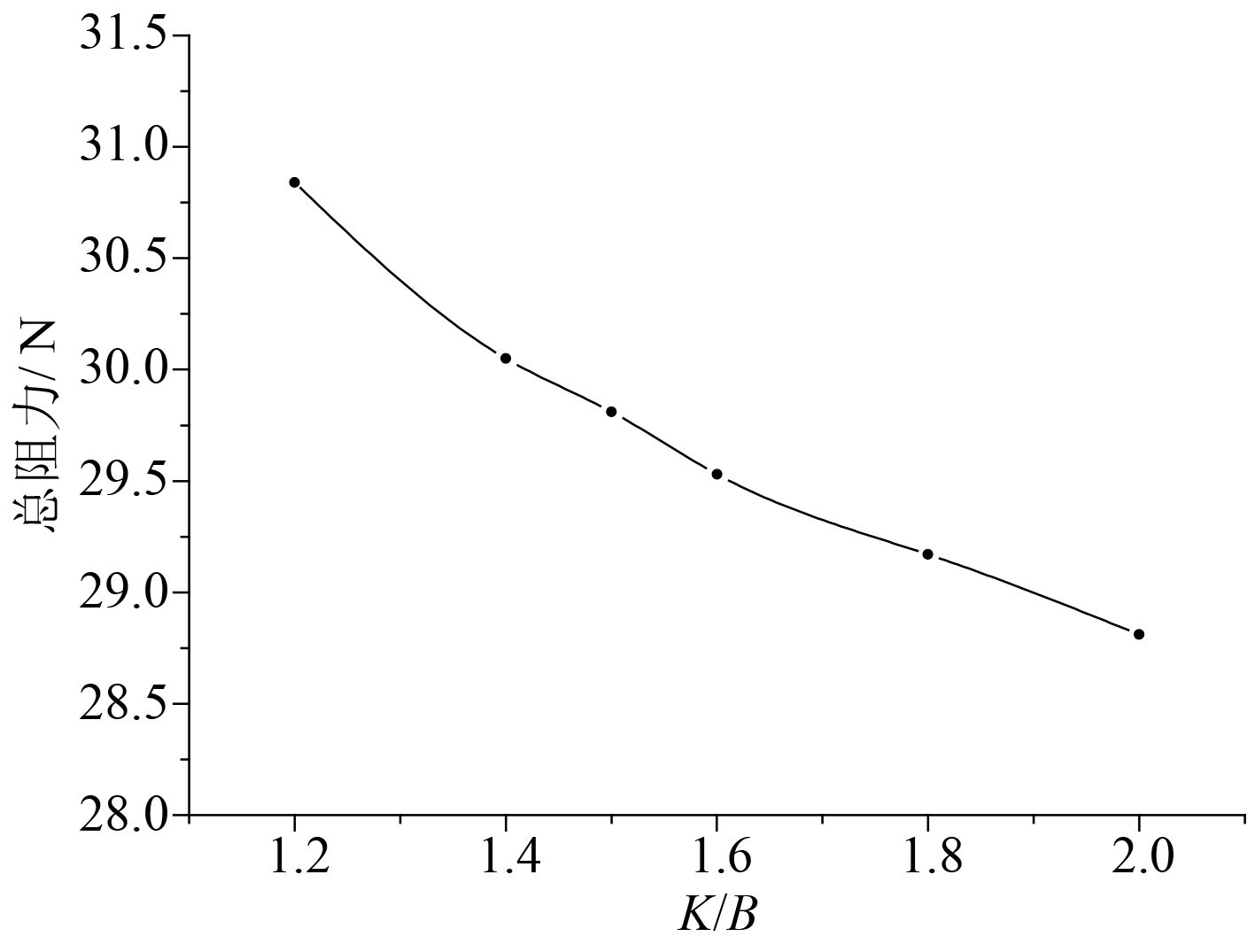
图 9 总阻力随K/B的变化曲线 Fig. 9 Curve of the total resistance with K/B changing |
由图9可知,随着两片体中纵剖面距离的不断加大,非对称船的阻力会不断降低,说明片体之间兴波的不利干扰效果不断降低,可以得出结论,当两片体之间的距离K不断加大时,总阻力趋于2个片体单独航行时的阻力之和。纵倾和升沉曲线如图10所示。
|
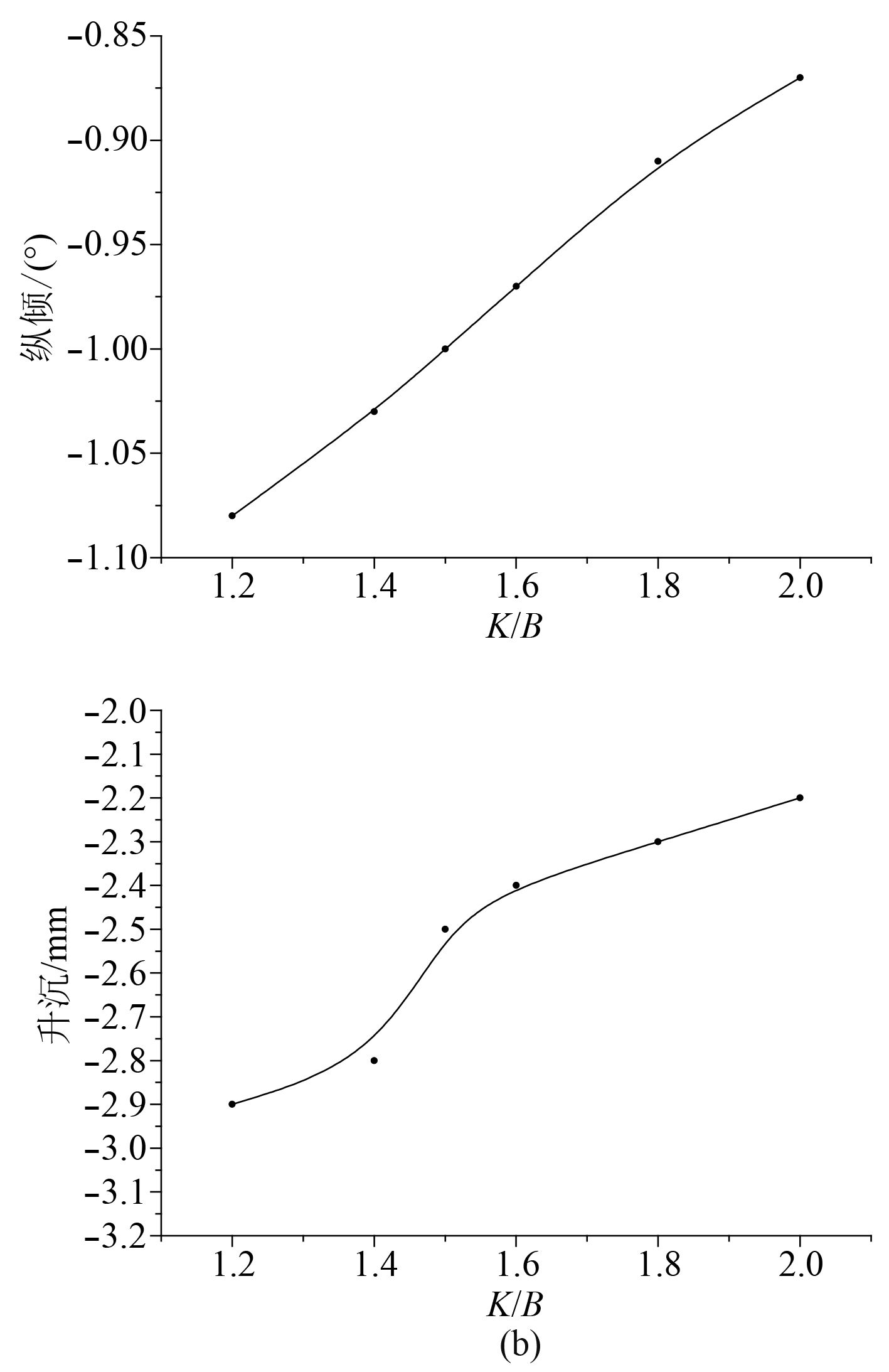
图 10 航行姿态随K/B的变化曲线 Fig. 10 Curve of the sailing gesture with K/B changing |
可以发现船体处于尾倾状态,随着片体间距的不断增加,尾倾的幅度不断减小。升沉图表示船的下沉幅度不断减小,总体来说,船的总体航行姿态随着片体间距K的增加而不断变好。
综合上述分析发现,K/B越大,非对称双体船的阻力越小,航行姿态越好,但是由于总宽度不宜过大,故选取K/B为1.8来进行计算研究。
2.4 改变主侧体中横剖面距离保持主侧体的长度、宽度以及中纵剖面距离不变,改变中横剖面的距离,取l/L为0.5,b/B为0.5,K/B为1.8,改变d/L。工况如表5所示,阻力曲线见图11。
|
|
表 5 工况 Tab.5 Working conditions |
|
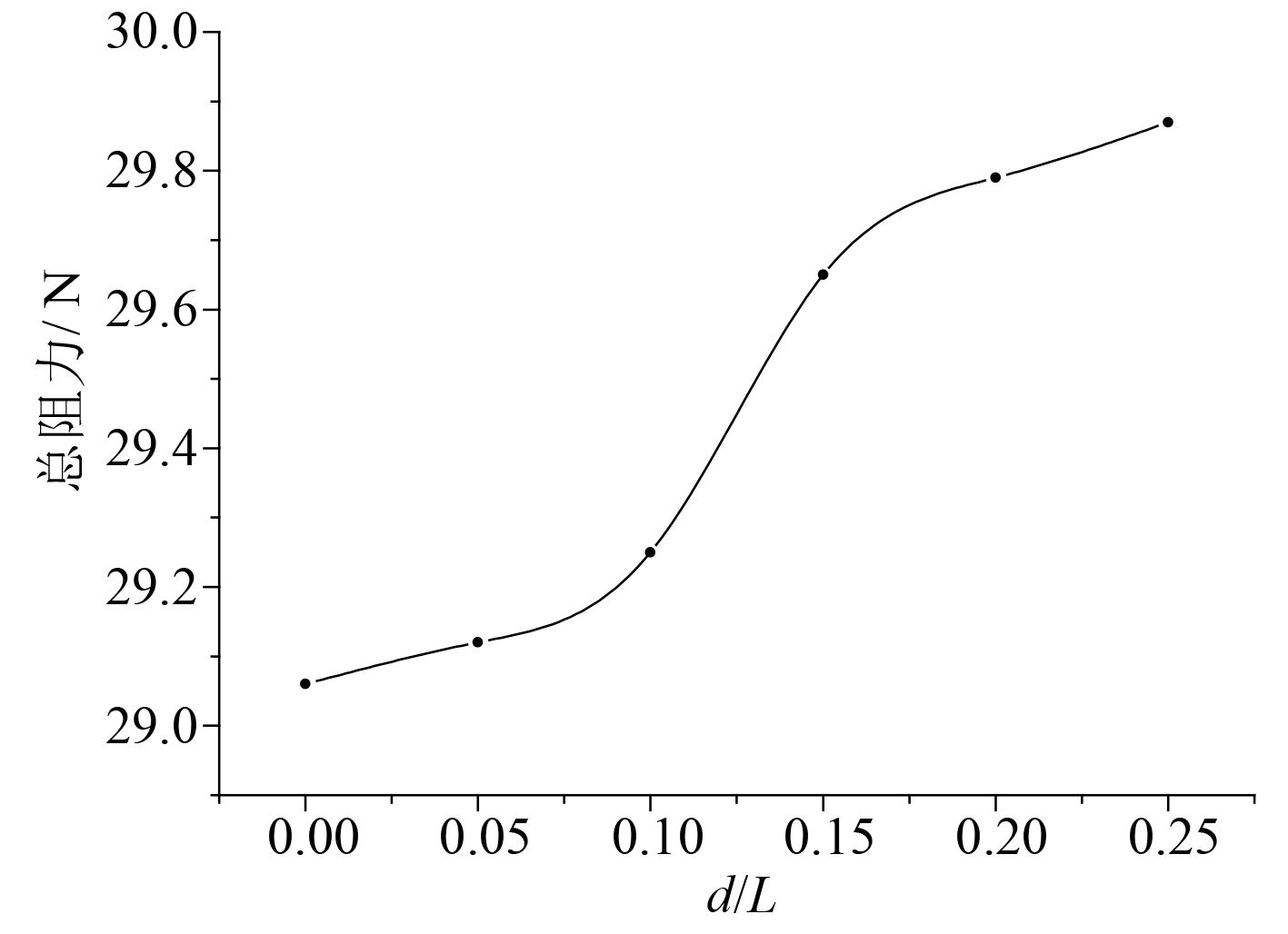
图 11 总阻力随d/L的变化曲线 Fig. 11 Curve of the total resistance with d/L changing |
由阻力曲线可知,阻力随着侧体位置不断向后移动而不断增加,但是并不呈现线性趋势。在d/L为0.1~0.17之间增加较快。
图12展示了侧体与主体中横剖面距离变化对航行姿态的影响。
|
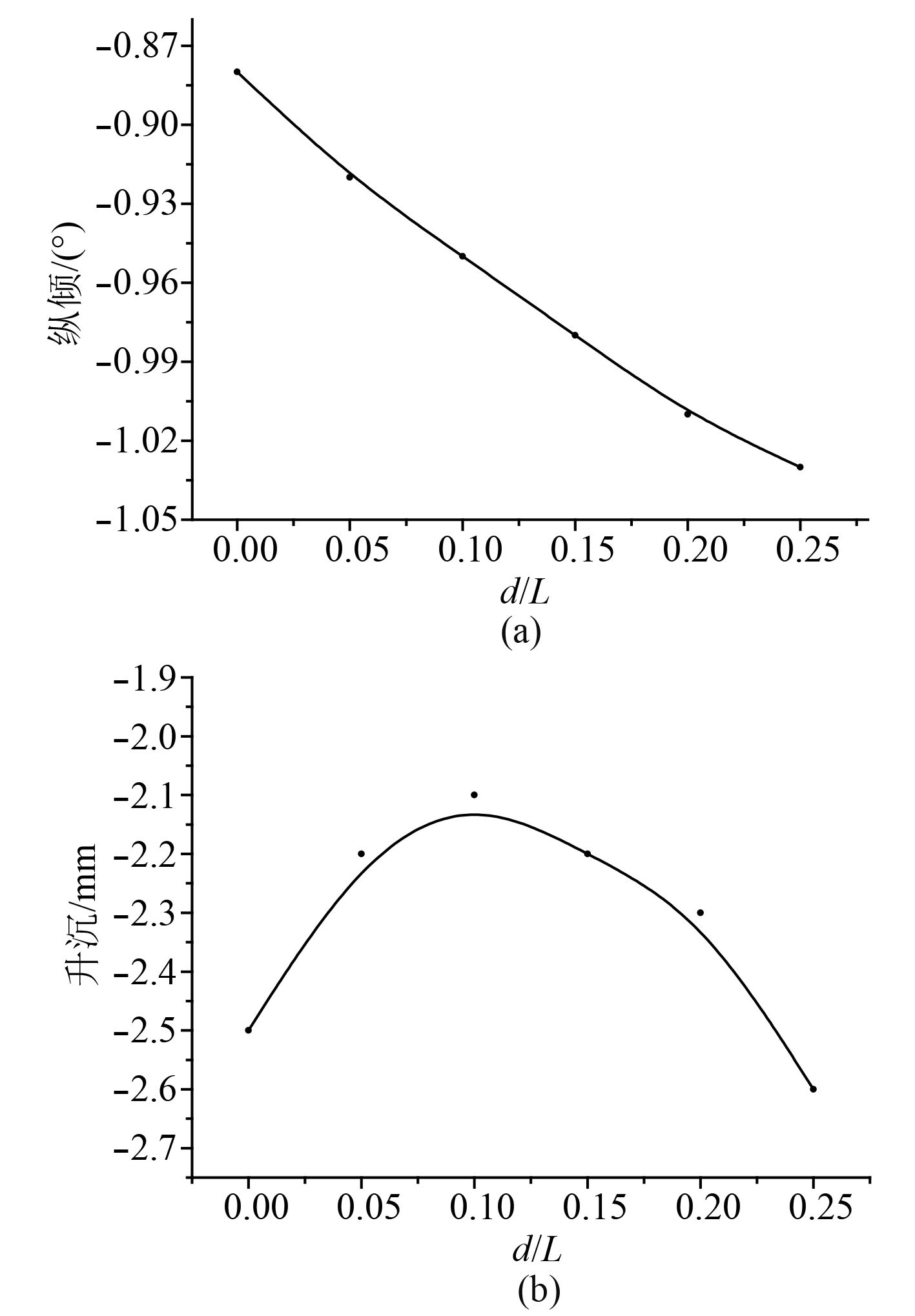
图 12 航行姿态随d/L的变化曲线 Fig. 12 Curve of the sailing gesture with d/L changing |
由图12可知,当d/L增加,即侧体相对主体向主体尾部移动时,纵倾不断幅度不断加大,航行姿态逐渐恶劣。而下沉幅度开始减小,在d/L达到0.1左右之后开始加大。
综合上述分析发现,当d/L取为0.1~0.15时有不错的航行姿态与阻力性能。
2.5 非对称船型阻力曲线与双体船比较根据上述分析选择船体布局l/L为0.5,b/B为0.5,K/B为1.8,d/L为0.1。模拟了其在不同傅汝德数下的静水阻力曲线,将所得阻力系数与Delft-372双体船试验数据进行对比,曲线如图13所示。
|
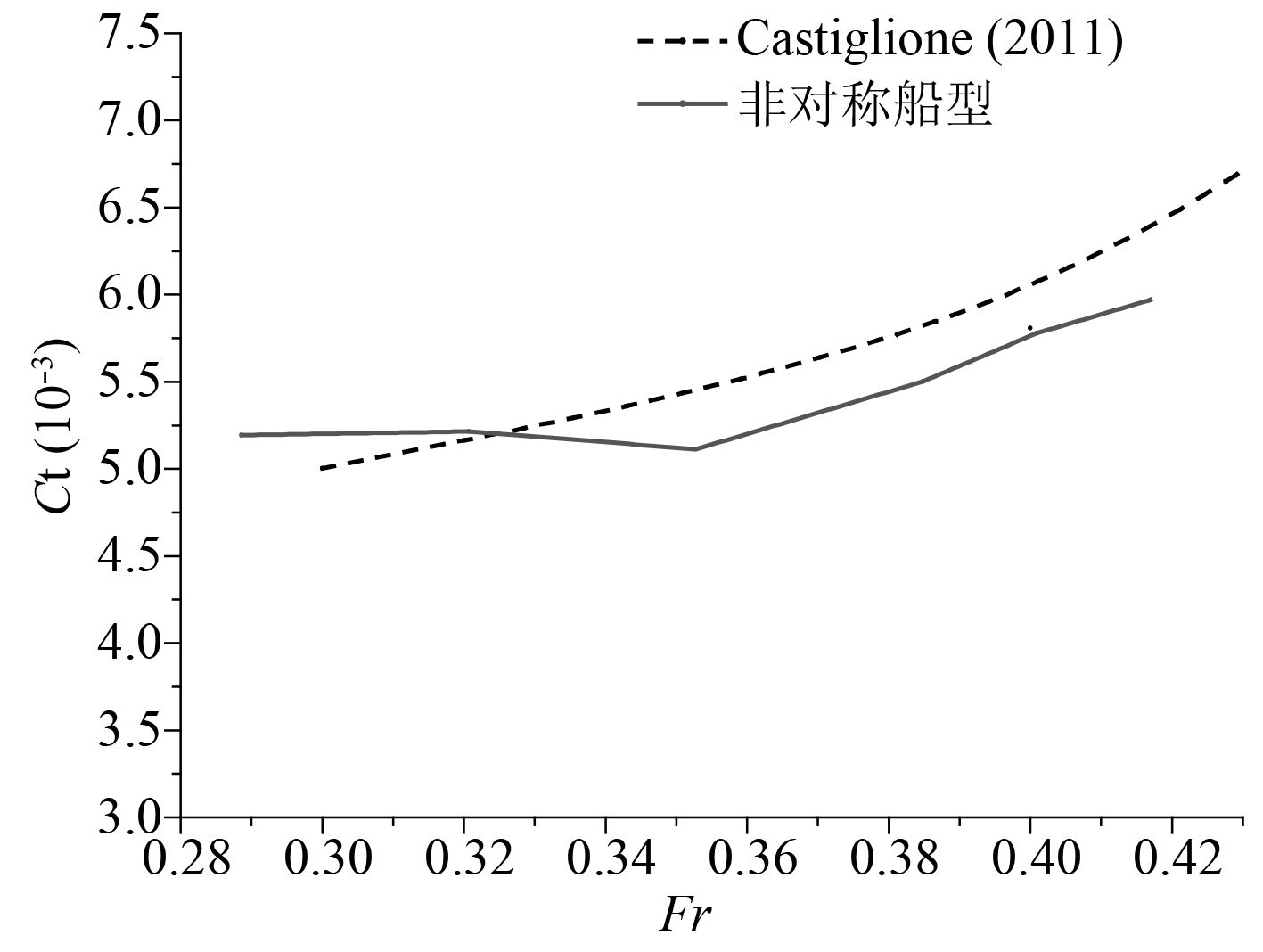
图 13 两种船型阻力系数比较 Fig. 13 Comparison of resistance coefficient of two hull form |
由图13可知,从阻力系数的角度来看,在所取傅汝德数范围内非对称双体船的阻力系数总体要低于常规双体船,仅在速度较低时(Fr小于0.3)阻力系数略微高于双体船,这说明非对称船型在阻力方面比常规双体船有一定的优势。
3 非对称双体船兴波阻力研究本节采用基于Dawson法的势流方法源程序对非对称双体船在不同构型下的兴波阻力进行计算。主要改变主体、侧体长度比、宽度比以及主侧体在横向、纵向的间距。船型变化的工况与第2节进行阻力与航行姿态研究时的工况一致,计算结果如图14所示。
|
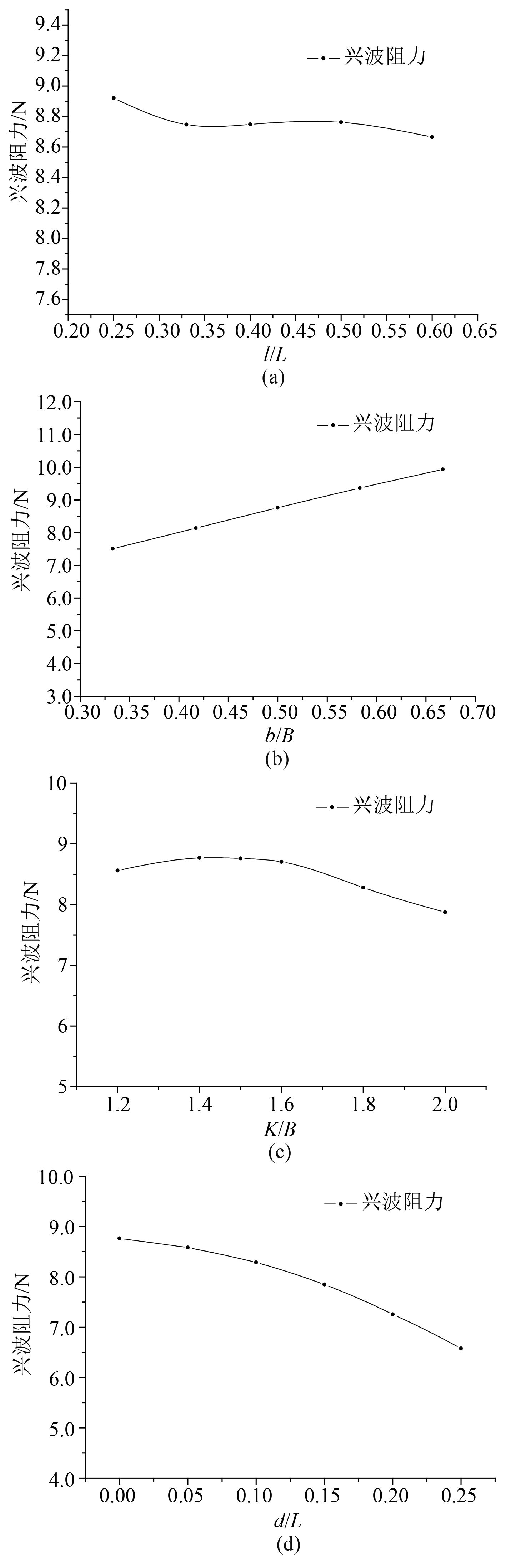
图 14 不同船体构型下的兴波阻力 Fig. 14 The wave-making resistance of different ship forms |
图14(a)为兴波阻力随长度比的变化曲线。可见,随着长度比增大,兴波阻力整体呈现减少趋势。开始是明显下降,之后趋势趋于缓和,到达0.5之后又明显下降,说明非对称船型两片体之间存在着较强的兴波干扰。在侧体与主体长度比较小时兴波干扰不利,从兴波阻力角度可见侧体船长不宜选取过小。图14(b)反应出兴波阻力随着侧体与主体宽度比b/B的增加大致呈现增加趋势,随着侧体宽度加大,两片体之间绝对距离减少,相互干扰程度加剧,会导致不利干扰;图14(c)是主体与侧体纵剖面间距变化时的兴波阻力变化情况,可见兴波阻力随着K/B增加逐渐减少,当K无限大时,两片体之间干扰为0,这时相当于2个片体单独航行。图14(d)显示兴波阻力随着侧体向主体尾部移动呈下降趋势,侧体向后移动会使侧体航行产生的开尔文波与主体产生的波浪进行叠加出现兴波的有利干扰,导致兴波阻力减少,从兴波的角度来看,侧体相对主体在纵向船长方向不宜太靠前。
综合考虑兴波阻力结果与第2节中的讨论结果,决定l/L取0.5~0.6,b/B取0.4~0.5,d/L取0.13~0.15,K/B取1.6~1.8,较为合适。
4 结 语本文基于CFD模拟方法研究了不同船型尺寸与布局下的非对称双体船在静水中航行时的水动力性能。分别改变非对称双体船的侧体与主体长度比、宽度比、中横剖面距离、中纵剖面距离,基于粘流方法对各种船型在静水中水动力性能进行模拟,并将阻力系数计算结果与常规双体船数据进行分析比较,发现非对称型双体船在阻力方面相对双体船具有一定的优势。同时采用势流方法对各种船体构型下的兴波阻力进行计算,分析了非对称双体船的兴波阻力变化特点。综合阻力与航行姿态及兴波阻力等多方面的影响提出了合理的具有较好综合性能的非对称双体船布局方案,可为以后此种船型的优化以及性能计算提供参考。
| [1] | 赵连恩, 韩端锋. 高性能船舶水动力原理与设计[M]. 哈尔滨工程大学出版社, 2007. |
| [2] |
贾静蓓, 宗智..不对称型双体船初稳性研究[J]. 中国舰船研究.2008(1): 13-17.
JIA Jing-bei, ZONG Zhi.Research of initial stability of unsymmetrical catamaran[J]. Chinese Journal of Ship Research.2008(1): 13-17. |
| [3] | 黄志敏.不对称双体船振动特性分析[D]. 大连: 大连理工大学.2007. |
| [4] |
李广年, 赵连恩.非对称双体船兴波问题与侧体布局优化分析[J]. 中国造船.2013(4): 55-62.
LI Guang-nian, ZHAO Lian-en.Wave and ship layout optimization analysis of unsymmetrical catamaran[J], Ship building of China, 2013(4): 55-62. |
| [5] | WILCOX D C.Turbulence modeling for CFD[M]. La Canada, CA:DCW industries, 1998. |
| [6] | LIN C W, PERCIVAL S, GOTIMEER E H.Viscous drag calculations for ship hull geometry[C]//9th International Conference on Numerical Metheds in Laminar and Turbulent Flow, Atlanta, GA, 1209-1222. |
 2018, Vol. 40
2018, Vol. 40

