船舶在中垂或中拱的情况下是最危险的时刻,船体梁将遭受很大的弯曲塑性变形。Budden[1]表示对于越来越多的在超过初始屈服应变下工作的构件,过去大多数的研究基于应力法都局限于小范围的屈服,而基于应力的断裂评估准则在很多有限元计算分析后表明现有的相关规范等过于保守。
为了描述含裂纹材料的韧性,Hutchinson[2]提出了J积分(能量释放率)和CTOD(裂纹尖端张口位移)同时作为2种断裂参数来进行金属的断裂评估。从Metzger M[3]的研究可以看出J积分与CTOD之间存在一定的关系,所以CTOD作为断裂参数是等价于J积分的。为了描述管道钢SE(T)试样的断裂行为,Cravero S[4]提出了J积分的计算式并进一步提出基于CMOD(裂尖张口位移)的裂纹扩展J积分评估方法。1984年,参考应力法率先被Ainsworth[5]提出,Ruggieri[6]的研究表明不管是全塑性方法还是参考应力法都可以通过J积分得到相似的断裂韧性估算,但是对于低硬化材料,由参考应力法可能会产生较高的J积分值。后来参考应力法经Linkens[7]等进一步推导为参考应变法,用来处理位移控制的载荷问题,并提出公式:
| $J = 2{F^2}\pi a{\sigma _{unc}}{\varepsilon _{unc}}\text{。}$ | (1) |
式中:
当材料最外层表面的进入屈服阶段的时候,裂纹深处裂尖还处于较安全的水平,此时式(1)中的
| $\frac{J}{{{\sigma _y}t}} = {f_1}{\varepsilon _{unc}} + {f_2}\text{,}$ | (2) |
式中:
Shih[9]推导出CTOD与J积分的单一的对应关系,并对海洋工程中的管道的断裂评估提出了基于测量CTOD的方法。所以本文基于J积分与CTOD的对应关系:
| $J \sim CTOD\text{,}$ | (3) |
得出:
| $CTOD \sim {\varepsilon _{unc}}\text{。}$ | (4) |
目前基本关于表面裂纹的研究都集中在海洋工程的管道等的焊接处表面裂纹,鲜有人关注到表面裂纹对船体板构件的损害。船体板表面裂纹是最常见也是最容易被忽视的一种结构缺陷,其在大应变条件下的扩展也是对结构安全的一种非常大的潜在危害。本文着眼于船舶在恶劣海况下,尤其是大型开口集装箱船和散货船船体板构件产生教大塑性的弯曲,此时船体板最外层表面的应变水平和裂纹深处尖端的CTOD之间的关系进行探讨。
1 有限元分析 1.1 材料模型考虑到结构受单向大塑性弯矩,本文采用的各项同性幂硬化模型,此模型适合描述单轴应力应变关系[10],表示如下:
| $\sigma = \left\{ {\begin{array}{*{20}{c}}{E\varepsilon \;\;\;\;\;\;\;\;\;\;\varepsilon \leqslant {\varepsilon _Y}}\text{,}\\{{\sigma _y}{{\left( {\displaystyle\frac{\varepsilon }{{{\varepsilon _Y}}}} \right)}^n}\;\;\;\;\varepsilon > {\varepsilon _Y}}\text{。}\end{array}} \right.$ | (5) |
其中,弹性模量
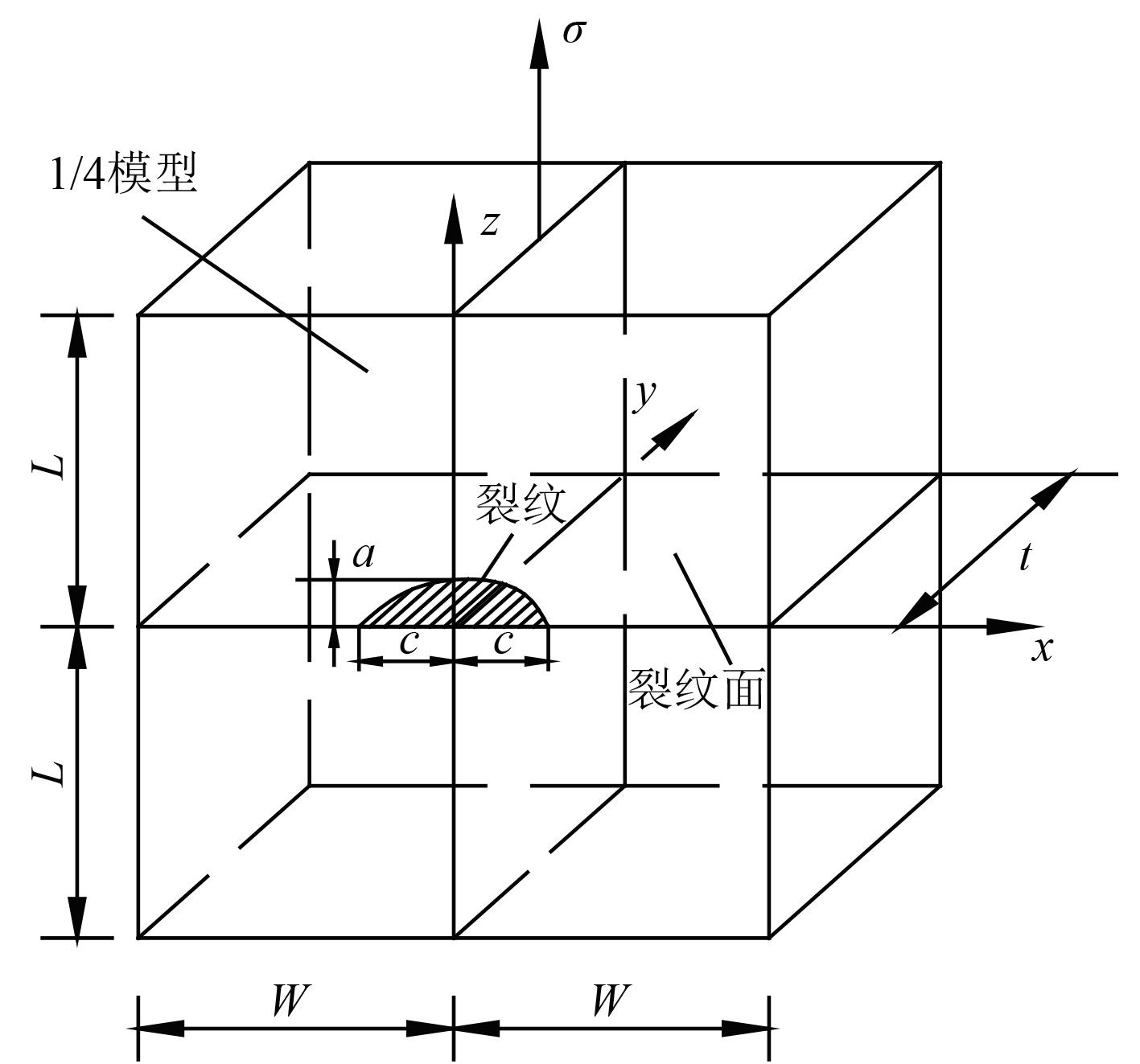
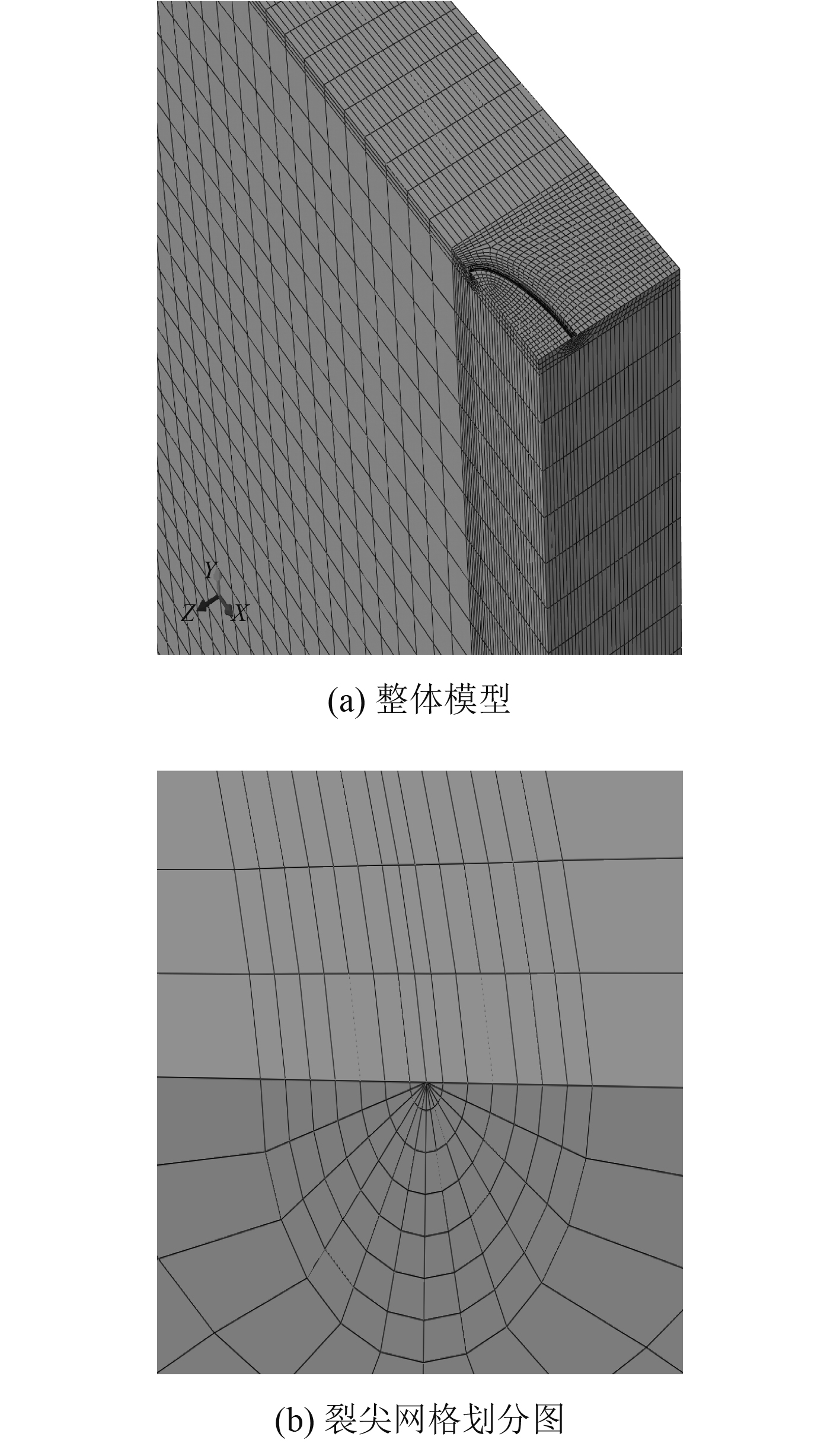
本文所取几何模型如图1所示,采用钢板尺寸L=150 mm,W=130 mm,t=20 mm来模拟无限大板中的表面裂纹。其中钢板弹性模量Es=206 GPa,泊松比Vs=0.3,钢板采取1/4模型,对称面采用对称边界条件,网格划分如图2所示。
|
图 1 含半椭圆表面裂纹钢板示意图 Fig. 1 A steel plate with semi elliptical surface crack |
|
图 2 有限元模型 Fig. 2 The mesh model |
Nourpanah N[8]提出当最外层表面的应变达到3%时,构件不含裂纹的塑性应变
| ${\varepsilon _{uncp}} = \sqrt {\frac{2}{3}({\varepsilon ^2}_{pL} + {\varepsilon ^2}_{pW} + {\varepsilon ^2}_{pt})}\text{。} $ | (6) |
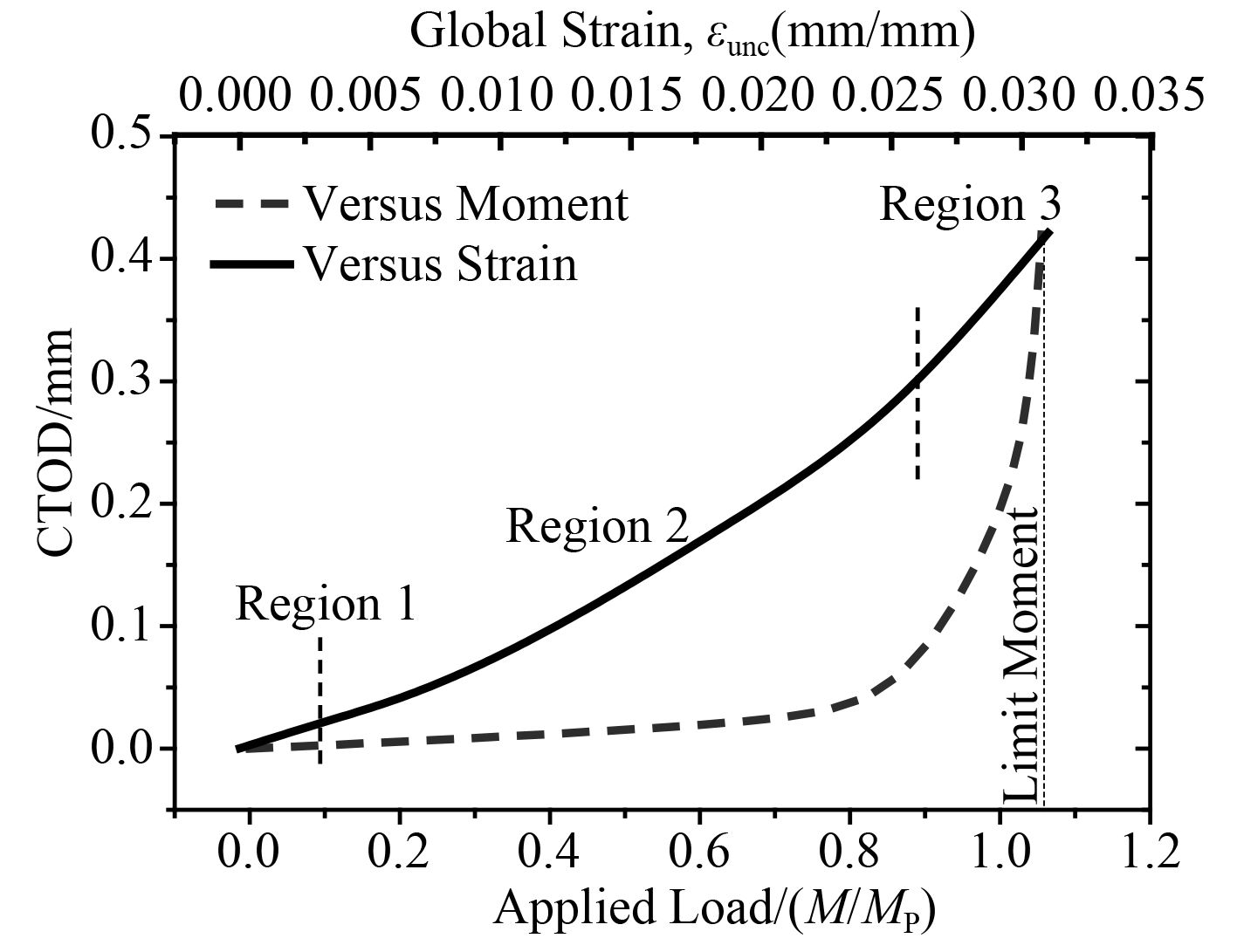
而对模型施加弯矩时会出现在很小的变化范围,导致J积分或者CTOD的陡增[11],本文对含表面裂纹板的断裂参数CTOD随着弯矩载荷控制和应变控制的变化做了计算,如图3所示。
|
图 3 两种弯曲施加方式的对比图 Fig. 3 The comparison of two kinds of bending methods |
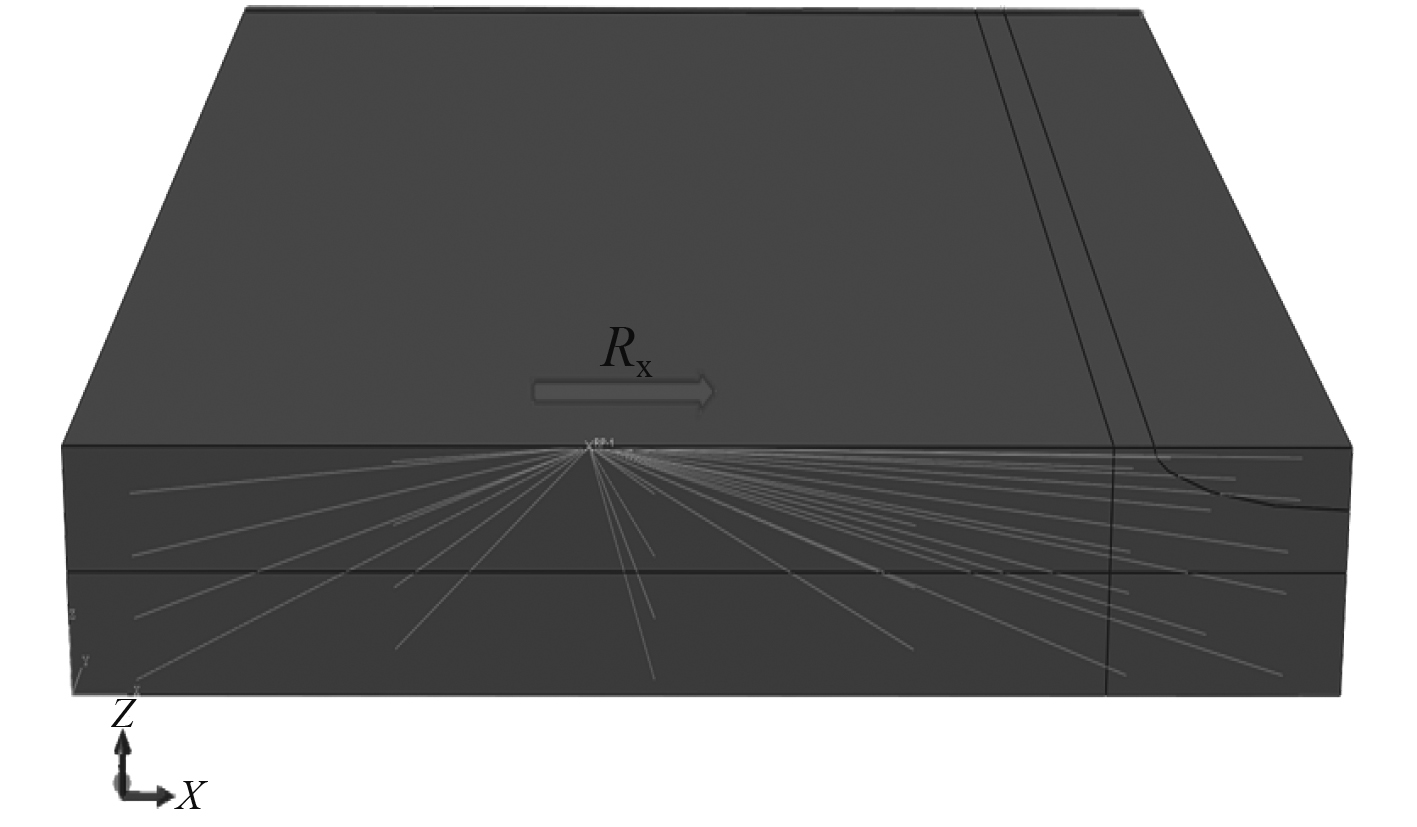
区域1表明大部分是弹性与局限在裂纹尖端塑性(小范围屈服),区域2表明塑性在整个板厚度方向发展,应变处在相对危险的水平,区域3是由韧性带崩溃导致极不稳定的区域。所以施加载荷时本文通过施加转角的方式施加弯曲,使板材的外层达到相应的屈服应变,依据欧拉-伯努利梁理论,假定在变形后横截面保持不变并在同一平面内,在不含裂纹的末端选取一个参考点,并使无裂纹的末端横截面与参考点之间进行运动耦合(MPCs),如图4所示。
|
图 4 运动约束与施加弯矩转角方向 Fig. 4 The motion constraint and the direction of bending moment |
|
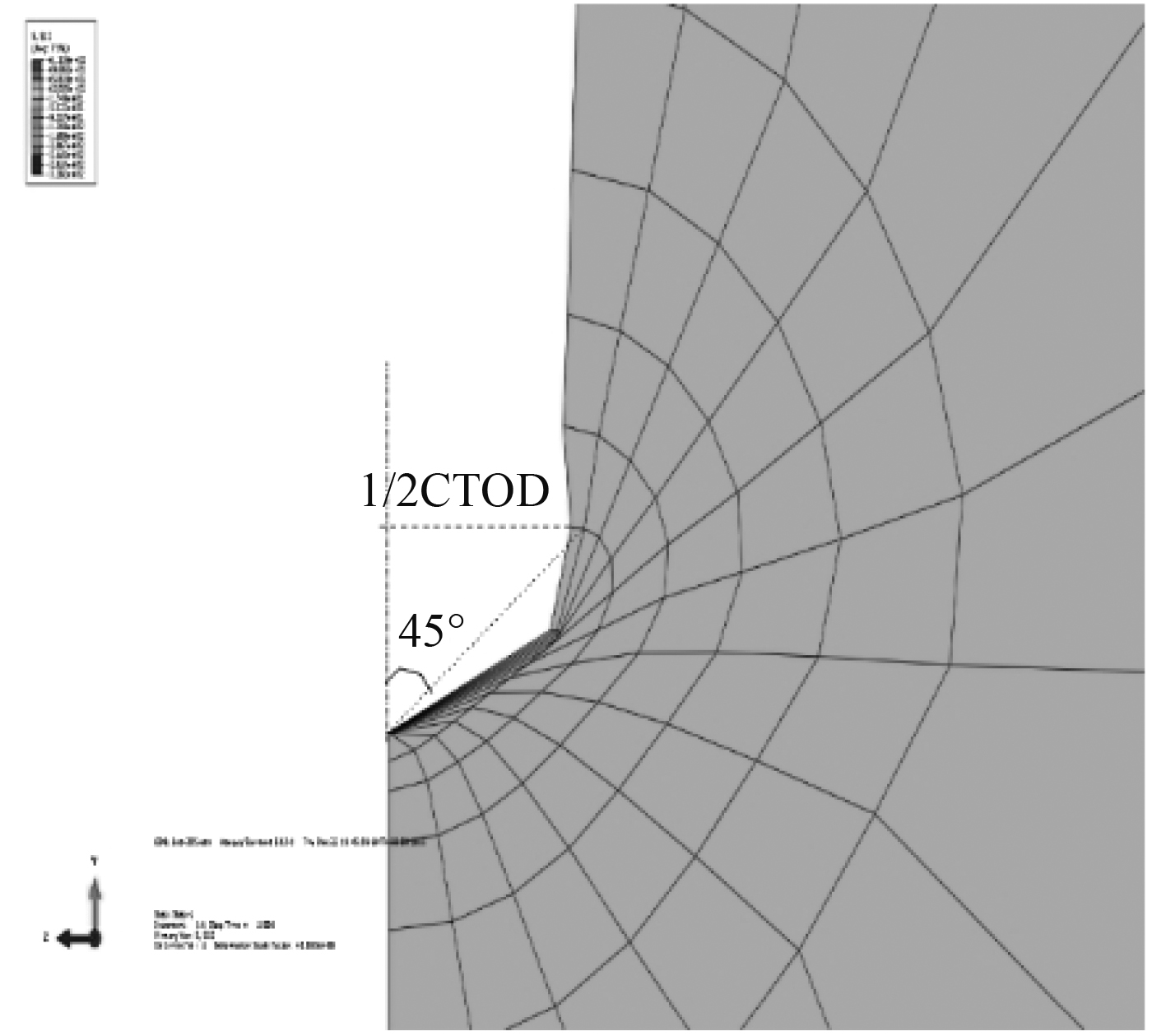
图 5 CTOD的示意图 Fig. 5 The schematic diagram of CTOD |
参考Nourpanah N[8]关于转动弧度和应变的关系,在前期做了一组无裂纹处表层等效塑性应变的模拟,提出应变与转角的关系约为:
| ${R_x} = \frac{{2{\varepsilon _{unc}}L}}{t}\text{。}$ | (7) |
为研究板材在受到大塑性弯曲时,其表面裂纹断裂参数CTOD随着应变的变化关系。本文探讨了裂纹形状因子c/a、裂纹深度a、裂纹深度与板厚比a/t及硬化指数n对CTOD的影响,CTOD的值为沿裂纹尖端做45°斜线与裂纹上下表而相交于两点,其间的距离而为裂纹尖端张开位移,图5为1/2CTOD示意图。

|
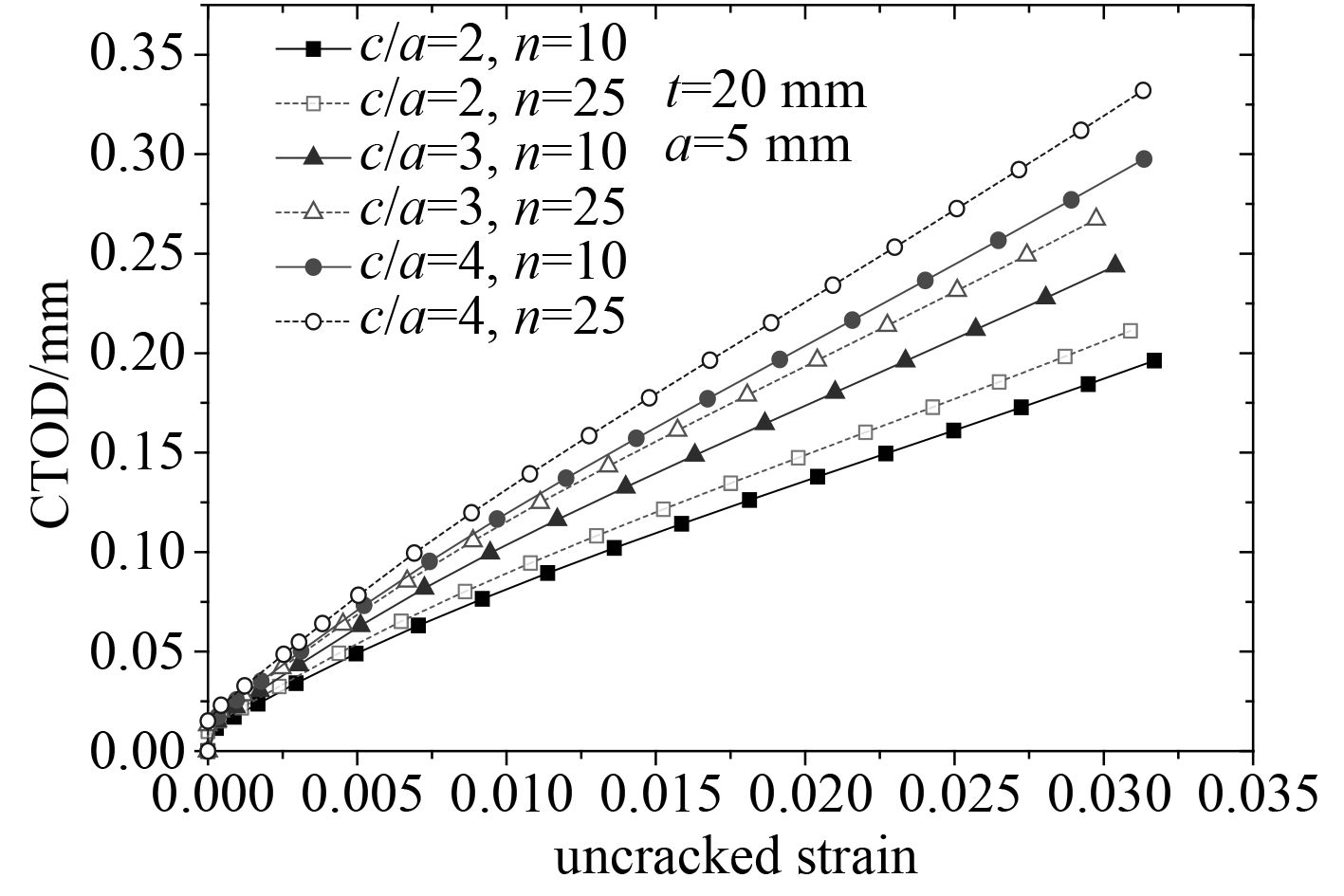
图 6 裂纹形状因子c/a对CTOD的影响 Fig. 6 The effect of crack shape factor c/a on CTOD |
|
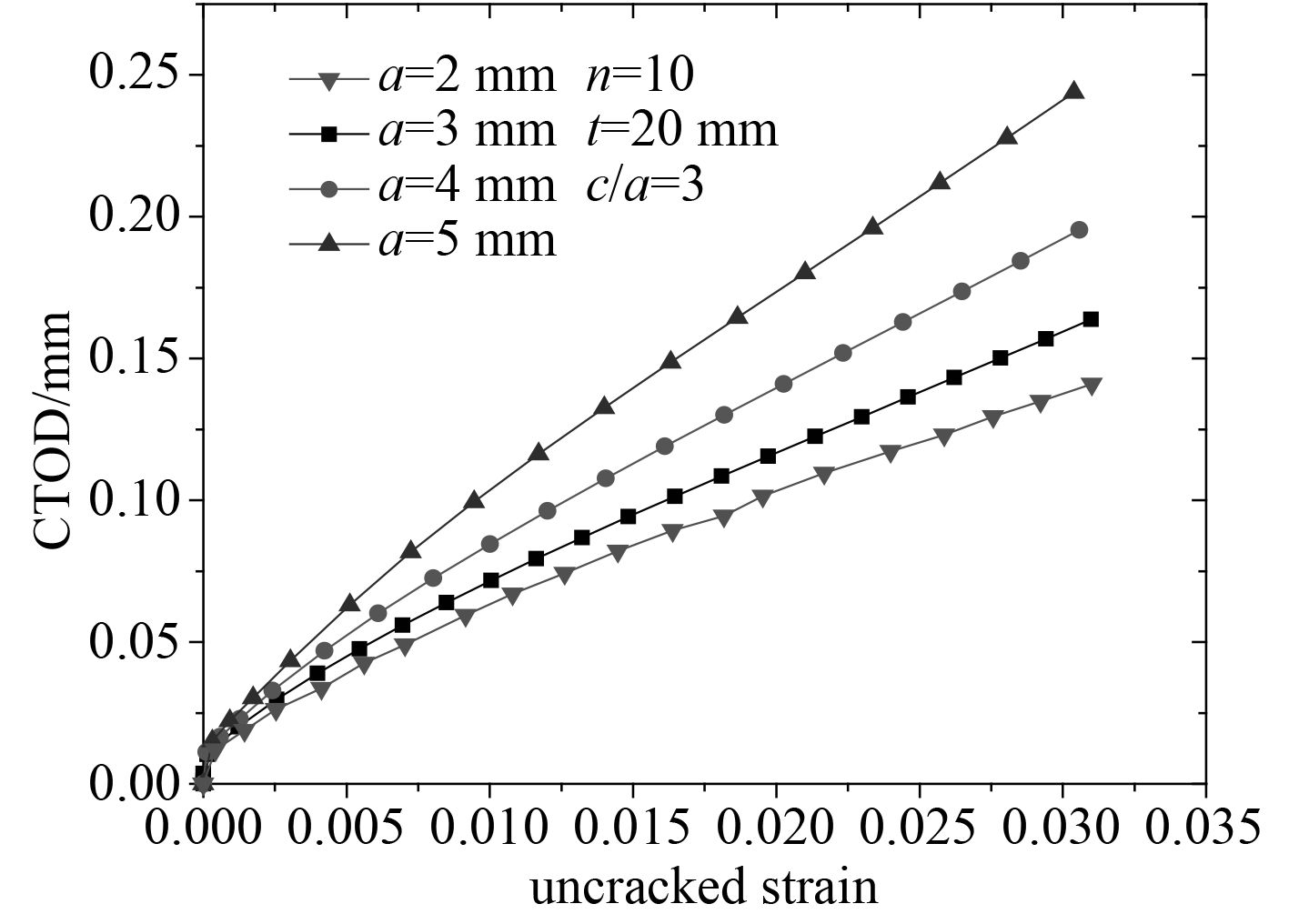
图 7 裂纹深度对CTOD的影响 Fig. 7 The effect of crack depth on CTOD |
在n=10,当裂纹深度给定为a=5 mm,板厚为t=20 mm时,图6中可以看出CTOD随着表面裂纹形状因子的c/a的增大而随之增大,并在同一塑性应变时,CTOD随裂纹形状因子的增长幅度逐渐降低。随着形状因子c/a和塑性应变水平的不断增长,裂纹的CTOD处于非常危险的水平。
2.2 裂纹深度a的影响从图7中可以看出,当给定裂纹形状因子c/a=3,板厚t=20 mm时且n=10时,表面裂纹沿板厚的深度a=2,3,4,5 mm时,随着裂纹深度的增大CTOD是增大的。随着裂纹深度的增大,CTOD的增长幅度很大,在同一应变下,随着裂纹深度a的不断增长,裂尖CTOD会产生更大变化,所以随着裂纹沿深度方向的扩展,结构处于更危险和容易破坏的状态。
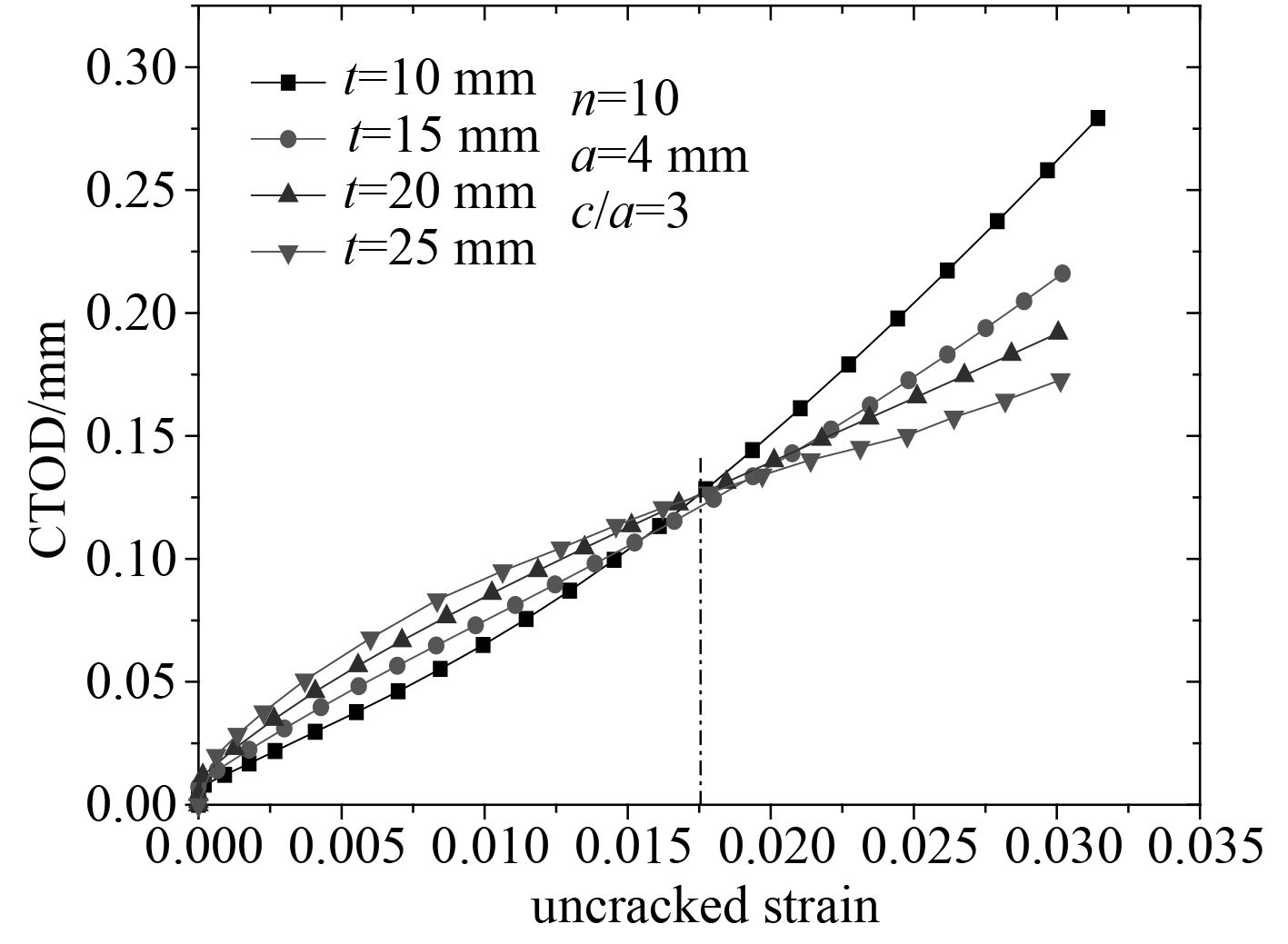
2.3 裂纹板厚度t的影响如图8在保持硬化指数n=10,裂纹深度a=4 mm,形状因子c/a=3即保持裂纹不变时,随着板厚增加裂纹尖端CTOD的变化随着板厚的增加并不是单一的变化趋势。并且在大约1.75%应变水平下板厚对CTOD的影响最小。在应变小于1.75%时,随着板厚的增长,CTOD随之变大,而在应变高于该水平时,则反之,且在同一应变水平之下随着板厚的减小,CTOD的增加速率逐步升高。
对于在前述板厚的影响趋势不单一的现象,是由于在上一节中裂纹深度的影响中,随着裂纹深度的增加,CTOD的值增加,但是保持裂纹形状因子c/a的不变,使得随着a的增大,c也跟着增大。但考虑板厚的影响因素时,保持了裂纹深度a=4 mm,裂纹形状因子c/a=3不变,随着板厚的减小,相当于裂纹深度的增加,但c的值却没有跟着变化,故而导致了上述变化。
|
图 8 板厚对CTOD的影响 Fig. 8 The effect of plate thickness on CTOD |
|
图 9 硬化指数对CTOD的影响 Fig. 9 The effect of hardening exponent on CTOD |
从图9可以很明显看出,在板厚t=20 mm,裂纹深度a=5 mm时,3种不同形状因子c/a下的CTOD随着硬化指数n的变化趋势,当n=25时的CTOD比n=10时的CTOD大,这表明了材料的应变硬化水平对CTOD的影响关系至关重要,工程中需要对材料严格要求。
3 塑性弯曲下表面裂纹板的CTOD评估方程应变方法现在越来越广泛地应用于各种海洋工程中管道的大塑性弯曲的断裂评估中,并且不断被接受。本文将其推广至船体表面裂纹板上,并提出大塑性弯曲下基于应变的CTOD评估多项式,考虑了影响船体表面裂纹板的各种表面裂纹特有的三维形状参数,这样更方便工程中的应用,CTOD评估多项式如下:
| $\begin{split}\frac{{CTOD}}{a} =& {\eta _0} + {\eta _1}\frac{a}{t} + {\eta _2}\frac{a}{c} + {\eta _3}{\varepsilon _{unc}} + {\eta _4}\frac{a}{t} \cdot \frac{a}{c}+ \\& {\eta _5}\frac{a}{t} \cdot {\varepsilon _{unc}}+ {\eta _6}\frac{a}{c} \cdot {\varepsilon _{unc}} + {\eta _7}{\left( {\frac{a}{t}} \right)^2} +\\& {\eta _8}{\left( {\frac{a}{c}} \right)^2} + {\eta _9}\varepsilon _{unc}^2\text{,}\end{split}$ | (8) |
式中和初始定义一样a为裂纹沿板厚的深度,t为板厚,c为裂纹长轴沿板宽方向。
|
|
表 1 CTOD公式拟合参数 Tab.1 The fitting parameters of CTOD formula |
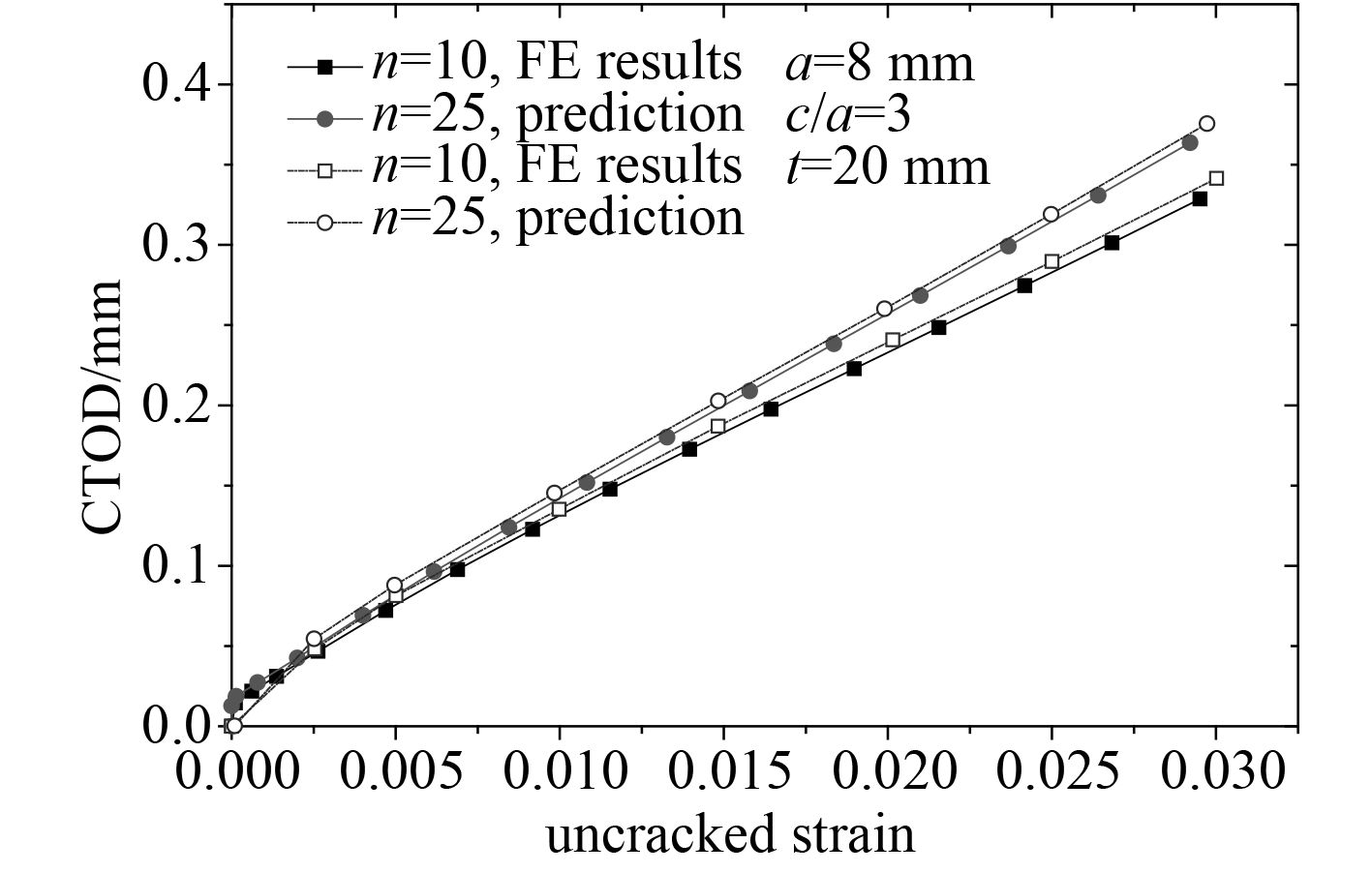
为了验证上述公式的可行性,取裂纹深度a=8 mm,c/a=3及板厚为20 mm时的情况进行有限元计算,将计算结果与公式的预测值进行对比如图10所示。从图中可以看出用基于有限元模拟的数据所拟合的CTOD预测公式计算值与有限元模拟的结果相比误差很小,且CTOD值计算结果偏大,偏于安全可行。
|
图 10 有限元计算与公式预测对比值 Fig. 10 Comparison between the FE calculation and the formula prediction |
当针对含表面裂纹船体板的断裂准则给出时,基于当前的工作,只需要使:
| $CTOD \leqslant {\delta _{critical}}\text{。}$ |
如果给定裂纹深度、形状因子、板厚及钢材的硬化指数n,并知道船舶在工作时船体板外层所遭受最大等效应变水平,就可以通过式(8)评估对应状态下的CTOD值,从而可以对含三维表面裂纹船体板构件的断裂韧性进行评估。
4 结 语本文针对含表明裂纹损伤的船体板在特定的中垂或中拱状态下,达到塑性状态后,此时θ=90°处裂尖的CTOD与不含裂纹处的等效塑性应变的关系进行了研究分析,并得到如下结论:
1)在各种影响因素的作用下,三维表面裂纹裂尖处CTOD的值随着应变的增加逐渐增加,但是增长趋势并趋于稳定。其中随着裂纹形状因子c/a的增大,CTOD在同一应变水平时逐步增大,且增长速率减小。随着裂纹深度a的增加,裂尖处CTOD在同一应变水平下也逐步增大,并且增长速率逐渐增大。
2)随着板厚的增加,对裂尖处CTOD的影响在某一应变水平可以忽略,并且在小于该应变大小时,板厚增加对CTOD呈现正作用,在大于该值时,则反之。此外硬化指数对CTOD的影响不可忽略,在n=25的硬化指数下,CTOD的值均大于n=10的情况。
3)在综合各种材料和半椭圆表面裂纹自身的形状因素的影响,本文给出了一个基于有限元模拟的CTOD评估公式。这为评估含表面裂纹板的断裂评估提供了一种新的思路。
| [1] | BUDDEN PJ. Failure assessment diagram methods for strain-based fracture [J]. Engineering Fracture Mechanics, 2006, 73(5): 537–552. |
| [2] | HUTCHINSON JW. Fundamentals of the phenomenological theory of nonlinear fracture mechanics. J. Appl. Mech., 1982, 49, 103–197. |
| [3] | METZGER M, SEIFERT T, SCHWEIZER C. Does the cyclic J -integral ΔJ describe the crack-tip opening displacement in the presence of crack closure? [J]. Engineering Fracture Mechanics, 2015, 134: 459–473. |
| [4] | CRAVERO S, RUGGIERI C. Estimation procedure of J-resistance curves for SE(T) fracture specimens using unloading compliance. Eng Fract Mech, 2007, 74: 2735e57. |
| [5] | AINSWORTH RA. The assessments of defects in structures of strain hardening materials. Eng Fract Mech, 1984, 19: 633e42. |
| [6] | RUGGIERI C. Comparison between fully-plastic solutions and the reference stress approach to evaluate J in circumferentially cracked pipes under bending. Procedia Eng, 2011, 10: 1703e8. |
| [7] | LINKENS D, FORMBY CL, AINSWORTH RA. A strain-based approach to fracture assessment-example applications. In: Proceedings of fifth international conference on engineering structural integrity assessment. Cambridge: EMAS; 2000. |
| [8] | NOURPANAH N, TAHERI F. Development of a reference strain approach for assessment of fracture response of reeled pipelines [J]. Engineering Fracture Mechanics, 2010, 77(12): 2337–2353. |
| [9] | SHIH CF. Relationship between the J-integral and the crack opening displacement for stationary and extending cracks. J Mech Phys Solids, 1981, 29: 305e26. |
| [10] | ZHANG YM, YI DK, XIAO ZM, et al. Elastic–plastic fracture analyses for pipeline girth welds with 3D semi-elliptical surface cracks subjected to large plastic bending[J]. International Journal of Pressure Vessels and Piping, 2013, 105–106: 90–102. |
| [11] | ØSTBY E, JAYADEVAN KR, THAULOW C. Fracture response of pipelines subject to large plastic deformation under bending. Int J Press Vessels Piping, 2005, 82: 201e15. |
 2018, Vol. 40
2018, Vol. 40
