焊接被广泛应用于型材加工、分段建造、船台合拢等船舶建造环节。由于焊缝附近区域的材料在焊接过程中的不均匀膨胀和收缩,使得结构不可避免地产生变形和残余应力,影响结构外形尺寸,降低装配精度。研究焊接结构变形规律,制定减少大型焊接结构变形的工艺方案,对于提高船体建造质量具有重要的工程价值。力学约束是控制结构焊接变形的有效方法[1-3],在甲板板架焊接过程中,采用力学方法限制其板格中部甲板板的垂向位移可控制焊接变形,本文研究此类垂向力学约束对焊接变形与残余应力的影响。对于大型甲板,不同的垂向力学约束方案在改善甲板板架结构变形和残余应力方面的效果有所不同,本文利用数值方法模拟各种垂向力学约束方案,寻求最佳约束方案条件,为实际焊接工程控制焊接变形工艺提供参考。
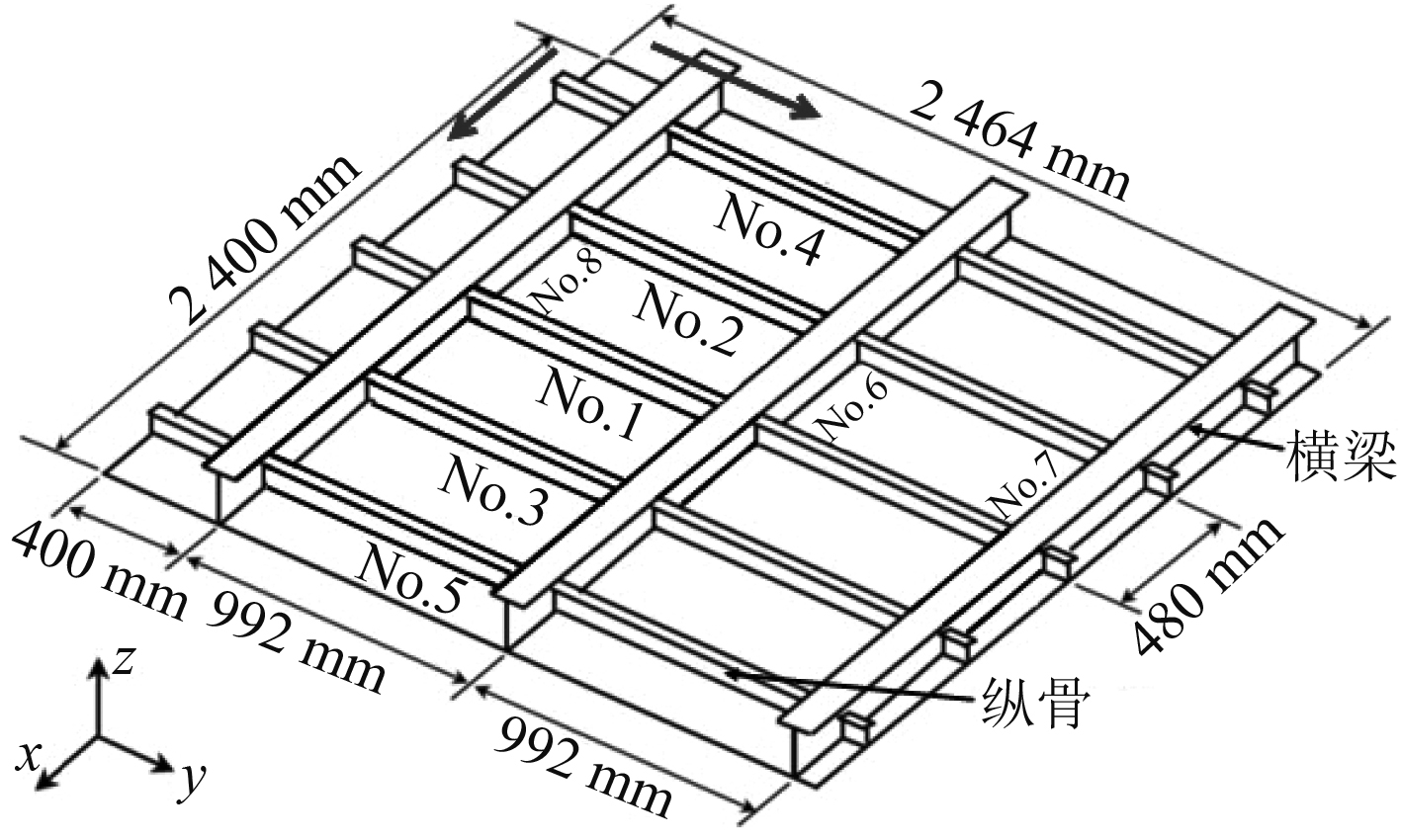
1 研究对象 1.1 甲板板架和焊接条件选取船体甲板板架为研究对象,板架尺寸和构件布置情况如图1所示。甲板板的尺寸为2 400 mm×2 464 mm,板厚6 mm;沿横向布置5根纵骨,其间距为480 mm,腹板高度和面板宽度均为80 mm,板厚均为8 mm;沿纵向布置3根横梁,其间距为992 mm,腹板高度和面板宽度分别为180 mm和120 mm,板厚均为8 mm。所有骨材在焊接前先通过定位点焊将其有效地连成整体,不考虑由于定位点焊所产生的初始变形和残余应力,加强筋和甲板板之间的角焊缝采用CO2气体保护焊,焊接参数见表1,纵骨和横梁两侧的角焊缝均采用同时同向连续施焊,纵骨与横梁的焊接顺序编号为No.1~No.8,焊接顺序和方向如图1所示。
|
图 1 甲板板架几何尺寸 Fig. 1 Deck grillage geometry |
|
|
表 1 焊接参数 Tab.1 Welding parameters |
将整个甲板板架按位置划分成4个板格区域,分别为:板格_A、板格_B、板格_C和板格_D,如图2所示。在焊接过程中,约束区域内甲板板的垂向位移被完全限制,待整个焊接过程结束板架温度降至室温后,释放垂向力学约束,甲板板架进入自由形变状态。本文计算方案设计为一个无约束的自由变形方案和5个垂向力学约束方案,6个计算方案如下:
方案1 板架不受约束,在焊接过程中可自由形变。
方案2 在板格_A的中心设置边长为64 mm的方形约束区域,分别在板格_B和板格_D的自由边上设置尺寸为32 mm×64 mm和64 mm×32 mm的矩形约束区域,在板格_C两自由边的交角处设置边长为32 mm的方形约束区域,如图2(a)所示。
方案3 板格中约束区域x和y方向的长度均是方案2中约束区域的2倍,如图2(b)所示。
方案4 板格中约束区域x方向的长度均与方案3中的约束区域相同;y方向的长度均是方案3中约束区域的2倍,如图2(c)所示。
方案5 在板格_A和板格_B中分别对称设置2个方案3中对应板格内的约束区域,板格_C和板格_D中的约束区域与方案3中相同,如图2(d)所示。
方案6 在板格_A和板格_B中分别对称设置3个方案3中对应板格内的约束区域,板格_C和板格_D中的约束区域与方案3中相同,如图2(e)所示。

|
图 2 垂向力学约束方案 Fig. 2 Vertical constraints cases |
本文首先利用顺序耦合的热弹塑性有限元法[4-5]模拟焊接过程,整个过程分为2步。第1步是建立能够反映焊接构件细节的有限元网格模型,根据焊接参数施加合理的热源数学模型于焊缝,依照焊接顺序模拟热源沿焊缝的移动,考虑焊接材料热物理性能和热分析边界条件,开展能够跟踪构件在整个焊接和冷却过程中的温度变化的热分析,获得焊接过程中模型的瞬时温度场分布。第2步将随时间变化的瞬时温度场结果作为温度载荷施加在力学模型上,考虑材料的力学参数性能,焊接时施加相应的边界条件,计算焊接过程中结构的应力和应变,其中垂向力学约束施加在约束区域内的甲板板上。待完成整个焊接过程的模拟之后,释放垂向力学约束,结构发生反弹变形,得到结构最终的焊接变形与残余应力分布。
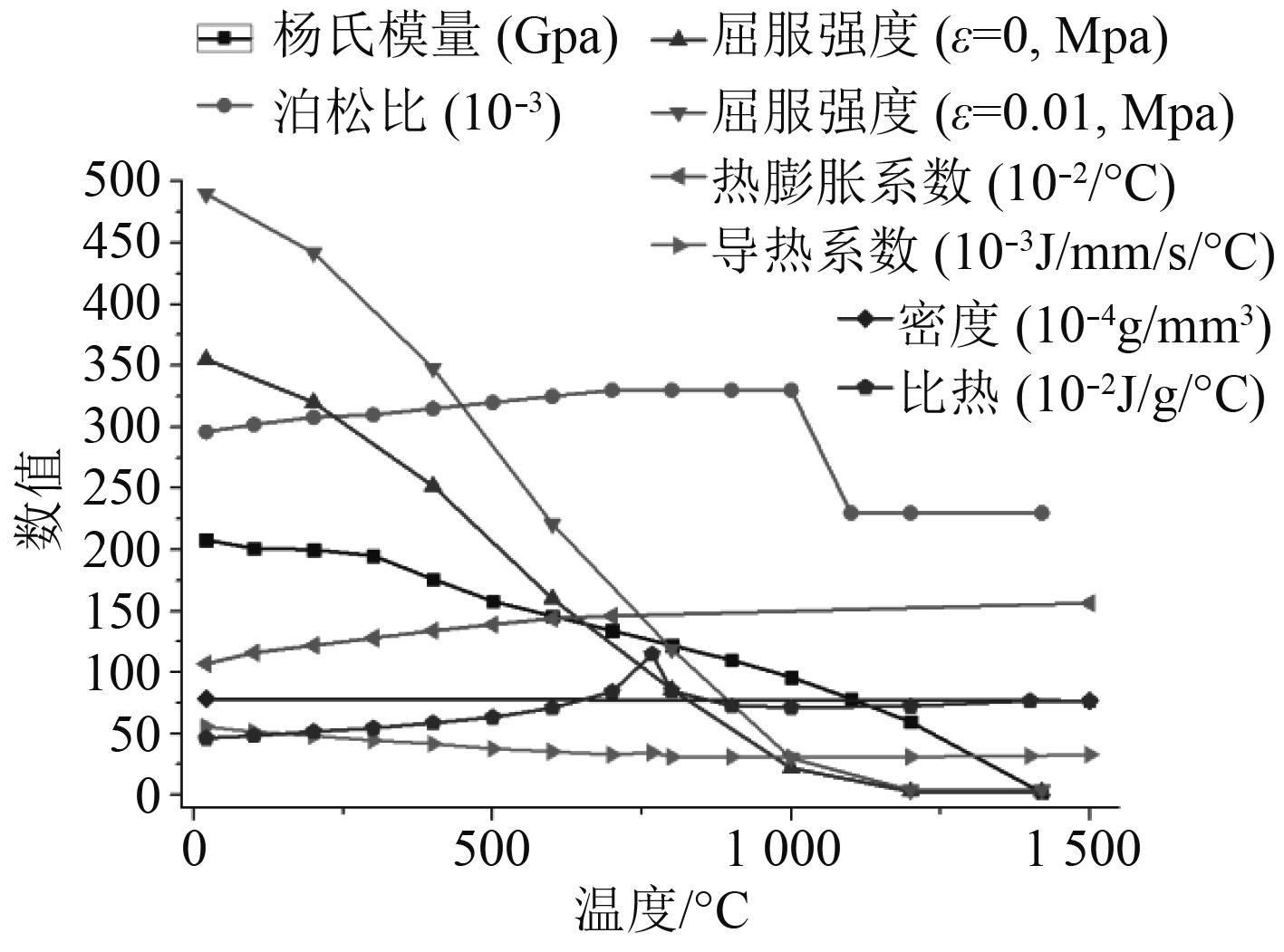
3 有限元模型甲板板架有限元模型如图3所示,采用shell/solid混合单元建模[6],整个模拟过程在Abaqus中实现。热焊接过程温度场的特点是热源附近和热影响区局部区域温度高、梯度大,随着距热源中心距离的增加,温度迅速降低。因此为了保证温度场模拟的精准性,模型在焊缝区域须采用细网格,其最小单元尺寸为2 mm×4 mm,模型在远离焊缝区域网格逐渐增大以提高计算效率,应力场计算模型网格划分与温度场模型相同,整个模型的单元数为250 435,节点数为318 479。材料为E36钢[7],其屈服极限、杨氏模量、热传导系数等物理量与温度的关系见图4。

|
图 3 有限元模型 Fig. 3 FE model |
温度场计算过程中空气对流换热系数设为15×10–6W/(mm2℃),环境温度设为20 ℃。应力场计算时,将温度场分析结果以温度载荷的形式施加到力学模型上。甲板板架在自由状态下施焊时,为了避免因刚体位移,采用三点约束边界条件(见图3)。在垂向力学约束方案的应力场计算过程中,限制约束区域内所有节点的垂向位移,待全部焊接完成后,释放垂向力学约束,同时施加三点约束边界条件。
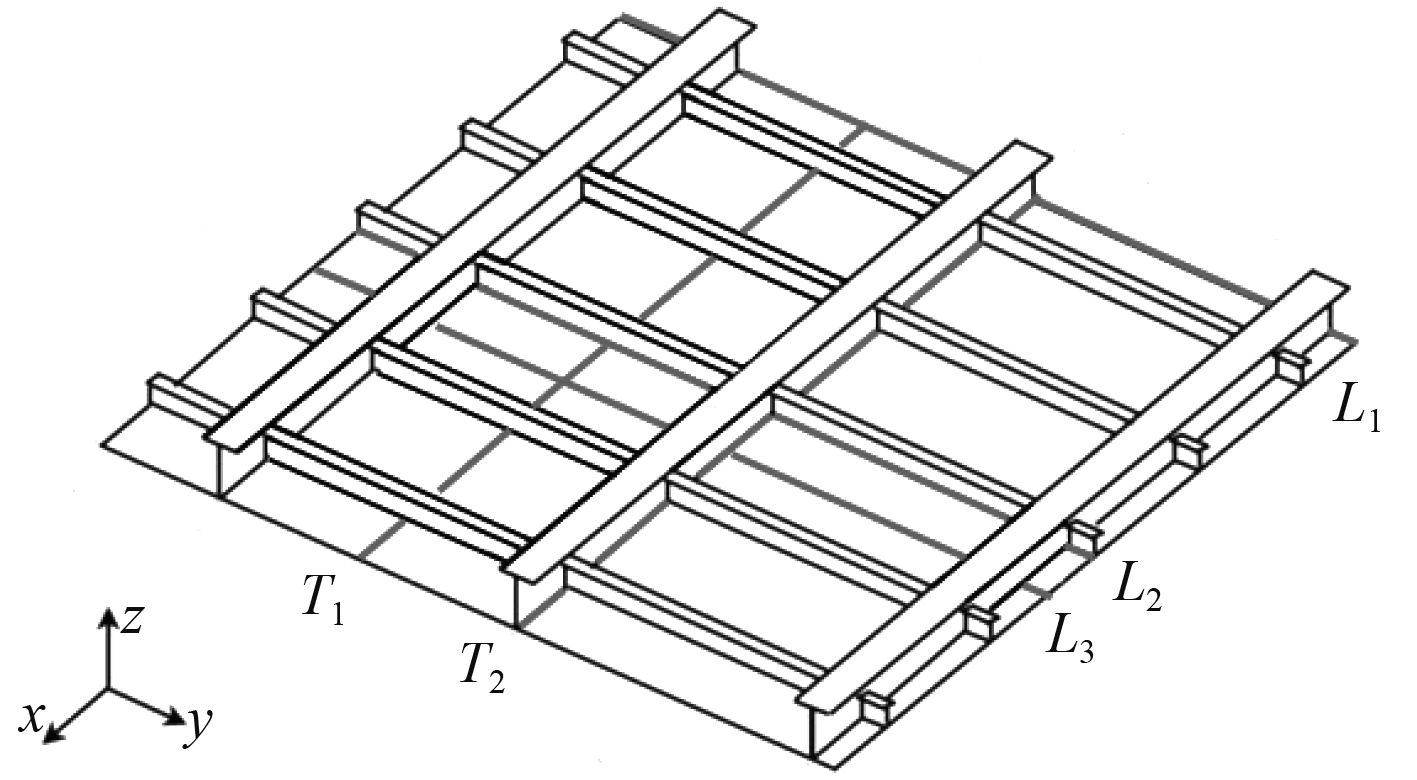
4 计算结果分析 4.1 焊接变形结果分析图5为各方案甲板板架的整体变形云图。由图可见,无约束方案和5种垂向力学约束方案下结构的焊接变形形式相近,整个板架中部拱起,甲板板纵向自由边处的变形大于板格的面外变形,纵横骨架范围之内的甲板板同样呈凸起变形特点,垂向力学约束使得板格内甲板板的变形减小。为了分析各焊接方案下的结构变形,选取甲板板上纵向剖面L1~L3、横向剖面T1~T2(见图6)分别绘制变形图。

|
图 5 各方案变形云图 Fig. 5 Welding deformation in different cases |
|
图 6 甲板剖面位置 Fig. 6 Five lines of the deck grillage |
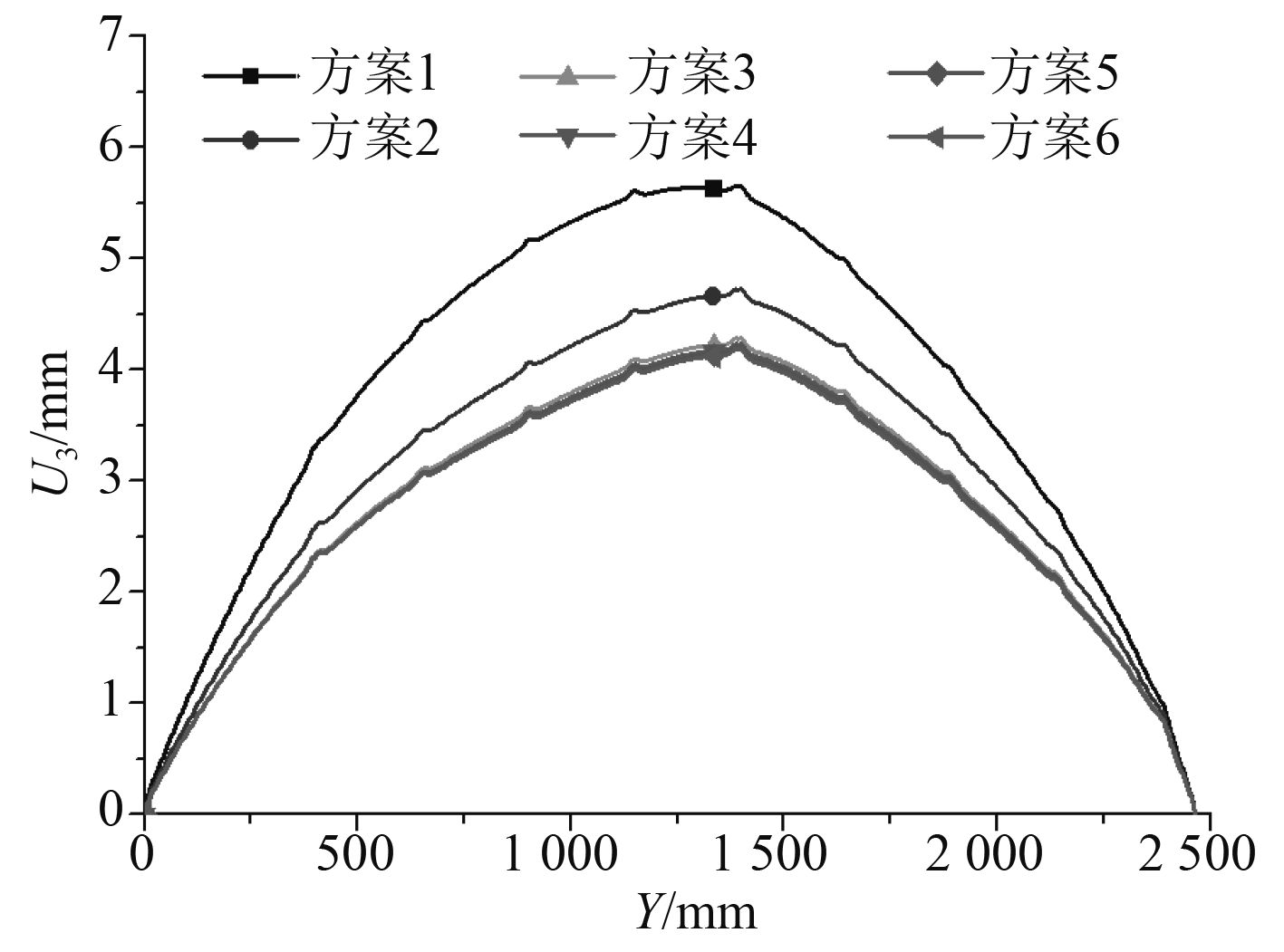
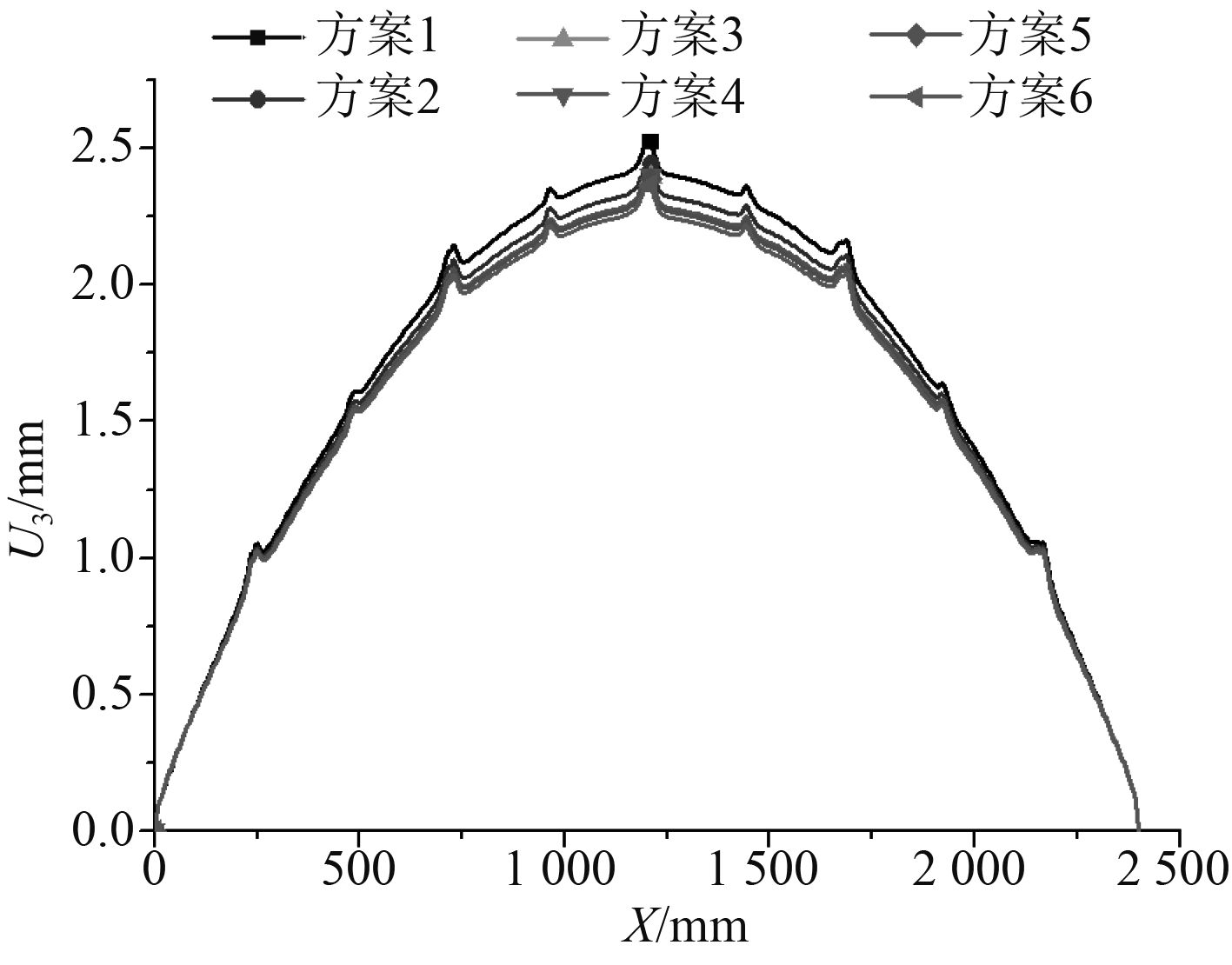
图7~图8为纵横加强筋位置L2和T2处的面外变形,反映了甲板分段焊接后整体的变形情况。纵骨变形较横梁变形更大,说明板架整体纵向弯曲程度大于其横向弯曲程度。相较于方案1,L2处板架整体纵向的变形在垂向力学约束方案中大幅减小,T2处板架整体横向的变形在垂向力学约束方案中有小幅减小;板架整体纵向和板架整体横向的变形均随着垂向力学约束区域面积的增大而逐渐减小。L2处板架整体纵向与T2处板架整体横向在各方案中的焊接变形最值见表2所示,在方案6中L2和T2处变形最值相较于方案1中的变形分别减小了25.9%和6.28%。
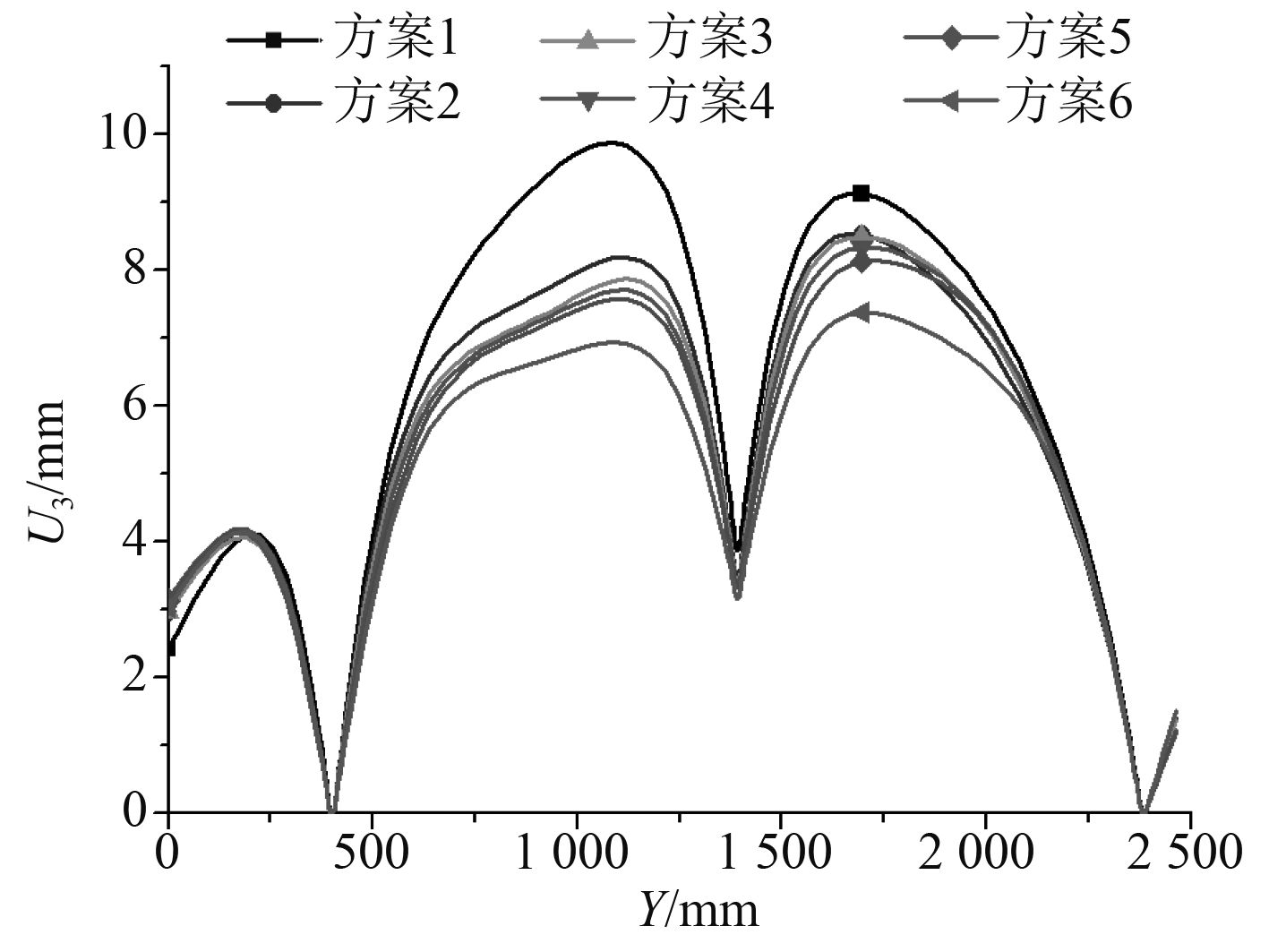
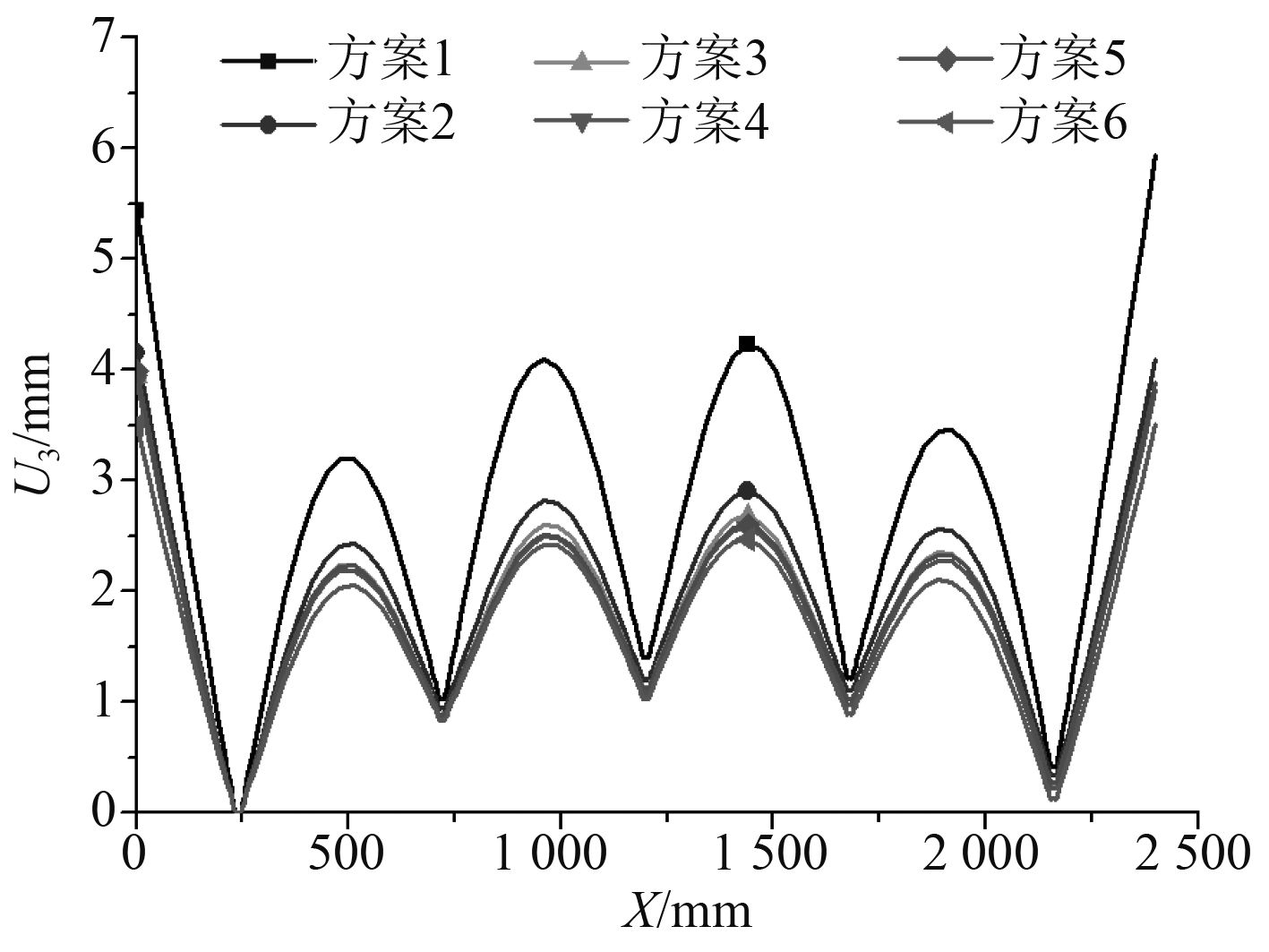
图9~图10分别为甲板板纵横方向的面外变形,在L1和T1剖面相邻骨材之间的甲板板均出现半波形的局部变形。垂向力学约束对减小局部焊接变形的作用明显,板格_A中的甲板板在约束方案中显著减小,自由边的变形同样明显改善,并且局部焊接变形随着垂向力学约束区域面积的增大而逐渐减小。甲板板的变形由板架整体变形与板格局部变形组成,仅考虑板格的局部变形情况,得到L1处自由边与T1处甲板板在各方案中的局部焊接变形最值如表2所示。在方案6中L1和T1处变形最值相较于方案1中的变形分别减小了27.2%和48.2%。对比方案4和方案5的变形最值,可以看出在此约束面积下,不同约束区域设置对焊接变形影响很小。方案6在L2,T2和T1处的变形最值相较于方案3减小不超过3.3%,而其约束面积是方案3的3倍,可见方案3在减小整体焊接变形与板格内局部变形中为相对更优的方案。
|
图 7 L2处面外变形 Fig. 7 Out-of-plane distortion at L2 |
|
图 8 T2处面外变形 Fig. 8 Out-of-plane distortion at T2 |
|
图 9 L1处面外变形 Fig. 9 Out-of-plane distortion at L1 |
|
图 10 T1处面外变形 Fig. 10 Out-of-plane distortion at T1 |
|
|
表 2 各方案焊接变形最值(mm) Tab.2 Maximum magnitudes of the welding distortions in different cases (mm) |
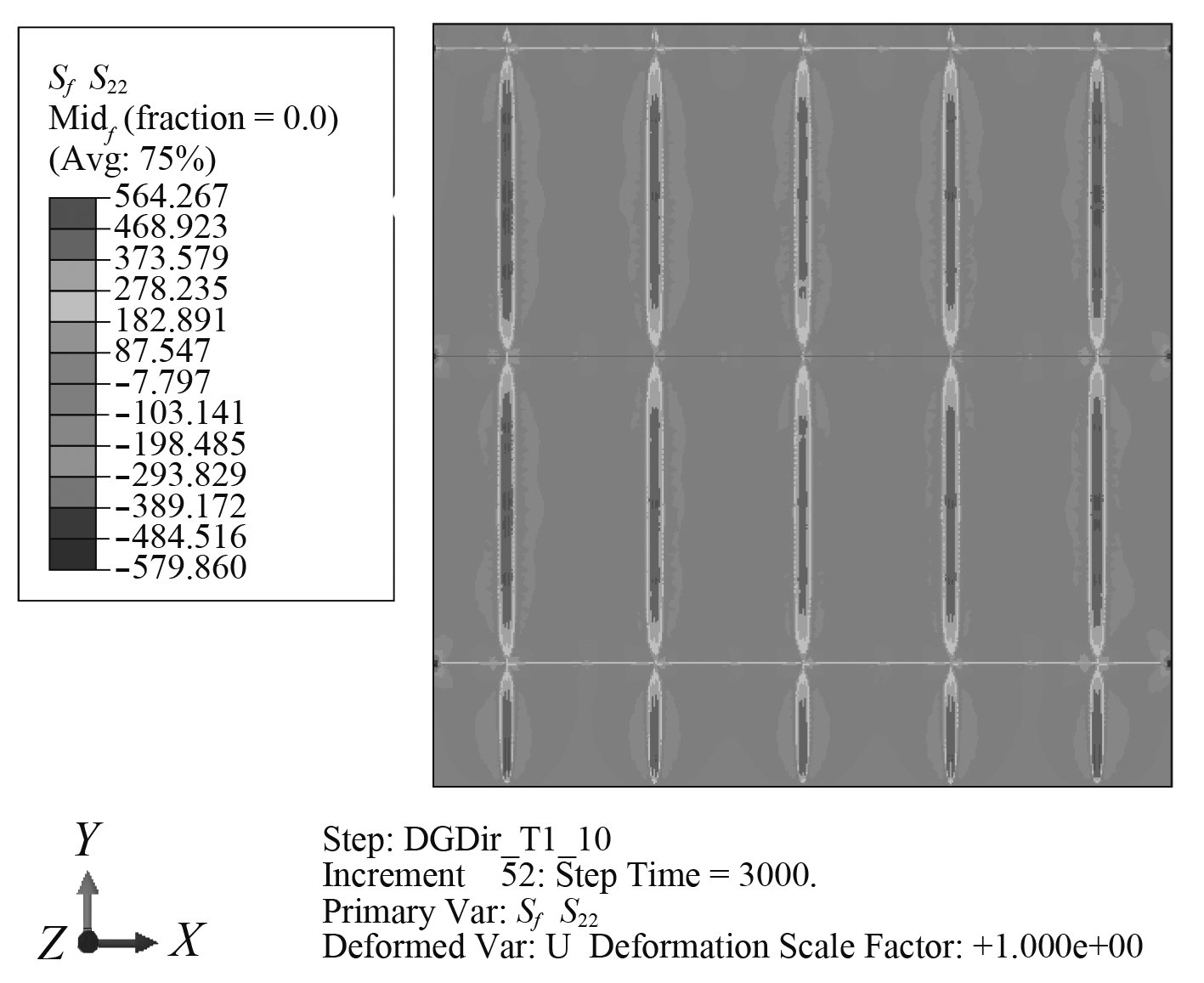
焊接完成后,在焊缝附近较窄区域内集中高量值的残余应力。图11为方案1中甲板板中面的纵向(y方向)残余应力云图,可以看出残余应力主要沿焊缝方向,高应力区域分布在焊缝附近区域,呈拉应力,量值达到材料的屈服极限,远离焊缝区域则为压应力,整体结构的拉压应力相平衡。约束方案中应力的分布规律与方案1中的分布规律相似。
|
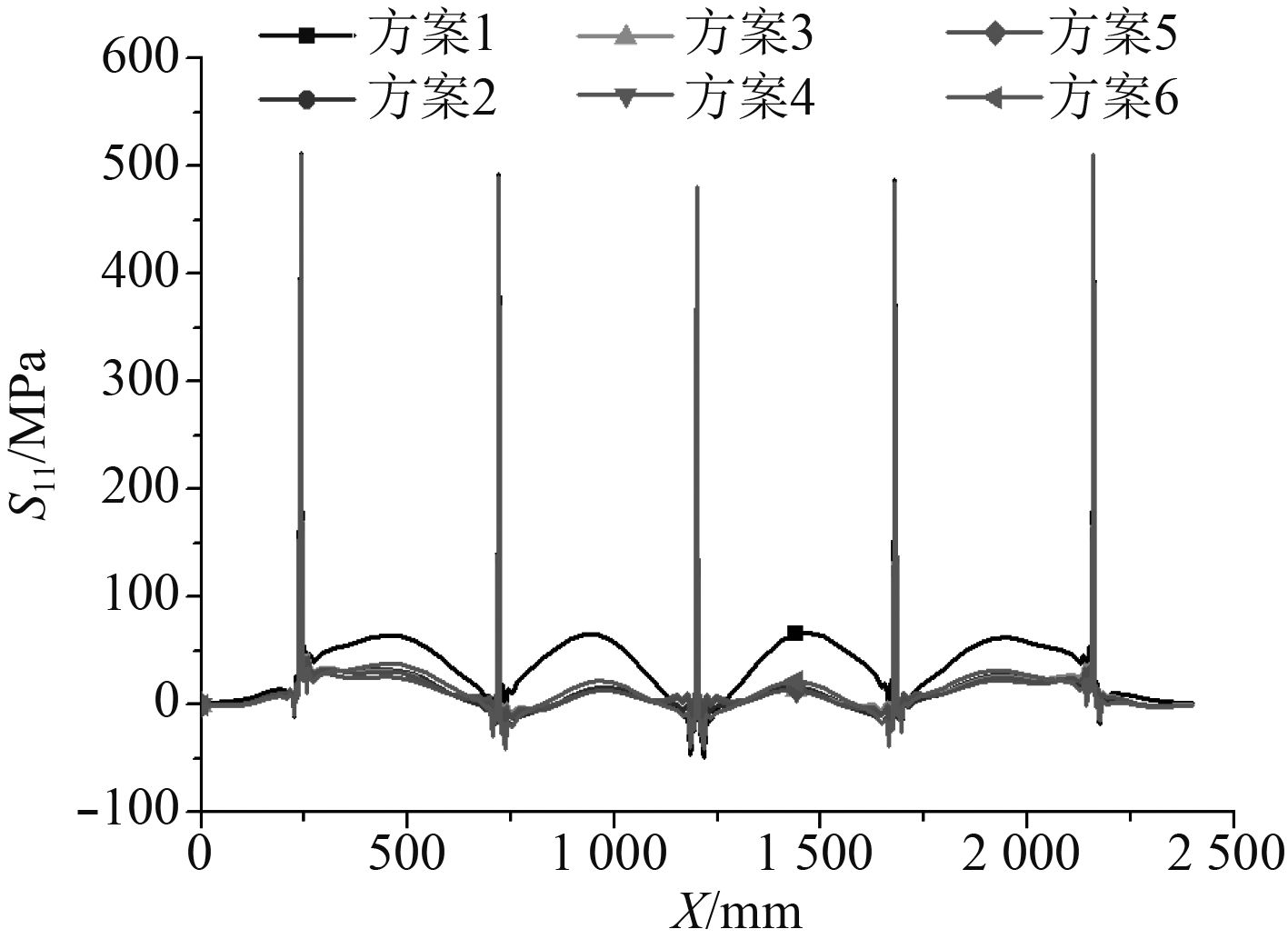
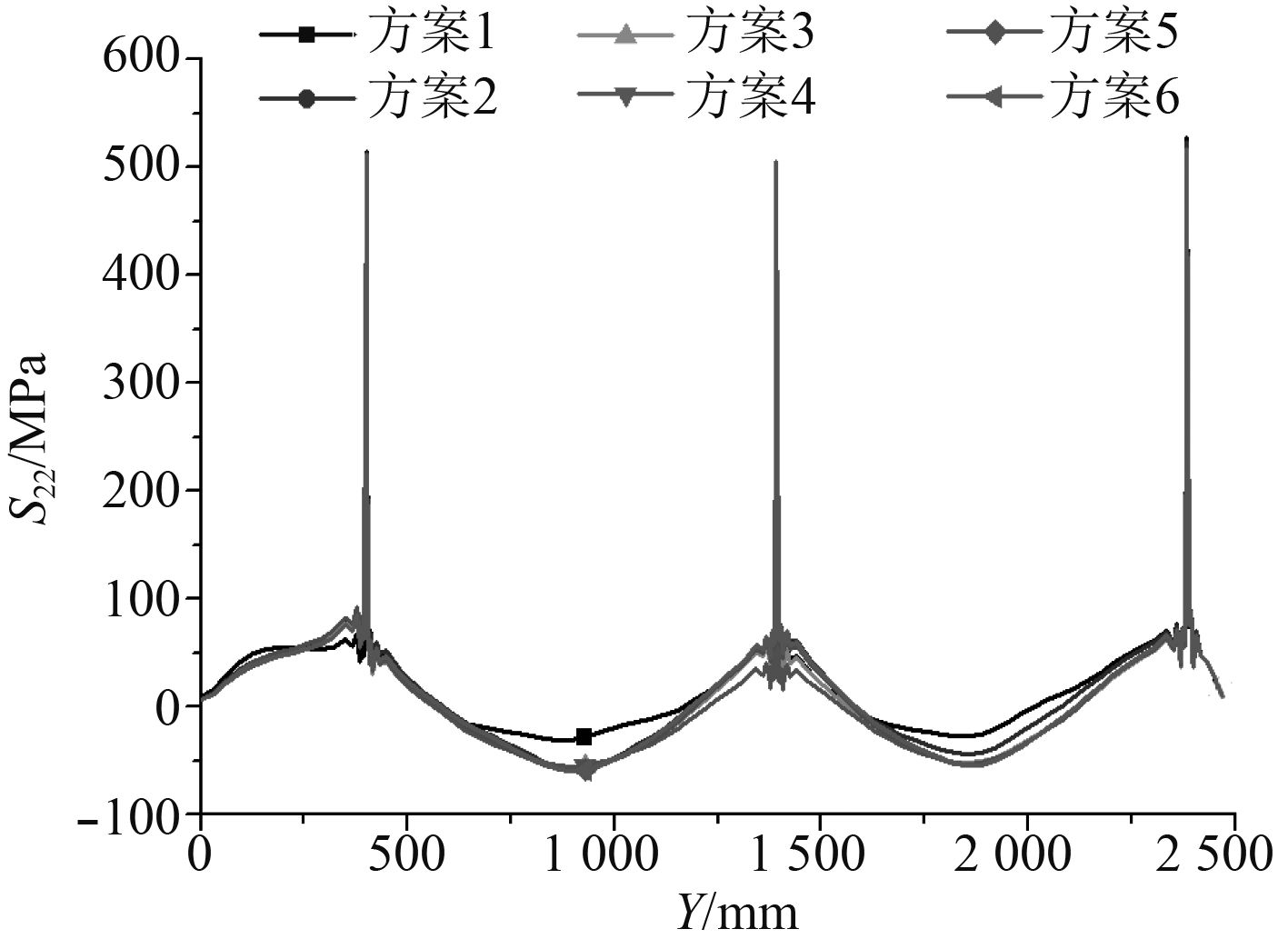
图 14 甲板板T1处上表面横向残余应力 Fig. 14 Transverse residual stress at T1 |
图12所示为各方案中甲板板T1剖面处中面纵向(y方向)残余应力S22的分布曲线,图13所示为各方案中甲板板L3剖面处中面横向(x方向)残余应力S11的分布曲线。图12和图13反映了甲板板由焊接引起的整体残余应力情况。焊接残余拉应力主要分布在焊缝附近的狭窄区域,其量值达到材料的屈服极限;压应力则主要位于纵横骨架的板格间,且纵骨间板格的纵向残余压应力(见图12)明显大于横梁间板格的横向残余应力(见图13)。这是由于纵骨数量较多,焊接产生的纵向收缩更严重。垂向力学约束方案对甲板板中面内横向和纵向的残余应力影响均不明显。
|
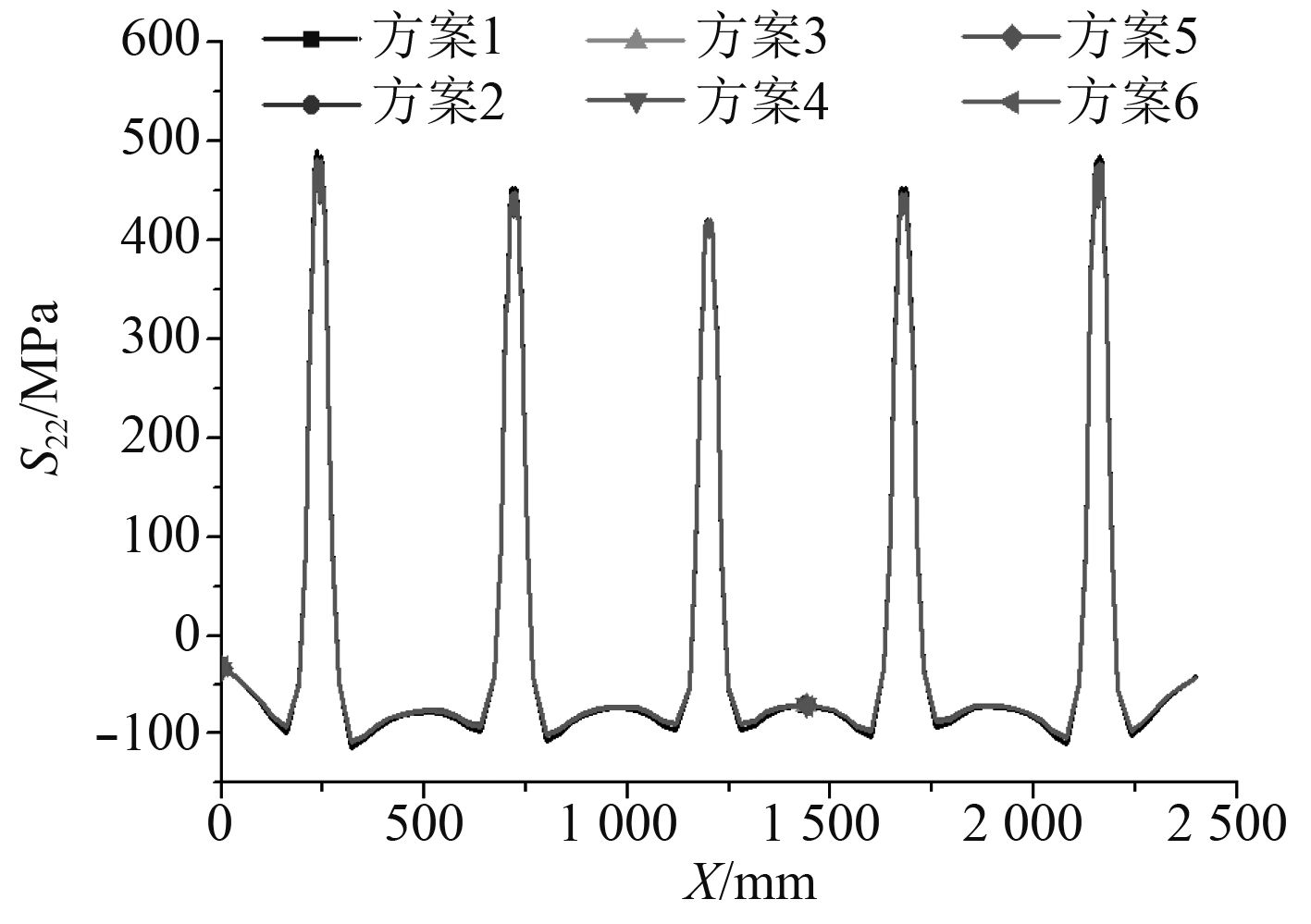
图 15 甲板板L3处上表面纵向残余应力 Fig. 15 Longitudinal residual stress at L3 |
|
图 12 甲板板T1处中面的纵向残余应力 Fig. 12 Longitudinal residual stress at T1 |

|
图 13 甲板板L3处中面的横向残余应力 Fig. 13 Transverse residual stress at L3 |
|
图 11 方案1纵向残余应力 Fig. 11 Llongitudinal residual stress in case one |
图14所示为各方案中甲板板T1剖面处上表面横向(x方向)残余应力的分布曲线,图15所示为各方案中甲板板L3剖面处上表面纵向(y方向)残余应力的分布曲线。由于甲板板产生角变形,使板格出现半波形局部弯曲,引起甲板板格的局部弯曲应力,因此甲板上表面的残余应力是由焊接收缩产生的压应力与局部弯曲导致的拉应力叠加形成。T1处横向弯曲拉应力大于横向收缩压应力,此处横向残余应力表现为拉应力;而在L3处情况相反,纵向弯曲拉应力小于纵向收缩压应力,此处纵向残余应力表现为压应力。在各约束方案中,由于垂向力学约束的作用导致局部弯曲变形减小,甲板上表面横向和纵向弯曲应力均减小,使得T1处板格中部甲板板上表面横向的残余应力减小,减小最多达到52 MPa;而L3处板格中部甲板板上表面纵向的残余应力略微增大,增大最多达到28 MPa。
5 结 语本文研究了垂向力学约束对甲板板架焊接的焊接变形与残余应力的影响规律,其主要结论如下:
1)对于该板架结构,垂向力学约束对减小板架焊接整体和局部变形的效果明显,可分别减小27%和48%。焊接变形随着约束面积增大而减小。
2)焊接引起的残余应力沿焊缝方向在狭窄区域内具有较高的拉应力,远离焊缝处为压应力。垂向力学约束对甲板板中面残余应力几乎没有影响;垂向力学约束使得板格中部甲板板上表面横向残余应力减小52 MPa,而纵向残余应力增大28 MPa。
3)针对本文研究的甲板板架及约束方案,方案3中焊接变形相较于方案2中变形有显著减小,而在方案4~方案6中增大约束面积对于进一步减小焊接变形效果有限,考虑到减小变形效果与约束面积成本,选择方案3为相对最优的约束方案。
| [1] | DENG D, ZHOU Y, BI T, et al. Experimental and numerical investigations of welding distortion induced by CO 2, gas arc welding in thin-plate bead-on joints[J]. Materials & Design, 2013, 52(24): 720–729. https://www.deepdyve.com/lp/elsevier/experimental-and-numerical-investigations-of-welding-distortion-wkeLpuusUc |
| [2] | FU G, LOURENCO M I, DUAN M, et al. Effect of boundary conditions on residual stress and distortion in T-joint welds[J]. Journal of Constructional Steel Research, 2014, 102(11): 121–135. |
| [3] | FANOUS I F Z, YOUNAN M Y A, WIFI A S. 3-D finite element modeling of the welding process using element birth and element movement techniques[J]. Journal of Pressure Vessel Technology, 2003, 125(2): 165–172. |
| [4] | DENG D, MURAKAWA H. Prediction of welding distortion and residual stress in a thin plate butt-welded joint[J]. Computational Materials Science, 2008, 43(2): 353–365. |
| [5] | 沈济超, 陈震, 罗宇. 船体T型接头分段移动热源焊接模拟[J]. 中国造船, 2014, 55(4): 66–72. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgzc201404008 |
| [6] | SHEN J, CHEN Z. Welding simulation of fillet-welded joint using shell elements with section integration[J]. Journal of Materials Processing Technology, 2014, 214(11): 2529–2536. |
| [7] | MATO P, ZDENKO T, ALAN R, et al. Numerical analysis and experimental investigation of welding residual stresses and distortions in a T-joint fillet weld[J]. Materials and Design, 2014, 53: 1052–1063. |
 2018, Vol. 40
2018, Vol. 40