0 引　言

船舶外板曲面展开一般通过三角形网格或者四边形网格进行展开。曲面网格划分成为外板曲面展开的重要部分，对船舶外板曲面展开的精度有着重要的影响。网格过于稀疏会使展开误差加大，过密则会降低展开效率。对于给定的船舶型值表数据，重构外板曲面后，曲面网格的划分引起了广泛的关注。在世博轴“阳光谷”工程设计中，李承铭^[1]先对参数域曲面进行人工细分后得到平面网格，之后将二维平面网格映射回三维空间曲面，实现了对该参数曲面的网格划分，网格划分效果较好，但其步骤繁琐，通用性不高。丁慧^[2]基于传统的映射方法，基于等参数线分割法的划分方法生成自由曲面网格，通过等弦长分割方式对曲面参数化不均匀的问题提出初步解决方案，但其生成的网格曲面单元仍存在划分混乱情况。江存^[3]提出自定义单元法的自由曲面网格划分，建立网格拓扑的参数化表达，改善了网格映射时的网格失真，但其方法试用范围单一，对非NURBS曲面不适用。王结臣^[4]通过栅格对空间散乱点集进行划分，以栅格为整体进行区域网格划分。陈永就^[5]与卫洪春^[6]分别通过直接剖分及递归程序分别对四边形及三角形网格进行了处理，网格扩展过程中变形量较小。石磊^[7]对现有的细分算法做出了分析，并同时指出了现有细分算法的劣势。针对船舶外板曲面的网格细分算法研究不多，由于船舶外板曲面曲率比较复杂，需考虑网格划分疏密对于以后外板曲面展开精度的影响。

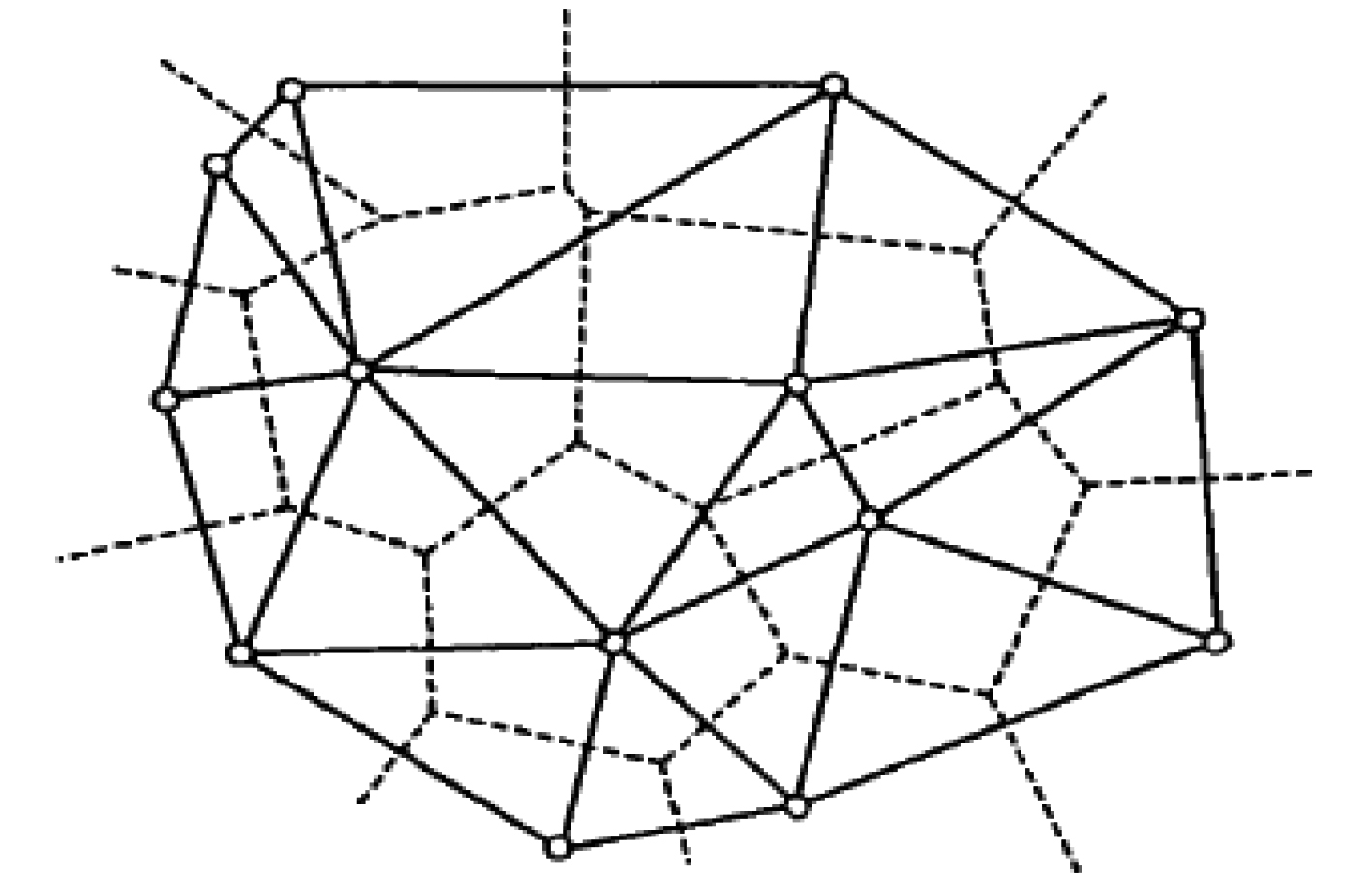
1 Delaunay三角网格化 1.1 Delaunay定义

Delaunay三角网格划分为数值分析及图形学方面重要技术手段，如图1所示，Delaunay三角网格是将空间测量数据点投影到平面来实现的二维划分法。算法基本思想为每一个Delaunay三角形的外接圆内部不包含其他结点，一旦检测到三角形外接圆含有其他结点后，就必须修改局部的网格划分，直至满足起始条件为止。

1.2 Delaunay三角网格划分算法

Delaunay三角网格划分步骤为：

1）构造大外接圆 ${G_0}$ ，使其包含所有结点，进行步骤2；

2）每次导入一个结点，重复进行步骤3～步骤5；

3）找出已有三角形中哪些外接圆包含新引入的结点，转步骤4；

4）删除这些三角形中离新结点最近的一条边，转步骤5；

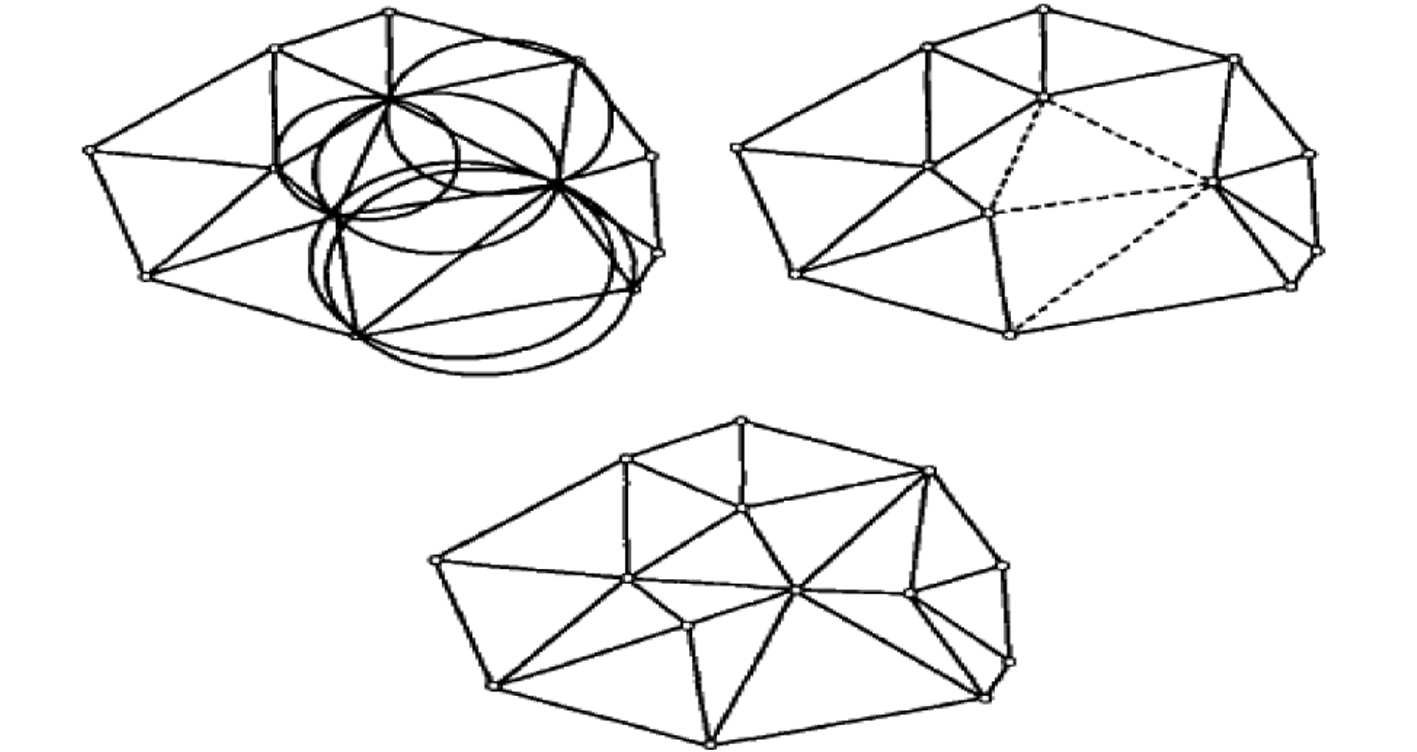
5）将新结点与老结点连接，产生新的三角形，算法示意图如图2所示。

多边形域由Delaunay三角网格划分后生成的网格还不能满足几何造型或者有限元分析的需求，为此需对初步划分后的网格作进一步的细化，在边界或者图形区域内部插入适当的节点，提高网格的质量。

2 细分曲面算法

对于给定的点云数据或者三角网格，构造细分曲面使得曲面插值于点云或者三角网格顶点，就是细分曲面插值问题。

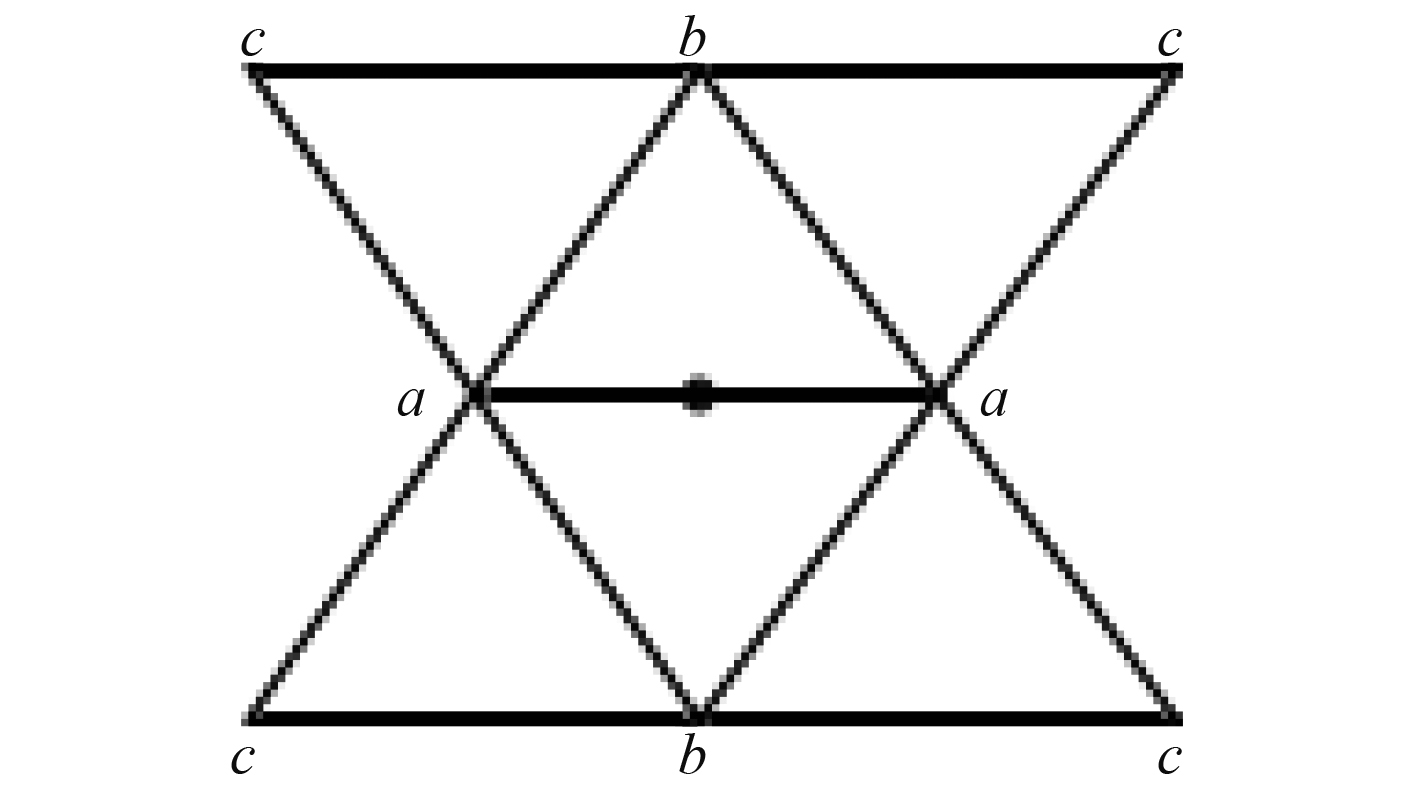
2.1 蝶形算法

蝶形算法为一种插值细分算法，如图3所示在每一条边上引入一个新顶点，顶点的值由模型中8个顶点的值加权平均得到。权重系数设置为：

$a = 1/2,b = 1/8 + 2w,c = - 1/16 - w{\text{。}}$

(1)

其中 $w$ 为张力系数 ，与表面的光滑程度有关。蝶形算法产生C₁连续的细分网格，但是对奇异点的处理不够。

2.2 多面体算法

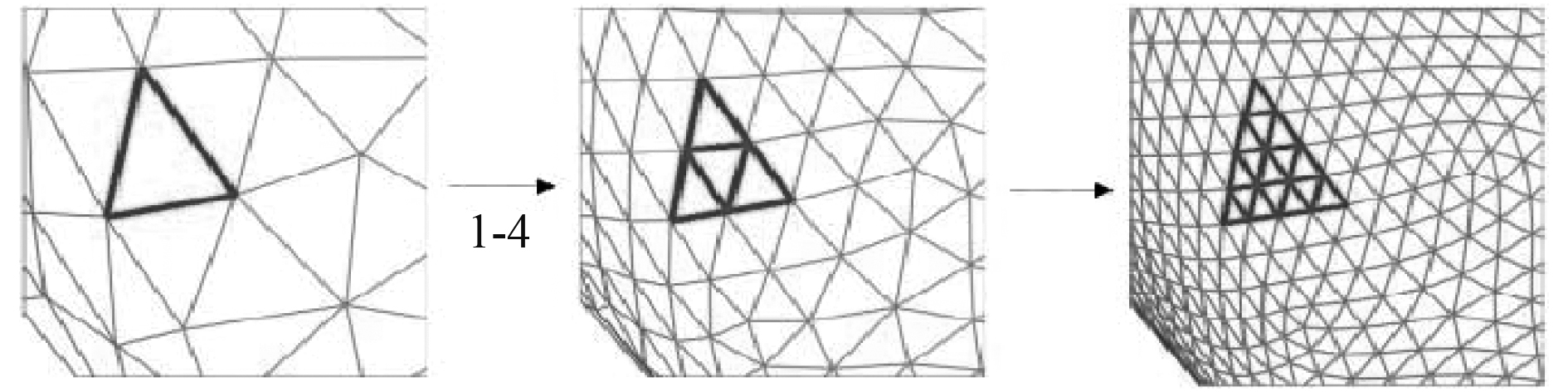
多面体算法在三角形网格细分中属于最简便的算法，算法基本思想是在三角形网格每2个顶点连线中间引入新的顶点，将原有单个三角形网格细分为4个三角网格。新引入顶点的位置通过取其所在连线两端2个顶点加权平均值确定，该算法不受奇异点影响，常用于细分算法的原理介绍。图4为多面体细分示意图。

2.3 Loop算法

Loop算法是一种逼近细分算法，其算法步骤主要分为3步，首先生成边界点，之后移动原有顶点，最后生成光滑表面（切平面连续）。

若以 $V_0^K$ 为曲面中心顶点， $V_1^K, \cdots \cdots V_n^K$ 为相邻顶点构成伞状网格，再根据Loop算法就可得到下式：

$V_0^{k + 1} = 1 - n\beta V_0^k + \beta \mathop \sum \limits_{i = 1}^n V_i^k, $

(2)

$V_0^{k + 1} = \frac{1}{8}\left( {3V_0^{k + 1} + V_{i - 1}^k + 3V_i^k + V_{1 + i}^k} \right),i = 1, \cdots \cdots ,n, $

(3)

综合上述两式得到如下局部细分矩阵形式：

$\begin{array}{l}\left[\!\!\!\!\!\!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}}{V_0^{k + 1}}\\{\begin{array}{*{20}{c}}{V_0^{k + 1}}\\{\begin{array}{*{20}{c}}{V_0^{k + 1}}\\ \vdots \end{array}}\\{V_0^{k + 1}}\end{array}}\\{V_0^{k + 1}}\end{array}}\!\!\!\!\!\!\!\!\!\!\!\!\! \right] = \frac{1}{8}\left[\!\!\!\!\! {\begin{array}{*{20}{c}}{8 - 8np}\!\!&\!\!{\begin{array}{*{20}{c}}{8\beta }\!\!&\!\!{8\beta }\!\!&\!\! \cdots \end{array}}\!\!&\!\!{8\beta }\!\!&\!\!{8\beta }\\{\begin{array}{*{20}{c}}3\\3\\ \vdots \end{array}}\!\!&\!\!{\begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}3\!\!&\!\!1\!\!&\!\! \cdots \!\!\end{array}}\\{\begin{array}{*{20}{c}}1\!\!&\!\!3\!\!&\!\! \cdots \!\!\end{array}}\\{\begin{array}{*{20}{c}} \vdots \!\!&\!\! \vdots \!\!&\!\! \cdots \!\!\end{array}}\end{array}}\!\!&\!\!{\begin{array}{*{20}{c}}0\\0\\ \vdots \end{array}}\!\!&\!\!{\begin{array}{*{20}{c}}1\\0\\ \vdots \end{array}}\\3\!\!&\!\!{\begin{array}{*{20}{c}}0\!\!&\!\!0\!\!&\!\! \cdots \!\! \end{array}}\!\!&\!\!3\!\!&\!\!1\\3\!\!&\!\!{\begin{array}{*{20}{c}}1\!\!&\!\!0\!\!&\!\! \cdots \!\!\end{array}}\!\!&\!\!1\!\!&\!\!3\end{array}}\!\!\!\!\! \right] \left[\!\!\!\!\!\!\!\! {\begin{array}{*{20}{c}}{V_0^k}\\{V_1^k}\\{\begin{array}{*{20}{c}}{V_2^k}\\ \vdots \\{V_{n - 1}^k}\end{array}}\\{V_n^j}\end{array}}\!\!\!\!\!\!\!\! \right]{\text{。}} (4)\end{array}$

中心顶点 $V_0^K$ 处的局部细分矩阵即为式（4）中的 $\left( {n + 1} \right) \times \left( {n + 1} \right)$ 矩阵，采用静态的网格细分模式，与网格顶点在网格中所处位置无关，只与阶数 $n$ 有关。

3 自适应三角网格划分算法（ATM） 3.1 ATM算法思想

自适应网格划分（Adaptive Triangular Meshing）算法通过自动估算曲面曲率的大小，结合Delaunay算法，自动选择合适的划分密度，避免了人工划分的繁琐，提高了划分效率。针对船舶外板曲面自适应网格划分算法基本步骤如下：

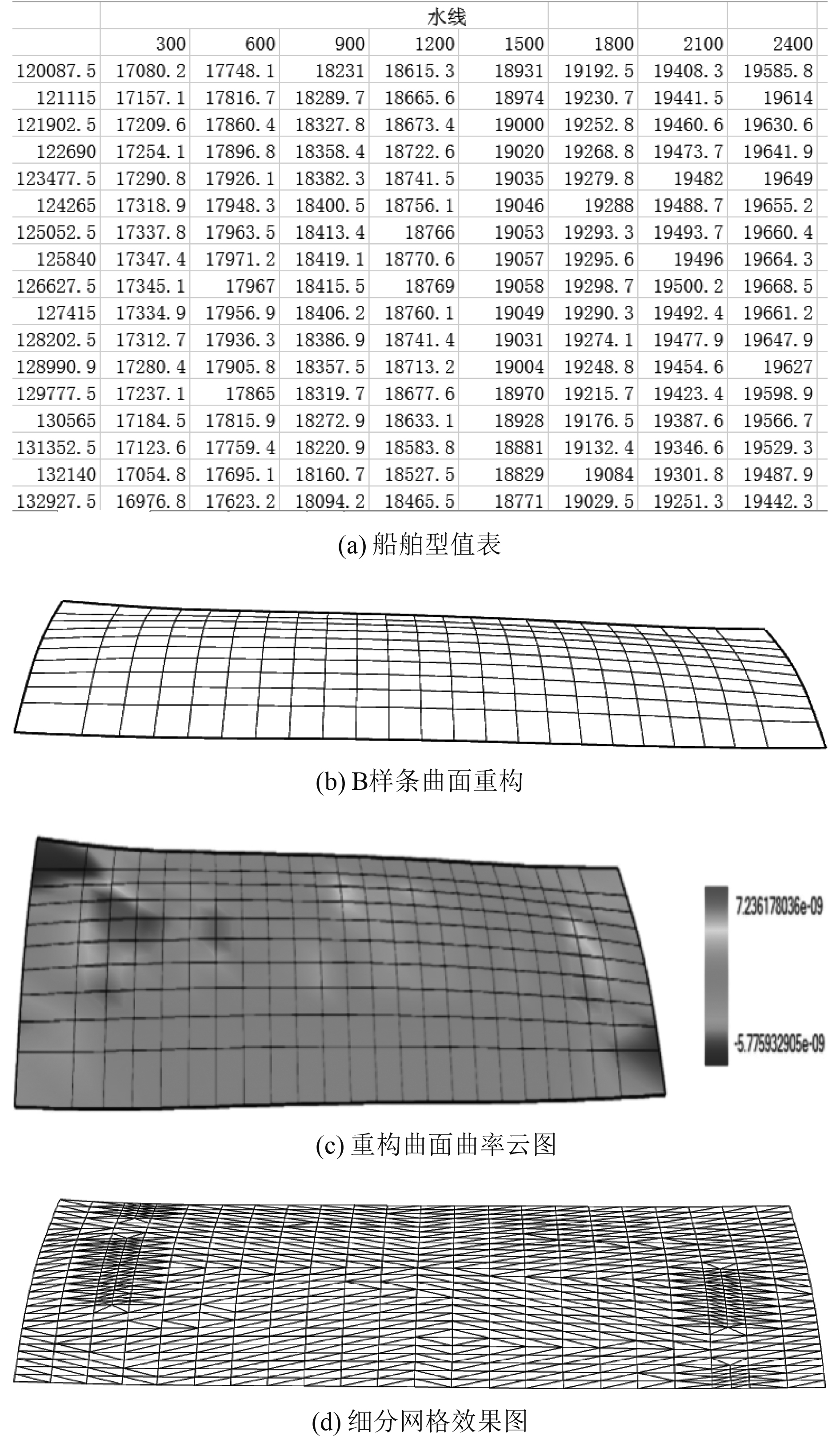
1）提取船舶型值表数据，通过B样条工具进行参数化曲面重构，得到参数化曲面 $r\left( {u,v} \right)$ ；

2）选定曲面适当区域，在参数化曲面 $u,v$ 方向上选取相向的2条曲线，从一端的顶点开始搜索，计算步长两端点弦长或者弧长（估算值）差的绝对值，将其值称为弦弧差；

3）设定弦弧差许用范围，将步骤2得到的值与弦弧差范围比较，如果在弦弧差范围之内，记录步长，并生成划分用网格线，否则步骤4；

4）调整步长重新判断，直至满足弦弧差范围；

5）重复步骤2～步骤4，直到搜索至边界的终点；

6）所有搜索完毕后得到的是四边形网格，此时进行Delaunay三角化生成细分网格。

3.2 步长划分准则

3.1节所述ATM算法步骤适用于矩形参数域。对于非矩形参数域而言，需要先对曲面进行扩展补充，通过 $uv$ 方向的最大与最小参数值 ${u_{\max }},{v_{\max }},{u_{\min }},{v_{\min }}$ 确定一个矩形域，此矩形域为原先非矩形参数域的最小外接矩形域。

以 $u$ 向网格划分为例，如图5所示，原先参数域为非矩形参数域，建立如图的 $uv$ 坐标系，通过最大参数值 ${u_{\max }},{v_{\max }}$ 及最小参数值 ${u_{\min }},{v_{\min }}$ 构建最小外接矩形参数域，包含原有的多边形域 $p_1p_2p_3p_4p_5$ 中所有点。B与b之间距离的绝对值为划分的步长值，将其与设定的弦弧差范围比较。

选中由 $uv$ 最值形成的参数化区域，由a、b两点开始搜索，给定初始步长l，求出a与A，b和B之间的弦弧差的值，其中较大的弦弧差的值记作 ${\delta _{\max }}$ ，较小的记作 ${\delta _{\min }}$ 。给定的许用弦弧差最小值为 ${\varepsilon _{\max }}$ ，许用弦弧差最大值为 ${\varepsilon _{\min }}$ 。判断当 ${\varepsilon _{\min }} \leqslant {\delta _{\min }} \leqslant {\delta _{\max }} \leqslant {\varepsilon _{\max }}$ 则满足条件，步长合适并生成划分网格线，否则需要重新修改步长再判定。

3.3 步长关系调整

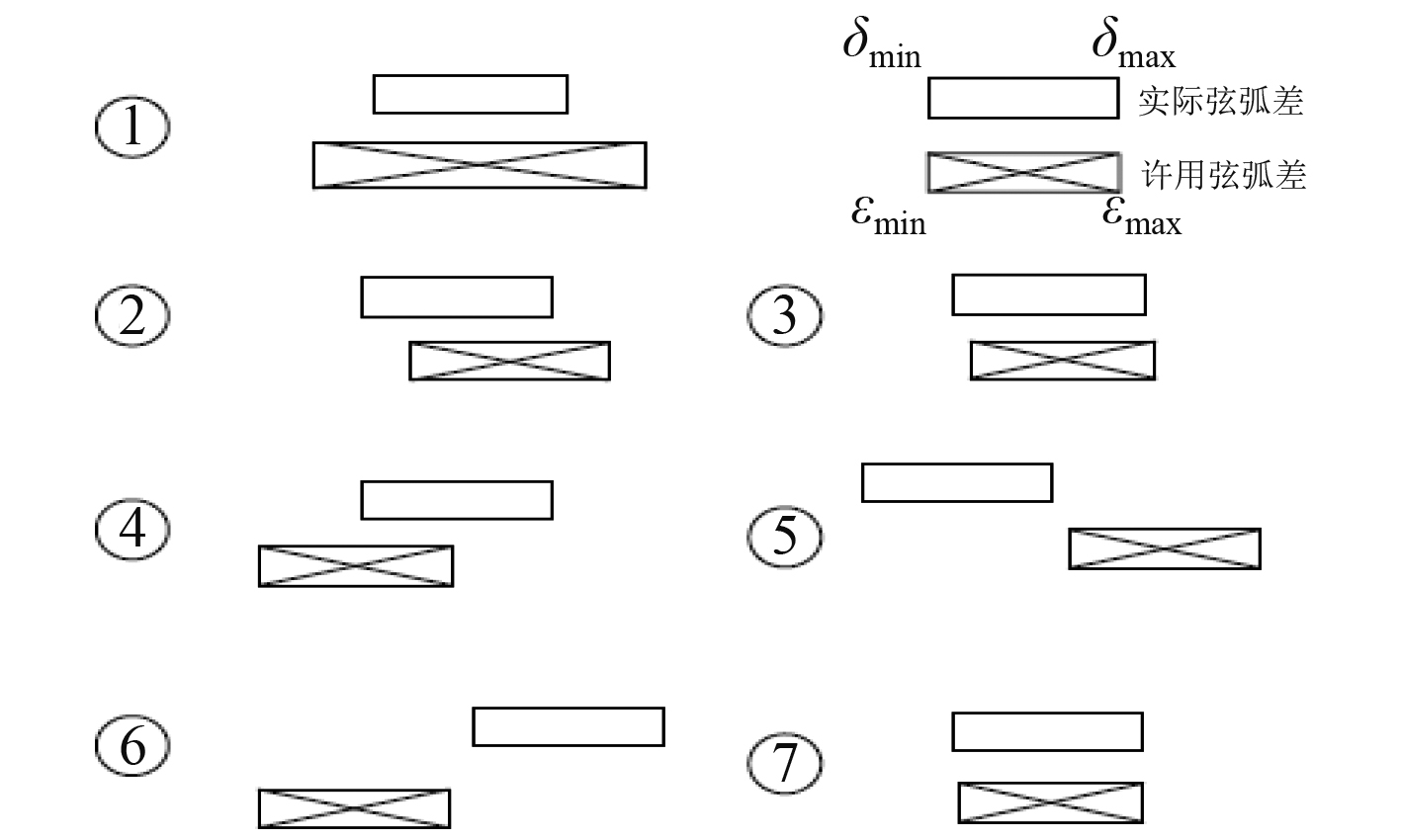
步长关系调整基于精度为主，效率为辅的原则。实际与许用弦弧差关系总共分为7种，如图6所示，上面部分图形为实际弦弧差绝对值，左端为最小值 ${\delta _{\min }}$ ，右端为最大值 ${\delta _{\max }}$ ，下面部分图形为许用弦长差绝对值，左端为许用弦弧差范围最小值 ${\varepsilon _{\min }}$ ，右端为许用弦弧差最大值 ${\varepsilon _{\max }}$ 。

针对7种步长关系图进行如下调整：

1）在情况1中，实际的弦弧差范围均处于许用弦弧差范围内， ${\delta _{\min }} \geqslant {\varepsilon _{\min }}$ ， ${\delta _{\max }} \leqslant {\varepsilon _{\max }}$ ，满足判断条件，可以记录步长，生成网格划分线，并进行下一步搜索；

2）在情况2中，实际弦弧差与许用弦弧差关系为 ${\delta _{\min }} < {\varepsilon _{\min }}$ ， ${\varepsilon _{\min }} < {\delta _{\max }} < {\varepsilon _{\max }}$ ，此时需要加大步长，在其满足判断条件后记录步长，生成网格划分线；

3）在情况3中，实际弦弧差最大值小于许用弦弧差最大值，关系为 ${\delta _{\min }} < {\varepsilon _{\min }}$ ， ${\varepsilon _{\min }} < {\delta _{\max }} < {\varepsilon _{\max }}$ ，跟情况2的不同之处在于此时实际弦弧差最大值 ${\delta _{\max }}$ 接近于许用弦弧差 ${\varepsilon _{\max }}$ ，不能加大步长，记录步长，生成网格划分线；

4）情况4中实际弦弧差与许用弦弧差关系为 ${\delta _{\min }} > {\varepsilon _{\min }}$ ， ${\delta _{\max }} > {\varepsilon _{\max }}$ ，此时需要缩小步长，使得 ${\delta _{\max }} \leqslant {\varepsilon _{\max }}$ ，即满足情况1或情况3的状态，当满足这个条件时记录步长，并生成网格划分线；

5）情况5中实际弦弧差与许用弦弧差关系为 ${\delta _{\min }} < {\varepsilon _{\min }}$ ， ${\delta _{\max }} < {\varepsilon _{\max }}$ ，此时需要增大步长值，在其满足判断条件后记录步长，生成网格划分线；

6）情况6中实际弦弧差与许用弦弧差关系为 ${\delta _{\min }} > {\varepsilon _{\max }}$ ，此时需要缩小步长，记录步长，在其满足判断条件后记录步长，生成网格划分线；

7）情况7中实际弦弧差与许用弦弧差关系为 ${\delta _{\min }} < {\varepsilon _{\min }}$ ， ${\delta _{\max }} > {\varepsilon _{\max }}$ ，此时减少步长值，使其达到情况3的状态。

4 实例应用

算法实现电脑配置为PC i3CPU，M350 @2.27 GHz RATM4G。根据提供的船舶型值表数据首先通过B样条进行曲面重构得到其参数化曲面，之后通过自适应算法得出船舶曲面外板实现网格划分效果。具体实现流程如图7所示。

船舶外板曲面实例效果如图8所示。经过自动调整划分的网格对于船舶外板的复杂曲面展开的精度更有益处。

下式为计算曲面展开面积误差的表达式：

${\varepsilon _j} = \frac{{\mathop \sum \nolimits_{i = 1}^v \frac{{\left| {{S_i} - {s_i}} \right|}}{{{S_i}}}}}{{{v}}}{\text{。}}$

(5)

其中 ${S_i}$ 和 ${s_i}$ 为展开前后的三角网格的对应三角形的面积值； $v$ 为空间曲面第 $j$ 个顶点相连的三角形的个数。

如表1所示，在对不同划分网格数的曲面进行展开后，得到的曲面面积变化误差也不同。对初始曲面分别进行划分处理，得到网格数为460，900，1 840的三角形网格曲面以及自适应细分后的1 386个三角片的曲面，借助现有的三角形展开方法进行展开后，得到相应的面积误差。可见，对于精细划分后的曲面展开来讲，其展开的面积误差较小，对于船板制造加工具有指导意义。

5 结　语

本文取船舶曲面分段进行曲面网格的划分研究，针对船舶曲面外板曲面的复杂特征而言，选择合适的网格划分方式对外板展开尤为重要。通过B样条工具进行曲面重构，之后对重构出的四边形网格作进一步的细分网格处理，并通过曲面展开验证细分网格的效果。现有的网格细分方法对划分网格的准确性存在一定缺陷，将Delaunay三角网格划分与自适应划分算法结合起来，利用自适应划分网格的准确性，实现船舶外板曲面的三角网格化处理，为曲面展开做好铺垫。