2. 武汉理工大学 船舶动力工程技术交通行业重点实验室,湖北 武汉 430063;
3. 中船黄埔文冲船舶有限公司,广东 广州 510725
2. Key Laboratory of Marine Power Engineering and Technology (Ministry of Transport), Wuhan University of Technology, Wuhan 430063, China;
3. CSSC Huangpu Wenchong Shipbuilding Company Limited, Guangzhou 510725, China
海运贸易对全球经济发展非常重要,目前,全球90%的贸易运输量由船舶航运承担[1]。同时,海运业会消耗大量的能源,并产生大量废气等污染物,因此保护环境、发展绿色船舶技术显得尤为重要。船舶减阻是一种重要的船舶节能、减排方法。球鼻首作为船体的特殊部位,可以有效地改善水面波系的分布,减小船体兴波阻力,对节能型船舶的发展有很重要的意义。
传统的球鼻首型线设计方法是针对具体的船型特点,根据一些基本规律和设计经验,确定几个型线方案,通过多组模型试验分析计算来改进型线并最终确定,这种设计过程非常繁琐,需要反复修改,消耗大量的人力物力,效率不高[2]。国外方面,C.Yang和H.Kim基于径向基函数修改船体曲面的参数化方法,完成了KCS船型的兴波阻力性能优化[3],但是由于船体曲面的复杂性,故很难用一个或者多个函数将曲面形状精确表达出来,这种方法也一直没有得到广泛应用。
为了快速获得球鼻首阻力最小最优型线,本文利用CAESES软件对2 200箱集装箱船球鼻首进行参数化建模,并集成Shipflow软件,利用遗传算法对球鼻首型线进行自动优化,获得具有最小阻力的该船型球鼻首型线。
1 球鼻首参数化模型的建立2 200箱集装箱船是广州文冲船厂建造的浅吃水支线集装箱船,适合全球航行,并满足巴拿马、苏伊士运河等航道的通航要求。该船尺度灵便,航速适中,节能环保,具有优秀的装载能力和油耗性能,满足最新的国际规范规则;布置合理紧凑,货舱利用率低,振动噪音性能佳,技术性能已经达到国际先进水平行列。该船的主要参数及数据如表1所示。
|
|
表 1 2 200箱集装箱船主要参数 |
球鼻首参数化是球鼻首进行优化设计的基础,采用CAESES软件对球鼻首进行参数化建模。建模思想为:首先构建控制船体面元的特征曲线以及曲面生成器Curve Engine,然后根据这些特征曲线和曲面生成器Curve Engine通过特征Feature生成横剖线,最后由曲面生成器Meta Surface将这些创建好的横剖线平滑连接起来,生成光顺曲面。
由于本文只对球鼻首部分进行优化研究,故只对球鼻首进行参数化建模。球鼻首创建的大致过程如下:
1)创建构成球鼻首曲面的特征轮廓线,并创建好相应的Feature,然后利用Curve Engine和Meta Surface功能生成球鼻首前段曲面bulb。
2)用Fillet Surface功能实现前端曲面到船体的光滑过渡,并将过渡面元分为两部分S1和S2。
3)为了实现前段和上部分船体的连接,需要创建球鼻首尖端bulbtip。和球鼻首前端曲面一样,创建好曲面控制线和Feature之后,启动Curve Engine,并利用Meta Surface生成球鼻首尖端面元bulbtip。
4)采用Coons Patch功能连接bulbtip、S2面元以及相邻船体2块面元的4条边,即可形成最后一块面元S4,并且与周围的4个曲面保持相切。
球鼻首参数化之后的模型如图1所示。

|
图 1 球鼻首参数化的船体模型 |
对于建立的船体模型,需要对船体进行静水力数据计算。获得球鼻首建模之后的船体模型的排水量、浮心位置、湿表面积等性能之后,分析和初始船型之间的误差,从而保证球鼻首建模之后船体型线精确度[4]。
通过在CAESES软件中添加静水力计算模块进行计算,并对数据进行分析之后,发现设计吃水时的排水体积误差仅为0.033%;浮心纵向位置误差为0.020%;一些其他静水力数据也符合设计要求,建模后船型的静水力数据误差保持在很小得到范围内,如表2所示。
|
|
表 2 设计吃水下的静水力数据对比 |
其中误差计算公式如下式:
| ${\text{误差}} = \frac{{{\text{参数}}{{\text{值}}_{{\text{建模后}}}} - {\text{参数}}{{\text{值}}_{{\text{原船型}}}}}}{{{\text{参数}}{{\text{值}}_{{\text{原船型}}}}}} \times 100{\rm{\% }}\text{。}$ | (1) |
在优化之前需要建立恰当的优化数学模型[5],对船型进行优化获得最小阻力是典型的优化问题。对于一个完整的优化问题,应该要包括设计变量、约束条件、优化目标和合适的优化算法。
2.1 优化变量的选择设计变量的选择取决于要研究的问题,选取对优化问题有关系、影响优化目标的参数作为优化变量。球鼻首是一个复杂的曲面空间,对球鼻首线型优化来说,需要选择一些能够表达和改变球鼻首线型的参数作为设计变量。在2 200箱集装箱船的参数化球鼻首中,选择具有代表性的特征参数作为设计变量,并根据实际情况确定设计变量的范围。本文选取球鼻首建模时创建的26个特征参数作为优化变量,并确定参数变化范围。这些参数包括控制轮廓线上点的坐标值,如长度、最前点高度、最大宽度、最大宽度线的高度等参数和控制面元丰满度的角度等参数。
2.2 约束条件的定义对于获得最小阻力球鼻首的问题,其约束条件必须满足船体的需要,在获得最小阻力的同时,要保证船体优化前后某些参数保持不变,例如排水体积的限制、浸水面的限制、吃水匹配和宽度的限制、耐波性要求等。本文选择无因次量排水体积V′和浮心纵向位置XCOF作为球鼻首优化的约束条件,控制其在1%以内变化[6]。
| $\frac{{V{'_{{\text{优化}}}}{\rm{ - }}V{'_{{\text{原始}}}}}}{{V{'_{{\text{原始}}}}}} \leqslant 1{\rm{\% }}\text{,}$ | (2) |
| $\frac{{XCO{F_{{\text{优化}}}}{\rm{ - }}XCO{F_{{\text{原始}}}}}}{{XCO{F_{{\text{原始}}}}}} \leqslant 1{\rm{\% }}\text{。}$ | (3) |
其中:
船型优化是一个综合权衡的过程,优化过程中要考虑到船舶的各项性能和经济指标,本文的研究只限于船舶型线的阻力性能优化,即在约束条件下以船体阻力为优化对象进行优化。在优化问题中,优化目标是核心,优化目标一般用目标函数来表示。根据优化设计变量的输入,按照某种计算规则获得一个优化指标,获得目标函数最优解即为优化问题的结果。在船型优化中,目标函数可以是耐波性、阻力、操纵性等。对球鼻首进行优化研究,文章中输出兴波阻力作为优化问题的目标函数。
| ${R_{wm}} = \frac{1}{2}\rho {v_m}^2{S_m} \cdot {C_{wm}}\text{。}$ | (4) |
式中:Rwm,vm,Sm,Cwm分别为兴波阻力,速度,湿表面积,兴波阻力系数。
2.4 优化算法的选择当一个实际的问题转化为数学问题时,需要采用数学优化算法来求解,在数学理论中有很多的优化算法,大部分传统算法是从单个初始值迭代求最优解,往往误入局部最优解,而且难以解决复杂的非线性的问题。遗传算法基于生物遗传和进化机制,适合于复杂系统优化问题的求解,是一种高效、全局的自适应概率优化技术,这里选取遗传算法作为2 200箱集装箱船球鼻首的优化算法。
3 基于遗传算法的球鼻首优化分析在自然界的生物进化中,每一种物种的子代都来源于父代,但其遗传物质又不完全同于父代。个体的性征由染色体决定,染色体上面又是由有序排列的基因组成的,染色体上的基因对环境有不同的适应性,通过基因杂交和变异也可以产生适应性强的个体被保留下来。遗传算法(GA)[7 – 8]是基于自然选择的生物进化机制的优化算法,把优化问题和自然遗传一一对应起来,优化解的搜索空间就是遗传空间,将优化问题的每一个可能出现的解编码为染色体的二进制串(二进制编码只是一种编码方法,还有其他的编码方法,比如浮点编码),每个染色体对应一个解,染色体二进制串的每一位称为基因;这里将每个染色体对应于个体,一定数量的个体(即一定数量的染色体)组成种群。
遗传算法首先随机产生一定数量的种群(即优化问题的解的集合),按照提前设置的优化问题的适应度函数计算每个个体(每个解)的适应度,再根据适应度值对每个个体对应的染色体进行选择,淘汰掉适应度值低的染色体,适应度值高的染色体就会保留下来,然后对染色体进行交叉、变异等遗传算法,进而产生新一代的种群,这样一代又一代的计算,最终达到满足某种优化约束条件而生成最优的群体,即是种群中最优解。
3.1 球鼻首优化的具体步骤遗传算法是一个以适应度函数(目标函数)为依据,通过对种群个体施加遗传操作实现种群内个体结构重组的迭代处理过程。在这一过程中,群体个体(问题的解)逐代优化并逐渐逼近最优解。
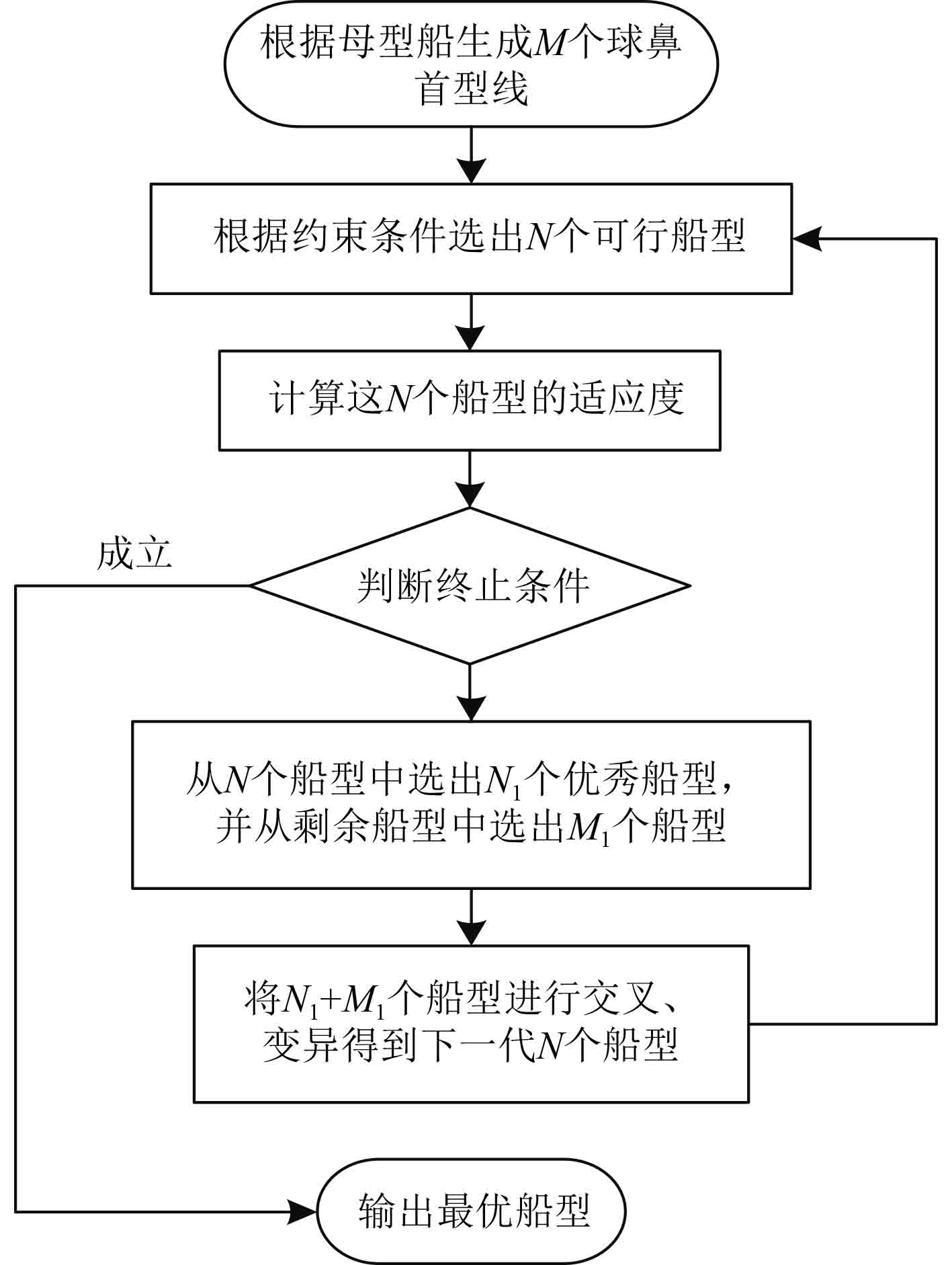
使用遗传算法NSGAII对球鼻首型线进行优化分析,应用于球鼻首的型线优化中的具体步骤如图2所示。
|
图 2 球鼻首优化具体步骤 |
在Shipflow进行计算时,需要导入相应的实船或船模尺度下的模型格式,接着设置好相关参数进行计算,其结果可以输出船模尺度下的,也可以输出实船尺度下的。文章中在进行计算结果分析时,导入实船模型对球鼻首进行参数化建模并分析静水力数据,并使用CAESES集成Shipflow软件计算,输出的优化结果为船模尺度下的解。
3.2.1 设计速度下优化结果分析使用CAESES软件集成Shipflow软件,运用遗传算法对参数化之后的2 200箱集装箱船球鼻首在设计吃水、设计航速下进行优化计算。使用建立好的优化模型,选择球鼻首建模时的26个参数作为设计变量,无因次量排水体积V′和浮心纵向位置XCOF作为约束条件,兴波阻力作为目标函数。利用遗传算法NSGAII进行优化,设置种群数量为28,遗传代数为20,交叉概率为0.8,变异概率为0.008,生成560组船型设计方案,剔除一部分出错的结果,得到模型优化之后的最优兴波阻力方案。计算并对比优化前后的目标和约束条件如表3所示。
|
|
表 3 优化前船型和优化后船型数据对比 |
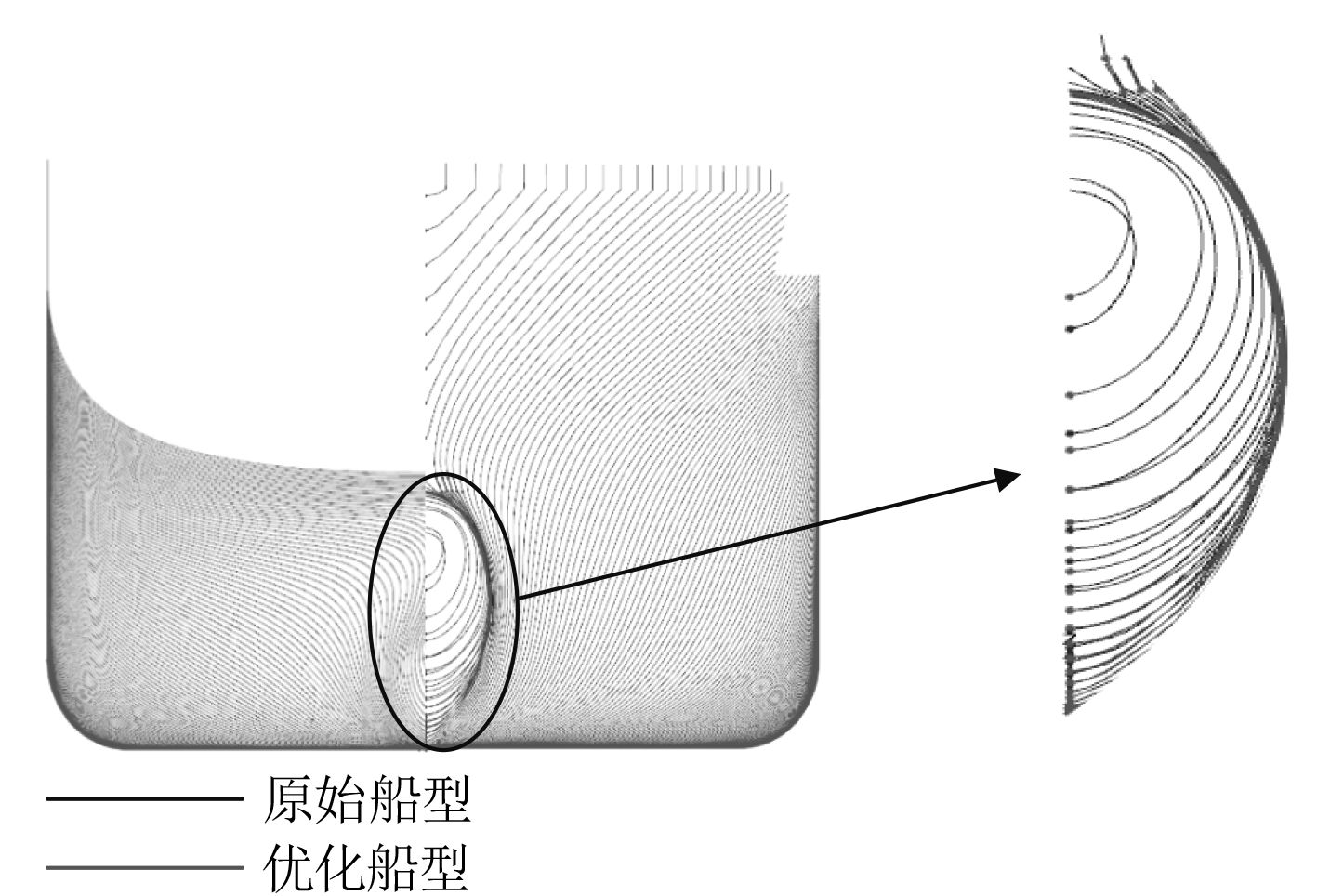
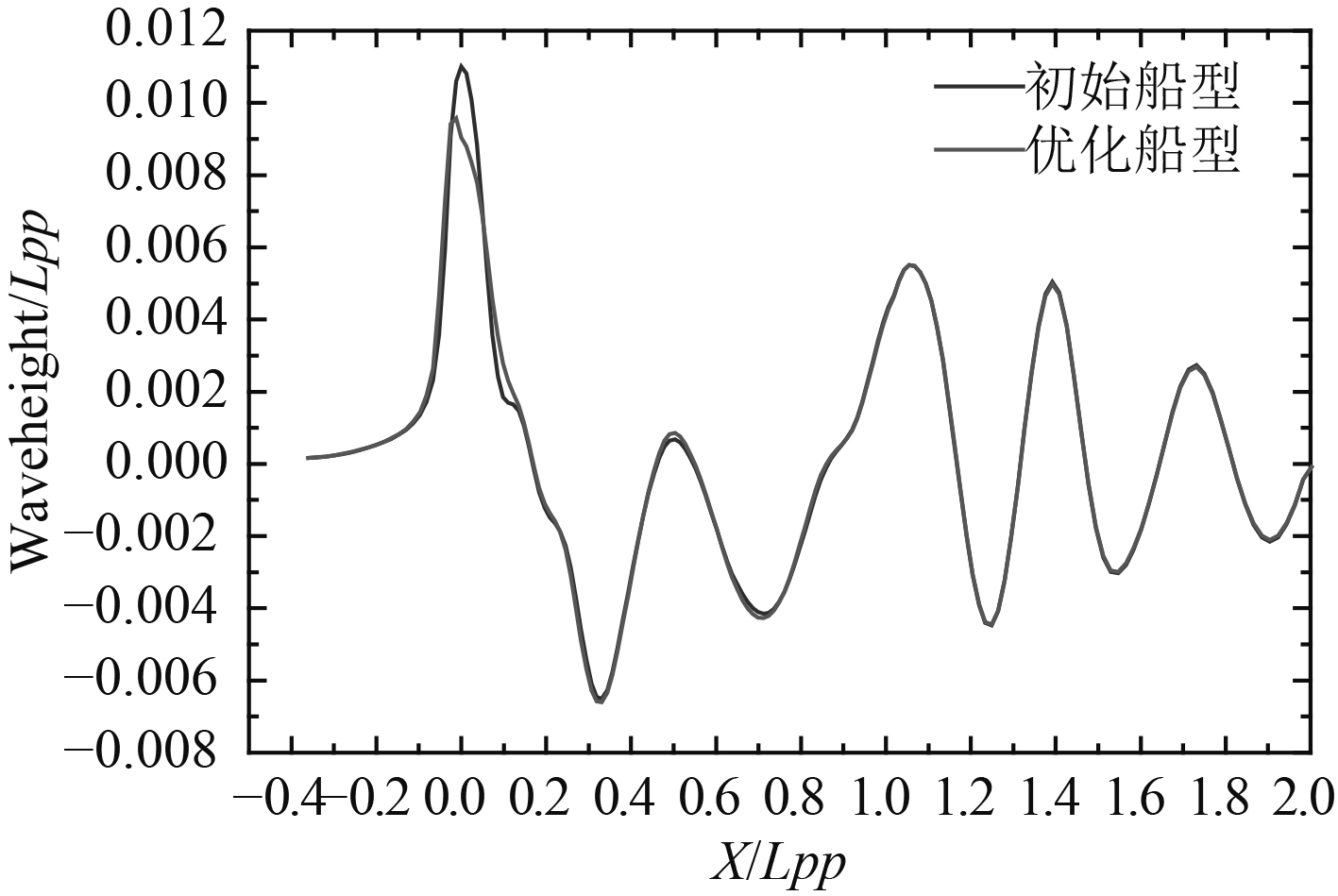
由表3可以看出,和初始方案相比,在船型设计吃水,航速为19 kn的情况下,经过NSGAII算法优化后的船型兴波阻力下降了4.137%,兴波阻力系数降低3.822%,而浮心纵向位置和排水体积的变化都维持在1%以内,误差计算同式(1)。图3为优化前后球鼻首面元对比图,图4为优化前后球鼻首部分型值组横剖线对比图,由图3和图4可以看出,优化之后的球鼻首相对初始球鼻首,长度有明显的增加,并且有上翘的趋势。图5和图6分别为航速19kn时,初始船型和优化后船型沿船体表面自由面波高对比图和波形对比图,比较图5和图6可以看出,优化之后的船型在球鼻首处的波高明显降低,并且船中后部的散波也有所改善。

|
图 3 优化前后球鼻首面元对比 |
|
图 4 优化前后球鼻首部分型值组横剖线对比 |
|
图 5 初始船型和优化后船型沿船体表面自由面波高对比(v=19 kn) |

|
图 6 初始船型和优化船型波形对比(v=19 kn) |
集装箱船逐渐向低速方向发展,一方面由于集装箱船在低速时能够减少运营成本;另一方面,在全球海运低迷期,低速行驶可以增加船舶的使用量,让更多闲置或者新增运力投入运营[9, 10]。对优化之后的船型在15 kn进行计算,并和原始船型进行对比。
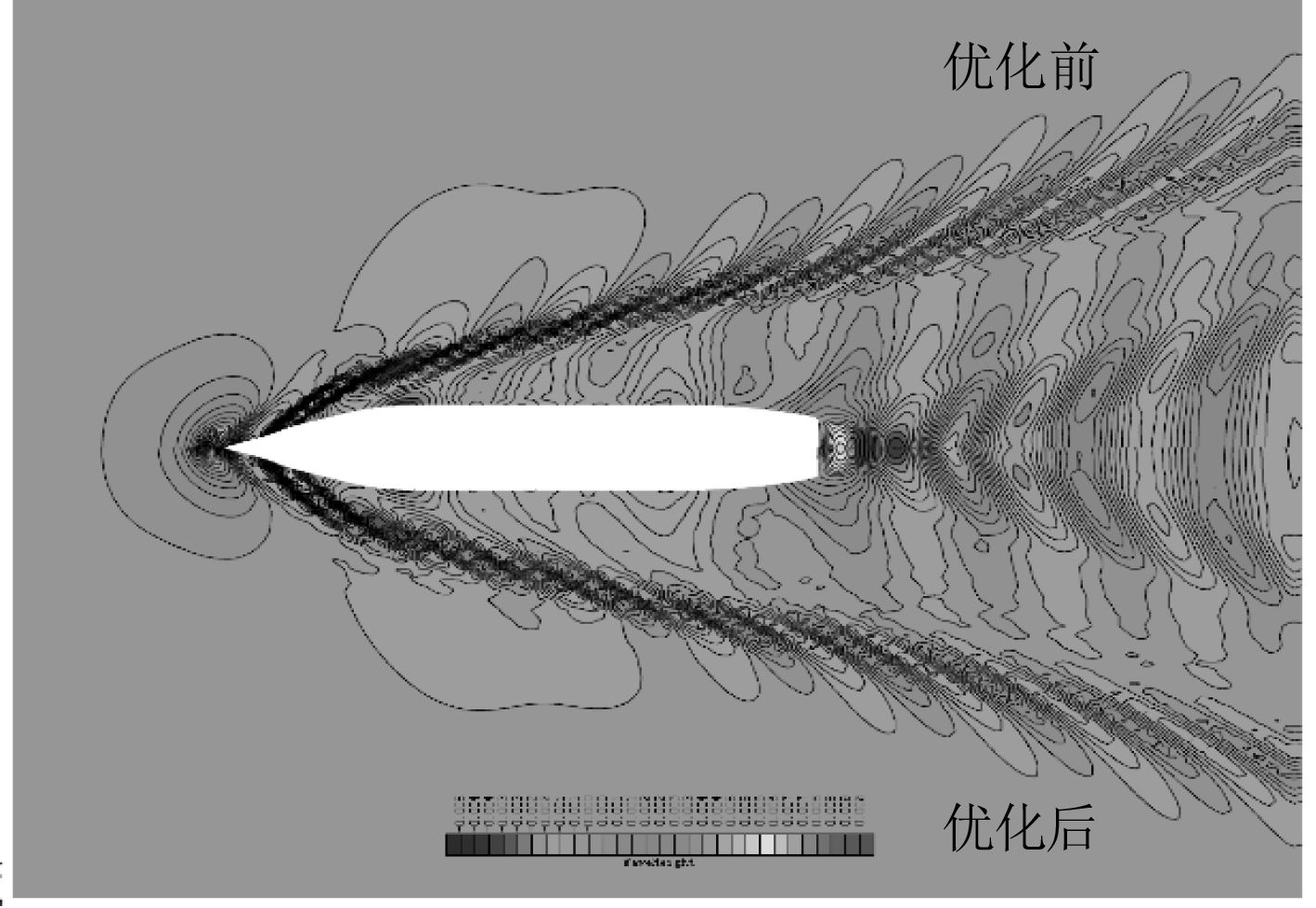
计算结果显示,航速为15 kn时,优化船型的兴波阻力系数相对初始船型下降了9.208%;总阻力系数也下降了1.010%,如表4所示。图7和图8分别为航速15 kn时,初始船型和优化后船型沿船体表面自由面波高对比图和波形对比图。由图7可以看出,在球鼻首优化之后船体中前部的波高有明显降低,由图8也可以看出优化之后船型的波形有明显的改善。
|
|
表 4 初始船型和优化后船型数据对比(v=15 kn) |

|
图 7 初始船型和优化船型沿船体表面自由面波高对比(v=15 kn) |
|
图 8 初始船型和优化船型波形对比(v=15 kn) |
使用CAESES软件对2 200箱集装箱船球鼻首进行了参数化建模,获得参数化之后的模型,基于Shipflow和CAESES软件集成平台,结合遗传算法对2 200箱集装箱船球鼻首在设计吃水,航速为19 kn下的型线进行了优化,并将优化好的船型在低速航行状态15 kn下进行了阻力验证。结果证明,最终获得阻力性能良好的球鼻首型线,提高该船型的水动力性能。
| [1] | 郝金凤, 强兆新, 石俊令, 等. 船舶设计节能减排技术策略[J]. 舰船科学技术, 2012, 9: 3–10. http://www.cqvip.com/QK/94984X/201209/43271026.html |
| [2] | 孙存楼, 徐炳香, 韩文玉. 基于母型船的船体线型优化设计研究[J]. 船舶工程, 2015, 1: 20–23. http://www.cnki.com.cn/Article/CJFDTotal-CANB201501008.htm |
| [3] | HYUNYUL KIM, CHI Yang. A new surface modification approach for CFD-based hull form optimization [C]// 9th International Conferences on Hydrodynamics, 2010, 10: 11-15. |
| [4] | 胡春平. 基于Friendship的船体型线优化技术研究[D]. 武汉: 武汉理工大学, 2012. |
| [5] | 黄金森. 基于最小阻力的船型优化研究[D]. 天津: 天津大学, 2006. |
| [6] | 邓贤辉, 方昭昭, 赵丙乾, 等. 基于计算流体动力学的最小阻力船型自动优化[J]. 中国舰船研究, 2015, 10(3): 19–25. http://www.cnki.com.cn/Article/CJFDTotal-JCZG201503004.htm |
| [7] | 谢宜, 王长雷. 基于小生境遗传算法的单体船船型参数优化[J]. 舰船科学技术, 2011, 33(3): 35–38. http://www.cnki.com.cn/Article/CJFDTOTAL-JCKX201103010.htm |
| [8] | 李华昌, 谢淑兰, 易忠胜. 遗传算法的原理与应用[J]. 矿冶, 2005, (1): 87–90. |
| [9] | 辛吉诚. 未来大型集装箱船发展趋势[J]. 中国船检, 2015, (2): 92–95. |
| [10] | 张华, 王超峰. 超低速航行及其经济效益浅析[J]. 航海, 2010, (2): 44–46. |
 2018, Vol. 40
2018, Vol. 40
