2. 海军驻郑州地区军事代表室,河南 郑州 450015
2. Military Representative Office, Navy Stationed in Zhengzhou, Zhengzhou 450015, China
弹药舱是舰船的重要舱室,属于高危险性和易爆炸区域,其安全性关乎弹药舱发生灾情时载舰的战斗力和生命力。舰船火灾发生原因复杂,危害性大,深入了解这类火灾的发生和发展规律,实现火灾探测设备在火灾发生初期探测报警,以便在事态严重之前采取有效应对措施[1]。本文采用数值模拟方法对邻舱发生火灾时通过公共壁面导热对研究弹药舱舱室内的温度影响进行了模拟,得到了在邻舱不同火源面积,不同火源热释放率的情况下,弹药舱内典型时刻舱室壁面温度以及舱室内各温度测点的变化特性,从而得到被研究舱室受邻舱火灾影响时的温度特性规律,所得结论对研究弹药舱内的火灾早期探测与消防应对等具有一定的指导意义。
1 舱室模型与火源设置弹药舱舱室为长方体结构,舱室内部尺寸为:长12 m,宽8 m,高3.5 m,舱室有一个门开口,环境温度为25 ℃。舱室两侧壁面上部各有6个对称分布的风口,各风口尺寸均为0.3 m×0.25 m,舱门所在的一侧6个风口为进风口,对面为出风口,每个风口的风速为2.5 m/s,风温20 ℃。舱室内地面上布置有6组弹药架。舱室结构的三维模型如图1所示。

|
图 1 舱室结构示意图 Fig. 1 Cabin structure diagram |
邻舱发生火灾时,火源设定为油类火,火源位置为邻舱靠近所研究舱室的公共壁面中心地面。建模后的邻舱火灾模型如图2所示,邻舱有一门开口,直接和外界相通。在弹药舱内的通风流场稳定以后,考察邻舱发生火灾后1 500 s时间内对弹药舱的影响。

|
图 2 邻舱火灾模型 Fig. 2 Adjacent compartment fire model |
在研究的舱室内距地面高3.2 m的平面上,布置有温度测点(T1~T8)、烟雾测点(S1~S4)和压力监测点(P1~P4),可对相应参数进行采集,采样周期0.2 s,采样频率5 Hz。各监测点的布置示意图如图3所示。假设邻舱与弹药舱之间没有直接相通的开口,邻舱火灾时产生的烟雾等燃烧产物不会进入被研究舱室内,邻舱火灾仅通过与被研究舱室的公共壁面导热作用于被研究舱室,因此本文只研究被研究舱室内温度测点的变化情况。

|
图 3 舱室内各监测点布置示意图(单位:m) Fig. 3 Booth arrangement diagram of the monitoring (unit: m) |
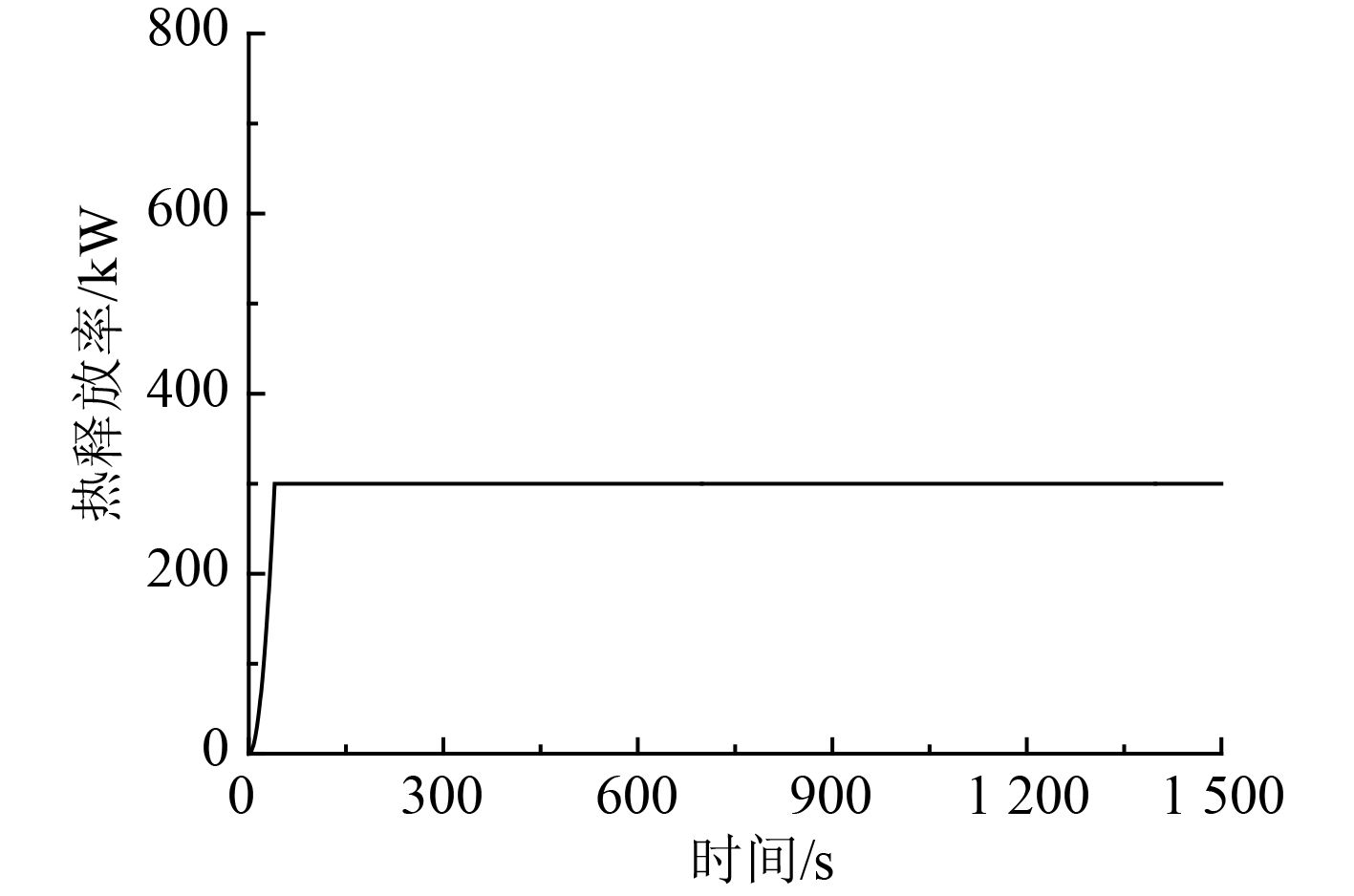
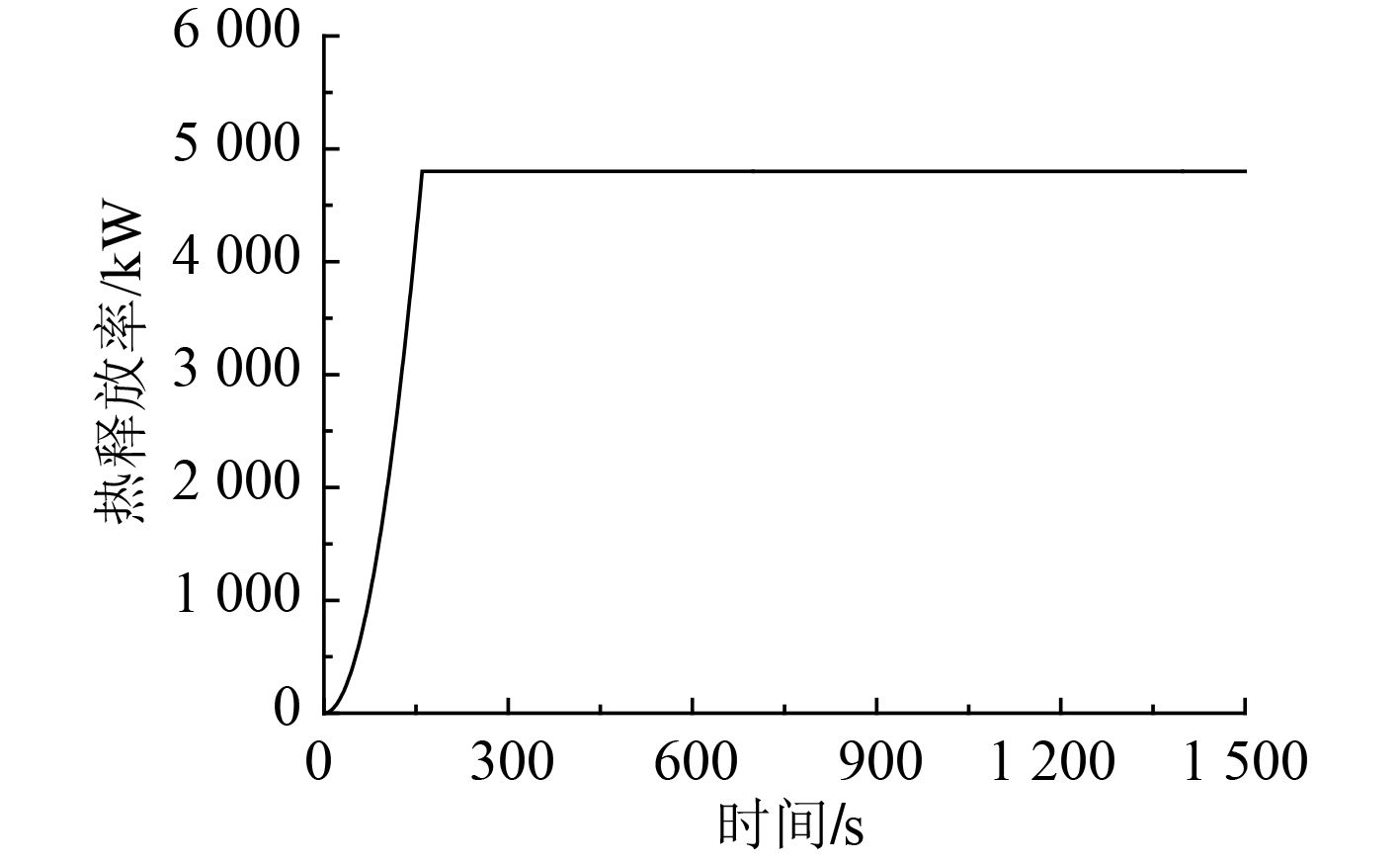
被研究舱室门关闭的条件下,将邻舱火源设定为油类火,分别考虑火源面积为0.5 m×0.5 m和2.0 m×2.0 m两种情况。假设当火源面积为0.5 m×0.5 m时,燃烧稳定阶段的火源热释放率约为300kW,火源发展规律为超快速火,燃烧稳定阶段火源最大热释放率的随时间变化曲线如图4所示。假设当火源面积为2.0 m×2.0 m时,火源发展规律为超快速火,燃烧稳定阶段的火源热释放率约为4.8 MW,火源热释放率随时间变化曲线如5所示。
|
图 4 热释放速率变化曲线 Fig. 4 The heat release rate curve |
|
图 5 热释放速率变化曲线 Fig. 5 The heat release rate curve |
基于所得结果的准确性、全面性等方面考虑,本文研究采用基于大涡模拟技术的数值模拟方法为主。受限空间内的火灾热流场主要为热浮力驱动的低马赫流动过程,在此类受重力作用的多组分理想气体的控制方程组的基础上,为了加快计算求解速度,根据火灾流场特性,需要对控制方程组进行一些必要的变形与简化[2 – 4],得到以下主要控制方程组:
连续性方程
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {{V}}} \right) = 0\text{,}$ |
组分方程
| $\frac{{\partial \left( {\rho {Y_l}} \right)}}{{\partial t}} + {{V}} \cdot \left( {\nabla \rho {Y_l}} \right) = - \rho {Y_l}\nabla \cdot {{V}} + \nabla \cdot \left( {\rho {D_l}\nabla {Y_l}} \right) + {\dot m'''_l}\text{,}$ |
动量方程
| $\frac{{\partial {{V}}}}{{\partial t}} - {{V}} \times {{\Omega }} + \nabla H = \frac{1}{\rho }\left[ {(\rho - {\rho _\infty }){{g}} + \nabla \cdot {{\tau }}} \right] - \left( {\frac{1}{\rho } - \frac{1}{{{\rho _\infty }}}} \right)\nabla \tilde P\text{,}$ |
速度散度约束方程
| $\begin{array}{l}\nabla \cdot {{V}} = \displaystyle\frac{1}{{\rho {C_P}T}}\left[ {\dot q + \nabla \cdot \left( {k\nabla T} \right) + \nabla \cdot \left( {\sum\limits_l {{h_{s,l}}\rho {D_l}\nabla {Y_l}} } \right) - \nabla \cdot {{{q}}_r}} - \right.\\\left. {\quad \sum\limits_l {{h_l}{{\dot m'''}_l} - \sum\limits_l {{h_l}\nabla \cdot \left( {\rho {D_l}\nabla {Y_l}} \right)} } } \right] + \displaystyle\frac{{\bar M}}{\rho }\sum\limits_l {\nabla \cdot \rho {D_l}\nabla \left( {{{{Y_l}} / {{M_l}}}} \right)} + \\\;\;\;\;\;\;\;\;\;\;\;\displaystyle\frac{1}{\rho }\sum\limits_l {\left( {\displaystyle\frac{{\bar M}}{{{M_l}}} - \displaystyle\frac{{{h_l}}}{{{C_P}T}}} \right){{\dot m'''}_l}} + \left( {\displaystyle\frac{1}{{\rho {C_p}T}} - \displaystyle\frac{1}{{{P_0}}}} \right)\displaystyle\frac{{D{P_0}}}{{Dt}}\text{,}\end{array}$ |
状态方程
| ${P_0}\left( t \right) = \rho TR\sum\limits_l {\frac{{{Y_l}}}{{{M_l}}}}\text{,} $ |
压力方程
| $\begin{array}{l}{\nabla ^2}H = - \displaystyle\frac{{\partial \left( {\nabla \cdot {{V}}} \right)}}{{\partial t}} - \nabla \cdot {{F}}\text{,}\\{{F}} = - {{V}} \times {{\varOmega }} + \left( {\displaystyle\frac{{\rm{1}}}{\rho } - \displaystyle\frac{1}{{{\rho _\infty }}}} \right)\nabla \tilde P - \frac{1}{\rho }\left[ {\left( {\rho - {\rho _\infty }} \right){{g}} + \nabla \cdot {{\tau }}} \right]\text{。}\end{array}$ |
式中:
数值计算时,采用大涡模拟技术对控制方程组进行处理,得到大尺度涡旋运动的控制方程组和小尺度涡旋给出的亚格子尺度模型[5];燃烧采用单步瞬时反应混合分数模型;热辐射采用有限体积法进行处理[6 – 10];舱室壁面导热使用的是一维导热模型[4]计算。对于邻舱火灾场景,流场属于典型的亚音速弱可压流动,计算过程中,为了对火灾热流场进行准确模拟,使用美国标准技术研究所开发的场模拟软件(FDS)来进行计算机物理建模与仿真。
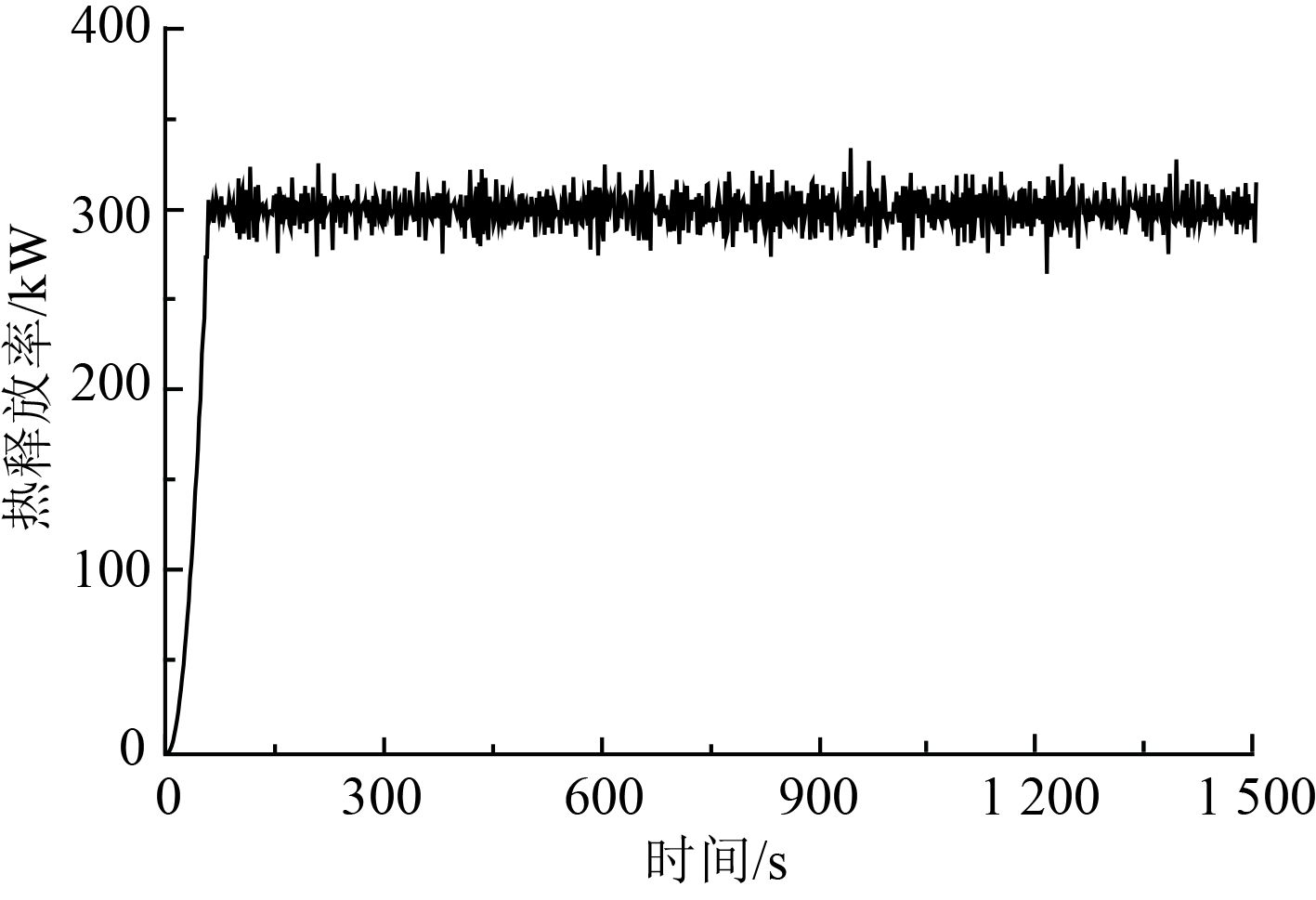
3 结果与分析 3.1 最大火源热释放率300 kW当火源面积为0.5 m×0.5 m时,若按假设火源最大热释放速率为300 kW作为模拟火源的输入条件,则经过模拟输出的火源热释放速率结果如图6所示。由图中可以看出,火源按设定的规律进行燃烧,并且在约60 s时刻达到最大值300 kW,之后的热释放速率值始终保持在300 kW附近波动,说明在邻舱内的火源可以按照设定的燃烧。
|
图 6 邻舱火灾的火源热释放率随时间变化 Fig. 6 The adjacent compartment fire heat release rate of change over time |
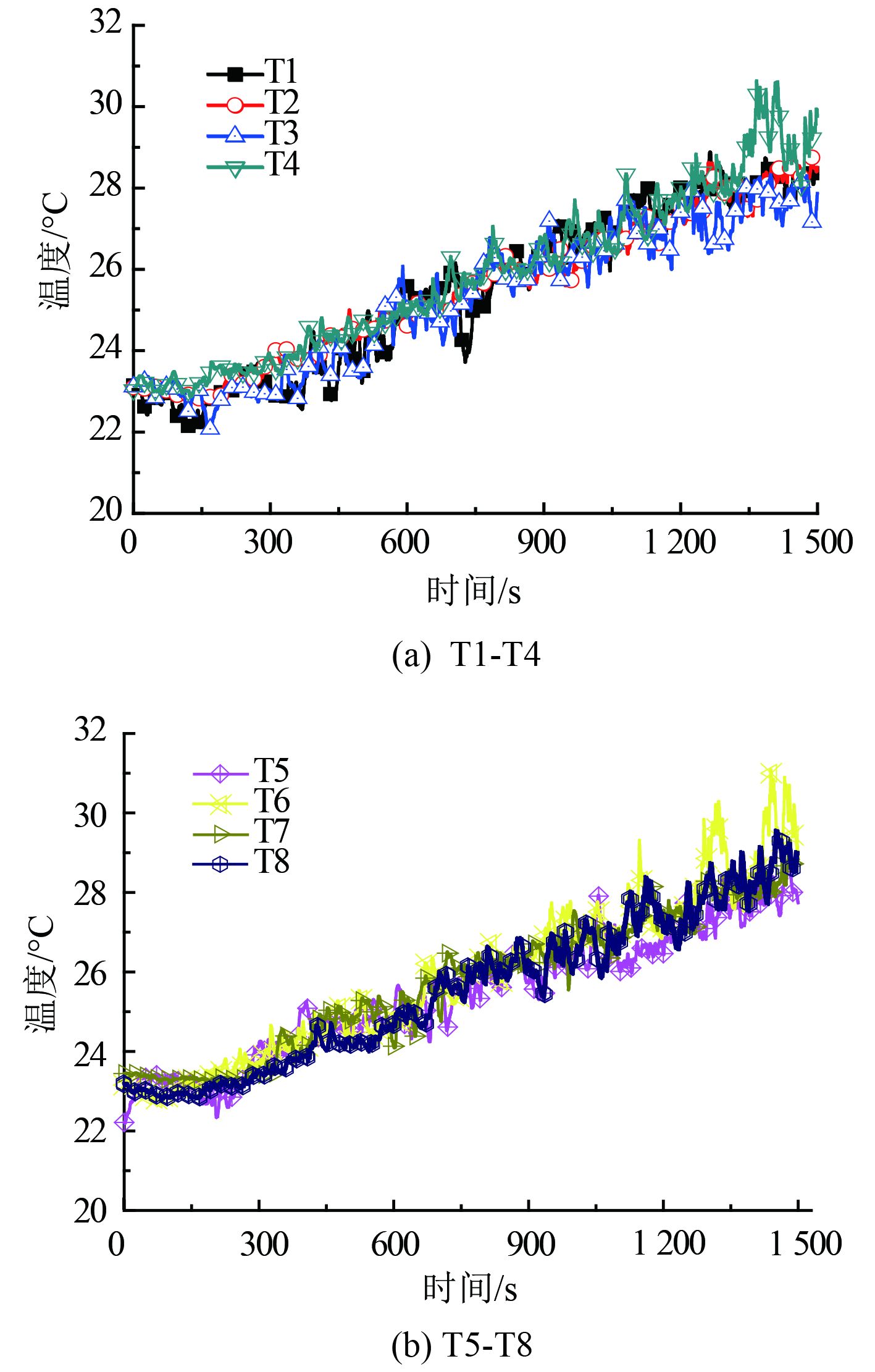
邻舱发生火灾时,被研究弹药舱内各温度测点输出随时间的变化如图7所示。由图中可以看出,尽管邻舱发生火灾,但是各温度测点在所模拟的500 s时间内,前350 s几乎没有任何变化,除测点T1和T3外,其余测点在约350 s以后才开始小幅度上升,随着时间的增加,在1 500 s时,所有温度测点处的温度均达到了28 ℃。
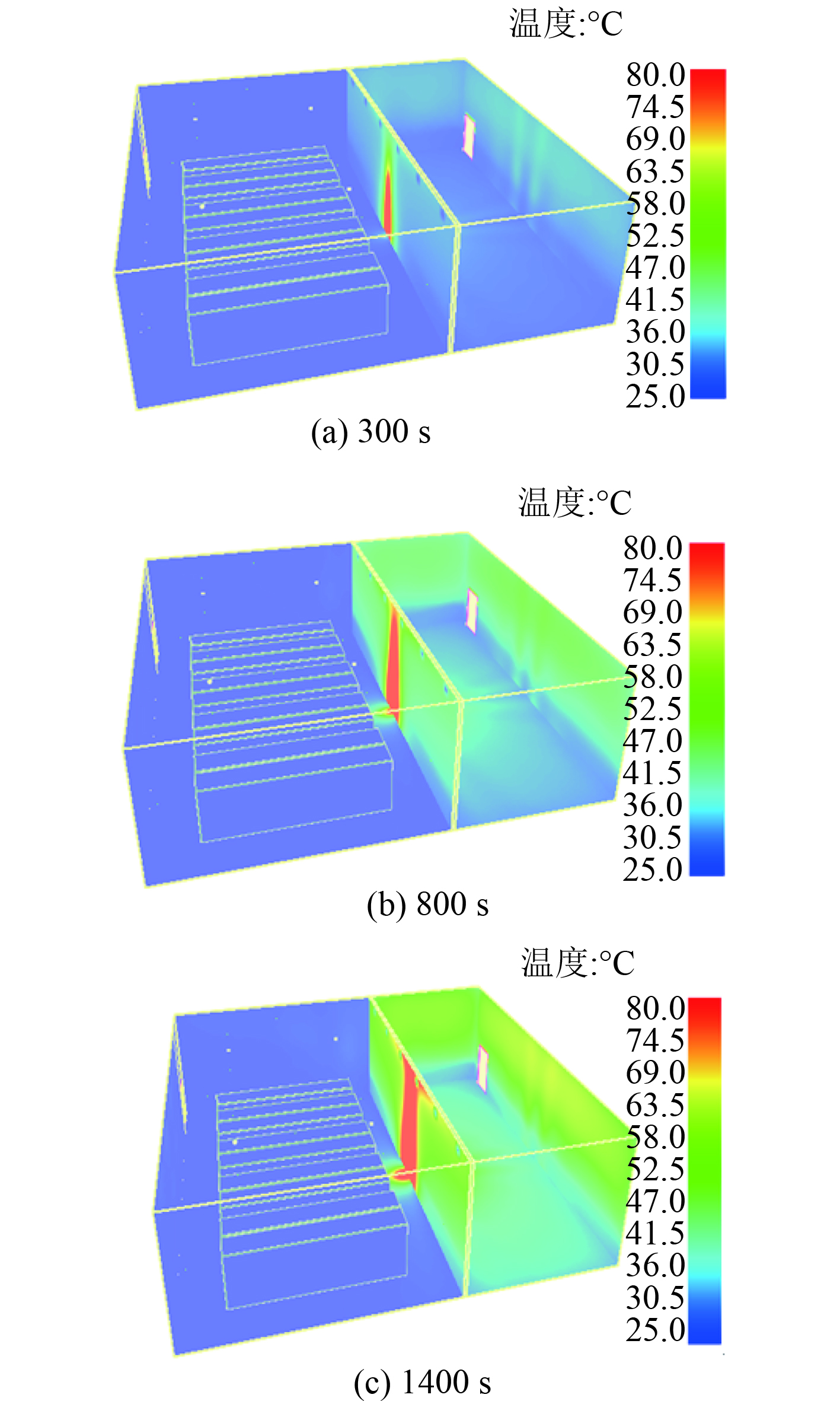
邻舱发生火灾时,各典型时刻的舱室壁面温度如图8所示。由图中可以看出,随着时间的增加,除火源所在房间的壁面外,两舱室相邻的共用壁面温度发生变化,说明火源产生的热量已经通过共用舱壁传入所研究的舱室中,而且共用舱壁面上火源所在位置的背面区域温度较其他区域高。随着时间增加,被研究舱室靠近与邻舱公共壁面中心的地面温度也开始逐渐由所升高,在1 400 s时壁面最高温度在70 ℃以上。
邻舱发生火灾时,各典型时刻研究舱室中各火灾探测器所在高度平面温度云图如图9所示。由图中可以看出,平面上高温源位于靠近公共壁面中部,随着时间的增加,相对高温的区域面积由高温源逐渐向周围扩大,到1 400 s时刻,平面上温度稍有升高,但是在靠近送风口一侧的通风上游区域,温度变化相对不明显,说明邻舱火灾时依靠公共壁面导热将热量传导至研究舱室时,由于热源在通风下游,所以热量在被研究舱室内扩散较慢,尤其是对靠近送风口的通风上游区域,使其升温较为困难。
|
图 7 邻舱火灾时舱室内各温度测点的变化 Fig. 7 Adjacent compartment fire booth the change of temperature measuring point |
|
图 8 邻舱火灾时各典型时刻舱室壁面温度 Fig. 8 Adjacent tank fire for typical cabin wall temperature |

|
图 9 邻舱火灾时测点所在平面的温度云图 Fig. 9 The plane adjacent compartment fire station temperature nephogram |
由于邻舱火源最大火源热释放率300 kW时,所研究舱室内温度变化幅度较小,因此考虑增大火源,来研究邻舱发生较大规模火灾时对研究舱室内的温度影响。假设邻舱火源面积为2.0 m×2.0 m,理论热释放速率为4.8 MW,经过模拟得到的热释放速率输出结果如图10所示。由图中可以看出,火源热释放速率在火灾初期阶段开始迅速上升,在约70 s热释放率达到了4.8 MW,随后在经过较大幅度的波动后,在约90s时刻开始迅速降低,100 s以后热释放率保持在1.5~2.0 MW之间波动,300 s后热释放率曲线呈现逐渐缓慢下降的趋势,到1 500 s时热释放率约1 MW。这是由于火源热释放率过大而舱室空间较小不足以提供燃烧需要的空气,所以不能按设定的释放率燃烧,只能在可提供的空气支持燃烧的范围内保持相对低的热释放率。

|
图 10 邻舱火源面积增大时的热释放速率 Fig. 10 Adjacent compartment fire area increases when the rate of heat release |
邻舱发生火灾时,被研究弹药舱内各温度测点输出随时间的变化如图11所示。由图中可以看出,各测点在约100 s后开始上升,100~200 s期间测点T6稍高于其他测点,约在900 s后各测点温度升高趋势放缓,T2的最高温度可以升至约36 ℃,远离热源壁面并且靠近通风上游一侧的测点T1,T3,T5和T7处的温度开始在32 ℃~35 ℃之间保持波动。
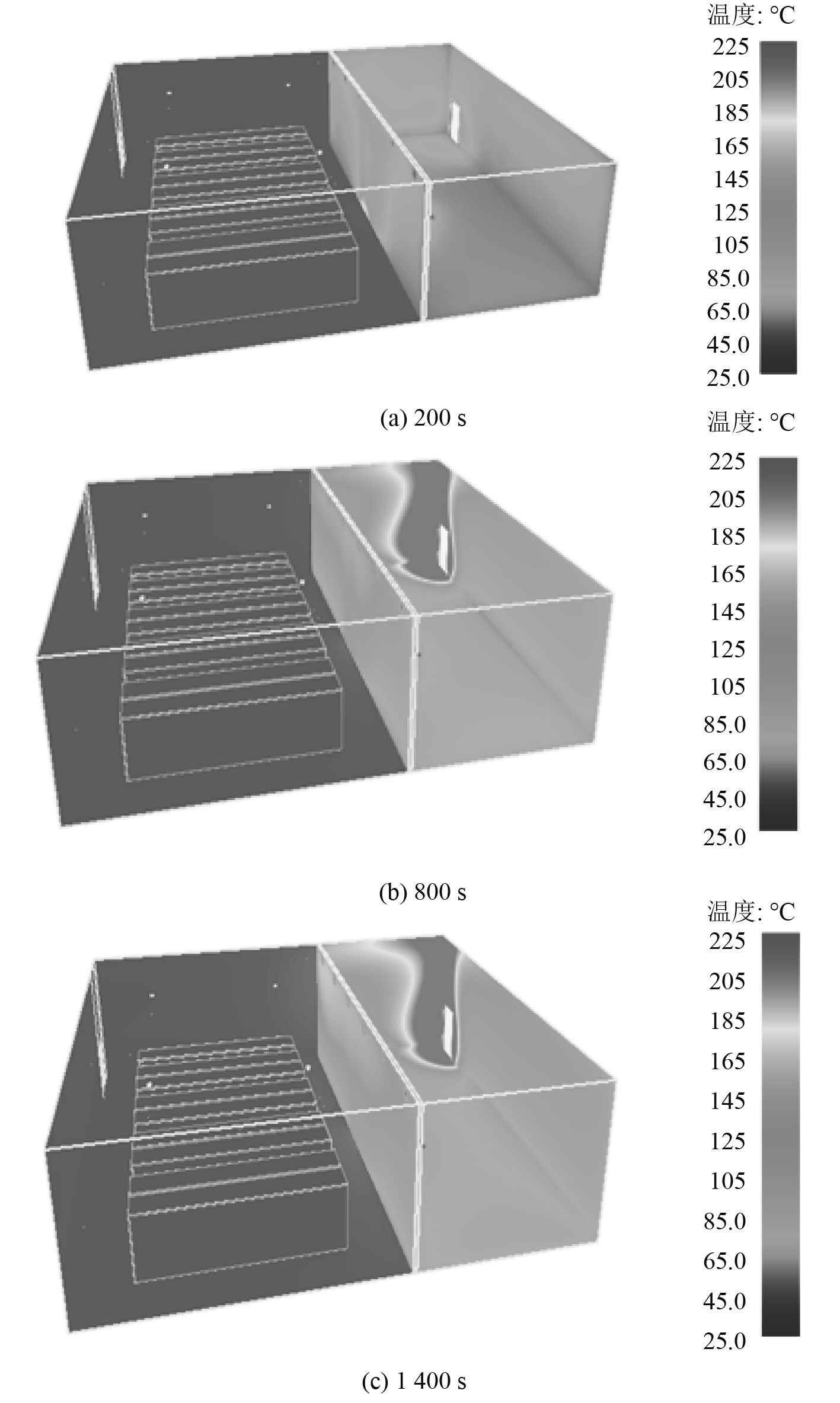
各典型时刻的舱室壁面温度如图12所示。由图中可以看出,随着时间的增加,两舱室相邻的共用壁面温度发生变化,说明火源产生的热量已经通过共用舱壁传入所研究的舱室中,而且共用舱壁面上火源所在位置区域温度较高,可以超过150 ℃。在弹药舱邻舱的火源所在舱室内,火灾发生100 s以后,在舱室门口附近的舱室壁面温度较高,由于舱室内的空气不足以支持如此大规模的火源燃烧,因此火源处有大量未燃烧的燃料气化产物,在接触到舱室门口的新鲜空气时,符合燃烧条件,因此在此区域内又发生燃烧,导致舱室门口附近壁面的温度升高。
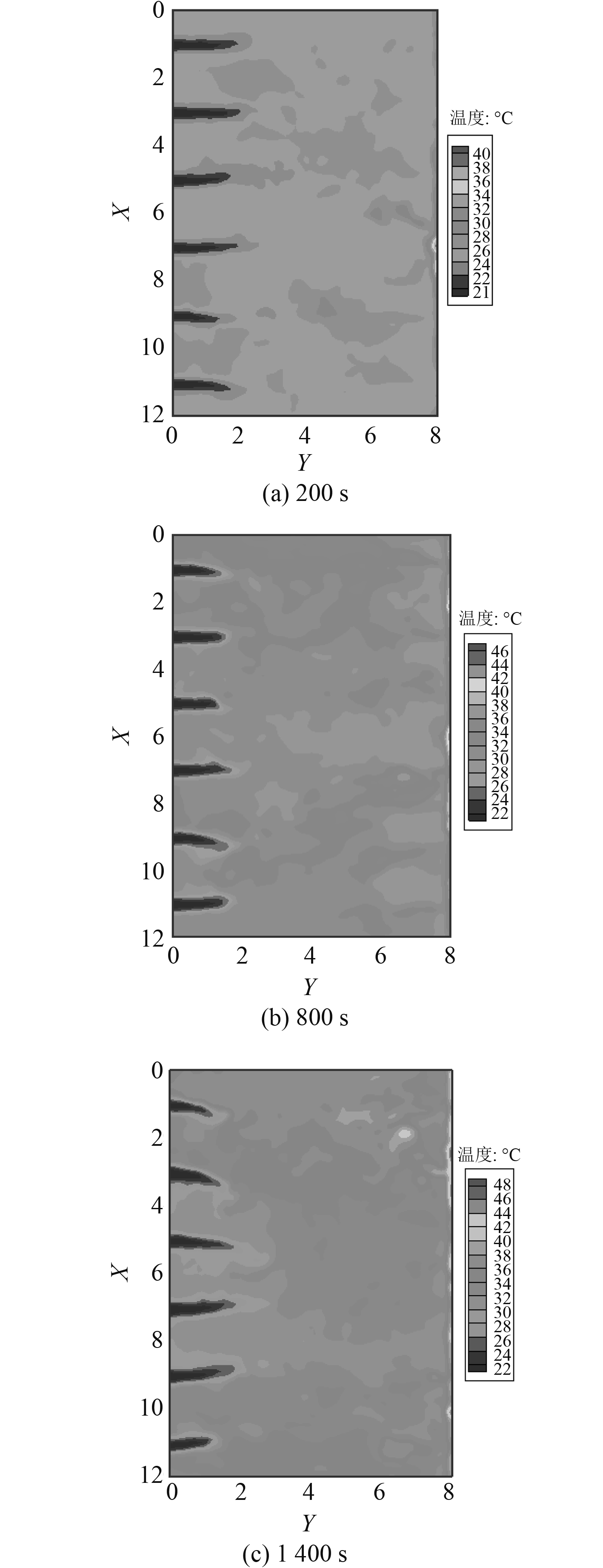
各典型时刻研究舱室中各火灾探测器所在高度平面温度云图如图13所示。由图中可以看出,由通风下游回风口所在的舱室共用壁面温度高温将热量传到舱室内,因此舱室共用壁面附近的区域温度较其他区域的温度高,在火灾后期,高温壁面的影响区域可以影响到舱室中部区域,但整个平面上整体的温度始终保持在未超过50 ℃。

|
图 11 邻舱火源面积增大时舱室内各温度测点的变化 Fig. 11 Adjacent compartment fire area increased booth when the change of temperature measuring point |
|
图 12 邻舱火源面积增大时各典型时刻舱室壁面温度 Fig. 12 Adjacent compartment fire area increases when the typical cabin wall temperature |
|
图 13 邻舱火源面积增大时测点所在平面的温度云图 Fig. 13 Adjacent compartment fire area increases when measuring point temperature contours of the plane |
利用数值方法对邻舱发生火灾时通过公共壁面导热对研究舱室内的温度影响进行模拟,通过对弹药舱内火灾温度参数结果进行分析得到:
1)邻舱火灾的火源面积为0.5 m×0.5 m最大热释放率为300 kW时,火源可以按照设定规律燃烧;公共壁面最高温度在70 ℃以上,研究舱室内各测点温度在1 500 s时升高至28 ℃以上,热量在被研究舱室测点所在高度平面扩散较慢,尤其是对靠近送风口的通风上游区域,使其升温较为困难。
2)邻舱火灾的火源面积为2 m×2 m最大热释放率为4.8 MW时,空间内的氧气不足以支持火源按设定的释放率燃烧,只能在可提供的空气支持燃烧的范围内保持在1~2 MW热释放率,并且在火源所在舱室门开口附近发生了回燃;共用舱壁面上火源所在位置区域温度较高,可以超过150 ℃;被研究弹药舱内各测点在约100 s后开始上升,100~200 s期间测点T6稍高于其他测点,约在900 s后各测点温度升高趋势放缓,T2的最高温度可以升至约36 ℃,远离热源壁面并且靠近通风上游一侧的测点T1,T3,T5和T7处的温度开始在32 ℃~35 ℃之间保持波动。
3)通过3次对比实验验证,火盆大小为0.5 m×0.5 m,燃料用量2 500 ml,燃烧时间为900 s,温度测点的最高温升分别为1.6 ℃,1.2 ℃,1.0 ℃,均没有引起传感器报警,温度上升趋势与仿真计算结果基本相吻合。伴随燃料用量及燃烧时间的增加,被研究舱室温度测点的温升也相应增加。
| [1] |
李玉峰, 张宏, 霍岩. 有通风弹药舱内慢速火灾特性数值研究[J]. 舰船科学技术, 2015, 37(12): 160–165.
LI Yu-feng, ZHANG Hong, HUO Yan. Numerical studies have slow fire ventilation ammunition hold characteristics [J]. Journal of Marine Science and Technology, 2015, 37 (12) : 160–165. |
| [2] |
霍岩. 有限开口空间热驱动流大涡模拟和实验研究[D]. 哈尔滨: 哈尔滨工程大学, 2010: 8–15.
HUO Yan. Limited open space thermal drive current large eddy simulation and experimental research [D]. Harbin: Harbin Engineering University, 2010: 8–15. |
| [3] |
邹高万. 船舶机舱火灾热流场特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2005: 86–97.
ZOU Gao-wan. Ship engine room fire heat flow field characteristics research [D]. Harbin: Harbin Engineering University, 2005: 86–97. |
| [4] | MCGRATTAN K B, HOSTIKKA S, FLOYD J E, et al. Fire dynamics simulator (Version 5), technical reference guide[M]. NIST Special Publication 1018–5, National Institute of Standards and Technology, Gaithersburg, Maryland, January 2007. |
| [5] | SMAGORINSKY J. General circulation experiments with the primitive equations[J]. Monthly Weather Review, 1963, 91(3): 99–164. |
| [6] | WANG H Y, COUTIN M, MOST J M. Large-eddy simulation of buoyancy-driven fire propagation behind a pyrolysis zone along a vertical wall[J]. Fire Safety Journal, 2002, 37(3): 259–285. |
| [7] | MCGRATTAN K B. Computational fluid dynamics and fire modeling[R]. NIST Technical Report Class2002, National Institute of Standards and Technology, 2001: 1–50. |
| [8] | INCROPERA F P, DEWITT D P. Introduction to Heat Transfer. Third Edition [M]. New York: John Wiley & Sons, 1996: 595–715. |
| [9] |
卞伯绘. 辐射换热的分析与计算[M]. 北京: 清华大学出版社, 1988: 244–315.
BIAN Bo-hui. Analysis and calculation of radiation heat transfer [M]. Beijing: Tsinghua University Press, 1988: 244–315. |
| [10] | FLOYD J E, MCGRATTAN K B, HOSTIKKA S, et al. CFD fire simulation using mixture fraction combustion and finite volume radiative heat transfer[J]. Journal of Fire Protection Engineering, 2003, 13(1): 34–34 |
 2018, Vol. 40
2018, Vol. 40
