2. 哈尔滨工程大学 青岛船舶科技有限公司,山东 青岛 266400
2. Harbin Engineering University, Qingdao Ship Science and Technology Co, Ltd, Qingdao 266400, China
舰载飞机与陆基飞机的着陆相比,在飞行甲板上着舰更为困难[1–2]。着舰环境涉及舰船的运动和海上的大气紊流扰动[3],在这种扰动环境下,舰载机必须精确控制航迹,保持合适的速度、姿态以及相对舰船的位置,对准着舰甲板中心线,在预定着舰点啮合,才能安全实施拦阻着舰[4]。本文将美国海军舰载机作为参考对象,综合考虑各种扰动对舰载机着舰的影响,设计一种飞机进舰着舰的控制系统,并通过仿真得到飞机着舰终端误差进而分析飞机的下落点的分布。
1 舰载飞机着舰环境数学建模飞机着舰时,舰尾大气扰动分为以下4部分:自由大气紊流分量u1,v1,w1;尾流稳态分量(雄鸡尾流)u2,w2;尾流的周期分量u3,w3;尾流的随机分量u4,v4,w4。设甲板风水平尾流为ug,横向尾流为vg,垂直尾流为wg,则
| $\left\{ \begin{aligned}& {u_g} = {u_1} + {u_2} + {u_3} + {u_4}\text{,}\\& {v_g} = {v_1} + {v_4}\text{,}\\& {w_g} = {w_1} + {w_2} + {w_3} + {w_4}\text{。}\end{aligned} \right.$ | (1) |
1)自由大气紊流分量
自由大气紊流分量u1,v1,w1与飞机相对于舰的位置无关,美国军标规定其空间功率谱:
| $\left\{ \begin{aligned}& {S_{{u_1}}}(\varOmega ) = \frac{{200}}{{1 + {{(100\varOmega )}^2}}}(\frac{{{{(ft/s)}^2}}}{{rad/ft}})\text{,}\\& {S_{{v_1}}}(\varOmega ) = \frac{{939[1 + {{(400\varOmega )}^2}]}}{{[1 + {{(1000\varOmega )}^2}][1 + {{(\frac{{400}}{3}\varOmega )}^2}]}}(\frac{{{{(ft/s)}^2}}}{{rad/ft}})\text{,}\\& {S_{{w_1}}}(\varOmega ) = \frac{{71.6}}{{1 + {{(100\varOmega )}^2}}}(\frac{{{{(ft/s)}^2}}}{{rad/ft}})\text{。}\end{aligned} \right.$ | (2) |
本文仅对自由大气紊流的水平分量u1及垂直分量w1对飞机轨迹运动的影响进行仿真研究,将它的空间功率谱形式S1(Ω)转化为时间功率谱S2(ω),可求得u1,w1在时间域中的有色大气紊流。

|
图 1 自由大气紊流仿真结果 Fig. 1 Atmospheric turbulence simulation results |
2)舰船尾流的稳态分量
舰尾气流是由于舰船迎风行驶,空气从其平坦的舰尾流出而造成的,其特点是在垂直方向产生一种特有的雄鸡尾形状的风力,其风向与距舰尾的距离有关。通过数据拟合,可得到雄鸡尾流模型的5阶多项式拟合的数学表达式:
| $\begin{split}{u_2}(t) = & - 0.0072{t^5} + 0.1137{t^4} - 0.5910{t^3} +\\ & 1.3552{t^2} - 0.6400t + 1.1715\text{,}\end{split}$ | (3) |
| $\begin{split}{w_2}(t) = & - 0.0001{t^5} - 0.0066{t^4} + 0.0698{t^3} +\\ & 0.3389{t^2} - 2.6679t - 0.1149\text{。}\end{split}$ | (4) |
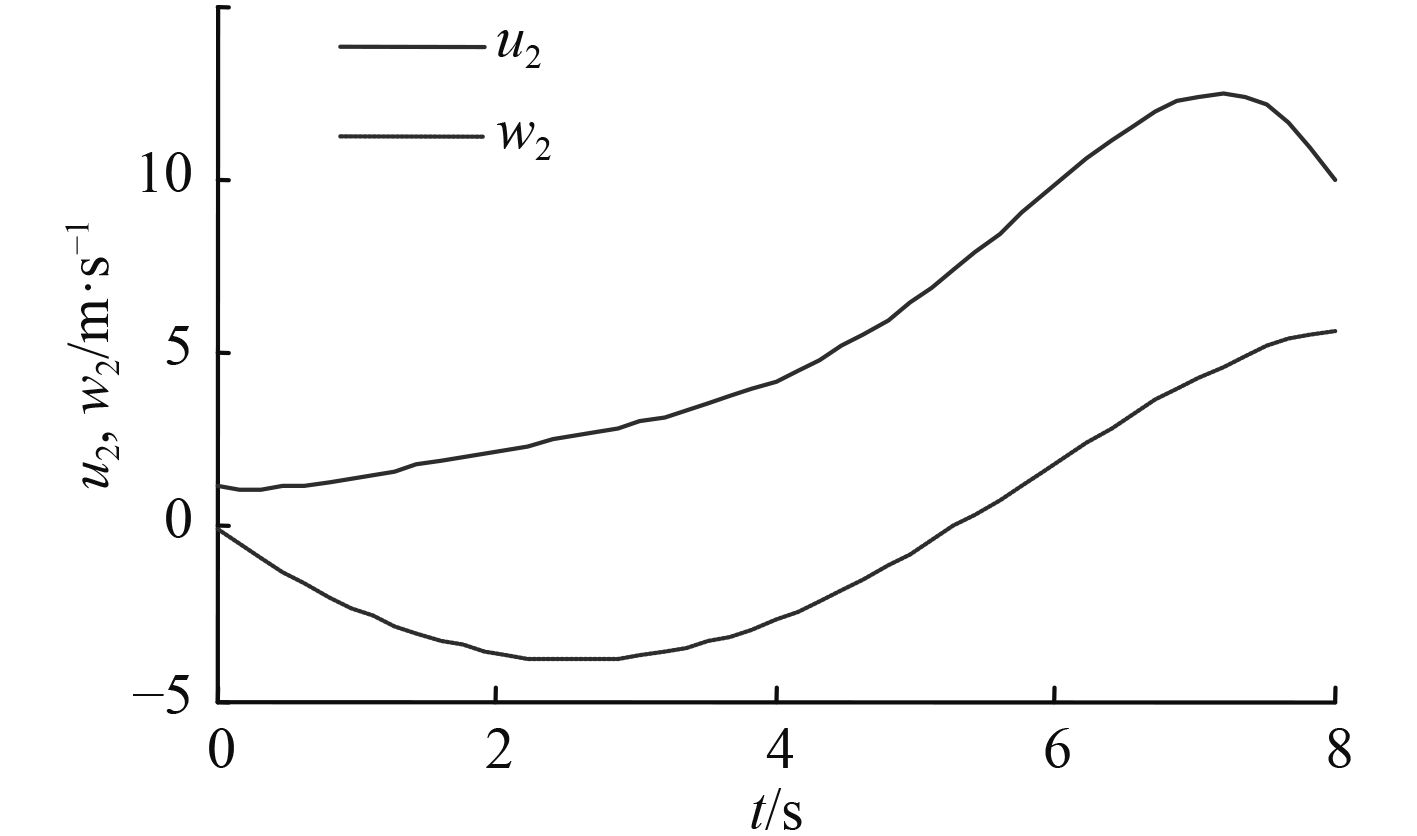
|
图 2 雄鸡尾气流仿真结果 Fig. 2 Cocktail air flow simulation results |
3)舰船尾流的周期分量
舰船纵摇产生的尾流是由于甲板的俯仰运动而形成的风力。它随舰的纵摇频率、纵摇大小、甲板上的风力以及飞机离舰的距离而变化,如下所示:
| ${u_3} = {\theta _s}{V_{w/d}}(2.22 + 0.0009X)C\text{,}$ | (5) |
| ${w_3} = {\theta _s}{V_{w/d}}(4.98 + 0.0018X)C\text{。}$ | (6) |
式中:
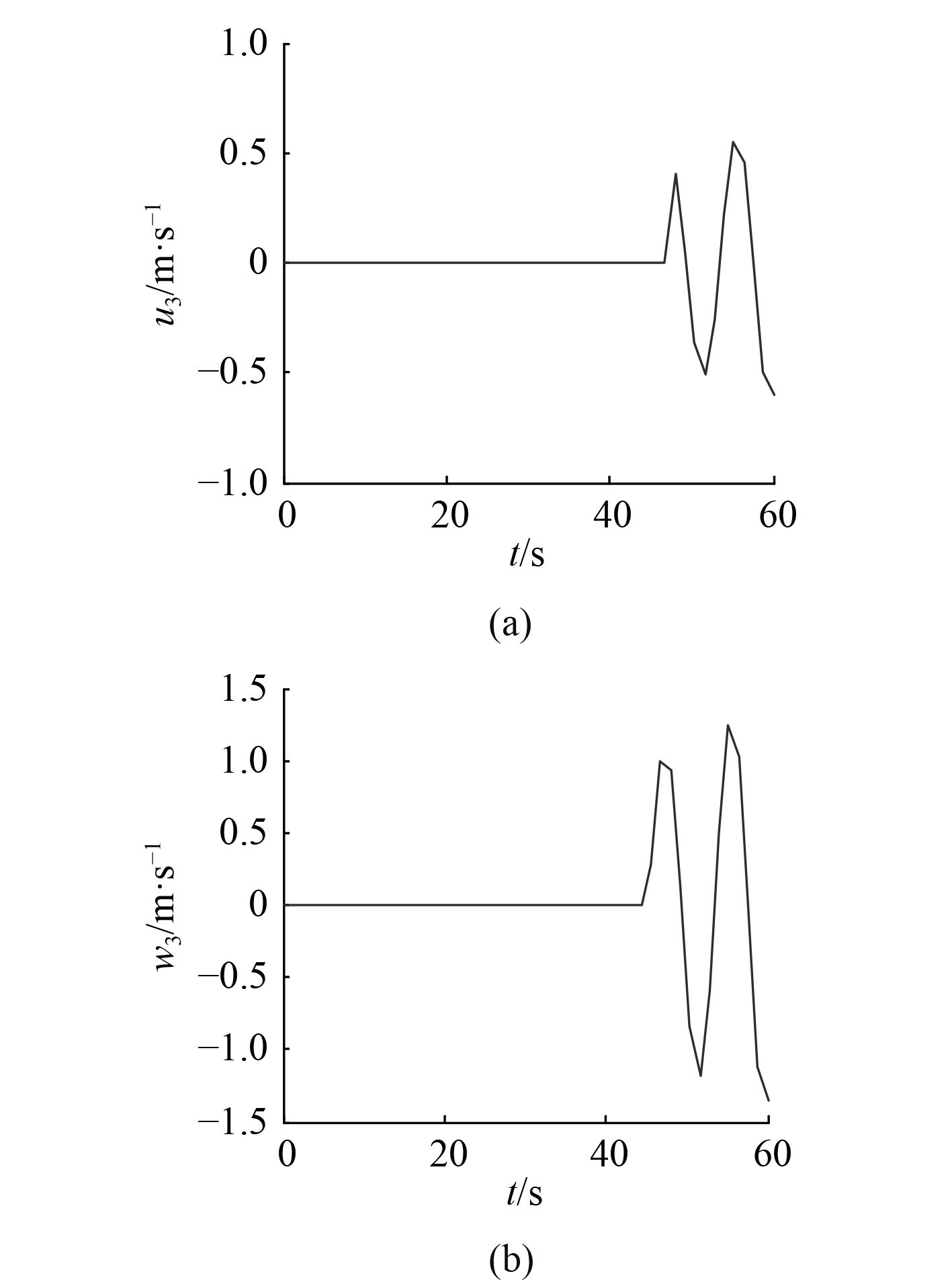
|
图 3 舰尾流周期分量仿真结果 Fig. 3 Periodic components of carrier air wake simulation results |
4)舰船尾流的随机分量
舰船尾流的随机分量如下所示:
| ${G_{{u_4}}}(s) = \frac{{\sigma (X)\sqrt {2\tau (X)} }}{{\tau (X)s + 1}}\text{,}$ | (7) |
| ${G_{{w_4}}}(s) = \frac{{0.035{V_{w/d}}\sqrt {6.66} }}{{3.33s + 1}}\text{。}$ | (8) |
式中σ(X)为与距离
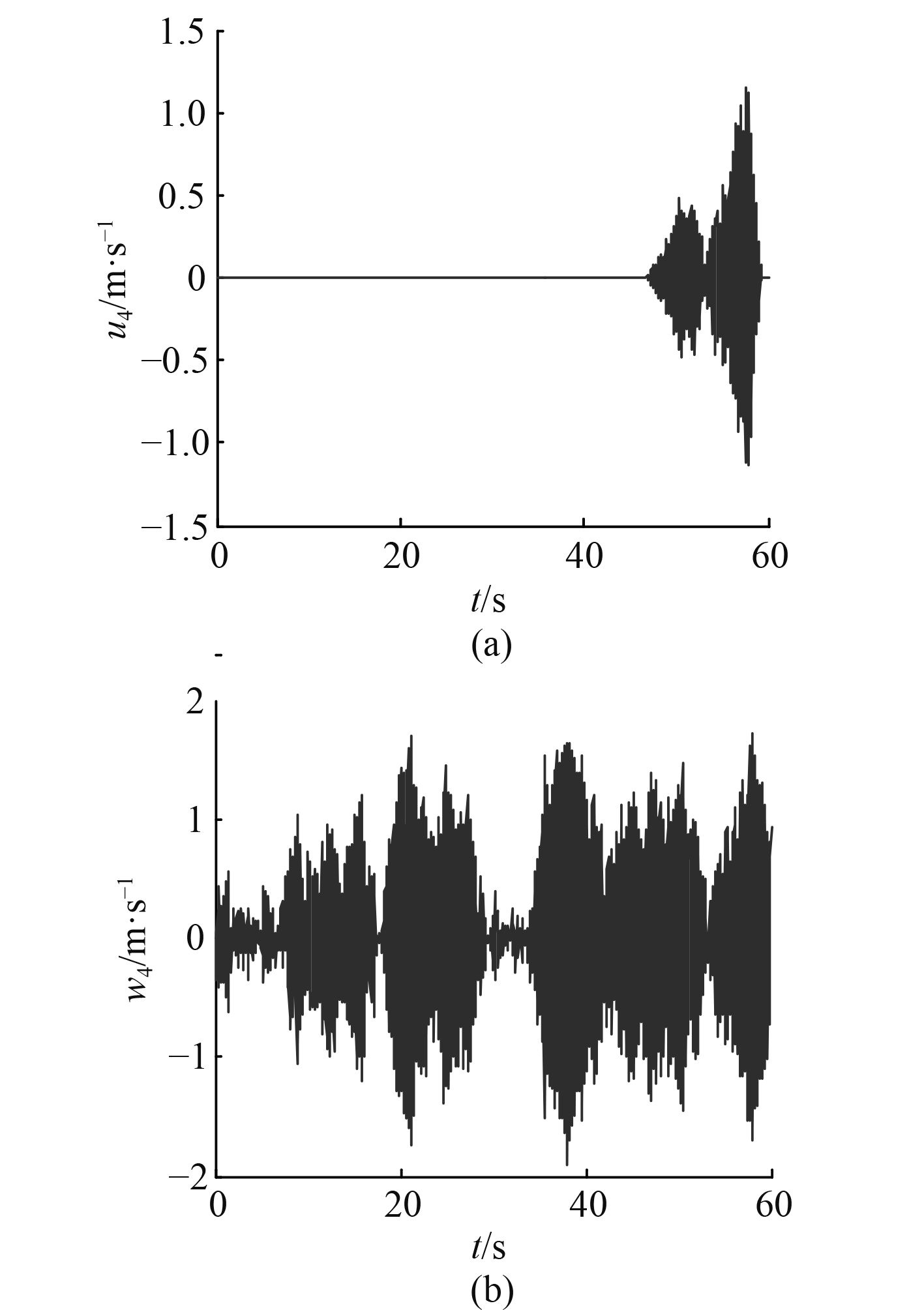
|
图 4 舰船尾流随机分量仿真结果 Fig. 4 Random components of warship wake simulation results |
取航母纵摇幅度设为1°,纵摇峰值频率0.6 rad/s,可以通过将上述的舰尾流4个分量模型叠加,生成舰载机进舰着舰前25 s内受到的紊流速度的大小,如图5所示。
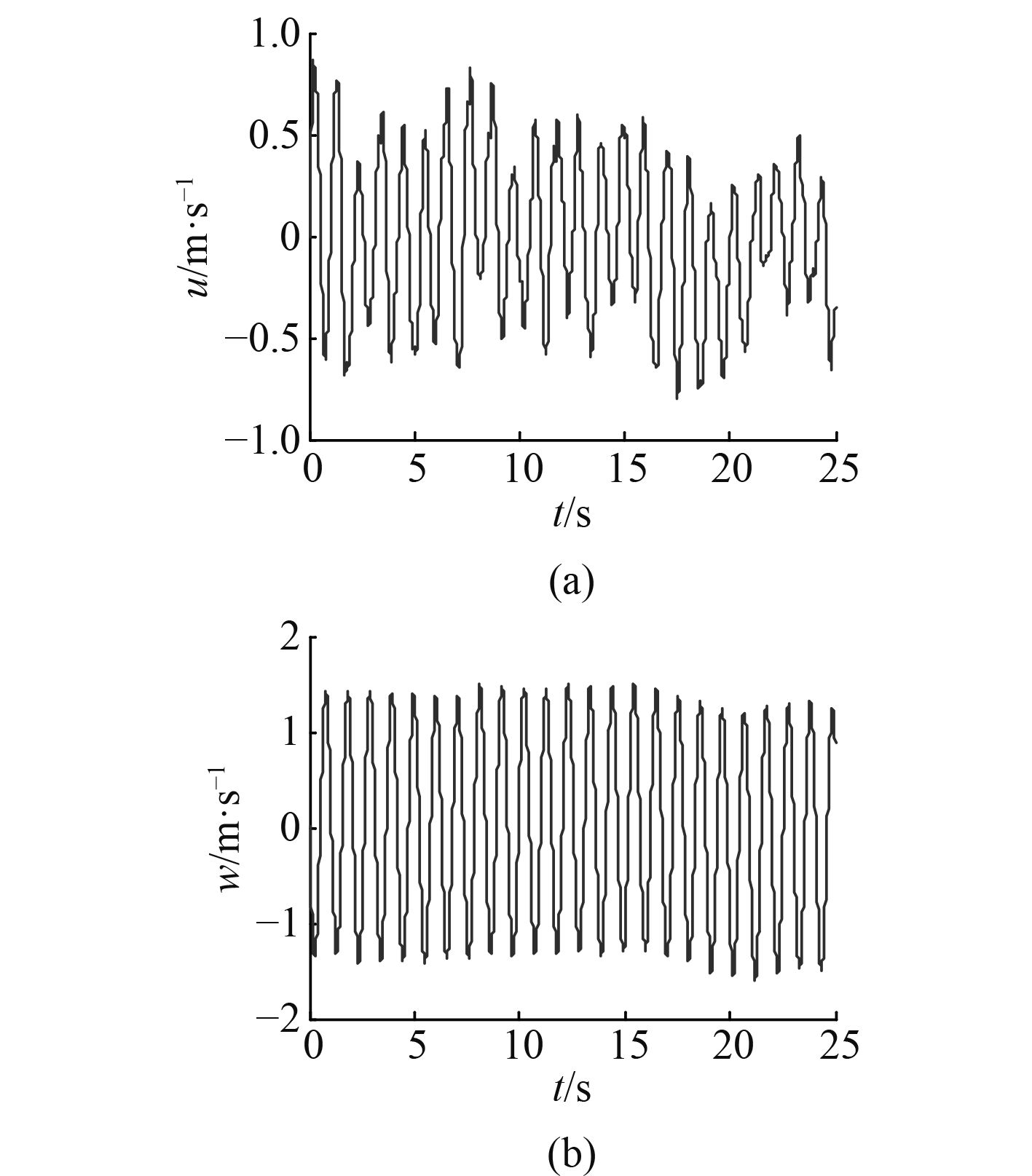
|
图 5 舰尾流水平和垂直速度分量 Fig. 5 Horizontal and vertical velocity components of warship wake simulation results |
当飞机装备有纵向增稳/控制增稳系统时,飞机的纵向稳定性、操纵性和机动性得到了有效的改善,使自动驾驶仪具有良好的稳定性、响应特性和控制精度[6]。图6给出了俯仰姿态保持的原理方框图。

|
图 6 俯仰姿态保持原理方框图 Fig. 6 Pitch attitude maintaining block diagram |
本文采用高度变化率指令控制下的飞行控制系统。由于内环的俯仰角速度的指令响应必须具备较高的增益和一定的超前,所以除了增大前向通道中的增益kωzc之外,还在俯仰角速度反馈回路中引入滞后一超前滤波器,使整个内环在相应的频率范围内具有一定的相位超前。由比例-积分控制器构成的动态补偿器Gc(s)提供快速、准确的俯仰角速度响应,从而保证整个系统有较好的高度变化率控制能力。外环引入航迹角γ和纵向过载ny作为反馈,达到对高度变化率的精确控制,对于舰载机克服下滑道中的舰尾流更有利[7]。
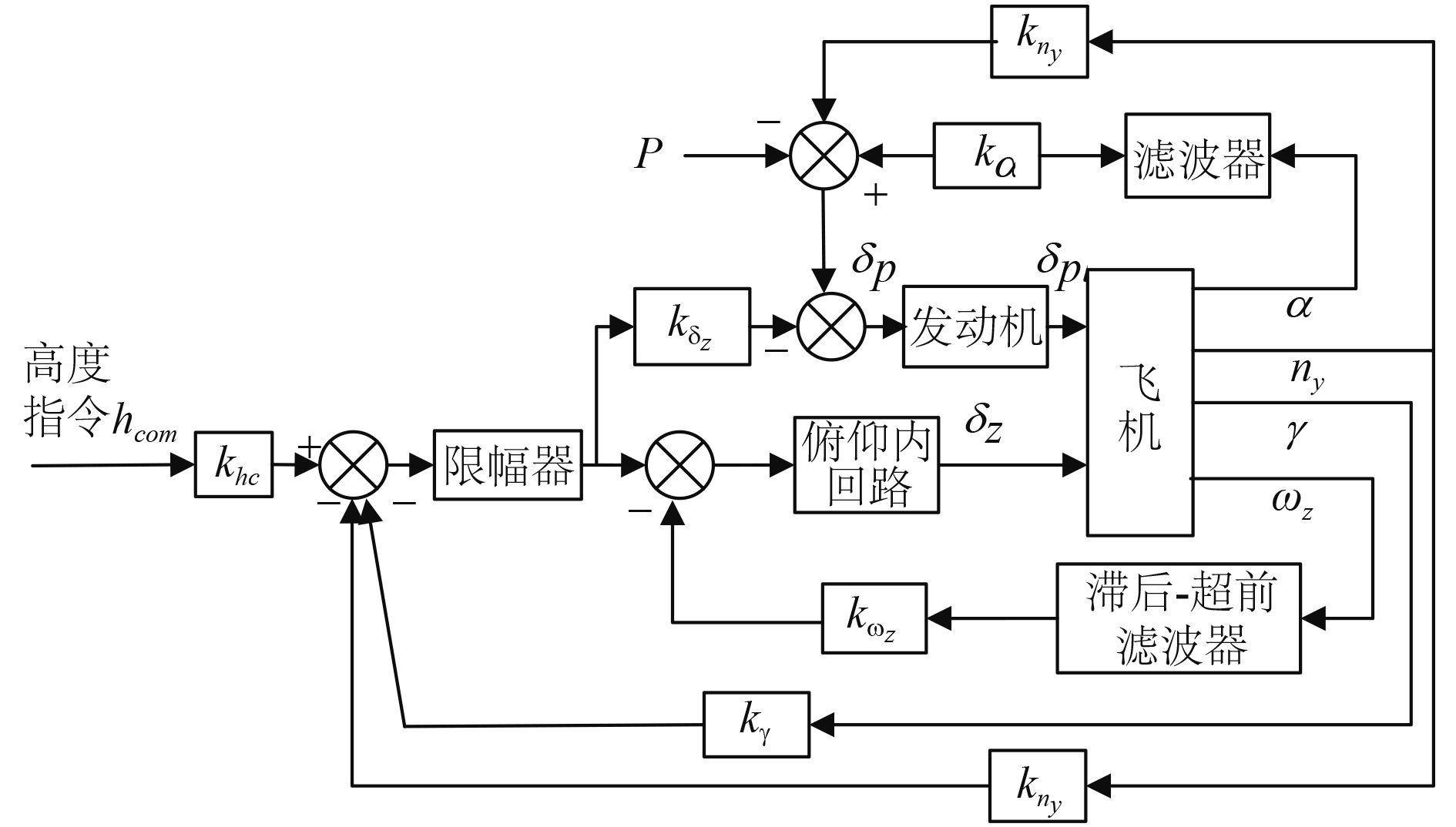
2.2 动力补偿系统为消除舰载机进舰着舰时的“速度不稳定”现象,引入油门控制。通过油门控制保持空速和迎角,使俯仰角变化将直接转化为航迹角变化。自动动力补偿系统(APCS)的控制目标是保持空速和迎角不变,通过反馈飞机的迎角α和纵向过载ny,并与高度控制指令飞行控制系统交联来实现的,如图7所示。
|
图 7 舰载机APCS交联结构框图 Fig. 7 Carrier aircraft APCS crosslink structure diagram |
根据参考文献[8],飞行员的数学模型为:
| ${Y_p} = {k_p} \cdot {e^{ - \tau s}}\frac{{({T_L} \cdot s + 1)}}{{({T_l} \cdot s + 1)({T_N} \cdot s + 1)}}\text{。}$ | (9) |
式中:τ为飞行员开始反应的时间常数;TN为飞行员动作滞后时间常数;kp为飞行员增益;TL为飞行员超前时间常数;Tl为飞行员滞后时间常数。
由于舰载飞机在进场着舰过程中,由飞行员和等效飞机所构成的高度回路具有低频特性,即使是由直接力构成的高度回路,其频带也只有1 rad/s左右。所以飞行员的开始反应时间τ及动作滞后时间TN在此频带内几乎不起作用,从而描述飞行员的传递函数可简化为用单一的比例环节来表示[9]:
| ${Y_p} = {k_p}\text{。}$ | (10) |
本文以参考文献给出的航母运动模型为例:ESSEX级航母,航速15.3 m/s,航向左舷60°,浪高5.18 m,海况主要为浪涌[10]。仿真在舰船速度为20 kn,即10.2 m/s航速时角稳定和点稳定2种方式下的落点分析。
3.1 角稳定
|
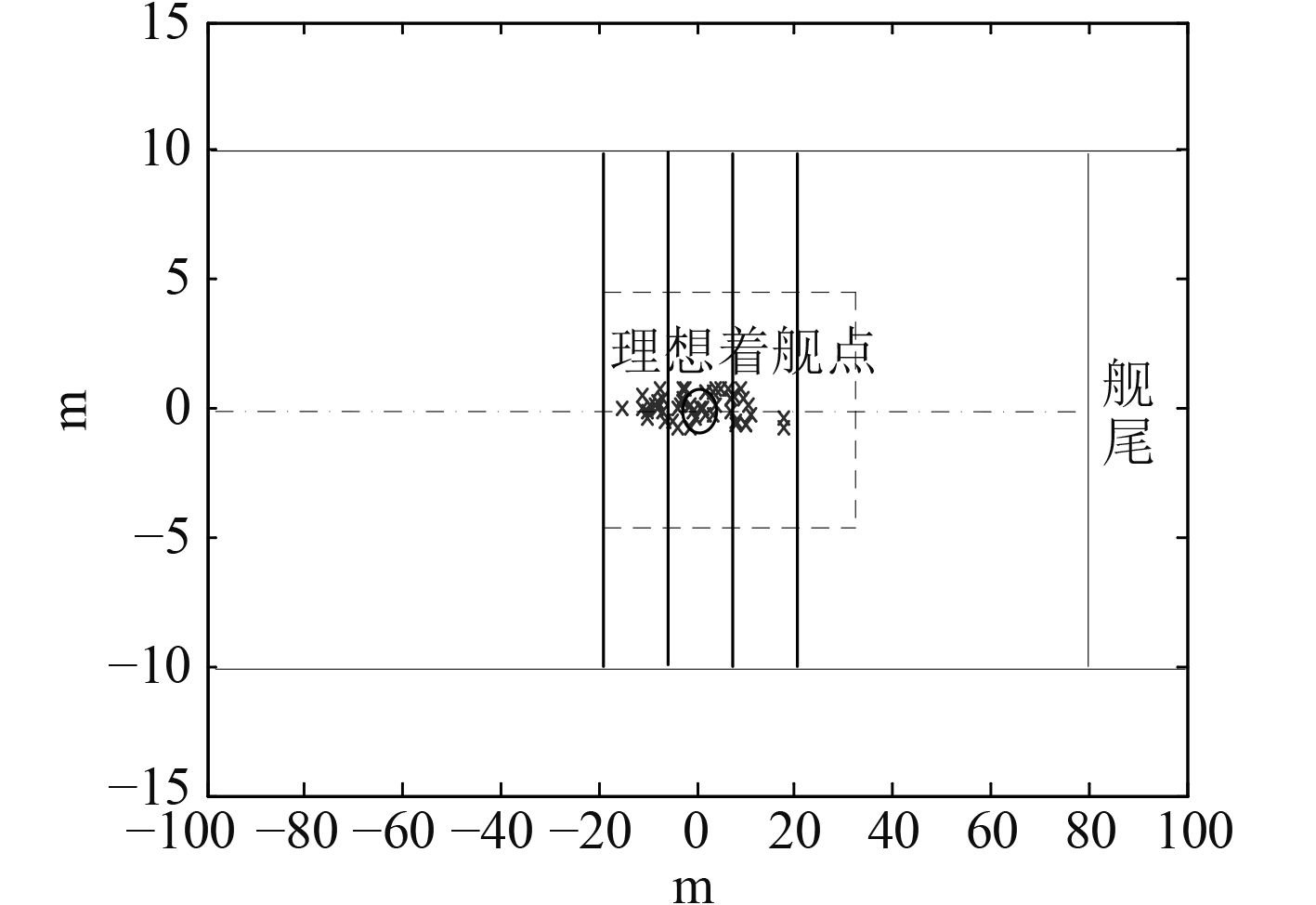
图 8 角稳定飞机落点分布图 Fig. 8 Angle stable carrier aircraft landing point distribution |
|
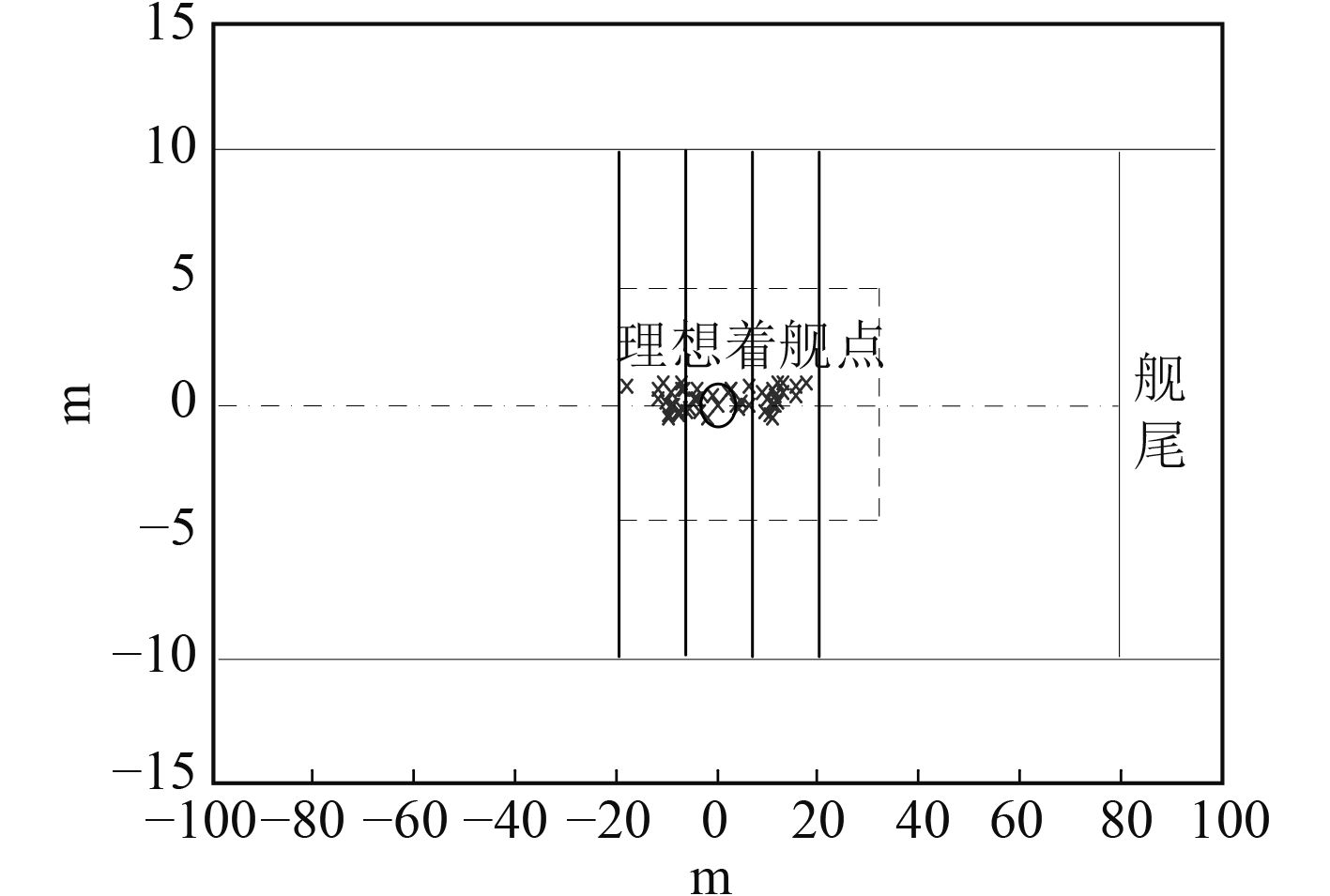
图 9 点稳定飞机落点分布图 Fig. 9 Point stable carrier aircraft landing point distribution |
着舰终端误差:σ(ΔhTD)=3.99 m,σ(ΔhR)=2.47 m,σ(ΔVTD)=2.14 m/s。
对于多次着舰仿真试验,考察舰载机下落点分布问题,得到如图8所示结果。由飞机多次着舰落点来看,飞机落点很大一部分分布在11 m之间。只有个别点接近20 m处及–18 m处,但是飞机大部分落点相对集中,着舰安全性较高。
3.2 点稳定着舰终端误差:σ(ΔhTD)=5.95 m,σ(ΔhR)=3.38 m,σ(ΔVTD)=4.64 m/s。
如图9所示,由飞机多次着舰落点来看,飞机落点基本大部分分布在–16 m~19 m之间,5 m~15 m与–5 m~–15 m范围之间较多。飞机所有落点都在20 m之内,但是有个别的落点已经接近20 m,着舰安全性降低。飞机落点分布范围较大,与理想着舰点之间的偏差更大。
4 结 语本文在Matlab/Simulink的仿真环境下建立了飞机进舰着舰导引控制系统的仿真模型。舰载机根据飞控系统的操纵指令及当时的飞行状态参数和风速计算生成下一时刻的飞行状态参数,并将输出高度反馈给光波束运动的实际高度,计算高度偏差,继续引导飞机下滑。最终由仿真结果给出了舰载飞机着舰系统的终端误差以及飞机在角稳定和点稳定2种导引方式引导下的落点分布。
| [1] | 贾新强, 林鹏, 王敏文, 等. 舰载机着舰甲板运动误差及其补偿仿真研究[J]. 航空计算技术, 2010, 1: 114–118. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkjsjs201001029 |
| [2] | 刘育. 环境扰动下的舰载机着舰响应分析与建模[J]. 舰船科学技术, 2017, 39(11A): 066. http://www.cnki.com.cn/Article/CJFDTotal-JSJZ201411016.htm |
| [3] | 许东松, 刘星宇, 王立新. 航母运动对舰载飞机着舰安全性的影响[J]. 北京航空航天大学学报, 2011, 37(3): 289–294. |
| [4] | 王延刚, 屈香菊. 舰载机进舰着舰过程仿真建模[J]. 系统仿真学报, 2008, 20(24): 6592–6594. http://www.cqvip.com/QK/95956X/201010/35495781.html |
| [5] | 申安玉, 申学仁, 李云保. 自动飞行控制系统[M]. 北京: 国防工业出版社, 2003: 48–64. |
| [6] | 郭锁凤, 申功璋, 吴成富. 先进飞行控制系统[M]. 北京: 国防工业出版社, 2003: 201–224. |
| [7] | HUFF R W, KESSLER G K. Enhanced displays, flight controls and guidance systems for approach and landing. AD/A244 869. 1978: 341–402. |
| [8] | 杨京. 舰载飞机着舰导引特殊技术研究[D]. 南京: 南京航空航天大学, 2000. |
| [9] | DURAND T S, TEPER G L. An analysis of terminal flight path control in carrier landing. AD606040. 1964: 9–13. |
| [10] | POWELL F, THEOCLITUS T. Study of an automatic carrier landing environment with the AN/SPN-10 landing control central. AD462348. 1965: 123–154. |
 2018, Vol. 40
2018, Vol. 40
