0 引　言

舰艇、飞机、导弹等平台常采用惯性导航系统（Inertal Navigation System，INS）与GPS（Global Positioning System）组合的方式进行导航定位，该方法可以提供精度相对较高的速度、位置信息，但对于某些对姿态信息要求较高的情况，需寻求新的解决方案^{[1 – 3]}。

天文导航系统（Celestial Navigation System，CNS）通过天体敏感器进行天体方位信息测量并经过解算输出载体的姿态信息，具有测量精度高、误差不随时间积累、可靠性高的特点，是一种较常用的姿态测定方法，但该方法受环境因素影响较大，输出导航信息不连续^{[4 – 5]}。

为改善INS/GPS的姿态精度低、误差随时间发散的问题，同时发挥CNS的优势，将INS/GPS与CNS进行组合是目前的研究热点，张科和吴坤峰分别设计了2类INS/GPS/CNS组合滤波算法，并进行仿真研究，但由于条件所限，2人未进行实物试验^{[6 – 7]}。

本文提出一种基于INS/GPS/CNS的联邦滤波算法，根据联邦滤波的特点，通过设计INS/CNS子滤波器、INS/GPS子滤波器和INS/GPS/CNS主滤波器，在有天文信息的情况下，进行3组合解算，在无天文的情况下，进行2组合解算，提高算法的稳定性和精度，并通过研制的INS/GPS/CNS组合测姿系统进行试验验证，验证了INS/GPS/CNS组合算法姿态精度和稳定收敛性，使系统姿态精度得到了很大的提高。

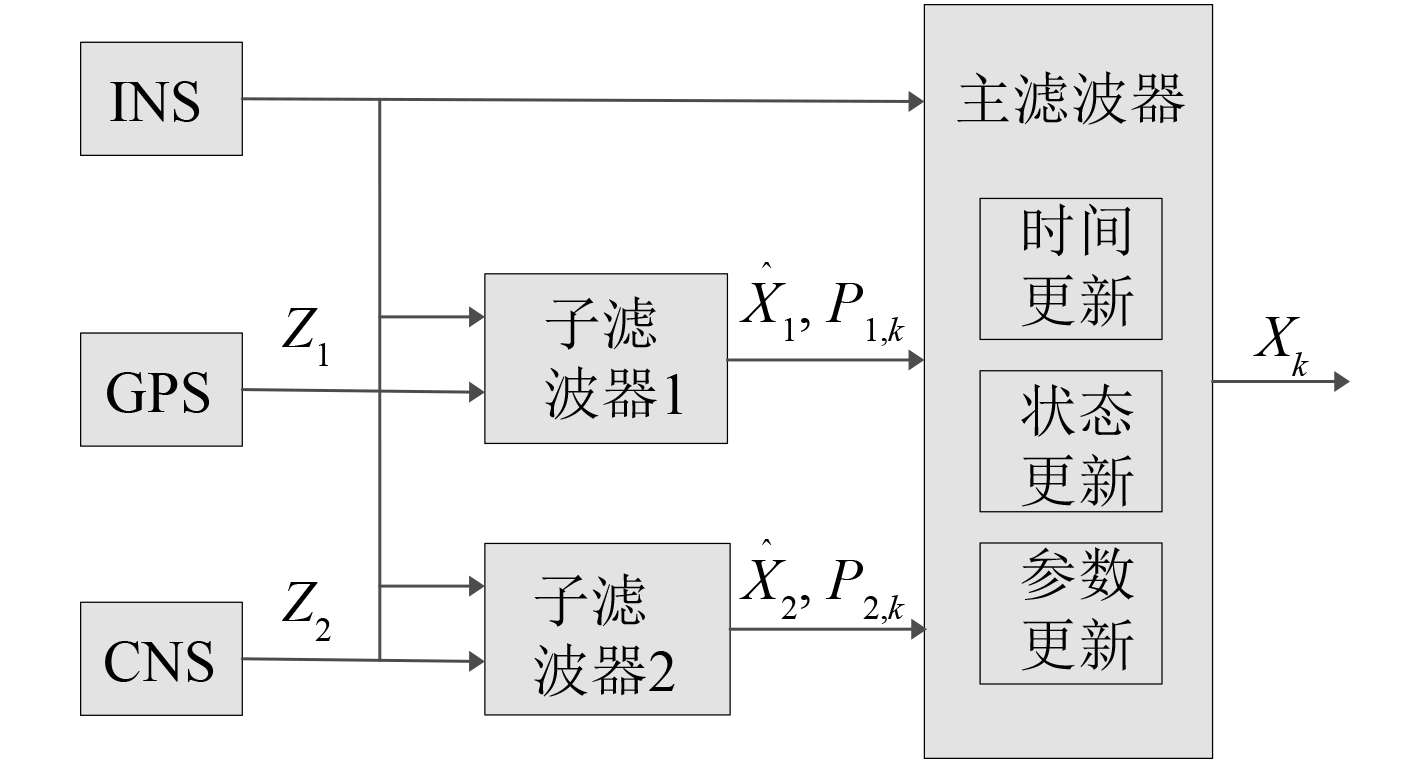
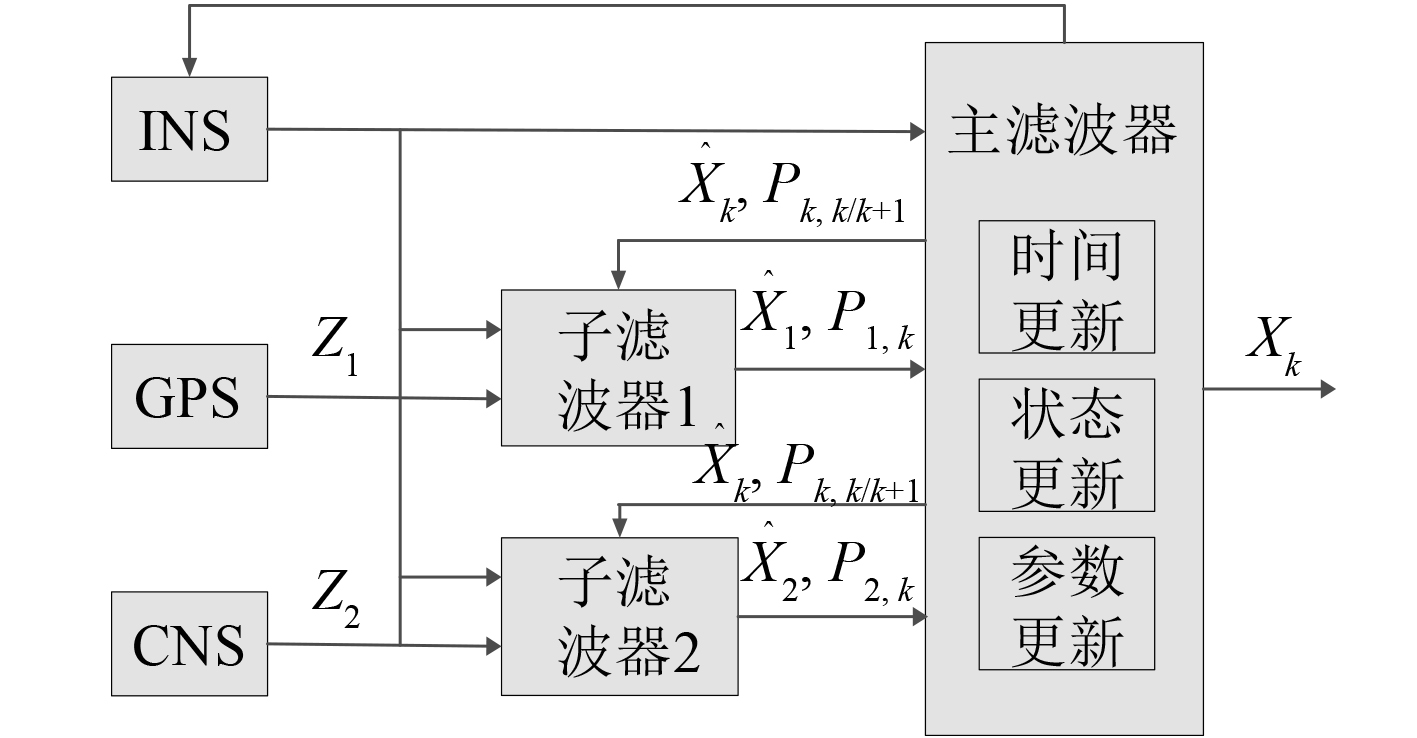
1 INS/GPS/CNS联邦滤波模型

联邦滤波器是Carlson提出^[8]，利用信息分配原则消除各子状态估计的相关联性，设计简单、容错性强，利用较小的计算量就可以获得全局最优或次优估计。根据信息分配策略的不同，联邦滤波器一般分为无复位方式和有复位方式2种。其中，无复位方式各子滤波器独立滤波，主滤波器只进行子滤波器滤波结果的简单融合，具有容错能力强的特点，但该方案精度取决于导航设备精度，要获得较高的姿态精度，对INS、GPS和CNS精度要求较高，方案结构如图1所示。有复位方式相对于无复位方式增加了主滤波器滤波结果对子滤波器的反馈校正，所以该方案精度较高，但可能会引起各滤波器之间的交叉污染，容错性能较低，方案结构如图2所示。

由于系统采用的导航设备精度很高，所以，本文算法采用无复位方式，以INS作为公共参考系统，GPS和CNS作为辅助系统进行方案设计。

2 基于INS/GPS/CNS的联邦滤波算法

联邦滤波算法基于卡尔曼滤波算法，状态参数包含导航系统误差（位置误差、速度误差和姿态误差）和惯性器件误差（陀螺误差和加速度计误差）。导航坐标系取当地地理坐标系，XYZ轴分为指向地理坐标系的东北天方向。

2.1 系统状态方程

根据文献[9]，建立如下状态方程：

1）速度误差方程

$\begin{aligned}\delta {{{\dot{ V}}}^n} = & {{{f}}^n} \times {{{\varphi }}^n} - \left( {2{{\omega }}_{ie}^n + {{\omega }}_{en}^n} \right) \times \delta {{{V}}^n} + \\ &{{{V}}^n} \times \left( {2\delta {{\omega }}_{ie}^n + \delta {{\omega }}_{en}^n} \right) + {\nabla ^n}\text{，}\end{aligned}$

(1)

式中： $i$ 为惯性坐标系； $e$ 为地球坐标系； ${{{f}}^n}$ 为加速度计测得的比力在导航系中的投影； $\delta {{{V}}^n} = $ $ {\left[ {\delta {V_E}\;\,\delta {V_N}\;\,\delta {V_U}} \right]^{\rm{T}}}$ 为东、北、天向的速度误差； ${{{\varphi }}^n} = $ ${\left[ {{\varphi _E}\;\,{\varphi _N}\;\,{\varphi _U}} \right]^{\rm{T}}}$ 为东、北、天向的平台失准角； ${\nabla ^n}$ 为加速度计零偏在导航坐标系中的投影； ${\omega _{en}}$ 为牵连角速度； ${\omega _{ie}}$ 为地球自转角速度。有

${{\omega }}_{ie}^n = {\left[ {\begin{array}{*{20}{c}} 0&{{\omega _{ie}}\cos L}&{{\omega _{ie}}\sin L} \end{array}} \right]^{\rm{T}}}\text{，}$

(2)

${{\omega }}_{en}^n = {\left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{{{V_N}}}{{R + h}}}&{\displaystyle\frac{{{V_E}}}{{R + h}}}&{\displaystyle\frac{{{V_E}}}{{R + h}}\tan L} \end{array}} \right]^{\rm{T}}}\text{，}$

(3)

$\delta {{\omega }}_{ie}^n = {\left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _{ie}}\sin L\delta L}&{{\omega _{ie}}\cos L\delta L} \end{array}} \right]^{\rm{T}}}\text{，}$

(4)

$\delta {{\omega }}_{en}^n = \left[ {\begin{array}{*{20}{c}} { - \displaystyle\frac{{\delta {V_N}}}{{R + h}} + \frac{{{V_N}\delta h}}{{{{\left( {R + h} \right)}^2}}}} \\ {\displaystyle\frac{{\delta {V_E}}}{{R + h}} - \frac{{{V_E}\delta h}}{{{{\left( {R + h} \right)}^2}}}} \\ {\displaystyle\frac{{\delta {V_E}}}{{R + h}}\tan L - \frac{{{V_E}\tan L\delta h}}{{{{\left( {R + h} \right)}^2}}} + - \frac{{{V_E}{{\sec }^2}L\delta L}}{{R + h}}} \end{array}} \right]\text{。}\!\!$

(5)

其中： $L$ 为当地地理纬度； $h$ 为车辆重心距地面高度； $R$ 为地球半径。

2）平台失准角误差方程

${{{\dot \varphi }}^n} = \delta {{\omega }}_{in}^n - ({{\omega }}_{ie}^n + {{\omega }}_{en}^n) \times {{{\varphi }}^n} + {{{\varepsilon }}^n}\text{。}$

(6)

其中， ${\varepsilon ^n}$ 表示陀螺常值漂移在导航坐标系中的投影， $\delta {{\omega }}_{in}^n = \delta {{\omega }}_{ie}^n + \delta {{\omega }}_{en}^n$ 。

3）位置误差方程

$\begin{split}\delta {{{\dot{ P}}}^n} = & \left[ {\begin{array}{*{20}{c}}0 & {\displaystyle\frac{1}{{R + h}}} & 0\\{\displaystyle\frac{{\sec L}}{{R + h}}} & 0 & 0\\0 & 0 & 1\end{array}} \right] \cdot \delta {{{V}}^n} + \\ & \left[ {\begin{array}{*{20}{c}}0 & 0 & { - \displaystyle\frac{{{V_N}}}{{{{\left( {R + h} \right)}^2}}}}\\{\displaystyle\frac{{{V_E}\sec L\tan L}}{{R + h}}} & 0 & { - \displaystyle\frac{{{V_E}\sec L}}{{{{\left( {R + h} \right)}^2}}}}\\0 & 0 & 0\end{array}} \right] \cdot \delta {{{P}}^n}\text{。}\end{split}$

(7)

其中， $\delta {{{P}}^n} = {\left[ {\begin{array}{*{20}{c}} {\delta \lambda }&{\delta L}&{\delta h} \end{array}} \right]^{\rm{T}}}$ ； $\delta \lambda $ ， $\delta L$ ， $\delta h$ 分别为当地经度，纬度和高度误差。

综合以上分析，考虑高度通道的影响，扩充器件误差参数为状态变量，得到15维状态变量如下：

$\begin{split}{{X}} = [\begin{array}{*{20}{c}}{\delta \lambda } & {\delta L} & {\delta h} & {\delta {V_E}} & {\delta {V_N}} & {\delta {V_U}} & {{\varphi _E}}\end{array}\\\begin{array}{*{20}{c}}{{\varphi _N}} & {{\varphi _U}} & {\varepsilon _x^b} & {\varepsilon _y^b} & {\varepsilon _z^b} & {\nabla _x^b} & {\nabla _y^b} & {\nabla _z^b}\end{array}{]^{\rm{T}}}\text{，}\end{split}$

(8)

其中， ${{{\varepsilon }}^b} = {\left[ {\begin{array}{*{20}{c}} {\varepsilon _x^b}&{\varepsilon _y^b}&{\varepsilon _z^b} \end{array}} \right]^{\rm T}}$ 为 $b$ 系三轴陀螺漂移； ${\nabla ^b} = $ ${\left[ {\begin{array}{*{20}{c}} {\nabla _x^b}&{\nabla _y^b}&{\nabla _z^b} \end{array}} \right]^{\rm{T}}}$ 为 $b$ 系加速度计零偏。

根据式（1）～式（7）可以建立卡尔曼滤波所需的状态方程

${\dot{ X}} = {{AX}} + {{BW}}\text{。}$

(9)

其中： ${{A}}$ 为状态矩阵； ${{B}}$ 为系统噪声矩阵； ${{W}}$ 为系统噪声，具体表达式可参见文献[9]。

2.2 系统量测方程

1）INS/GPS子滤波器1

取INS和GPS输出的位置和速度信息之差作为观测量，定义量测方程为：

${Z_1}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{L_I} - {L_G}} \\ {{\lambda _I} - {\lambda _G}} \\ {{h_I} - {h_G}} \\ {{v_{xI}} - {v_{xG}}} \\ {{v_{yI}} - {v_{yG}}} \\ {{v_{zI}} - {v_{zG}}} \end{array}} \right] = {H_1}{X_{1,k}} + {\gamma _k}\text{，}$

(10)

其中， ${H_1}$ 为量测矩阵 ${H_1} \!=\! [\!\!\!\! {\begin{array}{*{20}{c}} {diag[\!\!\! {\begin{array}{*{20}{c}} 1\!&\!1\!&\!1\!&\!1\!&\!1\!&\!1 \end{array}} \!\!\!\!]\!\!\!\!\!}&{{0_{6 \times 9}}} \end{array}}\!\!\! \!\!]$ ， ${\gamma _k}$ 为量测噪声。

2）INS/CNS子滤波器2

对于姿态组合子滤波器，由于INS输出为机体系下姿态（用 ${\varPhi _{Ib}}$ 表示），CNS为惯性系下姿态（用 ${\varPhi _{Cb}}$ 表示），所以在进行滤波前，需将两坐标系进行转换，将姿态信息转化到导航系下：

${\varPhi _{In}} = { C}_b^n{\varPhi _{Ib}}\;\;{{ \varPhi} _{Cn}} = { C}_i^n{\varPhi _{Ci}}\text{，}$

(11)

其中： ${ C}_b^n$ 为机体系（b系）转化到导航系（n系）的姿态转移矩阵； ${ C}_i^n$ 为惯性系（i系）转化到导航系（n系）的姿态转移矩阵。

所以量测方程为

${Z_2}\left( k \right) = \left[ {\begin{array}{*{20}{c}} {{\varPhi _{EIn}} - {\varPhi _{ECn}}} \\ {{\varPhi _{NIn}} - {\varPhi _{NCn}}} \\ {{\varPhi _{UIn}} - {\varPhi _{UCn}}} \end{array}} \right] = {H_2}{X_{2,k}} + {\kappa _k}\text{。}$

(12)

其中： ${H_2}$ 为量测矩阵 ${H_2} \!=\! [\!\!\!\!\! \begin{array}{*{20}{c}}{{0_{3 \times 6}}}\!\!&\!\!{C \bullet diag[\!\!\!\!\! \begin{array}{*{20}{c}}1\!\!&\!\!1\!\!&\!\!1\end{array}\!\!\!\!\!]}\!\!&\!\!{{0_{3 \times 6}}}\end{array}\!\!\!\!\!]$ ；C为姿态角误差与平台误差角之间的转移矩阵，具体表达形式可参考文献[10]； ${\kappa _k}$ 为量测噪声。

3）主滤波器

在无CNS信息时，主滤波器采用子滤波器1的状态更新结果，在有CNS信息时，主滤波器采用两子滤波器的的滤波结果对INS信息进行更新，构建量测方程如下：

$Z\left( k \right) = \left[ {\begin{array}{*{20}{c}} \!\!\!\! {{L_I} - L} \!\!\!\! \\ \!\!\!\! {{\lambda _I} - \lambda } \!\!\!\! \\ \!\!\!\! {{h_I} - h} \!\!\!\! \\ \!\!\!\! {{v_{xI}} - {v_x}} \!\!\!\! \\ \!\!\!\! {{v_{yI}} - {v_y}} \!\!\!\! \\ \!\!\!\! {{v_{zI}} - {v_z}} \!\!\!\! \\ \!\!\!\! {{\varPhi _{EIn}} - {\varPhi _{En}}} \!\!\!\! \\ \!\!\!\! {{\varPhi _{NIn}} - {\varPhi _{Nn}}} \!\!\!\! \\ \!\!\!\! {{\varPhi _{UIn}} - {\varPhi _{Un}}} \!\!\!\! \end{array}} \right]\left[ {\begin{array}{*{20}{c}}\!\!\!\! {{\varPhi _{EIn}} - {\varPhi _{ECn}}}\!\!\!\! \\ \!\!\!\! {{\varPhi _{NIn}} - {\varPhi _{NCn}}}\!\!\!\! \\ \!\!\!\! {{\varPhi _{UIn}} - {\varPhi _{UCn}}} \!\!\!\!\end{array}} \right] = H{X_{1,k}} + {\eta _k}\text{。}$

(13)

其中： $H$ 为量测矩阵 ${H_2} =[ {diag[\begin{array}{*{20}{c}}1&1&1&1&1&1\end{array}]}$ $C \cdot diag[\begin{array}{*{20}{c}}1&1&1\end{array}]\quad{0_{3 \times 9}}]$ ， ${\eta _k}$ 为量测噪声。

3 试验结果与分析

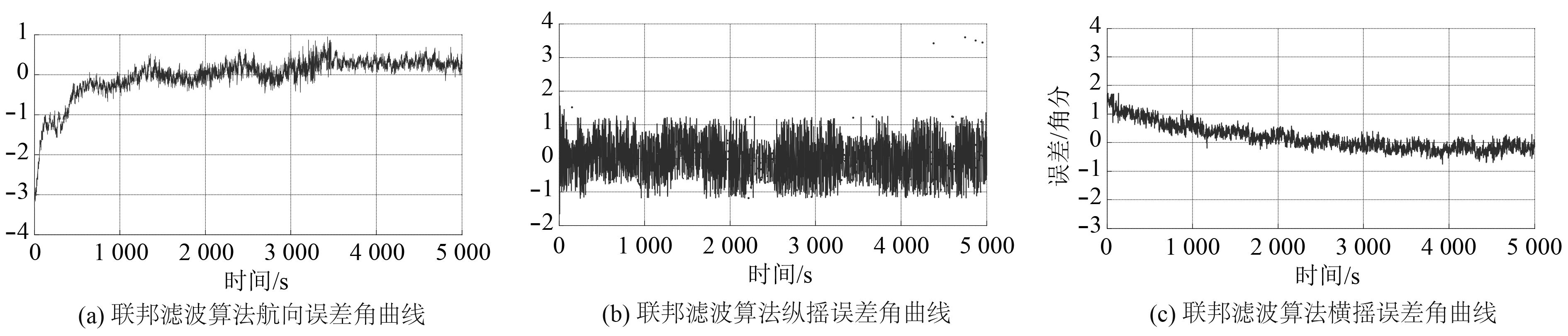
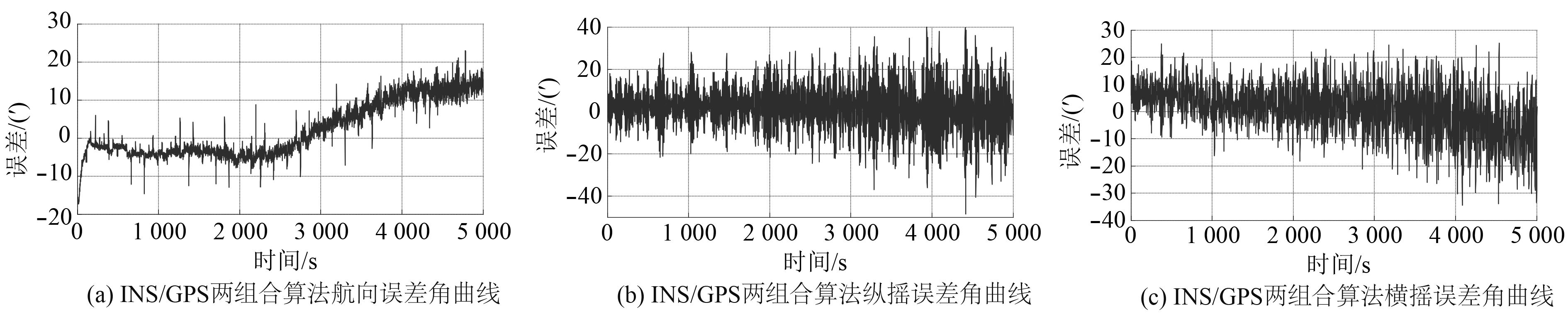
为验证本文所提算法的有效性，在实验室条件下，利用INS/GPS/CNS三组合试验装置进行试验，试验装置由光纤惯导、GPS接收机和天文相机组成。本文采用静态试验的方法进行系统及算法精度验证，同时采用INS/GPS两组合算法的平台误差角结果作为对照，试验时间5 000 s，试验结果如图3和图4所示。

从试验曲线可以看出：本文所提基于INS/GPS/CNS的联邦滤波算法平台误差角误差达到1′以内；相较于传统的INS/GPS两组合算法，平台误差角精度整体提高了一个数量级，同时算法收敛，未出现两组合算法平台误差角随时间发散的现象；由于CNS系统依赖受环境因素影响较大，而本试验是在无天文信号期间试验装置开机，待天文信号出现后记录数据，所以在图3的前1 000 s出现曲线收敛现象，而且收敛速度较快，证明CNS对姿态信息的校正能力很强，同时，试验期间存在间断无天文信号的现象，在此期间滤波器切换为子滤波器1，而曲线未出现发散和误差变大的现象，证明本算法在无天文期间也可以对INS/GPS两组合算法进行很好的调节。通过上述分析，证明了基于INS/GPS/CNS的联邦滤波算法的可行性、高精度性和可靠性。

4 结语

本文利用INS，GPS，CNS的特点，采用联邦滤波的思想提出了一种新的滤波器，实现了导航系统的高度融合及输出导航信息的完整性；并设计了基于INS/GPS/CNS的联邦滤波算法，该算法具有状态切换灵活、计算量小、容错性高的特点；实验室条件下，利用INS/GPS/CNS三组合试验装置进行了静态试验，试验结果表明，该算法平台误差角可达1′以内，远远高出传统的INS/GPS两组合算法精度，同时算法收敛性好、状态切换快、可靠性强。因此，该算法具有重要的工程应用意义。