舰船姿态[1]的精确测量是舰载跟踪设备实现精确测量的基础。目前,舰船姿态的实时和精确测量主要依靠惯性导航系统(INS)。惯性导航系统是完全自主的导航系统,它能高精度测量舰船的动态姿态,抗无线电干扰能力强,并能长期在水下潜航,但惯性导航也具有系统的结构复杂,价格昂贵,由陀螺漂移等因素引起的测量误差随时间积累等不足[2 – 3]。与INS相比,GPS测姿具有体积小、结构简单、成本低、没有误差积累等优点[4 – 5]。随着对GPS测姿技术的不断探索研究,用GPS独立测姿或与其他导航组合测姿已成为一种趋势[6]。
GPS测姿的精度与基线数量、基线长度和基线矢量间的夹角密切相关[7]。GPS测姿至少需要2条不平行的基线才能测定运动载体的3个姿态角,理论上来说基线数目越多,冗余度就越高,精度也随之提高,但增加基线的数目,提高了成本,且不利于解算[8 – 9]。本文研究在采用2条基线的条件下,如何改变基线的长度和基线矢量间的夹角来提高GPS测姿的精度。
1 相关坐标系及姿态角定义 1.1 相关坐标系在用GPS测量舰船姿态的过程中,常用坐标系的有以下3种:世界大地坐标系(WGS),当地水平坐标系(LLS)和舰船甲板坐标系(DOC)。
1)世界大地坐标系(WGS)
GPS坐标采用的是WGS-84坐标系,WGS-84坐标系是世界大地坐标系的一种,坐标系原点为地球质心,其下坐标用(L,B,H)表示。L,B和H分别为坐标系下点的经度、纬度和高度。
2)当地水平坐标系(LLS)
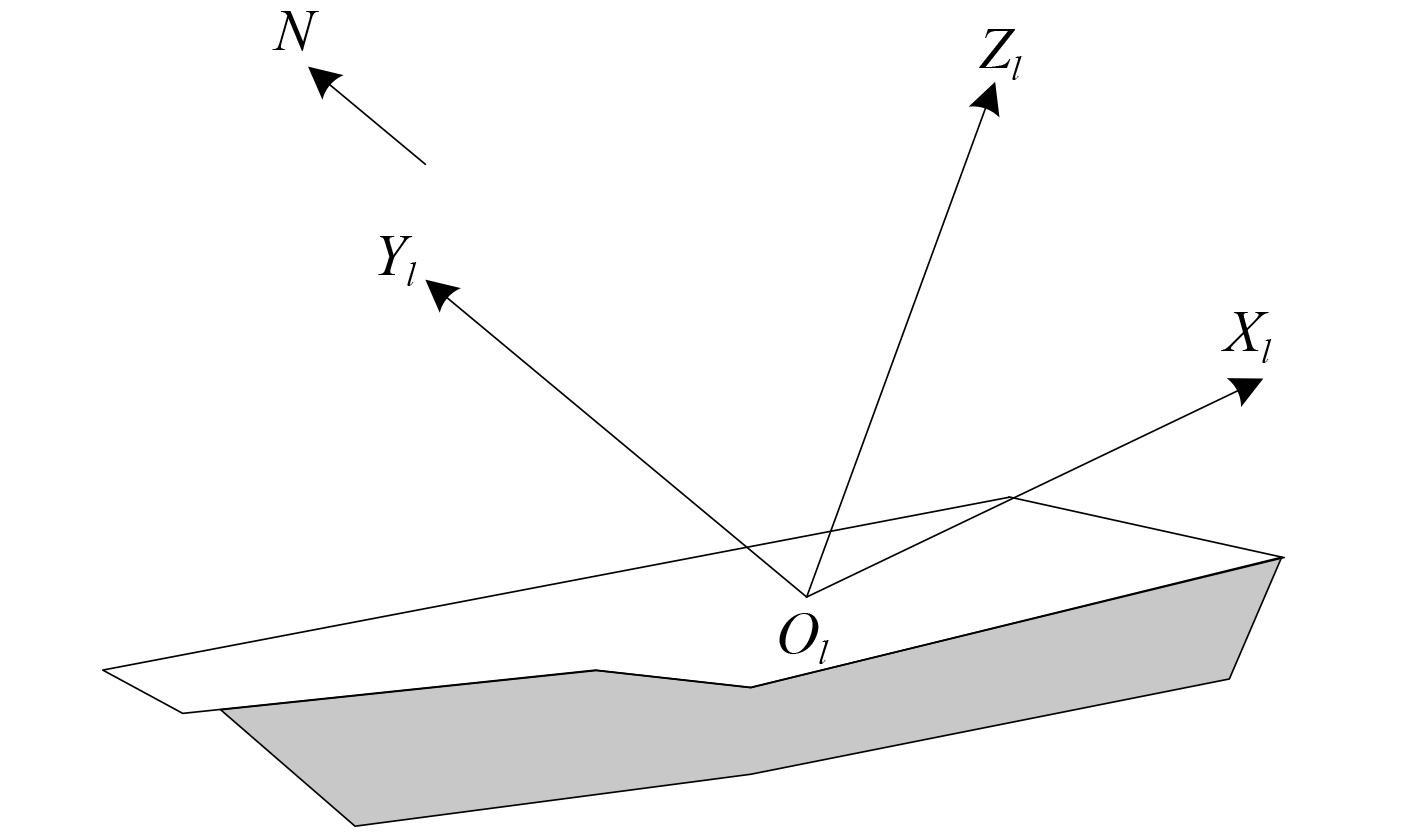
如图1所示,当地水平坐标系的坐标原点
|
图 1 当地水平坐标系 Fig. 1 LLS coordinate |
|
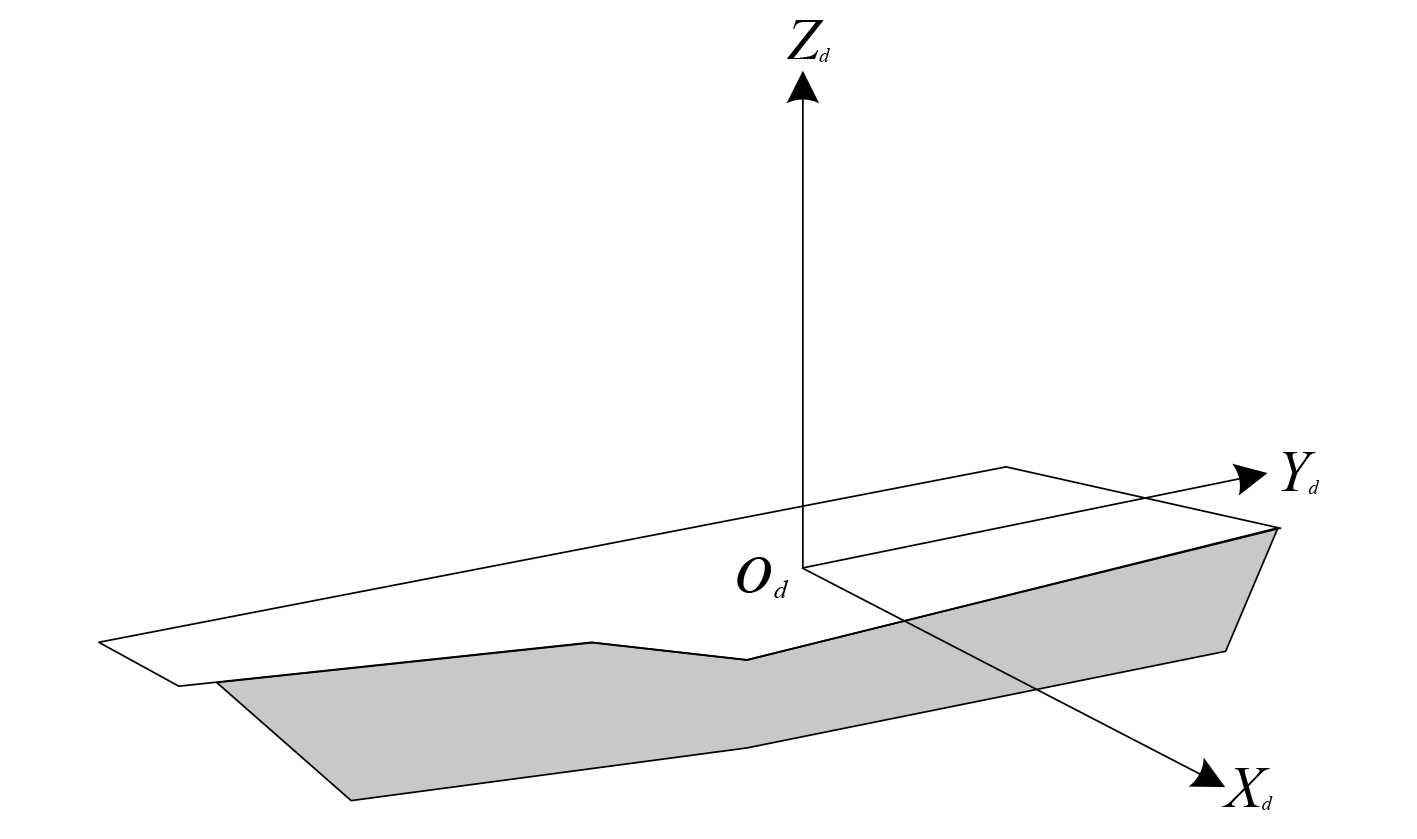
图 2 舰船甲板坐标系 Fig. 2 DOC coordinate |
3)舰船甲板坐标系(DOC)
如图2所示,舰船甲板坐标系的原点
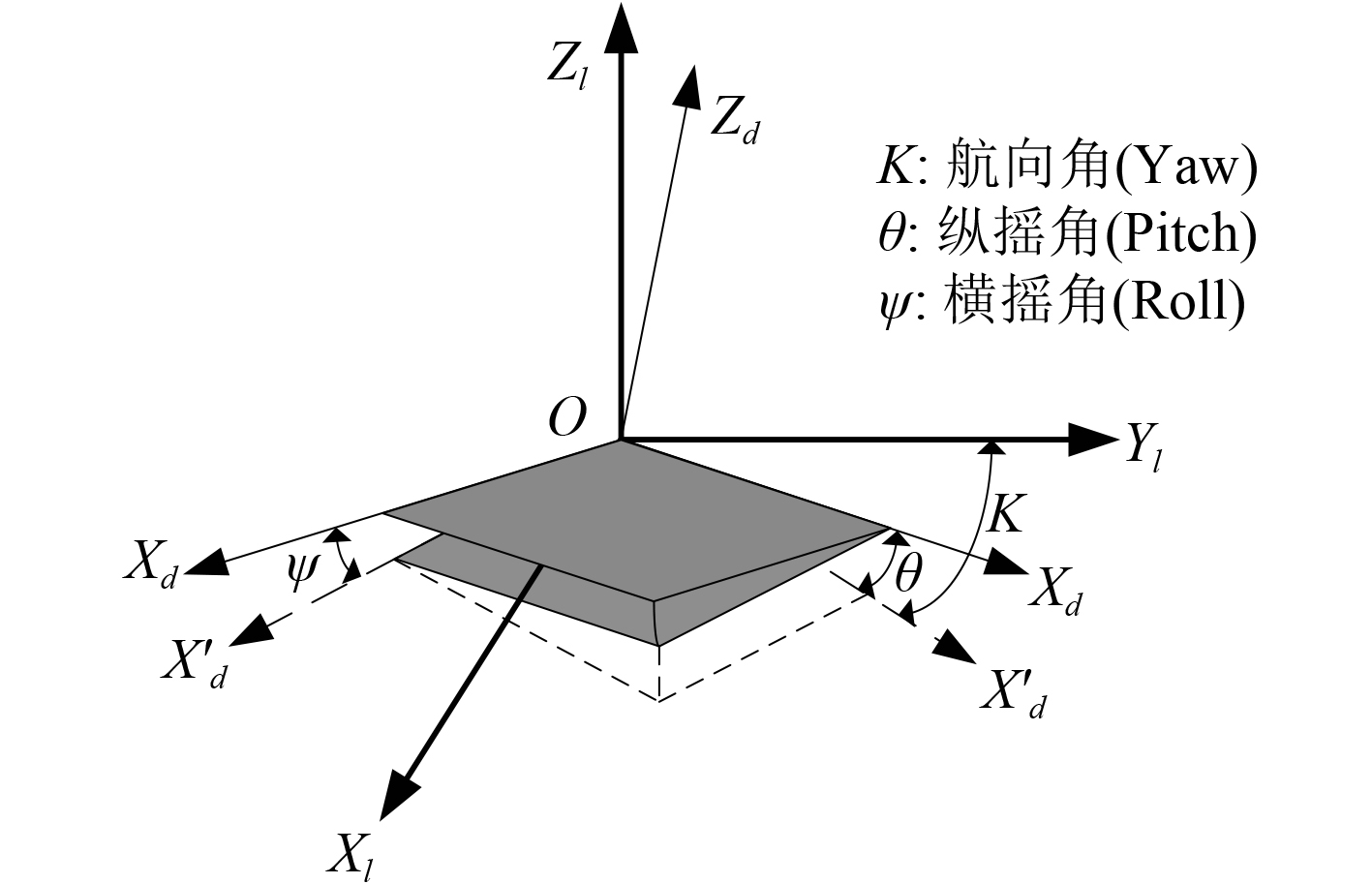
舰船的姿态由航向角(Yaw)、纵摇角(Pitch)和横摇角(Roll)3个姿态角表示。当舰船的3个姿态角都为0时,舰船甲板坐标系与当地水平坐标系重合。舰船运动时,舰船甲板坐标系相对于当地水平坐标系的3个轴之间的旋转角度即为舰船的姿态角。舰船姿态角定义如图3所示。
|
图 3 姿态角的定义 Fig. 3 The definition of attitude angle |
当地水平坐标系和舰船甲板坐标系的原点重合,2坐标系之间只有旋转变换,而旋转的角度就是舰船的3个姿态角。据研究,从当地水平坐标系到舰船甲板坐标系的变换可由3次绕轴旋转实现,但旋转顺序必须为先绕Z轴旋转(航向变换),再绕X轴旋转(纵摇变换),最后绕Y轴变换(横摇变换)[10]。旋转矩阵为:
| $\begin{array}{l}{T_{ld}} = {R_Y}(K){R_X}(\theta ){R_Z}(\psi ) = \left[ \begin{array}{l}\cos K\cos \psi + \sin K\sin \theta \sin \psi \\\cos \theta \sin \psi \\\sin K\cos \psi - \cos K\sin \theta \sin \psi \end{array} \right.\\\left. \begin{array}{l} - \cos K\sin \psi + \sin K\sin \theta \cos \psi \\\cos \theta \cos \psi \\ - \sin K\sin \psi - \cos K\sin \theta \cos \psi \end{array} \begin{array}{l} - \sin K\cos \theta \\\sin \theta \\\cos K\cos \theta \end{array} \right]{\text{。}}\quad\;\;\; (1)\end{array}$ |
GPS姿态测量技术是利用多幅天线间的相对定位,通过解算各天线接收的GPS卫星信号,计算出各基线向量在当地水平坐标系中的解,最后根据各天线的相对位置关系和姿态转换矩阵求解姿态角。
2个GPS天线中心的连线称为基线。要测量舰船的三维姿态,至少需要2条不平行的基线,即至少需要3个不共线的GPS天线。由沿舰船首尾线(舰船航向)布置的2个GPS天线可以解算出舰船的航向角和纵摇角,再利用第3个不在舰船首尾线上的GPS天线可解算出舰船的横摇角。
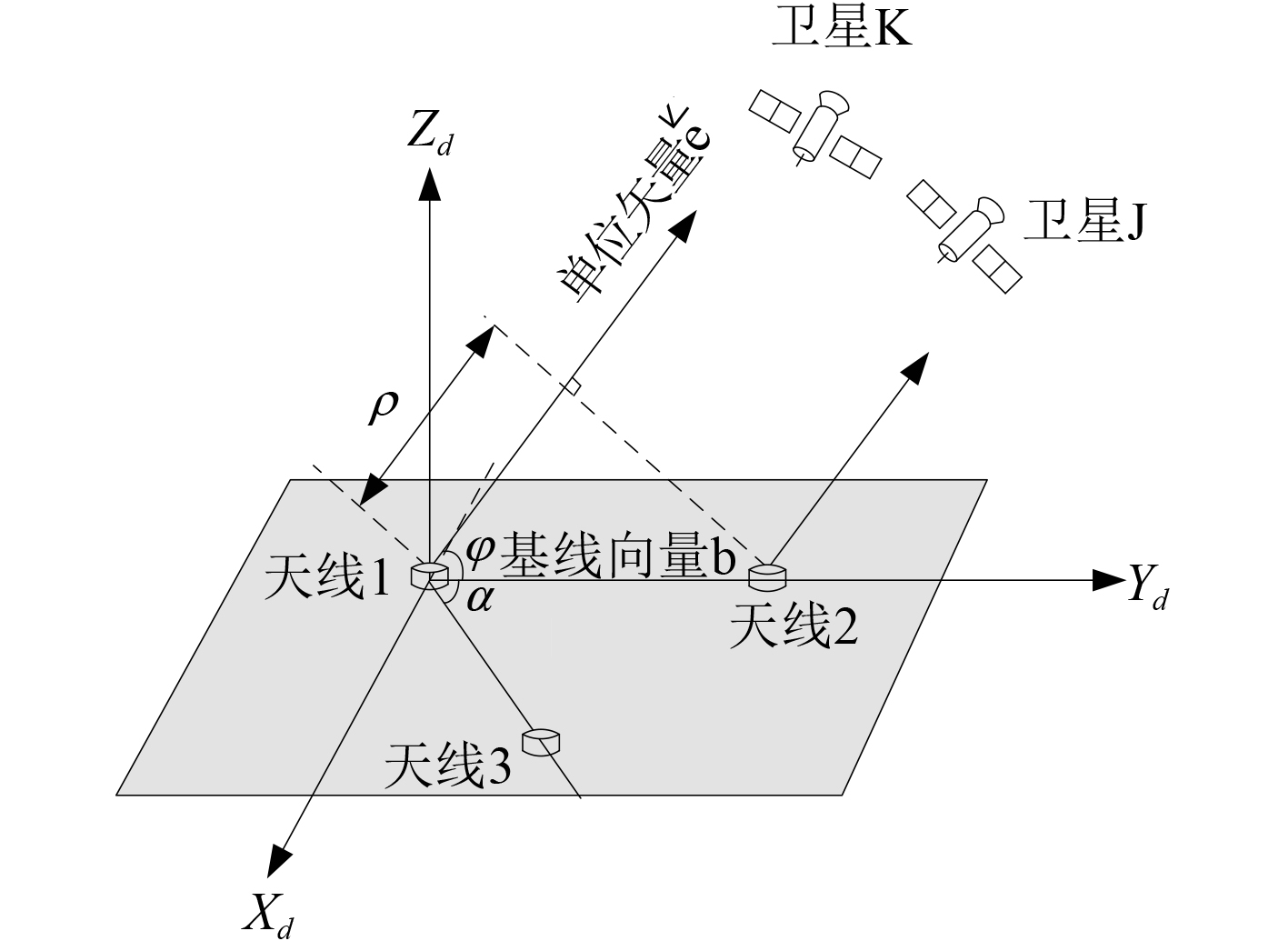
2.1 GPS基线矢量的解算如图4所示,GPS天线1和GPS天线2组成的基线矢量记为
|
图 4
载波相位差分测量
|
由图4可知:
| $\rho {{ = }}\rho _1^{{K}} - \rho _2^{{K}}{{ = }}\overrightarrow {{e^K}} \cdot \overrightarrow {{b}} {{ = }}\left| {\overrightarrow {{b}} } \right| \cdot \cos \phi {\text{,}}$ | (2) |
其中,
基线长度相对于站星距很小,相位差分几乎消除了电离层延迟误差、对流层误差、SA误差和钟差等空间相关性的误差源[12]。由载波相位单差观测方程得:
| $\lambda \varphi _{12}^K = \left( {\rho _1^K - \rho _2^K} \right) - \lambda N_{12}^K\text{,}$ | (3) |
将式(2)代入式(3)得:
| $\lambda \varphi _{12}^K = \overrightarrow {{e^K}} \cdot \overrightarrow b - \lambda N_{12}^K\text{,}$ | (4) |
同理,对于卫星J有:
| $\lambda \varphi _{12}^J = \overrightarrow {{e^J}} \cdot \overrightarrow b - \lambda N_{12}^J\text{,}$ | (5) |
式(4)–式(5)得双差观测方程:
| $\lambda \varphi _{12}^{{{K}}J} = \overrightarrow {{e^{{{K}}J}}} \cdot \overrightarrow b - \lambda N_{12}^{{{K}}J}\text{。}$ | (6) |
同一时刻GPS天线1和GPS天线2能同时观测到的GPS卫星数大于等于5(假设观测到5颗GPS卫星,为K、J、P、Q和T,设定卫星K为主星),则可构造4个双差观测方程,写成矩阵形式为:
| $\lambda \left( \begin{array}{l}\varphi _{12}^{KJ}\\[4pt]\varphi _{12}^{KP}\\[4pt]\varphi _{12}^{KQ}\\[4pt]\varphi _{12}^{KT}\end{array} \right) = \left( \begin{array}{l}\overrightarrow {{e^{KJ}}} \\\overrightarrow {{e^{KP}}} \\\overrightarrow {{e^{KQ}}} \\\overrightarrow {{e^{KT}}} \end{array} \right) \cdot \overrightarrow b - \lambda \left( \begin{array}{l}N_{12}^{KJ}\\[4pt]N_{12}^{KP}\\[4pt]N_{12}^{KQ}\\[4pt]N_{12}^{KT}\end{array} \right)\text{。}$ | (7) |
只要确定了整周模糊度,就可解算出基线矢量在地球坐标系中的坐标
假设舰船甲板为刚体,则固连在舰船甲板的GPS天线的位置相对于舰船甲板坐标系不改变,基线矢量在舰船甲板坐标系中的坐标
| ${b^L} = \left[ {\begin{array}{*{20}{c}} {{{\operatorname{sinB} }_0}\cos {L_0}}&{\sin {B_0}\sin {L_0}}&{ - \cos {B_0}} \\ { - \sin {B_0}}&{\cos {B_0}}&0 \\ {\cos {B_0}\cos {L_0}}&{\cos {B_0}\sin {L_0}}&{\sin {B_0}} \end{array}} \right] \cdot \overrightarrow b\text{。} $ | (8) |
当精准测得某一基线b在当地水平坐标系中的坐标
| ${b^L} = {T_{ld}} \cdot {b^b}\text{。}$ | (9) |
通过解算式(9)矩阵即可解算出舰船姿态K、
目前GPS测量姿态的姿态角解算有多种算法,例如:直接计算法[13]、融合TRIAD算法[14]、最小二乘法[15]和四元数法[16]等。直接计算法求解载体3个姿态角,具有原理简单、计算快等优点,本文采用直接计算法来解算舰船的姿态。
利用3个GPS天线,安装位置如图4所示,天线1和天线2组成基线矢量
| $b_{12}^L = \left[ {x_{12}} \right.,y_{12}{\left. {,z_{12}} \right]^{\rm{T}}}\text{,}b_{13}^L = \left[ {x_{13}} \right.,y_{13}{\left. {,z_{13}} \right]^{\rm{T}}}\text{。}$ |
根据基线
| $K = - \arctan \frac{{{x_{12}}}}{{{y_{12}}}}\text{,}$ | (10) |
| $\theta = \arctan \frac{{{z_{12}}}}{{\sqrt {x_{12}^2 + y_{12}^2} }}\text{。}$ | (11) |
将基线
| $\begin{aligned}b_{13}^{'L} = & {\left[ {x_{13}',y_{13}',z_{13}'} \right]^{\rm{T}}} = \\ &\left[ {\begin{array}{*{20}{c}}\!\!\!\!\!\! 1 & 0 &0 \!\!\!\!\!\!\\\!\!\!\!\!\! 0 & {\cos \theta } & {\sin \theta } \!\!\!\!\!\!\\\!\!\!\!\!\! 0 & { - \sin \theta } & {\cos \theta } \!\!\!\!\!\!\end{array}} \right]\left[ {\begin{array}{*{20}{c}}\!\!\!\!\!\! {\cos K} & {\sin K} & 0 \!\!\!\!\!\! \\\!\!\!\!\!\! { - \sin K} & {\cos K} & 0 \!\!\!\!\!\! \\\!\!\!\!\!\! 0 & 0 & 1 \!\!\!\!\!\!\end{array}} \right]\left[ \begin{array}{l}\!\!\!\!\!\! {x_{13}} \!\!\!\!\!\! \\\!\!\!\!\!\! {y_{13}} \!\!\!\!\!\! \\\!\!\!\!\!\! {z_{13}} \!\!\!\!\!\!\end{array} \right]\text{。}\end{aligned}$ | (12) |
| $\begin{split}\psi = & - \arctan \displaystyle\frac{{z_{13}'}}{{x_{13}'}} = \\ & -\arctan \displaystyle\frac{{{x_{13}}\sin K\sin \theta \!-\! {y_{13}}\cos K\sin \theta \!+\! {z_{13}}\cos \theta }}{{{x_{13}}\cos K \!+\! {y_{13}}\sin K}}\text{。}\!\!\!\!\!\end{split}$ | (13) |
根据式(9),对航向角
| $dK = - \frac{{{y_{12}}d{x_{12}} - {x_{12}}d{y_{12}}}}{{x_{12}^2 + y_{12}^2}}\text{,}$ | (14) |
航向角
| $\begin{split}{\sigma _K} = & \sqrt {y_{12}^2\sigma _{{x_{12}}}^2 + x_{12}^2\sigma _{{y_{12}}}^2} /\left( {x_{12}^2 + y_{12}^2} \right) = \\ &\sqrt {{{\cos }^2}(K)\sigma _{{x_{12}}}^2 + {{\sin }^2}(K)\sigma _{{y_{12}}}^2} /{b_{12}}\cos \theta \text{,}\end{split}$ | (15) |
同理,纵摇角
| ${\sigma \!_\theta } \!=\! \frac{{\sqrt {{{\left( {cosK\sin \theta } \right)}^2}\sigma _{{x_{12}}}^2 \!+\! {{(\sin K\sin \theta )}^2}\sigma _{{y_{12}}}^2 \!+\! {{(\cos \theta )}^2}\sigma _{{z_{12}}}^2} }}{{{b_{12}}}}\text{,}$ | (16) |
| ${\sigma _\psi } = \sqrt {{{(\sin \psi )}^2}\sigma _{x_{13}'}^2 + {{(\cos \psi )}^2}\sigma _{z_{13}'}^2} /{b_{13}}\sin \alpha\text{。} $ | (17) |
分析式(14)~式(16),得航向角和纵摇角的测量精度与
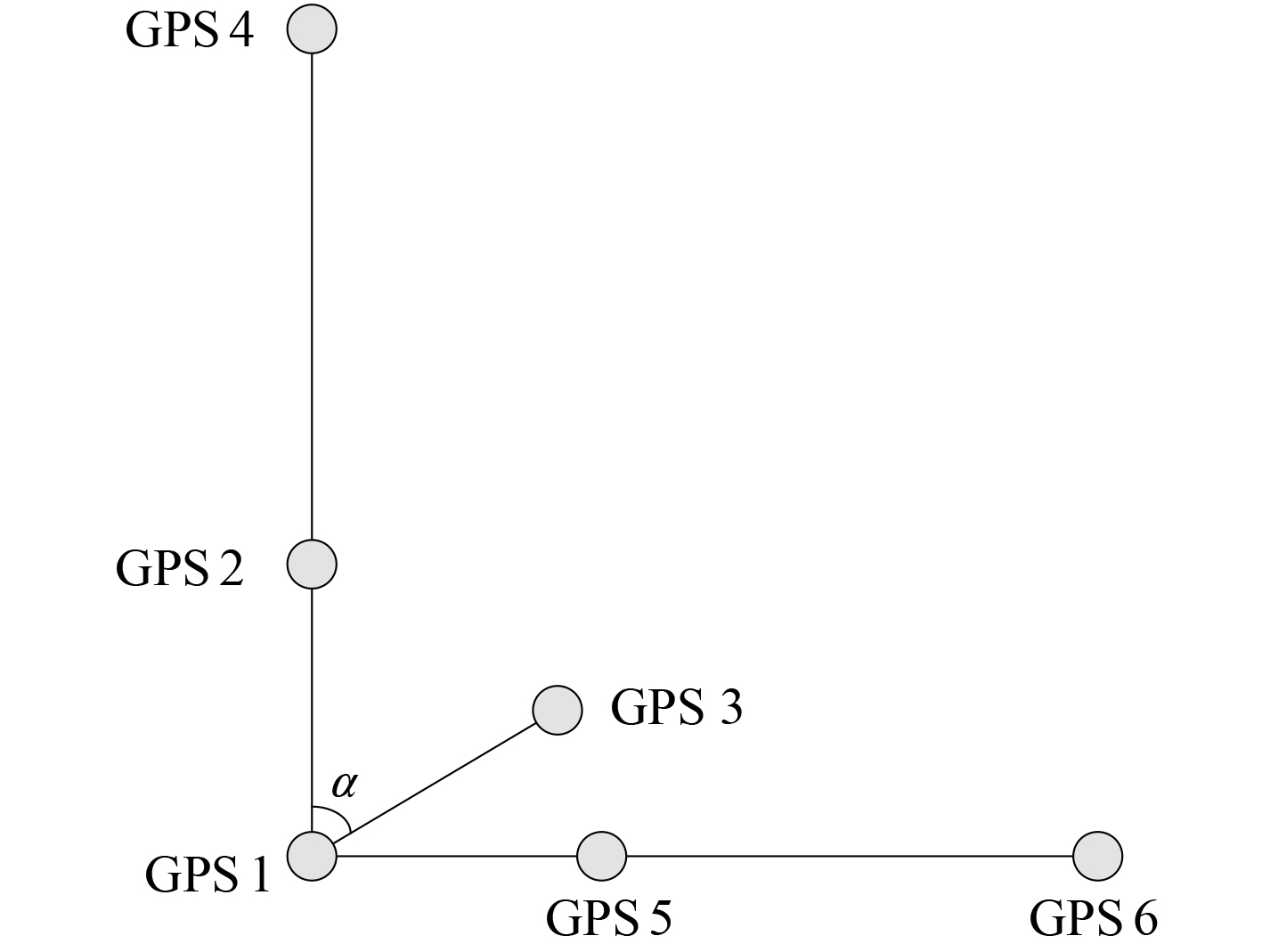
为了验证上述结论,利用7个GPS接收机天线来采集舰船的航行数据,GPS天线在舰船甲板上的布局如图5所示。
|
图 5 数据采集天线布局图 Fig. 5 Antenna layout diagram of date collection |
天线1位于舰船甲板中心;天线1、天线2和天线4沿舰船首尾线布置;天线1、天线5和天线6沿一条与首尾线垂直的直线布置;天线3与天线1间的基线与首尾线成60°夹角;天线2、天线3、天线5与天线1之间基线的长度均为1 m;天线4、天线6与天线1之间的基线均为10 m。选用不同组合的GPS测量数据解算舰船的实时姿态角,然后减去该时刻舰载高精度INS测得的舰船姿态(将舰载高精度INS的姿态测量值作为真值),得到GPS姿态测量误差序列。
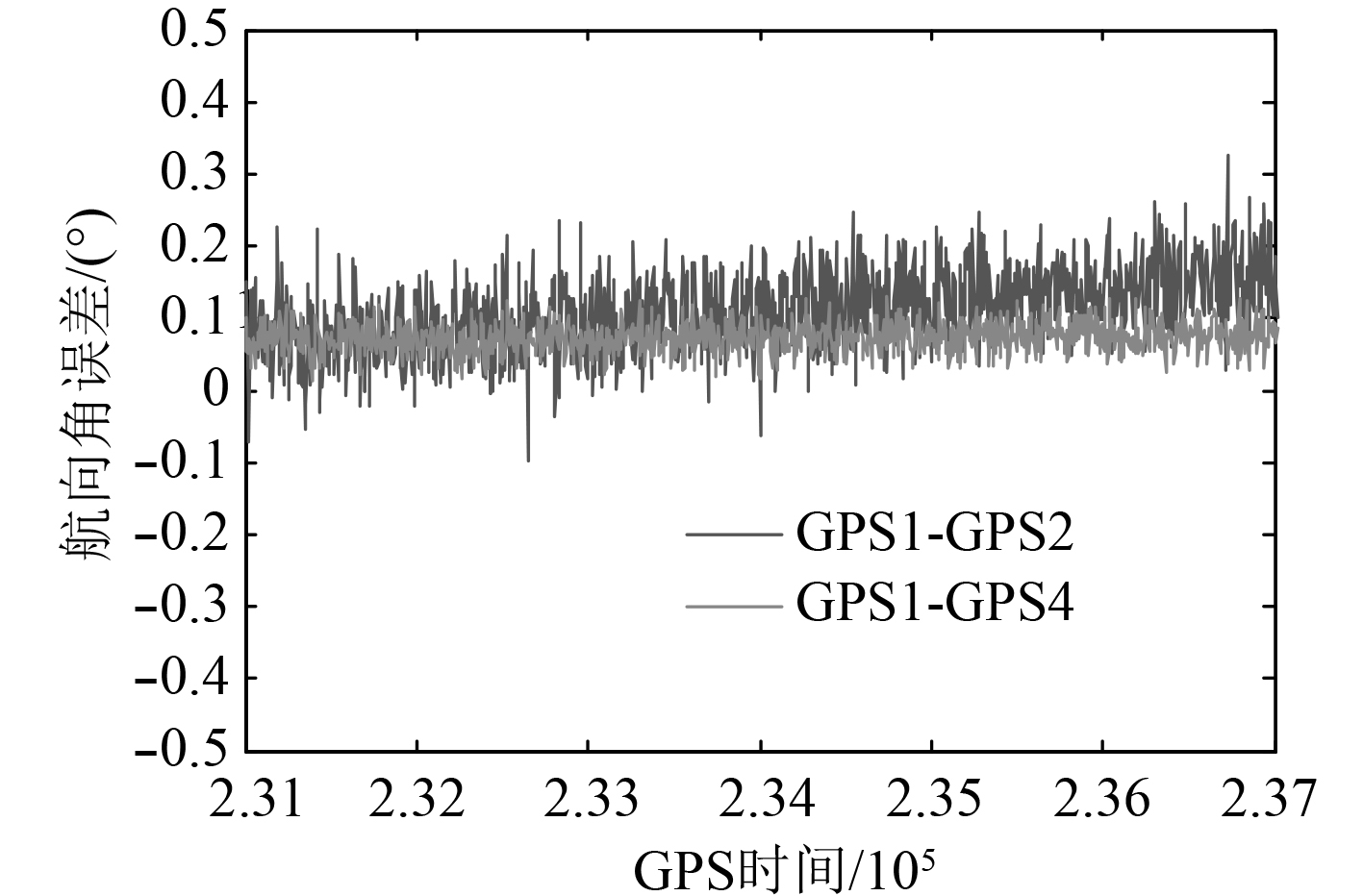
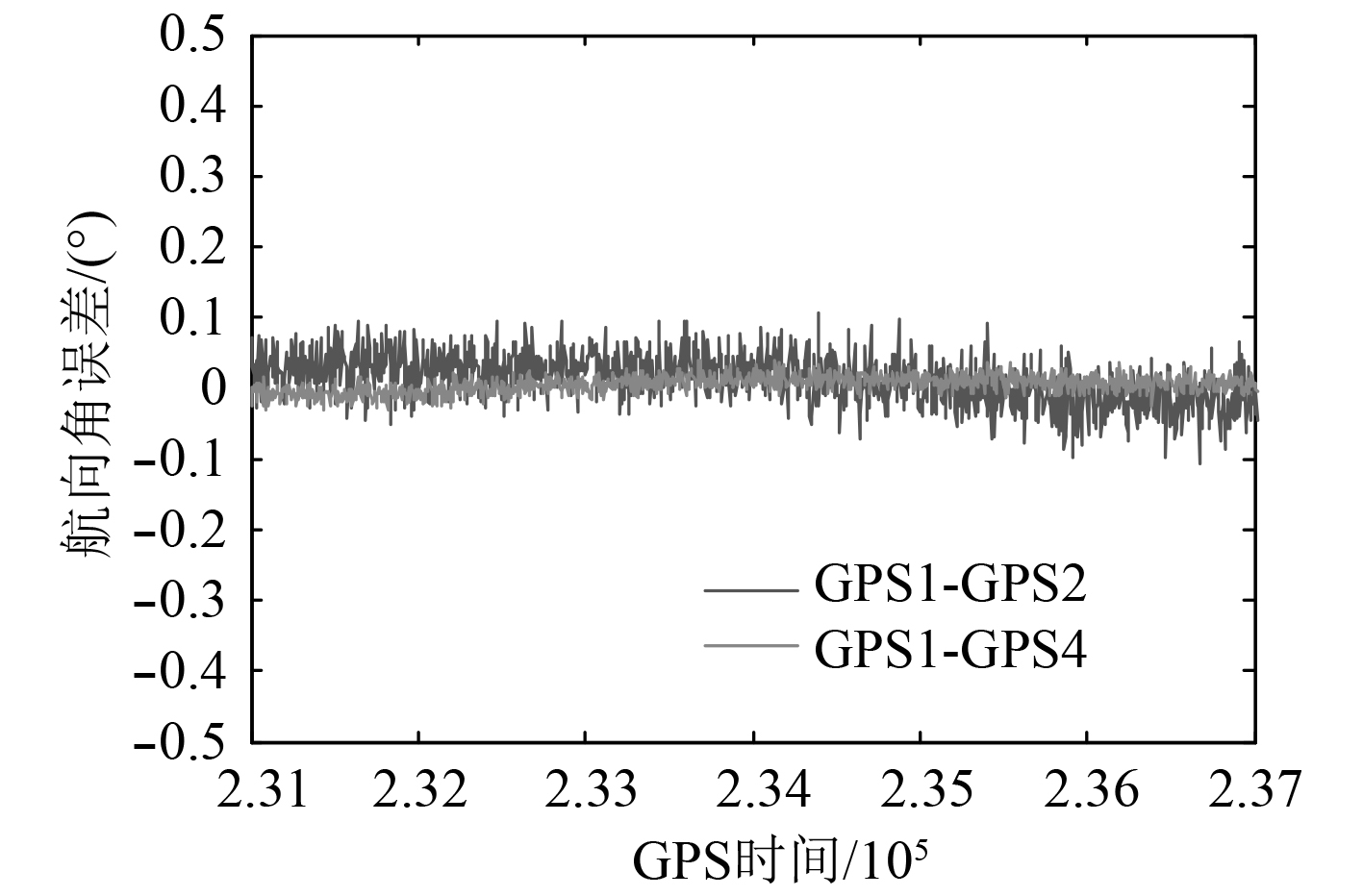
解算天线1与天线2,天线1与天线4组成的2条基线,得到不同基线长度下舰船的航向角和纵摇角测量误差,分别如图6和图7所示。
|
图 6 航向角测量误差 Fig. 6 Yaw measurement error |
|
图 7 纵摇角测量误差 Fig. 7 Pitch measurement error |
由图6和图7可知,基线长度1 m时的航向角和纵摇角测量误差明显大于基线长度10 m时的测量误差。
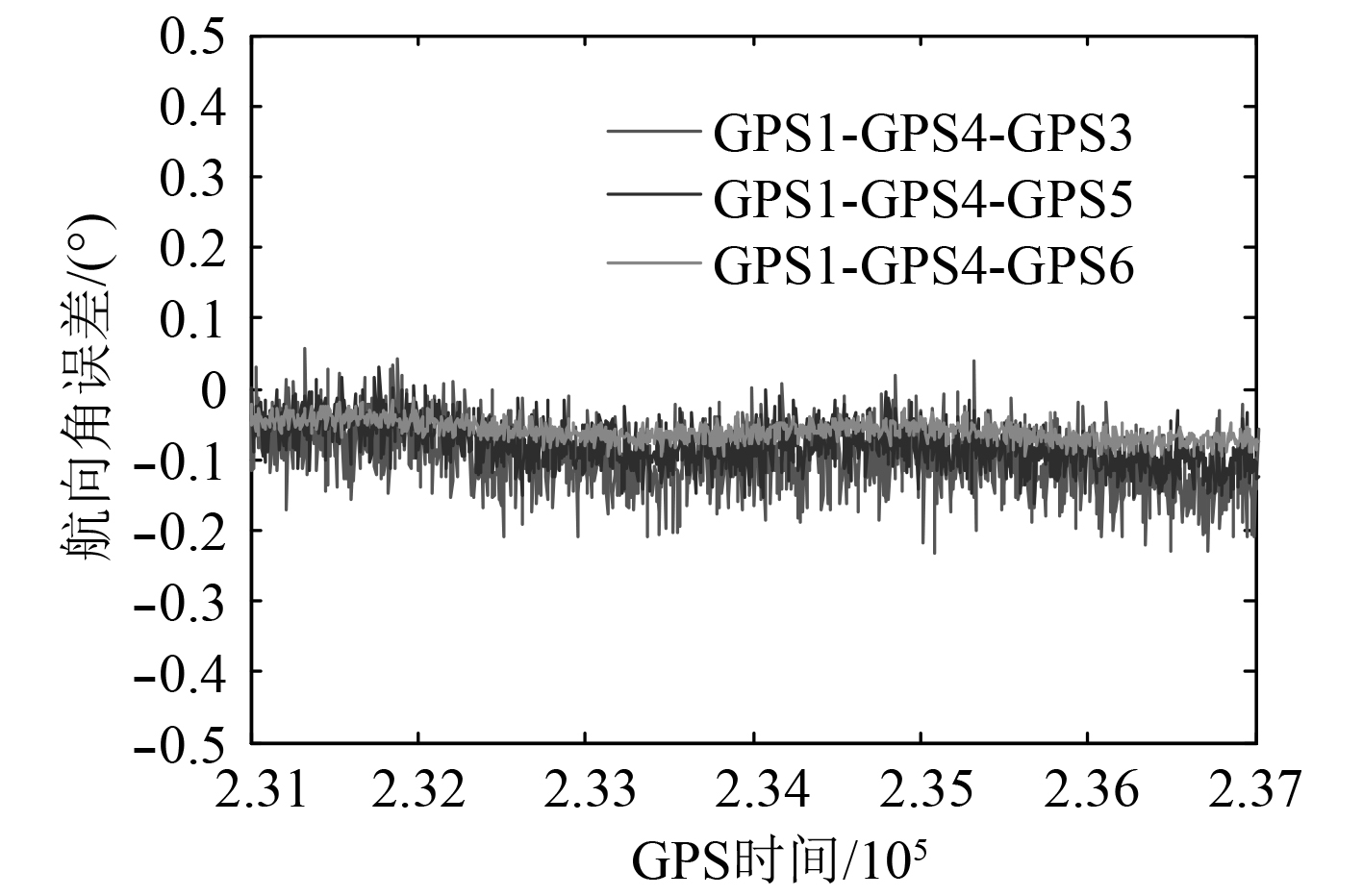
解算①天线1、天线4和天线3;②天线1、天线4和天线5;③天线1、天线4和天线6三种天线组合下舰船的横摇角,得到不同情况下的舰船横摇角测量误差,如图8所示。
|
图 8 横摇角测量误差 Fig. 8 Roll measurement error |
由图8可知,基线长度相同时,2条基线间夹角为90°时横摇角的测量误差明显小于夹角为60°时的测量误差;2条基线夹角相同时,基线长度为10 m时的横摇角测量误差明显小于基线长度为1 m时的测量误差。
5 结 语仿真试验对姿态测量精度与天线布局的关系进行了验证,试验结果与推导的结论一致,即:航向角和纵摇角与航向基线长度有关,基线越长,测量精度越高;横摇角测量精度与横向基线长度和基线夹角有关,基线越长,两基线越接近正交布设,横摇角的测量精度越高。因此,利用GPS测量舰船姿态时,应该适当增加基线长度,并使2条基线正交分布,以提高舰船姿态的测量精度。
| [1] | 利娜, 张瑜. 舰船姿态的GPS测定方法研究[J]. 河南师范大学学报(自然科学版), 2006, 34(3): 58–60, 63. http://www.cnki.com.cn/Article/CJFDTOTAL-HNSX200603017.htm |
| [2] | 许江林, 朱涛, 卞鸿魏. 姿态测量技术综述[J]. 海军工程大学学报, 2003, 5(3): 17–23, 36. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tcykzxb201005003 |
| [3] | 郭万禄, 潘玉纯, 瞿峥嵘. 基于双天线GPS接收机航向姿态测量方法[J]. 专题技术与工程应用, 2012, 42(5): 50–52. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wxdgc201205016 |
| [4] | 钟林, 周海渊. 测姿GPS系统在测量船上的应用[J]. 科学技术与工程, 2013, 13(3): 641–644, 651. https://www.wenkuxiazai.com/doc/9acfca06581b6bd97f19ea30.html |
| [5] | 刘新明, 赵李健, 王珏, 等. 一种GPS测姿系统的设计及精度分析[J]. 中国惯性技术学报, 2013, 21(1): 76–79. |
| [6] | 贺浩, 郑玉航, 杨东方, 等. 一种新的GPS/SINS组合测姿模型[J]. 计算机测量与控制, 2015, 23(7): 2302–2304. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jsjzdclykz201507018 |
| [7] | 鲁洋为, 王振杰, 聂志喜, 等. 不同天线组合对GPS姿态测量精度的影响分析[J]. 海洋测绘, 2014, 34(6): 43–45, 48. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hych201406011 |
| [8] | 刘若普. GPS三维姿态测量技术研究[D]. 上海: 上海交通大学, 2008. |
| [9] | 高源骏. GPS测姿算法与天线布局研究[D]. 哈尔滨: 哈尔滨工程大学: 2011. |
| [10] | 张志远, 罗国富. 舰船姿态坐标变换及稳定补偿[J]. 舰船科学技术, 2009, 31(4): 34–40. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=jckxjs200904008 |
| [11] | 程建华, 王晶, 董建明. 基于GPS直接求解姿态矩阵算法的精度分析研究[J]. 传感与微系统, 2011, 30(11): 51–55. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=cgqjs201111016 |
| [12] | 潘良. 航天测量船船姿船位测量技术[M]. 北京: 国防工业出版社, 2009. |
| [13] | 张方照, 柴艳菊, 柴华, 等. 两种多天线GNNS定姿方法的精度分析[J]. 中国惯性技术学报, 2016, 24(2): 30–35. http://www.cqvip.com/QK/83064X/201601/668526681.html |
| [14] | 黎湧, 吴宏鑫, 刘良栋. 融合TRIAD算法用于GPS姿态确定[J]. 中国空间科学技术, 2000(2): 30–35. http://www.cnki.com.cn/Article/CJFDTotal-DKXB201301028.htm |
| [15] | 王立红, 郝继平, 汤云. 基于最小二乘法的GPS多天线测姿及精度分析[J]. 测控技术学报, 2007, 21(1): 1–5. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hbgxycsjsxb200701001 |
| [16] | 张荣辉, 贾宏光, 陈涛, 等. 基于四元数法的捷联式惯性导航系统的姿态解算[J]. 光学精密工程, 2008, 6(10): 1963–1970. |
 2018, Vol. 40
2018, Vol. 40
